统计学计算题61083
《统计学》计算题型与参考答案

《统计学》计算题型(第二章)1.某车间40名工人完成生产计划百分数(%)资料如下:90 65 100 102 100 104 112 120 124 98110 110 120 120 114 100 109 119 123 107110 99 132 135 107 107 109 102 102 101110 109 107 103 103 102 102 102 104 104要求:(1)编制分配数列;(4分)(2)指出分组标志及其类型;(4分)(3)对该车间工人的生产情况进行分析。
(2分)解答:(1)(2类型:数量标志(3)从分配数列可以看出,该计划未能完成计划的有4人,占10%,超额完成计划在10%以内的有22人,占55%,超额20%完成的有7人,占17.5%。
反映该车间,该计划完成较好。
(第三章)2.2005年9份甲、乙两农贸市场某农产品价格和成交量、成交额资料如下:解答:(1)x 甲=∑∑m x m 1=248.416.36.314.24.21246.34.2⨯+⨯+⨯++=30/7=4.29(元)x 乙=∑∑fxf =12418.426.344.2++⨯+⨯+⨯=21.6/7=3.09(元)(2)原因分析:甲市场在价格最高的C 品种成交量最高,而乙市场是在最低的价格A 品种成交量最高,根据权数越大其对应的变量值对平均数的作用越大的原理,可知甲市场平均价格趋近于C ,而乙市场平均价格却趋近于A ,所以甲市场平均价格高于乙市场平均价格。
(第三章)3.甲、乙两企业产量资料如下表:工人人数比重(%)产量(件)甲企业 乙企业 100以下 2 4 100-110 8 5 110-120 30 28 120-130 35 31 130-140 20 25 140-150 3 4 150以上 2 3 合 计 100 100要求:(1)分别计算甲、乙两企业的平均产量?(5分)(2)计算有关指标比较两企业职工的平均产量的代表性。
统计学试题库计算题部分练习题.doc

统计学试题库计算题部分:知识点四:统计综合指标1、某局所属企业某年下半年产值资料如下:试通过计算填写表中空缺2、现有某市国内生产总值资料如下,通过计算填写表中空缺。
(单位:亿元)(2)计算标准差(3)计算方差(2)比较哪个企业职工平均年龄更具代表性7、甲、乙两企业工人有关资料如下:要求:(1)比较哪个企业职工工资偏高(2)比较哪个企业职工平均工资更具代表性10、甲、乙两钢铁生产企业某月上旬的钢材供货量资料如下:试比较甲、乙Array两企业该月上旬钢材供货的均衡性11、某校甲、乙两班学生的统计学原理考试成绩分组情况如下:要求:(1)计算各班学生的平均成绩(2)通过计算说明哪个班学生平均成绩的代表性强12、某公司所属40个企业资金利润及有关资料如下表:求平均利润率。
13、设甲乙两公司进行招员考试,甲公司用百分制记分,乙公司用五分制记分,有关资料如下表所示:问哪一个公司招员考试的成绩比较整齐?(用标准差)知识点五:时间数列及动态分析(2)预测2004年存款余额将达到多少4、1997—2002年某企业职工人数和非生产人数资料如下:人员占全部职工人数的平均比重(2)计算上半年平均计划完成程度(2)计算四年平均工业增加值占国内生产总值的比重(2)用最小平方法配合直线趋势方程11、试通过计算填写表中所缺的环比动态指标:知识点六:统计指数要求:(1)计算每种产品的产量和出厂价格个体指数(2)编制产量总指数、计算由于产量变动而增减的产值(3)编制出厂价格总指数,计算由于价格变动而增减的产值(2)计算销售量总指数(3)对总销售额的变动进行因素分析(2)三种商品价格及销售量的综合变动指数(3)由于价格提高和销售量的增加各使销售额增加多少?(2)物价总指数(3)由于物价变动所引起的总产值的增加或减少额(2)销售量总指数以及由于销售量变动对销售额的影响8、某商店出售三种商品,资料如下:试计算价格总指数11、某工业企业生产甲、乙两种产品,基期和报告期的产量、单位产品成本和出厂价格资料如下:试计算:(1)以单位成本为同度量因素的产量总指数; (2)单位成本总指数;(3)对总成本进行两因素分析。
统计学练习题——计算题
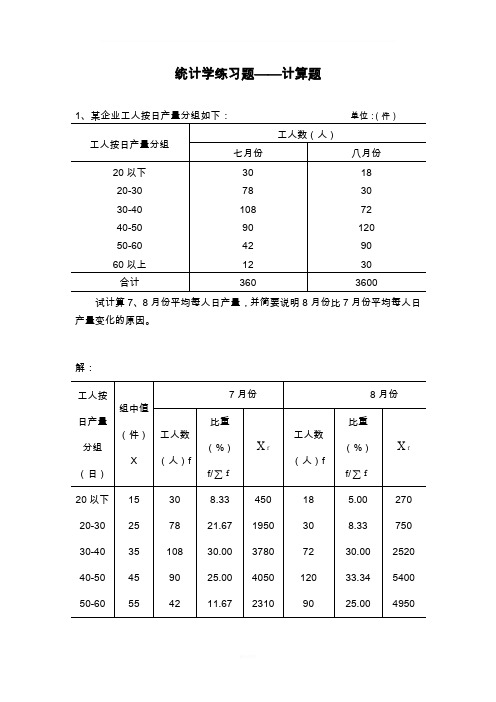
统计学练习题——计算题试计算7、8月份平均每人日产量,并简要说明8月份比7月份平均每人日产量变化的原因。
解:7月份平均每人日产量为:3736013320===∑∑f Xf X (件) 8月份平均每人日产量为:4436015840===∑∑fXf X (件)根据计算结果得知8月份比7月份平均每人日产量多7件。
其原因是不同组日产量水平的工人所占比重发生变化所致。
7月份工人日产量在40件以上的工人只占全部工人数的40%,而8月份这部分工人所占比重则为66.67%。
试比较这两年产品的平均等级,并说明该厂棉布生产在质量上有何变化及其因。
解:2009年棉布的平均等级=25010 34022001⨯+⨯+⨯=1.24(级)2010年棉布的平均等级=3006 32422701⨯+⨯+⨯=1.12(级)可见该厂棉布产品质量2010年比2009年有所提高,其平均等级由1.24级上升为1.12级。
质量提高的原因是棉布一级品由80%上升为90%,同时二级品和三级品分别由16%及4%下降为8%及2%。
试比较和分析哪个企业的单位成本高,为什么?解:甲企业的平均单位产品成本=1.0×10%+1.1×20%+1.2×70%=1.16(元)乙企业的平均单位产品成本=1.2×30%+1.1×30%+1.0×40%=1.09(元)可见甲企业的单位产品成本较高,其原因是甲企业生产的3批产品中,单位成本较高(1.2元)的产品数量占70%,而乙企业只占30%。
试计算各地区平均价格和此种商品在四个地区总的平均价格。
解:总平均价格=23010600=销售总量销售总额=46.09根据上表计算该商店售货员工资的全距,平均差和标准差,平均差系数和标准差系数。
⑴2010200==∑∑fXf X =510(元); ⑵全距=690-375=315(元) ⑶156020X XfA D f-⋅==∑∑=78(元); ⑷)(202085002==∑∑-ffXX σ=102.1(元)⑸%10051078%100⨯=⨯⋅=⋅XD A V D A =15.29%; ⑹%1005101.102%100⨯=⨯=XV σσ=20.02%6、某班甲乙两个学习小组某科成绩如下:试比较甲乙两个学习小组该科平均成绩的代表性大小。
国家开放大学电大《统计学》计算题题库

计算分析题(要求写出公式和计算过程,结果保留两位小数)1、按照某市城市社会发展十年规划,该市人均绿化面积要在2010年的人均4平方米的基础上十年后翻一番。
试问:(1)若在2020年达到翻一番的目标,每年的平均发展速度是多少?(2)若在2018年就达到翻一番的目标,每年的平均增长速度是多少?(3)若2011年和2012年的平均发展速度都为110%,那么后8年应该以怎样的平均发展速度才能实现这一目标?(4)假定2017年的人均绿化面积为人均6.6平方米,以2010年为基期,那么其平均年增长量是多少?2、某地区市场销售额报告期为40万元,比上年增加了5万元,销售量与上年相比上升了3%,试计算:(1)市场销售量总指数;(2)市场销售价格指数;(3)由于销售量变动对销售额的影响。
3、某乡有5000农户,按随机原则重复抽取100户调查,得平均每户年纯收入12000元,标准差2000元。
要求:(1)以95%的概率(Z=1.96)估计全乡平均每户纯收入的区间。
(2)以同样概率估计全乡农户年纯收入总额的区间范围。
4、某企业工人的日产量情况如下表所示:试计算该企业工人平均日产量。
(10分)1、某乡2012-2013年三种鲜果产品收购资料如下:试计算三种鲜果产品收购价格指数,说明该地区2013年较之2012年鲜果收购价格的提高程度,以及由于收购价格提高使当地农民增加的收入。
2、某企业2013年上半年进货计划执行情况如下表:试计算:(1)各季度进货计划完成程度。
(2)上半年进货计划完成情况。
(3)上半年累计计划进度执行情况。
3、按照某市城市社会发展十年规划,该市人均绿化面积要在2010年的人均4平方米的基础上十年后翻一番。
试问:(1)若在2020年达到翻一番的目标,每年的平均发展速度是多少?(2)若在2018年就达到翻一番的目标,每年的平均增长速度是多少?(3)若2011年和2012年的平均发展速度都为110%,那么后8年应该以怎样的平均发展速度才能实现这一目标?(4)假定2017年的人均绿化面积为人均6.6平方米,以2010年为基期,那么其平均年增长量是多少?4、设某总体服从正态分布,其标准差为12,现抽取了一个样本容量为400的子样,计算得平均值=21,试以显著性水平确定总体的平均值是否不超过20?(10分)1又知乙车间工人日产量的标准差为12件,日产量为40件,试根据资料说明:(1)哪一个车间的平均产量高。
统计学考试计算题答案统计学试题及答案

统计学考试计算题答案统计学试题及答案一、填空题(每空1分,共10分)1.从标志与统计指标的对应关系来看,标志通常与( )相同。
2.某连续变量数列,其首组为开口组,上限为80,又知其邻组的组中值为95,则首组的组中值为( )。
3.国民收入中消费额和积累额的比例为1:0.4,这是( )相对指标。
4.在+A的公式中,A称为( )。
5.峰度是指次数分布曲线项峰的( ),是次数分布的一个重要特征。
6.用水平法求平均发展速度本质上是求( )平均数。
7.按习惯做法,采用加权调和平均形式编制的物量指标指数,其计算公式实际上是( )综合指数公式的变形。
8.对一个确定的总体,抽选的样本可能个数与( )和( )有关。
9.用来反映回归直线代表性大小和因变量估计值准确程度的指标称( )。
二、是非题(每小题1分,共10分)1.统计史上,将国势学派和图表学派统称为社会经济统计学派。
2.统计总体与总体单位在任何条件下都存在变换关系统计学原理试题及答案统计学原理试题及答案。
3.学生按身高分组,适宜采用等距分组。
4.根据组距数列计算求得的算术平均数是一个近似值。
5.基尼系数的基本公式可转化为2(S1+S2+S3)。
6.对连续时点数列求序时平均数,应采用加权算术平均方法。
7.分段平均法的数学依据是Σ(Y-YC)2=最小值。
8.平均数、指数都有静态与动态之分。
9.在不重复抽样下,从总体N中抽取容量为n的样本,则所有可能的样本个数为Nn个10.根据每对____和y的等级计算结果ΣD2=0,说明____与y之间存在完全正相关。
三、单项选择题(每小题2分,共10分)1.在综合统计指标分析^p 的基础上,对社会总体的数量特征作出归纳、推断和预测的方法是A.大量观察法B.统计分组法C.综合指标法D.模型推断法2.对同一总体选择两个或两个以上的标志分别进行简单分组,形成A.复合分组B.层叠分组C.平行分组体系D.复合分组体系3.交替标志方差的最大值为A.1B.0.5C.0.25D.04.如果采用三项移动平均修匀时间数列,那么所得修匀数列比原数列首尾各少A.一项数值B.二项数值C.三项数值D.四项数值5.可变权数是指在一个指数数列中,各个指数的A.同度量因素是变动的B.基期是变动的C.指数化因数是变动的D.时期是变动的四、多项选择题(每小题2分,共10分)1.反映以经济指标为中心的三位一体的指标总体系包括A.社会统计指标体系B.专题统计指标体系C.基层统计指标体系D.经济统计指标体系E.科技统计指标体系2.典型调查A.是一次性调查B.是专门组织的调查C.是一种深入细致的调查D.调查单位是有意识地选取的E.可用采访法取得资料3.下列指标中属于总量指标的有A.月末商品库存额B.劳动生产率C.历年产值增加额D.年末固定资金额E.某市人口净增加数4.重复抽样的特点是A.各次抽选互不影响B.各次抽选相互影响C.每次抽选时,总体单位数逐渐减少D.每次抽选时,总体单位数始终不变E.各单位被抽中的机会在各次抽选中相等5.下列关系中,相关系数小于0的现象有A.产品产量与耗电量的关系B.单位成本与产品产量的关系C.商品价格与销售量的关系D.纳税额与收入的关系E.商品流通费用率与商品销售额的关系五、计算题(每小题10分,共60分)要求:(1)写出必要的计算公式和计算过程,否则,酌情扣分。
统计学计算题和答案精编版

统计学计算题和答案 GE GROUP system office room 【GEIHUA16H-GEIHUA GEIHUA8Q8-三个企业生产的同一型号空调在甲、乙两个专卖店销售,有关资料如下:企业型号价格(元/台)甲专卖店销售额(万元)乙专卖店销售量(台)A250050.0340B3400115.6260C4100106.6200合计—272.2—要求:分别计算两个专卖店空调的平均销售价格,并分析平均价格差异的原因。
答案:2某企业甲、乙两个生产车间,甲车间平均每个工人日加工零件数为65件,标准差为11件;乙车间工人日加工零件数资料如下表。
试计算乙车间工人加工零件的平均数和标准差,并比较甲、乙两个生产车间哪个车间的平均日加工零件数更有代表性?60以下60—7070—8080—9090—100日加工零件数(件)工人数(人)59121410答案:三、某地区2009—2014年GDP资料如下表,要求:1、计算2009—2014年GDP的年平均增长量;2、计算2009—2014年GDP的年平均发展水平;3、计算2009—2014年GDP的年平均发展速度和平均增长速度。
年份20092010201120122013201487431062711653147941580818362GDP(亿元)答案:年平均增长速度:100%100%22.9%x-==四,某百货公司2010—2014年的商品销售额资料如下:试用最小平方法配合销售额的直线趋势方程,并预测2016年的销售额将达到什么水平?答案: 2010年—2014年的数据有5项,是奇数,所以取中间为0,以1递增。
设定x为-2、-1、0、1、2、年份/销售额(y) x xy x22010 320 -2 -640 42011 332 -1 -332 12012 340 0 0 02013 356 1 356 12014 380 2 760 4合计 1728 0 144 10b=∑xy/∑x2=144/10=14.4a=∑y/n=1728/5=345.6y=345.6+14.4x预测2016年,按照设定的方法,到2016年应该是5y=345.6+14.4*5=417.6元五、某企业生产三种产品,2013年三种产品的总生产成本分别为20万元,45万元,35万元,2014年同2013年相比,三种产品的总生产成本分别增长8%,10%,6%,产量分别增长12%,6%,4%。
统计学计算题例题及计算分析

μp=√σp2/n(1-n/N) =√0.16/100*(1-100/10000) =3.98%
△p=zμp=2*3.98%=7.96%
户数所占比重的下限=p-△p=20%-7.96%=12.04%
户数所占比重的上限=p+△p=20%+7.96%=27.96%
∴ μp=√σp2/n =√0.0736/100 =2.71%
△p=zμ
合格率下限=p-△p=92%-5.31%=86.69%
合格率上限=p+△p=92%+5.31%=97.31%
合格品数量下限=10000*86.69%=8669(只)
合格品数量上限=10000*97.31%=9731(只)
即在95%概率保证下,该新型灯泡合格率区间范围为86.69%~97.31%,合格品数量的区间范围为8669~9731只。
(1)这种新的电子元件平均寿命的区间范围;
(2)这种新的电子元件合格率的区间范围。
解:已知N=10000只n=100只x=1192小时σ=101.17小时p=88% z=1.96
(1)μx=√σ2/n(1-n/N) =√101.172/100*(1-100/10000) =10.07(小时)
△x=zμx=1.96*10.07=19.74(小时)
即全部农户中,户均月收入在6000元以上的户数所占比重的范围为12.04%~27.96%。
(3)户数下限=10000*12.04%=1204(户)
户数上限=10000*27.96%=2796(户)
即全部农户中,户均月收入在6000元以上的户数范围为1204~2796户。
3.2.某企业生产一种新的电子元件10000只,用简单随机不重复抽样方法抽取100只作耐用时间试验,试验得到的结果:平均寿命1192小时,标准差101.17小时,合格率88%;试在95%概率保证度下估计:
统计学计算题要点

第三章、综合指标六、计算题试计算平均月奖金.试计算该企业工人的平均工资。
4、设有甲、乙班组工人日产量资料如下:试判断甲、乙哪个班组的平均日产量代表性大。
试研究两个品种的平均亩产量,确定哪一品种具有较好的稳定性?试计算该企业平均计划完成百分比。
8、在过去5年中,某国家因受严重通货膨胀的困扰,银行为吸收存款而提高利息率。
5年的年利息率分别是25%、40%、60%、100%、120%,问:(1)若存入100美元,按算术平均数计算平均利率,第五年末的实际存款额是多少?(2)若存入100美元。
按几何平均数计算平均利率,第五年末的实际存款额是多少?(3)何种方法最合适?为什么?试计算全县2005年粮食平均亩产量。
第四章动态数列六、计算题要求:(1)计算一季度月平均工业总产值:(2)计算一季度月平均工人数。
要求:(1)计算一季度、二季度月平均商品纯销售额:(2)计算一季度、二季度月平均商品流动资金占用额。
试计算该企业4月份平均人数。
试计算该生活区居民平均拥有彩电台数。
(2)计算一季度、上半年平均人数。
试计算:(1)一季度月平均劳动生产率。
(2)一季度平均劳动生产率。
(2)第二季度平均工人数。
(3)第二季度产量平均计划完成%。
试计算:(1)逐期增长量、累积增长量、平均增长量。
(2)环比发展速度、定基发展速度。
(3)平均发展速度。
13、某煤矿1990年煤炭产量为25万吨(1)规定“八五”期间每年平均增长4%,以后每年平均增长5%,问到本世纪末年煤炭产量将达到什么水平?(2)如果规定本世纪末年煤炭产量是1990年产量的4倍,且“八五”期间每年平均增长速度为5%。
问以后需要每年平均增长速度多少才能达到预定的产量水平?14、1982年我国人口数为10亿人,1990年我国人口数为11.3亿人。
试问在这期间我国人口平均增长率为多少?如果按这个人口平均增长速度发展,则本世纪我国人口数将达到多少亿?15、某工厂计划工业总产值从1980年的400万元发展到2000年的800万元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计学计算题27、【104199】(计算题)某班级30名学生统计学成绩被分为四个等级:A .优;B .良;C .中;D .差。
结果如下:B C B A B D B C C B C D B C A B B C B A B A B B D C C B C A BDAACDCABD(1)根据数据,计算分类频数,编制频数分布表;(2)按ABCD 顺序计算累积频数,编制向上累积频数分布表和向下累计频数分布表。
【答案】28、【104202】(计算题)某企业某班组工人日产量资料如下:根据上表指出:(1)上表变量数列属于哪一种变量数列;(2)上表中的变量、变量值、上限、下限、次数; (3)计算组距、组中值、频率。
【答案】(1)该数列是等距式变量数列。
(2)变量是日产量,变量值是50-100,下限是,、、、、9080706050上限是,、、、、10090807060次数是111625199、、、、; (3)组距是10,组中值分别是 9585756555、、、、,频率分别是13.75%31.25%.20%23.75%11.25% 、、。
29、【104203】(计算题) 甲乙两班各有30名学生,统计学考试成绩如下:(1)根据表中的数据,制作甲乙两班考试成绩分类的对比条形图; (2)比较两班考试成绩分布的特点。
【答案】乙班学生考试成绩为优和良的比重均比甲班学生高,而甲班学生考试成绩为中和差的比重比乙班学生高。
因此乙班学生考试成绩平均比乙班好。
两个班学生都呈现出"两头大,中间小"的特点,即考试成绩为良和中的占多数,而考试成绩为优和差的占少数。
30、【104205】(计算题)科学研究表明成年人的身高和体重之间存在着某种关系,根据下面一组体重身高数据绘制散点图,说明这种关系的特征。
体重(Kg )5053 57 60 66 70 76 75 80 85 身高(cm ) 150155160165168172178180182185【答案】散点图:可以看出,身高与体重近似呈现出线性关系。
身高越高,体重越重。
31、【150771】(计算题) 某班40名学生统计学考试成绩分别为:66 89 88 84 86 87 75 73 72 68 75 82 97 58 81 54 79 76 95 76 71 6090 65 76 72 76 85 89 92 64 57 83 81 78 77 72 61 70 81 学校规定:60分以下为不及格,60-70为及格,70-80分为中,80-90分为良,90-100分为优。
要求:(1)将该班学生分为不及格、及格、中、良、优五组,编制一张次数分配表。
(2)指出分组标志及类型;分组方法的类型;分析本班学生考试情况。
【答案】(1)"学生考试成绩"为连续变量,需采组距式分组,同时学生考试成绩变动均匀,故可用等距式分组来编制变量分配数列。
(2)分组标志为考试成绩,属于数量标志,简单分组;从分配数列中可看出,该班同学不及格人数和优秀生的人数都较少,分别为%5.7和%10。
大部分同学成绩集中在70-90分之间,说明该班同学成绩总体良好。
考试成绩一般用正整数表示时,可视为离散变量也可用单项式分组,但本班学生成绩波动幅度大,单项式分组只能反映成绩分布的一般情况,而组距分组分配数列可以明显看出成绩分配比较集中的趋势,便于对学生成绩分配规律性的掌握。
62、【104275】(计算题)设某产品的完整生产过程包括3道流水作业的连续工序,这3道生产工序的产品合格率分别为80%、90%和95%。
则整个生产流程的产品总合格率是多少?—【答案】%1.88684.095.09.08.033==⨯⨯63、【145013】(计算题) 某学院一年级两个班的学生高等数学考试成绩如下表:试分别计算两个班的平均成绩和标准差,并比较说明哪个班的高等数学考试成绩差异程度更大。
【答案】甲班成绩均值:804032005151===∑∑==i ii ii f f x x 甲甲班成绩标准差:()()()()()()62.10406809517808510807558065280552222251512=⨯-+⨯-+⨯-+⨯-+⨯-=-=∑∑--i ii i i f f x x s 甲甲甲班成绩离散系数:1328.08062.10===甲甲甲x s V乙班成绩均值:4.785039205151===∑∑==i ii ii f f x x 乙乙班成绩标准差:()()()()()36.115074.7895184.7885144.786544.7855222251512=⨯-+⨯-+⨯-+⨯-=-=∑∑--i ii i i f f x x s 乙乙乙班成绩离散系数:1449.04.7836.11===乙乙乙x s V乙甲V V <,因此,乙班的高等数学考试成绩差异更大。
64、【145019】(计算题)根据下表资料,计算众数和中位数。
【答案】次数最多的是168万人,众数所在组为15~30这一组,故15=L X ,30=U X人261421681=-=∆,人72961682=-=∆,98.181572262615211=⨯++=⋅∆+∆∆+=d X M L o 或:98.181572267230212=⨯+-=⋅∆+∆∆-d M o26125222===∑f中位数位置,说明这个组距数列中的第262位所对应的人口年龄是中位数。
从累计(两种方法)人口数中可见,第261位被包括在第2组,即中位数在15~30这组中。
15=L X ,30=U X ,168=m f ,1421=-m S ,2121=+m S625.25151681422611521=⨯-+=⨯-+=-∑d f S fX M mm L e或者:625.25151682122613021=⨯--=⨯--=+∑d f S fX M mm U e65、【145089】(计算题) 有甲乙两个生产小组,甲组平均每个工人的日产量为32件,标准差为8件。
乙组工人日产量资料如下:要求:(1)计算乙组平均每个工人的日产量和标准差。
(2)比较甲、乙两生产小组哪个组的日产量差异程度大?【答案】(1)03.281234382512453435382525154141i =+++⨯+⨯+⨯+⨯==∑∑==i iii f f x x 乙()()()()()43.9123438251203.28453403.28353803.28252503.2815222241412=+++⨯-+⨯-+⨯-+⨯-=-=∑∑==i ii i i f f x x s 甲乙(2)25.0328===甲甲甲x s V34.003.2843.9===乙乙乙x s V说明乙组日产量差异程度大于甲组。
66、【163301】(计算题)某年度两家工厂采购同一种原材料的价格和批量情况如下表。
试分别计算这两个厂的平均采购价格。
【答案】74.74054.04007804577052755827251067001154552821061155151==++++++++==∑∑--i iii i x mm x 甲(元/吨)27.74667.05007801007701007551007251007001001001001001001005151==+++++++===∑∑--i iii ix mm x x 甲乙(元/吨)67、【173857】(计算题)某农场在不同自然条件的地段上用同样的管理技术试种两个粮食新品种,有关资料如下表所示:试计算有关指标,并从作物收获率的水平和稳定性两方面综合评价,哪个品种更有推广价值?【答案】平均值18.412133.5358134203.53942.43855.14500.24141==⨯+⨯+⨯+⨯==∑∑==i ii ii f f x x 甲标准差()()()()()90.20133.518.4124202.418.4123945.118.4123850.218.412450222241412==⨯-+⨯-+⨯-+⨯-=-=∑∑==i ii i i f f x x s 甲甲标准差系数0507.018.41290.20===甲甲甲x S V平均值75.390137.5079133725.54212.34058.13835.24141==⨯+⨯+⨯+⨯==∑∑==i ii ii f f x x 乙标准差()()()()()34.20135.575.3903722.375.3904218.175.3904055.275.390383222241412=⨯-+⨯-+⨯-+⨯--=∑∑==i ii ii f f x x s 乙乙标准差系数0521.075.39034.20===乙乙乙x s V87、【104322】(计算题)某车间有20台机床,在给定的一天每一台机床不运行的概率都是0.05,机床之间相互独立。
问在给定的一天内,至少有两台机床不运行的概率是多少?(结果保留三位小数) 【答案】设x 表示在给定的一天内不运行的机床台数, 则),(~p n B X ,20=n ,05.0=p 解法一:[]264.03774.03585.01)95.0()05.0()95.0()05.0(1)1()0(1)2(1)2(191120200020=--=--==+=-=<-=≥c c x p x p x p x p解法二:因为20=n ,05.0=p ,51≤=np ,可以用泊松分布近似计算二项分布 1==np λ,则有:3679.0!01!)0(10==≈=--e e x x p xλλ3679.0!11!)1(11==≈=--e ex x p xλλ则264.0)1()0(1)2(1)2(==-=-=<-=≥x p x p x p x p88、【150764】(计算题)某厂生产的螺栓的长度服从均值为10cm ,标准差为0.05的正态分布。
按质量标准规定,长度在9.9~10.1cm 范围内的螺栓为合格品。
试求该厂螺栓的不合格率是多少。
(查概率表知,()()97725.022=Φ=<X P ) 【答案】螺栓的长度)05.0,10(~N X ,则)1,0(~05.010N X Z -=,合格的概率为9545.0197725.021)2(2)2()2(}05.0101.1005.01005.0109.9{}1.109.9{=-⨯=-Φ=-Φ-Φ=-≤-≤-=≤≤X P X P0455.09545.01=-故不合格率为。
110、【122755】(计算题)一家调查公司进行一项调查,其目的是为了了解某市电信营业厅大客户对该电信的服务满意情况。
调查人员随机访问了30名去该电信营业厅办理业务的大客户,发现受访的大客户中有9名认为营业厅现在的服务质量比两年前好。
