捷联惯导算法与组合导航原理讲义(20170220)
捷联惯导与组合导航解读

3)惯性仪表的校准,对陀螺的标度系数进行测 定,对陀螺的漂移进行测定并补偿,对加速度 计也同样测定标度系数并存入计算机。初始过 程中对惯性仪表的校准是提高系统精度的重要 保证,相关内容在第五章中已有详细讨论。
3、惯性仪表的误差补偿,对捷联式惯导系统来说, 由于惯性仪表直接安装在机体上,因此,飞行 器的线运动和角运动都引起较大的误差,为了 保证系统的精度,必须对惯性仪表的误差进行 补偿,最好的补偿方法是计算补偿,一般通过 专用的软件来实现误差补偿,相关内容在第五 章中已有详细讨论。
? 1.3.1 四元数的基本概念
? 四元数是由一个实数单位 1和一个虚数单位 i、j、k 组成的含有四个元的数,其形式为:
Q? (q0,q1,q2,q3) ? q0 ? q1i ? q2 j ? q3k ? q0 ? q
? 我们知道,在平面问题中,一个复数 以表示二维空间中的一个矢量:
Z ? z1 ? jz2可
? 2)利用陀螺输出角速率信号,通过求解 四元数微分方程实时更新姿态矩阵:
四 元
q?(t)
?
1 q(t) ? ?
2
b
数 微 分 方 程
?q?0 ? ?0
??q?1 ?? ???qq??32 ???
?
1 ??? 2 ??
?
??
bx by bz
? ? bx
0
? ? bz ? by
? ? by ? bz
cos ? 0
2
sin ? 0
2
cos ? 0
2
cos ? 0
?
sin ? 0
?
sin
0
22
?
?
sin
0
?
sin
捷联惯性导航系统的解算方法ppt课件

的 分量构成的矩阵,则
r rnT n r nT Cnb n rnT r nT Cbn
由于坐标系不动而是矢量转动,它 相应于矢量固定时坐标系方向转动
rn
n
C
n b
r
2010-03-19
方向余弦矩阵微分方程
由矢量相对导数和绝对导数的关系式
dr dt
n
dr dt
b
ω nb r
假定地理坐标系为参考坐标系,作为参考 坐标系认为它在空间是不动的,即
如把OXbYbZb作为动坐标系, ENU作为参考坐标系,则航向 角H,纵摇角(俯仰角)P和横 摇角(横滚角、倾斜角)R。就 是一组欧拉角。
Zb Zb'' U Zb' P
欧拉角没有严格的定义,根 据
需要,可以选用不同的欧拉 角
组。第一次转动,可以绕三 个
轴中的任一个转动,故有3种 可
能,第二次有2种可能,第三 次
启动
自检 测
初始 化
返回9
姿态
迭 数
代
次阵计 算
N O
YES
导 航 计 控 制 信 息算提 取
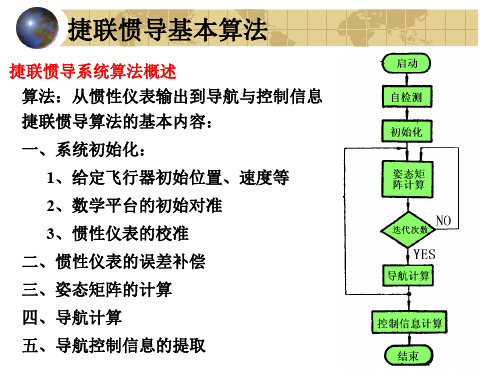
3.2 姿态矩阵的计算
捷联式惯导中,载体地理位置就是地理坐标系相对 地球坐标系的方位。而载体的姿态和航向则是载体 坐标系相对于地理坐标系的方位关系。确定两个坐 标系的方位关系问题,是力学中的刚体定点转到理 论。在刚体定点转动理论中,描述动坐标系相对参 考坐标系方位关系的方法有多种。
求解方程可以直接得到航向和姿态信息,
欧 拉角法得到的姿态阵永远是正交阵,用这
个矩 阵将比力fb→fn信息的坐标变换时,变换后的信 息
中不存在非正交误差。因此,用欧拉角法得 到的姿态矩阵无
捷联惯导系统算法.ppt
cos
b Ebz
注意事项:当 θ= 90 度时,方程出现奇点
姿态计算 矩阵方程精确解1
二、方向余弦矩阵微分方程及其解 C C
其中
C bE
CbE
b Eb
0
b Eb
z
z
0
y
x
y x
0
由于陀螺仪直接测得的是载体 相对惯性空间的角速度,所以:
CbE
b ib
E iE
C
E b
或四元数微分方程:
q(t)
(
b ib
b iE
)q(t)
注意事项: 1、上述两个方程中的角速度表达式不一样 2、方程第二项较小,计算时速度可以低一些
增量算法 矩阵方程精确解
一、角增量算法
角增量:陀螺仪数字脉冲输出,每个脉冲代表一个角增量
一个采样周期内,陀螺输出脉冲数对应的角增量为:
C
0
0
c os
0 0 0 sin
sin
sin
c os
cos cos
求解欧拉角速率得
1 0
0
cos
0 sin
惯性器件的误差补偿
姿态计算 欧拉角微分方程1
姿态矩阵的计算 假设数学坐标系模拟地理坐标系 飞行器姿态的描述:
航向角ψ、俯仰角θ、滚动角γ 一、欧拉微分方程
从地理坐标系到载体坐标系 的旋转顺序:
Ψ →θ →γ
捷联式惯性导航系统原理

1、方向余弦表cos cos sin sin sin sin cos cos sin sin cos sin sin cos cos cos sin cos sin sin sin cos sin sin cos sin cos cos cos C ψϕψθϕψϕψθϕθϕψθψθθψϕψθϕψϕψθϕθϕ-+-⎡⎤⎢⎥=-⎢⎥⎢⎥+-⎣⎦(1.0.1)X E Y C N Z ζ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(1.0.2) 在列写惯导方程需要采用方向余弦表,因为错误!未找到引用源。
α较小,经常采用两个假设,即:cos 1sin 1αα≈≈ (1.0.3)式中 α-两坐标系间每次相对转动的角度。
由于在工程实践中可以使其保持很小,所以进一步可以忽略如下形式二阶小量,即:sin sin 0αβ≈ (1.0.4)式中β-两坐标系间每次相对转动的角度。
可以将C 近似写为:111C ψϕψθϕθ-⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦(1.0.5) 2、用四元素表示坐标变换对于四元素123q p i p j p k λ=+++,可以表示为如下形式cossincos sincos sincos 2222q i j k θθθθαβγ=+++ (2.0.1)式(2.0.1)的四元数称为特殊四元数,它的范数1q =。
1'R q Rq -= (2.0.2)式中''''R xi yj zk R x i y j z k=++=++ (2.0.3)将q 和1q -的表达式及式(2.0.3)带入(2.0.2),然后用矩阵表示为:()()()()()()()()()22221231231322222123213231222213223131222''22'22p p p p p p p p p x x y p p pp p p p p p yz z p p p p p p p p p λλλλλλλλλ⎡⎤+--+-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-+--+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥+-+--⎣⎦(2.0.4)由四元素到方向余弦表的建立123cos cos22sin cos22sin sin22cos sin22p p p θψϕλθψϕθψϕθψϕ-=-=-=+= (2.0.5) 将式(2.0.5)带入式(2.0.4),有cos cos sin cos sin cos sin sin cos cos sin sin sin cos cos cos sin sin sin cos cos cos cos sin sin sin sin cos cos C ϕψϕθψϕψϕθψϕθϕψϕθψϕψϕθψϕθθψθψθ-+⎡⎤⎢⎥=---+⎢⎥⎢⎥-⎣⎦(2.0.6)3、四元数转动公式的进一步说明采用方向余弦矩阵描述飞行器姿态运动时,需要积分姿态矩阵微分方程式,即C C =Ω (3.0.1)式中 C -动坐标系相对参考坐标系的方向余弦阵Ω-动坐标系相对参考坐标系角速度ω的反对称矩阵表达式 其中C 为公式(1.0.5)提供000z y zx y xωωωωωω⎡⎤-⎢⎥Ω=-⎢⎥⎢⎥-⎣⎦(3.0.2)采用(3.0.1)计算需要列写9个一阶微分方程式,计算量大。
捷联惯性导航系统的解算方法课件

02
CATALOGUE
捷联惯性导航系统组成及工作 原理
主要组成部分介绍
惯性测量单元
包括加速度计和陀螺仪,用于测量载体在三个正交轴上的加速度 和角速度。
导航计算机
用于处理惯性测量单元的测量数据,解算出载体的姿态、速度和 位置信息。
控制与显示单元
用于实现人机交互,包括设置导航参数、显示导航信息等。
工作原理简述
学生自我评价报告
知识掌握情况
学生对捷联惯性导航系统的基本原理、解算 方法和实现技术有了深入的理解和掌握。
实践能力提升
通过实验和仿真,学生的动手实践能力得到了提升 ,能够独立完成相关的实验和仿真验证。
团队协作能力
在课程项目中,学生之间的团队协作能力得 到了锻炼和提升,能够相互协作完成项目任 务。
对未来发展趋势的预测和建议
捷联惯性导航系统的解算 方法课件
CATALOGUE
目 录
• 捷联惯性导航系统概述 • 捷联惯性导航系统组成及工作原理 • 捷联惯性导航系统解算方法 • 误差分析及补偿策略 • 实验验证与结果展示 • 总结与展望
01
CATALOGUE
捷联惯性导航系统概述
定义与基本原理
定义
捷联惯性导航系统是一种基于惯性测量元件(加速度计和陀螺仪)来测量载体(如飞机、导弹等)的加速度和角 速度,并通过积分运算得到载体位置、速度和姿态信息的自主导航系统。
01
高精度、高可靠性
02
多传感器融合技术
随着科技的发展和应用需求的提高, 捷联惯性导航系统需要进一步提高精 度和可靠性,以满足更高层次的应用 需求。
为了克服单一传感器的局限性,可以 采用多传感器融合技术,将捷联惯性 导航系统与其他传感器进行融合,提 高导航系统的性能和鲁棒性。
捷联惯导算法与组合导航原理讲义

捷联惯导算法与组合导航原理讲义一、捷联惯导算法捷联惯导(Inertial Navigation System,INS)是一种通过测量惯性传感器的运动参数实现导航定位的技术。
惯性导航系统中包括了加速度计和陀螺仪等传感器,通过测量物体的加速度和角速度,可以推算出物体的位置、速度和姿态等信息。
1.1加速度计加速度计是一种测量物体加速度的传感器。
常见的加速度计有基于压电效应的传感器和基于微机电系统(Microelectromechanical System,MEMS)的传感器。
加速度计的原理是通过测量物体受到的惯性力,推算出物体的加速度。
由于加速度是速度对时间的导数,因此通过对加速度的积分操作,可以计算出物体的速度和位移。
1.2陀螺仪陀螺仪是一种测量物体角速度的传感器。
常见的陀螺仪有机械陀螺仪和MEMS陀螺仪等。
陀螺仪的原理是基于角动量守恒定律,通过测量转动惯量的变化,推算出物体的角速度。
与加速度计类似,通过对角速度的积分操作,可以计算物体的姿态。
1.3捷联惯导算法离散时间模型中,位置、速度和姿态等状态变量通过积分加速度和角速度来更新。
由于加速度计和陀螺仪测量结果存在噪声,因此在积分操作时需要加入误差补偿算法来消除误差。
常见的误差补偿算法有零偏校正和比例积分修正等。
连续时间模型中,位置、速度和姿态等状态变量通过微分方程来描述,并通过求解微分方程来更新状态。
由于计算量较大,通常需要使用数值积分方法来求解微分方程。
常见的数值积分方法有欧拉法、中点法和四阶龙格-库塔法等。
二、组合导航原理组合导航是一种融合多种导航技术的导航方式。
常见的组合导航方式有捷联惯导与GPS组合导航。
组合导航通过融合多种导航系统的测量结果,可以提高导航定位的精度和可靠性。
2.1捷联惯导与GPS组合导航捷联惯导与GPS组合导航是一种常见的组合导航方式。
在这种方式下,捷联惯导提供了高频率的惯导数据,可以提供较高的定位精度,但是由于其测量结果累积误差较大,会逐渐偏离真实轨迹。
捷联惯导系统

作业思考题
1、简要说明捷联惯导系统的基本组成和原理。 2、什么是数学平台?它有什么作用?
惯性导航系统
第四十四讲 捷联惯导系统 力学编排方程(一)
捷联式惯导系统(SINS)
加速度计
fb
数学平台
姿态矩阵 Cbp
f p 导航 速度、位置
计算机 姿态、航向
姿态矩阵计算
陀螺
ibb
pbb
b ip
姿态航向
-
C11 C21 C31
Cep 1 Cep T
C12 C13 1 C11 C21
C22
C23
C12
C22
C32 C33 C13 C23
C11 C22C33 C23C32 C21 C13C32 C12C33 C31 C12C23 C22C13
C31
C32
C33
位置矩阵微分方程组
Cep 0 f 0,0,0
1
p p epx epy
g g egx egy
R VeggxVeggy
VeppxVeppy
三、位置速率方程
11
p p epx epy
g g egx egy
RN RE
捷联惯导的发展
1、1950年起,德雷珀实验室捷联系统得到成熟的探索; 2、1969年,在“阿波罗-13”宇宙飞船,备份捷联惯导系统; 3、20世纪80~90年代,波音757/767、A310民机以及F-20战 斗机上使用激光陀螺惯导系统,精度达到1.85km/h的量级; 4、20世纪90年代,美国军用捷联式惯导系统已占有90% 。光 纤陀螺的捷联航姿系统已用于战斗机的机载武器系统中及波 音777飞机上。 5、国内由90年代挠性捷联惯导到现在激光捷联惯导、光纤陀 螺捷联航姿系统。
捷联惯导结算原理

0 cos sin , Rz sin 0 cos
sin cos 0
0 0 1
cos cos sin sin sin cos cos sin sin cos sin cos T11 T12 T13 Ry Rx Rz cos sin cos cos sin T21 T22 T23 sin cos cos sin sin sin sin cos sin cos cos cos T T T 31 32 33 b 由姿态矩阵 C n 反解飞行器姿态欧拉角:
(5) 速度的计算
t t t t t 0 2iez etz ety 2iey Vxt Vx 0 t t b t t t t 0 2iex etx Vyt 0 Vy Cb f 2iez etz t Vz g Vzt 2 t t 2 t t 0 iey ety iex etx
o o sin 1 T23 , 90 , 90
tg 1
T13 180o , 180o , T33
tg 1
T21 o o , 180 , 180 T 22
图 6 东向北向速度变化曲线
阶段总结:1.学习了平台式和捷联式惯导的惯导解算方法并进行了仿真计算。 2.平台式惯导物理平台时刻跟踪当地水平东北天地理系, 加速计的比 力信息直接投影在导航系中,可直接进行导航速度和位置解算。载体的姿态可直 接从平台框架直接得出;而捷联式惯导用数学平台取代实体的物理平台,通过求
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
捷联惯导算法与组合导航原理讲义严恭敏,翁浚编著西北工业大学2016-9前言近年来,惯性技术不论在军事上、工业上,还是在民用上,特别是消费电子产品领域,都获得了广泛的应用,大到潜艇、舰船、高铁、客机、导弹和人造卫星,小到医疗器械、电动独轮车、小型四旋翼无人机、空中鼠标和手机,都有惯性技术存在甚至大显身手的身影。
相应地,惯性技术的研究和开发也获得前所未有的蓬勃发展,越来越多的高校学生、爱好者和工程技术人员加入到惯性技术的研发队伍中来。
惯性技术涉及面广,涵盖元器件技术、测试设备和测试方法、系统集成技术和应用开发技术等方面,囿于篇幅和作者知识面限制,本书主要讨论捷联惯导系统算法方面的有关问题,包括姿态算法基本理论、捷联惯导更新算法与误差分析、组合导航卡尔曼滤波原理、捷联惯导系统的初始对准技术、组合导航系统建模以及算法仿真等内容。
希望读者参阅之后能够对捷联惯导算法有个系统而深入的理解,并能快速而有效地将基本算法应用于解决实际问题。
本书在编写和定稿过程中得到以下同行的热心支持,指出了不少错误之处或提出了许多宝贵的修改建议,深表谢意:西北工业大学自动化学院:梅春波、赵彦明、刘洋、沈彦超、肖迅、牟夏、郑江涛、刘士明、金竹、冯理成、赵雪华;航天科工第九总体设计部:王亚军;辽宁工程技术大学:丁伟;北京腾盛科技有限公司:刘兴华;东南大学:童金武;中国农业大学:包建华;南京航空航天大学:赵宣懿;武汉大学:董翠军;网友:Zoro;山东科技大学:王云鹏。
书中缺点和错误在所难免,望读者不吝批评指正。
作者2016年9月目录第1章概述 (6)1.1捷联惯导算法简介 (6)1.2 Kalman滤波与组合导航原理简介 (7)第2章捷联惯导姿态解算基础 (10)2.1反对称阵及其矩阵指数函数 (10)2.1.1 反对称阵 (10)2.1.2 反对称阵的矩阵指数函数 (12)2.2方向余弦阵与等效旋转矢量 (13)2.2.1 方向余弦阵 (13)2.2.2 等效旋转矢量 (14)2.3方向余弦阵微分方程及其求解 (17)2.3.1 方向余弦阵微分方程 (17)2.3.2 方向余弦阵微分方程的求解 (17)2.4姿态更新的四元数表示 (20)2.4.1 四元数的基本概念 (20)2.4.2 四元数微分方程 (23)2.4.3 四元数微分方程的求解 (25)2.5等效旋转矢量微分方程及其泰勒级数解 (26)2.5.1 等效旋转矢量微分方程 (26)2.5.2 等效旋转矢量微分方程的泰勒级数解 (29)2.6圆锥运动条件下的等效旋转矢量算法 (31)2.6.1 圆锥运动的描述 (31)2.6.2 圆锥误差补偿算法 (33)第3章地球形状与重力场基础 (40)3.1地球的形状描述 (40)3.2地球的正常重力场 (46)3.3地球重力场的球谐函数模型 (50)3.3.1 球谐函数的基本概念 (50)3.3.2 地球引力位函数 (58)3.3.3 重力位及重力计算 (63)第4章捷联惯导更新算法及误差分析 (69)4.1捷联惯导数值更新算法 (69)4.1.1 姿态更新算法 (69)4.1.2 速度更新算法 (70)4.1.3 位置更新算法 (76)4.2捷联惯导误差方程 (76)4.2.1惯性传感器测量误差 (76)4.2.2姿态误差方程 (78)4.2.3速度误差方程 (79)4.2.4位置误差方程 (79)4.2.5误差方程的整理 (80)4.3静基座误差特性分析 (82)4.3.1 静基座误差方程 (82)4.3.2 高度通道 (83)4.3.3 水平通道 (83)4.3.4 水平通道的简化 (88)4.3.5 水平通道误差方程的仿真 (90)第5章卡尔曼滤波基本理论 (92)5.1递推最小二乘法 (92)5.2 Kalman滤波方程的推导 (94)5.3连续时间随机系统的离散化与连续时间Kalman滤波 (101)5.4噪声相关条件下的Kalman滤波 (107)5.5序贯滤波 (111)5.6信息滤波与信息融合 (114)5.7平方根滤波 (116)5.8遗忘滤波 (124)5.9 Sage-Husa自适应滤波 (125)5.10最优平滑算法 (127)5.11非线性系统的EKF滤波、二阶滤波与迭代滤波 (130)5.12间接滤波与滤波校正 (136)5.13联邦滤波(待完善) (136)5.14滤波的稳定性与可观测度分析 (141)第6章初始对准及组合导航技术 (147)6.1捷联惯导粗对准 (147)6.1.1矢量定姿原理 (147)6.1.2解析粗对准方法 (149)6.1.3间接粗对准方法 (152)6.2捷联惯导精对准 (153)6.3惯性/卫星组合导航 (157)6.3.1空间杆臂误差 (157)6.3.2时间不同步误差 (158)6.3.3状态空间模型 (159)6.4车载惯性/里程仪组合导航 (159)6.4.1航位推算算法 (159)6.4.2航位推算误差分析 (161)6.4.3惯性/里程仪组合 (164)6.5低成本姿态航向参考系统(AHRS) (167)6.5.1简化的惯导算法及误差方程 (168)6.5.2地磁场测量及误差方程 (169)6.5.3低成本组合导航系统模型 (170)6.5.4低成本惯导的姿态初始化 (171)6.5.5捷联式地平仪的工作原理 (173)第7章捷联惯导与组合导航仿真 (176)7.1飞行轨迹和惯性器件信息仿真 (176)7.1.1飞行轨迹设计 (176)7.1.2 捷联惯导反演算法 (177)7.1.3 仿真 (178)7.2捷联惯导仿真 (180)7.2.1 Matlab子函数 (180)7.2.2捷联惯导仿真主程序 (185)7.3惯导/卫星组合导航仿真 (186)7.3.1Matlab子函数 (186)7.3.2组合导航仿真主程序 (187)附录 (190)A一些重要的三维矢量运算关系 (190)B 运载体姿态的欧拉角描述 (192)C 姿态更新的毕卡算法、龙格—库塔算法及精确数值解法 (199)D 从非直角坐标系到直角坐标系的矩阵变换 (207)E 线性系统基本理论 (211)F 加权最小二乘估计 (216)G 矩阵求逆引理 (217)H 几种矩阵分解方法(QR、Cholesky与UD) (219)I 二阶滤波中的引理证明 (223)J 方差阵上界的证明 (225)K 三阶非奇异方阵的奇异值分解 (226)L Matlab仿真程序 (231)M 练习题 (237)参考文献 (241)第1章概述第1章概述 (6)1.1捷联惯导算法简介 (6)1.2 Kalman滤波与组合导航原理简介 (7)1.1捷联惯导算法简介在捷联惯导系统(SINS)中惯性测量器件(陀螺和加速度计)直接与运载体固联,通过导航计算机采集惯性器件的输出信息并进行数值积分求解运载体的姿态、速度和位置等导航参数,这三组参数的求解过程即所谓的姿态更新算法、速度更新算法和位置更新算法。
特别在恶劣的高动态环境下,高精度的SINS对惯性器件性能和导航算法精度的要求都非常苛刻,由于高精度惯性器件往往价格昂贵并且进一步提升精度异常困难,所以在影响SINS精度的所有误差源中要求因导航算法引起的误差比重必须很小,一般认为应小于5%。
姿态更新算法是SINS算法的核心,对整个系统的解算精度影响最为突出,具有重要的研究和应用价值。
传统的姿态更新算法有欧拉角法、方向余弦阵法和四元数法等方法,这些方法直接以陀螺采样输出作为输入,使用泰勒级数展开或龙格—库塔等方法求解姿态微分方程,未充分考虑转动的不可交换性误差问题。
传统姿态更新算法在理论上可以通过提高采样和更新频率来提高解算精度,但实际陀螺采样频率又受限于传感器的带宽和噪声水平,因此传统算法的精度提升空间相对有限,仅适用于对解算精度要求不太高的场合。
早在1775年,欧拉就提出了等效旋转矢量的概念,指出刚体的定点转动(即绕固定点的任何有限角位移)均可用绕经过该固定点的某轴的一次转动来实现,建立了刚体上单位矢量在转动前后的变换公式。
1840年,罗德里格使用后人称之为罗德里格参数的表示方法,推导了相继两次转动的合成公式,它与W. R. Hamilton在1843年发明的四元数乘法表示是一致的。
研究表明,相继多次的定点转动问题可用一系列的姿态变化量(变化四元数或变化矩阵)相乘来描述,每个姿态变化量与对应转动的等效旋转矢量之间存在转换公式,使用等效旋转矢量计算姿态变化量不存在任何原理上的误差。
因此,现代的SINS姿态更新算法研究的关键就在于如何使用陀螺输出构造等效旋转矢量,以尽量减小和避免不可交换性误差,后续再使用等效旋转矢量计算姿态变化量和进行姿态更新将变得非常简单,而不像传统方法那样,直接使用陀螺输出进行姿态更新容易引起不可交换性误差。
1949年,J. H. Laning在研究火控系统的过程中详细地分析了空间转动合成的性质,推导了由等效旋转矢量确定转动角速度的公式,但是由于缺少更好的应用背景驱动(比如后来SINS发展的迫切需求),未能获得广泛的研究重视。
20世纪50年代是机械陀螺仪飞速发展的一个重要时期,也正是在那时发现了著名的圆锥运动现象,即当陀螺仪在其旋转轴和输出轴出现同频不同相的角振动时,尽管其输入轴净指向不变(在整体上没有随时间改变的趋势项),但陀螺仪还是会敏感到并输出常值角速率。
1958年,为揭示圆锥运动现象产生的根源,L. E. Goodman建立了刚体转动的等效旋转矢量与角速度之间的关系式,后人称之为Goodman-Robinson定理,该定理从几何上将转动不可交换性误差的坐标分量描述为单位球面上的一块有向面积,其面积由对应动坐标轴在单位球面上扫过的曲线与连接该曲线端点的大圆围成,Goodman借助二维Green积分理论获得了不可交换性误差的近似公式。
1969年,基于Goodman近似公式,J. W. Jordan在假设陀螺角增量输出为二次多项式条件下提出了等效旋转矢量的“pre-processor”算法,它与后来发展的等效旋转矢量二子样算法完全一致。
1969年,J. E. Bortz在其博士论文中详细推导了等效旋转矢量微分方程(1971年正式发表,后人称之为Bortz方程),它是利用陀螺输出求解等效旋转矢量的基本公式,奠定了等效旋转矢量多子样算法的理论基础。
在实际应用时一般需对较复杂的Bortz方程做近似处理,事实上,其简化结果与Goodman公式完全一致,它也可以根据Laning公式简化获得。
1983年,R. B. Miller采用在圆锥运动条件下使算法漂移误差最小作为评价标准,推导了等效旋转矢量三子样优化算法。
1990年,J. E. Lee研究了四子样优化算法。
