matlab实验报告--定积分的近似计算
matlab蒙特卡洛法求定积分

matlab蒙特卡洛法求定积分摘要:一、蒙特卡洛法简介二、蒙特卡洛法求定积分的步骤1.确定积分区间2.生成随机点3.计算原函数在随机点的值4.计算积分三、Matlab 编程实现蒙特卡洛法求定积分1.编写蒙特卡洛积分函数2.生成随机点3.计算原函数在随机点的值4.计算积分四、结论正文:蒙特卡洛法是一种通过随机抽样来估算数学期望值的方法。
在求解定积分问题时,蒙特卡洛法可以通过模拟原函数在区间上的取值,用随机点代替实际点,从而近似计算定积分。
Matlab 提供了丰富的工具箱,可以方便地实现蒙特卡洛法求定积分。
首先,我们需要确定积分区间。
例如,对于积分区间[a, b],我们需要确定a 和b 的值。
接下来,生成随机点。
在Matlab 中,我们可以使用rand 函数生成随机数。
在[a, b] 区间内生成足够多的随机点,例如n 个点。
然后,计算原函数在随机点的值。
这需要我们先编写一个原函数的Matlab 函数。
例如,如果原函数是f(x),我们可以使用f(x) = ...来计算原函数在随机点的值。
最后,计算积分。
根据蒙特卡洛法的原理,我们可以用生成随机点的个数n 来近似计算定积分。
具体地,定积分的值约等于(1/n) * Σ[f(xi)],其中xi 是随机点。
在Matlab 中,我们可以使用sum 函数计算Σ[f(xi)]。
综上所述,我们可以通过以下步骤在Matlab 中实现蒙特卡洛法求定积分:1.确定积分区间。
2.生成随机点。
3.计算原函数在随机点的值。
4.计算积分。
通过这种方法,我们可以有效地求解定积分问题。
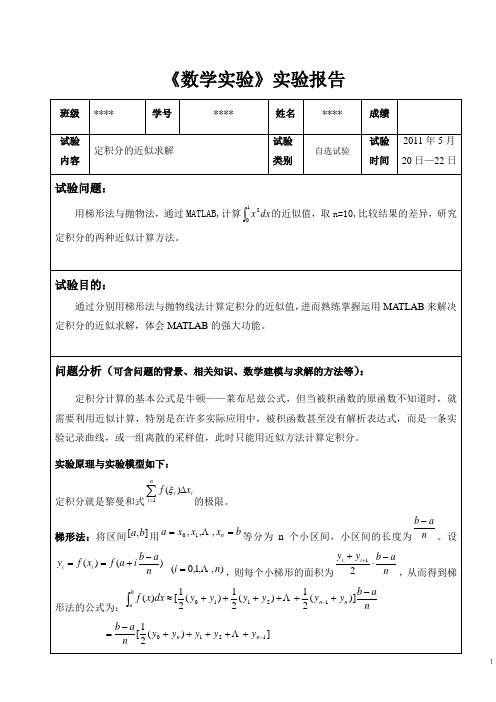
《数学实验》实验报告——定积分的近似求解
3
2 梯形法程序如下: f=input('请输入被积函数 f(x)='); qujian=input('请输入积分区间[a,b]='); n=input('请输入子区间个数 n='); s=0; for i=1:n-1 x=qujian(1)+(qujian(2)-qujian(1))/n*i; y=eval(f); s=s+y; end x=qujian(1); y=eval(f); s=s+y/2; x=qujian(2); y=eval(f); s=s+y/2; disp('定积分的近似值是:'); s=s*(qujian(2)-qujian(1))/n
《数学实验》实验报告
班级 试验 内容 **** 学号 **** 姓名 试验 类别
自选试验
****
成绩 试验 时间 2011 年 5 月 20 日—22 日
定积分的近似求解
试验问题:
用梯形法与抛物法,通过 MATLAB,计算 x 2 dx 的近似值,取 n=10,比较结果的差异,研究
0 1
定积分的两种近似计算方法。
1 1 1 2 ph 3 6rh h(2 ph 2 6r ) h( y 0 4 y1 y 2 ) 3 3 3 。 ba n ,则上面所求的 S 等于区间 [ x0 , x2 ] 上以抛物线为曲边的曲边梯形的面积。同理可
取
以得到区间 [ xi 1 , xi 1 ] 上以抛物线为曲边的曲边梯形的面积:
试验目的:
通过分别用梯形法与抛物线法计算定积分的近似值, 进而熟练掌握运用 MATLAB 来解决 定积分的近似求解,体会 MATLAB 的强大功能。
matlab实验报告--定积分的近似计算

○2 使用函数 quad()
quad('sin(x)./x',0,inf) 【调试结果】 ans =
NaN
○3 程序法
%矩阵法
format long
n=inf;a=0;b=inf;
syms x fx
fx=sin(x)./x;
i=1:n;
xj=a+(i-1)*(b-a)/n; xi=a+i*(b-a)/n;
%左点
xi=a+i*(b-a)/n;
%右点
xij=(xi+xj)/2;
fxj=subs(fx,'x',xj);
%左点值
fxi=subs(fx,'x',xi);
%右点值
fxij=subs(fx,'x',xij);
%中点值
f=(fxj+4*fxij+fxi)*(b-a)/(6*n);
inum=sum(f)
xj=a+(i-1)*(b-a)/n; xi=a+i*(b-a)/n; xk=(xi+xj)/2;
%左点 %右点 %中点
fxj=subs(fx,'x',xj); fxi=subs(fx,'x',xi); fxk=subs(fx,'x',xk); inum=inum+(fxj+4*fxk+fxi)*(b-a)/(6*n); end inum integrate=int(fx,1,2); integrate=double(integrate); fprintf('The relative error between inum and real-value is about:%g/n/n',... abs((inum-integrate)/integrate)) 【调试结果】 inum =
MATLAB数值积分求值实验报告

fori=1:n
x=rand;%产生(0,1)区间的随机数
y=rand;
ify<=1/(1+x^2);%对y=1/(1+x^2)面积投点
k=k+1;
end
end
z=k/n
pi=4*k/n%由积分pi/4=k/n而来,前者是概率,后者是频率
四.蒙特卡罗均值估计法:
n=10000;
x=rand(1,n);
姓名:
2011年11月27日
学号
班级
统计1001
姓名
指导教师
易昆南
实验题目
用多种方法计算数值积分
评 分
1、设计(实习)目的:
1.了解MATLAB在实际问题中的应用
2.通过实践加深对这门语言中M文件的了解
3.熟悉简单程序结构,如循环结构(for循环、while循环)选择结构(if-else-if)、分支语句(switch-case-otherwise)。
y=x.^2;
z=sum(y)/n%均值估计法
4:实验结果:
一.左、右矩形法和梯形法:
z1 =
0.3308
z2 =
0.3358
z3 =
0.3333
二.复化辛普森公式法:
z1 =
0.3Байду номын сангаас33
z2 =
0.3333
Warning: QUAD8 is obsolete. We use QUADL instead.
2、实验内容:
(1).分别用左、右矩形法,梯形法,复化辛普森公式计算y=x^2在[0,1]上的定积分;
(2).用蒙特卡罗随机投点法计算y=1/(1+x^2)在[0,1]上的定积分,并求出pi的近似值;
matlab蒙特卡洛法求定积分

matlab蒙特卡洛法求定积分摘要:一、引言二、蒙特卡洛法简介三、用MATLAB 实现蒙特卡洛法求定积分的方法四、实例:用MATLAB 实现蒙特卡洛法求定积分五、结论正文:一、引言在数学中,定积分是一种常见的计算方式,它可以用来求解曲线下的面积、长度、体积等。
在实际应用中,有些定积分的具体形式难以求解,这时就可以采用蒙特卡洛法来近似求解。
蒙特卡洛法是一种通过随机抽样来估算数学期望值的方法,其在求解定积分方面有着广泛的应用。
本文将介绍如何在MATLAB 中使用蒙特卡洛法求解定积分。
二、蒙特卡洛法简介蒙特卡洛法是一种基于随机抽样的数值计算方法,通过大量模拟实验来近似求解问题。
在求解定积分时,蒙特卡洛法通过随机生成一定数量的样本点,然后计算这些样本点对应的函数值之和,再乘以样本点的权重,最后得到定积分的近似解。
蒙特卡洛法的优点在于它不需要求解积分的具体形式,只需要知道积分函数的表达式即可。
同时,蒙特卡洛法的精度可以通过增加样本点数量来提高。
三、用MATLAB 实现蒙特卡洛法求定积分的方法在MATLAB 中,可以使用内置的random 函数生成随机数,结合定积分的表达式,就可以实现蒙特卡洛法求解定积分。
具体步骤如下:1.创建一个函数文件,输入定积分的表达式;2.使用random 函数生成一定数量的随机数;3.将随机数代入定积分的表达式,计算每个样本点对应的函数值;4.计算所有样本点函数值之和,再乘以样本点的权重,得到定积分的近似解。
四、实例:用MATLAB 实现蒙特卡洛法求定积分例如,求解定积分∫(0~π) sin x dx。
首先,创建一个函数文件,输入以下代码:```matlabfunction integral = montecarlo_integration(n, a, b, f)% n 为样本点数量,a 和b 为积分区间,f 为积分函数x = linspace(a, b, n+1);y = f(x);integral = mean(y);end```然后,在命令窗口中输入以下命令:```matlab= 10000;a = 0;b = pi;f = @(x) sin(x);integral = montecarlo_integration(n, a, b, f);```最后,得到定积分∫(0~π) sin x dx 的近似解为:```matlabintegral =2.5717```五、结论蒙特卡洛法是一种强大的数值计算方法,可以用来求解各种定积分。
概率统计定积分近似计算实验报告

概率统计定积分近似计算实验报告
实验五、定积分的近似计算实验序号:5
日期:xxx 年 5 月 15 日班级
学号
姓名
实验名称定积分的近似计算
问题的背景和目的:
加深对大数定律的理解,学会用 o Monte Carlo 方法近
似计算定积分的值.掌握利用随机投点法和平均值法近似计算定积分的方法.:
实验内容:
(随机投点法)
估计定积分11011xeJ dxe.(当 0 1 x
时,10 ( ) 11xef xe).随机投点法的具体步骤为:
(1) 独立地产生 2n 个服从(0,1)上均匀分布的随机数,
1 2 1 2, , , ; , , ,n nx x x y y y ; (2) 统计 ( )i iy
f x 的次数 k ; (3) 用kn来估计1J .
(平均值法)
估计定积分1101.1xeJ dxe(当 0 1 x
时,10 ( ) 11xef xe).平均值法的具体步骤为:
(1) 独立地产生 n 个服从 (0,1) 区间上的均匀分布的随机数1 2, , ,nx x x ; (2) 计算 ( )if x ; (3) 用
11( )niif xn来估计1J .(4)自己从《数学分析》教材中找一个“积不出来”的定积分,利用上述方法近似计算积分。
实验所用软件及版本:
Excel 2003 实验过程:
实验结果总结:
教师评语与成绩:
挺有创意的!
范文自然,朴实。
很受用的一篇范文,谢谢分享!。
MATLAB实验三 定积分的近似计算
实验三定积分的近似计算一、问题背景与实验目的利用牛顿—莱布尼兹公式虽然可以精确地计算定积分的值,但它仅适用于被积函数的原函数能用初等函数表达出来的情形.如果这点办不到或者不容易办到,这就有必要考虑近似计算的方法.在定积分的很多应用问题中,被积函数甚至没有解析表达式,可能只是一条实验记录曲线,或者是一组离散的采样值,这时只能应用近似方法去计算相应的定积分.本实验将主要研究定积分的三种近似计算算法:矩形法、梯形法、抛物线法.对于定积分的近似数值计算,Matlab有专门函数可用.二、相关函数(命令)及简介1.sum(a):求数组a的和.2.format long:长格式,即屏幕显示15位有效数字.(注:由于本实验要比较近似解法和精确求解间的误差,需要更高的精度).3.double():若输入的是字符则转化为相应的ASCII码;若输入的是整型数值则转化为相应的实型数值.4.quad():抛物线法求数值积分.格式:quad(fun,a,b) ,注意此处的fun是函数,并且为数值形式的,所以使用*、/、^等运算时要在其前加上小数点,即.*、./、.^等.例:Q = quad('1./(x.^3-2*x-5)',0,2);5.trapz():梯形法求数值积分.格式:trapz(x,y)其中x为带有步长的积分区间;y为数值形式的运算(相当于上面介绍的函数fun)例:计算0sin()dx xπ⎰x=0:pi/100:pi;y=sin(x);trapz(x,y)6.dblquad():抛物线法求二重数值积分.格式:dblquad(fun,xmin,xmax,ymin,ymax),fun可以用inline定义,也可以通过某个函数文件的句柄传递.例1:Q1 = dblquad(inline('y*sin(x)'), pi, 2*pi, 0, pi)顺便计算下面的Q2,通过计算,比较Q1 与Q2结果(或加上手工验算),找出积分变量x、y的上下限的函数代入方法.Q2 = dblquad(inline('y*sin(x)'), 0, pi, pi, 2*pi)例2:Q3 = dblquad(@integrnd, pi, 2*pi, 0, pi)这时必须存在一个函数文件integrnd.m:function z = integrnd(x, y) z = y*sin(x);7.fprintf (文件地址,格式,写入的变量):把数据写入指定文件.例:x = 0:.1:1; y = [x; exp(x)];fid = fopen('exp.txt','w'); %打开文件 fprintf(fid,'%6.2f %12.8f\n',y); %写入 fclose(fid) %关闭文件 8.syms 变量1 变量2 …:定义变量为符号. 9.sym('表达式'):将表达式定义为符号.解释:Matlab 中的符号运算事实上是借用了Maple 的软件包,所以当在Matlab 中要对符号进行运算时,必须先把要用到的变量定义为符号. 10.int(f,v,a,b):求f 关于v 积分,积分区间由a 到b .11.subs(f ,'x',a):将 a 的值赋给符号表达式 f 中的 x ,并计算出值.若简单地使用subs(f),则将f 的所有符号变量用可能的数值代入,并计算出值.三、实验内容1. 矩形法根据定积分的定义,每一个积分和都可以看作是定积分的一个近似值,即1()d ()nbi i ai f x x f x ς==∆∑⎰在几何意义上,这是用一系列小矩形面积近似小曲边梯形的结果,所以把这个近似计算方法称为矩形法.不过,只有当积分区间被分割得很细时,矩形法才有一定的精确度.针对不同i ς的取法,计算结果会有不同,我们以 120d 1xx +⎰为例(取100=n ),(1) 左点法:对等分区间b x i n ab a x x a x n i =<<-+=<<<=ΛΛ10,在区间],[1i i x x -上取左端点,即取1-=i i x ς,12 01d ()1ni i i xf x x ς==∆≈+∑⎰0.78789399673078, 理论值 12 0d 14x x π=+⎰,此时计算的相对误差0.7878939967307840.0031784ππ-=≈(2)右点法:同(1)中划分区间,在区间],[1i i x x -上取右端点,即取i i x =ς,12 01d ()1ni i i xf x x ς==∆≈+∑⎰0.78289399673078, 理论值 12 0d 14x x π=+⎰,此时计算的相对误差 0.7828939967307840.0031884ππ-=≈(3)中点法:同(1)中划分区间,在区间1[,]i i x x -上取中点,即取12i ii x x ς-+=, 12 01d ()1ni i i xf x x ς==∆≈+∑⎰0.78540024673078, 理论值 12 0d 14x x π=+⎰,此时计算的相对误差 60.7854002467307842.653104ππ--=≈⨯如果在分割的每个小区间上采用一次或二次多项式来近似代替被积函数,那么可以期望得到比矩形法效果好得多的近似计算公式.下面介绍的梯形法和抛物线法就是这一指导思想的产物.2. 梯形法等分区间b x i n a b a x x a x n i =<<-+=<<<=ΛΛ10,nab x -=∆ 相应函数值为n y y y ,,,10Λ(n i x f y i i ,,1,0),(Λ==).曲线)(x f y =上相应的点为n P P P ,,,10Λ(n i y x P i i i ,,1,0),,(Λ==)将曲线的每一段弧i i P P 1-用过点1-i P ,i P 的弦i i P P 1-(线性函数)来代替,这使得每个],[1i i x x -上的曲边梯形成为真正的梯形,其面积为x y y ii ∆⨯+-21,n i ,,2,1Λ=. 于是各个小梯形面积之和就是曲边梯形面积的近似值,11 11()d ()22nnbi i i i ai i y y x f x x x y y --==+∆≈⨯∆=+∑∑⎰, 即11 ()d ()22bn n ay y b a f x x y y n --≈++++⎰L , 称此式为梯形公式.仍用 12 0d 1x x +⎰的近似计算为例,取100=n ,10112 0d ()122n n y y x b a y y x n --≈++++=+⎰L 0.78539399673078, 理论值 12 0d 14x x π=+⎰,此时计算的相对误差 60.7853939967307845.305104ππ--=≈⨯很显然,这个误差要比简单的矩形左点法和右点法的计算误差小得多.3. 抛物线法由梯形法求近似值,当)(x f y =为凹曲线时,它就偏小;当)(x f y =为凸曲线时,它就偏大.若每段改用与它凸性相接近的抛物线来近似时,就可减少上述缺点,这就是抛物线法.将积分区间],[b a 作n 2等分,分点依次为b x i n a b a x x a x n i =<<-+=<<<=2102ΛΛ,nab x 2-=∆, 对应函数值为n y y y 210,,,Λ(n i x f y i i 2,,1,0),(Λ==),曲线上相应点为n P P P 210,,,Λ(n i y x P i i i 2,,1,0),,(Λ==).现把区间],[20x x 上的曲线段)(x f y =用通过三点),(000y x P ,),(111y x P ,),(222y x P 的抛物线)(12x p x x y =++=γβα来近似代替,然后求函数)(1x p 从0x 到2x 的定积分:21 ()d x x p x x =⎰22 ()d x x x x x αβγ++=⎰)()(2)(30220223032x x x x x x -+-+-γβα]4)(2)()()[(62022022202002γβαγβαγβα++++++++++-=x x x x x x x x x x 由于2201x x x +=,代入上式整理后得 21 ()d x x p x x ⎰)](4)()[(612122202002γβαγβαγβα++++++++-=x x x x x x x x )4(621002y y y x x ++-=)4(6210y y y nab ++-= 同样也有422 ()d x x p x x ⎰)4(6432y y y n ab ++-=……222 ()d n n x nx p x x -⎰)4(621222n n n y y y nab ++-=-- 将这n 个积分相加即得原来所要计算的定积分的近似值:22222212 11()d ()d (4)6ii nnbx i i i i ax i i b af x x p x x y y y n---==-≈=++∑∑⎰⎰, 即021******* ()d [4()2()]6bn n n ab af x x y y y y y y y y n---≈++++++++⎰L L 这就是抛物线法公式,也称为辛卜生(Simpson )公式.仍用 12 0d 1x x +⎰的近似计算为例,取100=n ,102132124222 0d [4()2()]16n n n x b ay y y y y y y y x n ---≈+++++++++⎰L L=0.78539816339745,理论值 12 0d 14x x π=+⎰,此时计算的相对误差 160.7853981633974542.827104ππ--=≈⨯4. 直接应用Matlab 命令计算结果(1) 数值计算 120d .1xx +⎰ 方法1:int('1/(1+x^2)','x',0,1) (符号求积分)方法2:quad('1./(1+x.^2)',0,1) (抛物线法求数值积分)方法3:x=0:0.001:1; y=1./(1+x.^2);trapz(x,y) (梯形法求数值积分) (2)数值计算 212 01d d x x y y -+⎰⎰方法1:int(int('x+y^2','y',-1,1),'x',0,2) (符号求积分)方法2:dblquad(inline('x+y^2'),0,2,-1,1) (抛物线法二重数值积分)四、自己动手1. 实现实验内容中的例子,即分别采用矩形法、梯形法、抛物线法计算 120d 1xx +⎰,取258=n ,并比较三种方法的精确程度.2. 分别用梯形法与抛物线法,计算 2 1d xx⎰,取120=n .并尝试直接使用函数trapz()、quad()进行计算求解,比较结果的差异.3. 试计算定积分 0sin d xx x+∞⎰.(注意:可以运用trapz()、quad()或附录程序求解吗?为什么?)4. 将 120d 1xx +⎰的近似计算结果与Matlab 中各命令的计算结果相比较,试猜测Matlab 中的数值积分命令最可能采用了哪一种近似计算方法?并找出其他例子支持你的观点.5. 通过整个实验内容及练习,你能否作出一些理论上的小结,即针对什么类型的函数(具有某种单调特性或凹凸特性),用某种近似计算方法所得结果更接近于实际值?6. 学习fulu2sum.m 的程序设计方法,尝试用函数 sum 改写附录1和附录3的程序,避免for 循环.五、附录附录1:矩形法(左点法、右点法、中点法)(fulu1.m ) format long n=100;a=0;b=1;inum1=0;inum2=0;inum3=0; syms x fx fx=1/(1+x^2); for i=1:nxj=a+(i-1)*(b-a)/n; %左点 xi=a+i*(b-a)/n; %右点 fxj=subs(fx,'x',xj); %左点值fxi=subs(fx,'x',xi); %右点值fxij=subs(fx,'x',(xi+xj)/2); %中点值inum1=inum1+fxj*(b-a)/n;inum2=inum2+fxi*(b-a)/n;inum3=inum3+fxij*(b-a)/n;endinum1inum2inum3integrate=int(fx,0,1)integrate=double(integrate)fprintf('The relative error between inum1 and real-value is about: %d\n\n',...abs((inum1-integrate)/integrate))fprintf('The relative error between inum2 and real-value is about: %d\n\n',...abs((inum2-integrate)/integrate))fprintf('The relative error between inum3 and real-value is about: %d\n\n',...abs((inum3-integrate)/integrate))附录2:梯形法(fulu2.m)format longn=100;a=0;b=1;inum=0;syms x fxfx=1/(1+x^2);for i=1:nxj=a+(i-1)*(b-a)/n;xi=a+i*(b-a)/n;fxj=subs(fx,'x',xj);fxi=subs(fx,'x',xi);inum=inum+(fxj+fxi)*(b-a)/(2*n);endinumintegrate=int(fx,0,1)integrate=double(integrate)fprintf('The relative error between inum and real-value is about: %d\n\n',...abs((inum-integrate)/integrate))附录2sum:梯形法(fulu2sum.m),利用求和函数,避免for 循环format longn=100;a=0;b=1;syms x fxfx=1/(1+x^2);i=1:n;xj=a+(i-1)*(b-a)/n; %所有左点的数组xi=a+i*(b-a)/n; %所有右点的数组fxj=subs(fx,'x',xj); %所有左点值fxi=subs(fx,'x',xi); %所有右点值f=(fxi+fxj)/2*(b-a)/n; %梯形面积inum=sum(f) %加和梯形面积求解integrate=int(fx,0,1)integrate=double(integrate)fprintf('The relative error between inum and real-value is about: %d\n\n',...abs((inum-integrate)/integrate))附录3:抛物线法(fulu3.m)format longn=100;a=0;b=1;inum=0;syms x fxfx=1/(1+x^2);for i=1:nxj=a+(i-1)*(b-a)/n; %左点xi=a+i*(b-a)/n; %右点xk=(xi+xj)/2; %中点fxj=subs(fx,'x',xj);fxi=subs(fx,'x',xi);fxk=subs(fx,'x',xk);inum=inum+(fxj+4*fxk+fxi)*(b-a)/(6*n);endinumintegrate=int(fx,0,1)integrate=double(integrate)fprintf('The relative error between inum and real-value is about: %d\n\n',...abs((inum-integrate)/integrate))。
试验定积分的近似计算
实验一特殊函数与图形一、问题背景与实验目的著名的Riemann函数大家都很熟悉了,但是关于它的图像你是否清楚呢?除了最上面那几点,其他都很难画吧?你想不想看看下面那些“挤在一起”的点是怎样分布的呢?还有几何中的马鞍面、单叶双曲面等是怎样由直线生成的,是不是也想目睹一下呢?这些,都离不开绘图.实际上绘图一直是数学中的一种重要手段,借助图形,往往可以化繁为简,使抽象的对象得到明白直观的体现.比如函数的基本性质,一个图形常可以使之一目了然,非常有效.它虽不能代替严格的分析与证明,但在问题的研究过程中,可以帮助研究人员节约相当一部分精力.此外,它还可以使计算、证明、建模等的结果得到更明白易懂的表现,有时,这比科学论证更有说服力.同时,数学的教学与学习过程也离不开绘图.借助直观的图形,常可以使初学者更容易接受新知识.如数学分析中有不少函数,其解析式着实让人望而生畏,即使对其性质作了详尽的分析,还是感到难明就里;但如果能看到它的图形,再配合理论分析,则问题可以迎刃而解.又如在几何的学习中,会遇到大量的曲线与曲面,也离不开图形的配合.传统的手工作图,往往费力耗时,效果也不尽理想.计算机恰恰弥补了这个不足,使你可以方便地指定各种视角、比例、明暗,从各个角度进行观察.本实验通过对函数的图形表示和几个曲面(线)图形的介绍,一方面展示它们的特点,另一方面,也将就Matlab软件的作图功能作一个简单介绍.大家将会看到,Matlab 的作图功能非常强大.二、相关函数(命令)及简介1.平面作图函数:plot,其基本调用形式:plot(x,y,s)以x作为横坐标,y作为纵坐标.s是图形显示属性的设置选项.例如:x=-pi:pi/10:pi;y=sin(x);plot(x,y,'--rh','linewidth',2,'markeredgecolor','b','markerfacecolor','g')图1在使用函数plot时,应当注意到当两个输入量同为向量时,向量x与y必须维数相同,而且必须同是行向量或者同是列向量.绘图时,可以制定标记的颜色和大小,也可以用图形属性制定其他线条特征,这些属性包括:linewidth 指定线条的粗细.markeredgecolor 指定标记的边缘色markerfacecolor 指定标记表面的颜色.markersize 指定标记的大小.若在一个坐标系中画几个函数,则plot的调用格式如下:plot(x1,y1,s1,x2,y2,s2,……)2.空间曲线作图函数:plot3,它与plot相比,只是多了一个维数而已.其调用格式如下:plot3(x,y,z,s).例如:x=0:pi/30:20*pi;y=sin(x);z=cos(x);plot3(x,y,z)得到三维螺旋线:图23.空间曲面作图函数:(1)mesh函数.绘制彩色网格面图形.调用格式:mesh(z),mesh(x,y,z)和mesh(x,y,z,c).其中,mesh(x,y,z,c)画出颜色由c指定的三维网格图.若x、y均为向量,则length(x)=n,length(y)=m,[m,n]=size(z).(2)surf在矩形区域内显示三维带阴影曲面图.调用格式与mesh类似.(3)ezmesh用符号函数作三维曲面网格图.调用格式:ezmesh(x,y,z)其中x = x(s,t), y = y(s,t),z = z(s,t).画图区域默认为:-2*pi < s < 2*pi 且-2*pi < t < 2*pi.或者用格式:ezmesh(x,y,z,[smin,smax,tmin,tmax])(4)ezsurf用符号函数作三维曲面图.调用格式与ezmesh类似.(5)sphere画球体命令.4.meshgrid,调用格式:[x,y]=meshgrid(m,n),这里的m,n为给定的向量,可以定义网格划分区域和划分方法.矩阵x和矩阵y是网格划分后的数据矩阵.5.图像的修饰与其他函数:(1)axis equal 控制各个坐标轴的分度,使其相等;(2)colormap设置绘图颜色.调用格式:colormap([r g b])其中r,g,b都是0-1之间的数.或者用格式:colormap(s)s为颜色映像.下面举几个常用的例子:(3)grid网格函数grid on添加网格.grid off取消网格.(4)find找出符合条件的元素在数组中的位置.调用格式:y=find(条件)例如:输入:a=[4 5 78 121 4 665 225 4 1];b=find(a>7)输出:b =3 4 6 7三、实验内容数学分析中,特别是积分部分,我们接触了不少有趣的函数,由于其中有的不是一一对应的,用上面的方法无法画出它们的图像,这时就只能用参数了.此外还有些图形只能用参数来画,比如空间曲线,在计算机上不接受“两个曲面的交线”这种表示,所以也只能用参数来实现.用参数方式作图的关键在于找出合适的参数表示,尤其是不能有奇点,最好也不要用到开方.所以要找的参数最好是有几何意义的.当然这也不可一概而论,需要多积累经验.1.利用函数plot在一个坐标系中画以下几个函数图像,要求采用不同颜色、不同线形、不同的符号标记.函数为:===∈.x t y t z t tπsin(),cos(),sin(2),(0,2)程序如下:t=0:pi/20:2*pi;x=sin(t);y=cos(t);z=sin(2*t);plot(t, x, '--k*', t, y, '-rs', t, z, ':bo')图像如下:图32.绘制类似田螺线的一条三维螺线(方程自己设计).程序如下:t=0:.1:30;x=2*(cos(t)+t.*sin(t));y=2*(sin(t)-t.*cos(t));z=1.5*t;plot3(x,y,-z) %取–z 主要是为了画图看起来更清楚axis equal图像如下:图43.利用函数z=绘制一个墨西哥帽子的图形.程序如下:[a,b]=meshgrid(-8:.5:8); %先生成一个网格c=sqrt(a.^2+b.^2)+eps;z=sin(c)./c;mesh(a,b,z)axis square图像如下:图5思考:这里的 eps 是什么?其作用是什么?4.利用surf 绘制马鞍面图形(函数为:2294x y z =-). 程序如下:[x,y]=meshgrid(-25:1:25,-25:1:25); z=x.^2/9-y.^2/4; surf(x,y,z) title('马鞍面') grid off图像如下:图65.分别用ezmesh 和ezsurf 各绘制一个圆环面,尝试将两个圆环面放在一个图形界面内,观察它们有什么不同之处.提示:圆环面的方程为: 2 ,6 ,)(22222===+-+r R r z R y x ,而圆环面的参数方程为:]2,0[ ],2,0[ ,sin sin )cos (cos )cos (ππ∈∈⎪⎩⎪⎨⎧=+=+=v u u r z v u r R y v u r R x 程序参见附录1. 图像如下:图76.绘制黎曼函数图形,加深对黎曼函数的理解.说明:黎曼函数的定义为1(0,1) 01[01]p p p q x qq q y x x ⎧=∈⎪=⎨⎪=∈⎩,当、为正整数,为既约分数,0,当,及无理点,, 程序参见附录2. 图像如下:图8四、自己动手1. 作出下图所示的三维图形:图9提示:图形为圆环面和球面的组合.2.作出下图所示的墨西哥帽子及其剪裁图形:图10 3.画出球面、椭球面、双叶双曲面、单叶双曲面.4.若要求田螺线的一条轴截面的曲边是一条抛物线:0y时25==.试重新x z设计田螺线的参数方程,并画出该田螺线.5.作出下图所示的马鞍面(颜色为灰色,并有一个标题:“马鞍面”):图116.绘制图8所示的黎曼函数图形,要求分母的最大值n的数值由键盘输入(提示:使用input语句).五、附录附录1:(fulu1.m)程序如下:subplot(1,2,1)ezmesh('(6+2*cos(u))*cos(v)','(6+2*cos(u))*sin(v)','2*sin(u)',[0,2*pi,0,2*pi]) axis equalsubplot(1,2,2)ezsurf('(6+2*cos(u))*cos(v)','(6+2*cos(u))*sin(v)','2*sin(u)',[0,2*pi,0,2*pi])axis equal附录2:(fulu2.m)程序如下:n=100;x=[];y=[];k=1;for i=2:nfor j=1:i-1if gcd(i,j)==1 %用函数gcd(m,n)可求m和n的最大公约数x(k)=j/i;y(k)=1/i;k=k+1;endendendplot(x,y,'.b');axis([0,1,0,1])。
Matlab实验报告四(矩形法梯形法抛物线法求定积分)
functionf=f1(x)
f=sqrt(1+0.5^2*cos(x).^2);
x=0.9的方程:
functionf=f1(x)
f=sqrt(1+0.9^2*cos(x).^2);
3.结果
f=zuoye(@f1,0,2e1(@f1,0,2*pi,100)
functionf=zuoye(fun,a,b,n)
h=(b-a)/n;
x=a:h:b;
y=x;
fori=2:n+1
y(i)=fun((x(i)+x(i-1))/2);
end
f=h*sum(y(1:end))
梯形法:
functionf=zuoye1(fun,a,b,n)
h=(b-a)/n;
x=a:h:b;
f = 6.2989
f=zuoye3(@f1,0,2*pi,100)
x = 6.2989
4.结论及分析
三、实验小结
y=x;
fori=1:n+1
y(i)=fun(x(i));
end
f=h*(sum(y)-1/2*y(1)-1/2*y(end));
抛物线法:
functionf=zuoye3(fun,a,b,n)
h=(b-a)/(2*n);
x=a:h:b;
y=x;
fori=1:2*n+1
y(i)=fun(x(i));
数学与信息科学系实验报告
实验名称定积分的近似计算
所属课程数学软件与实验
实验类型综合型实验
专业信息与计算科学
班级
学号
姓名
指导教师
一、实验概述
【实验目的】
matlab定积分及应用
实验四 定积分及应用实验的目的1、掌握利用Matlab 进行积分运算;2、掌握积分在计算面积、体积等问题中的应用;3、掌握各种积分指令的区别与特点。
实验的基本理论与方法1、定积分定义:函数)(x f 在区间],[b a 上的定积分定义为:设函数)(x f 在],[b a 上有界,在区间],[b a 上任取1-n 个分点:b x x x x x a n n =<<<<<=-1210 ,把],[b a 分成n 个小区间],[1i i i x x -=∆, n i ,,2,1 =。
这些分点构成对区间],[b a 的一个分割,用T 表示。
小区间i ∆的长度为1--=∆i i i x x x 。
记{}i ni x T ∆=≤≤1ma x ,称为分割T 的模。
在区间],[1i i ix x -=∆上取点i ξ)(1i i i x x ≤≤-ξ,做函数值)(i f ξ与小区间长度i x ∆的乘积),2,1()(n i x f i i =∆ξ,并作和∑=∆=ni i i x f S 1)(ξ。
当0→T 时,和S 总趋于确定的极限,这时这个极限为函数)(x f 在区间],[b a 上的定积分,记作⎰badx x f )(。
即i ni i T bax f dx x f ∆=∑⎰=→1)(lim )(ξ。
2、定积分的应用①计算平面图形的面积:由连续曲线)0)()((≥=x f x f y ,直线)(,b a b x a x <==及x 轴所围成的曲边梯形面积为⎰=badx x f S )(;②计算旋转体的体积:由连续曲线)(x f y =,直线)(,b a b x a x <==及x 轴所围成的曲边梯形绕x 轴旋转一周所成立体的体积为⎰=badx x f V 2)]([π;③计算平面曲线的弧长:设曲线弧由直线坐标方程))((b x a x f y ≤≤=给出,其中)(x f 在],[b a 上具有一阶连续导数,则曲线弧长dx y l ba⎰'+=21;设曲线弧由参数方程⎩⎨⎧≤≤==)(,)()(βαt t y y t x x 给出,其中)(),(t y t x 在],[βα上具有连续导数,则曲线弧长dt t y t x l ⎰'+'=βα22)()(;设曲线弧由极坐标方程))((βθαθ≤≤=r r 给出,其中)(θr 在],[βα上具有连续导数,则曲线弧长θθθβαd r r l ⎰'+=22)()(。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
abs((inum2-integrate)/integrate))
fprintf('the relative error between inum3 and real-value is about: %g\n\n',...
abs((inum3-integrate)/integrate)) 【调试结果】
○2 使用函数 quad()
quad('sin(x)./x',0,inf) 【调试结果】 ans =
NaN
○3 程序法
%矩阵法
format long
n=inf;a=0;b=inf;
syms x fx
fx=sin(x)./x;
i=1:n;
xj=a+(i-1)*(b-a)/n; xi=a+i*(b-a)/n;
实验目的:
本实验将主要研究定积分的三种近似计算算法:矩形法、梯形法、抛物线法。对于定 积分的近似数值计算,Matlab 有专门函数可用。
实验原理与数学模型:
1. 矩形法 根据定积分的定义,每一个积分和都可以看作是定积分的一个近似值,即
在几何意义上,这是用一系列小矩形面积近似小曲边梯形的结果,所以把这个近似计 算方法称为矩形法.不过,只有当积分区间被分割得很细时,矩形法才有一定的精确度.
【调试结果】
inum =
0.78539816339745
the relative error between inum and real-value is about: 2.82716e-016
【情况记录】
1、梯形法和抛物线法程序设计较为顺利。但要注意使用 for 循环函数和求和函数时
的不同 matlab 命令,避免混淆出错。使用函数 trapz(),quad()时要注意被积函数是数 值形式,应使用数组计算,应用点除即 ./ ,否则将出错,不能调试出结果。
the relative error between inum3 and real-value is about: 2.65258e-006
○2 抛物线法:使用求和函数
%抛物线
format long
n=100;a=0;b=1;
syms x fx
fx=1/(1+x^2);
i=1:n;
xj=a+(i-1)*(b-a)/n;
1/2*pi
3:
○1 矩形法:利用求和函数
%矩阵法
format long
n=100;a=0;b=1;
syms x fx
fx=1/(1+x^2);
i=1:n;
xj=a+(i-1)*(b-a)/n;
%左点
xi=a+i*(b-a)/n;
%右点
xij=(xi+xj)/2;
fxj=subs(fx,'x',xj);
针对不同 的取法,计算结果会有不同。 (1) 左点法:对等分区间
在区间
上取左端点,即取
。
(2)右点法:同(1)中划分区间,在区间
,
上取右端点,即取
。
(3)中点法:同(1)中划分区间,在区间
上取中点,即取
。
2. 梯形法 等分区间
相应函数值为
,
(
).
曲线
上相应的点为
(
)
将曲线的每一段弧 用过点 , 的弦 上的曲边梯形成为真正的梯形,其面积为
同样也有 ……
将这 个积分相加即得原来所要计算的定积分的近似值: ,
即 这就是抛物线法公式,也称为辛卜生(Simpson)公式.
实验所用软件及版本: Matlab 7.0
主要内容(要点):
1. 分别用梯形法与抛物线法,计算 ,取 quad()进行计算求解,比较结果的差异.
.并尝试直接使用函数 trapz()、
0.69314718056936
The relative error between inum and real-value is about:1.35886e-011/n/n>>
○3 使用函数 trapz()
x=1:1/120:2; y=1./x; trapz(x,y)
【调试结果】 ans =
0.69315152080005
%左点值
fxi=subs(fx,'x',xi);
%右点值
fxij=subs(fx,'x',xij);
%中点值
f1=fxj*(b-a)/n;
f2=fxi*(b-a)/n;
f3=fxij*(b-a)/n;
inum1=sum(f1)
inum2=sum(f2)
inum3=sum(f3)
integrate=int(fx,0,1);
inum=sum(f)
%加和梯形面积求解
integrate=int(fx,1,2);
integrate=double(integrate)
fprintf('The relative error between inum and real-value is about:%g/n/n',...
abs((inum-integrate)/integrate))
2. 试计算定积分
.(注意:可以运用 trapz()、quad()或附录程序求解吗?
为什么?) 3. 学习 fulu2sum.m 的程序设计方法,尝试用函数 sum 改写附录 1 和附录 3 的程序, 避免 for 循环。
实验过程记录(含基本步骤、主要程序清单及异常情况记录等):
1:
○1 梯形法
format long
【调试结果】 inum =
0.69315152080005 integrate =
0.69314718055995
The relative error between inum and real-value is about:6.26164e-006/n/n
○2 抛物线法:
%抛物线法 format long n=120;a=1;b=2; inum=0; syms x fx fx=1/x; for i=1:n
2、使用函数 trapz(),quad()和附录程序求解,均不能调试出获得出正确答案。最 后尝试用 matlab 命令中的符号求积分才得出正确结果。
3、参照附录 B 中的求和函数程序设计顺利改变了附录 A 和 C。发现使用求和函数时, inum 不需要赋初值,应用了积分理论中分割、近似、求和、取极限的思想方法,避免了 for 循环的冗杂性,较容易理解。
%左点 %右点
xij=(xi+xj)/2;
fxj=subs(fx,'x',xj);
%左点值
fxi=subs(fx,'x',xi);
%右点值
fxij=subs(fx,'x',xij);
%中点值
f1=fxj*(b-a)/n;
f2=fxi*(b-a)/n;
f3=fxij*(b-a)/n;
inum1=sum(f1)
inum2=sum(f2)
inum3=sum(f3)
integrate=int(fx,0,inf);
integrate=double(integrate);
fprintf('the relative error between inum1 and real-value is about: %g\n\n',...
数学实验报告
实验序号: 班级 实验名称 问题背景描述:
日期: 年 月 日
姓名
学号
定积分的近似计算
利用牛顿—莱布尼兹公式虽然可以精确地计算定积分的值,但它仅适用于被积函数的 原函数能用初等函数表达出来的情形.如果这点办不到或者不容易办到,这就有必要考虑 近似计算的方法.在定积分的很多应用问题中,被积函数甚至没有解析表达式,可能只是 一条实验记录曲线,或者是一组离散的采样值,这时只能应用近似方法去计算相应的定积 分.
(线性函数)来代替,这使得每个
,
.
于是各个小梯形面积之和就是曲边梯形面积的近似值,
,
即
,
称此式为梯形公式。 3. 抛物线法
将积分区间 作 等分,分点依次为
对应函数值为 (
曲线上相应点为 (
现把区间
上的曲线段
用通过三点
,
,
),
).
,
,
的抛物
线 来近似代替,然后求函数 从 到 的定积分:
由于Leabharlann ,代入上式整理后得inum1 =
0.78789399673078
inum2 = 0.78289399673078
inum3 = 0.78540024673078
the relative error between inum1 and real-value is about: 0.00317779
the relative error between inum2 and real-value is about: 0.0031884
n=120;a=1;b=2;
syms x fx
fx=1/x;
i=1:n;
xj=a+(i-1)*(b-a)/n; %所有左点的数组
xi=a+i*(b-a)/n;
%所有右点的数组
fxj=subs(fx,'x',xj); %所有左点值
fxi=subs(fx,'x',xi); %所有右点值
f=(fxi+fxj)/2*(b-a)/n; %梯形面积
○4 使用函数 quad()
quad('1./x',1,2) 【调试结果】
