概率与统计2版(陈萍[等]编)思维导图
考研数学思维导图概率论与数理统计篇

1
1
指数分布
E(X) = , D(X) =
随
λ
λ2
机 变
正态分布 E(X) = μ, D(X) = σ 2
量
的
X是随机变量,E(Xⁿ)称为x的n阶原点矩
数
矩
字
X是随机变量,E[(X-E(X))ⁿ]称为x的n阶中心矩。
特
征
协方差
cov(X, Y) = E[X − E(X)][Y − E(Y)]
cov(X, Y)
随机试验:1.条件相同可重复;2.结果具有多样性;3.实验前无法预测
基本概练
样本空间:随机试验的每一种结果称为样本点,样本点的全集是样本空间 事件:样本空间的子集称为随机事件
事件之间的关系
事件的差:记作A-B:事件A发生而事件B不发生 事件的交:记作AB:事件AB同时发生 事件的并:记作A+B或AUB:事件A或B至少有一个发生
超几何分布
C Ck n − k
P(X = k) = M N −M , k = l , l , l , l
Cn
1234
N
泊松分布
如果随机变量x的分布率为。
λk P(X = k) = e−λ , k = 0.1.2
记作X~P(λ)
第 二
k!
1 ,a ≤ x ≤ b
章
f (x) = b − a
随
常用分布Biblioteka 0, 其他二项分布,X~B(n,p)
E (X) = np, D(X) = np(1 − p)
泊松分布,X~P(λ)
E (X) = λ , D(X) = λ
几何分布。
1
1− p
E(X) = , D(X) =
高校统计学专业概率论知识点整理思维导图

高校统计学专业概率论知识点整理思维导图概率论是统计学中重要的基础学科,它研究的是不确定事件的数量关系和规律性。
对于高校统计学专业的学生来说,掌握概率论知识是非常重要的。
本文将通过整理概率论的知识点,并以思维导图的形式展示,帮助读者更好地理解和记忆。
一、概率基本概念1. 随机试验- 随机试验的定义- 试验的分类- 样本空间和样本点2. 事件与事件的关系- 事件的定义- 事件的运算- 事件关系的性质3. 概率的定义与性质- 古典概型- 几何概型- 组合概型二、概率分布1. 随机变量- 随机变量的定义- 随机变量的分类- 随机变量的分布函数2. 离散型随机变量及其分布- 离散型随机变量的定义- 二项分布、泊松分布等常见分布 - 离散型随机变量的期望和方差 3. 连续型随机变量及其分布- 连续型随机变量的定义- 均匀分布、正态分布等常见分布 - 连续型随机变量的期望和方差三、概率密度函数与分布函数1. 概率密度函数- 概率密度函数的定义- 连续型随机变量的概率计算2. 分布函数- 分布函数的定义- 连续型和离散型随机变量的分布函数性质 - 分布函数的计算方法四、多维随机变量1. 二维随机变量- 二维随机变量的定义- 二维随机变量的概率密度函数和分布函数 2. 边缘分布与条件分布- 边缘分布的定义与计算- 条件分布的定义与计算3. 相关性与独立性- 相关性与协方差的关系- 独立性的定义与判定五、大数定律与中心极限定理1. 大数定律- 弱大数定律与强大数定律- 大数定律的应用2. 中心极限定理- 中心极限定理的定义- 中心极限定理的应用六、抽样与统计推断1. 抽样方法- 简单随机抽样- 分层抽样- 系统抽样2. 参数估计- 点估计与区间估计的概念 - 极大似然估计- 置信区间估计3. 假设检验- 假设检验的原理- 单侧与双侧假设检验- 显著性水平与p值总结:概率论作为统计学的基础学科,对于高校统计学专业的学生来说是非常重要的。
思维导图之统计概率

统计概率应用
概率
性质
P(A+B)=P(A)+P(B)-P(AB)互斥加法公式P(AB)=0
P(A+B)=P(A)+P(B)独立乘法公式
P(AB)=P(A)P(B)
条件概率公式
B发生的条件下A发生的概率
P (A |B )=
=
n (AB )n (B )
P (AB )P (B )
辨析
互斥定性分析水火不容对立你死我活
独立
定量判断
P(B)=P(B|A)
或P(AB)=P(A)P(B)
随机变量
离散型
古典概型
有限等可能基本事件
可数的等可能的
P (A )=
n (A )n (Ω)
分布列、期望、方差
常见分布
非常见分布⇒常见分布
两点分布二项分布
有放回抽签一批产品已知次品率超几何分布
不放回抽签
已知产品数及次品数
典例恰好第k次检测出全部次品
亦可测出全部正品前k-1次未测出
连续型
几何概型
无线等可能基本事件
不可数、连续均匀变化
P (A )=
μ(A )μ(Ω)
是否不可数?谁等可能?有几个?
分布列、期望、方差正态分布标准正态非标准正态
卡方分布
统计
图形特征
频率分布直方图面积表示频率
平均数=Σ组中点×组面积
数字特征
众数、中位数
平均数、方差(标准差)相关关系独立性假设检验
卡方
回归分析
线性回归方程相关系数
非线性⇒线性。
初中数学《统计与概率》教学设计以及思维导图

初中数学《统计与概率》教学设计以及思维导图1. 教学目标1.1 知识与技能- 能够理解统计与概率的基本概念;- 能够运用统计与概率的方法解决实际问题。
1.2 过程与方法- 能够运用数据分析的方法,对数据进行整理、描述和分析;- 能够运用概率计算的方法,解决随机事件的概率问题。
1.3 情感态度与价值观- 培养学生的数据意识,提高学生运用数学方法解决实际问题的能力;- 培养学生对数学学科的兴趣和热情。
2. 教学内容2.1 统计- 数据收集和整理- 描述统计- 分析统计2.2 概率- 随机事件- 概率计算- 概率的应用3. 教学方法- 讲授法:讲解统计与概率的基本概念和方法;- 案例分析法:分析实际问题,引导学生运用统计与概率的方法解决问题;- 小组讨论法:分组讨论,培养学生的合作能力和思维能力。
4. 教学步骤4.1 导入- 通过生活中的实例,引入统计与概率的概念;- 引导学生思考为什么需要统计与概率的方法。
4.2 统计1. 数据收集和整理- 讲解数据收集和整理的方法;- 让学生动手实践,收集和整理数据。
2. 描述统计- 讲解描述统计的方法,如平均数、中位数、众数等;- 让学生动手实践,描述数据。
3. 分析统计- 讲解分析统计的方法,如相关系数、回归方程等;- 让学生动手实践,分析数据。
4.3 概率1. 随机事件- 讲解随机事件的定义和特点;- 让学生动手实践,观察和分析随机事件。
2. 概率计算- 讲解概率计算的方法,如古典概率、条件概率等;- 让学生动手实践,计算概率。
3. 概率的应用- 讲解概率在实际问题中的应用;- 让学生动手实践,解决实际问题。
4.4 总结与拓展- 总结本节课所学的内容,让学生形成知识体系;- 给出一些拓展问题,激发学生的学习兴趣。
5. 教学评价- 课堂表现:观察学生在课堂上的参与程度、提问回答等情况;- 作业完成情况:检查学生对课堂所学内容的掌握程度;- 小组讨论:评价学生在小组讨论中的表现,如合作能力、思维能力等。
概率思维导图

概率思维导图
表示一个事件发生的可能性大小。
越接近1,该事件更可能发生;越接近0,则该事件更不可能发生,其是客观论证,而非主观验证。
概率思维导图是总结概率知识的一种快捷方便的方法。
概率思维导图可以把各类知识内容给联系起来,建立一个联系网,更好的把知识面给体现出来。
是对于同一事件,可以从不同的等可能性角度算出不同的概率,从而产生了种种悖论。
另一方面,随着经验的积累,人们逐渐认识到,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示一
率定义。
从理论上讲,概率的频率定义是不够严谨的。
几何概率若随机试验中的基本事件有无穷多个,且每个基本事件发生是等可能的,这时就不能使用古典概率,于是产生了几何概率。
几何概率的基本思想是
问题是应用几何概率的一个典型例子。
在概率论发展的早期,人们就注意到古典概率仅考虑试验结果只有有限个的情况是不够的,还必须考虑试验结果是无限
具有所谓“均匀分布”的性质,关于“均匀分布”的精确定义类似于古典概率中“等可能”只一概念。
而这些概率的内容和解释就可以用概率思维导图来整体的联系起来,使这些
内容更加清晰和有条理性,概率思维导图可以为你打开概率大门。
概率知识框架图
构成事件A的区域 长度(面积或体积) 概率公式:P(A)= 试验的全部结果所构成 的区域长度(面积或体积)
计算机模拟试验
3.概率框架图
随机事件频率ຫໍສະໝຸດ 概率,概率的 意义与性质古典概型
几何概型
应 用 概 率 解 决 实 际 问 题
随机数与随机模拟
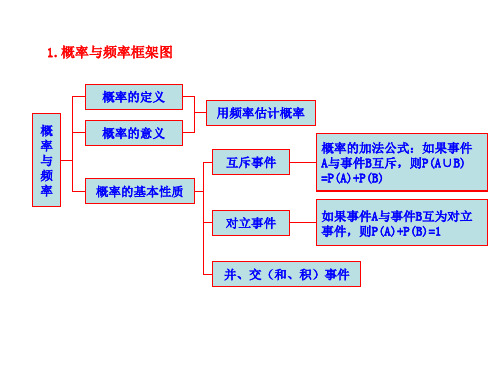
1.概率与频率框架图
概率的定义 用频率估计概率 概 率 与 频 率 概率的意义 互斥事件 概率的加法公式:如果事件 A与事件B互斥,则P(A∪B) =P(A)+P(B)
概率的基本性质
对立事件
如果事件A与事件B互为对立 事件,则P(A)+P(B)=1
并、交(和、积)事件
2.随机事件的概率知识框架图
A包含的基本事件的个数 概率公式:P(A)= 基本事件的总数
