直角三角形的边角关系专题复习
中考数学专题复习:直角三角形的边角关系

中考数学专题复习:直角三角形的边角关系一、选择题1.在直角三角形ABC中,sinA的值为12,则cosA的值等于()A.12B.√22C.√32D.√32.如图,在Rt△ABC中,BC=4,AC=3,∠C=90∘,则sinB的值为()A.45B.34C.35D.433.如图,在平面直角坐标系xOy中,点P(4,3),OP与x轴正半轴的夹角为α,则tanα的值为()A.35B.45C.34D.434.如图,为方便行人推车过天桥,市政府在10m高的天桥两端分别修建了50m长的斜道,用科学计算器计算斜道的倾斜角,下列按键顺序正确的是()A.sin0⋅2=B.2ndF sin0⋅2=C.tan0⋅2=D.2ndF tan0⋅2=5.在锐角△ABC中,(tanC−√3)2+∣∣√2−2sinB∣∣=0,则∠A=()A.30∘B.45∘C.60∘D.75∘6.如图,在8×8的网格中,点A,B,C都在格点上,每个小正方形的边长为1,则sin∠ABC的值为()A.√22B.√105C.√23D.13√10507.如图,在Rt△ABC中∠CAB=90∘,AD⊥BC于点D,BD=2,tanC=12,则线段AC 的长为()A.10B.8C.8√5D.4√58.如图,大坝横截面的迎水坡AB的坡比为1:2,即BC:AC=1:2,若坡面AB的水平宽度AC为12米,则斜坡AB的长为()A.4√3米B.6√3米C.6√5米D.24米9.如图,在四边形ABCD中,∠DAB=90∘,AD∥BC,BC=12AD,AC与BD交于点E,AC⊥BD,则tan∠BAC的值是()A.14B.√24C.√22D.1310.钓鱼是一项特别锻炼心性的运动,如图,小南在江边垂钓,河堤AB的坡度为1:2.4,AB长为3.9米,钓竿AC与水平线的夹角是60∘,其长为 4.5米,若钓竿AC与钓鱼线CD的夹角也是60∘,则浮漂D与河堤下端B之间的距离约为(参考数据:√3≈1.732)()A.1.732米B.1.754米C.1.766米D.1.823米二、填空题11.计算:cos230∘−tan60∘=__________.12.如图,在Rt△ABC中,∠C=90∘,BC=5,AC=12,则cosB=__________.,则13.如图,在直角三角形ABC中,点D是AC边的中点,∠C=90∘,sin∠DBC=35 sin∠ABC的值为__________.14.如图,在△ABC中,tanB=2,∠ACB=45∘,AD⊥BC于点D,CE⊥AB于点E,AD,CE交于点F,若AC=5√10,则线段EF的长为__________.15.如图是某种晾衣架的平面示意图,AB和CD分别是两根不同长度的支撑杆,夹角α=60∘,若AO=85cm,BO=DO=65cm,则较长支撑杆的端点A离地面的高度ℎ(单位:cm)约为__________.(结果精确到0.01,√3≈1.732),延长BC至点D,使CD:AC=1:3,则16.如图,在△ABC中,AB=AC,sinB=45tan∠CAD=__________三、解答题17.计算:(1) 2sin30∘−√12+tan60∘;(2) sin260∘+∣tan45∘−√2∣−2cos45∘.18.如图,在Rt△ABC中,设a,b,c分别为∠CAB,∠B,∠C的对边,∠C=90∘,b=8,△ABC的角平分线AD=16√3,求∠B,a,c的值.319.某校改造教室照明设备,在黑板前加装三盏带有灯罩的荧光灯(如图①),图①是荧光灯的安装截面图.黑板的高度BC=1.2米,黑板的下沿C与地面HG的距离CG=1米,天花板EF与地面HG的距离FG=3.2米,荧光灯A发出的光线夹角∠BAC=30∘,∠ACB=45∘.若使荧光灯发出的光线刚好覆盖黑板的上下沿,则电工师傅在安装荧光灯时,荧光灯A与墙面CF的距离AD是多远?固定荧光灯的吊绳AE的长度是多长?(结果精确到0.1m)(参考数据:tan15∘≈0.27,tan30∘≈0.58)20.2019年12月17日,国产航母山东舰正式交付中国海军,中国海军建设迈上了一个新台阶.如图,在一次训练中,笔直的海岸线l上有A,B两个观测站,A在B的正东方向,AB=(12+4√3)海里,山东舰在点P处,从A测得山东舰在北偏西60∘的方向,从B测得山东舰在北偏东45∘的方向.(1) 求B,P两点之间的距离;(结果保留根号)(2) 山东舰从点P处沿射线AP的方向航行,航行30分钟后到达点C处,此时,从B测得山东舰在北偏西15∘的方向.在这次训练中,山东舰的航行速度是多少?参考答案一、选择题 1. 【答案】C【解析】因为在直角三角形 ABC 中,sinA 的值为 12, 所以 ∠A =30∘, 所以 cosA =cos30∘=√32. 2. 【答案】C【解析】由勾股定理得 AB =√AC 2+BC 2=5, ∴sinB =ACAB =35. 3. 【答案】C【解析】过 P 作 PN ⊥x 轴于 N ,PM ⊥y 轴于 M ,则 ∠PMO =∠PNO =90∘, ∵x 轴 ⊥y 轴,∴∠MON =∠PMO =∠PNO =90∘, ∴ 四边形 MONP 是矩形, ∴PM =ON ,PN =OM , ∵P (4,3),∴ON =PM =4,PN =3, ∴tanα=PNON =34.4. 【答案】B【解析】 sinA =1050=0.2,所以用科学计算器求这条斜道倾斜角的度数时,按键顺序为2ndF sin 0 ⋅ 2 =.故选B . 5. 【答案】D【解析】 ∵(tanC −√3)2+∣∣√2−2sinB ∣∣=0, ∴tanC =√3,sinB =√22,∴∠C=60∘,∠B=45∘,∴∠A=75∘.故选:D.6. 【答案】D【解析】如图,过点C作CD⊥AB于点D,易得S△ABC=5×6−6−5−6=13,AB=√32+42=5,∴AB边上的高CD=265,在Rt△CBD中,BC=√22+62=2√10,∴sin∠ABC=CDBC =2652√10=13√1050.7. 【答案】D【解析】∵∠CAB=90∘,AD⊥BC,∴∠B+∠C=90∘,∠B+∠BAD=90∘,∴∠BAD=∠C.在Rt△ABD中,∠ADB=90∘,BD=2,∵tan∠BAD=BDAD =12,∴AD=2BD=4,∴AB=√BD2+AD2=2√5.在Rt△ABC中,∠CAB=90∘,AB=2√5,∵tanC=ABAC =12,∴AC=2AB=4√5.8. 【答案】C【解析】∵大坝横截面的迎水坡AB的坡比为1:2,AC=12米,∴BCAC =12=BC12,∴BC=6,∴AB=√AC2+BC2=√122+62=6√5(米).9. 【答案】C【解析】∵AD∥BC,∠DAB=90∘,∴∠ABC=180∘−∠DAB=90∘,∠BAC+∠EAD=90∘,∵AC⊥BD,∴∠AED=90∘,∴∠ADB+∠EAD=90∘,∴∠BAC=∠ADB,∴△ABC∽△DAB,∴ABDA =BCAB,∵BC=12AD,∴AD=2BC,∴AB2=BC×AD=BC×2BC=2BC2,∴AB=√2BC,在Rt△ABC中,tan∠BAC=BCAB =√2BC=√22.10. 【答案】C【解析】如图,延长CA交DB的延长线于点E,过点A作AF⊥BE于点F,则∠CED=60∘,∵河堤AB的坡度为1:2.4,∴AFBF =12.4=512,设AF=5x米,则BF=12x米,∵AB=3.9米,∴在直角△ABF中,由勾股定理得3.92=25x2+144x2,解得x=310(舍负).∴AF=32米,BF=185米.∴EF=AFtan60∘=32√3=√32(米),AE=AFsin60∘=32√32=√3(米),∵∠C=∠CED=60∘,∴△CDE是等边三角形,∵AC=4.5米,∴DE=CE=AC+AE=(4.5+√3)米,则BD=DE−EF−BF=4.5+√3−√32−185≈1.766(米).二、填空题11. 【答案】34−√3【解析】原式=(√32)2−√3=34−√3.12. 【答案】513【解析】在Rt△ABC中,∠C=90∘,BC=5,AC=12,∴AB=√52+122=13,∴cosB=BCAB =513.13. 【答案】3√1313【解析】在Rt△BCD中,sin∠DBC=DCDB =35,设DC=3x,则BD=5x,根据勾股定理可得BC=4x,∵点D是AC的中点,∴AC=6x,∴AB=√AC2+BC2=√(6x)2+(4x)2=2√13x,∴sin∠ABC=ACAB =2√13x=3√1313.14. 【答案】52【解析】∵∠ACB=45∘,AD⊥BC,∴△ADC为等腰直角三角形,∴AD=CD,∵AC=5√10,∴AD=CD=AC⋅sin45∘=5√10×√22=5√5,∵AD⊥BC,CE⊥AB,∴∠B+∠BAD=∠AFE+∠BAD=90∘,∴∠DFC=∠AFE=∠B,∵tanB=2,∴tan∠DFC=2,∴CDDF=2,∴DF=CD2=5√52,∴AF=AD−DF=5√5−5√52=5√52,∵tan∠AFE=tanB=2,∴设AE=2x,则EF=x,由勾股定理得AF=√5x,∴√5x=5√52,∴x=52,∴EF=52,故答案为52.15. 【答案】129.90【解析】过点A作AE⊥直线BD于点E,如图所示,在△BOD中,∠BOD=α=60∘,BO=DO,∴△BOD为等边三角形,∴∠OBD=60∘,在Rt△ABE中,∠AEB=90∘,∠ABE=60∘,AB=AO+OB=150cm,∴AE=AB⋅sin∠ABE=150×√32≈129.90(cm).16. 【答案】29【解析】过点D作DE⊥AC,与AC的延长线交于点E,因为AB=AC,所以∠B=∠ACB,因为∠DCE=∠ACB,所以∠DCE=∠B,因为sinB=45,所以sin∠DCE=DECD =45,不妨设DE=4x,则CD=5x,所以CE=√CD2−DE2=3x,因为CD:AC=1:3,所以AC=3CD=15x,所以AE=AC+CE=18x,所以tan∠CAD=DEAE =4x18x=29.故答案为29.三、解答题17. 【答案】(1) 原式=2×12−2√3+√3=1−√3.(2) 原式=(√32)2+√2−1−2×√22 =34+√2−1−√2=−14.18. 【答案】∵∠C=90∘,b=8,△ABC的角平分线AD=163√3,∴cos∠CAD=ACAD =16√33=√32,∴∠CAD=30∘,∴∠CAB=60∘,∴∠B=30∘,∴c=2b=16,a=btan30∘=√33=8√3,即∠B=30∘,a=8√3,c=16.19. 【答案】由题意知AD⊥FG,∴∠CAD=45∘=∠ACB,∴AD=DC,∠BAD=∠CAD−∠CAB=45∘−30∘=15∘,在Rt△ADB中,tan∠BAD=BDAD,∴BD=AD⋅tan∠BAD≈0.27AD=0.27CD,∴BC=CD−BD=CD−0.27CD=0.73CD=1.2米,∴CD≈1.64米,∴AD=CD≈1.6米,AE=DF=FG−CD−CG=3.2−1.64−1=0.56≈0.6(米).答:荧光灯A与墙面CF的距离AD约是 1.6米,固定荧光灯的吊绳AE的长度约是0.6米.20. 【答案】(1) 如图,过点P作PH⊥AB于点H,设PH=x海里,在Rt△PBH中,∠BHP=90∘,∠PBH=90∘−45∘=45∘,∴BH=PH=x海里,PB=√2x海里,在Rt△PAH中,∠AHP=90∘,∠PAB=90∘−60∘=30∘,∴AH=√3PH=√3x海里,∵BH+AH=AB,∴x+√3x=12+4√3,解得x=4√3,∴BP=√2x=4√6(海里).答:B,P两点之间的距离为4√6海里.(2) 如图,过点P作PM⊥BC于点M,在Rt△BPM中,∠PMB=90∘,∠PBM=45∘+15∘=60∘,∴PM=PBsin∠PBM=4√6×√32=6√2(海里).在Rt△PMC中,∠PMC=90∘,易得∠CPM=45∘,∴PC=PMcos∠CPM =√2√22=12(海里),∴航行速度为12÷0.5=24(海里/时).答:在这次训练中,山东舰的航行速度是24海里/时.。
中考数学综合题专题复习【直角三角形的边角关系】专题解析附答案解析

中考数学综合题专题复习【直角三角形的边角关系】专题解析附答案解析一、直角三角形的边角关系1.(6分)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).【答案】.【解析】试题分析:作AD⊥BC于D,于是有∠ABD=45°,得到AD=BD=,求出∠C=60°,根据正切的定义求出CD的长,得到答案.试题解析:作AD⊥BC于D,∵∠EAB=30°,AE∥BF,∴∠FBA=30°,又∠FBC=75°,∴∠ABD=45°,又AB=60,∴AD=BD=,∵∠BAC=∠BAE+∠CAE=75°,∠ABC=45°,∴∠C=60°,在Rt△ACD中,∠C=60°,AD=,则tanC=,∴CD==,∴BC=.故该船与B港口之间的距离CB的长为海里.考点:解直角三角形的应用-方向角问题.2.如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.(1)求证:直线CP是⊙O的切线.(2)若BC=2,sin∠BCP=,求点B到AC的距离.(3)在第(2)的条件下,求△ACP的周长.【答案】(1)证明见解析(2)4(3)20【解析】试题分析:(1)利用直径所对的圆周角为直角,2∠CAN=∠CAB,∠CAB=2∠BCP判断出∠ACP=90°即可;(2)利用锐角三角函数,即勾股定理即可.试题解析:(1)∵∠ABC=∠ACB,∴AB=AC,∵AC为⊙O的直径,∴∠ANC=90°,∴∠CAN+∠ACN=90°,2∠BAN=2∠CAN=∠CAB,∵∠CAB=2∠BCP,∴∠BCP=∠CAN,∴∠ACP=∠ACN+∠BCP=∠ACN+∠CAN=90°,∵点D在⊙O上,∴直线CP是⊙O的切线;(2)如图,作BF⊥AC∵AB=AC,∠ANC=90°,∴CN=CB=,∵∠BCP=∠CAN,sin∠BCP=,∴sin∠CAN=,∴∴AC=5,∴AB=AC=5,设AF=x,则CF=5﹣x,在Rt△ABF中,BF2=AB2﹣AF2=25﹣x2,在Rt△CBF中,BF2=BC2﹣CF2=2O﹣(5﹣x)2,∴25﹣x2=2O﹣(5﹣x)2,∴x=3,∴BF2=25﹣32=16,∴BF=4,即点B到AC的距离为4.考点:切线的判定3.下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)【答案】2.5m.【解析】试题分析:设DF=x,在Rt△DFC中,可得CF=DF=x,则BF=4-x,根据线段的和差可得AN=5-x,EN=DM=BF=4-,在Rt△ANE中,∠EAB=,利用∠EAB的正切值解得x的值.试题解析:解:设DF=,在Rt△DFC中,∠CDF=,∴CF=tan·DF=,又∵CB=4,∴BF=4-,∵AB=6,DE=1,BM= DF=,∴AN=5-,EN=DM=BF=4-,在Rt△ANE中,∠EAB=,EN=4-,AN=5-,tan==0.60,解得=2.5,答:DM和BC的水平距离BM为2.5米.考点:解直角三角形.4.如图,在⊙O的内接三角形ABC中,∠ACB=90°,AC=2BC,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.(1)求证:△PAC∽△PDF;(2)若AB=5,,求PD的长;(3)在点P运动过程中,设=x,tan∠AFD=y,求y与x之间的函数关系式.(不要求写出x的取值范围)【答案】(1)证明见解析;(2);(3).【解析】试题分析:(1)应用圆周角定理证明∠APD=∠FPC,得到∠APC=∠FPD,又由∠PAC=∠PDC,即可证明结论.(2)由AC=2BC,设,应用勾股定理即可求得BC,AC的长,则由AC=2BC得,由△ACE∽△ABC可求得AE,CE的长,由可知△APB是等腰直角三角形,从而可求得PA的长,由△AEF是等腰直角三角形求得EF=AE=4,从而求得DF的长,由(1)△PAC∽△PDF得,即可求得PD的长.(3)连接BP,BD,AD,根据圆的对称性,可得,由角的转换可得,由△AGP∽△DGB可得,由△AGD∽△PGB可得,两式相乘可得结果.试题解析:(1)由APCB内接于圆O,得∠FPC=∠B,又∵∠B=∠ACE=90°-∠BCE,∠ACE=∠APD,∴∠APD=∠FPC.∴∠APD+∠DPC=∠FPC+∠DPC,即∠APC=∠FPD.又∵∠PAC=∠PDC,∴△PAC∽△PDF.(2)连接BP,设,∵∠ACB=90°,AB=5,∴.∴.∵△ACE∽△ABC,∴,即. ∴.∵AB⊥CD,∴.如图,连接BP,∵,∴△APB是等腰直角三角形. ∴∠PAB=45°,.∴△AEF是等腰直角三角形. ∴EF=AE=4. ∴DF=6.由(1)△PAC∽△PDF得,即.∴PD的长为.(3)如图,连接BP,BD,AD,∵AC=2BC,∴根据圆的对称性,得AD=2DB,即.∵AB⊥CD,BP⊥AE,∴∠ABP=∠AFD.∵,∴.∵△AGP∽△DGB,∴.∵△AGD∽△PGB,∴.∴,即.∵,∴.∴与之间的函数关系式为.考点:1.单动点问题;2.圆周角定理;3.相似三角形的判定和性质;4.勾股定理;5.等腰直角三角形的判定和性质;6.垂径定理;7.锐角三角函数定义;8.由实际问题列函数关系式.5.如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.(1)判断DE与⊙O的位置关系,并说明理由;(2)求证:BC2=2CD•OE;(3)若314cos,53BAD BE∠==,求OE的长.【答案】(1)DE为⊙O的切线,理由见解析;(2)证明见解析;(3)OE =356.【解析】试题分析:(1)连接OD,BD,由直径所对的圆周角是直角得到∠ADB为直角,可得出△BCD为直角三角形,E为斜边BC的中点,由直角三角形斜边上的中线等于斜边的一半,得到CE=DE,从而得∠C=∠CDE,再由OA=OD,得∠A=∠ADO,由Rt△ABC中两锐角互余,从而可得∠ADO与∠CDE互余,可得出∠ODE为直角,即DE垂直于半径OD,可得出DE为⊙O的切线;(2)由已知可得OE是△ABC的中位线,从而有AC=2OE,再由∠C=∠C,∠ABC=∠BDC,可得△ABC∽△BDC,根据相似三角形的对应边的比相等,即可证得;(3)在直角△ABC中,利用勾股定理求得AC的长,根据三角形中位线定理OE的长即可求得.试题解析:(1)DE为⊙O的切线,理由如下:连接OD,BD,∵AB为⊙O的直径,∴∠ADB=90°,在Rt△BDC中,E为斜边BC的中点,∴CE=DE=BE=BC,∴∠C=∠CDE,∵OA=OD,∴∠A=∠ADO,∵∠ABC=90°,∴∠C+∠A=90°,∴∠ADO+∠CDE=90°,∴∠ODE=90°,∴DE⊥OD,又OD为圆的半径,∴DE为⊙O的切线;(2)∵E是BC的中点,O点是AB的中点,∴OE是△ABC的中位线,∴AC=2OE,∵∠C=∠C,∠ABC=∠BDC,∴△ABC∽△BDC,∴,即BC2=AC•CD.∴BC2=2CD•OE;(3)解:∵cos∠BAD=,∴sin∠BAC=,又∵BE=,E是BC的中点,即BC=,∴AC=.又∵AC=2OE,∴OE=AC=.考点:1、切线的判定;2、相似三角形的判定与性质;3、三角函数6.如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm.点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M 同时同方向以相同的速度运动,以MN为边在BC的上方作正方形MNGH.点M到达点D 时停止运动,点N到达点C时停止运动.设运动时间为t(s).(1)当t为何值时,点G刚好落在线段AD上?(2)设正方形MNGH与Rt△ABC重叠部分的图形的面积为S,当重叠部分的图形是正方形时,求出S关于t的函数关系式并写出自变量t的取值范围.(3)设正方形MNGH的边NG所在直线与线段AC交于点P,连接DP,当t为何值时,△CPD是等腰三角形?【答案】(1)3;(2);(3)t=9s或t=(15﹣6)s.【解析】试题分析:(1)求出ED的距离即可求出相对应的时间t.(2)先求出t的取值范围,分为H在AB上时,此时BM的距离,进而求出相应的时间.同样当G在AC上时,求出MN的长度,继而算出EN的长度即可求出时间,再通过正方形的面积公式求出正方形的面积.(3)分DP=PC和DC=PC两种情况,分别由EN的长度便可求出t的值.试题解析:∵∠BAC=90°,∠B=60°,BC=16cm∴AB=8cm,BD=4cm,AC=8cm,DC=12cm,AD=4cm.(1)∵当G刚好落在线段AD上时,ED=BD﹣BE=3cm∴t=s=3s.(2)∵当MH没有到达AD时,此时正方形MNGH是边长为1的正方形,令H点在AB 上,则∠HMB=90°,∠B=60°,MH=1∴BM=cm.∴t=s.当MH到达AD时,那么此时的正方形MNGH的边长随着N点的继续运动而增大,令G点在AC上,设MN=xcm,则GH=DH=x,AH=x,∵AD=AH+DH=x+x=x=4,∴x=3.当≤t≤4时,S MNGN=1cm2.当4<t≤6时,S MNGH=(t﹣3)2cm2∴S关于t的函数关系式为:.(3)分两种情况:①∵当DP=PC时,易知此时N点为DC的中点,∴MN=6cm∴EN=3cm+6cm=9cm.∴t=9s故当t=9s的时候,△CPD为等腰三角形;②当DC=PC时,DC=PC=12cm∴NC=6cm∴EN=16cm﹣1cm﹣6cm=(15﹣6)cm∴t=(15﹣6)s故当t=(15﹣6)s时,△CPD为等腰三角形.综上所述,当t=9s或t=(15﹣6)s时,△CPD为等腰三角形.考点:1.双动点问题;2.锐角三角函数定义;3.特殊角的三角函数值;4.正方形的性质;5.由实际问题列函数关系式;6.等腰三角形的性质;7.分类思想的应用.7.在正方形ABCD中,AC是一条对角线,点E是边BC上的一点(不与点C重合),连接AE,将△ABE沿BC方向平移,使点B与点C重合,得到△DCF,过点E作EG⊥AC于点G,连接DG,FG.(1)如图,①依题意补全图;②判断线段FG与DG之间的数量关系与位置关系,并证明;(2)已知正方形的边长为6,当∠AGD=60°时,求BE的长.BE【答案】(1)①见解析,②FG=DG,FG⊥DG,见解析;(2)3【解析】【分析】(1)①补全图形即可,②连接BG,由SAS证明△BEG≌△GCF得出BG=GF,由正方形的对称性质得出BG=DG,得出FG=DG,在证出∠DGF=90°,得出FG⊥DG即可,(2)过点D作DH⊥AC,交AC于点H.由等腰直角三角形的性质得出DH=AH=2FG=DG=2GH=6,得出DF2DG=3Rt△DCF中,由勾股定理得出CF=3得出结果.【详解】解:(1)①补全图形如图1所示,②FG=DG,FG⊥DG,理由如下,连接BG,如图2所示,∵四边形ABCD是正方形,∴∠ACB=45°,∵EG ⊥AC , ∴∠EGC =90°,∴△CEG 是等腰直角三角形,EG =GC , ∴∠GEC =∠GCE =45°, ∴∠BEG =∠GCF =135°, 由平移的性质得:BE =CF ,在△BEG 和△GCF 中,BE CF BEG GCF EG CG =⎧⎪∠=∠⎨⎪=⎩,∴△BEG ≌△GCF (SAS ), ∴BG =GF ,∵G 在正方形ABCD 对角线上, ∴BG =DG , ∴FG =DG ,∵∠CGF =∠BGE ,∠BGE+∠AGB =90°, ∴∠CGF+∠AGB =90°, ∴∠AGD+∠CGF =90°, ∴∠DGF =90°, ∴FG ⊥DG.(2)过点D 作DH ⊥AC ,交AC 于点H .如图3所示, 在Rt △ADG 中, ∵∠DAC =45°, ∴DH =AH =2在Rt △DHG 中,∵∠AGD =60°, ∴GH 33236,∴DG =2GH =6, ∴DF 2DG =3 在Rt △DCF 中,CF ()22436-3∴BE =CF =3.【点睛】本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质、勾股定理、解直角三角形的应用等知识;本题综合性强,证明三角形全等是解题的关键.8.如图,在平面直角坐标系中,菱形ABCD 的边AB 在x 轴上,点B 坐标(﹣6,0),点C 在y 轴正半轴上,且cos B =35,动点P 从点C 出发,以每秒一个单位长度的速度向D 点移动(P 点到达D 点时停止运动),移动时间为t 秒,过点P 作平行于y 轴的直线l 与菱形的其它边交于点Q .(1)求点D 坐标;(2)求△OPQ 的面积S 关于t 的函数关系式,并求出S 的最大值;(3)在直线l 移动过程中,是否存在t 值,使S =320ABCDS 菱形?若存在,求出t 的值;若不存在,请说明理由.【答案】(1)点D 的坐标为(10,8).(2)S 关于t 的函数关系式为S =24(04)220(410)33t t t t t ⎧⎪⎨-+<⎪⎩剟…,S 的最大值为503.(3)3或7. 【解析】【分析】(1)在Rt △BOC 中,求BC,OC,根据菱形性质再求D 的坐标;(2)分两种情况分析:①当0≤t ≤4时和②当4<t ≤10时,根据面积公式列出解析式,再求函数的最值;(3)分两种情况分析:当0≤t ≤4时,4t =12,;当4<t ≤10时,22201233t t -+= 【详解】解:(1)在Rt △BOC 中,∠BOC =90°,OB =6,cos B =35, 10cos OB BC B∴==8OC ∴==∵四边形ABCD 为菱形,CD ∥x 轴,∴点D 的坐标为(10,8).(2)∵AB =BC =10,点B 的坐标为(﹣6,0),∴点A 的坐标为(4,0).分两种情况考虑,如图1所示.①当0≤t ≤4时,PQ =OC =8,OQ =t ,∴S =12PQ •OQ =4t , ∵4>0, ∴当t =4时,S 取得最大值,最大值为16;②当4<t ≤10时,设直线AD 的解析式为y =kx +b (k ≠0),将A (4,0),D (10,8)代入y =kx +b ,得:4k b 010k b 8+=⎧⎨+=⎩,解得:4k 316b 3⎧=⎪⎪⎨⎪=-⎪⎩, ∴直线AD 的解析式为41633y x =-. 当x =t 时,41633y t =-, 41648(10)333PQ t t ⎛⎫∴=--=- ⎪⎝⎭ 21220233S PQ OP t t ∴=⋅=-+ 22202502(5),033333S t t t =-+=--+-<Q ∴当t =5时,S 取得最大值,最大值为503. 综上所述:S 关于t 的函数关系式为S =24(04)220(410)33t t t t t ⎧⎪⎨-+<⎪⎩剟…,S 的最大值为503. (3)S 菱形ABCD =AB •OC =80.当0≤t ≤4时,4t =12,解得:t =3;当4<t ≤10时,222033t t -+=12, 解得:t 1=5﹣7(舍去),t 2=5+ 7. 综上所述:在直线l 移动过程中,存在t 值,使S =320ABCD S 菱形,t 的值为3或5+7.【点睛】考核知识点:一次函数和二次函数的最值问题.数形结合,分类讨论是关键.9.关于三角函数有如下的公式: sin (α+β)=sinαcosβ+cosαsinβ①cos (α+β)=cosαcosβ﹣sinαsinβ②tan (α+β)=③利用这些公式可将某些不是特殊角的三角函数转化为特殊角的三角函数来求值,如: tan105°=tan (45°+60°)==﹣(2+).根据上面的知识,你可以选择适当的公式解决下面的实际问题: 如图,直升飞机在一建筑物CD 上方A 点处测得建筑物顶端D 点的俯角α=60°,底端C 点的俯角β=75°,此时直升飞机与建筑物CD 的水平距离BC 为42m ,求建筑物CD 的高.【答案】建筑物CD 的高为84米.【解析】分析:如图,过点D作DE⊥AB于点E,由题意易得∠ACB=75°,∠ABC=90°,DE=BC=42m,∠ADE=60°,这样在Rt△ABC和在Rt△ADE中,结合题中所给关系式分别求出AB和AE的长,即可由CD=BE=AB-AE求得结果了.详解:如图,过点D作DE⊥AB于点E,由题意可得∠ACB=75°,∠ABC=90°,DE=BC=42m,CD=BE,∠ADE=60°,∴在Rt△ABC和Rt△ADEAB=BC•tan75°=42tan75°=,AE=,∴CD=AB﹣AE=(米).答:建筑物CD的高为84米.睛:读懂题意,把已知量和未知量转化到Rt△ABC和Rt△ADE中,这样利用直角三角形中边角间的关系结合题目中所给的“两角和的三角形函数公式”即可使问题得到解决.10.如图,正方形ABCD的边长为2+1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,(1)求证:△ABF∽△ACE;(2)求tan∠BAE的值;(3)在线段AC上找一点P,使得PE+PF最小,求出最小值.【答案】(1)证明见解析;(2)tan∠EAB2﹣1;(3)PE+PF的最小值为22【解析】【分析】(1)根据两角对应相等的两个三角形相似判断即可;(2)如图1中,作EH ⊥AC 于H .首先证明BE=EH=HC ,设BE=EH=HC=x ,构建方程求出x 即可解决问题;(3)如图2中,作点F 关于直线AC 的对称点H ,连接EH 交AC 于点P ,连接PF ,此时PF+PE 的值最小,最小值为线段EH 的长;【详解】(1)证明:∵四边形ABCD 是正方形,∴∠ACE =∠ABF =∠CAB =45°,∵AE 平分∠CAB ,∴∠EAC =∠BAF =22.5°,∴△ABF ∽△ACE .(2)解:如图1中,作EH ⊥AC 于H .∵EA 平分∠CAB ,EH ⊥AC ,EB ⊥AB ,∴BE =EB ,∵∠HCE =45°,∠CHE =90°,∴∠HCE =∠HEC =45°,∴HC =EH ,∴BE =EH =HC ,设BE =HE =HC =x ,则EC 2,∵BC 2+1,∴x+x 2+1,∴x =1,在Rt △ABE 中,∵∠ABE =90°,∴tan ∠EAB =221BE AB == 1. (3)如图2中,作点F 关于直线AC 的对称点H ,连接EH 交AC 于点P ,连接PF ,此时PF+PE 的值最小.作EM ⊥BD 于M .BM =EM =2, ∵AC =22AB BC +=2+2,∴OA =OC =OB =12AC =22+ , ∴OH =OF =OA•tan ∠OAF =OA•tan ∠EAB =22+ •(2﹣1)=2, ∴HM =OH+OM =222+, 在Rt △EHM 中,EH =2222222EM HM 22⎛⎫⎛⎫+++ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭= =22+.. ∴PE+PF 的最小值为22+..【点睛】 本题考查正方形的性质,相似三角形的判定,勾股定理,最短问题等知识,解题的关键是学会添加常用辅助线,学会利用轴对称解决最短问题,属于中考常考题型.11.如图,在航线l 的两侧分别有观测点A 和B ,点B 到航线l 的距离BD 为4km ,点A 位于点B 北偏西60°方向且与B 相距20km 处.现有一艘轮船从位于点A 南偏东74°方向的C 处,沿该航线自东向西航行至观测点A 的正南方向E 处.求这艘轮船的航行路程CE 的长度.(结果精确到0.1km )(参考数据:3≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)【答案】20.9km【解析】分析:根据题意,构造直角三角和相似三角形的数学模型,利用相似三角形的判定与性质和解直角三角形即可.详解:如图,在Rt △BDF 中,∵∠DBF=60°,BD=4km ,∴BF=cos 60BD o =8km , ∵AB=20km ,∴AF=12km , ∵∠AEB=∠BDF ,∠AFE=∠BFD ,∴△AEF ∽△BDF , ∴AE BD AF BF, ∴AE=6km , 在Rt △AEF 中,CE=AE•tan74°≈20.9km .故这艘轮船的航行路程CE 的长度是20.9km .点睛:本题考查相似三角形,掌握相似三角形的概念,会根据条件判断两个三角形相似.12.如图所示,小华在湖边看到湖中有一棵树AB ,AB 与水面AC 垂直.此时,小华的眼睛所在位置D 到湖面的距离DC 为4米.她测得树梢B 点的仰角为30°,测得树梢B 点在水中的倒影B′点的俯角45°.求树高AB (结果保留根号)【答案】AB=(3)m .【解析】【分析】设BE=x ,则BA=x+4,B′E=x+8,根据∠ADB′=45°,可知DE=B′E=x+8,再由tan30°=BE DE即可得出x 的值,进而得到答案,【详解】如图:过点D 作DE ⊥AB 于点E ,设BE=x ,则BA=x+4,B′E=x+8,∵∠ADB′=45°,∴DE=B′E=x+8,∵∠BDE=30°,∴tan30°=383BE x DE x ==+ ,解得x=4+43 , ∴AB=BE+4=(8+43 )m .【点睛】本题考查了解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解答此题的关键。
中考数学复习指导:《直角三角形的边角关系》专题专练及答案

《直角三角形的边角关系》专题专练专题一:锐角三角函数考点分析:在理解三角函数定义的基础上,理解并掌握三角函数有关的概念及性质; 典例剖析例1. 如图1,角α的顶点为O ,它的一边在x 轴的正半轴上,另一边OA 上有一点P (3,4),则 sin α= .分析:先用勾股定理求出第三边,再利用三角函数的定义求解 解:根据点P 的坐标利用勾股定理可以求得OP=2243+=5. 所以sin α=54=斜边的对边α. 点评:过已知点向坐标轴引垂线构造直角三角形,利用这点的坐标求出对应线段的长度,便可计算要求的锐角的三角函数值.例2.在Rt ABC △中,90C ∠=°,a b c ,,分别是A B C ∠∠∠,,的对边,若2b a =,则tan A = .分析:由于正切与两条直角边有关,故直接利用三角函数的定义求解 解:因为tan A =122a ab a == 点评:本题重点考查学生对正切定义的理解和运用情况,只要记住定义,就可以把边的比转化为正切了专练一:1、在△ABC 中,∠C=90°,则cosB 的值为( ) A.1D.122、若且α为锐角,则cos α等于( ) A.12B.23、在△ABC 中,若21sin tan 02A B ⎫-+-=⎪⎪⎝⎭,则∠C 的度数为( ) A.30° B.60° C.90° D.120°图14、把Rt △ABC 的三边都扩大十倍,关于锐角A 的正弦值:甲同学说扩大十倍;乙同学说不变;丙同学说缩小十倍.那么你认为正确的说法应是A.甲B.乙C.丙D.都不正确5、(1)已知tan α则锐角α的度数为_____; (2)若cos 0α,则锐角α的度数为_____. 6、在Rt △ABC 中,∠C =900,AC =12,BC =15。
(1)求AB 的长; (2)求sinA 、cosA 的值; (3)求A A 22cos sin +的值; (4)比较sinA 、cosB 的大小。
《直角三角形的边角关系》复习课件

(1)2 3 2 0 2sin 30 3
2
题型2 解直角三角形
1∠.如AD图E4=,a,在且矩c形osAαB=CD3 中,DE⊥A B )
A.3
B.16
3
C. 20 3
D.16 5
2.2002年8月在北京召开的国际数学家大会会标
如图5所示,它是由四个相同的直角三角形与中
间的小正方形拼成的一个大正方形. 若大正方形
的面积是13,小正方形的面积是1,直角三角形 的较长直角边为a,较短直角边为b,
则a+b的值为( B )
A.35 B.43 C.89 D.97
题型3 解斜三角形
1.如图所示,已知:在△ABC中,∠A=60°, ∠B=45°,AB=8, 求△ABC的面积(结果可保留根 号).
AC=12,则cosA等于( D )
A. 2 , B. 5 , C.12 , D.12 12 13 5 13
4. 如图,在Rt△ABC中,∠ACB =90°, CD⊥AB于点D,已知AC= 5 ,
BC=2,那么sin∠ABC=( A )
A. 5
B. 2
C. 2 5
D. 5
3
3
5
2
5.计算:
.
|- 2 |+(cos60°-tan30°)+ 8
3.已知∠A,b. 解直角三角形
4. 已知∠A,c. 解直角三角形
【热点试题归类】
题型1 三角函数 1. 在Rt△ABC中,∠C=90°,AB=5,AC=4, 则sinA的值为_______. 2. 在Rt△ABC中,∠C =90°,BC=4,AC=3, 则cosA的值为______. 3. 如图,在△ABC中,∠C =90°,BC=5,
直角三角形边角关系知识点

直角三角形边角关系专题复习一. 知识体系:1. 三种三角函数与直角三角形中边与角的关系,在Rt△中在此应注意的问题是无论是求哪一个角的三角函数,一定要先把这个角放在直角三角形中 2. 特殊角的三角函数值3. 三角函数的有关计算(对于一般角的三角函数值可利用计算器)41 2 3 4.三角函数的应用()测山的高度()测楼的高度()测塔的高度()其它⎧⎨⎪⎪⎩⎪⎪题型一:三角形内的计算问题(计算三角函数值、面积等) 例1.在ABC Rt ∆中,∠C=90° ,且21sin =A ,AB=3,求BC ,AC 及B ∠.例2.已知,四边形ABCD 中,∠ABC = ∠ADB =090,AB = 5,AD = 3,BC = 32,求四边形ABCD 的面积。
例3.如图,在Rt ABC ∆中,90BCA ∠=︒,CD 是中线,5,4BC CD ==,求AC 的长。
B变式训练:1、ABC Rt ∆中,∠C=90°,AC=4,BC=3,B cos 的值为…………………【 】 A 、51 B 、53 C 、 34 D 、 432、在菱形ABCD 中,∠ABC=60° , AC=4,则BD 的长是…………………【 】 A 、 38 B 、34 C 、32 D 、83、在ABC Rt ∆中,∠C=90° ,A tan =3,AC=10,则S △ABC 等于………【 】 A 、 3 B 、300 C 、350D 、150 4、在Rt △ABC 中,如果各边长度都扩大为原来的2倍,那么锐角A 的正弦值( ) A.扩大2倍 B.缩小2倍 C.扩大4倍 D.没有变化5、在ABC Rt ∆中,∠C=90°,∠A 、∠B 、∠C 的对边分别为a 、b 、c 三边,则下列式子一定成立的是………………………………………………………………【 】 A 、B c a sin ⋅= B 、B c a cos ⋅= C 、Bac tan =D 、A a c sin ⋅= 6、等腰三角形的腰长为10cm ,顶角为120,此三角形面积为 。
中考数学专题复习:直角三角形的边角关系
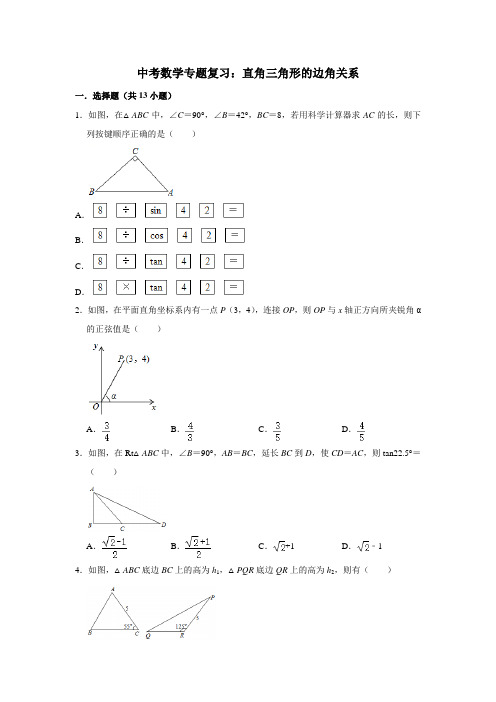
中考数学专题复习:直角三角形的边角关系一.选择题(共13小题)1.如图,在△ABC中,∠C=90°,∠B=42°,BC=8,若用科学计算器求AC的长,则下列按键顺序正确的是()A.B.C.D.2.如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是()A.B.C.D.3.如图,在Rt△ABC中,∠B=90°,AB=BC,延长BC到D,使CD=AC,则tan22.5°=()A.B.C.+1 D.﹣14.如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有()A.h1=h2B.h1<h2C.h1>h2D.以上都有可能5.如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD 的值是()A.B.2 C.D.6.如图是某一段索道的示意图.已知A、B两点间的距离为30米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为()A.30sinα米B.米C.30cosα米D.米7.如图所示为该地区某滑雪场的一段赛道示意图,AB段为助滑段,长为12米,坡角α为16°,一个曲面平台BCD连接了助滑坡AB与着陆坡DE.已知着陆坡DE的坡度为i=1:2.4,DE长度为19.5米,B,D之间的垂直距离为5.5米,则一人从A出发到E处下降的垂直距离约为(参考数据sin16°≈0.28,cos16°≈0.96,tan16°≈0.29,结果保留一位小数)()A.15.9米B.16.0米C.16.4米D.24.5米8.小宇和小轲两位同学准备利用所学数学知识对某亭的高度进行测量.他们在临时搭建的一个坡度为12:5的钢板斜坡上的F点测得亭顶A点的仰角为13°,F点到地面的垂直高度FG=1.8米,从钢板斜坡底的E点向前走16.2米到D点,测得亭前阶梯CD的长度为2.5米,坡度为3:4.C点到亭中心O点的距离为1米.根据测量结果,该亭的高度AO大约为()米.(参考数据:sin13°≈0.22,cos13°≈0.97,tan13°≈0.23,A,B,C,D,E,F,G各点均在同一平面内)A.4.9 B.4.6 C.6.4 D.6.19.如图,某栋教学楼AB顶部竖有一块宣传牌BC,某同学从建筑物底端A点出发,沿水平方向向右走12米到达D点,在D处测得宣传牌底部B点的仰角是54°,再经过一段坡比为1:2.4,坡长为6.5米的斜坡DE到达E点(A,B,C,D,E均在同一平面内).在E 处测得宣传牌的顶部C点的仰角是45°,则宣传牌BC的高度为()(参考数据:sin54°≈0.80,cos54°≈0.59,tan54°≈1.38,结果精确到0.1米)A.1.4米B.3.9米C.4.0米D.16.6米10.如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即EF=15米,在点E处看点D的仰角为64°,则CD的长用三角函数表示为()A.15sin32°B.15tan64°C.15sin64°D.15tan32°11.如图,测量人员计划测量山坡上一信号塔的高度,测量人员在山脚点C处,测得塔顶A 的仰角为45°,测量人员沿着坡度i=1:的山坡BC向上行走100米到达点E处,再测得塔顶A的仰角为53°,则山坡的高度BD约为()(精确到0.1米,参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈,≈1.73,≈1.41)A.100.5米B.110.5米C.113.5米D.116.5米12.如图,为了测量某建筑物BC的高度,某数学兴趣小组采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,先沿斜坡AD行走390米至坡顶D处,再从D处沿水平方向继续前行一定距离后至点E处,在E点处测得该建筑物顶端C的仰角为68°,建筑物底端B的俯角为57°,其中A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4,根据数学兴趣小组的测量数据,计算得出建筑物BC的高度约为()(计算结果精确到0.1米,参考数据:sin68°≈0.93,tan68°≈2.48,sin57°≈0.84,tan57°≈1.54)A.241.6米B.391.6米C.422.9米D.572.9米13.如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=25米,则此时AB的长约为()(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)A.10.4米B.12.4米C.27.4米D.22.4米二.填空题(共7小题)14.如图,△ABC的顶点都在正方形网格的格点上,则sin∠ACB的值为________.15.如图,△ABC的顶点B、C的坐标分别是(1,0)、(0,),且∠ABC=90°,∠A=30°,则顶点A的坐标是________.16.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为点D,线段AE与线段CD相交于点F,且AE=AB,连接DE,∠E=∠C,若AD=3DE,则cos E的值为________.17.某型号的机翼形状如图所示,根据图中的数据,可求AB的长度为________m.(≈1.732,结果保留两位小数)18.如图,从楼顶A处看楼下荷塘C处的俯角为45°,看楼下荷塘D处的俯角为60°,已知楼高AB为30米,则荷塘的宽CD为________米(结果保留根号).19.如图,从飞机A看一栋楼顶部B的仰角为30°,看这栋楼底部的俯角为60°,飞机A与楼的水平距离为240m,这栋楼的高度BC是________m(≈1.732,结果取整数).20.如图,测高仪CD距建筑物AB底部5m,DC⊥BC,AB⊥BC,在测高仪D处观测建筑物顶端的仰角为50°,测高仪高度为1.5m,则建筑物AB的高度为________m.(精确到0.1m,sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)三.解答题(共4小题)21.如图,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.(1)若AE=1,求△ABD的周长;(2)若AD=BD,求tan∠ABC的值.22.如图,一架无人机在空中A处观测到山顶B的仰角为36.87°,山顶B在水中的倒影C 的俯角为63.44°,此时无人机距水面的距离AD=50米,求点B到水面距离BM的高度.(参考数据:sin36.87°≈0.60,cos36.87°≈0.80,tan36.87°≈0.75,sin63.44°≈0.89,cos63.44°≈0.45,tan63.44°≈2.00)23.如图,一段河流自西向东,河岸笔直,且两岸平行.为测量其宽度,小明在南岸边B 处测得对岸边A处一棵大树位于北偏东60°方向,他以1.5m/s的速度沿着河岸向东步行40s后到达C处,此时测得大树位于北偏东45°方向,试计算此段河面的宽度(结果取整数,参考数据:≈1.732)24.如图,斜坡AB的坡角∠BAC=13°,计划在该坡面上安装两排平行的光伏板.前排光伏板的一端位于点A,过其另一端D安装支架DE,DE所在的直线垂直于水平线AC,垂足为点F,E为DF与AB的交点.已知AD=100cm,前排光伏板的坡角∠DAC=28°.(1)求AE的长(结果取整数);(2)冬至日正午,经过点D的太阳光线与AC所成的角∠DGA=32°,后排光伏板的前端H在AB上.此时,若要后排光伏板的采光不受前排光伏板的影响,则EH的最小值为多少(结果取整数)?参考数据:≈1.41,≈1.73,≈2.45.13°28°32°锐角A三角函数sin A0.22 0.47 0.53cos A0.97 0.88 0.850.62tan A0.23 0.53参考答案1.解:在△ABC中,因为∠C=90°,所以tan∠B=,因为∠B=42°,BC=8,所以AC=BC•tan B=8×tan42°.故选:D.2.解:作P A⊥x轴于A,如右图.∵P(3,4),∴OA=3,AP=4,∴OP==5,∴sinα=.故选:D.3.解:在Rt△ABC中,∠B=90°,AB=BC,∴∠ACB=45°,∵CD=AC,∴∠D=22.5°,设AB=BC=x,在Rt△ABC中,由勾股定理得,AC==x,∴AC=CD=x,∴BD=BC+CD=(+1)x,∴tan D=tan22.5°===﹣1,故选:D.4.解:如图,分别作出△ABC底边BC上的高为AD即h1,△PQR底边QR上的高为PE 即h2,在Rt△ADC中,h1=AD=5×sin55°,在Rt△PER中,h2=PE=5×sin55°,∴h1=h2,故选:A.5.解:如图:作OF⊥AB于F,∵AB=AC,AD平分∠BAC.∴∠ODB=90°.BD=CD=6.∴根据勾股定理得:AD==8.∵BE平分∠ABC.∴OF=OD,BF=BD=6,AF=10﹣6=4.设OD=OF=x,则AO=8﹣x,在Rt△AOF中,根据勾股定理得:(8﹣x)2=x2+42.∴x=3.∴OD=3.在Rt△OBD中,tan∠OBD===.故选:A.6.解:由图可知,在△ABC中,AC⊥BC,∴sinα==,∴BC=30sinα米.故选:A.7.解:作BF⊥AP于F,DG⊥AP于G,DH⊥PE于H,在Rt△AFB中,sinα=,AB=12米,∴AF=AB•sinα≈12×0.28=3.36,设DH=x米,∵DE的坡度为i=1:2.4,∴HE=2.4x,由勾股定理得,(2.4x)2+x2=19.52,解得,x=7.5,∴一人从A出发到E处下降的垂直距离=3.36+5.5+7.5≈16.4(米),故选:C.8.解:由题意可知,∠AFM=13°,CD=2.5.CD的坡比是3:4,EF的坡比是12:5,FG =1.8,DE=16.2,MF∥NG,ON⊥NG,CH⊥NG,FG⊥NG,OC=NH=1(米),∴四边形MNGF是矩形,∴FM=NG,在Rt△CDH中,设CH=3x,DH=4x,∴CD=2.5,∴(3x)2+(4x)2=2.52,∴x=0.5,∴DH=2(米),CH=1.5(米),在Rt△EFG中,,FG=1.8,∴,∴EG=0.75(米),∴FM=GN=EG+DE+DH+NH=19.95(米),在Rt△AMF中,tan∠AFM==tan13°,∴AM≈19.95×0.23=4.5885(米),∴AO=AM+MO=AM+(FG﹣CH)≈4.9(米),故选:A.9.解:(1)过E作EF⊥AD,交AD的延长线于F,作EG⊥AB于G.∴则四边形EF AG是矩形,∴AG=EF,AF=EG,Rt△DEF中,i=tan∠EDF=1:2.4,∵DE=6.5米,∴EF=2.5米,DF=6米,∵AD=12米,∴AF=EG=AD+DF=18米,在Rt△CEG中,∠CEG=45°,∴CG=EG=18米,Rt△ABD中,∠ADB=54°,AD=12米,∴AB=AD•tan54°≈12×1.38=16.56(米),∴BC=CG+GA﹣AB=18+2.5﹣16.56=3.94(米)≈3.9米,即宣传牌BC的高度为3.9米.故选:B.10.解:∵∠CED=64°,∠F=32°,∠CED=∠F+∠EDF,∴∠EDF=∠CED﹣∠F=64°﹣32°=32°,∴∠EDF=∠F,∴DE=EF,∵EF=15米,∴DE=15米,在Rt△CDE中,∵sin∠CED=,∴CD=DE sin∠CED=15sin64°,故选:C.11.解:如图作EF⊥AD于F,EH⊥CD于H.在Rt△ADC中,∠ACD=45°,∴AD=CD,在Rt△CEH中,EC=100米,EH:CH=1:,∴EH=50米,CH=50米,∵四边形EFDH是矩形,∴EF=DH,EH=DF=50米,设BF=x,则EF=x,∴CD=AD=50+x,BD=x+50,AF=50+x﹣50,在Rt△AEF中,tan53°=,∴≈,∴x=150﹣50≈63.5(米),∴BD=BF+DF=63.5+50≈113.5(米).故选:C.12.解:如图作DH⊥AB于H,延长DE交BC于F.在Rt△ADH中,AD=390米,DH:AH=1:2.4,∴DH=150(米),∵四边形DHBF是矩形,∴BF=DH=150米,在Rt△EFB中,tan57°=,∴EF=,在Rt△EFC中,FC=EF•tan68°,∴CF≈×2.48≈241.6(米),∴BC=BF+CF=391.6米.故选:B.13.解:如图,延长DE交AB延长线于点P,作CQ⊥AP于点Q,∵CE∥AP,∴DP⊥AP,∴四边形CEPQ为矩形,∴CE=PQ=2(米),CQ=PE,∵i===,∴设CQ=4x、BQ=3x,由BQ2+CQ2=BC2可得(4x)2+(3x)2=252,解得:x=5或x=﹣5(舍),则CQ=PE=20(米),BQ=15(米),∴DP=DE+PE=23(米),在Rt△ADP中,∵AP==≈27.4(米),∴AB=AP﹣BQ﹣PQ=27.4﹣15﹣2=10.4(米)故选:C.14.解:作如图所示的辅助线,则BD⊥AC,∵BC=,BD=,∴sin∠ACB=,故答案为.15.解:过点A作AG⊥x轴,交x轴于点G.∵B、C的坐标分别是(1,0)、(0,),∴OC=,OB=1,∴BC==2.∵∠ABC=90°,∠BAC=30°,∴AB====2.∵∠ABG+∠CBO=90°,∠BCO+∠CBO=90°,∴∠ABG=∠BCO.∴sin∠ABG===,cos∠ABG===,∴AG=,BG=3.∴OG=1+3=4,∴顶点A的坐标是(4,).故答案为:(4,).16.解:在AD上取一点G,使AG=DE,连接BG,如图所示:∵AD=3DE,∴DG=2AG,∵∠BAC=90°,AD⊥BC,∴∠ABC+∠C=∠ABC+∠BAG=90°,∴∠C=∠BAG,∵∠C=∠E,∴∠BAG=∠E,在△ABG和△EAD中,,∴△ABG≌△EAD(SAS),∴BG=AD=3DE=3AG,∴BD=,∴AB==AG,∴cos E=cos∠BAD=;故答案为:.17.解:如图,延长BA交过点C的水平线于点E,作DF⊥BE于点F,在Rt△CEA中,∠ACE=45°,∴AE=CE=5(m),在Rt△BDF中,∠BDF=30°,∵cos∠BDF=,∴DB==10(m),∴BF=BD=5(m),∵AB+AE=EF+BF,∴AB=5.40+5﹣5≈1.74(m).故答案为:1.74.18.解:由题意可得,∠ADB=60°,∠ACB=45°,AB=30m,在Rt△ABC中,∵∠ACB=45°,∴AB=BC,在Rt△ABD中,∵∠ADB=60°,∴BD=AB=10(m),∴CD=BC﹣BD=(30﹣10)m,故答案为:(30﹣10).19.解:过点A作AD⊥BC,垂足为D,根据题意有∠DAC=60°,∠BAD=30°,AD=240m,在Rt△ADC中,∵∠DAC=60°,AD=240m,∴DC=tan60°•AD=240(m),在Rt△ADB中,∵∠DAB=30°,AD=240m,∴DB=tan30°•AD=80(m),∴BC=240+80=320≈554(m),故答案为:554.20.解:如图,过点D作DE⊥AB,垂足为点E,∵∠DCB=∠CBE=∠DEB=90°,∴四边形BEDC是矩形,∴DE=BC=5m,DC=BE=1.5m,在Rt△ADE中,∵tan∠ADE=,∴AE=DE•tan∠ADE=5tan50°≈5×1.19=5.95(m),∴AB=AE+BE=5.95+1.5≈7.5(m),答:建筑物AB的高度约为7.5m,21.解:(1)如图,连接BD,设BC垂直平分线交BC于点F,∴BD=CD,C△ABD=AB+AD+BD=AB+AD+DC=AB+AC,∵AB=CE,∴C△ABD=AC+CE=AE=1,故△ABD的周长为1.(2)设AD=x,∴BD=3x,又∵BD=CD,∴AC=AD+CD=4x,在Rt△ABD中,AB===2.∴tan∠ABC===.22.解:过点A作AH⊥BM交于点H,由题意可得:AD=HM=50米,设BM=x米,则MC=BM=x米∵BH=BM﹣HM∴BH=(x﹣50)米,∴在Rt△ABH中,∵HC=HM+MC∴HC=(50+x)米,在Rt△AHC中,,∴,解得x=110,即BM=110米,答:点B到水面距离BM的高度约为110米.23.解:如图,作AD⊥BC于D.由题意可知:BC=1.5×40=60(m),∠ABD=90°﹣60°=30°,∠ACD=90°﹣45°=45°,在Rt△ACD中,∵tan∠ACD=tan45°==1,∴AD=CD,在Rt△ABD中,∵tan∠ABD=tan30°=,∴BD=,∵BC=BD﹣CD=﹣AD=60(m),∴AD=30(+1)≈82(m),答:此段河面的宽度约82m.24.解:(1)在Rt△ADF中,cos∠DAF=,∴AF=AD•cos∠DAF=100×cos28°=100×0.88=88(cm),在Rt△AEF中,cos∠EAF=,∴AE===≈91(cm);(2)设DG交AB于M,过点A作AN⊥DG于N,如图所示:∴∠AMN=∠MAG+∠DGA=13°+32°=45°,在Rt△ADF中,DF=AD•sin∠DAC=100×sin28°=100×0.47=47(cm),在Rt△DFG中,tan∠DGA=,∴tan32°=,∴FG==≈75.8(cm),∴AG=AF+FG=88+75.8=163.8(cm),在Rt△AGN中,AN=AG•sin∠DGA=163.8×sin32°=163.8×0.53≈86.8(cm),∵∠AMN=45°,∴△AMN为等腰直角三角形,∴AM=AN≈1.41×86.8≈122.4(cm),∴EM=AM﹣AE≈122.4﹣91≈31(cm),当M、H重合时,EH的值最小,∴EH的最小值约为31cm.。
直角三角形的边角关系专题复习

直角三角形的边角关系测试题1、在Rt △ABC 中,∠A=90º,AB=6,AC=8,则sinB= ,cosC=2、在△ABC 中,∠B=90º,21cos =C ,则∠C=3、在△ABC 中,∠C=90º,∠A=60º,AC=34,则BC=4、在△ABC 中,∠C=90º,BC=3,AB=32,则∠A=5、在△ABC 中,∠C=90º,若tanA=21,则sinA= 6、在△ABC 中,若∠C=90º,∠A=45º,则tanA+sinB=7、如图1,在△ABC 中,∠C=90º,∠B=30º,AD 是∠BAC 的平分线。
已知AB=34, 那么AD= 8、正方形ABCD 中,AM 平分∠BAC 交BC 于M ,AB=2,BM=1,则cos ∠MAC= 9、如果3)20tan(3=︒+α,那么锐角α=10、某校数学课外活动小组的同学测量英雄纪念碑的高,如图2所示,测得的数据为: BC=42m ,倾斜角º︒=30α,测得测角仪高CD=1.5m ,则AB= 。
(结果保留四位 有效数字)11、在△ABC 中,∠C=90º,BC=5,AC=12,则tanA=( ) A 、512 B 、125 C 、513 D 、135 12、在Rt △ABC 中,∠C=90º,53cos =A ,AC=6cm ,则BC=( )cm A 、8B 、4.8C 、3.6D 、1.2 13、菱形ABCD 的对角线AC=10cm ,BD=6cm ,那么=2tan A ( ) A 、53 B 、54C 、34343 D 、3434514、已知:如图3,梯形ABCD 中,AD//BC ,∠B=45º,∠C=120º,AB=8,则CD 的长为( ) A 、638 B 、64 C 、238D 、24 15、在平面直角坐标系内P 点的坐标为(cos30º,tan45º),则P 点关于y 轴对称点A 的坐标为( ) A 、(23,1) B 、(—1,23) C 、(1,23-) D 、(1,23--) 16、若等腰三角形的腰长为10cm ,顶角为60º,则等腰三角形的面积为( )cm 2A 、25B 、325C 、350D 、5017、如图4,某游乐场一山顶滑梯的高为h ,滑梯的坡角为a ,那么滑梯长l 为 A .h sin a B . h tan a C . hcos aD . h ·sin a 18、在△ABC 中,∠A 、∠B 均为锐角,且0)3sin 2(3tan 2=-+-A B ,则△ABC 是( ) A 、等腰三角形 B 、等边三角形 C 、直角三角形 D 、等腰直角三角形19、河堤横断面如图5所示,堤高BC =5米,迎水坡AB 的坡比1:3(坡比是坡面的铅直高度BC 与水平宽度AC 之比),则AC 的长是( ) A .53米 B .10米 C .15米 D .103米 20、计算:(1)、︒+︒+︒-︒45tan 30cos 230tan 330sin (2)、︒-︒+︒-︒-︒60tan 45tan 30sin 160cos 45cos 222图2a CA E BD ACD B 图1 BC DA图3图4图521、在△ABC 中,AB=AC ,且AB=2BC ,求∠B 的三个三 22、在△ABC 中,AB=4,∠B=30º,∠C=45º,求△ABC 角函数值。
(完整)直角三角形的边角关系全章总结复习,推荐文档

2017—2018学年寒假辅导第1讲直角萨娇新的边角关系一、知识清单梳理知识点一:锐角三角函数的定义关键点拨与对应举例1.锐角三角函数正弦: sin A=∠A的对边斜边=ac余弦: cos A=∠A的邻边斜边=bc正切: tan A=∠A的对边∠A的邻边=ab.根据定义求三角函数值时,一定根据题目图形来理解,严格按照三角函数的定义求解,有时需要通过辅助线来构造直角三角形.2.特殊角的三角函数值度数三角函数30°45°60°sinA 122232cosA 322212tanA 331 3知识点二:解直角三角形3.解直角三角形的概念在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形.科学选择解直角三角形的方法口诀:已知斜边求直边,正弦、余弦很方便;已知直边求直边,理所当然用正切;已知两边求一边,勾股定理最方便;已知两边求一角,函数关系要记牢;已知锐角求锐角,互余关系不能少;已知直边求斜边,用除还需正余弦.例:在Rt△ABC中,已知a=5,∠A=30°,则c=,b=.4.解直角三角形的常用关系(1)三边之间的关系:a2+b2=c2;(2)锐角之间的关系:∠A+∠B=90°;(3)边角之间的关系:sinA==cosB=ac,cosA=sinB=bc,tanA=ab.(4)相等的角①商的关系:tanA= ;②平方关系:sin2A+cos2A=1.(5)互余的两角:若∠A+∠B=90°,则sinA=cosB, cosA=sinB.知识点三:解直角三角形的应用5.仰角、俯角、坡度、坡角和方向角(1)仰、俯角:视线在水平线上方的角叫做仰角.视线在水平线下方的角叫做俯角.(如图①)(2)坡度:坡面的铅直高度和水平宽度的比叫做坡度(或者叫做坡比),用字母i表示.坡角:坡面与水平面的夹角叫做坡角,用α表示,则有i=tanα. (如图②)(3)方向角:平面上,通过观察点Ο作一条水平线(向右为东向)和一条铅垂线(向上为北向),则从点O出发的视线与水平线或铅垂线所夹的角,叫做观测的方向角.(如图③)解直角三角形中“双直角三角形”的基本模型:(1)叠合式(2)背靠式解题方法:这两种模型种都有一条公共的直角边,解题时,往往通过这条边为中介在两个三角形中依次求边,或通过公共边相等,列方程求解.6.解直角三角形实际应用的一般步骤(1)弄清题中名词、术语,根据题意画出图形,建立数学模型;(2)将条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形问题;(3)选择合适的边角关系式,使运算简便、准确;(4)得出数学问题的答案并检验答案是否符合实际意义,从而得到问题的解.二、 专题讲座专题一:锐角三角函数的概念注意:1.sinA 、∠cosA 、tanA 表示的是一个整体,是两条线段的比,没有 ,这些比值只与 有关,与直角三角形的 无关2.取值范围 <sinA< ; < cosA< ; tanA> 例1.如图所示,在Rt △ABC 中,∠C =90°.①斜边)(sin =A =______, 斜边)(sin =B =______;②斜边)(cos =A =______, 斜边)(cos =B =______;③的邻边A A ∠=)(tan =______,)(tan 的对边B B ∠==______.例2. 锐角三角函数求值:在Rt △ABC 中,∠C =90°,若a =9,b =12,则c =______,sin A =__ ___,cos A =___ ___,tan A =____ __, sin B =___ ___,cos B =_____ _,tan B =___ ___.例3.已知:如图,Rt △TNM 中,∠TMN =90°,MR ⊥TN 于R 点,TN =4,MN =3.求:sin ∠TMR 、cos ∠TMR 、tan ∠TMR .类型一:直角三角形求值例4.已知Rt △ABC 中,,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cos B .例5.已知A ∠是锐角,178sin =A ,求A cos ,A tan 的值类型二. 利用角度转化求值:例6.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点.DE ∶AE =1∶2. 求:sinB 、cosB 、tanB .例7.如图,角α的顶点为O ,它的一边在x 轴的正半轴上,另一边OA 上有一点P (3,4),则 sin α= .A D ECBF例7图 例8图 例9图 例13图例8.如图,菱形ABCD 的边长为10cm ,DE ⊥AB ,3sin 5A =,则这个菱形的面积= cm 2. 例9.如图,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边的点F 处.已知8AB =,10BC =,AB=8,则tan EFC ∠的值为 ( ) A.34 B.43 C.35 D.45类型三. 化斜三角形为直角三角形例10.如图,在△ABC 中,∠A=30°,∠B=45°,AC=23,求AB 的长.例11.已知:如图,△ABC 中,AC =12cm ,AB =16cm ,⋅=31sin A (1)求AB 边上的高CD ;(2)求△ABC 的面积S ;(3)求tan B .例12.已知:如图,在△ABC 中,∠BAC =120°,AB =10,AC =5.求:sin ∠ABC 的值.类型四:利用网格构造直角三角形例13如图所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为( ) A .12 B .55 C .1010D .255对应训练:1.在Rt △ABC 中,∠ C =90°,若BC =1,AB =5,则tan A 的值为( )A .55 B .255 C .12D .2 2.在△ABC 中,∠C =90°,sin A=53,那么tan A 的值等于( ) A .35 B. 45 C. 34 D. 433. 如图,在等腰直角三角形ABC ∆中,90C ∠=︒,6AC =,D 为AC 上一点,若1tan 5DBA ∠= ,则AD 的长为( ) A .2 B .2 C .1 D .224. 如图,在Rt △ABC 中,∠C =90°,AC =8,∠A 的平分线AD =3316;求∠B 的度数及边BC 、AB 的长.DABC5.如图,在Rt △ABC 中,∠BAC=90°,点D 在BC 边上,且△ABD 是等边三角形.若AB=2,求△ABC 的周长.(结果保留根号)6.已知:如图,△ABC 中,AB =9,BC =6,△ABC 的面积等于9,求sin B .7. 在△ABC 中,∠A=60°,AB=6 cm ,AC=4 cm ,则△ABC 的面积是 ( )A.23 cm 2B.43 cm 2C.63 cm 2D.12 cm 28.如图,△ABC 的顶点都在方格纸的格点上,则sin A =_______.9.如图,A 、B 、C 三点在正方形网络线的交点处,若将ABC ∆绕着点A 逆时针旋转得到''B AC ∆,则'tan B 的值为( ) A.41 B. 31 C.21D. 110.正方形网格中,AOB ∠如图放置,则tan AOB ∠的值是( )A .5 5 B. 2 5 5 C.12D. 2CB A ABO专题二:特殊角的三角函数值当 时,正弦和正切值随着角度的增大而 余弦值随着角度的增大而例1.求下列各式的值.(1)︒-︒+︒60tan 45sin 230cos 2 (2)︒-︒+︒30cos 245sin 60tan 2(3)3-1+(2π-1)0-33tan30°-tan45°(4)30tan 2345sin 60cos 221⎪⎪⎭⎫ ⎝⎛︒-︒+︒+ (5) tan 45sin 301cos 60︒+︒-︒;例2.求适合下列条件的锐角α . (1)21cos =α (2)33tan =α (3)222sin =α(4)33)16cos(6=- α (5)已知α 为锐角,且3)30tan(0=+α,求αtan 的值(6)在ABC ∆中,若0)22(sin 21cos 2=-+-B A ,B A ∠∠,都是锐角,求C ∠的度数.例3. 三角函数的增减性 1.已知∠A 为锐角,且sin A <21,那么∠A 的取值范围是( ) A. 0°< ∠A < 30° B. 30°< ∠A <60° C. 60°< ∠A < 90° D. 30°< ∠A < 90° 2. 已知∠A 为锐角,且030sin cos <A ,则 ( )A. 0°<∠ A < 60°B. 30°<∠ A < 60°C. 60°< ∠A < 90°D. 30°<∠ A < 90°例4. (三角函数在几何中的应用)已知:如图,在菱形ABCD 中,DE ⊥AB 于E ,BE =16cm ,⋅=1312sin A 求此菱形的周长.对应练习:1.计算:10123tan 45(2 1.41)3-⎛⎫--++- ⎪⎝⎭2.计算:1201314.330sin 21)()(-++---π3.计算:212322cos602°. 4计算:(2014-5)0-(cos60°)-2+38-3tan30°;5.计算:6.计算:|1﹣|﹣()﹣1﹣4cos30°+(π﹣3.14)0.7.已知α是锐角,且sin(α+15°)=32. 计算10184cos ( 3.14)tan 3απα-⎛⎫---++ ⎪⎝⎭的值.8.已知:如图,Rt △ABC 中,∠C =90°,3==BC AC ,作∠DAC =30°,AD 交CB 于D 点,求: (1)∠BAD ; (2)sin ∠BAD 、cos ∠BAD 和tan ∠BAD .9. 已知:如图△ABC 中,D 为BC 中点,且∠BAD =90°,31tan =∠B ,求:sin ∠CAD 、cos ∠CAD 、tan ∠CAD .10. 如图,在Rt △ABC 中,∠C=90°,53sin =B ,点D 在BC 边上,DC= AC = 6,求tan ∠BAD 的值.11.(本小题5分)如图,△ABC 中,∠A=30°,3tan 2B =,43AC =.求AB 的长.DCBAACB专题三:解直角三角形的应用例1.(2012•福州)如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是()例1图例2图A.200米B.200米C.220米D.100()米例2.如图,某水库堤坝横断面迎水坡AB的坡比是1:3,堤坝高BC=50m,则应水坡面AB的长度是()A.100m B.1003m C.150m D.503m例3. “兰州中山桥”位于兰州滨河路中段白搭山下、金城关前,是黄河上第一座真正意义上的桥梁,有“天下黄河第一桥”之美誉。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直角三角形的边角关系测试题
1、在Rt △ABC 中,∠A=90º,AB=6,AC=8,则sinB= ,cosC=
2、在△ABC 中,∠B=90º,2
1
cos =C ,则∠C=
】
3、在△ABC 中,∠C=90º,∠A=60º,AC=34,则BC=
4、在△ABC 中,∠C=90º,BC=3,AB=32,则∠A=
5、在△ABC 中,∠C=90º,若tanA=
2
1
,则sinA= 6、在△ABC 中,若∠C=90º,∠A=45º,则tanA+sinB=
7、如图1,在△ABC 中,∠C=90º,∠B=30º,AD 是∠BAC 的平分线。
已知AB=34,
那么AD=
#
8、正方形ABCD 中,AM 平分∠BAC 交BC 于M ,AB=2,BM=1,则cos ∠MAC= 9、如果3)20tan(3=︒+α,那么锐角α=
10、某校数学课外活动小组的同学测量英雄纪念碑的高,如图2所示,测得的数据为: BC=42m ,倾斜角º︒=30α,测得测角仪高CD=1.5m ,则AB= 。
(结果保留四位 有效数字)
11、在△ABC 中,∠C=90º,BC=5,AC=12,则tanA=( ) A 、512 B 、125 C 、513 D 、13
5 12、在Rt △ABC 中,∠C=90º,5
3
cos =
A ,AC=6cm ,则BC=( )cm A 、8
B 、
C 、
D 、 !
13、菱形ABCD 的对角线AC=10cm ,BD=6cm ,那么=2tan
A ( ) A 、53
B 、54
C 、34
343 D 、34345
14、已知:如图3,梯形ABCD 中,AD
63864238242
3
23
1,23-1,2
3
--3253500
)3sin 2(3tan 2=-+-A B 5
米
353103︒+︒+︒-︒45tan 30cos 230tan 330sin ︒-︒+︒
-︒
-
︒60tan 45tan 30sin 160cos 45cos 2226—1为平地
上一幢建筑物与铁塔图,题6-2图为其示意图.建筑物AB 与铁塔CD 都垂直于底面,BD=30m ,在A 点测得D 点的俯角为45°,测得C 点的仰角为60°.求铁塔CD 的高度.
…
图6-1 图6-2
图2
a C
A
E B
)
图1 B
C
D
A
图3
图4 图5
24、如图,小明家在A 处,门前有一口池塘,隔着池塘有一条公路l ,AB 是A 到l 的小路。
现新修一条路AC 到公路l .小 明测量出∠ACD =30°,∠ABD =45°,BC =50m .请你帮小明计算他家到公路l 的距离AD 的长度(精确到0.1m ;参考数据:
2 1.414,
3 1.732≈≈)
—
25、如图,某船向正东方向航行,在A 处望见某岛C 在北偏东60º方向,前进6海里到B 点,测得该岛在北偏东30º方向,已知该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁危险试说明理由。
]
、
26、综合实践课上,小明所在小组要测量护城河的宽度。
如图所示是护城河的一段,两岸ABCD ,河岸AB 上有一排大 树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD 的M 处测得∠α=36°,然后沿河岸走50米到达N 点,测得∠β=72°。
请你根据这些数据帮小明他们算出河宽FR (结果保留两位有效数字). (参考数据:sin 36°≈,cos 36°≈,tan36°≈,sin 72°≈,cos 72°≈,tan72°≈)
A
B C
北 东
A
B
)
E
F
α
β。
