四川省新津县高二数学12月月考试题
四川省新津中学高二数学12月月考试题文
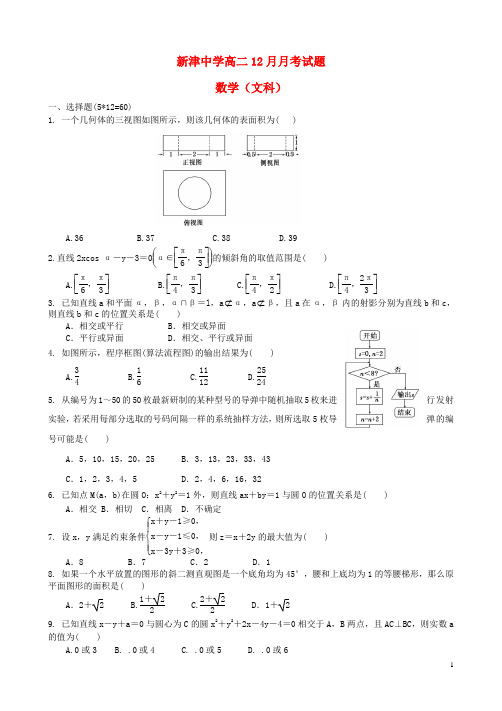
新津中学高二12月月考试题数学(文科)一、选择题(5*12=60)1. 一个几何体的三视图如图所示,则该几何体的表面积为( )A.36B.37C.38D.392.直线2xcos α-y -3=0⎝ ⎛⎭⎪⎫α∈⎣⎢⎡⎦⎥⎤π6,π3的倾斜角的取值范围是( ) A.⎣⎢⎡⎦⎥⎤π6,π3 B.⎣⎢⎡⎦⎥⎤π4,π3 C.⎣⎢⎡⎦⎥⎤π4,π2 D.⎣⎢⎡⎦⎥⎤π4,2π33. 已知直线a 和平面α,β,α∩β=l ,a ⊄α,a ⊄β,且a 在α,β内的射影分别为直线b 和c ,则直线b 和c 的位置关系是( )A .相交或平行B .相交或异面C .平行或异面D .相交、平行或异面 4. 如图所示,程序框图(算法流程图)的输出结果为( )A.34B.16C.1112D.25245. 从编号为1~50的50枚最新研制的某种型号的导弹中随机抽取5枚来进行发射实验,若采用每部分选取的号码间隔一样的系统抽样方法,则所选取5枚导弹的编号可能是( )A .5,10,15,20,25B .3,13,23,33,43C .1,2,3,4,5D .2,4,6,16,326. 已知点M(a ,b)在圆O :x 2+y 2=1外,则直线ax +by =1与圆O 的位置关系是( )A .相交B .相切C .相离D .不确定7. 设x ,y 满足约束条件⎩⎪⎨⎪⎧x +y -1≥0,x -y -1≤0,x -3y +3≥0,则z =x +2y 的最大值为( )A .8B .7C .2D .18. 如果一个水平放置的图形的斜二测直观图是一个底角均为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )A .2+ 2 B.1+22 C.2+22D .1+ 29. 已知直线x -y +a =0与圆心为C 的圆x 2+y 2+2x -4y -4=0相交于A ,B 两点,且AC ⊥BC,则实数a 的值为( )A.0或3B. .0或4C. .0或5D. .0或610.在正四棱锥S-ABCD 中,SO ⊥平面ABCD 于O ,SO=2底面边长为2,点P ,Q 分别在线段BD ,SC 上移动,则PQ 两点的最短距离为( )A .55 B.552 C.2 D.1 11.若圆x 2+y 2=r 2(r >0)上仅有4个点到直线x -y -2=0的距离为1,则实数r 的取值范围为( ) A .(2+1,+∞) B.(2-1, 2+1) C .(0, 2-1) D .(0, 2+1)12.如图,四棱锥PABCD 的底面是边长为8的正方形,四条侧棱长均为217.点G ,E ,F ,H 分别是棱 PB ,AB ,CD ,PC 上共面的四点,平面GEFH 平面ABCD ,BC ∥平面GEFH .若EB =2,则四边形GEFH 的面积为( )A .16 B. 17 C. 18 D.19二、填空题(5*4=20)13. 甲、乙两套设备生产的同类型产品共4 800件,采用分层抽样的方法从中抽取一个容量为80的样本进行质量检测.若样本中有50件产品由甲设备生产,则乙设备生产的产品总数为_______件. 14.n =10S =100 DO S =S -n n =n -1LOOP UNTIL S<=70 PRINT n END程序运行的结果为________15. 若圆C 的半径为1,其圆心与点(1,0)关于直线y =x 对称,则圆C 的标准方程为________________. 16.如图,在三棱锥DABC 中,若AB =CB ,AD =CD ,E 是AC 的中点,则下列命题中正确的有________(写出全部正确命题的序号).①平面ABC⊥平面ABD ; ②平面ABD⊥平面BCD ;③平面ABC⊥平面BDE ,且平面ACD⊥平面BDE ; ④平面ABC⊥平面ACD ,且平面ACD⊥平面BDE. 三.解答题(共70分)17. (本小题满分12分) 已知两条直线l 1:ax -by +4=0,l 2:(a -1)x +y +b =0,求分别满足下列条件的a ,b 的值.(1)直线l 1过点(-3,-1),并且直线l 1与l 2垂直;(2)直线l 1与直线l 2平行,并且坐标原点到l 1,l 2的距离相等.18.(本小题满分12分)如图,三棱柱ABC A 1B 1C 1中,侧面BB 1C 1C 为菱形,B 1C 的中点为O ,且AO ⊥平面BB 1C 1C .(1)证明:B 1C ⊥AB ; (2)若AC ⊥AB 1,∠CBB 1=60°,BC =1,求三棱柱ABC A 1B 1C 1的高.19.(本小题满分12分)从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测(1)在下表中作出这些数据的频率分布直方图:(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);方差公式:S 2=21()nii i x x P =-∑(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?20.(本小题满分12分)已知点P (2,2),圆C :x 2+y 2-8y =0,过点P 的动直线l 与圆C 交于A ,B 两点,线段AB 的中点为M ,O 为坐标原点.(1)求M 的轨迹方程;(2)当|OP |=|OM |时,求l 的方程及△POM 的面积. 21. (本小题满分12分) (1) 甲、乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服中选择1种,则他们选择相同颜色运动服的概率为多少?(2) (2)设x ∈[0,3],y ∈[0,4],求点M 落在不等式组:⎩⎪⎨⎪⎧x +2y -3≤0,x ≥0,y ≥0所表示的平面区域内的概率.22. (本小题满分10分)如图所示,已知二面角αMNβ的大小为60°,菱形ABCD在面β内,A,B两点在棱MN上,∠BAD =60°,E是AB的中点,DO⊥平面α,垂足为O.(1)证明:AB⊥平面ODE;(2)求异面直线BC与OD所成角的余弦值.文科数学参考答案一.1.C 2.B 3.D 4.C 5.B 6.A 7.B 8.A 9.D 10.B 11.A 12C 12. 连接AC ,BD 交于点O ,BD 交EF 于点K ,连接OP ,GK. 因为PA =PC ,O 是AC 的中点,所以PO ⊥AC , 同理可得PO ⊥BD.又BD∩AC=O ,且AC ,BD 都在底面内, 所以PO ⊥底面ABCD.又因为平面GEFH ⊥平面ABCD ,且PO ⊄平面GEFH ,所以PO ∥平面GEFH. 因为平面PBD∩平面GEFH =GK , 所以PO ∥GK ,且GK ⊥底面ABCD , 从而GK ⊥EF.所以GK 是梯形GEFH 的高.由AB =8,EB =2得EB∶AB=KB∶DB=1∶4,从而KB =14DB =12OB ,即K 为OB 的中点.再由PO ∥GK 得GK =12PO ,即G 是PB 的中点,且GH =12BC =4.由已知可得OB =42,PO =PB 2-OB 2=68-32=6, 所以GK =3.故四边形GEFH 的面积S =GH +EF 2·GK=4+82×3=18.二.13.1800 14.615. x 2+(y -1)2=1. 16. 三.解答题17.解:(1)∵l 1⊥l 2,∴a(a-1)+(-b)·1=0,即a 2-a -b =0.①又点(-3,-1)在l 1上, ∴-3a +b +4=0② 由①②得a =2,b =2.(2)∵l 1∥l 2,∴a b =1-a ,b =a1-a ,故l 1和l 2的方程可分别表示为: (a -1)x +y +4(a -1)a =0,(a -1)x +y +a1-a=0,又原点到l 1与l 2的距离相等.∴4⎪⎪⎪⎪⎪⎪a -1a =⎪⎪⎪⎪⎪⎪a 1-a ,∴a=2或a =23, ∴a=2,b =-2或a =23,b =2.18.解析:(1)(2)质量指标值的样本平均数为x =80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.质量指标值的样本方差为s 2=(-20)2×0.06+(-10)2×0.26+0×0.38+102×0.22+202×0.08=104.所以这种产品质量指标值的平均数的估计值为100,方差的估计值为104.(3)质量指标值不低于95的产品所占比例的估计值为0.38+0.22+0.08=0.68.由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定.19.解析:(1)连接BC 1,则O 为B 1C 与BC 1的交点.因为侧面BB 1C 1C 为菱形,所以B 1C ⊥BC 1.又AO ⊥平面BB 1C 1C ,所以B 1C ⊥AO ,故B 1C ⊥平面ABO . 由于AB ⊂平面ABO ,故B 1C ⊥AB .(2)作OD ⊥BC ,垂足为D ,连接AD .作OH ⊥AD ,垂足为H .由于BC ⊥AO ,BC ⊥OD ,故BC ⊥平面AOD ,所以OH ⊥BC .又OH ⊥AD ,所以OH ⊥平面ABC .因为∠CBB 1=60°,所以△CBB 1为等边三角形,又BC =1,可得OD =34. 由于AC ⊥AB 1,所以OA =12B 1C =12.由OH ·AD =OD ·OA ,且AD =OD 2+OA 2=74,得OH =2114.又O 为B 1C 的中点,所以点B 1到平面ABC 的距离为217.故三棱柱ABC A 1B 1C 1的高为217. 20.解析:(1)圆C 的方程可化为x 2+(y -4)2=16,所以圆心为C (0,4),半径为4.由于点P 在圆C 的内部,所以M 的轨迹方程是(x -1)2+(y -3)2=2.(2)由(1)可知M 的轨迹是以点N (1,3)为圆心,2为半径的圆.由于|OP |=|OM |,故O 在线段PM 的垂直平分线上,又P 在圆N 上,从而ON ⊥PM . 因为ON 的斜率为3,所以l 的斜率为-13,故l 的方程为y =-13x +83.又|OM |=|OP |=22,O 到l 的距离为4105,|PM |=4105,所以△POM 的面积为165.21.(1) 甲、乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服中选择1种的所有可能情况为(红,白),(白,红),(红,蓝),(蓝,红),(白,蓝),(蓝,白),(红,红),(白,白),(蓝,蓝),共9种,他们选择相同颜色运动服的所有可能情况为(红,红),(白,白),(蓝,蓝),共3种.故所求概率为P =39=13.(2)依条件可知,点M 均匀地分布在平面区域⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫(x ,y )⎪⎪⎪⎩⎪⎨⎪⎧0≤x ≤3,0≤y ≤4内,该平面区域的图形为图中矩形OABC 围成的区域,面积为S =3×4=12.而所求事件构成的平面区域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫(x ,y )⎪⎪⎪⎩⎪⎨⎪⎧x +2y -3≤0,x ≥0,y ≥0,其图形如图中的三角形OAD (阴影部分).又直线x +2y -3=0与x 轴、y 轴的交点分别为A (3,0),D ⎝ ⎛⎭⎪⎫0,32,则三角形OAD 的面积为S 1=12×3×32=94.故所求事件的概率为P =S 1S =9412=316.22. 解:(1)证明:如图,因为DO ⊥α,AB ⊂α,所以DO ⊥AB.连接BD ,由题设知,△ABD 是正三角形.又E 是AB 的中点,所以DE ⊥AB.而DO∩DE=D ,故AB ⊥平面ODE. (2)因为BC∥AD,所以BC 与OD 所成的角等于AD 与OD 所成的角,即∠ADO 是BC 与OD 所成的角.由(1)知,AB ⊥平面ODE ,所以AB ⊥OE. 又DE ⊥AB ,于是∠DEO 是二面角αMNβ的平面角, 从而∠DE O =60°.不妨设AB =2,则AD =2,易知DE = 3.在Rt△DOE 中,DO =DE·sin 60°=32.连接AO ,在Rt△AOD 中,cos∠ADO=DO AD =322=34.故异面直线BC 与OD 所成角的余弦值为34.。
新津县二中2018-2019学年上学期高二数学12月月考试题含解析

新津县二中2018-2019学年上学期高二数学12月月考试题含解析班级__________ 姓名__________ 分数__________一、选择题1. 已知△ABC 的周长为20,且顶点B (0,﹣4),C (0,4),则顶点A 的轨迹方程是( )A .(x ≠0)B .(x ≠0)C .(x ≠0)D .(x ≠0)2. 已知实数a ,b ,c 满足不等式0<a <b <c <1,且M=2a ,N=5﹣b ,P=()c ,则M 、N 、P 的大小关系为( )A .M >N >PB .P <M <NC .N >P >M3. 已知双曲线kx 2﹣y 2=1(k >0)的一条渐近线与直线2x+y ﹣3=0垂直,则双曲线的离心率是( )A .B .C .4D .4. 直线l 将圆x 2+y 2﹣2x+4y=0平分,且在两坐标轴上的截距相等,则直线l 的方程是( )A .x ﹣y+1=0,2x ﹣y=0B .x ﹣y ﹣1=0,x ﹣2y=0C .x+y+1=0,2x+y=0D .x ﹣y+1=0,x+2y=05. 设函数()()()21ln 31f x g x ax x ==-+,,若对任意1[0)x ∈+∞,,都存在2x ∈R ,使得()()12f x f x =,则实数的最大值为( )A .94B . C.92D .4 6. 已知向量与的夹角为60°,||=2,||=6,则2﹣在方向上的投影为( ) A .1B .2C .3D .47. 如果集合 ,A B ,同时满足{}{}{}{}1,2,3,41,1,1AB B A B =≠≠,A =,就称有序集对(),A B 为“ 好集对”. 这里有序集对(),A B 是指当A B ≠时,(),A B 和(),B A 是不同的集对, 那么“好集对” 一共有( )个A .个B .个C .个D .个 8. 已知圆C :x 2+y 2=4,若点P (x 0,y 0)在圆C 外,则直线l :x 0x+y 0y=4与圆C 的位置关系为( ) A .相离 B .相切 C .相交 D .不能确定9. 设m ,n 表示两条不同的直线,α、β表示两个不同的平面,则下列命题中不正确的是( ) A .m ⊥α,m ⊥β,则α∥β B .m ∥n ,m ⊥α,则n ⊥α C .m ⊥α,n ⊥α,则m ∥nD .m ∥α,α∩β=n ,则m ∥n10.已知全集R U =,集合{|||1,}A x x x R =≤∈,集合{|21,}xB x x R =≤∈,则集合U AC B 为( )A.]1,1[-B.]1,0[C.]1,0(D.)0,1[- 【命题意图】本题考查集合的运算等基础知识,意在考查运算求解能力.11.若复数z=(其中a ∈R ,i 是虚数单位)的实部与虚部相等,则a=( )A .3B .6C .9D .1212.△ABC 的外接圆圆心为O ,半径为2, ++=,且||=||,在方向上的投影为( )A .﹣3B .﹣C .D .3二、填空题13.已知n S 是数列1{}2n n -的前n 项和,若不等式1|12n n n S λ-+<+|对一切n N *∈恒成立,则λ的取值范围是___________.【命题意图】本题考查数列求和与不等式恒成立问题,意在考查等价转化能力、逻辑推理能力、运算求解能力. 14.数列{a n }是等差数列,a 4=7,S 7= .15.如图,一个空间几何体的正视图和侧视图都是边长为2的正三角形,俯视如图是一个圆,那么该几何体的体积是 .16.已知(ax+1)5的展开式中x 2的系数与的展开式中x 3的系数相等,则a= .17.抛物线y 2=6x ,过点P (4,1)引一条弦,使它恰好被P 点平分,则该弦所在的直线方程为 .18.已知函数()f x 是定义在R 上的奇函数,且当0x ≥时,2()2f x x x =-,则()y f x =在R 上的解析式为三、解答题19.一台还可以用的机器由于使用的时间较长,它按不同的转速生产出来的某机械零件有一些会有缺陷,每小时生产有缺陷零件的多少随机器运转的速率而变化,下表为抽样试验结果:转速x (转/秒)1614 12 8 每小时生产有缺陷的零件数y (件) 11985(1)画出散点图; (2)如果y 与x 有线性相关的关系,求回归直线方程;(3)若实际生产中,允许每小时的产品中有缺陷的零件最多为10个,那么机器的转运速度应控制在什么范围内?参考公式:线性回归方程系数公式开始=, =﹣x .20.【无锡市2018届高三上期中基础性检测】已知函数()()2ln 1.f x x mx m R =--∈ (1)当1m =时,求()f x 的单调区间;(2)令()()g x xf x =,区间1522,D e e -⎛⎫= ⎪⎝⎭,e 为自然对数的底数。
新津县高中2018-2019学年上学期高二数学12月月考试题含解析

新津县高中2018-2019学年上学期高二数学12月月考试题含解析 班级__________ 座号_____ 姓名__________ 分数__________一、选择题1. 如图甲所示, 三棱锥P ABC - 的高8,3,30PO AC BC ACB ===∠= ,,M N 分别在BC 和PO 上,且(),203CM x PN x x ==∈(,,图乙的四个图象大致描绘了三棱锥N AMC -的体积y 与 的变化关系,其中正确的是( )A .B . C. D .1111] 2. 若函数2()48f x x kx =--在[5,8]上是单调函数,则k 的取值范围是( )A .(][),4064,-∞+∞ B .[40,64] C .(],40-∞ D .[)64,+∞3. 已知函数x x x f 2sin )(-=,且)2(),31(log ),23(ln 3.02f c f b f a ===,则( )A .c a b >>B .a c b >>C .a b c >>D .b a c >>【命题意图】本题考查导数在单调性上的应用、指数值和对数值比较大小等基础知识,意在考查基本运算能力. 4. 在圆的一条直径上,任取一点作与该直径垂直的弦,则其弦长超过该圆的内接等边三角形的边长概率为( )A .B .C .D .5. 若如图程序执行的结果是10,则输入的x 的值是( )A .0B .10C .﹣10D .10或﹣106. 在复平面内,复数(﹣4+5i )i (i 为虚数单位)的共轭复数对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限7. 函数f (x )=ax 2+2(a ﹣1)x+2在区间(﹣∞,4]上为减函数,则a 的取值范围为( ) A .0<a ≤ B .0≤a ≤ C .0<a < D .a >8. 在ABC ∆中,b =3c =,30B =,则等于( )A B . C D .2 9. 集合{}1,2,3的真子集共有( )A .个B .个C .个D .个 10.阅读如下所示的程序框图,若运行相应的程序,则输出的S 的值是( )A .39B .21C .81D .10211.利用计算机在区间(0,1)上产生随机数a ,则不等式ln (3a ﹣1)<0成立的概率是( )A .B .C .D .12.在ABC ∆中,22tan sin tan sin A B B A =,那么ABC ∆一定是( )A .锐角三角形B .直角三角形C .等腰三角形D .等腰三角形或直角三角形二、填空题13.已知实数x ,y 满足,则目标函数z=x ﹣3y 的最大值为14.如图所示,正方体ABCD ﹣A ′B ′C ′D ′的棱长为1,E 、F 分别是棱AA ′,CC ′的中点,过直线EF 的平面分别与棱BB ′、DD ′交于M 、N ,设BM=x ,x ∈[0,1],给出以下四个命题:①平面MENF ⊥平面BDD ′B ′;②当且仅当x=时,四边形MENF 的面积最小; ③四边形MENF 周长l=f (x ),x ∈0,1]是单调函数; ④四棱锥C ′﹣MENF 的体积v=h (x )为常函数; 以上命题中真命题的序号为 .15.已知函数f (x )=x 2+x ﹣b+(a ,b 为正实数)只有一个零点,则+的最小值为 .16.对于集合M ,定义函数对于两个集合A ,B ,定义集合A △B={x|f A (x )f B (x )=﹣1}.已知A={2,4,6,8,10},B={1,2,4,8,12},则用列举法写出集合A △B 的结果为 .17.如果椭圆+=1弦被点A (1,1)平分,那么这条弦所在的直线方程是 .18.已知||2=a ,||1=b ,2-a 与13b 的夹角为3π,则|2|+=a b . 三、解答题19.某校为了解2015届高三毕业班准备考飞行员学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右前3个小组的频率之比为1:2:4,其中第二小组的频数为11.(Ⅰ)求该校报考飞行员的总人数;(Ⅱ)若经该学校的样本数据来估计全省的总体数据,若从全省报考飞行员的学生中(人数很多)任选3人,设X 表示体重超过60kg 的学生人数,求X 的数学期望与方差.20.已知函数3()1xf x x =+,[]2,5x ∈. (1)判断()f x 的单调性并且证明; (2)求()f x 在区间[]2,5上的最大值和最小值.21.【2017-2018学年度第一学期如皋市高三年级第一次联考】设函数()1ln 1f x a x x=+-. (1)当2a =时,求函数()f x 在点()()11f ,处的切线方程; (2)讨论函数()f x 的单调性;(3)当102a <<时,求证:对任意1+2x ⎛⎫∈∞ ⎪⎝⎭,,都有1e x aa x +⎛⎫+< ⎪⎝⎭.22.(本题满分14分)已知函数x a x x f ln )(2-=.(1)若)(x f 在]5,3[上是单调递减函数,求实数a 的取值范围;(2)记x b x a x f x g )1(2ln )2()()(--++=,并设)(,2121x x x x <是函数)(x g 的两个极值点,若27≥b , 求)()(21x g x g -的最小值.23.已知二次函数f (x )的图象过点(0,4),对任意x 满足f (3﹣x )=f (x ),且有最小值是. (1)求f (x )的解析式;(2)求函数h (x )=f (x )﹣(2t ﹣3)x 在区间[0,1]上的最小值,其中t ∈R ;(3)在区间[﹣1,3]上,y=f (x )的图象恒在函数y=2x+m 的图象上方,试确定实数m 的范围.24.(本小题满分10分)已知函数f (x )=|x -a |+|x +b |,(a ≥0,b ≥0). (1)求f (x )的最小值,并求取最小值时x 的范围; (2)若f (x )的最小值为2,求证:f (x )≥a +b .新津县高中2018-2019学年上学期高二数学12月月考试题含解析(参考答案)一、选择题1. 【答案】A 【解析】考点:几何体的体积与函数的图象.【方法点晴】本题主要考查了空间几何体的体积与函数的图象之间的关系,其中解答中涉及到三棱锥的体积公式、一元二次函数的图象与性质等知识点的考查,本题解答的关键是通过三棱锥的体积公式得出二次函数的解析式,利用二次函数的图象与性质得到函数的图象,着重考查了学生分析问题和解答问题的能力,是一道好题,题目新颖,属于中档试题.2. 【答案】A 【解析】试题分析:根据()248f x x kx =--可知,函数图象为开口向上的抛物线,对称轴为8kx =,所以若函数()f x 在区间[]5,8上为单调函数,则应满足:58k ≤或88k≥,所以40k ≤或64k ≥。
四川省 高二数学 12月月考试题 文

高二上(12月)月考试题数 学 试 题(文)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷第3至4页。
满分150分,考试时间120分钟。
考试结束后,将答题卷和机读卡一并收回。
第Ⅰ卷(选择题 共60分)一、选择题(共12小题,每小题5分,共60分;每小题给出的四个选项中,只有一项是符合题目要求的)。
4.由y=︱x ︱和圆422=+y x 所围成的较小图形的面积( ) (A )4π (B )43π (C ) π (D ) 23π5.动点在圆122=+y x 上运动,它与定点B (3,0)连线的中点的轨迹方程式( ) (A)4)3(22=++y x (B)1)3(22=+-y x (C)14)32(22=+-y x (D)21)23(22=++y x 6 在下列关于直线l 、m 与平面α和β的命题中,真命题的是( )A.若β⊂l 且α⊥β,,则l ⊥α;B.若l ⊥β且α∥β,则l ⊥α; C.若l ⊥β且α⊥β,则l ∥α; D.若m =⋂βα且l ∥m ,则l ∥α7.某公司现有职员160人,中级管理人员30人,高级管理人员10人,要从其中抽取20个人进行身体健康检查,如果采用分层抽样的方法,则职员、中级管理人员和高级管理人员各应该抽取( )人A .8,15,7B .16,2,2C .16,3,1D .12,3,5 8.一个袋中装有2个红球和2个白球,现从袋中取出1球,然后放回袋中再取出一球,则取出的两个球同色的概率是( ) A .B .C .D .9. 从区间内任取两个数,则这两个数的和小于的概率是 ( )A. B. C. D.10.在长为10 cm 的线段AB 上任取一点P ,并以线段AP 为边作正方形,这个正方形的面积介于25 cm 2与49 cm 2之间的概率为( )A.B.C.D.11.直线3y kx =+与圆()()22324x y -+-=相交于M,N 两点,若MN ≥则k 的取值范围是A. 304⎡⎤-⎢⎥⎣⎦,B. []304⎡⎤-∞-+∞⎢⎥⎣⎦ ,,C. ⎡⎢⎣⎦D. 203⎡⎤-⎢⎥⎣⎦, 12.已知点A (-1,0),B(0,2),点P 是圆(x-1)2+y 2=1上任意一点,则△PAB 面积的最大值是( )A. 2 B .254+ C. 25 D . 252+ 第Ⅱ卷(选择题 共90分)二. 填空题(共4题,每题4分)13.掷两枚骰子,出现点数之和为5的概率是____。
高二数学12月月考试题 文 试题 (2)(共13页)

民族(mínzú)中学2021-2021学年度上学期12月月考试卷高二文科数学本套试卷分第I卷〔选择题〕和第II卷〔非选择题〕两局部。
满分是150分,考试时间是是120分钟。
请在答题卷上答题。
第I卷选择题〔一共60分〕一、选择题:本大题一一共12小题,每一小题5分,一共60分。
在每一小题给出的四个选项里面,只有一项是哪一项符合题目要求的。
1.p:∀x∈R,ax2+2x+3>0,假如p是真命题,那么a的取值范围是( )A.a< B. 0<a≤ C.a≤D.a≥p:x<-3或者x>1,条件q:x>a,且p是q的充分不必要条件,那么a的取值范围是( )A.a≥-1 B.a≤1C.a≥1D.a≤-3+=1(a>b>0)的左,右焦点分别为F1,F2,上顶点为B.假设|BF2|=|F1F2|=2,那么该椭圆的方程为( )A.+=1 B.+y2=1 C.+y2=1 D.+y2=1-=1(a>0,b>0),过其右焦点且垂直于实轴的直线与双曲线交于M、N两点,O是坐标原点.假设OM⊥ON,那么双曲线的离心率为( )A.B.C. D.P是抛物线y2=2x上的动点,点P到准线(zhǔn xiàn)的间隔为d,且点P在y轴上的射影是M,点A(,4),那么|PA|+|PM|的最小值是( )A.B. 4 C.D. 5f(x)在定义域内可导,y=f(x)的图象如下图,那么导函数y=f′(x)的图象可能为( )+y2=1的一个焦点作倾斜角为45°的直线l,交椭圆于A、B两点.设O为坐标原点,那么·等于( )A.-3 B.- C.-或者-3 D.±y=2x2上两点A(x1,y1)、B(x2,y2)关于直线y=x+m对称,且x1·x2=-,那么m等于( )A. B. 2 C.D. 3g(x)=x(x2-1),那么g(x)在区间[0,1]上的最小值为( )A.-1 B. 0 C.-D.f(x)=ax3-3x2+1,假设(jiǎshè)f(x)存在唯一的零点x0,且x0>0,那么a的取值范围是( )A. (2,+∞) B. (1,+∞) C. (-∞,-2) D. (-∞,-1)P在曲线y=上,α为曲线在点P处的切线的倾斜角,那么α的取值范围是( )A.[0,) B.[,) C.(,] D.[,π)12.F1,F2是双曲线-y2=1的两个焦点,P是双曲线上一点,且∠F1PF2=90°,那么△F1PF2的面积是( )A.1 B.C.2 D.第II卷非选择题〔一共90分〕二、填空题:本大题一一共4小题,每一小题5分,一共20分。
高二数学12月月考试题 18(共10页)

2021-2021学年(xuénián)高二数学12月月考试题本套试卷分第I卷(选择题)和第二卷(非选择题)两局部,满分是l50分,考试时间是是120分钟。
在在考试完毕之后以后,将本套试卷和答题卡一起交回.考前须知:1.答第I卷前,所有考生必须将本人的姓名,考号填写上在答题卡上2.选择题答案使需要用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号,非选择题答案使用0.5毫米的黑色中性(签字)笔或者碳素笔书写,字体工整,笔迹清楚.第I卷(选择题一共60分)]一、选择题:本大题一一共l2小题,每一小题5分.一共60分,在每一小题给出的四个选项里面.只有一项是哪一项符合题目要求的.1.假设复数,那么其虚部为A.-1B.2C.-2D.2.设函数〔为自然对数的底数〕.假设,那么A.e B.C.D.3.,是间隔为2的两定点,动点M满足∣∣+∣∣=4,那么M点的轨迹是4.与双曲线有一共同的渐近线,且过点〔2,2〕的双曲线HY方程为A. B. C. D.5.在区间(qū jiān)上的最小值是A. B. 0 C. 1 D.6.与向量〔-3,-4,5〕一共线的单位向量是〔〕A.〔〕和〔〕B.〔32222,,1052-〕C.〔〕和〔〕D.〔32222,, 1052--〕7.假设,那么等于A. B. C. D.以上都不是8.设是函数的导数,的图像图--1所示,那么的图象最有可能的是〔〕图--19.正方形的顶点为椭圆的焦点,顶点在椭圆上,那么此椭圆的离心率为A. B. C. D.10.如图—2,是直三棱柱(léngzhù),∠BCA=90°,点、分别是、的中点,假设,那么与所成角的余弦值是A .B .C .D .的图像在区间上连续不断,且,,那么对任意的都有 A . B . C .D .和,定义运算“〞:,设函数假设函数的图像与轴恰有三个公一共点,那么实数的取值范围是〔 〕 A .B .C .D .第二卷(非选择题一共90分)二、填空题:本大题一一共4小题,每一小题5分,一共20分. 13.抛物线的准线方程为 .14.设复数满足〔为虚数单位〕,那么的值是 .四棱锥P -ABCD 中,ABCD 为平行四边形,AC 与BD 交于O ,G 为BD 上一点,BG =3GD ,PA →=a ,PB →=b ,PC →=c , PG →= .〔用基底{a ,b ,c }表示向量PG →〕 图--316.,函数(h ánsh ù))(x f 定义域中任意的,有如下结论:①;②;③ ④上述结论中正确结论的序号是 .三.解答题:本大题一一共6小题.一共70分,解答写出文字说明、证明过程或者推演步骤.17.〔此题满分是10分〕 复数.〔Ⅰ〕假设z 是纯虚数,务实数的值;〔Ⅱ〕假设,设,试求.18.〔此题满分是12分〕 函数.〔I 〕当时,求曲线()y f x 在处的切线方程;(II)假设()f x 在是单调递增函数,务实数a 的取值范围.19.〔此题满分是12分〕如图,在三棱锥P-ABC中,PA⊥底面ABC,.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.〔Ⅰ〕求证(qiúzhèng):MN∥平面BDE;〔Ⅱ〕求二面角C-EM-N的正弦值;20.〔此题满分是12分〕某地建一座桥,两端的桥墩已建好,这两墩相距640米,余下工程只需要建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为256万元,间隔为x米的相邻两墩之间的桥面工程费用为万元.假设桥墩等间隔分布,所有桥墩都视为点,且不考虑其他因素,设需要新建个桥墩,记余下工程的费用为万元.〔Ⅰ〕试写出y关于x的函数关系式;〔注意:〕〔Ⅱ〕需新建多少个桥墩才能使y最小?21.〔此题满分是12分〕椭圆的离心率为22,点在上.〔I〕求C的方程(fāngchéng);〔II〕直线不经过原点O,且不平行于坐标轴,l与C有两个交点A,B,线段AB中点为M,证明:直线OM的斜率与直线l的斜率乘积为定值.22.〔此题满分是12分〕函数.f x的单调性;〔Ⅰ〕讨论()〔Ⅱ〕当时,证明2021-2021学年度12月月考数学(shùxué)参考答案一、选择题1—5 BDABC 6—10 AACDD 11—12 BB 二、填空题 13.14.15.PG →==a -b +43c . 16.①③ 三、解答题17.解:〔Ⅰ〕假设是纯虚数,那么解得 . ……………………………………………………………4分 〔Ⅱ〕假设,那么. ……………………………………5分∴, ………………………8分∴,∴. …………………………………10分18.解:〔I 〕()f x 的定义域为.当4=a 时,,所以曲线()=y f x 在处的切线方程为(II)因为又()f x 在(1,)+∞是单调递增函数; 所以在(1,)+∞恒成立即在(1,)+∞恒成立令,所以(su ǒy ǐ)1()ln 1(1)F x x x x=++>在(1,)+∞单增, 所以,即, 故实数a 的取值范围为.19.解:如图,以A 为原点,分别以,,方向为x轴、y 轴、z 轴正方向建立空间直角坐标系.依题意可得A 〔0,0,0〕,B 〔2,0,0〕,C 〔0,4,0〕,P 〔0,0,4〕,D 〔0,0,2〕,E 〔0,2,2〕,M 〔0,0,1〕,N 〔1,2,0〕. 〔Ⅰ〕易得=〔0,2,0〕,=〔2,0,〕.设为平面BDE 的法向量,那么,即.不妨设,可得.又=〔1,2,〕,可得.因为平面BDE ,所以平面BDE .20.解 〔Ⅰ〕640)1(=+x n 即所以〔〕〔Ⅱ〕 由〔Ⅰ〕知,令,得,所以(su ǒy ǐ)x =64 w.w.w.k.s.5.u.c.o.m 当0<x <64时<0, ()f x 在区间〔0,64〕内为减函数; 当时,'()f x >0. ()f x 在区间〔64,640〕内为增函数,所以()f x 在x =64处获得最小值,此时,故需新建9个桥墩才能使y 最小 21.解:22.解:当0<a 时,那么(n à me))(x f 在单调递增,在单调递减.〔2〕由〔1〕知,当0<a 时,,,令〔〕,那么,解得.∴y 在单调递增,在单调递减, ∴,∴,即,∴.内容总结(1)2021-2021学年高二数学12月月考试题本套试卷分第I 卷(选择题)和第二卷(非选择题)两局部,满分是l50分,考试时间是是120分钟 (2)8分 ∴,∴.。
四川省新津中学学年高二数学12月月考试题 理(答案不全)

四川省新津中学2014-2015学年高二数学12月月考试题 理(答案不全)一、选择题:本大题共10个小题,每小题5分,共50分。
1.下列问题中,最适合用系统抽样抽取样本的是( ) A .从10名学生中,随机抽取2名参加义务劳动 B.从全校3000名学生中,随机抽取100名参加义务劳动C .从某市30000名学生中,其中小学生14000人,初中生10000人,高中生6000人,抽取300名了解该市学生的近视情况D.从某班周二值日小组6人中,随机抽取1人擦黑板2、直线3470x y ++=和直线210x y --=的交点坐标是( ) A 、()1,3- B 、 ()1,3 C 、(-1,-1) D 、()1,1- 3.已知一个k 进制数132与十进制数30相等,那么k 等于( ) A .5 B .4 C .3 D. 24.若点(2,1,1)P x x -在点(1,0,0),(0,1,0),(0,0,1A B C 所确定的平面内,则实数x 的值为( ) A.1-B.0C.1D.25.已知点)0,2(-A 和)2,0(B 在直线1-+=k kx y 的同侧,则实数k 的取值范围是 A.),3()1,(+∞--∞ B. ),1()3,(+∞--∞ C.)3,1(- D.)1,3(- 6 .已知,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是( ) A.若//,,m n αβαβ⊂⊂,则//m n B.若,,m n m n αβ⊥⊂⊂,则αβ⊥ C.若,,m n αβαβ⊥⊂⊂,则m n ⊥D.若,//,//m m n n αβ⊥,则αβ⊥7.某算法的程序如右下图所示,若输入2x =,则电脑屏上显示的结果为( )A.16B.4C.0y =D.08棱长为1的正方体ABCD-A 1B 1C 1D 1中,四面体AB 1CD 1的体积为( ) A.14 B.13 C.12 D.239.设,x y 满足约束条件360,20,0,0,x y x y x y --≤⎧⎪-+≥⎨⎪≥≥⎩若目标函数(0,z ax by a b =+>>0)的最大值为12,则23a b+的最小值为( )A.256B.83C.113 D.410.在四面体PA B C 中,有下列命题: INPUT ; IF 0 THEN (2)2ELSEIF 0 THEN 4 ELSE (-2)2 END IF END IF PRINT ; ENDx x x y x x y y x y y ∧∧=<=+====〝〞〝〞CD1A 1B 1C 1D P①若P A B C 为正三棱锥,则相邻两侧面所成二面角的取值范围是3ππ(,); ②若PA 、PB 、PC 两两垂直,底面ABC 上的高为h ,则22221111PCPB PA h ++=;③若P A B C 为正四面体,点E 在棱PA 上,点F 在棱B C 上,使得(0)P E B FE AF cλλ==>,设f(λ)=λλβα+,λα与λβ分别表示EF 与A C P B、所成的角,则f(λ)是定值; ④若它的四个顶点均在半径为1的球面上,且满足0=⋅PB PA ,0=⋅PC PB ,0=⋅PA PC ,则三棱锥P —ABC 的侧面积可以等于3.其中正确命题的个数( )A .4B .3C .2 D. 1二、填空题:本大题共5小题,每小题5分,共25分.答案填在答题卡上.11.如图,是计算111124620++++的值的一个程序框图,其中判断框内应填入的条件是 ________ 12.930与868的最大公约数是________.13。
新津县高级中学2018-2019学年上学期高二数学12月月考试题含解析

新津县高级中学2018-2019学年上学期高二数学12月月考试题含解析 班级__________ 座号_____ 姓名__________ 分数__________一、选择题1. 设全集U={1,3,5,7,9},集合A={1,|a ﹣5|,9},∁U A={5,7},则实数a 的值是( ) A .2B .8C .﹣2或8D .2或82. 在正方体1111ABCD A BC D -中,,E F 分别为1,BC BB 的中点,则下列直线中与直线EF 相交的是( )A .直线1AAB .直线11A B C. 直线11A D D .直线11BC 3. 在等差数列{}n a 中,首项10,a =公差0d ≠,若1237k a a a a a =++++,则k =A 、22B 、23C 、24D 、254. 在正方体8个顶点中任选3个顶点连成三角形,则所得的三角形是等腰直角三角形的概率为( )A .B .C .D .5. 已知函数f (x )=31+|x|﹣,则使得f (x )>f (2x ﹣1)成立的x 的取值范围是( )A .B .C .(﹣,)D .6. 已知a 为常数,则使得成立的一个充分而不必要条件是( )A .a >0B .a <0C .a >eD .a <e7. 与椭圆有公共焦点,且离心率的双曲线方程为( )A .B .C .D .8. 一个长方体去掉一个小长方体,所得几何体的正视图与侧(左)视图分别如图所,则该几何体的俯视图为( )A. B. C. D.9. 四棱锥P ABCD -的底面ABCD 为正方形,PA ⊥底面ABCD ,2AB =,若该四棱锥的所有顶点都在体积为24316π同一球面上,则PA =( ) A .3 B .72 C. D .92【命题意图】本题考查空间直线与平面间的垂直和平行关系、球的体积,意在考查空间想象能力、逻辑推理能力、方程思想、运算求解能力.10.由小到大排列的一组数据x 1,x 2,x 3,x 4,x 5,其中每个数据都小于﹣1,则样本1,x 1,﹣x 2,x 3,﹣x 4,x 5的中位数为( )A.B.C.D.11.sin570°的值是( ) A.B.﹣ C.D.﹣12.在极坐标系中,圆的圆心的极坐标系是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四川省新津中学高2015级高二12月月考数学试题
一、选择题:(共60分)
1. 在长方体ABCD -A 1B 1C 1D 1中,若D (0,0,0),A (4,0,0),B (4,2,0),A 1(4,0,3),则对角线AC 1的长为( )
A .9
B.
C .5
D .2
2. 命题“
”的否定是( ) A . B .
C .
D .
3. 如果表示焦点在x 轴上的椭圆,则实数a 的取值范围为( )
A.(-2,+
) B.(-2,-1)
(2,+
) C. (-,-1)
(2,+
) D.任意实数R
4. 十进制数2004等值于八进制数( )。
A. 3077
B. 3724
C. 2766
D. 4002 5. 已知直线
平行,则K 得值是( )
(A ) 1或3 (B )1或5 (C )3或5 (D )1或2 6.设变量x ,y 满足约束条件⎩⎪⎨⎪
⎧
y≤x x +y≥2
y≥3x-6
, 则目标函数z =2x +y 的最小值为( )
A .2
B .3
C .5
D .7
7.执行如图所示的程序框图.若输出
,则输入角( )
A .
B .
C .
D .
8. 一名小学生的年龄和身高(单位:cm)的数据如下: 年龄x 6 7 8 9 身高y
118
126
136
144
,预测该学生10岁时的身
高为 (A) 154
(B ) 153
(C) 152 (D) 151
9. 已知圆M 方程:x 2
+(y+1)2
=4,圆N 的圆心(2,1),若圆M 与圆N 交于A B 两点,且|AB|=2,
则圆N 方程为: ( ) A .(x-2)2
+(y-1)2
=4
B .(x-2)2+(y-1)2
=20
C.(x-2)2+(y-1)2=12 D.(x-2)2+(y-1)2=4或(x-2)2+(y-1)2=20
10. 如图,椭圆的中心在坐标原点0,顶点分别是A1, A2, B1, B2,焦点分别为F1 ,F2,延长B1F2与
A2B2交于P点,若为钝角,则此椭圆的离心率的取值范围为( )
A. B.
C. D.
11. 已知直线:4x-3y+6=0和直线:x=-1,,抛物线y2=4x上一动
点P到直线和直线的距离之和的最小值是( )
A.2
B.3
C.
D.12. 已知以T=4为周期的函数
,其中。
若方程恰有5个实数解,则m的取值范围为()
A.B.C.D.
二、填空题(共20分)
13. 从新津中学高三学生中随机抽取100名同学,
将他们的考试成绩(单位:分)绘制成频率分布直
方图(如图).则图中a= ,由图中数据可知
此次成绩平均分为 .
14.已知双曲线的准线过椭圆
的焦点,则y=kx+2与椭圆至多有一个交点的充要条件是
15. 是分别经过A(1,1),B(0,1)两点的两条平行直线,当,间的距离最大时,直线的方程是.
16.给出下列命题:①直线的倾斜角是;②已知过抛物线C:y2=2px(p>0)的焦点F 的直线与抛物线C交于A(x1,y1),B(x2,y2)两点,则有x1x2=,y1y2=-p2;③已知F1、F2为双曲线
C: 的左、右焦点,点P为双曲线右支上异于顶点的任意一点,则的内心I始终在一条直线上.其中所有正确命题的序号为 .
三、解答题(共70分)
17.(本题满分10分)已知且;q:集合A={x|x2+(a+2)x+1=0,x R},且A.若p∨q为真命题,p∧q为假命题,求实数a的取值范围.
18. (本题满分12分)已知直线l的方程为3x+4y-12=0,求满足下列条件的直线l′的方程.
(1)l′与l平行且过点(-1,3);
(2)l′与l垂直且l′与两坐标轴围成的三角形面积为4;
(3)l′是l绕原点旋转180°而得到的直线.
19.(本题满分12分)为了了解某中学高二女生的身高情况,该校对高二女生的身高进行了一次随机抽样测量,所得数据整理后列出了频率分布表如下:(单位:cm)
(1)表中m、n、M、N所表示的数分别是多少?
(2)绘制频率分布直方图;
(3)估计该校女生身高小于162.5cm的百分比.
20. (本题满分12分)
已知一圆经过点A(3,1),B(-1,3),且它的圆心在直线3x-y-2=0上.
(1)求此圆的方程;
(2)若点D为所求圆上任意一点,且点C(3,0),求线段CD的中点M的轨迹方程.
21.(本题满分12分)
给定直线:y=2x-16,抛物线G:y2=ax(a>0),
(1)当抛物线G的焦点在直线上时,求a的值;
(2)若ABC的三个顶点都在(1)所确定的
抛物线G上,且点A的纵坐标y A=8,ABC 的重心恰是抛物线G的焦点F,求直线BC的方程.
22. (本题满分12分)已知椭圆C: 的离心率为,以原点为圆心,椭圆
的短半轴为半径的圆与直线x-y+=0相切,过点P(4,0)且不垂直于x轴直线与椭圆C 相交于A、B两点。
(1)求椭圆C的方程;
(2)求的取值范围;
(3)若B点在于x轴的对称点是E,证明:直线AE与x轴相交于定点。
12月月考数学试题参考答案
一. BDBBC BDBDD AB
二.13. 0.035,64.5 14. 充分必要条件 15. 16. ② ③
三.17.
18. 解 (1)直线l :3x +4y -12=0,k l =-,
又∵l ′∥l ,∴k l ′=k l =-.
∴直线l ′:y = - (x +1)+3,即3x +4y -9=0.
(2)∵l ′⊥l ,∴k l ′=.
设l ′与x 轴截距为b ,则l ′与y 轴截距为-4
3b ,
由题意可知,S =|b |·⎪⎪⎪⎪
⎪⎪-43b =4, ∴b =±
.
∴直线l ′:y =(x +)或y =(x -).
(3)∵l ′是l 绕原点旋转180°而得到的直线, ∴l ′与l 关于原点对称.
任取点(x 0,y 0)在l 上,则在l ′上对称点为(x ,y ).
x=-x0,y=-y0,则-3x-4y-12=0.
∴l′为3x+4y+12=0.
19.
解答:解:(1)在统计中,由于频率和为1,所以N=1,
所以n=1﹣(0.02+0.08+0.4+0.3+0.16)=0.04
所以M=,
m=50﹣(1+4+20+15+8)=2
故有m=2,n=0.04,M=50,N=1;…(4分)
(2);;;;;
频率分布直方图为:
…(10分)(3)该校女生身高小于162.5cm的百分比(0.02+0.08+0.4)×100%=50%…(14分)
20. 解:(1)法一:由已知可设圆心,又由已知得,从而有
,解得:.……(2分)
于是圆的圆心,半径.……(4分)
所以,圆的方程为. ……(5分)
法二:∵,,∴,线段的中点坐标为,……(1分)从而线段的垂直平分线的斜率为,方程为即……(2分)
由方程组解得,
所以圆心,半径, ……(4分)
故所求圆的方程为. ……(5分)
(2)设,,则由及为线段的中点得:
解得:. …… (7分)
又点在圆上,所以有,化简得:
. ……(9分)
故所求的轨迹方程为. ……(10分)
21. 解:(1)∵抛物线的焦点在轴上,且其坐标为
∴对方程,令得:.
从而由已知得,.
(2)由(1)知:抛物线的方程是,.
又∵点在抛物线上,且,∴.
延长交于点,则由点是的重心得:点为线段的中点.
设点,则由得:,解之得:.
∴
设,则由点在抛物线上得:,两式相减得:
,又由点为线段的中点得,. ……(9分)∴直线的方程为,即.
22.。
