被除数、除数、商的关系(1)
乘除法的关系和运算律

【知识要点】(一)、乘除法各部分之间的关系:(1)乘法各部分之间的关系:因数×因数=积一个因数=积÷另一个因数(2)除法各部分之间的关系:没有余数的除法:有余数的除法:被除数=商×除数被除数=商×除数+余数除数=被除数÷商除数=(被除数-余数)÷商商=被除数÷除数商=(被除数-余数)÷除数(3)乘、除法之间的关系:除法是乘法的逆运算注意:0不能作除数。
(4)整除:a÷b(b≠0)=c 则a能被b整除,b能整除a。
(二)乘法运算律1、乘法交换律:两个数相乘,交换因数的位置,它们的积不变。
这个规律叫做乘法交换律。
用字母表示为:a·b=b·a2、乘法结合律:三个数相乘,先把前两个数相乘再乘第三个数,或先将后两个数相乘再乘第一个数,它们的积不变。
这个规律叫做乘法结合律。
用字母表示为:(a·b)·c=a·(b·c) 3、乘法分配律:两个数的和与一个数相乘,可以把这两个加数分别与这个数相乘,再把积相加。
这个规律叫做乘法分配律。
用字母表示为:(a+b)·c=a·c+b·c a·c+b·c=(a+b)·c乘法分配律的拓展:两个数的差与一个数相乘,可以用这个数分别去乘相减的两个数,再把积相减。
用字母表示为:(a-b)·c=a·c-b·c a·c-b·c=(a-b)·c(三)减法简便运算:1、一个数连续减去两个数,可以用这个数减去这两个数的和。
用字母表示:a-b-c=a-(b+c)2、一个数连续减去两个数,可以用这个数先减去后一个数再减去前一个数。
用字母表示:a-b-c=a—c-b(四)除法简便运算:1、一个数连续除以两个数,可以用这个数除以这两个数的积。
除数是一位数的除法

三年级数学知识:除数是一位数的除法1、有关除法的3条公式:(没有余数)被除数÷除数=商被除数÷商=除数商×除数=被除数2、有关除法的3条公式:(有余数)被除数÷除数=商------余数(被除数一余数)÷商=余数商×除数+余数=被除数。
3、关于余数(1)、余数与除数的关系很大,余数不能大于除数。
余数不能是0, 0不是余数。
整除就没有余数。
(2)、在一位数除法中,最大的余数是8,最小的余数是1。
4、关于商有几多位的问题一定要看被除数有几多位,被除数是两位数的时候,商就有可能是1位或者2位数。
被除数是三位数的时候,商就有可能是2位或者3位数。
决定商到底有几多位数的时候,一定要看被除数的最高位与除数的大小关系,就可以算出来了。
4、被除数是两个数的时候,当被除数的最高位(十位数)大于或等于除数时,商就是2位数。
当被除数的最高位(十位数)小于除数时,商就是1位数。
如:51÷3商就是2位数。
13÷3商就是1位数。
5、被除数是三位数的时候,当被除数的最高位(百位数)大于或等于除数时,商就是3位数。
当被除数的最高位(百位数)小于除数时,商就是2位数。
如:456÷4商就是有3位数。
324÷6商就是有2位数。
6、最大余数和最小余数的算法在一位数除法当中,最大的除数是9,最大的余数是8,最小的余数是1。
在每一道除法中,最小的余数是1是没有改变的。
最大的余数就具体看除数了。
要看规则:余数不能大于除数就可以了。
例如:除数是5的时候,最大的余数就是4、最小就是1,其中4、3、2、1 都是可能是余数。
按照这样的方法类推,其中除数是9的时候,余数是最多的,最大余数是8,最小是1,其中8、7、6、5、4、3、2、1都是可能是余数。
7、特殊情况,除数是整数和整百的时候,(超出了一位数)可以与被除数后面相互去掉一个零或两个零就可以了。
例如:100÷10=10 20000÷100=200 相互在后面去掉相应的零就可以了。
商与被除数的关系教案

微课《商与被除数的大小关系》教学设计黄山市歙县行知小学方邦道教学内容:商与被除数的大小关系教学目标:1、使学生理解并掌握判断商与被除数的大小关系的方法。
2、培养学生判断、推理、归纳,总结的思维能力。
教学重点:理解并掌握判断商与被除数的大小关系的方法。
教学难点:运用商与被除数的大小关系的方法正确地判断商与被除数的大小。
教学过程:一、问题导入1、计算下面各题,你能从中发现什么规律?0÷1212÷350÷1 12÷1 12÷2 12÷322、导入新课,板书:探究商与被除数的大小关系。
二、新课讲解1、计算上面各题的结果:0 ÷12= 0 12÷35= 560 ÷1= 01 2÷1 = 1212÷2 = 1412÷32= 13想一想:除数与1比较有什么特点?2、观察商与被除数的关系,再将其分类。
0 ÷12= 0 除数<1 商= 01 2÷35= 56除数<1 商>被除数0 ÷1= 0 除数= 1 商= 01 2÷1 = 12除数= 1 商= 被除数12 ÷ 2 = 14 除数 > 1 商 < 被除数 12÷ 32 = 13 除数 > 1 商 < 被除数 3、 归纳总结:当除数小于1, 商大于被除数。
(1)、两个不为0的数相除: 当除数等于1, 商等于被除数。
当除数大于1 商小于被除数。
(2)、0除以任何不为0的数都得0三、 运用规律:1、在下面 里填上>、<、=。
310÷76 310 8÷23 8 89÷1 89 0÷1241250 2、不用计算,你会填吗?67÷ 3 149÷730 9 ÷ 34 57÷52 45 ÷45 38 ÷1 0÷711 商大于被除数 商小于被除数4、 判断题:(1)一个不为0的数除以真分数,商一定小于这个数。
四年级数学下册第一单元四则运算知识点归纳总结

四年级下册数学知识点归纳总结第一单元四则运算四则运算:加法、减法、乘法和除法统称四则运算。
1、加减法的意义和各部分间的关系。
(1)把两个数合并成一个数的运算,叫做加法。
加法各部分间的关系:和=加数+加数加数=和-另一个数(2)已知两个数的和与其中一个加数,求另一个数的运算,叫做减法。
减法各部分间的关系:差=被减数-减数减数=被减数-差被减数=差+减数(3)加法和减法是互逆运算。
2、乘除法的意义和各部分间的关系。
(1)求几个相同加数的和的简便运算,叫做乘法。
乘法各部分间的关系:积=因数×因数因数=积÷另一个因数(2)已知两个因数的积与其中一个因数,求另一个因数的运算,叫做除法。
除法各部分间的关系:商=被除数÷除数除数=被除数÷商被除数=商×除数(3)乘法和除法是互逆运算。
3、关于“0”的运算(1)“0”不能做除数;字母表示:a÷0错误(2)一个数加上0还得原数;字母表示:a+0 = a (3)一个数减去0还得原数;字母表示:a-0 = a (4)被减数等于减数,差是0;字母表示:a-a = 0 (5)一个数和0相乘,仍得0;字母表示:a×0 = 0(6)0除以任何非0的数,还得 0;字母表示:0÷a(a≠0)=0 (7)被减数等于减数,差是0。
字母表示:A-A=0(8)被除数等于除数,商是1。
字母表示:A÷A=1(a不为0)4、四则运算顺序(1)在没有括号的算式里,如果只有加、减法或者只有乘、除法,都要从左往右按顺序计算。
(2)在没有括号的算式里,有乘、除法和加、减法、要先算乘除法,再算加减法。
(3)一个算式里既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的,最后算括号外面的有括号,要先算括号里面的,再算括号外面的;括号里面的算式计算顺序遵循以上的计算顺序。
5、租船问题两个原则:(1)尽可能多的租单座便宜的;(2)尽可能坐满。
被除数,除数,商和余数的和为383已知商为7余数4求被除数和除数各是多少?

被除数,除数,商和余数的和为383已知商为7余数4求被除
数和除数各是多少?
先上答案:被除数为326,除数为46。
这个题目中有四个数量,分别是带余数除法中的被除数,除数,商,余数。
我是王老师,致力于小学数学的精品问答!下面是我的解题思路
四者关系图
被除数,除数,商,余数的基本关系如下:
被除数=除数×商+余数
→ 被除数与除数的和:383-7-4=372
→ 被除数除以除数商7余4
解题思路一:设份数
设除数为1份,被除数则为7份+4
等量关系为:1份+7份+4=372
除数为1份量:(372-4)÷8=46;
被除数则为:46×7+4=326。
验算:326÷46=7……4 ,326+46+7+4=383 √
解题思路二:倍数关系
被除数除以除数商7余4,被除数+除数=372
被除数是除数的7倍多4,在两者和中减去4,正好是整数倍
→ (7+1)倍的除数=372-4=368
→ 除数为:368÷8=46
→ 被除数:372-46=326
解题思路三:列方程
解:设除数为X,被除数则为7X+4
→ 7X+4+X+7+4=383
→ X=46
解题思路都很明确,找准未知被除数和除数的数量关系,小心不要掉入陷阱哦。
练习题
你学会了吗?做下练习题吧!
1,被除数,除数,商和余数的和为933,已知商为40,余数16。
求被除数和除数各是多少?
2,143除以一个两位数,余数为11,那么商最大是多少,最小是多少?。
数字的商与余数知识点

数字的商与余数知识点在数学中,我们经常会遇到对除法运算的商和余数感兴趣的情况。
商和余数是除法运算的两个重要结果,对于解决实际问题和进行数学推理都起到关键作用。
本文将介绍商和余数的概念、性质以及在实际问题中的应用。
一、商和余数的定义1. 商:在除法运算中,被除数除以除数所得的整数部分,叫做商。
商可以表示为整数或小数,取决于是否能整除。
例如,将12除以5,得到商为2,表示为12 ÷ 5 = 2。
2. 余数:在除法运算中,被除数除以除数所得的余数,叫做余数。
余数永远是一个非负整数,并且小于除数。
例如,将12除以5,得到余数为2,表示为12 ÷ 5 = 2,余2。
商和余数的关系:被除数 = 商 ×除数 + 余数。
这个等式一般称为除法的基本性质。
二、商和余数的性质1. 商的性质:(1)如果被除数能整除除数,即余数为0,那么商为一个整数。
例如,将15除以5,得到商为3,没有余数。
(2)如果被除数不能整除除数,即余数不为0,那么商为一个小数或分数。
例如,将17除以5,得到商为3.4,保留一位小数。
2. 余数的性质:(1)余数总是非负整数,并且小于除数。
例如,将23除以7,得到商为3,余数为2,满足0 ≤ 余数< 除数。
(2)如果余数为0,说明被除数能整除除数。
例如,将15除以5,得到商为3,余数为0,说明15能被5整除。
三、商与余数的应用1. 整除判定:根据商和余数的定义,我们可以判断一个数能否被另一个数整除。
例如,判断120是否能被8整除,只需要计算120 ÷ 8,如果余数为0,则能整除;如果余数不为0,则不能整除。
2. 分配物品:商和余数的概念在实际生活中也有应用,例如,将一袋糖果平均分给几个人。
例如,有50颗糖果,要平均分给8个人,每个人能得到的糖果数量为商,剩下的不够分的糖果数量为余数。
3. 计算时间:商和余数的概念在计算时间上也有应用,例如,计算小时和分钟的转换。
小学二年级下册数学测量知识点总结归纳

小学二年级下册数学测量知识点总结归纳学校二班级下册数学测量知识点总结归纳 1数学测量知识点认识分米、毫米、千米分米用字母dm表示,1分米写成1dm毫米用字母mm表示,1毫米写成1mm千米用字母km表示,1千米写成1km米、分米、厘米、毫米、千米之间的换算1厘米=10毫米或1cm=10mm1分米=10厘米或1dm=10cm1米=100厘米或1m=100cm1米=10分米或1m=10dm1千米=1000米或1km=1000m苏教版学校二班级下册数学测量知识点:感受1分米、1毫米、1千米间的实际长度一张IC卡的厚度大约是1毫米1扎的长度大约是1分米公共汽车两站地间的距离大约是1千米依据详细情境选择合适的长度单位铅笔有多长(分米、毫米的认识)知识点:1. 通过实际测量,了解米、分米、厘米、毫米之间的关系。
1分米=10厘米或1dm=10cm;1米=10分米或 1m=10dm;1厘米=10毫米或1cm=10mm;2.知道1分米或1毫米的实际长度。
3.能利用长度单位之间关系进行单位换算1千米有多长(千米的认识)知识点:1.体验1千米有多长。
2.了解千米和米之间的关系; 1千米=1000米或1km=1000m。
3、能正确运用长度单位。
学校二班级下册数学测量知识点总结归纳 2一、用7、8、9的乘法口诀求商求商方法:想“除数×()=被除数”,再依据乘法口诀计算得商。
二、解决问题求一个数里有几个几,和把一个数平均分成几份,求每份是多少,都用除法计算。
混合计算一、混合计算混合运算,先乘除,后加减,有括号的要先算括号里面的,再算括号外面的。
只有加、减法或只有乘、除法,都要从左到右按顺次计算。
二、解决两步计算的实际问题1、想好先解决什么问题,再解决什么问题。
2、可以画图援助分析。
3、可以分布计算,也可以列综合算式。
有余数的除法一、有余数的除法1、有余数的除法的意义:在平均分一些物体时,有时会有剩余。
2、余数与除数的关系:在有余数的除法中,余数需要比除数小。
小学数学关系式
单价×数量 =Βιβλιοθήκη 总价 单产量×数量 = 总产量单产 = 总产÷ 数量
数量= 总产÷单产
工效×工时 = 工总量
工效=工总量÷工时
工时=工总量÷工效
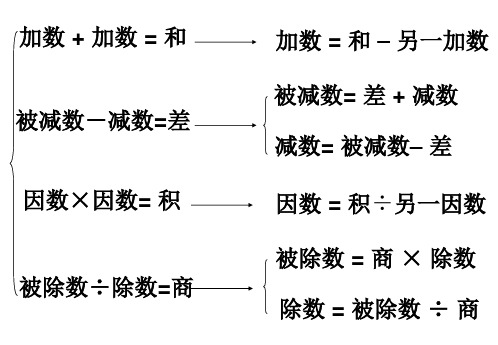
加数 + 加数 = 和
加数 = 和 – 另一加数 被减数= 差 + 减数
被减数-减数=差 因数×因数= 积
减数= 被减数– 差 因数 = 积÷另一因数
被除数 = 商 × 除数 被除数÷除数=商 除数 = 被除数 ÷ 商
加数 + 加数 = 和
加数 = 和 – 另一加数 被减数= 差 + 减数
被减数-减数=差 因数×因数= 积
减数= 被减数– 差 因数 = 积÷另一因数
被除数 = 商 × 除数 被除数÷除数=商 除数 = 被除数 ÷ 商
速度×时间 = 路程
速度 = 路程÷时间 时间= 路程÷速度 单价 =总价÷数量 数量=总价÷单价
分数与除法
真分数 (<1) 假分数 (≥1)
带分数(或整数)
约分(分子分母同时缩小相同的倍数) 分数的基本性质
通分(分子分母同时扩大相同的倍数)
倍数 约数
公倍数
公约数 质数 合数 互质数
最小公倍数
最大公约数
, 质因数
分解质因数
个位上是0、2、4、6、8的数,都能被2整除.
.
个位上是0或5的数,都能被5整除.
一个数的各位上的数的和能被3整除,这个数就 能被3整除.
单位“1” 分数的意义
分数单位 分数大小的比较
同分子
同分母 不同分子 (通分) 不同分母
速度×时间 = 路程
速度=路程÷时间 时间=路程÷速度 单价 =总价÷数量 数量=总价÷单价
