Gold序列与m序列仿真应用
扩频编码M序列和gold序列
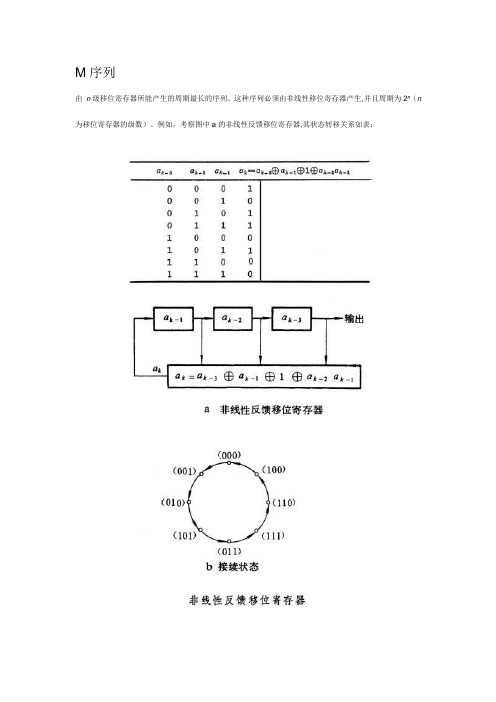
M序列由n级移位寄存器所能产生的周期最长的序列。
这种序列必须由非线性移位寄存器产生,并且周期为2n(n 为移位寄存器的级数)。
例如,考察图中a的非线性反馈移位寄存器,其状态转移关系如表:状态(a k-3,a k-2,a k-1)的接续状态是(a k-2,a k-1,a k),其中a k=a k-3嘰a k-1嘰1嘰a k-2a k-1是一种非线性逻辑。
从任一状态出发,例如从(000)出发,其接续状态恰好构成一个完全循环(图b),由此产生一个周期为23=8的3级序列。
M序列最早是用抽象的数学方法构造的。
它出现于组合数学的一些数学游戏中,例如L.欧拉关于哥尼斯堡的七桥问题等。
后来发现这种序列具有某些良好的伪随机特性。
例如,M序列在一个周期中,0与1的个数各占一半。
同时,同样长度的0游程与1游程也各占一半。
所有这些性质在数据通信、自动控制、光学技术和密码学诸领域中均有重要应用。
隐蔽通信内容的通信方式。
为了使非法的截收者不能理解通信内容的含义,信息在传输前必须先进行各种形式的变化,成为加密信息,在收信端进行相应的逆变化以恢复原信息。
电报通信、电话通信、图像通信和数据通信,都有相应的保密技术问题。
另一方面,为了从保密通信中获得军事、政治、经济、技术等机密信息,破译技术也在发展。
保密技术和破译技术是在相互对立中发展起来的。
1881年世界上出现了第一个电话保密专利。
电话保密开始是采用模拟保密或置乱的方法,即把话音的频谱或时间分段打乱。
置乱后的信号仍保持连续变化的性质。
在第二次世界大战期间,频域和时域的置乱器在技术上已基本成熟。
70年代以来,由于采用集成电路,电话保密通信得到进一步完善。
但置乱器仍是有线载波和短波单边带电话保密通信的主要手段。
模拟保密还可以采用加噪声掩盖、人工混响或逆向混响等方法,但因恢复后话音的质量大幅度下降或保密效果差,这些方法没有得到推广应用。
数字保密是由文字密码发展起来的。
数字信号(包括由模拟信号转换成的数字信号),由相同速率的密码序列加密,成为数字保密信号;保密信号传输到收信端后由同一密码序列去密,恢复原数字信号。
扩频编码M序列和gold序列

M序列由n级移位寄存器所能产生的周期最长的序列。
这种序列必须由非线性移位寄存器产生,并且周期为2n(n 为移位寄存器的级数)。
例如,考察图中a的非线性反馈移位寄存器,其状态转移关系如表:状态(a k-3,a k-2,a k-1)的接续状态是(a k-2,a k-1,a k),其中a k=a k-3嘰a k-1嘰1嘰a k-2a k-1是一种非线性逻辑。
从任一状态出发,例如从(000)出发,其接续状态恰好构成一个完全循环(图b),由此产生一个周期为23=8的3级序列。
M序列最早是用抽象的数学方法构造的。
它出现于组合数学的一些数学游戏中,例如L.欧拉关于哥尼斯堡的七桥问题等。
后来发现这种序列具有某些良好的伪随机特性。
例如,M序列在一个周期中,0与1的个数各占一半。
同时,同样长度的0游程与1游程也各占一半。
所有这些性质在数据通信、自动控制、光学技术和密码学诸领域中均有重要应用。
隐蔽通信内容的通信方式。
为了使非法的截收者不能理解通信内容的含义,信息在传输前必须先进行各种形式的变化,成为加密信息,在收信端进行相应的逆变化以恢复原信息。
电报通信、电话通信、图像通信和数据通信,都有相应的保密技术问题。
另一方面,为了从保密通信中获得军事、政治、经济、技术等机密信息,破译技术也在发展。
保密技术和破译技术是在相互对立中发展起来的。
1881年世界上出现了第一个电话保密专利。
电话保密开始是采用模拟保密或置乱的方法,即把话音的频谱或时间分段打乱。
置乱后的信号仍保持连续变化的性质。
在第二次世界大战期间,频域和时域的置乱器在技术上已基本成熟。
70年代以来,由于采用集成电路,电话保密通信得到进一步完善。
但置乱器仍是有线载波和短波单边带电话保密通信的主要手段。
模拟保密还可以采用加噪声掩盖、人工混响或逆向混响等方法,但因恢复后话音的质量大幅度下降或保密效果差,这些方法没有得到推广应用。
数字保密是由文字密码发展起来的。
数字信号(包括由模拟信号转换成的数字信号),由相同速率的密码序列加密,成为数字保密信号;保密信号传输到收信端后由同一密码序列去密,恢复原数字信号。
基于Gold序列的直接扩频通信系统仿真

频 技术 中应 用最 为广 泛 的就是 直接 扩频 技术 (i c Sqec pedS et m, Dr t eune ra pc u 简称 D S ) e S r SS。
1 God序 列 l
m序列是一种应用较为广泛的伪随机序列 , 是 带 由线 性 反馈 的移 位 寄 存 器 产 生 的 周期 最 长 的一种二进制序列 , 然而其优选特性较差 , 能 不
第 2 卷 第 2期 6
2 1 年 4月 02
商洛 学院学报
J un lo h n hoUnv ri o r a f a g ies y S t
V0.6 No2 1 . 2
Ap . 2 2 r 01
基 于 God序 列的直接扩频通信 系统仿真 l
李 亚 文
( 商洛学院物理与电子信息工程系, 陕西商洛 760) 200
定的, 除了军事 中应用外, 民用 中扩频技术也 在 正在显示 出它的强大生命力。 扩频技术正广泛用
76 0) 20 0
Ab t a t T e wo k n rn i l f d r c p e d s e t m o sr c : h r i g p i cp e o ie t s r a p cr u c mmu ia i n s se a a ay e i h i n c t y t mi n l s d wh c s o s r a e p cr m y G l o e・ q e c , n i l t g t i c mmu i a o t t b S mu i k y ped d se t u b o d c d s u n e a d smu a i h s o e n n c tn wi Ma l / i l .B h a n
gold序列的生成与相关特性仿真

Gold序列生成与相关性仿真1.1 references[1] 基于Matlab的Gold码序列的仿真与实现.[2] Code Selection for CDMA Systems.1.2 m序列的生成原理1.2.1生成本原多项式利用Matlab编程环境求解本原多项式,其运行结果如表1所示.选择n=7,采用7级移位寄存器,产生的序列周期是127,其程序如下所示.N=7; %以7级寄存器为例,并组其中的一组优选对:211,,217connections=gfprimfd(N,'all');表(1)n=7 本原多项式上面的多项式中,仅有9个是独立的.因为第一行和第十行,第二行和四行,第三行和第十六行,第五行和第八行,第六行和第十四行,第七行和第十三行,第九行和第十八行,第十一行和第十二行,第十五行和第十七行是两两对称的.用八进制数表示时,所选择的本原多项式为211、217、235、367、277、325、203、313和345共9条.在这9条本原多项式中,选择一个基准本原多项式,再按要求选择另一本原多项式与之配对,构成m序列优选对,对7级m序列优选对如下表:表(2)n=7 m序列所以优选对1.2.2构成移位寄存器根据产生Gold码序列的方法,从上述本原多项式中选择一对m序列优选对,以211作为基准本原多项式,217作为配对本原多项式,通过并联结构形式来产生Gold序列,生成gold 序列的结构如图(6)所示:图(6)Gold序列生成结构1.3 自相关函数仿真参数及初始值设定如下:N=7; %以7级寄存器为例,并组其中的一组优选对:211,,217connections=gfprimfd(N,'all');f1=connections(4,:); %取一组本原多项式序列,211f2=connections(16,:); %取另一组本原多项式序列,217registers1=[1 0 0 0 0 0 0];%给定寄存器的初始状态registers2=[1 0 0 0 0 0 0];%取相同的初始状态生成的gold 序列自相关函数如图(7)、(8)所示图(7) Gold 序列周期自相关函数结论:自相关函数取值集合{127,15,-1,-17}图(8)Gold 序列非周期自相关函数020406080100120140gold 序列周期自相关函数020406080100120140-40-2020406080100120140gold 序列非周期自相关函数1.4 互相关函数仿真时改变m序列寄存器初始状态,从而生成两个gold序列,求得互相关函数如图(9)(10)所示。
m序列产生及其特性实验

3G移动通信实验报告实验名称:扩频码仿真学生姓名:学生学号:学生班级:所学专业:实验日期:1.实验目的1.掌握m序列的特性、产生方法及应用。
2.. 掌握Gold序列的特性、产生方法及应用。
3. 掌握Gold序列与m序列的区别。
4. 掌握Walsh码的产生原理及特性。
5. 了解它们在3G系统中的应用。
2.实验内容找一个127长度的m序列,验证其特性自相关性之+互相关性质m+m=goldwalsh 128位长度求 2个互相关自相关m+walsh 互相关自相关3.实验代码clear all;A1=[0 0 0 0 0 1 1];A1=A1';D1=[0 0 0 0 0 0 1];Dm1=zeros(1,127);A2=[0 0 0 1 0 0 1];A2=A2';D2=[0 0 0 0 0 0 1];Dm2=zeros(1,127);for i=1:127;Dm1(1,i)=D1(1,7);Dm2(1,i)=D2(1,7);Dr1=mod(D1*A1,2);Dr2=mod(D2*A2,2);for n=7:-1:2D1(1,n)=D1(1,n-1);D2(1,n)=D2(1,n-1);endD1(1,1)=Dr1;D2(1,1)=Dr2;end%m序列自相关特性验证Dm11=zeros(1,127)Dm12=zeros(1,127)Dm1n=[Dm1,Dm1,Dm1];p1=zeros(1,253);Dm11=Dm1n(1,128:254);for i=-126:1:126n1=i+128;Dm12=Dm1n(1,n1:1:(n1+126));Dm1s=mod(Dm11+Dm12,2);sum0=0;sum1=0;for i1=1:127if Dm1s(1,i1)==0 sum0=sum0+1; else sum1=sum1+1;endendp1(1,i+127)=(sum0-sum1)/127;endsubplot(4,2,1);plot(-126:1:126,p1);title('m序列自相关特性');%m序列互相关特性验证Dm21=zeros(1,127)Dm22=zeros(1,127)Dm2n=[Dm2,Dm2,Dm2];p2=zeros(1,253);pmax=0;pmax_n1=0;pmin=0;pmin_n1=0;Dm21=Dm2n(1,128:254);for i=-126:1:126n1=i+128;Dm22=Dm1n(1,n1:1:(n1+126));Dm2s=mod(Dm21+Dm22,2);sum0=0;sum1=0;for i1=1:127if Dm2s(1,i1)==0 sum0=sum0+1; else sum1=sum1+1;endendp=(sum0-sum1)/127;if p>pmaxpmax=p;pmax_n1=n1;endif p>pminpmin=p;pmin_n1=n1;endp2(1,i+127)=p;endsubplot(4,2,2);plot(-126:1:126,p2);title('m序列互相关特性');%gold序列的自相关特性Dmg11=Dm21;Dmg12=Dm1n(1,pmax_n1:1:(pmax_n1+126)); Dmg1=mod(Dmg11+Dmg12,2);Dmg1n=[Dmg1,Dmg1,Dmg1];pg1=zeros(1,253);Dmg11=Dmg1n(1,128:254);for i=-126:1:126n1=i+128;Dmg12=Dmg1n(1,n1:1:(n1+126));Dmg1s=mod(Dmg11+Dmg12,2);sum0=0;sum1=0;for i1=1:127if Dmg1s(1,i1)==0 sum0=sum0+1; else sum1=sum1+1;endendpg1(1,i+127)=(sum0-sum1)/127;endsubplot(4,2,3);plot(-126:1:126,pg1);title('gold序列自相关特性');%gold序列的互相关特性Dmg21=Dm21;Dmg22=Dm1n(1,pmin_n1:1:(pmin_n1+126)); Dmg2=mod(Dmg21+Dmg22,2);Dmg2n=[Dmg2,Dmg2,Dmg2];pg2=zeros(1,253);for i=-126:1:126n1=i+128;Dmg22=Dmg2n(1,n1:1:(n1+126));Dmg2s=mod(Dmg1+Dmg22,2);sum0=0;sum1=0;for i1=1:127if Dmg2s(1,i1)==0 sum0=sum0+1; else sum1=sum1+1;endendpg2(1,i+127)=(sum0-sum1)/127;;endsubplot(4,2,4);plot(-126:1:126,pg2);title('gold序列自相关特性');%walsh序列产生H1=0;H2=[H1,H1;H1,H1*(-1)+1];H4=[H2,H2;H2,H2*(-1)+1];H8=[H4,H4;H4,H4*(-1)+1];H16=[H8,H8;H8,H8*(-1)+1];H32=[H16,H16;H16,H16*(-1)+1];H64=[H32,H32;H32,H32*(-1)+1];H128=[H64,H64;H64,H64*(-1)+1];%walsh序列的自相关特性W11=H128(2,1:128);W1n=[W11,W11,W11]pw1=zeros(1,253);for i=-126:1:126n1=i+128;W12=W1n(1,n1:1:(n1+127));W1s=mod(W11+W12,2);sum0=0;sum1=0;for i1=1:128if W1s(1,i1)==0 sum0=sum0+1; else sum1=sum1+1;endendpw1(1,i+127)=(sum0-sum1)/128;endsubplot(4,2,5);plot(-126:1:126,pw1);title('walsh序列自相关特性');%walsh序列的互相关特性W21=W11;W22=H128(8,1:128);W2n=[W22,W22,W22];pw2=zeros(1,253);for i=-126:1:126n1=i+128;W22=W1n(1,n1:1:(n1+127));W2s=mod(W21+W22,2);sum0=0;sum1=0;for i1=1:128if W2s(1,i1)==0 sum0=sum0+1; else sum1=sum1+1;endendpw2(1,i+127)=(sum0-sum1)/128;endsubplot(4,2,6);plot(-126:1:126,pw2);title('walsh序列互相关特性');%m+walsh序列产生mw1=mod([Dm1,0]+H128(2,1:128),2);mw2=mod([Dm2,0]+H128(8,1:128),2);%mw序列的自相关特性mwa1=mw1;mwan=[mwa1,mwa1,mwa1];pmwa=zeros(1,253);for i=-126:1:126n1=i+128;mwa2=mwan(1,n1:1:(n1+127));mwas=mod(mwa1+mwa2,2);sum0=0;sum1=0;for i1=1:128if mwas(1,i1)==0 sum0=sum0+1; else sum1=sum1+1;endendpmwa(1,i+127)=(sum0-sum1)/128; endsubplot(4,2,7);plot(-126:1:126,pmwa);title('m+walsh序列自相关特性');%mw序列的互相关特性mwb1=mw1;mwb2=mw2;mwbn=[mwb2,mwb2,mwb2];pmwb=zeros(1,253);for i=-126:1:126n1=i+128;mwb2=mwbn(1,n1:1:(n1+127));mwbs=mod(mwb1+mwb2,2);sum0=0;sum1=0;for i1=1:128if mwbs(1,i1)==0 sum0=sum0+1;else sum1=sum1+1;endendpmwb(1,i+127)=(sum0-sum1)/128;endsubplot(4,2,8);plot(-126:1:126,pmwb);title('m+walsh序列互相关特性'); 4.实验结果。
m 序列与gold 序列性能分析比较 包含程序

m序列与gold序列性能分析比较赵新宁北京邮电大学信息工程学院,北京(100876)E-mail:zhaoxinning106@摘要:在扩频系统中,伪随机序列具有十分重要的作用。
m序列和gold序列作为最常用和实用的伪随机序列,各有其特点。
本文分析其基本原理和产生方式,并特别对其性能方面做了仿真比较。
关键词:扩频;m序列;gold序列中图分类号:TN91在扩频通信系统中,伪随机序列是关键技术之一。
伪随机序列码的码型影响码序列的相关特性,序列长度决定了扩展频谱的宽度。
因此,在扩频系统中,对于伪随机序列有如下的要求:首先,伪随机序列的长度(即伪码比特率)应该足够长,能够满足扩展带宽的需要;第二,伪随机序列要具有尖锐的自相关特性(用作地址码),和良好的互相关特性;第三,伪随机序列要有足够多的数量,以满足码分多址的需求;第四,应具有近似噪声的频谱特性,即近似连续谱,且均匀分布;工程上易于实现。
通常,作为扩频通信系统工程实现上的伪随机序列一般是m序列和gold序列。
目前,在cdma2000系统中采用伪随机序列中的m序列(长码)来区分用户,wcdma系统中则用gold码来区分用户。
1.m序列的原理和产生在所有的伪随机序列中,m序列是最重要、最基本的一种伪随机序列。
而另外的多种伪随机序列都是由它引出并且产生的。
m序列是一种周期性的伪随机序列,又被称作最长线性移位寄存器序列;是由带线性反馈的移位寄存器产生的周期最长的序列[1]。
其周期为2n-1(n 为移位寄存器级数)。
m序列具有与随机噪声类似的尖锐的自相关特性,但它不是真正随机的,而是按照一定的规律周期性的变化。
这种特性使得m序列适合于工程应用。
m序列最大长度决定于移位寄存器的级数,而序列构成则决定于反馈系数的不同设置。
并非所有的反馈系数的设置都可以产生对应长度的m序列。
m序列具有平衡性和其游程特性,即一个序列周期中,“1”的数目与“0”的数目最多相差一个;同时,长度为n的元素游程出现的次数比长度为n+1的游程出现的次数多一倍。
Gold序列与m序列仿真应用

1. 绪论m序列具有优良的双值自相关特性,但互相关特性不是很好。
作为CDMA通信地址码时,由于互相关特性不理想,使得系统内多址干扰影响增大,且可用地址码数量较少。
在某些应用场合,利用狭义伪随机序列复合而成复合序列更为有利。
这是因为通过适当方法构造的复合序列具有某些特殊性质。
Gold序列就是一种复合序列,而且具有良好的自相关与互相关特性,地址码数量远大于m序列,且易于实现、结构简单,在工程上得到广泛应用。
表1是m序列和Gold序列的主要性能比较,表中为m序列的自相关峰值,为自相关主峰;为Gold序列的互相关峰值,为其自相关主峰。
从表1中可以看出:当级数n一定时,Gold序列中可用序列个数明显多于m序列数,且Gold序列的互相关峰值和主瓣与旁瓣之比都比m序列小得多,这一特性在实现码分多址时非常有用。
表1. m序列和Gold序列性能比较在引入Gold序列概念之前先介绍一下m序列优选对。
m序列优选对,是指在m序列集中,其互相关函数绝对值的最大值(称为峰值互相关函数)最接近或达到互相关值下限(最小值)的一对m序列。
设{ai}是对应于r次本原多项式F1(x)所产生的m序列, {bi} 是另一r次本原多项式F2(x)产生的m序列,峰值互相关函数满足(1)则m序列{ai}与{bi}构成m序列优选对。
例如:的本原多项式与所产生的m序列与,其峰值互相关函数。
满足式(1),故与构成m序列优选对。
而本原多项式所产生的m序列,与m序列的峰值互相关函数,不满足上式,故与不是m序列优选对。
2. Gold序列1967年,R·Gold指出:“给定移位寄存器级数r时,总可找到一对互相关函数值是最小的码序列,采用移位相加方法构成新码组,其互相关旁瓣都很小,且自相关函数和互相关函数均有界”。
这样生成的序列称为Gold码(Gold序列)。
Gold序列是m序列的复合序列,由两个码长相等、码时钟速率相同的m序列优选对的模2和序列构成。
m 序列与Gold 序列比较

中图分类号:TN914 . 42 文献标识码:A 文章编号:1009 - 2552(2006)06 - 0069 - 03
图 5(b) Gold 序列的互相关图形
面考虑,m 序 列 性 能 要 比 Glod 序 列 优 越 一 些,当 然 这同时也要付出占 用 更 多 的 频 带 资 源 的 代 价,在 这 个领 域,已 经 有 人 提 出 双 m 序 列 伪 随 机 序 列 扩 频[7] 的 观 点 ,所 以 对 这 一 课 题 还 有 待 进 一 步 深 入 研 究 。 参 考 文 献:
Abstract:As often used as spread sequence in all PN sequences,m sequence and Gold sequence have its respective characteristic,but there are some differences between them . The article compares the differences about performances from the basic principle,property and constructing means of the two sequences,and simulats them in relation part with MATLAB . Key words:spread spectrum;PN sequence
位的 m 序列之一为 111101011001000。 同 理,我 们 不
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 绪论m 序列具有优良的双值自相关特性,但互相关特性不是很好。
作为CDMA 通信地址码时,由于互相关特性不理想,使得系统内多址干扰影响增大,且可用地址码数量较少。
在某些应用场合,利用狭义伪随机序列复合而成复合序列更为有利。
这是因为通过适当方法构造的复合序列具有某些特殊性质。
Gold 序列就是一种复合序列,而且具有良好的自相关与互相关特性,地址码数量远大于m 序列,且易于实现、结构简单,在工程上得到广泛应用。
表1是m 序列和Gold 序列的主要性能比较,表中max ϕ为m 序列的自相关峰值,(0)s ϕ为自相关主峰;()t n 为Gold 序列的互相关峰值,(0)g ϕ为其自相关主峰。
从表1中可以看出:当级数n 一定时,Gold 序列中可用序列个数明显多于m 序列数,且Gold 序列的互相关峰值和主瓣与旁瓣之比都比m 序列小得多,这一特性在实现码分多址时非常有用。
表1. m 序列和Gold 序列性能比较在引入Gold 序列概念之前先介绍一下m 序列优选对。
m 序列优选对,是指在m 序列集中,其互相关函数绝对值的最大值(称为峰值互相关函数)max ()R τ最接近或达到互相关值下限(最小值)的一对m 序列。
设{a i }是对应于r 次本原多项式F 1(x )所产生的m 序列, {b i } 是另一r 次本原多项式F 2(x )产生的m 序列,峰值互相关函数满足12max2221()214r ab r r R τr ++⎧+⎪≤⎨⎪+⎩为奇数为偶数但不是的整倍数(1)则m 序列{a i }与{b i }构成m 序列优选对。
例如:6r =的本原多项式61()1F x x x =++与6522()1F x x x x x =++++所产生的m 序列{}i a 与{}i b ,其峰值互相关函数26222max ()17212117r ab R τ++=≤+=+=。
满足式(1),故{}i a 与{}i b 构成m 序列优选对。
而本原多项式65323()1F x x x x x =++++所产生的m 序列{}i c ,与m 序列{}i a 的峰值互相关函数max ()2317ac R τ=>,不满足上式,故{}i a 与{}i c 不是m 序列优选对。
2. Gold 序列1967年,R·Gold 指出:“给定移位寄存器级数r 时,总可找到一对互相关函数值是最小的码序列,采用移位相加方法构成新码组,其互相关旁瓣都很小,且自相关函数和互相关函数均有界”。
这样生成的序列称为Gold 码(Gold 序列)。
Gold 序列是m 序列的复合序列,由两个码长相等、码时钟速率相同的m 序列优选对的模2和序列构成。
每改变两个m 序列相对位移就可得到一个新的Gold 序列。
当相对位移1,2,…,2r -1个比特时,就可得到一族2r -1个Gold 序列,加上原来的两个m 序列,共有2r +1个Gold 序列,即21r r G =+ (2) 产生Gold 序列的移位寄存器结构有两种形式。
一种是乘积型,将m 序列优选对的特征多项式乘积作为新的特征多项式,根据此2r 次特征多项式构成新的线性移位寄存器,参见图(1),图中特征多项式为652()1G x x x x x =++++,6()1F x x x =++,其乘积多项式为12118653()()1F x G x x x x x x x =++++++。
另一种结构是模2和型,直接求两m 序列优选对输出序列的模2和序列,参见图(2)。
图1. 码长2为N=63的乘积型Gold 码发生器图2. 码长2为N=63的模2和型Gold 码发生器理论上可以证明,这两种结构是完全等效的。
它们产生的Gold 序列周期都是N=2r -1。
可以证明:复码的周期是组成复码的子码周期的最小公倍数。
由于组成复码Gold 序列的子码的周期都是N=2r -1,故Gold 序列的周期是N=2r -1。
由m 序列优选对模2和产生的Gold 序列族中2r -1个序列不再是m 序列,不再具有m 序列的特性。
任意两序列之间的互相关函数满足12max2221()214r ab r r R τr ++⎧+⎪≤⎨⎪+⎩为奇数为偶数但不是的整倍数(3)由于Gold 序列的这一特性,使得码族中任一码序列都可作为地址码,这样采用Gold 码族作地址码,其地址数大大超过了用m 序列作地址码的数量,所以Gold 序列在多址技术中得到了广泛的应用。
表2. Gold 序列的三值互相关函数特性Gold 码序列具有三值互相关函数的特性:当r 为奇数时,码族中约有50%的码序列有很低的互相关函数值(-1)(非归一化);当r 为偶数但不是4的整倍数时,码族中约有75%的码序列有很低的互相关函数值(-1) (非归一化)。
其三值互相关函数特性见表(2)。
Gold 序列自相关函数值的旁瓣取三值,互相关函数值也取三值,只是出现的位置不同。
Gold 码族同族(周期长度相同的序列)内互相关函数取值已有理论结果,但不同族之间互相关函数的取值尚无理论结果。
不同Gold 码族之间的互相关函数取值已不是三值而是多值,且互相关值已大大超过同族内的互相关值。
3. m 序列优选对的寻找前面在介绍Gold 码序列的构造时已指出,Gold 序列可由m 序列的优选对来构成,即要想构造出或求出Gold 码序列,首先要找到m 序列的优选对。
下面介绍一种寻找m 序列优选对的方法。
3.1优选对寻找方法1若a 是2r 阶有限域GF(2)的一个本原元,f 1(x )与f t (x )是2r 阶有限域GF(2)上的r 次本原多项式,a 是f 1(x )的首根,取122221214r r r t r ++⎧+⎪=⎨⎪+⎩为奇数为偶数,但不是的倍数 (4)使a t 为r 次本原多项式f t (x )的一个根,则以r 次本原多项式f 1(x )与f t (x )为特征多项式的m 序列就构成m 序列优选对。
例:对于r =7,N=2r -1=127,设a 是27阶有限域GF(2)的一个本原元,以a 为首根的本原多项式为731()1f x x x =++(附录1 r =7 1 211E) 由式(4)可求出17122212117r t ++=+=+=则以a 17为根的本原多项式f t (x )所产生的m 序列和f 1(x )所产生的m 序列构成m 序列优选对。
a 17是本原多项式f t (x )的一个根,但可能不是首根。
根据有限域的理论:若a t 是r 次不可约多项式f t (x )的一个根,那么121222,,,r ttta aa- 是f t (x ) 其余的r -1个根。
在计算时,需要注意由于a是2r 阶有限域的本原元,则有211r a-=。
据此,可以求出以a 17为根的本原多项式f t (x )的所有根:按幂次大小排列为91718346872,,,,,a a a a a a ,其中a 9为()t f x 的首根。
由附录1得75432()1t f x x x x x x x =++++++(附录1:r =7 9 277 E)上面介绍的方法有一个最大的局限,这就是该方法只能求出附录1中第一个多项式对应的m 序列优选对,事实上求解m 序列优选对的方法很多,下面再介绍一种。
3.2 优选对寻找方法2若a 是2r 阶有限域GF(2)的一个本原元,1()f x 与()t f x 是2r 阶有限域GF(2)上的r 次本原多项式,a k 是1()f x 的首根,t 按照式(4) 取值,令kt 的共轭类首元[kt ]r 为r 次本原多项式()t f x 首根的幂指数,即它的首根为[]rkt a,则以本原多项式()t f x 和1()f x 为特征多项式的m 序列构成m 序列优选对。
下面介绍kt 的共轭类首元的求法。
对于任意的正整数kt ,模N (21r =-)运算后,可用 r 位二进制数来表示为12310r r r ννννν---将其循环移位得到的一组(r 个)二进制数12310012311012223101r r r r r r r r r r r νννννννννννννννννννν-----------称为kt 的共轭类,而其中最小者称为kt 的共轭类首元,用符号[]r kt 来表示。
例:对于r =7,N =2r -1=127 ,设a 是27阶有限域GF(2)的一个本原元,设k =1,以a k =a 作为首根的本原多项式为731()1f x x x =++ (附录1: r =7 1 211 E) 由式(4)得17122212117r t ++=+=+=11717kt =⨯=的共轭类为0010001,1001000,0100100,0010010, 0001001,1000100,0100010共轭类首元7[][117]9r kt =⨯=,以a 9为首根的()t f x 为75432()1t f t x x x x x x =++++++4. 平衡Gold 序列及其产生方法4.1 平衡Gold 码Gold 码就其平衡性来讲,可以分为平衡码和非平衡码。
平衡码序列中一周期内1码元和0码元的个数之差为1,非平衡码中1码元和0码元的个数之差多于1。
平衡Gold 码和非平衡Gold 码的数量关系如下表所示。
表3.r 为奇数时的平衡Gold 码和非平衡Gold 码数量表表4.r 为偶数时的平衡Gold 码和非平衡Gold 码数量表例如,9r =的Gold 序列族,平衡码序列的数量为257个(包括2个m 序列),非平衡码序列的数量为256个。
在扩频通信中,扩频码平衡性(序列中0与1的均匀性)影响系统质量,平衡码具有更好的频谱特性。
在DS-SS 系统中,码的平衡性与载波抑制度有密切关系。
码不平衡时直接序列系统的载波泄漏增大,从而破坏扩频通信系统的保密性、抗干扰与抗侦破能力。
下表给出9~18级Gold 码对载波抑制度的影响,从表中可以看出:平衡码使载波抑制性能下降一半(分贝数),增加码长对载波抑制性能改善不是十分明显。
因此在DS-SS 系统中选用Gold码作扩频码时,应选用平衡Gold 码。
表5. 码的平衡性对载波抑制的影响4.2平衡Gold 码的产生方法为了寻找平衡码,R·Gold 给出特征相位描述:每一个最大长度序列都具有特征相位(序列的初始状态),当序列处于特征相位时,具有每隔一位抽样与原序列一样的特性。
这就是序列处于特征相位的特性。
设序列{}i a 的特征多项式()a f x 是一个r 次本原多项式,其特征相位由()/()a a g x f x 之比来确定。
其中()a g x 是生成函数,其次数等于或小于r ,求取算法[][]d ()d ()d ()()4d a a a a xf x r xg x xf x f x r x ⎧⎪⎪=⎨⎪+⎪⎩为奇数为偶数但不是的倍数(5)特征相位多项式定义为()()()a a g x G x f x =(6) 例:对于本原多项式3()1a f x x x =++,根据式(5),得()3d 1()1(mod 2)d a x x x g x x⎡⎤++⎣⎦==根据式(6)得特征相位多项式为3()11()()()1a a a g x G x f x f x x x===++ 长除得24789()1G x x x x x x x =+++++++因而得特征相位为111(r =3)。
