滤波器电路知识-经典版
滤波器基本知识

有源滤波器Active Filter(信号分离电路) 测量系统从传感器拾取的信号往往包含噪声和许多与被测量无关的信号,并且原始的测量信号经传输、放大、变换、运算及各种其它处理过程,也会混入各种不同形式的噪声,从面影响测量精度。
这些噪声一般随机性很强,很难从时域中直接分离,但限于其产生的机理,其噪声功率是有限的,并按一定规律分布于频率域中某一特定频带中。
滤波器(信号分离电路):从频域中实现对噪声的抑制,提取所需要的信号,是各种测控系统中必不可少的组成部分。
对滤波器的要求:(1)滤波特性好;(2)级联特性好(输入,输出);(3)滤波频率便于改变滤波器举例:心电信号的滤波:主要受到50Hz的工频干扰,采用50Hz陷波(带阻)滤波器。
一.滤波器的基本知识⒈按处理信号的形式分类:模拟:连续的模拟信号(又分为:无源和有源)数字:离散的数字信号。
⒉理想滤波器对不同频率的作用:通带内,使信号受到很小的衰减而通过。
阻带内,使信号受到很大的衰减而抑制,无过渡带。
⒊按频谱结构分为5种类型:滤波器对信号不予衰减或以很小衰减让其通过的频段称为通带;对信号的衰减超过某一规定值的频段称为阻带;位于通带和阻带之间的频段称为过渡带。
根据通带和阻带所处范围的不同,滤波器功能可分为以下几种:低通(Low Pass Filter)高通(High Pass Filter)带通(Band Pass Filter)带阻(Band Elimination Filter)全通(All Pass Filter)(理想)各种频率信号都能通过,但不同的频率信号的相位有不同的变化,一种移相器。
图2-2 按频谱结构分类的各种滤波器的衰减(1-幅频)特性几个定义:(1)通带的边界频率:一般来讲指下降—3dB即对应的频率。
(2)阻带的边界频率:由设计时,指定。
(3)中心频率:对于带通或带阻而言,用f0或ω0表示。
(4)通带宽度:用Δf0或Δω0表示。
(5)品质因数:衡量带通或带阻滤波器的选频特性。
滤波电路原理分析

滤波电路原理分析
滤波电路是一种电子电路,用于去除信号中的噪声或频率分量,只保留所需的信号成分。
其原理基于信号的频域特性,通过选择合适的滤波器类型和参数来实现。
滤波电路通常由被滤波的信号输入端、滤波器和输出端组成。
滤波器是该电路的核心部件,根据信号的频率特性选择适当的滤波器类型。
常见的滤波器类型包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
低通滤波器用于去除高频信号,只保留低频部分。
其工作原理是将高频信号的能量耗散或削弱,使得只有低频信号可以通过。
高通滤波器则相反,只保留高频信号。
带通滤波器用于选择一个特定频率范围内的信号,滤除其他频率的信号。
其原理是在一定频率范围内提供通路,而在其他频率上提供阻断。
带阻滤波器则用于滤除某个特定频率范围内的信号,只传递其他频率的信号。
其原理是在一定频率范围内提供阻断,而在其他频率上提供通路。
滤波电路根据滤波器的类型和参数,可以实现不同程度的滤波效果。
常见的滤波电路包括RC滤波器、RL滤波器、LC滤波
器和活动滤波器等。
它们通过选择合适的电容、电感或运算放大器等元件参数,实现对信号的滤波功能。
此外,滤波电路还需要考虑一些其他因素,如滤波器的频率响应、相移以及失真等。
这些因素会影响滤波电路对信号的处理效果,需要通过合理设计和选择元器件来解决。
总之,滤波电路的原理是根据信号的频域特性选择合适的滤波器类型和参数,实现对信号的滤波功能。
它在电子电路中起到去噪和频率选择的作用,广泛应用于各种电子设备和通信系统中。
各种滤波器及其典型电路

第一章滤波器1.1 滤波器的基本知识1、滤波器的基本特性定义:滤波器是一种通过一定频率的信号而阻止或衰减其他频率信号的部件。
功能:滤波器是具有频率选择作用的电路或运算处理系统,具有滤除噪声和分离各种不同信号的功能。
类型:按处理信号形式分:模拟滤波器和数字滤波器。
按功能分:低通、高通、带通、带阻、带通。
按电路组成分:LC无源、RC无源、由特殊元件构成的无源滤波器、RC有源滤波器按传递函数的微分方程阶数分:一阶、二阶、…高阶。
如图1.1中的a、b、c、d图分别为低通滤波器、高通滤波器、带通滤波器、带阻滤波器传输函数的幅频特性曲线。
图1.1 几种滤波器传输特性曲线.2、模拟滤波器的传递函数与频率特性(一)模拟滤波器的传递函数模拟滤波电路的特性可由传递函数来描述。
传递函数是输出与输入信号电压或电流拉氏变换之比。
经分析,任意个互相隔离的线性网络级联后,总的传递函数等于各网络传递函数的乘积。
这样,任何复杂的滤波网络,可由若干简单的一阶与二阶滤波电路级联构成。
(二)模拟滤波器的频率特性模拟滤波器的传递函数H(s)表达了滤波器的输入与输出间的传递关系。
若滤波器的输入信号Ui是角频率为w的单位信号,滤波器的输出Uo(jw)=H(jw)表达了在单位信号输入情况下的输出信号随频率变化的关系,称为滤波器的频率特性函数,简称频率特性。
频率特性H(jw)是一个复函数,其幅值A(w)称为幅频特性,其幅角∮(w)表示输出信号的相位相对于输入信号相位的变化,称为相频特性(三)滤波器的主要特性指标1、特征频率:(1)通带截止频f p=wp/(2π)为通带与过渡带边界点的频率,在该点信号增益下降到一个人为规定的下限。
(2)阻带截止频f r=wr/(2π)为阻带与过渡带边界点的频率,在该点信号衰耗(增益的倒数)下降到一人为规定的下限。
(3)转折频率f c=wc/(2π)为信号功率衰减到1/2(约3dB)时的频率,在很多情况下,常以fc作为通带或阻带截频。
滤波器电路基础
术 物
电容器CH 上的电压uH 等于输入电压ua ,即uH =ua ;而在开 理
关K1 打开、K2 闭合时,电容CH 上的电压反向加在运算放大器 基
输入端。这样,因运算放大器虚短路,在每个开关周期内, 础
端口上电压恰好反向。
第一章 上一页 回首页 下一页 回末页 结束 回目录
1
§1.3.2 滤波器 filter
1
§1.3.2 滤波器 filter
三、开关电容滤波器
开关电容滤波器是由 MOS开关、电容器和运算放大器构
成的一种离散时间模拟滤波器。
第
1、基本原理
一 章
最简单的开关电容滤波器见图1.3.2-13 。开关K置于左边
时,信号电压源u1向电容器C1充电;K倒向右边时,电容器C1 向电压源u2放电。当开关以高于信号的频率fc工作时,使C1
§1.3.2 滤波器 filter
第 一 章
光
电
信
息
技
术
物
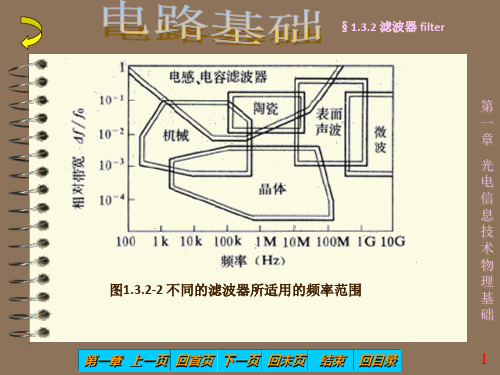
图1.3.2-2 不同的滤波器所适用的频率范围
理 基
础
第一章 上一页 回首页 下一页 回末页 结束 回目录
1
§1.3.2 滤波器 filter
滤波器工作在内阻抗为ZS的电压源与负载ZL 之间(见图 1.3.2-3),
第 一 章
光
电
信
息
技
图1.3.2-3 滤波器原理图
术
递函数为
H(s)
R
3 R R3
4
R1R
1 2 C1C 2
s2
R
1 1C1
1 R 2C1
R4 R 2R3C2
s
1 R1R 2C1C2
物 理 基 础
滤波器知识--侯飞飞版权

滤波器:(filter)是一种用来消除干扰杂讯的通讯器件,将输入或输出经过过滤而得到纯净的交流电。
概述:对特定频率的频点或该频点以外的频率进行有效滤除的电路,就是滤波器。
其功能就是得到一个特定频率或消除一个特定频率,利用这个特性可以将通过滤波器的一个方波群或复合噪波,而得到一个特定频率的正弦波原理图:滤波器的原理图滤波器:分类:按所通过信号的频段分为低通、高通、带通和带阻滤波器四种。
---A图示(图A)低通滤波器:它允许信号中的低频或直流分量通过,抑制高频分量或干扰和噪声。
高通滤波器:它允许信号中的高频分量通过,抑制低频或直流分量。
带通滤波器:它允许一定频段的信号通过,抑制低于或高于该频段的信号、干扰和噪声。
带阻滤波器:它抑制一定频段内的信号,允许该频段以外的信号通过。
滤波器性能的技术指标主要有:中心频率f0,即工作频带的中心带宽BW通带衰减,即通带内的最大衰减阻带衰减对于实际滤波器而言,考虑到实际的组成元件的品质因数的取值是一有限值(因为受限于材料与工艺的水平),所以所有工程上的实用滤波器都是有损滤波器,因此对于这些滤波器还应考虑通带内的最小插入衰减。
现代滤波器设计,多是采用滤波器变换的方法加以实现。
主要是通过对低通原型滤波器进行频率变换与阻抗变换,来得到新的目标滤波器。
理解带通滤波器的波形与调试方法:整个滤波器的仿真响应,可以理解为由n(n 为滤波器腔数)个相关联的单腔谐振,通过一定的组合构成。
除两个抽头腔外的每个谐振腔,形成一个在通带内的谐振峰,谐振峰之间通过不同大小的窗口耦合,排列在通带内的不同位置,形成通带。
左下图为滤波器的回波草图。
对于带通滤波器,有几个谐振腔(包括两个抽头腔)就会在通带内形成几个传输极点(即对应的图中红色圆圈内的波谷)。
回波与驻波相对应,回波曲线中的波谷,对应在驻波曲线中,也是一个波谷。
基站的基本结构带通滤波器的工作原理原始信号滤波器响应滤波后的信号带通滤波器的主要电气参数1. 带外抑制:带外抑制指,滤波器在工作频段以外的频点处对信号的衰减。
滤波器基本知识介绍课件

二维信号滤波器原理
图像处理
二维信号滤波器主要用于图像处 理,以改善图像的质量或提取图
像中的特定信息。
卷积与滤波
二维信号滤波器通过与图像进行卷 积来处理图像,以实现图性, 对图像中的特定方向进行增强或抑 制。此外,它们也可以在空间域内 对图像进行处理。
滤波器的主要功能是提取感兴趣的频率成分,同时抑制不需要的频率成分。它广 泛应用于通信、音频处理、图像处理、电力等领域。
滤波器的分类
根据不同的分类方法,滤波器可以分为 多种类型。常见的分类包括
4. 带阻滤波器(Notch Filter):允许 特定频率范围以外的信号通过,抑制特 定频率范围内的信号。
滤波器的优化设计
最优准则的选择
01
最小均方误差准则( MMSE)
该准则以最小化输出信号的均方误差 为目标,通过优化滤波器参数,使得 输出信号与期望信号之间的误差最小 。
02
最大信噪比准则( MSNR)
该准则以最大化滤波器输出信号的信 噪比为目标,通过优化滤波器参数, 使得输出信号的信噪比最大化。
03
号处理和控制系统等领域。
基于变换域的滤波器
频域
频域滤波器是基于傅里叶变换的,它可以将时域信号转换到频域,从而更容易 地去除噪声和干扰。
小波变换域
小波变换域滤波器是基于小波变换的,它可以将信号分解成不同的频率分量, 并对每个分量进行独立的滤波处理。这种方法在信号处理中得到了广泛应用。
05
CATALOGUE
在保证滤波器稳定性的前提下,尽量减小滤波器 的参数数量。
设计过程的优化算法
梯度下降法
该算法通过计算目标函数对优化变量的梯度,并按照负梯度方向 更新优化变量的值,从而逐渐逼近最优解。
滤波器电路分析

图5-3 m推演型LPF的特性示例
图5-5
表2 m推演型低通滤波电路元件归一化参数表
续表2
(9) 将上式(6)~(9)带入电路中得下图m推演型低通滤波电路,陷波点为 130MHZ,截止频率为100MHZ。
m推演型低通滤波电路,在f=130MHZ处有一个陷波点
仿真结果
回波损耗频率特性曲线,当在陷波点f=130MHZ时,电路的回拨损 耗最大,信号反射最厉害
2A
63.66 V
u1 (t ) [63.66 42.44cos(t ) 8.488cos(2t ) 3.638cos(3t ) ...]V
2. 对于基波,先计算转移电压比
| H ( j ) | 1 1 C
2
1 1 10
设计RC二阶低通滤波器电路,可以通过将两个RC一阶低通滤波电路 级联等到,RC二阶低通滤波电路。
图 14-9
下面给出一个fc=200KHZ的RC二阶低通滤波电路的仿真电路图
仿真结果:RC二阶电路的幅频特性 曲线,截止频率为28.199KHZ,
RC二阶高通滤波电路相频特性曲线
3.3RC二阶高通滤波电路
RC一阶高通滤波电路仿真原理图
RC一阶高通滤波电路幅频特性曲线,从图中可以看 出电路在幅度增益下降3.232dB时,截止为 100.901KHZ,滤波电路的性能能满足设计指标。
RC一阶高通滤波电路相频特性曲线,从图中可任意看 出当f=100.697KHZ时,相角超前46.497 deg。
3.3RC二阶低通滤波电路
图10
RC二阶高通滤波电路幅度表达式
RC二阶高通滤波电路截止频率
RC滤波电路所实现的频率特性,也可由相应的 RL电路来实现。在低频率应用的条件下,由于
什么是滤波电路

什么是滤波电路滤波电路是一种常见的电子电路,用于去除信号中的噪声或者选择特定频率范围内的信号。
滤波电路在各个电子设备中广泛应用,包括音频设备、通信设备、电源设备等等。
本文将介绍滤波电路的基本原理、分类、常见应用及工作原理。
一、滤波电路的基本原理滤波电路通过选择特定频率范围内的信号,或者去除信号中的杂波和干扰,实现信号的处理和提取。
其基本原理是利用电容、电感或者二者的组合,对不同频率的信号进行衰减或放大。
电容或电感可以根据频率的不同,阻止或允许信号通过。
二、滤波电路的分类滤波电路按照频率特性的不同可以分为低通滤波电路、高通滤波电路、带通滤波电路和带阻滤波电路。
1. 低通滤波电路低通滤波电路允许低频信号通过,而阻止高频信号通过。
通常用于去除高频噪声或提取低频信号。
常见的低通滤波电路有RC低通滤波电路和RL低通滤波电路。
2. 高通滤波电路高通滤波电路允许高频信号通过,而阻止低频信号通过。
通常用于去除低频噪声或提取高频信号。
常见的高通滤波电路有RC高通滤波电路和RL高通滤波电路。
3. 带通滤波电路带通滤波电路允许特定范围内的信号通过,而阻止其他频率范围内的信号通过。
常见的带通滤波电路有RC带通滤波电路和LC带通滤波电路。
4. 带阻滤波电路带阻滤波电路阻止特定范围内的信号通过,而允许其他频率范围内的信号通过。
常见的带阻滤波电路有RC带阻滤波电路和LC带阻滤波电路。
三、滤波电路的常见应用滤波电路在各个领域中都有广泛的应用。
以下是滤波电路的一些常见应用:1. 音频设备中的滤波电路音频设备中常用的滤波电路有低通滤波器,用于去除高频噪声,以确保音频信号的清晰度和质量。
2. 通信设备中的滤波电路通信设备中使用滤波电路用于信号处理和频率选择。
例如,在收音机中使用带通滤波电路选择特定的广播频率。
3. 电源设备中的滤波电路电源设备中常用的滤波电路有电源滤波器,用于去除电源信号中的噪声和纹波电压,以确保电子设备的正常工作和稳定性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x ( t ) (t )
Y (S ) H (S ) X (S )
y (t ) h(t )
H ( j )
Y ( j ) 热能工程系 X ( j )
2
无源滤波 R, C, L 模拟滤波器
有源滤波 R, C, 运算放大器
一、滤波器的传递函数 理想幅频特性 H(j) H(j)
H() 巴特沃思 贝塞尔 切比雪夫
2018/5/20 热能工程系
/
0
9
二、RC有源滤波器
无限增益多路反馈电路 设A0 , Ib vi
根据电流守恒定律,则
Y1 Y4 Y3 Y5
v1
Y2
v2
vo
(vi v1 )Y1 (v1 vo )Y4 v1Y2 (v1 v2 )Y3
n=1,2,...
H ( s)
1 1 Bn ( s) ( s s1 )(s s2 ) ( s sn )
2
例: n = 1 s1= -1 Bn(s)=s+1 H(s)=1/(s+1)
1 1 j H ( j ) j 1 1 2
H ( j )
与
H ( s) s2
2 H 00
0
q
比较得
2 s 0
0
1 R3 R4C2C5
截止角频率
H0
R4 R1
增益因子
RR 1 C5 3 4 q C2 R1
2018/5/20
R4 R3
R2 R4
选择性因子
11
热能工程系
2. 高通滤波器
例:低通归一化二阶滤波器
H ( s) H0 s s2 1 q
H0
1 s s
2018/5/20
H0s2 H ( s) 2 s 2 1 1 1 s 1 1 q s q s
热能工程系 5
1. 巴特沃思近似
幅频函数 传递函数
H ( j )
2
1 1 2n
• 将Y1,Y3,Y4电容,Y2,Y5 用电阻,带入上式 vi
– 高频下:C1,C3,C4相当于 短路,传输函数为1 – 低频下: C1,C3,C4相当 于开路,传输函数= 0 C1 C4 C3 R5
v1
R2
vo
C1 2 s C4 H ( s) s C1 1 1 1 s2 R5 C3C4 C4 C3 R2 R5C3C4
(v1 v2 )Y3 (v2 vo )Y5
v2 vo 0 Ao
H ( s) vo ( s) Y1Y3 vi ( s) Y5 (Y1 Y2 Y3 Y4 ) Y3Y4
热能工程系 10
由此解得
2018/5/20
1. 低通滤波器
• 将Y1,Y3,Y4用电阻1/R, Y2,Y5用电容CS,带入上 vi 式
6
热能工程系
2. 切比雪夫近似
H ( j )
2
1 2 1 Tn ( )
H ( s)
H0 Vn ( s )
Tn() Vn()
n阶切比雪夫多项式 切比雪夫滤波多项式
n=1 n=2
0.5db波纹 S+2.863 S2+1.425S+1.516
切比雪夫多项式Vn()
n=1 n=2
2
1 12
2
1 12
n=2
H ( s)
Bn (s) s2 2s 1
H ( j )
2
巴特沃思多项式
1 ( j )2 2 j 1
1 s2 2s 1
H ( j )
2018/5/20
2
1 (1 2 ) 2 ( 2 ) 2
1 1 1 (1 2 ) 2 2 2 1 2 2 4 2 2 1 4
热工实验技术与数据处理
第 三 讲
李
2018/5/20
彦
1
热能工程系
第三节
模拟滤波
模拟滤波器是对模拟信号实行线性滤波的一种线性非 时变系统 ha(t) xa(t) ya(t) H(j) X(j) Y(j) X(j) Y(j) H(j)
动态特性的描述
(1)单位冲激响应 (2)传递函数 (3)频率特性
1db波纹 S+1.965 S2+1.098S+1.103
2018/5/20
热能工程系
7
3. 贝塞尔近似
H ( s) H0 En ( s )
En()贝塞尔滤波多项式
n=1 n=2
S+1 S2+3S+3
2018/5/20
热能工程系
8
4. 三种近似方法的特点
巴特沃思: 通带内幅频曲线的幅度平坦,最平幅度逼近, 相移与频率的关系不是很线性的,阶跃响应有过冲。 切比雪夫: 下降最陡,但通带之间幅频曲线有波纹。 贝塞尔: 相移和频率之间有良好的线性关系,阶跃响应过冲 小,但幅频曲线的下降陡度较差。
H0 0 H0 0 H0
H(j) H0 1 2
H(j)
1 2
an s n an1s n1 a0 H ( s) n s bn1s n1 b0
二阶传输函数
a2 s 2 a1s a0 H ( s) 2 s b1s b0
热能工程系 3
2018/5/20
低通
H ( s) s2
2 H 00
0
q
2 s 0
带通
H ( s)
H 0 0 s2
0
q
s q
2 s 0
高通
H ( s) s
2
0
q
H 0s2 s
2 0
带阻
H ( s)
2 H 0 (0 s2 )
s2
0
q
2 s 0
其中: H0:任意增益因子 0:特征频率, 对低通,高通, 0是截止频率 带通,带阻, 0是截止频率 q: 选择性因子
近似方法
巴特沃思近似 切比雪夫近似 贝塞尔近似
热能工程系 4
2018/5/2 得到带阻滤波器
通过保角变换
1 (s ) s s 1 ( s ) 1 s s
– 高频下:C2,C5相当于短 路,传输函数为0 – 低频下: C2,C5相当于开 路,传输函数-R4/R1 R1 R4 R3 C5
v1
C2
v2
vo
H ( s)
1 / R1R3C2C5 s 1 1 1 1 s2 C2 R1 R3 R4 R3 R4C2C5
