(完整word版)高中数学符号意义
(完整word版)高数符号大全

高等数学常用符号大全及符号的含义acsc xy,余割函数反函数在x处的值,即 x = csc y θ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a•ba、b向量的点积(a•b)a、b向量的点积|v|向量v的模|x|数x的绝对值表示求和,通常是某项指数。
下边界值写在其下部,上边界值写在Σ其上部。
如j从1到100 的和可以表示成:。
这表示 1+ 2 + … + nM表示一个矩阵或数列或其它|v>列向量,即元素被写成列或可被看成k×1阶矩阵的向量<v|被写成行或可被看成从1×k阶矩阵的向量dx变量x的一个无穷小变化,dy, dz, dr等类似ds长度的微小变化ρ变量 (x2+ y2+ z2)1/2或球面坐标系中到原点的距离r 变量 (x2+ y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式,其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值,为一个面积、体积或超体积d2f/dx2f关于x的二阶导数f(2)(x)同样也是f关于x的二阶导数f(k)(x)f关于x的第k阶导数,f(k-1)(x)的导数T 曲线切线方向上的单位向量,如果曲线可以描述成 r(t), 则T =(dr/dt)/|dr/dt|ds沿曲线方向距离的导数κ曲线的曲率,单位切线向量相对曲线距离的导数的值:|dT/ds|NdT/ds投影方向单位向量,垂直于TB平面T和N的单位法向量,即曲率的平面τ曲线的扭率: |dB/ds|g重力常数F力学中力的标准符号k弹簧的弹簧常数pi第i个物体的动量H物理系统的哈密尔敦函数,即位置和动量表示的能量{Q, H}Q, H的泊松括号以一个关于x的函数的形式表达的f(x)的积分函数f 从a到b的定积分。
(完整word版)高中数学公式及知识点总结大全(精华版)

高中文科数学公式及知识点速记一、函数、导数1、函数的单调性(1)设2121],,[x x b a x x <∈、那么],[)(0)()(21b a x f x f x f 在⇔<-上是增函数; ],[)(0)()(21b a x f x f x f 在⇔>-上是减函数.(2)设函数)(x f y =在某个区间内可导,若0)(>'x f ,则)(x f 为增函数;若0)(<'x f ,则)(x f 为减函数.2、函数的奇偶性对于定义域内任意的x ,都有)()(x f x f =-,则)(x f 是偶函数; 对于定义域内任意的x ,都有)()(x f x f -=-,则)(x f 是奇函数。
奇函数的图象关于原点对称,偶函数的图象关于y 轴对称。
3、函数)(x f y =在点0x 处的导数的几何意义函数)(x f y =在点0x 处的导数是曲线)(x f y =在))(,(00x f x P 处的切线的斜率)(0x f ',相应的切线方程是))((000x x x f y y -'=-.*二次函数: (1)顶点坐标为24(,)24b ac b a a --;(2)焦点的坐标为241(,)24b ac b a a-+- 4、几种常见函数的导数①'C 0=;②1')(-=n n nxx ; ③x x cos )(sin '=;④x x sin )(cos '-=;⑤a a a xx ln )('=;⑥xx e e =')(; ⑦a x x a ln 1)(log '=;⑧xx 1)(ln '= 5、导数的运算法则(1)'''()u v u v ±=±. (2)'''()uv u v uv =+. (3)'''2()(0)u u v uv v v v -=≠. 6、会用导数求单调区间、极值、最值7、求函数()y f x =的极值的方法是:解方程()0f x '=.当()00f x '=时: (1) 如果在0x 附近的左侧()0f x '>,右侧()0f x '<,那么()0f x 是极大值; (2) 如果在0x 附近的左侧()0f x '<,右侧()0f x '>,那么()0f x 是极小值. 指数函数、对数函数分数指数幂(1)m na =0,,a m n N *>∈,且1n >).(2)1m nm naa-==(0,,a m n N *>∈,且1n >).根式的性质(1)当na =; 当n,0||,0a a a a a ≥⎧==⎨-<⎩.有理指数幂的运算性质(1) r sa a⋅=(2) ()r s rsa a=(3)()r rab a b=注:若a>0,指数幂都适用..(0,1,0)a a N>≠>..1a≠,0m>,且1m≠,0N>).对数恒等式:).推论logmnab).常见的函数图象822sin cosθθ+9απ±kα看成锐角时该函数的符号;αππ±+2kα看成锐角时该函数的符号。
(完整word版)高中数学公式及知识点总结大全(精华版)

高中文科数学公式及知识点速记一、函数、导数1、函数的单调性(1)设2121],,[x x b a x x <∈、那么],[)(0)()(21b a x f x f x f 在⇔<-上是增函数; ],[)(0)()(21b a x f x f x f 在⇔>-上是减函数.(2)设函数)(x f y =在某个区间内可导,若0)(>'x f ,则)(x f 为增函数;若0)(<'x f ,则)(x f 为减函数.2、函数的奇偶性对于定义域内任意的x ,都有)()(x f x f =-,则)(x f 是偶函数; 对于定义域内任意的x ,都有)()(x f x f -=-,则)(x f 是奇函数。
奇函数的图象关于原点对称,偶函数的图象关于y 轴对称。
3、函数)(x f y =在点0x 处的导数的几何意义函数)(x f y =在点0x 处的导数是曲线)(x f y =在))(,(00x f x P 处的切线的斜率)(0x f ',相应的切线方程是))((000x x x f y y -'=-.*二次函数: (1)顶点坐标为24(,)24b ac b a a --;(2)焦点的坐标为241(,)24b ac b a a-+- 4、几种常见函数的导数①'C 0=;②1')(-=n n nxx ; ③x x cos )(sin '=;④x x sin )(cos '-=;⑤a a a xx ln )('=;⑥xx e e =')(; ⑦a x x a ln 1)(log '=;⑧xx 1)(ln '= 5、导数的运算法则(1)'''()u v u v ±=±. (2)'''()uv u v uv =+. (3)'''2()(0)u u v uv v v v -=≠. 6、会用导数求单调区间、极值、最值7、求函数()y f x =的极值的方法是:解方程()0f x '=.当()00f x '=时: (1) 如果在0x 附近的左侧()0f x '>,右侧()0f x '<,那么()0f x 是极大值; (2) 如果在0x 附近的左侧()0f x '<,右侧()0f x '>,那么()0f x 是极小值. 指数函数、对数函数分数指数幂(1)m na =0,,a m n N *>∈,且1n >).(2)1m nm naa-==(0,,a m n N *>∈,且1n >).根式的性质(1)当na =; 当n,0||,0a a a a a ≥⎧==⎨-<⎩.有理指数幂的运算性质(1) r sa a⋅=(2) ()r s rsa a=(3)()r rab a b=注:若a>0,指数幂都适用..(0,1,0)a a N>≠>..1a≠,0m>,且1m≠,0N>).对数恒等式:).推论logmnab).常见的函数图象822sin cosθθ+9απ±kα看成锐角时该函数的符号;αππ±+2kα看成锐角时该函数的符号。
(完整word版)物理公式和符号汇总(word文档良心出品)

数学物理里面的公式符号读法:A :阿尔法AlphaB :贝塔Betar :丫伽玛Gamma△ 3德尔塔DelteE飞艾普西龙Epsilonz z捷塔ZetaE n依塔Eta0刃西塔ThetaI:艾欧塔IotaK K喀帕KappaA入:拉姆达LambdaM 口缪MuN v拗NuS辽克西XiO o欧麦克轮Omicronn n 派PiP p 柔Rho 刀:(r西格玛SigmaT T套TauY u宇普西龙Upsilon① © fai PhiX x器ChiW书普赛PsiQ ①欧米伽Omega 符号大全(1)数量符号:女口:i, 2 + i, a, x,自然对数底e,圆周率n(2)运算符号:如加号(+),减号(-),乘号(X或•,除号(^或/),两个集合的并集(U),交集(0),根号(),对数(log, lg,ln),比(:),微分(d),积分(力等。
(3)关系符号:如“堤等号,“或“是近似符号,“是不等号,'”是大于符号,是小于符号,“表示变量变化的趋势,为'是相似符号,奎”是全等号, 是平行符号,1 ”是垂直符号,& ”是正比例符号,& '是属于符号等。
4)结合符号:如圆括号“()”方括号“[,]”花括号“{括}”线“—”(5)性质符号:如正号“ +,负号-“”绝对值符号11(6)省略符号:如三角形(△),正弦(sin) , X的函数(f(x)),极限(lim), 因为(•.•),所以(•••),总和(刀),连乘(n,从N个元素中每次取出R 个元素所有不同的组合数(C ),幕(aM),阶乘(!)等。
符号意义g无穷大PI 圆周率|x| 函数的绝对值U集合并n集合交>大于等于<小于等于三恒等于或同余In(x)以e为底的对数lg(x) 以10 为底的对数floor(x) 上取整函数ceil(x) 下取整函数x mod y 求余数小数部分x - floor(x)/ f(x)不定积分/ [a:b]f(x) 到X^a的定积分P 为真等于1 否则等于0刀[1 < k < n]f对n进行求和,可以拓广至很多情况如:刀[n is prime][n < 10]f(n)刀刀[1 < i奇〃2c n] lim f(x) (x->?) 求极限f(z) f 关于z 的m 阶导函数C(n:m)组合数,n 中取m P(n:m) 排列数m|n m 整除n m丄n m与n互质a € Aa属于集合A #A 集合A 中的元素个数初中物理公式:物理量(单位) 公式备注公式的变形速度V (m/S) v= S :路程/t :时间重力G (N) G=mg m :质量g:9.8N/kg 或者10N/kg密度P(kg/m3 ) p =m/V m:质量V :体积合力F合(N) 方向相同:F合=F1+F2 方向相反:F合=F1 —F2方向相反时,F1>F2 浮力F 浮(N) F浮=G物一G视G视:物体在液体的重力浮力 F 浮(N) F浮=G物此公式只适用物体漂浮或悬浮浮力F 浮(N) F浮=G排=m排g= p液gV排G 排:排开液体的重力m 排:排开液体的质量p液:液体的密度V 排:排开液体的体积(即浸入液体中的体积)杠杆的平衡条件F1L1= F2L2 F1 :动力L1 :动力臂F2 :阻力L2 :阻力臂定滑轮F=G 物S=h F :绳子自由端受到的拉力G 物:物体的重力S :绳子自由端移动的距离h :物体升高的距离动滑轮F= (G物+G轮)S=2 h G 物:物体的重力G 轮:动滑轮的重力滑轮组F= (G物+G轮) S=n h n :通过动滑轮绳子的段数机械功W(J) W=Fs F :力s :在力的方向上移动的距离有用功W有总功W总W有=G物hW总=Fs适用滑轮组竖直放置时机械效率n = x 100%功率P(w)P=W :功t :时间压强p (Pa)P=F :压力S:受力面积液体压强p(Pa)P=p gh p液体的密度h :深度(从液面到所求点的竖直距离)热量Q(J)Q=cm △ t c:物质的比热容m :质量△ t:温度的变化值燃料燃烧放出的热量Q(J)Q=mq m :质量q:热值常用的物理公式与重要知识点一.物理公式单位)公式备注公式的变形串联电路电流I(A) 1=11=12= ..... 电流处处相等串联电路电压U(V) U=U1+U2+……串联电路起分压作用串联电路电阻R ( Q)R=R1+R2•+…• •并联电路电流I(A) 1=11+12+……干路电流等于各支路电流之和(分流)并联电路电压U(V) U=U仁U2……并联电路电阻R ( Q)= + + ……欧姆定律I= 电路中的电流与电压成正比,与电阻成反比电流定义式I=Q:电荷量(库仑)t:时间(S)电功W(J)W=Ult=Pt U :电压I:电流t:时间P:电功率电功率P=UI=I2R=U2/R U:电压I :电流R:电阻电磁波波速与波长、频率的关系C=Xv C物理量单位公式名称符号名称符号质量m 千克kg m=pv 温度t 摄氏度°C 速度v 米/秒m/s v=s/t 密度p 千克/米3 kg/m3 p=m/v 力(重力)F 牛顿(牛)N G=mg 压强P 帕斯卡(帕)Pa P=F/S功W 焦耳(焦)J W=Fs功率P 瓦特(瓦)w P=W/t电流I 安培(安) A I=U/R电压U 伏特(伏)V U=IR电阻R 欧姆(欧)R=U/I电功W 焦耳(焦)J W=UIt电功率P 瓦特(瓦)w P=W/t=UI热量Q 焦耳(焦)J Q=cm(t-t °)比热 c 焦/(千克°C) J/(kg °C)真空中光速3X108米/秒g 9.8 牛顿/千克15°C 空气中声速340 米/秒初中物理公式汇编【力学部分】1、速度: V=S/t2、重力:G=mg3、密度:p =m/V4 、压强:p=F/S5、液体压强:p=p gh6、浮力:(1)、F浮二F' —F (压力差)(2)、F浮二G —F (视重力)(3)、F浮二G (漂浮、悬浮)(4)、阿基米德原理:F浮=G排二p液gV排7、杠杆平衡条件:F1 L1 = F2 L28、理想斜面:F/G = h/L9、理想滑轮:F=G/n10、实际滑轮:F= (G + G动” n (竖直方向)11、功:W = FS = Gh (把物体举高)12、功率:P =W/t = FV13、功的原理:W手=W机14、实际机械:W总=W有+ W额外15、机械效率:n= W 有/W总16 、滑轮组效率:(1)、n= G/ nF(竖直方向)(2)、n= G/(G + G动)(竖直方向不计摩擦)(3)、n= f / nF (水平方向)【热学部分】1、吸热:Q 吸=Cm(t —tO) = Cm^t2、放热:Q 放=Cm(tO —t) = Cm^t3、热值:q = Q/m4、炉子和热机的效率:n= Q有效利用/Q燃料5、热平衡方程:Q放=Q吸6、热力学温度:T = t + 273K【电学部分】1、电流强度:1= Q电量/t2、电阻:R=p L/S3、欧姆定律:I= U/R4、焦耳定律:(1)、Q = I2Rt普适公式)(2)、Q=UIt=Pt=UQ 电量= U2t/R (纯电阻公式) 5、串联电路:(1)、I=I1=I2(2)、U = U1 + U2(3)、R = R1 + R2(4)、U1/U2 = R1/R2 (分压公式)(5)、P1/P2 = R1/R26 、并联电路:(1)、1= 11 + I2(2)、U = U1 = U2(3)、1/R=1/R1+1/R2 [ R=R1R2/(R1 +R2)](4)、I1/I2 = R2/R1 (分流公式)(5)、P1/P2=R2/R17 定值电阻:(1)、I1/I2=U1/U2(2)、P1/P2=I12/I22(3)、P1/P2=U12/U228 电功:(1)、W=UIt=Pt=UQ (普适公式)(2)、W=I2Rt=U2t/R (纯电阻公式)9 电功率:(1)、P=W/t=UI (普适公式)(2)、P=I2R=U2/R (纯电阻公式)【常用物理量】1、光速:C = 3x108m/s (真空中)2、声速:V = 340m/s (15 C)3、人耳区分回声:>0 1s4、重力加速度:g = 9. 8N/kg〜10N/kg5、标准大气压值:760毫米水银柱高=1 . 01 X105Pa6、水的密度:p= 1 . 0X03kg/m37、水的凝固点:0C8、水的沸点:100C9、水的比热容:C= 4.2X103J/(kg? C )10 、元电荷:e= 1 .6X10-19C11 、一节干电池电压:1.5V12 、一节铅蓄电池电压:2V13、对于人体的安全电压: < 36V(不高于36V)14、动力电路的电压:380V15 、家庭电路电压:220V16、单位换算:(1 )、1m/s = 3. 6km/h(2)、1g/cm3 = 103kg/m3(3)、1kw?h = 3. 6X106J 初中物理公式汇编【力学部分】1 、速度:V=S/t2、重力:G=mg3、密度:p =m/V4 、压强:p=F/S5、液体压强:p=p gh6、浮力:(1)、F浮二F' —F (压力差)(2)、F浮二G —F (视重力)(3)、F浮二G (漂浮、悬浮)(4)、阿基米德原理:F浮=G排二p液gV排7、杠杆平衡条件:F1 L1 = F2 L28、理想斜面:F/G = h/L9、理想滑轮:F=G/n10、实际滑轮:F= (G + G动” n (竖直方向)11、功:W = FS = Gh (把物体举高)12、功率:P =W/t = FV13、功的原理:W手=W机14、实际机械:W总=W有+ W额外15、机械效率:n= W 有/W总16 、滑轮组效率:(1)、n= G/ nF(竖直方向)(2)、n= G/(G + G动)(竖直方向不计摩擦)(3)、n= f / nF (水平方向)【热学部分】1、吸热:Q 吸=Cm(t —10) = Cm^t2、放热:Q 放=Cm(t0 —t) = Cm^t3、热值:q = Q/m4、炉子和热机的效率:n= Q有效利用/Q燃料5、热平衡方程:Q放=Q吸6、热力学温度:T = t + 273K 【电学部分】1、电流强度:1= Q电量/t2、电阻:R=p L/S3、欧姆定律:1= U/R4、焦耳定律:(1)、Q=I2Rt 普适公式)(2)、Q = Ult = Pt = UQ 电量=U2t/R (纯电阻公式) 5、串联电路:( 1)、l= l1= l2(2)、U=U1+U2( 3)、R= R1+R2(4)、U1/U2 = R1/R2 (分压公式)(5)、P1/P2 = R1/R26 、并联电路:( 1)、l= l1+l2(2)、U=U1=U2(3)、1/R=1/R1+1/R2 [ R = R1R2/(R1+R2)](4)、I1/I2 = R2/R1(分流公式)(5)、P1/P2=R2/R17 定值电阻:(1)、I1/I2=U1/U2(2)、P1/P2=I12/I22(3)、P1/P2=U12/U228 电功:(1)、W=UIt=Pt=UQ (普适公式)(2)、W=I2Rt=U2t/R (纯电阻公式)9 电功率:(1)、P=W/t=UI (普适公式)(2)、P=I2R=U2/R (纯电阻公式) 【常用物理量】1、光速:C = 3x108m/s (真空中)2、声速:V = 340m/s (15 C)3、人耳区分回声:>0 1s4、重力加速度:g = 9. 8N/kg〜10N/kg5、标准大气压值:760毫米水银柱高=1 . 01 X105Pa6、水的密度:p= 1 . 0X103kg/m37、水的凝固点:0 C8、水的沸点:100 C9、水的比热容:C= 4. 2X103J/(kg? C)10、元电荷:e = 1 . 6X10-19C11、一节干电池电压:1.5V12 、一节铅蓄电池电压:2V13、对于人体的安全电压: < 36V(不高于36V)14 、动力电路的电压:380V15 、家庭电路电压:220V16 、单位换算:(1 )、1m/s = 3. 6km/h(2)、1g/cm3 = 10A3kg/m A3物理量单位公式名称符号名称符号质量m千克kg m=p v温度t 摄氏度°C速度v 米/秒m/s v=s/t密度p 千克/米 3 kg/m3p =m/v力(重力)F 牛顿(牛) N G=mg压强P Pa 帕斯卡(帕)P=F/S功W J 焦耳(焦)W=Fs功率:P 瓦特(瓦)w P=W/t电流:I 安培(安)A I=U/R电压:U 伏特(伏)V U=IR电阻:R 欧姆(欧)R=U/I电功:W 焦耳(焦)J W=UIt电功率:P 瓦特(瓦)w P=W/t=UI热量:Q 焦耳(焦)J Q=cm(t-t°)比热: c 焦/(千克°C) J/(kg °C)真空中光速3X108米/秒g :9.8 牛顿/千克15°C 空气中声速340 米/秒初中物理公式汇编【力学部分】1 、速度:V=S/t2、重力:G=mg3、密度:p =m/V4、压强:p=F/S5、液体压强:p=p gh6、浮力:(1)、F浮二F' —F (压力差)(2)、F浮二G —F (视重力)(3)、F浮二G (漂浮、悬浮)(4)、阿基米德原理:F浮=G排二p液gV排7、杠杆平衡条件:F1 L1 = F2 L28、理想斜面:F/G = h/L9、理想滑轮:F=G/n10、实际滑轮:F= (G + G动” n (竖直方向)11、功:W = FS = Gh (把物体举高)12、功率:P =W/t = FV13、功的原理:W手=W机14、实际机械:W总=W有+ W额外15、机械效率:n= W 有/W总16 、滑轮组效率:(1)、n= G/ nF(竖直方向)(2)、n= G/(G + G动)(竖直方向不计摩擦)(3)、n= f / nF (水平方向)【热学部分】1、吸热:Q 吸=Cm(t —tO) = CmX t2、放热:Q 放=Cm(t0 —t) = Cm^ t3、热值:q = Q/m4、炉子和热机的效率:n= Q有效利用/Q燃料5、热平衡方程:Q放=Q吸6、热力学温度:T = t + 273K【电学部分】1、电流强度:1= Q电量/t2、电阻:R=p L/S3、欧姆定律:I= U/R4、焦耳定律:(1)、Q = I2Rt普适公式)(2)、Q=UIt=Pt=UQ 电量= U2t/R (纯电阻公式) 5、串联电路:(1)、I=I1=I2( 2)、U= U1 + U2(3)、R=R1+R2 (1)、W=UIt=Pt=UQ (普适公式) (2)、W=I2Rt=U2t/R (纯电阻公式)6、并联电路:(1)、1= 11 + 12(2)、U = U1 = U2(3)、1/R=1/R1+1/R2 [ R=R1R2/(R1 +R2)](4)、11/12 = R2/R1(分流公式)(5)、P1/P2=R2/R17 定值电阻:(1)、I1/I2=U1/U2(2)、P1/P2=I12/I22(3)、P1/P2=U12/U228 电功:(1)、W=UIt=Pt=UQ (普适公式)(2)、W=I2Rt=U2t/R (纯电阻公式)9 电功率:(1)、P=W/t=UI (普适公式)(2)、P=I2R=U2/R (纯电阻公式)【常用物理量】1、光速:C = 3x108m/s (真空中)2、声速:V = 340m/s (15 C)3、人耳区分回声:> 0.1s4、重力加速度:g = 9.8N/kg〜10N/kg5、标准大气压值:760毫米水银柱高=1.01 X05Pa6、水的密度:p= 1.0 X103kg/m37、水的凝固点:0C8、水的沸点:100C9、水的比热容:C = 4.2 X103J/(kg? C)10、元电荷:e = 1.6 X10-19C11、一节干电池电压:1.5V12、一节铅蓄电池电压:2V13、对于人体的安全电压:< 36V(不高于36V)14、动力电路的电压:380V15、家庭电路电压:220V16、单位换算:(1)、1m/s=3.6km/h(2)、1g/cm3 =103kg/m3(3)、1kw?h = 3.6 X106J重力G (N) G=mg m :质量g:9.8N/kg 密度P(kg/m3 ) p =m/V m:质量V :体积合力F合(N)F合=F1+F2方向相同F合=F1-F2方向相反时,F1>F2方向相反:浮力F浮(N) F浮=G物-G视G视:物体在液体的重力浮力F浮(N) F浮=G物此公式只适用浮力F浮(N) F浮=G排=m排g= p液gV排杠杆的平衡条件F1L1= F2L2动滑轮F= G物+G轮压强p(Pa)P= F/S热量Q(J)Q=cm △ t 机械功W(J)W=Fs 功率P(w)P=W/t机械效率n = x 100%液体压强p(Pa )P=p gh燃料燃烧放出的热量Q (J)Q=mq m :质量q:热值物体漂浮或悬浮G 排:排开液体的重力m排:排开液体的质量p液:液体的密度V排:排开液体的体积(即浸入液体中的体积):动力L1 :动力臂F2 :阻力L2:阻力臂定滑轮F=G 物S=h F :绳子自由端受到的拉力G物:物体的重力S :绳子自由端移动的距离h :物体升高的距离S=2 h G 物:物体的重力G 轮:动滑轮的重力滑轮组F= (G物+G轮)S=n h n:通过动滑轮绳子的段数F:力s:在力的方向上移动的距离有用功W有总功W总W有=G物hW总=Fs适用滑轮组竖直放置时W :功t :时间F :压力S :受力面积P:液体的密度h :深度(从液面到所求点的竖直距离):物质的比热容m :质量t :温度的变化值物理量(单位) 公式备注公式的变形重力 G (N ) G=mg m :质量 g : 9.8N/kg 或者 10N/kg密度P (kg/m3 ) p =m/V m :质量 V :体积合力F 合(N ) 方向相同:F 合=F1+F2方向相反:F 合=F1-F2方向相反时,F1>F2 浮力F 浮(N)F 浮=G 物-G 视 G 视:物体在液体的重力 浮力F 浮(N)F 浮=G 物 此公式只适用物体漂浮或悬浮 浮力F 浮(N)F 浮=G 排=m 排g= p 液gV 排 G 排:排开液体的重力 m 排:排开液体的质量 p 液:液体的密度 V 排:排开液体的体积(即浸入液体中的体积 )杠杆的平衡条件 F1L 仁F2L2F1:动力L1 :动力臂 F2 :阻力 L2 :阻力 臂定滑轮 F=G 物S=h F :绳子自由端受到的拉力G 物:物体的重力 S :绳子自由端移动的距离 h :物体升高的距离 动滑轮F= (G 物+G 轮)S=2 h G 物:物体的重力 G 轮:动滑轮的重力滑轮组F= (G 物+G 轮)S=n h n :通过动滑轮绳子的段数 机械功W (J ) W=Fs F :力 s :在力的方向上移动的距离 有用功W 有总功W 总 W 有=G 物hW 总=Fs 适用滑轮组竖直放置时机械效率n = x 100%功率P (w ) P=W/t W :功 t :时间压强p (Pa ) P= F/S F :压力 S :受力面积液体压强p (Pa ) P=p gh p :液体的密度 h :深度(从液面到所求点的竖 直距离) 热量Q (J ) Q=cm △ t c :物质的比热容 m :质量 △ t :温度的变化值燃料燃烧放出的热量Q (J ) Q=mq m :质量 q :热值1=11=12= .... 电流处处相等 U=U1+U2+… 串联电路起分压作用 R=R1+R2+ ……I=I1+I2+ …… 干路电流等于各支路电流之和(分流)U=U 仁U2…… 串联电路:电流 I (A ) 串联电路:电压 U (V ) 串联电路:电阻R (Q) 并联电路:电流 I (A ) 并联电路:电压U (V ) 并联电路电阻R ( Q)R= 1/R1+ 1/R2+ ……电路中的电流与电压成正比,与电阻成反比 Q :电荷量(库仑)t :时间(S ) U :电压I :电流 t :时间P :电功率 U:电压I :电流R :电阻 电磁波波速与波长、频率的关系 C=Xv C :真空中的光速速度 V (m/S ) v=S/tS :路程 t :时间重力 G (N )G=mgm :质量g :重力加速度,常数,9.8N/kg 或者10N/kg密度 P (kg/m3) p =m/vm :质量V :体积合力F 合(N )方向相同:F 合=F1+F2方向相反:F 合=F1-F2方向相反时,F1>F2浮力F 浮(N )F 浮=G 物-G 视G 视:物体在液体的重力浮力F 浮(N )F 浮=G 物 此公式只适用物体漂浮或悬浮浮力F 浮(N )F 浮=G 排=m 排g=p 液gV 排G 排:排开液体的重力 m 排:排开液体的质量 p 液:液体的密度 V 排:排开液体的体积(即浸入液体中的体积)杠杆的平衡条件F1L 仁F2L2F1 :动力L1 :动力臂 F2 :阻力L2:阻力臂 定滑轮 F=G 物S=hF :绳子自由端受到的拉力G 物:物体的重力S :绳子自由端移动的距离h :物体升高的距离动滑轮 F=(G 物 +G 轮)/2S=2hG 物:物体的重力G 轮:动滑轮的重力滑轮组 F=(G 物 +G 轮) 欧姆定律 I= U/R 电流定义式 I=Q/t 电功 W (J )W=UIt=Pt 电功率P=UI=I2R=U2/RS=nhn :通过动滑轮绳子的段数机械功W(J)W=FsF :力s :在力的方向上移动的距离有用功W有=G物h总功W总W总=Fs适用滑轮组竖直放置时机械效率n =W W/W总X100%功率P(w)P=w/tW :功t:时间压强p(Pa )P=F/sF :压力S:受力面积液体压强p (Pa)P=p ghp:液体的密度h :深度(从液面到所求点的竖直距离)热量Q(J)Q=cm △tc:物质的比热容m :质量△ t:温度的变化值燃料燃烧放出的热量Q(J)Q=mqm :质量q:热值常用的物理公式与重要知识点.物理公式(单位)公式备注公式的变形串联电路电流I (A) 1=11=12=……电流处处相等串联电路电压U (V) U=U1+U2+•… 串联电路起分压作用串联电路电阻R ( Q) R=R1+R2……并联电路电流I (A) I=I1+I2+ ••…干路电流等于各支路电流之和(分流)并联电路电压U(V) U=U1=U2=……并联电路电阻R ( Q) 1/R=1/R1+1/R2+……欧姆定律I=U/I电路中的电流与电压成正比,与电阻成反比电流定义式I=Q/tQ:电荷量(库仑)t:时间(S)电功W(J) W=UIt=PtU:电压I:电流t:时间P:电功率电功率P=UI=I2R=U2/RU:电压I :电流R :电阻电磁波波速与波长、频率的关系C=Xv C波速(电磁波的波速是不变的,等于3X108m/s ) 入:波长V频率需要记住的几个数值a •声音在空气中的传播速度:340m/sb光在真空或空气中的传播速度:3x108m/sc.水的密度:1.0 %03kg/m3d •水的比热容:4.2 X103J/ (kgo C)e .一节干电池的电压:1.5Vf .家庭电路的电压:220Vg.安全电压:不高于36V。
高中数学 第二章 数与符号 2.3 数学符号课件 北师大版

-8-
§3 数学符号
Y预习导引 U XI DAO YIN
H 互动课堂 U DONG KE TANG
重难点拨
思悟升华
例1
例2
这段话的意思用表格表示计算过程就是: 把每人所出的钱数写出来(表第 1 行:所出率),多余、不足的钱数分别写在
它们的下面(表第 2 行:盈不足).将它们分别与所出的钱数交错相乘(“维乘”即
§3 数学符号
-1-
§3 数学符号
激趣诱思
新知预习
Y预习导引 U XIDAO YIN
H 互动课堂 U DONG KE TANG
数学除了记数以外,还需要一套数学符号来表示数和数、数和形 的相互关系.数学符号的发明和使用比数字晚,但是数量多得多.现在 常用的数学符号有 200 多个,初中数学书里就不下 20 多种.你了解它 们的经历吗?学完本节,你就会有答案了.
平方根号曾经用拉丁文“Radix”(根)的首尾两个字母合并起来 表示,17 世纪初,法国数学家笛卡儿在他的《几何学》中,第一次用“ ” 表示根号.
-5-
§3 数学符号
重难点拨
思悟升华
Y预习导引 U XI DAO YIN
H 互动课堂 U DONG KE TANG
例1
例2
16 世纪法国数学家维叶特用“=”表示两个量的差别.可是英国 牛津大学数学、修辞学教授雷科德觉得:用两条平行而又相等的直线 来表示两数相等是最合适不过的了,于是等于符号“=”就从 1540 年 开始使用起来.
-4-
§3 数学符号
Y预习导引 U XI DAO YIN
H 互动课堂 U DONG KE TANG
重难点拨
思悟升华
例1
例2
乘号曾经用过十几种,现在通用两种.一个是“×”,一个是“·”,最 早是由英国数学家奥特雷德 1631 年提出的.德国数学家莱布尼茨认 为:“×”号像拉丁字母“X”,加以反对,而赞成用“·”号.他自己还提出 用“n”表示相乘.可是这个符号现在应用到集合论中去了.
(word版)人教版高中数学知识点汇总,文档

人教版高中数学高中数学主要知识点必修1数学知识第一章、集合与函数概念、集合1、把研究的对象统称为元素,把一些元素组成的总体叫做集合。
集合三要素:确定性、互异性、无序性。
2、只要构成两个集合的元素是一样的,就称这两个集合相等。
3、常见集合:正整数集合:N*或N,整数集合:Z,有理数集合:Q,实数集合:R.4、集合的表示方法:列举法、描述法.§、集合间的根本关系1、一般地,对于两个集合A、B,如果集合A中任意一个元素都是集合B中的元素,那么称集合A是集合B的子集。
记作A B.2、如果集合A B,但存在元素xB,且x A,那么称集合A是集合B的真子集.记作:A B.3、把不含任何元素的集合叫做空集.记作:.并规定:空集合是任何集合的子集.4、如果集合A中含有n个元素,那么集合A有2n个子集.§、集合间的根本运算1、一般地,由所有属于集合A或集合B的元素组成的集合,称为集合A与B的并集.记作:A B.2、一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集.记作:A B.3、全集、补集?C U A{x|x U,且x U}运算交集并集类型定由所有属于A且属由所有属于集合A或义于B的元素所组成属于集合B的元素所的集合,叫做A,B的组成的集合,叫做A,B交集.记作AB〔读的并集.记作:AB作‘A交B’〕,即〔读作‘A并B’〕,即补集设S是一个集合,A是S的一个子集,由S中所有不属于A的元素组成的集合,叫做S中子集A的补集〔或余集〕记作C S A,即A B={x|x A,且 A B={x|x A,或xB}.xB}).{x|xS,且xA}C S A=-1-人教版高中数学韦恩A B A B SA图示图1图2性A A=A A A=A(C u A)(C u B)AΦ=ΦAΦ=A=C u(A B)A B=BA A B=B A(C u A)(C u B)A BA A BA质ABB ABB=C u(AB)A(C u A)=UA(C u A)=Φ.§、函数的概念1、设A、B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有惟一确定的数fx和它对应,那么就称f:A B为集合A到集合B的一个函数,记作:y fx,x A.2、一个函数的构成要素为:定义域、对应关系、值域.如果两个函数的定义域相同,并且对应关系完全一致,那么称这两个函数相等.§、函数的表示法1、函数的三种表示方法:解析法、图象法、列表法.、单调性与最大〔小〕值单调性的定义:见书P281、注意函数单调性证明的一般格式:解:设x1,x2a,b且x1x2,那么:fx1fx2=、奇偶性1、一般地,如果对于函数fx的定义域内任意一个x,都有f x fx,那么就称函数fx为偶函数.偶函数图象关于y轴对称.2、一般地,如果对于函数fx的定义域内任意一个x,都有f x fx,那么就称函数fx为奇函数.奇函数图象关于原点对称.第二章、根本初等函数〔Ⅰ〕§、指数与指数幂的运算1、一般地,如果x n a,那么x叫做a的n次方根。
(完整word)高等数学符号
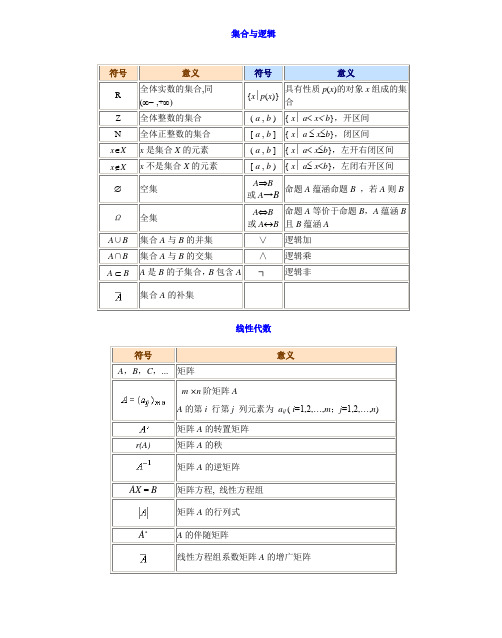
集合与逻辑符号意义符号意义R 全体实数的集合,同(∞- ,+∞){x∣p(x)}具有性质p(x)的对象x组成的集合Z 全体整数的集合( a , b ) { x∣a<x< b},开区间N 全体正整数的集合[ a , b ] { x∣a≤x≤b},闭区间x∈X x是集合X的元素( a , b ] { x∣a< x≤b},左开右闭区间x∉X x不是集合X的元素[ a , b ) { x∣ a≤ x<b},左闭右开区间∅空集A⇒B或A→B命题A蕴涵命题B ,若A则BΩ全集A⇔B或A↔B命题A等价于命题B,A蕴涵B且B蕴涵AA∪B集合A与B的并集∨逻辑加A∩B集合A与B的交集∧逻辑乘A⊂B A是B的子集合,B包含A┐逻辑非集合A的补集线性代数符号意义A,B,C,... 矩阵m×n阶矩阵AA的第i 行第j列元素为a ij (i=1,2,…,m;j=1,2,…,n)矩阵A的转置矩阵r(A)矩阵A的秩矩阵A的逆矩阵AX= B 矩阵方程, 线性方程组矩阵A的行列式A*A的伴随矩阵线性方程组系数矩阵A的增广矩阵数列、函数与极限符号意义符号意义u1,u2,…,u n,…或{u n} 以u n为通项的数列n趋于无穷大时数列{y n} 的极限以u n为通项的无穷级数和x 趋于无穷大时函数f(x)的极限有限项u1+u2+…+u n的和x趋于正无穷大时函数f(x)的极限x在对应规律f下对应到yx趋于负无穷大时函数f(x)的极限函数f :X为定义域,f为对应规律,x为自变量,y为因变量x趋于a时函数f(x)的极限D f函数f的定义域x>a且x趋于a时函数f(x)的右极限R f函数f的值域x<a且x趋于a时函数f(x)的左极限Γf函数f 的图像x→✉,f(x) ~ g(x) 在x→✉的变化过程中,无穷小(大)量f(x)与g(x)的等价函数 f :X→Y 与g : Y →Z的复合函数函数y=y(x)在自变量x0处的值f-1函数f的反函数函数f(x)在[a,b]上的平均值f( x , y ) 以x , y为自变量的二元函数符号意义符号意义函数y关于x的导(函)数函数f(x , y)在(x0 , y0)处关于x的偏导数函数f(x)关于x的导(函)数函数f(x , y)在(x0 , y0)处关于y的偏导数函数y在x0的导数函数f(x)的不定积分函数f(x)在x0的导数函数f(x)的黎曼和函数f(x)在x0的右导数函数f(x)在[a, b]上的定积分函数f(x)在x0的左导数差数F(b) F(a)变量u的改变量f(x)在无穷区间[a, +∞)上的无穷(广义)积分du 变量u的微分f(x)在无穷区间(-∞, b]上的无穷(广义)积分函数y关于x的n 阶导数,n∈N f(x)在无穷区间(-∞, +∞)上的无穷(广义)积分二元函数z=f(x,y)关于x或y 的偏导数概率论与数理统计∅不可能事件ω基本事件Ω={ω1,ω2,…,ωn} 样本空间,基本事件组A⊂ B或B⊃ A事件B包含事件AA + B事件A与B的和AB事件A与事件B的积事件A1,A2,…,A n的积A– B事件A与事件B的差事件A的对立事件, 或称为事件A的互补事件P(A) 事件A的概率ξ、η、ζ或X、Y、Z 随机变量χ2(n) 自由度为n的χ2分布t(n) 自由度为n的t分布F( n1, n2) 第一自由度为n1和第二自由度为n2的F分布χ2分布的临界值tα(n) t分布的临界值Fα(n1,n2) F分布的临界值其它符号意义[x] 不超过x的最大整数a ( mod n )用n除a所得的余数(n∈N,a∈N)e极限,自然对数的底经济学函数y= f(x)的弹性⊥直线或线段的垂直∥直线或线段的平行。
(完整word版)向量的点乘和叉乘,以及几何意义

所谓点乘(也常称作内积),数学定义如下:点乘只是表达这个结果的一种方式,符号不重要,叫法也不重要,我可以叫点乘,内积,也可以叫"相乘",定义"#"字符代替“·” 符号都可以,只是人们约束习惯这么这么写,那我们就也都这么写。
而且,也不要纠结为什么是这么定义,没有为什么,人们就是这么“龟腚”这个公式的,我们要研究的是这个规定到底能干嘛?有啥具体意义?a.点乘的具体几何意义:根据公式,我们可以得出a·b=|a| |b|cosθ我试着证明为什么会是这样(为了能让大家看的方便,我将向量标为蓝色,具体长度标为红色):定义向量c=a - b这样就形成了一个封闭的三角形,c向量为他的第三边由于余弦定理我们可以知道c² =a² +b² - 2ab cos(θ) (这里的a,b,c全部都是每一边的具体长度)根据定义我们可以推导出c·c=c²(有兴趣的朋友可以去试着推导一下)所以:c·c=a·a+b·b- 2ab cos(θ)因为向量的点乘满足分配率:a·(b+c)=a·b+a·cc=a - bc·c=(a -b)·(a - b)c·c=(a·a-2a·b+b·b)(a·a - 2a·b + b·b)=a²+b²- 2ab cos(q)约掉a·a=a²,b·b=b²;-2a·b= -2ab cos(θ)a·b=ab cos(θ)因为a=|a|所以a·b=|a| |b|cosθ跟据这个公式,我们能拿到两个向量之间的夹角,这对于判断两个向量是否同一方向,是否正交(也就是垂直),很有用处。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
符号意义
∞ 无穷大
PI 圆周率
|x| 函数的绝对值
∪集合并
∩ 集合交
≥ 大于等于
≤ 小于等于
≡ 恒等于或同余
ln(x) 自然对数
lg(x) 以2为底的对数
log(x) 常用对数
floor(x) 上取整函数
ceil(x) 下取整函数
x mod y 求余数
{x} 小数部分x - floor(x)
∫f(x)δx 不定积分
∫[a:b]f(x)δx a到b的定积分
[P] P为真等于1否则等于0
∑[1≤k≤n]f(k) 对n进行求和,可以拓广至很多情况
如:∑[n is prime][n < 10]f(n)
∑∑[1≤i≤j≤n]n^2
lim f(x) (x->?) 求极限
f(z) f关于z的m阶导函数
C(n:m) 组合数,n中取m
P(n:m) 排列数
m|n m整除n
m⊥n m与n互质
a ∈A a属于集合A
#A 集合A中的元素个数
∑(n=p,q)f(n) 表示f(n)的n从p到q逐步变化对f(n)的连加和,如果f(n)是有结构式,f(n)应外引括号;
∑(n=p,q ; r=s,t)f(n,r) 表示∑(r=s,t)[∑(n=p,q)f(n,r)],
如果f(n,r)是有结构式,f(n,r)应外引括号;
∏(n=p,q)f(n) 表示f(n)的n从p到q逐步变化对f(n)的连乘积, 如果f(n)是有结构式,f(n)应外引括号;
∏(n=p,q ; r=s,t)f(n,r) 表示∏(r=s,t)[∏(n=p,q)f(n,r)],
如果f(n,r)是有结构式,f(n,r)应外引括号;
lim(x→u)f(x) 表示f(x) 的x 趋向u 时的极限,
如果f(x)是有结构式,f(x)应外引括号;
lim(y→v ; x→u)f(x,y) 表示lim(y→v)[lim(x→u)f(x,y)],
如果f(x,y)是有结构式,f(x,y)应外引括号;
∫(a,b)f(x)dx 表示对f(x) 从x=a 至x=b 的积分,
如果f(x)是有结构式,f(x)应外引括号;
∫(c,d ; a,b)f(x,y)dxdy 表示∫(c,d)[∫(a,b)f(x,y)dx]dy,
如果f(x,y)是有结构式,f(x,y)应外引括号;
∫(L)f(x,y)ds 表示f(x,y) 在曲线L 上的积分,
如果f(x,y)是有结构式,f(x,y)应外引括号;
∫∫(D)f(x,y,z)dσ 表示f(x,y,z) 在曲面D 上的积分,
如果f(x,y,z)是有结构式,f(x,y,z)应外引括号;
∮(L)f(x,y)ds 表示f(x,y) 在闭曲线L 上的积分,
如果f(x,y)是有结构式,f(x,y)应外引括号;
∮∮(D)f(x,y,z)dσ 表示f(x,y,z) 在闭曲面 D 上的积分, 如果f(x,y)是有结构式,f(x,y)应外引括号;
∪(n=p,q)A(n) 表示n从p到q之A(n)的并集,
如果A(n)是有结构式,A(n)应外引括号;
∪(n=p,q ; r=s,t)A(n,r) 表示∪(r=s,t)[∪(n=p,q)A(n,r)], 如果A(n,r)是有结构式,A(n,r)应外引括号;
∩(n=p,q)A(n) 表示n从p到q逐步变化对A(n)的交集, 如果A(n)是有结构式,A(n)应外引括号;
∩(n=p,q ; r=s,t)A(n,r) 表示∩(r=s,t)[∩(n=p,q)A(n,r)],
如果A(n,r)是有结构式,A(n,r)应外引括号。
