多速率数字信号处理Ch10_4
北京交通大学数字信号处理04DSP研究性学习报告多速率信号处理

《数字信号处理》课程研究性学习报告姓名学号同组成员指导教师时间多速率信号处理专题研讨【目的】(1) 掌握序列抽取运算与内插运算的频谱变化规律。
(2) 掌握确定抽取滤波器与内插滤波器的频率指标。
(3) 掌握有理数倍抽样率转换的原理及方法。
(4) 培养学生自主学习能力,以及发现问题、分析问题和解决问题的能力。
【研讨题目】 基本题1.抽取、内插信号特征的时域/频域分析对于给定的单频模拟信号y (t )=sin(1000πt ),确定一个合适的采样频率f sam ,获得离散信号y [k ],试进行以下问题的分析:(1) 对离散信号y [k ]进行M=2倍抽取,对比分析y [k ]和y [M k ]在时域/频域的关系; (2) 对离散信号y [k ]进行L=2倍内插,对比分析y [k ]和y [k /L]在时域/频域的关系。
【温磬提示】在多速率信号分析中,离散序列的抽取和内插是多速率系统的基本运算,抽取运算将降低信号的抽样频率,内插运算将提高信号的抽样频率。
两种运算的变换域描述中,抽取运算可能出现频谱线性混叠,而内插运算将出现镜像频谱。
【设计步骤】1、 已知y (t )=sin(1000πt )频率为500Hz ,周期为0.002s ,可取时间范围T 为0到0.004秒,两个周期,根据抽样定理取Hz f sam 8000=,每个周期抽取16个点。
2、 用函数xD=x(1:M:end)对离散信号进行M=2倍的抽取,用fft 计算频谱。
3、 用函数xL=zeros(1,L*length(x));xL(1:L:end)=x;对离散信号进行L=2的内插,用fft 计算频谱。
【仿真结果】对离散信号y [k ]抽取和内插的时域/频域对比分析结果。
抽取:内插:【结果分析】1、抽取运算在频域描述:对x[k]进行M 倍抽取后得到][k x D 的频谱为∑-=-ΩΩ=102)(1)(M l Ml jj D eX Me X π,即将x[k]的频谱)(Ωj eX 扩展M 倍,得到)(Mj e X Ω,再以π2为周期进行周期化并乘以因子M1。
数字信号处理(第四版)第9章数字信号处理的实现

第9章 数字信号处理的实现
2. 极点位置敏感度 下面分析系数量化误差对极零点位置的影响。如果 极零点位置改变了,严重时不仅IIR系统的频率响应会 发 生变化,还会影响系统的稳定性。因此研究极点位置 的 改变更加重要。为了表示系数量化对极点位置的影响,引 入极点位置灵敏度的概念,所谓极点灵敏度, 是指每 个极 点对系数偏差的敏感程度。相应的还有零点位置灵 敏度 ,分析方法相同。下面讨论系数量化对极点位置的 影响 。
就是量化后的数值。x可以是标量、向量和矩阵。将数取
整的方法有四舍五入取整、向上取整、向下取整、向零
取整,对应的MATLAB取整函数分别为 round(x)、
ceil(x)、floor(x)、fix(x)。round最常用,对应的MATLAB
量化语句为xq=q*round(x/q)。
第9章 数字信号处理的实现
解 求解本例的系数量化与绘图程序为ep911.m。
第9章 数字信号处理的实现
%ep911.m: 例题9.1.1 系数量化与图9.1.3绘图程序 B=1; A=[1, -0.17, 0.965];%量化前系统函数系数向量
b=4; Aq=quant(A, b);
进行b位量化
%量化2进制位数 %对系统函数分母系数向量A
p=roots(A) pq=roots(Aq) ap=abs(p) a pq=abs(pq) %以下为绘图部分省略
%计算量化前的极点 %计算量化后的极点 %计算量化前极点的模 %计算量化后极点的模
第9章 数字信号处理的实现
运行程序,得到量化后的系统函数
为
并求出H(z)和
的极点分别为
显然,因为系数的量化,使极点位置发生变化,算出极点
的模为: |p1, 2|=0.9823,
多速率数字信号处理
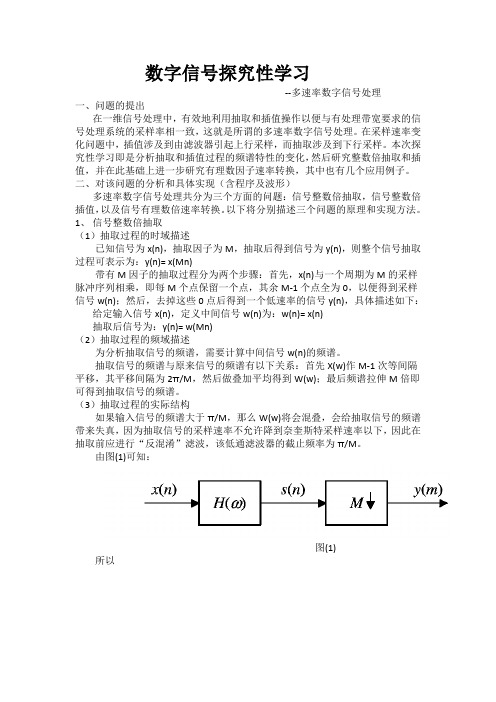
数字信号探究性学习--多速率数字信号处理一、问题的提出在一维信号处理中,有效地利用抽取和插值操作以便与有处理带宽要求的信号处理系统的采样率相一致,这就是所谓的多速率数字信号处理。
在采样速率变化问题中,插值涉及到由滤波器引起上行采样,而抽取涉及到下行采样。
本次探究性学习即是分析抽取和插值过程的频谱特性的变化,然后研究整数倍抽取和插值,并在此基础上进一步研究有理数因子速率转换,其中也有几个应用例子。
二、对该问题的分析和具体实现(含程序及波形)多速率数字信号处理共分为三个方面的问题:信号整数倍抽取,信号整数倍插值,以及信号有理数倍速率转换。
以下将分别描述三个问题的原理和实现方法。
1、信号整数倍抽取(1)抽取过程的时域描述已知信号为x(n),抽取因子为M,抽取后得到信号为y(n),则整个信号抽取过程可表示为:y(n)= x(Mn)带有M因子的抽取过程分为两个步骤:首先,x(n)与一个周期为M的采样脉冲序列相乘,即每M个点保留一个点,其余M-1个点全为0,以便得到采样信号w(n);然后,去掉这些0点后得到一个低速率的信号y(n),具体描述如下:给定输入信号x(n),定义中间信号w(n)为:w(n)= x(n)抽取后信号为:y(n)= w(Mn)(2)抽取过程的频域描述为分析抽取信号的频谱,需要计算中间信号w(n)的频谱。
抽取信号的频谱与原来信号的频谱有以下关系:首先X(w)作M-1次等间隔平移,其平移间隔为2π/M,然后做叠加平均得到W(w);最后频谱拉伸M倍即可得到抽取信号的频谱。
(3)抽取过程的实际结构如果输入信号的频谱大于π/M,那么W(w)将会混叠,会给抽取信号的频谱带来失真,因为抽取信号的采样速率不允许降到奈奎斯特采样速率以下,因此在抽取前应进行“反混淆”滤波,该低通滤波器的截止频率为π/M。
由图(1)可知:图(1)所以令“反混叠”低通滤波器为理想滤波器,表示为:那么整个过程可描述为:信号X(w)通过低通滤波器H(w)(wc=π/M),然后伸长M倍即得抽取信号的频谱Y(w)。
《数字信号处理CH》PPT课件

k 2 ) / T )
周期采样后的信号频谱为原信号频谱的平移叠加
精选PPT
4
平移叠加
当横轴分别为f, Ω,ω 时,平 移周期对应为 fs, Ωs, 2π
当 Ωs <2ΩN 时,信号频谱 产生混叠
幅度因子1/T
精选PPT
5
连续时间信号的恢复
当 Ωs >2ΩN时,原理 上可找到合适的理想
低通滤波器完全恢复
原来的连续时间信号
Xr(j)Xs(j)Hr(j)Xc(j)
T Hr(j)0
||c ||c
精选PPT
6
5 .Nyquist sampling theorems :
奈奎斯特采样定理 let xc (t ) be a band lim ited signal with X c ( j ) 0, | | N
]
|
( 2 ) H c ( j ) H ( e j ) | T e j T
Y c ( j ) X c ( j ) H c ( j ) X c ( j ) e j T
yc (t) xc (t T )
(3) y[ n ] y c [nT ] x c (nT T )
x [ k ] sin[ ( t kT ) / T ] | t nT T
H
(e
j T
)H
r(
j ) 1 T
X c(
k
j(
2 k
/ T ))
H
(e
j T
)
X 0
c
(
j )
| | / T | | / T
X
c(
j )H
(e
j T
), |
|
0 ,
现代数字信号处理ch推荐优秀PPT

18
19
三、相关接收系统模型
假定信号码元宽度为T,接收信号
为
,相关器输出的相关值为:
,
离散时间模型为:
,其中
为脉冲能量,
为零均值加性高斯
白噪声,
。
代表发射的数
字信号序列。
20
此时检测变量是一个均值为 ,方差为 的
12
五、角度分集
接收端使用方向天线,不同接收方向对准不同 多径来波,这样每个方向天线接收信号互不相 关,从而实现分集。
13
2 相关接收机
在二进制通信系统中,接收信号处理问题在数学上归 结为一个二元假设检验问题:
设计最佳接收机意味着使接收系统总的错误概率为最 小
为假定 H0为真、检测结果为 H1的错误概率,
3
1 分集接收
分集接收是指对信号进行不同的接收,通过选择多条 信号传输路径,改善接收端瞬时信噪比和平均信噪比。 分集(diversity)是一种有效的通信接收方式,突出 优点是低投入、高性能由于多径信号是相关信号甚至 是相干信号,分集技术的主要任务就是如何将这种多 径信号变成互不相干信号,分集处理不同于信道均衡, 无需训练信号就可以实现信号分离。
衰落分为大尺寸衰落和小尺寸衰落,相应的分集有宏 分集技术(macroscopic diversity techniques) 和微分 集技术(microscopic diversity techniques) 。
4
一、空间分集
空间分集(space diversity)也就是天线分集 (antenna diversity) ,通过天线阵列实现信 号分集。空间分集接收信号的方法分为(1) 选择分集; (2)反馈分集; (3)最大合并 比分集; (4)等增益合并比分集。在移动通 信系统中,移动用户考虑用一个天线,基站才 用天线阵列,而且要求各个阵元之间距离足够 大,以保证各个阵元输出信号的衰落特性相互 独立,一般地, d ≥λ/2。
数字信号处理(第四版)第四章ppt

Digital Signal Processing
© 2013 Jimin Liang
Discrete-Time Systems Outline Discrete-time system examples Classification of DT systems Impulse and step responses Time-domain characteristics of LTI Simple interconnection schemes
Process a given sequence, called the input system, to generate another sequence, called the output sequence, with more desirable properties or to extract certain information about the input signal. DT system is usually also called the digital filter
12
Digital Signal Processing
© 2013 Jimin Liang
Discrete-Time Systems 4.2 Classification of DT systems Stable system
A system is stable if and only if for every bounded input, the output is also bounded, called BIBO stable.
Discrete-Time Systems 4.1 Discrete-time system examples (4) Linear Interpolator Linear factor-2 interpolator
数字信号处理 名词解释-概述说明以及解释

数字信号处理名词解释-概述说明以及解释1.引言1.1 概述数字信号处理(Digital Signal Processing,简称DSP)是一种广泛应用于信号处理领域的技术,它利用数字化的方式对连续时间信号进行处理和分析。
数字信号处理可以实现信号的滤波、频谱分析、模拟与数字信号的转换、信息编码解码等功能,是现代通信、音视频处理、生物医学领域等各个领域中不可或缺的技术手段。
通过数字信号处理技术,我们可以更加精确和高效地处理各种类型的信号,包括声音、图像、视频等。
数字信号处理可以使信号的处理过程更加稳定可靠,同时也可以方便地与计算机等数字系统进行集成,实现更多复杂功能。
在本篇文章中,我们将深入探讨数字信号处理的定义、应用领域以及基本原理,以期让读者对这一重要领域有更加全面的认识和理解。
1.2 文章结构本文将分为三个主要部分,分别是引言、正文和结论。
在引言部分,我们将对数字信号处理进行简要的概述,并介绍文章的结构和目的。
正文部分将详细讨论数字信号处理的定义、应用领域和基本原理。
最后,在结论部分,我们将总结数字信号处理的重要性,探讨未来数字信号处理的发展趋势,并做出最终的结论。
通过这样的结构安排,读者能够清晰地了解数字信号处理的基本概念、应用以及未来发展方向。
1.3 目的:本文旨在介绍数字信号处理的概念、应用领域和基本原理,旨在帮助读者更深入了解数字信号处理的重要性和作用。
通过对数字信号处理的定义和应用领域的介绍,读者可以了解数字信号处理在各个领域中的广泛应用和重要性。
同时,通过对数字信号处理的基本原理的讲解,读者可以更好地理解数字信号处理的工作原理和技术特点。
通过本文的阐述,希望读者能够全面了解数字信号处理的基本概念和工作原理,进而认识到数字信号处理在现代科学技术中的重要性和必要性。
同时,本文也将展望未来数字信号处理的发展趋势,希望能够启发读者对数字信号处理领域的进一步研究和探索。
最终,通过本文的阐述,读者可以更加深入地理解数字信号处理这一重要的科学技术领域。
赵雪英10版《数字信号处理》实验讲义..

《数字信号处理》实验讲义信息学院赵雪英2013.1前言数字信号处理是利用计算机或专用数字处理设备,采用数值计算的方法对信号进行处理的一门学科,它包括数据采集,变换、分析、综合、滤波、估值与识别等加工处理,以便于提取信息和应用。
数字信号处理的主要优点有:(1)灵活性好。
适合用计算机、可编程器件(如通用单片机、DSP、可编程逻辑器件等)实现,通过编程很容易改变数字信号处理系统得参数,从而使系统实现各种不同的处理功能。
如数字电话系统中采用的时分复用技术。
(2)稳定可靠。
(3)处理精度高。
(4)便于加解密。
(5)便于大规模集成化、小型化。
(6)便于自动化、多功能化。
(7)可实现模拟系统无法实现的复杂处理功能。
数字信号处理原理、实现和应用是本学科研究和发展的三个主要方面。
数字信号处理应用非常广泛,涉及语音、雷达、声呐、地震、图像处理、通信系统、系统控制、生物医学工程、机械振动、遥感遥测、航空航天、电力系统、故障检测和自动化仪表等领域。
MATLAB是美国MathWorks公司开发的一种功能极其强大的高技术计算语言和内容极其丰富的软件库。
其中的信号处理工具箱是一个内容丰富的信号处理软件库,是学习、应用数字信号处理的一个极好工具。
在学习数字信号处理理论的同时,熟练掌握MATLAB的使用,对理工科的学生是非常必要的。
目录实验一时域离散信号和系统 (4)实验二时域离散信号和系统的频域分析 (6)实验三离散傅里叶变换及其快速算法 (8)实验四特殊滤波器 (9)实验五IIR数字滤波器设计 (10)实验六FIR数字滤波器设计 (12)实验七综合实验-数字滤波器设计 (14)实验八时域离散系统的实现 (15)实验一 时域离散信号和系统一、实验目的(一)常用时域离散信号的MATLAB 表示(二)应用MATLAB 求线性卷积(三)应用MATLAB 求解差分方程二、实验内容(一)常用时域离散信号的MATLAB 表示用两个参数向量x 和n 表示有限长序列x(n),x 是x(n)的样值向量,n 是位置向量; n 与x 长度相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8
Copyright © S. K. Mitra
Two-Channel QMF Bank
• The analysis and the synthesis filters are chosen so as to ensure that the reconstructed output y[n] is a reasonably close replica of the input x[n]
• Because of the lower sampling rate, the processing of the down-sampled signals can be carried out more efficiently
2
Copyright © S. K. Mitra
Quadrature-Mirror Filter Bank
Copyright © S. K. Mitra
Alias-Free Filter Bank
• Since the up-sampler and the down-sampler are linear time-varying components, in general, the 2-channel QMF structure is a linear time-varying system
6
Copyright © S. K. Mitra
-Channel QMF Bank
• The analysis filters H0(z) and H1(z) have typically a lowpass and highpass frequency responses, respectively, with a cutoff at p/2
12
Copyright © S. K. Mitra
Analysis of the Two-Channel QMF Bank
• From the first and the last equations we obtain after some algebra
V^ k
(z)
1 2
{Vk
(
z)
Vk
16
Copyright © S. K. Mitra
Alias-Free Filter Bank
• To cancel aliasing we need to ensure that
A(z) = 0, i.e.,
H0(z)G0(z) H1(z)G1(z) 0
• For aliasing cancellation we can choose G0 (z) H1( z)
• Moreover, they are also designed to provide good frequency selectivity in order to ensure that the sum of the power of the subband signals is reasonably close to the input signal power
• Making use of the input-output relations of the down-sampler and the up-sampler in the z-domain we arrive at Vk (z) Hk (z)X (z), Uk (z) 12{Vk (z1/ 2) Vk (z1/ 2)}, k = 0, 1 V^k (z) Uk (z2)
Quadrature-Mirror Filter Bank
• In many applications, a discrete-time signal
x[n] is split into a number of subband signals {vk [n]}by means of an analysis filter bank
3
Copyright © S. K. Mitra
Quadrature-Mirror Filter Bank
• If the down-sampling and up-sampling factors are equal to or greater than the number of bands of the filter bank, then the output y[n] can be made to retain some or all of the characteristics of the input signal x[n] by choosing appropriately the filters in the structure
• This yields G1(z) H0(z)
G0(z) C(z)H1(z), G1(z) C(z)H0(z),
where C(z) is an arbitrary rational function
17
Copyright © S. K. Mitra
(
z)}
1 {H
2
k
(
z)
X
(z)
H
k
(
z)
X
(
z)}
• The reconstructed output of the filter bank
is given by
Y (z) G0(z)V^0(z) G1(z)V^1(z)
13
Copyright © S. K. Mitra
Analysis of the Two-Channel QMF Bank
• To this end, we consider the QMF bank structure without the coders and the decoders as shown below
11
Copyright © S. K. Mitra
Analysis of the Two-Channel QMF Bank
9
Copyright © S. K. Mitra
Two-Channel QMF Bank
• In practice, various errors are generated in this scheme
• In addition to the coding error and errors caused by transmission of the coded signals through the channel, the QMF bank itself introduces several errors due to the sampling rate alterations and imperfect filters
7
Copyright © S. K. Mitra
Two-Channel QMF Bank
• Each down-sampled subband signal is encoded by exploiting the special spectral properties of the signal, such as energy levels and perceptual importance
1
Copyright © S. K. Mitra
Quadrature-Mirror Filter Bank
• If the subband signals {vk [n]} are bandlimited to frequency ranges much smaller than that of the original input signal x[n], they can be down-sampled before processing
• The subband signals are then processed
• Finally, the processed subband signals are combined by a synthesis filter bank resulting in an output signal y[n]
Y (z) T (z)X (z) A(z)X (z)
where T(z), called the distortion transfer
function, is given by
T (z) 12{H0(z)G0(z) H1(z)G1(z)}
and
15
A(z) 12{H0(z)G0(z) H1(z)G1(z)}
• The most common application of this scheme is in the efficient coding of a signal x[n]
5
Copyright © S. K. Mitra
Two-Channel QMF Bank
• Figure below shows the basic two-channel QMF bank-based subband codec (coder/decoder)
• After processing, these signals are then upsampled before being combined by the synthesis filter bank into a higher-rate signal
• The combined structure is called a quadrature-mirror filter (QMF) bank
