《机械原理MATLAB辅助分析》
matlab平面连杆结构分析(机械原理课程设计)

优化参数:连杆 长度、角度、质 量等
优化结果:得到 最优的连杆结构 设计
感谢观看
汇报人:
平面连杆结构的应用范围
机械工程:用于设计、分析和优化机械设 备
生物医学:用于设计、分析和优化假肢、 康复设备等
航空航天:用于设计、分析和优化飞机、 火箭等航天器
机器人技术:用于设计、分析和优化机器 人关节、机械臂等
汽车工业:用于设计、分析和优化汽车底 盘、悬挂系统等
建筑工程:用于设计、分析和优化建筑结 构、桥梁等
03
平面连杆结构的运动学分析
平面连杆结构的运动学方程
平面连杆结构的运动学方程是描述连杆系统运动状态的数学模型 运动学方程包括位移方程、速度方程和加速度方程 运动学方程的建立需要知道连杆系统的几何参数和运动参数 运动学方程的求解可以通过数值积分方法或解析方法进行
平面连杆结构的运动学特性
运动学方程:描述连杆结构的运动状态 运动学参数:包括位移、速度、加速度等 运动学约束:限制连杆结构的运动范围 运动学仿真:通过计算机模拟连杆结构的运动过程
平面连杆结构的形状优化
优化目标:提 高连杆结构的 稳定性和刚度
优化方法:有 限元分析、拓
扑优化等
优化参数:连 杆的长度、宽
度、厚度等
优化效果:提 高连杆结构的 承载能力和使
用寿命
平面连杆结构的拓扑优化
拓扑优化:通过改变材料的分布和形状, 约束条件:结构的刚度、强度、稳定
以实现最优的结构性能
性等性能要求
目标函数:最小化重量或体积,同时 满足给定的性能要求
优化方法:遗传算法、粒子群算法、 模拟退火算法等
设计变量:材料的分布和形状
应用领域:汽车、航空航天、机械制 造等
matlab机械原理运动解析

matlab机械原理运动解析MATLAB机械原理运动解析是指使用MATLAB软件进行机械系统的运动学和动力学分析的过程。
通过建立数学模型,运用MATLAB进行编程计算,可以实现对机械系统的运动规律、动态特性和性能进行评估和预测。
具体来说,MATLAB机械原理运动解析包括以下步骤:1.建立数学模型:根据机械系统的物理模型,建立相应的数学模型,包括运动学和动力学方程。
这些方程可以描述系统的位移、速度、加速度、力矩等物理量之间的关系。
2.编写MATLAB程序:根据建立的数学模型,使用MATLAB编程语言编写程序,进行数值计算和分析。
MATLAB提供了丰富的数值计算函数库和图形界面工具,方便用户进行数据处理和可视化。
3.数值求解:通过MATLAB的数值计算功能,求解数学模型中的方程,得到机械系统的运动学和动力学特性。
这包括求解位置、速度、加速度等物理量的时间历程,以及分析系统的稳定性和振动等动态行为。
4.结果分析和优化:根据计算结果,对机械系统的性能进行分析和评估。
如果需要改进系统的性能,可以对数学模型进行优化设计,并重新进行数值计算和验证。
至于具体的MATLAB机械原理运动解析示例,比如平面连杆机构的分析,可以通过封闭矢量多边形法求解位置方程,得到构件的位置、速度和加速度;或者采用解析法进行机构运动分析,通过建立数学模型并对其进行封闭矢量多边形法求解,得到构件的运动规律。
此外,还可以使用MATLAB对其他类型的机械系统进行运动学和动力学分析,例如齿轮传动系统、凸轮机构等。
总之,MATLAB机械原理运动解析是一种基于数学模型的计算机辅助分析方法,通过MATLAB编程实现机械系统的运动学和动力学分析,有助于优化机械系统的设计和性能。
Matlab求解理论力学问题系列(二)典型机构的运动分析

—血內 sin(pi — «3^2 sin 巾 一QiS sin 0 = 0 ]
恋91 COS0 +COS02 + 如30 COS0 = 0
〉(5) j
由于0,0,02已在前面求出,因此得到关于內,02 的一组线性方程组。类似X=inv(A)*B可解出角速 度,从而可以获得角速度随时间或随6变化的关系 (图 5)。
步骤(4):类似一元函数的泰勒展开式,= f(xo) + f'(xo){x — X0) + o(x — ®0)> 多兀函数为
fi(x) = f,(x*) + J(x*)dx + o(dx)
1 Matlab中非线性方程的求解及动画演示
案例1:如图1,已知四连杆机构ABCD, AB 杆长为如,BC杆长为a2, CD杆长为a3, AD距离 为cm。若AB杆以匀角速度5转动,初始d0 = Oo 求BC和CD杆的角度、角速度变化规律。
编程计算得到角度的变化关系后,可以算出任 意时刻各较的位置,以及BC杆上不同点的运动轨 迹(图3):很明显B点轨迹是圆,C点轨迹是圆的 一部分(AB杆大范围运动时,CD杆只在小范围运 动),而在BC杆上不同的点轨迹就很复杂了。
各较点的位置并连接起来,就得到了四连杆机构在 某一时刻的图象,延迟一定的时间后再画出下一时 刻的图象,就形成了动画。本问题中动画的源代码 见图4,其中plot函数表示画线段;hl是句柄,定义
ai COS & + Q2 COS 01 + Q3 COS(P2 — «4 = 0 1 ⑴
ai sin 9 + 恋 sin 休 + sin 0 = 0
J
方程(1)是关于转角0和02的非线性方程组,通 常没有解析解,下面给出一般的处理方法。
基于 matlab 的机械故障诊断技术案例教程

基于 matlab 的机械故障诊断技术案例教程机械故障诊断技术是通过分析机械设备的运行状态、振动、声波等数据,以识别和定位故障的技术手段。
在此案例教程中,我们将详细介绍基于MATLAB的机械故障诊断技术。
一、故障诊断技术的基本原理故障诊断技术是通过对机械设备的振动、声音等信号进行分析来判断设备运行是否正常。
在机械故障诊断过程中,需要收集设备的振动和声音数据,并进行合理的处理和分析。
二、使用 MATLAB 进行机械故障诊断的案例在此案例中,我们将以离心泵为例,介绍基于 MATLAB 的机械故障诊断技术的应用。
1. 数据采集:从离心泵中采集振动和声音数据,并将其存储为数值形式的文件。
2. 数据预处理:使用MATLAB 对采集到的数据进行预处理,包括去噪、滤波、降采样等操作,以便后续的信号分析和故障诊断。
3. 特征提取:使用 MATLAB 对预处理后的数据提取特征。
常用的特征包括频域特征、时域特征、小波包特征等。
4. 特征选择:根据实际情况,使用 MATLAB 对提取到的特征进行选择,筛选出与故障相关的特征。
5. 故障诊断模型建立:使用 MATLAB 构建故障诊断模型,可以采用机器学习算法、人工智能技术等。
6. 故障诊断与预测:使用构建好的故障诊断模型,对新的数据进行诊断和预测。
通过与已知故障样本进行比对,可以准确判断设备是否出现故障,并预测故障类型。
三、案例教程中的注意事项在进行机械故障诊断时,需要注意以下几点:1. 数据采集要准确可靠,确保采集到的数据具有代表性。
2. 数据预处理要注意去除噪声、滤除干扰,并保留有用的信号。
3. 特征提取要选择合适的特征,能够准确反映机械设备的运行状态。
4. 模型建立要根据实际情况选择合适的算法和技术,同时需要考虑模型的准确性和计算效率。
5. 故障诊断与预测要结合实际情况进行判断,并及时修复设备故障,避免进一步损坏。
综上所述,通过基于 MATLAB 的机械故障诊断技术案例教程,我们可以学习到使用 MATLAB 进行机械故障诊断的基本原理和方法,帮助我们有效提高设备故障的诊断准确性和效率。
MATLAB在机械设计与动力学仿真中的应用实例

MATLAB在机械设计与动力学仿真中的应用实例1. 引言机械设计与动力学仿真是现代工程领域非常重要的一个环节。
通过仿真软件可以在设计前对机械系统进行全面的分析和验证,大大减少了实际试制的时间和成本。
而MATLAB作为一种功能强大的科学计算软件,被广泛应用于机械设计与动力学仿真中。
本文将通过几个实际应用例子来展示MATLAB在这一领域的应用。
2. 机械结构分析机械结构的分析是机械设计的基础。
MATLAB提供了各种方法和工具,可以帮助工程师对机械结构进行静力学和动力学分析。
例如,可以利用MATLAB的有限元分析工具对机械结构进行强度校核。
通过输入结构的几何参数和材料性质,MATLAB可以计算出结构的应力和变形情况,从而判断是否满足设计要求。
此外,还可以利用MATLAB的多体动力学分析工具对机械结构的振动和冲击响应进行模拟和优化,以确保结构的安全性和可靠性。
3. 机械传动系统分析机械传动系统是机械设备中的重要组成部分,对于许多机械设备的运转效果和精度起着至关重要的作用。
MATLAB可以对不同类型的机械传动系统进行仿真分析,从而帮助工程师优化设计参数和减小误差。
例如,可以利用MATLAB的信号处理工具箱对传动系统中的振动和噪音进行分析和消除,提高系统的稳定性和准确性。
此外,还可以利用MATLAB的优化工具箱对传动系统的传动比、齿轮模数等参数进行优化,以满足设计要求。
4. 机械控制系统仿真机械控制系统在现代机械设备中起着至关重要的作用。
MATLAB提供了强大的控制系统设计和仿真工具,可以帮助工程师进行各种机械控制系统的仿真分析和优化设计。
例如,可以利用MATLAB的控制系统工具箱对机械控制系统的稳定性和性能进行评估和改进。
此外,还可以利用MATLAB的仿真工具对机械控制系统进行实时仿真,通过改变输入信号,观察输出响应,从而优化控制算法和参数。
5. 系统性能优化在机械设计与动力学仿真中,系统性能优化是一个重要的目标。
机械原理matlab分析大作业3-28
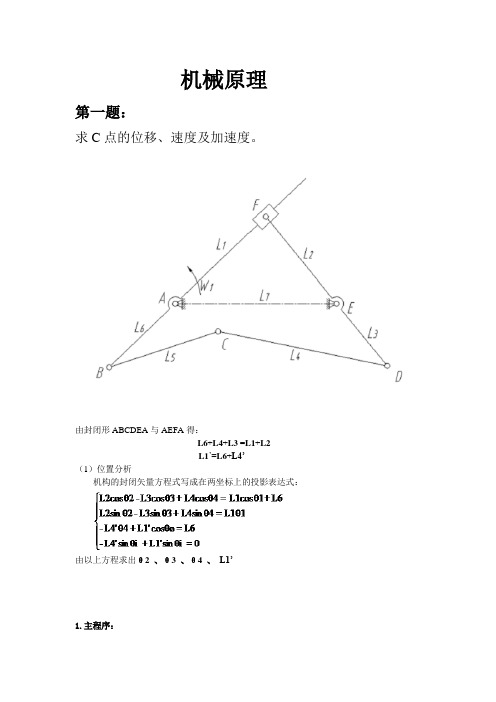
机械原理第一题:求C点的位移、速度及加速度。
由封闭形ABCDEA与AEFA得:L6+L4+L3 =L1+L2L1’=L6+L4’(1)位置分析机构的封闭矢量方程式写成在两坐标上的投影表达式:由以上方程求出θ2 、θ3 、θ4 、L1’1.主程序:%输入已知数据l2=60;l3=35;l4=75;l5=50;l6=40;l7=70;hd=pi/180;du=180/pi;omega1=10;alpha1=0;%调用子函数计算角位移,角速度及角加速度for n1=1:66 %曲柄转角范围theta1(n1)=(n1-1)*hd;ll=[l2,l3,l4,l5,l6,l7];[theta,omega,alpha]=six_bar(theta1(n1),omega1,ll);l1(n1)=theta(1);theta2(n1)=theta(2);theta4(n1)=theta(3);theta3(n1)=theta(4);v1(n1)=omega(1);omega2(n1)=omega(2);omega3(n1)=omega(3);omega4(n1)=omega(4);a1(n1)=alpha(1);alpha2(n1)=alpha(2);alpha3(n1)=alpha(3);alpha4(n1)=alpha(4);e nd%图像输出figure(1);n1=1:66;t=(n1-1)*2*pi/360;subplot(2,2,1);%滑块F线位移L1图像输出plot(theta1*du,l1,'k');title('L1线位移图');xlabel('角位移\theta_1/\circ')ylabel('线位移/mm')grid on;hold on;gtext('L1')pause(1);subplot(2,2,2);%theta2、theta3、theta4角位移图像输出plot(theta1*du,theta2*du,'g',theta1*du,theta3*du,'r',theta1*du,th eta4*du);title('\theta_2、\theta_3、\theta_4角位移图');xlabel('角位移\theta_1/\circ')ylabel('角位移/\circ')grid on;hold on;legend('\theta_2','\theta_3','\theta_4');pause(1);subplot(2,2,3);%滑块F的速度图像输出plot(theta1*du,v1,'k');title('滑块F的速度图');xlabel('角位移\theta_1/\circ')ylabel('速度/mm\cdots^{-1}')grid on;hold on;gtext('v1')pause(1);subplot(2,2,4);%滑块F的加速度图像输出plot(theta1*du,a1,'k');title('滑块F的加速度图');axis auto;xlabel('角位移\theta_1/\circ')ylabel('加速度/mm\cdots^{-2}')grid on;hold on;gtext('a1');pause(5);figure(2);subplot(1,2,1);%omega2、omega3和omega4角位移图像输出plot(theta1*du,omega2,'g',theta1*du,omega3,'r',theta1*du,omega4,' b');title('\omega_2、\omega_3、\omega_4角速度图');axis auto;grid on;hold on;xlabel('角位移\theta_1/\circ')ylabel('角速度/rad\cdots^{-1}')box on;legend('\omega_2','\omega_3','\omega_4');pause(1);subplot(1,2,2);%alpha2、alpha3和alpha4角加速度图像输出plot(theta1*du,alpha2,'g',theta1*du,alpha3,'r',theta1*du,alpha4,' b');title('\alpha_2、\alpha_3、\alpha_4角加速度图');axis auto;grid on;hold on;xlabel('角位移\theta_1/\circ')ylabel('角加速度/rad\cdots^{-2}')box on;legend('\alpha_2','\alpha_3','\alpha_4');pause(5);figure(3);xC=-l6*cos(theta1+pi)+l5*cos(theta3);yC=l6*sin(theta1+pi)+l5*sin(theta3);% rC=sqrt(xC.*xC+yC.yC)vCX=-omega1*l6*sin(theta1+pi)-omega3*l5.*sin(theta3);vCY=omega1*l6*cos(theta1+pi)+omega3*l5.*cos(theta3);% v3=sqrt(vCX.*vCX+vCY.*vCY);subplot(2,2,1);hold on;grid on;%C点x、y方向位移图像输出plot(theta1*du,xC,'r',theta1*du,yC);axis auto;hold on;grid on;title('C点位移图');xlabel('角位移\theta_1/\circ')ylabel('位移/mm')grid on;hold on;legend('xC','yC');pause(1);subplot(2,2,2);grid on;hold on;%C点x、y方向速度图像输出plot(theta1*du,vCX,'k',theta1*du,vCY);title('C点速度图');xlabel('角位移\theta_1/\circ')ylabel('速度/mm\cdots^{-1}')legend('vCX','vCY');pause(1);aCX=omega1*omega1*l6*cos(theta1)-omega3.*omega3.*l5.*cos(theta3)-alpha3.*l5.*sin(theta3);aCY=omega1*omega1*l6*sin(theta1)-omega3.*omega3.*l5.*sin(theta3)+ alpha3.*l5.*cos(theta3);%a3=sqrt(aCX.*aCX+aCY.*aCY);subplot(2,2,3);%C点x、y方向加速度图像输出plot(theta1*du,aCX,'r',theta1*du,aCY,'b');title('C点加速度图');grid on;hold on;xlabel('角位移\theta_1/\circ')ylabel('加速度/mm\cdots^{-2}')box on;legend('aCX','aCY');%主程序结束2.子程序:%子函数function[theta,omega,alpha]=six_bar(theta1,omega1,ll)l2=ll(1);l3=ll(2);l4=ll(3);l5=ll(4);l6=ll(5);l7=ll(6);%1.计算角位移和线位移l1=l7*cos(theta1)+sqrt((l7*cos(theta1))*(l7*cos(theta1))-l7*l7+l2 *l2);theta2=asin((l1*sin(theta1))/l2);A=2*l4*(l6*sin(theta1)-l3*sin(theta2).*sin(theta2));B=2*l4*(l6*cos(theta1)+l7-l3*cos(theta2));C=l4*l4-l5*l5+l6*l6+l7*l7+l3*l3-2*l3*l6*(cos(theta1)*cos(theta2)+ sin(theta1)*sin(theta1))-2*l7*l3*cos(theta2)+2*l6*l7*cos(theta1); theta4=2*atan((A+sqrt(A.*A+B.*B-C.*C))/(B-C));theta3=asin((l6*sin(theta1)+l4*sin(theta4)-l3*sin(theta2))/l5); theta(1)=l1;theta(2)=theta2;theta(3)=theta4;theta(4)=theta3;%2利用矩阵计算角速度和线速度D=[-l5*sin(theta3),l4*sin(theta4),-l3*sin(theta2+pi),0l5*cos(theta3),-l4*cos(theta4),-l3*cos(theta2+pi),00,0,l2*sin(theta2),cos(theta1)0,0,-l2*cos(theta2),sin(theta1)];E=[l6*sin(theta1+pi);-l6*cos(theta1+pi);l1*sin(theta1);-l1*cos(theta1)];omega=D\(omega1*E);v1=omega(4);omega2=omega(3);omega3=omega(1);omega4=omega(2);%3利用矩阵计算角加速度和加速度Dt=[-l5*omega3*cos(theta3),l4*omega4*cos(theta4),-l3*omega2*cos(t heta2),0-l5*omega3*sin(theta3),l4*omega4*sin(theta4),-l3*omega2*sin(theta 2),00,0,l2*omega2*cos(theta2),-omega1*sin(theta1)0,0,l2*omega2*sin(theta2),omega1*cos(theta1)];Et=[l6*omega1*cos(theta1);l6*omega1*sin(theta1);l1*omega1*cos(theta1)+v1*sin(theta1);l1*omega1*sin(theta1)-v1*cos(theta1)];alpha=D\(-Dt*omega+omega1*Et);a1=alpha(4);alpha2=alpha(3);alpha3=alpha(1);alpha4=alpha(2);%3子程序结束3.图像输出:%1.滑块F线位移L1图像输出%2.theta2、theta3、theta4角位移图像输出%3.滑块F的速度图像输出%4.滑块F的加速度图像输出%5.omega2、omega3和omega4角位移图像输出%6.alpha2、alpha3和alpha4角加速度图像输出%7.C点x、y方向位移图像输出%8.C点x、y方向速度图像输出%9.C点x、y方向加速度图像输出。
matlab在机械原理中的应用实例

matlab在机械原理中的应用实例在机械原理中,MATLAB是一种常用的计算工具,可以应用于诸多领域,包括机械设计、力学分析、动力学仿真等。
下面将介绍几个MATLAB在机械原理中的应用实例。
1.机构设计与分析MATLAB可以用于机构的设计和分析,例如平面机构、空间机构、曲柄机构等。
它提供了多种机构建模方法,如刚体模型、柔性模型等。
利用MATLAB的强大计算能力和绘图功能,可以进行机构分析和优化。
例如,可以计算机构的运动学性能、动力学性能和静力学性能,并进行动态仿真。
2.动力学仿真MATLAB可以进行各种机械系统的动力学仿真,包括振动系统、运动系统和控制系统。
通过对机械系统建立微分方程或差分方程,利用MATLAB进行数值解求解,并绘制相应的图形,可以得到机械系统的响应。
例如,可以模拟机械系统的自由振动、强迫振动和阻尼振动等。
3.控制系统设计与分析MATLAB在机械原理中的应用还包括控制系统的设计与分析。
通过MATLAB中的控制系统工具箱,可以进行控制系统的模型建立、系统分析和控制器设计。
例如,可以利用MATLAB对机械系统进行稳定性分析、频域分析和时域分析,并设计相应的控制器,实现机械系统的控制。
4.声学分析MATLAB也可以用于机械系统的声学分析。
通过建立机械系统的声学模型,利用MATLAB进行声场分布和声压级分析。
可以计算机械系统的声辐射特性,例如机械振动引起的噪声。
同时,还可以进行声学优化设计,减少机械系统的噪声。
5.优化设计MATLAB在机械原理中广泛应用于优化设计。
通过建立数学模型和定义目标函数,利用MATLAB进行优化计算。
例如,可以利用MATLAB进行机械系统的拓扑优化、形状优化和尺寸优化,实现机械系统的性能优化。
同时,还可以利用MATLAB的优化算法进行参数优化和控制器设计。
综上所述,MATLAB在机械原理中具有广泛的应用,可以应用于机构设计与分析、动力学仿真、控制系统设计与分析、声学分析和优化设计等方面。
Matlab软件在机械原理课程OBE教学改革中的应用

Internal Combustion Engine &Parts0引言机械原理课程主要包括三大分析(即结构分析、运动分析和力分析)、三大机构(即连杆机构、凸轮机构和齿轮机构)和三大机械(即机械的效率、机械的平衡和机械的运动),简称“机原三三制”。
其分析设计主要采用解析法和作图法,数学运用多,而我校培养的应用型本科生的数学理论基础不够好,在学习该课程时较吃力,甚至畏惧。
如何提高学生课堂知识获得感一直是机械原理课程OBE 教学改革中待解决的重要问题。
Matlab 是一种在数学、自动控制等领域得到广泛应用的数学软件。
为提高学生知识获得感,培养学生软件应用能力等,我们将Matlab 引入到机械原理课程的OBE 教学改革中。
1相关研究现状一些教师已对Matlab 在机械原理课程教学中的应用进行了研究。
例如:刘相权将Matlab 应用于六杆牛头刨床的运动分析[1]。
王宪磊研究了Matlab 在自动控制原理建模分析中的应用[2]。
王俊峰和田丽萍在机原课程设计教学中应用了SimMechanics 模块[3]。
杨绿云将Simulink 模块与———————————————————————基金项目:贵州工程应用技术学院2018年本科教学质量提升工程项目(2018JG097,2018JG100);贵州工程应用技术学院高层次人才科研项目(院科合字G2018009);国家自然科学基金资助项目(51375168)。
作者简介:李永湘(1981-),男,博士,研究方向为OBE 教学改革、云制造;何晓芬(1990-),女,硕士,研究方向为现代设计方法;张卫华(1984-),男,硕士,研究方向为先进制造装备。
Matlab 软件在机械原理课程OBE 教学改革中的应用Application of Matlab in OBE Teaching Reform of Mechanical Principle Course李永湘LI Yong-xiang ;何晓芬HE Xiao-fen ;张卫华ZHANG Wei-hua(贵州工程应用技术学院机械工程学院,毕节551700)(College of Mechanical Engineering ,Guizhou University of Engineering Science ,Bijie 551700,China )摘要:将Matlab 应用于机械原理课程OBE 教学改革,针对机械原理三三制将课程分为三大模块:三大分析、三大机构和三大机械,规划了Matlab 在机械原理教学中应用专题,提出了实施措施,案例研究结果表明,机制专业学生学习成绩和多项能力得到提高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点击此处查看更多内容
《机械原理 MATLAB 辅助分析》既可作为高校机械类专业选修课的教材,也可作为学 习机械原理和机械原理课程设计的参考书。
目录
第一章 平面连杆机构的运动分析 第一节 平面连杆机构运动分析概述 第二节 铰链四杆机构的运动分析 第三节 曲柄滑块机构的运动分析 第四节 导杆机构的运动分析 第五节 六杆机构的运动分析 习题
第四章 凸轮机构设计 第一节 推杆常用的运动规律 第二节 凸轮轮廓曲线的设计 第三节 程序设计实例 习题
第五章 齿轮机构设计 第一节 渐开线函数的计算 第二节 渐开线标准直齿圆柱齿轮的设计计算 第三节 直齿圆柱齿轮机构传动设计计波动的调节
第二章 平面连杆机构的力分析 第一节 平面连杆机构力分析概述 第二节 铰链四杆机构的力分析 第三节 曲柄滑块机构的力分析 第四节 导杆机构的力分析 第五节 六杆机构的力分析 习题
第三章 连杆机构设计 第一节 铰链四杆机构类型判断 第二节 几何法按连杆上活动铰链已知位置设计四杆机构 第三节 位移矩阵法按连杆预定位置设计四杆机构 第四节 解析法按连杆预定位置设计四杆机构 第五节 按预定的运动规律设计四杆机构 第六节 按行程速比系数及有关参数设计四杆机构 习题
内容提要
李滨城等编著的《机械原理 MATLAB 辅助分析》介绍了数学软件 MATLAB 辅助机械 原理分析的方法。运用解析法,通过建立数学模型,对机构与机器进行精确的分析与综合, 是机械原理学科发展的重要方向。全书分为七章,分别应用 MATLAB 进行了平面连杆机构 的运动分析、平面连杆机构的力分析、连杆机构设计、凸轮机构设计、齿轮机构设计、机械 的运转及其速度波动的调节和机构优化设计,每一专题内容通过数学模型的建立、计算实例 的介绍、MATLAB 程序的编制,深入浅出地介绍了 MATLAB 在机械原理中的应用。书中大 量的程序实例不但实用,更包含作者多年在机械原理教学中使用 MATLAB 的经验。
