三棱锥的外接球半径
三棱锥外接球公式

三棱锥外接球公式
三棱锥外接球公式是指一个三棱锥的外接球半径与其四个面的
面积和体积有关的公式。
在数学上,三棱锥外接球公式是三维几何中一个重要的定理,在几何学、物理学、工程学等领域应用广泛。
三棱锥是由一个三角形和一个顶点连接三条棱所组成的多面体。
它的外接球是指可以完全覆盖住三棱锥的球。
三棱锥外接球公式的推导过程可以通过数学计算得出。
具体来说,它可以表示为:
R = (3V/(4πS))^(1/3)
其中,R表示三棱锥外接球半径,V表示三棱锥体积,S表示三
棱锥四个面的总面积。
通过这个公式,我们可以得出一个三棱锥的外接球半径,从而求出它在空间中的位置和大小。
这对于几何学、物理学和工程学领域的研究非常有用。
例如,在建筑结构中,三棱锥外接球公式可以帮助建筑师计算出三棱锥结构的固定点和材料使用量,从而确保建筑物的稳定性和安全性。
总之,三棱锥外接球公式是一个重要的数学定理,在几何学、物理学和工程学等领域有着广泛的应用。
熟练掌握这个公式的计算方法,可以帮助我们更好地理解三维几何学,提高我们的数学和科学素养。
- 1 -。
三棱锥外接球半径常见解法(含答案解析)
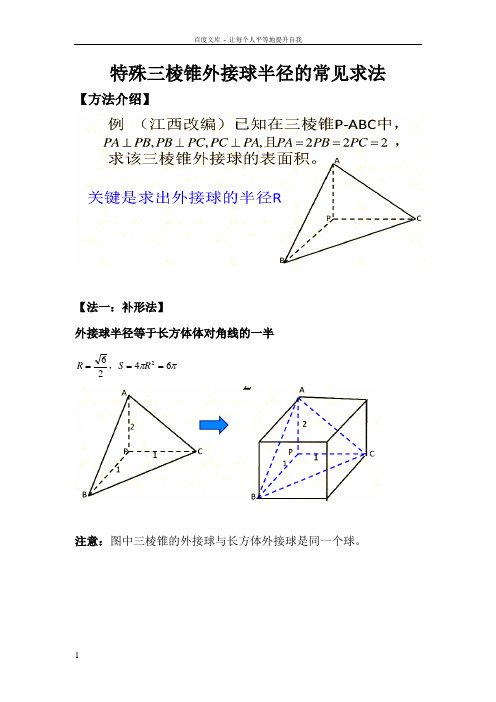
特殊三棱锥外接球半径的常见求法
【方法介绍】
【法一:补形法】
外接球半径等于长方体体对角线的一半
ππ642
6
2===
R S R ,
注意:图中三棱锥的外接球与长方体外接球是同一个球。
【法二:轴截面法】
1、 寻找底面△PBC 的外心;
2、 过底面的外心作底面的垂线;
3、 外接球的球心必在该垂线上,利用轴截面计算出球心的位置。
【法三:向量法】
设外接球的球心坐标为:),,(z y x O .由→
→
→
→
===OC OB OA OP 可得:
【方法总结】
三棱锥外接球半径的常见解法:
1、 补形法;
2、轴截面法;
3、向量法.
【练习巩固】
【参考答案】
练习1 【补形法】
【轴截面法】
【轴截面法】
练习3 【补形法】。
对棱相等的三棱锥外接球半径公式

对棱相等的三棱锥外接球半径公式对于棱相等的三棱锥,我们可以利用其几何特征来推导其外接球的半径公式。
首先,我们先来了解一下什么是外接球。
外接球是指能够同时接触到三棱锥的每一个顶点的球形体,它是一个球心位于三棱锥外部并和三棱锥顶点连成的线段相切。
要推导外接球的半径公式,我们可以利用欧拉公式来解决。
欧拉公式是指,对于所有的凸多面体,其顶点数、棱数和面数满足以下关系:顶点数+面数=棱数+2现在我们来考虑一个有n个棱边的三棱锥。
根据三棱锥的定义,它有n+1个顶点(其中一个顶点是顶点,其余n个顶点是底面的顶点)。
同时,它有n个面(一个是底面,其余n-1个是三角面)。
由于三棱锥的每个面都是一个三角形,所以它共有3n个棱边(每个三角形有3个边)。
将这些数据代入欧拉公式中,我们可以得到:n+1+n=3n+2化简得:2n+1=3n+2n=1这意味着棱相等的三棱锥只有一个边,也就是说它是一个等边三角形。
在等边三角形中,每个角度都是60度。
接下来,我们来推导等边三角形的外接球半径公式。
为了方便推导,我们假设等边三角形的边长为a。
根据三角形的性质,我们可以知道等边三角形的高等于边长的一半乘以根号3(即h=(a√3)/2)。
外接球的半径可以通过等边三角形的高来计算。
根据立体几何的知识,我们可以知道外接球的半径r等于等边三角形的高的三分之二(即r=(a√3)/3)。
将等边三角形的边长a代入到外接球半径公式中,我们可以得到:r=(a√3)/3所以,棱相等的三棱锥的外接球半径公式就是r=(a√3)/3综上所述,对棱相等的三棱锥来说,其外接球半径公式是r=(a√3)/3,其中a代表等边三角形的边长。
三棱锥外接球的半径常见解法-锥形外接圆半径

通过相似三角形性质,将锥形的高与底面圆半径之间的关系转化为相似三角形边 长的比例关系,从而求解锥形外接圆半径。
详细描述
首先,将锥形的高与底面圆半径分别作为相似三角形的一组对应边。然后,利用 相似三角形的性质,即相似三角形的对应边长比例相等,求出锥形外接圆半径。
利用三角函数性质求解
总结词
利用三角函数性质,将锥形的角度信 息转化为锥形外接圆半径的表达式, 进而求解锥形外接圆半径。
详细描述
首先,根据锥形的角度信息,利用三 角函数性质计算出锥形底面圆的半径 。然后,利用锥形外接圆与底面圆的 关系,求出锥形外接圆半径。
利用几何定理求解
总结词
利用几何定理,如勾股定理、毕达哥 拉斯定理等,建立锥形外接圆半径与 其他几何量之间的关系,从而求解锥 形外接圆半径。
详细描述
首先,根据锥形的几何量信息,如锥 形的高、底面圆的半径等,选择适当 的几何定理建立求解方程。然后,解 方程求出锥形外接圆半径。
01
02
03
实际意义
锥形外接圆半径是工程中 常用的参数,如建筑设计、 机械制造等领域。
计算方法
根据实际需求和工程条件, 选择合适的计算公式或方 法求得锥形外接圆半径。
应用案例
建筑设计中的锥形屋顶、 机械制造中的锥形齿轮等。
经典案例解析与探讨
案例选择
选取具有代表性的经典案例,如历年高考数 学题、竞赛题等。
总结词
公式法是一种通过已知的三棱锥的边长和角度,利用公式来求解外接球半径的 方法。
详细描述
首先,我们需要知道三棱锥的边长和角度,然后利用这些已知条件代入公式中 计算出外接球的半径。这种方法需要熟练掌握三棱锥的公式,并且已知三棱锥 的边长和角度。
三棱锥外接球半径常见解法

三棱锥外接球半径常见解法三棱锥是立体几何中最具挑战性的几何形体之一,它具有奇妙的几何美,是许多数学家和几何学家的景点和玩游戏的佳境。
学习解决三棱锥外接球半径的问题,给人带来一种全新的愉悦感。
三棱锥外接球半径的概念有多个描述。
它定义为将一个三棱锥置于某种情况中的最小球体的半径。
三棱锥可以由三条 / 有关的侧延长线构成,或三角形的底部和顶部来构建。
因此,三棱锥外接球半径因其外表形状而变化。
最经典的解决三棱锥外接球半径问题的方法是利用几何进行计算。
该方法主要利用三角函数来检验三角形底部给定点和外接球中心之间的距离。
首先,三角形的底面上的三点应该被指定。
这三点成为被研究三角形的顶点。
以此为基础,计算三个顶点的位置,并确定它们的关系,以确定三边的范围。
当三边的范围被确定以后,通过三角原理,可以得出中线边的长度,并以此决定外接球的半径。
通过三角函数,还可以确定外接球与三角形底部点之间的坐标距离。
首先,应该找出两个顶点形成的直角边的斜率,并利用其斜率式定义斜线方程。
这样就可以展开对应的三角函数,并根据相应的函数求出外接球的中心点与底部点的坐标距离。
另一种解决三棱锥外接球半径问题的方法是借助几何软件。
几何软件提供三棱锥具体定义,并支持求解三棱锥外接球半径的功能,使用者可以更加方便快捷地获得所需要的数据。
通过利用几何软件解决三棱锥外接球半径问题,只需输入三角形底面上的三点坐标即可用几何软件计算出三棱锥外接球半径。
用户还可以根据所输入的点的值,计算出三角形底面的长和宽,从而得出外接球的半径。
当外接球的半径计算出来以后,用户将获得一个完整的三棱锥外接球的数据,借此可以通过算法模拟三棱锥的外观以及三棱锥与球体的关系,为研究三棱锥的几何性质提供参考。
以上就是三棱锥外接球半径常见解法的介绍,它是一种有趣却又挑战性强的数学问题,让人有种新奇解决前所未有问题的乐趣。
高三复习题型:三棱锥外接球半径问题(含答案)
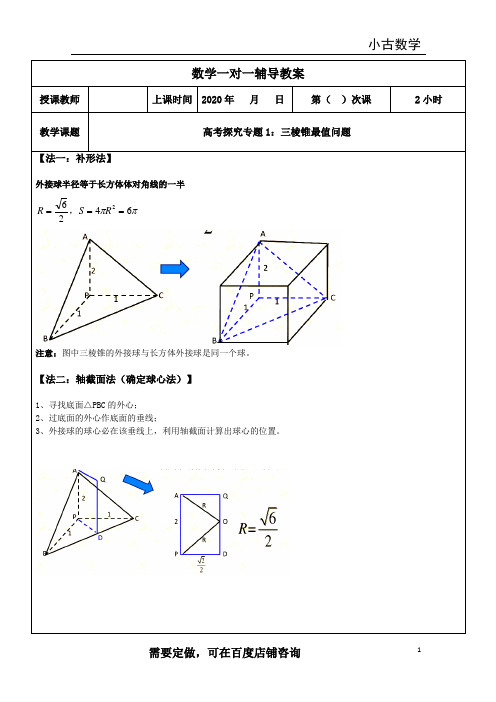
数学一对一辅导教案授课教师 上课时间 2020年 月 日 第( )次课 2小时教学课题 高考探究专题1:三棱锥最值问题【法一:补形法】外接球半径等于长方体体对角线的一半ππ64262===R S R ,注意:图中三棱锥的外接球与长方体外接球是同一个球。
【法二:轴截面法(确定球心法)】1、寻找底面△PBC 的外心;2、过底面的外心作底面的垂线;3、外接球的球心必在该垂线上,利用轴截面计算出球心的位置。
【题型分析】【利用轴截面法1】例1.在三棱锥ABC P -中,︒=∠===⊥120,BAC AC AB PA ABC PA 2,底面,求其外接球的半径【变式1】已知在三棱锥ABC P -,222===⊥⊥⊥PC PB PA PA PC PC PB PB PA ,且,,,求该三棱锥外接球的表面积与体积。
【变式2】在四面体S ABC -中,SA ⊥平面ABC ,90ABC ∠=°,2SA AC ==,1AB =,则该四面体的外接球的表面积为【变式3】三棱锥P ABC -中,PA ⊥平面,,1,3ABC AC BC AC BC PA ⊥===,则该三棱锥外接球的表面积为( ) A .5π B .2π C .20π D .4π【变式4】如图,已知点A、B、C、D是球O的球面上四点,DA⊥平面ABC,AB⊥BC,DA=AB=BC=3,则球O 的表面积等于_________.【利用轴截面法2】例2.三棱锥P-ABC 内接于半径为2的球中,PA ⊥平面ABC ,∠BAC=90°,BC=22,则三棱锥P-ABC 的体积最大值是【变式1】三棱锥P-ABC 内接于半径为4的球中,PA ⊥平面ABC ,∠BAC=45°,BC=22,则三棱锥P-ABC 的体积最大值是【变式2】已知球的直径4SC =,A 、B 是该球球面上的两点,30ASC BSC ∠=∠=︒,则棱锥S ABC -的体积最大为( ) A .2 B .83C .3D .23 【答案】A【解析】如图所示,∵线段SC 是球的直径且4SC =,30ASC BSC ∠=∠=︒, ∴2AC =,=2BC ,23AS =,=23BS ,13A SBC SBC V S h -=⨯⋅△, (其中h 为点A 到底面SBC 的距离),故当h 最大时,A SBC V -的体积最大,由图可得当面ASC ⊥面BSC 时,h 最大且满足4223h =⋅,即3h =,此时112233232A SBC V -=⨯⨯⨯⨯=,故选A .【变式3】在三棱锥BCD A -中,BD AB DB AB DC DB AC AB ⊥=+==,4,,,则三棱锥BCD A -外接球的体积的最小值为( ) A .3264π B .332πC .328πD .34π【利用图形的特殊性】例3.已知在三棱锥ABC P -,222===⊥⊥⊥PC PB PA PA PC PC PB PB PA ,且,,,求该三棱锥外接球的表面积与体积。
三棱锥外接球半径常见解法
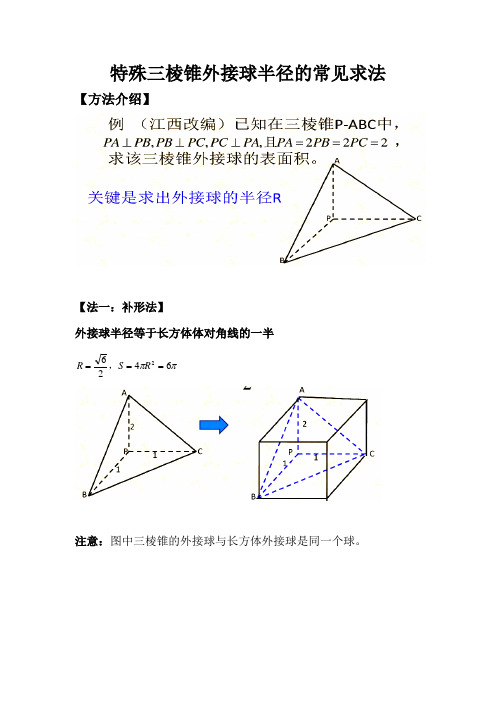
特殊三棱锥外接球半径的常见求法
【方法介绍】
【法一:补形法】
外接球半径等于长方体体对角线的一半
ππ642
6
2===
R S R ,
注意:图中三棱锥的外接球与长方体外接球是同一个球。
【法二:轴截面法】
1、 寻找底面△PBC 的外心;
2、 过底面的外心作底面的垂线;
3、 外接球的球心必在该垂线上,利用轴截面计算出球心的位置。
【法三:向量法】
设外接球的球心坐标为:),,(z y x O .由→
→
→
→
===OC OB OA OP 可得:
【方法总结】
三棱锥外接球半径的常见解法:
1、 补形法;
2、轴截面法;
3、向量法.
【练习巩固】
【参考答案】
练习1 【补形法】【轴截面法】
【轴截面法】
练习3 【补形法】。
几何体外接球常用结论及方法(如何求几何体的外接球半径)

几何体外接球常用结论及方法(如何求几何体的外接球半径)几何体的外接球是一个常见的问题,其中有一些常用的结论和方法:1.对于三棱锥P-ABC,如果PA垂直于PB和PC,则该三棱锥的外接球半径2R可以用公式2R=PA²+PB²+PC²求得。
2.对于等边三角形,其外接圆的半径等于连长的1/3倍。
3.直角三角形的外接圆半径等于斜边的一半。
4.对于一般的三角形ABC,可以用正弦定理求得外接圆半径R,而内切圆的半径r可以用海龙公式S=Cr求得。
5.如果已知三棱锥P-ABC中PA=a,且△ABC的外接圆半径为r,则该三棱锥的外接球半径2R可以用公式2R=2r+a²求得。
6.正方体的外接球、内切球和棱切球的直径分别为正方体的体对角线长2R=3a、棱长2R=a和面对角线长2R=2√2a。
7.对于四面体P-ABC,如果∠APC=90°且∠ABC=90°,则该四面体的外接球直径为AC。
8.对于正三棱锥V-ABC,可以用射影定理求得其外接球半径,即VA²=h(2R-h)。
9.对于正四面体,其高h=2/3√2a,外接球半径和内切球半径均为a。
10.对于有内切球的多面体,其内切球半径可以用公式V=Sr/3求得。
11.如果三棱锥A-BCD中的面ABD和面BCD互相垂直且其外接圆半径分别为r1和r2,公共棱BD的长度为a,则该三棱锥的外接球半径2R可以用公式2R=2r1+2r2-a²/2√(r1²+r2²)求得。
的公共弦AD和BC的垂线,分别交于点E和F。
连接OE和OF,则OE=OF=R,且OE和OF分别是三棱锥P-ABC 和A-BCD的外接球的直径。
由于三棱锥P-ABC和A-BCD的外接球是重合的,因此它们的直径相等,即2R=2r1+2r2-a。
对于三棱锥P-ABC,已知面PAC与ABC所形成的二面角为θ(θ<θ≤90°),且已知ΔPAC和ΔABC的外接圆的半径分别为r1,r2,AC=a,则该棱锥的外接球半径R满足:left(2R+2\cos\theta\right)\left(R-r_1\right)\left(R-r_2\right)=2\left(r_1+r_2\right)^2-4\left(r_1-r_2\right)^2\cos^2\frac{\theta}{2}$这个公式可以通过对三棱锥P-ABC和A-BCD的共面直角投影,推导出它们的公共弦长等于$\sqrt{a^2+\left(r_1+r_2\right)^2-2r_1r_2\cos\theta}$。
