2012考研数学模拟题带答案数学三
2012年考研数学三真题及标准答案

2012年考研数学三真题一、选择题(1~8小题,每小题4分,共32分。
下列每题给出的四个选项中,只有一个选项是符合题目要求的。
)(1)曲线y=x 2+xx2−1渐近线的条数为(A)0 (B)1 (C)2 (D)3 【答案】C。
【解析】由limx→+∞y=limx→+∞x2+xx2−1=1=limx→−∞y=limx→−∞x2+xx2−1,得y=1是曲线的一条水平渐近线且曲线没有斜渐近线;由limx→1y=limx→1x2+xx−1=∞得x=1是曲线的一条垂直渐近线;由limx→−1y=limx→−1x2+xx−1=12得x=−1不是曲线的渐近线;综上所述,本题正确答案是C【考点】高等数学—一元函数微分学—函数图形的凹凸、拐点及渐近线(2)设函数f(x)=(e x−1)(e2x−2)⋯(e nx−n),其中n为正整数,则f′(0)=(A)(−1)n−1(n−1)! (B)(−1)n(n−1)!(C)(−1)n−1(n)! (D)(−1)n(n)!【答案】A【解析】【方法1】令g (x )=(e 2x −2)⋯(e nx −n),则f (x )=(e x −1)g (x )f ′(x)=e xg (x )+(e x −1)g′(x )f ′(0)=g (0)=(−1)(−2)⋯(−(n −1))=(−1)n−1(n −1)!故应选A.【方法2】由于f (0)=0,由导数定义知f ′(0)=lim x→0f(x)x =lim x→0(e x −1)(e 2x −2)⋯(e nx −n)x =lim x→0(e x −1)x ∙lim x→0(e 2x −2)⋯(e nx −n)=(−1)(−2)⋯(−(n −1))=(−1)n−1(n −1)!.【方法3】排除法,令n =2,则f (x )=(e x −1)(e 2x −2)f ′(x )=e x (e 2x −2)+2e 2x (e x −1)f ′(0)=1−2=−1则(B)(C)(D)均不正确综上所述,本题正确答案是(A )【考点】高等数学—一元函数微分学—导数和微分的概念(3)设函数f(t)连续,则二次积分∫dθπ20∫f(r 2)rdr 22cos θ= (A )∫dx 20∫√x 2+y 2f(x 2+y 2)dy √4−x 2√2x−x 2(B) ∫dx 20∫f(x 2+y 2)dy √4−x 2√2x−x 2。
2012考研数学三真题与答案

2012年考研数学三真题一、选择题(18小题,每小题4分,共32分。
下列每题给出的四个选项中,只有一个选项是符合题目要求的。
)(1)曲线渐近线的条数为(A)0 (B)1(C)2 (D)3【答案】C。
【解析】由,得是曲线的一条水平渐近线且曲线没有斜渐近线;由得是曲线的一条垂直渐近线;由得不是曲线的渐近线;综上所述,本题正确答案是C【考点】高等数学—一元函数微分学—函数图形的凹凸、拐点及渐近线(2)设函数,其中为正整数,则(A) (B)(C) (D)【答案】A【解析】【方法1】令,则故应选A.【方法2】由于,由导数定义知.【方法3】排除法,令,则则(B)(C)(D)均不正确综上所述,本题正确答案是(A)【考点】高等数学—一元函数微分学—导数和微分的概念(3)设函数连续,则二次积分(A)(B)(C)(D)【答案】B。
【解析】令,则所对应的直角坐标方程为,所对应的直角坐标方程为。
由的积分区域得在直角坐标下的表示为所以综上所述,本题正确答案是(B)。
【考点】高等数学—多元函数微积分学—二重积分的概念、基本性质和计算(4)已知级数绝对收敛,级数条件收敛,则(A) (B)(C) (D)【答案】D。
【解析】由级数绝对收敛,且当时,故,即由级数条件收敛,知综上所述,本题正确答案是(D)【考点】高等数学—无穷级数—数项级数敛散性的判定(5)设,其中为任意常数,则下列向量组线性相关的为(A) (B)(C) (D)【答案】C。
【解析】个维向量相关显然所以必线性相关综上所述,本题正确答案是(C)。
【考点】线性代数—向量—向量组的线性相关和线性无关(6)设为3阶矩阵,为3阶可逆矩阵,且.若,则(A) (B)(C) (D)【答案】B。
【解析】由于经列变换(把第2列加至第1列)为,有那么=综上所述,本题正确答案是(B)。
【考点】线性代数—矩阵—矩阵运算、初等变换(7)设随机变量相互独立,且都服从区间上的均匀分布,则(A) (B)(C) (D)【答案】D。
2012考研数学三真题及答案解析

,
1 0
a 0 0 1
0
(Ⅰ)计算行列式 A ;
(Ⅱ)当实数 a 为何值时,方程组 Ax 有无穷多解,并求其通解.
1 0 1
(21)已知
A
0 1
1 0
1 a
,二次型
f
x1,
x2 ,
x3
xT
AT A x 的秩为 2,
0
a 1
(Ⅰ)求实数 a 的值;
(Ⅱ)求正交变换 x Qy 将 f 化为标准形.
(13)设 A 为 3 阶矩阵, A 3 , A* 为 A 的伴随矩阵。若交换 A 的第 1 行与第 2 行得矩 阵 B ,则 BA*
(14)设 A 、 B 、 C 是随机事件, A 与 C 互不相容, P( AB) 1 , P(C) 1 ,则 P( AB | C)
2
3
三、解答题:15~23 小题,共 94 分.请将解答写在答.题.纸.指定位置上.解答应写出文字说 明、证明过程或演算步骤.
0
2
0
0 0 1
(7)设随机变量 X 与 Y 相互独立,且都服从区间(0.1)上的均匀分布,则
P X 2 Y 2 1 ( )
(A) 1 4
(B) 1 2
(C) 8
(D) 4
(8)设 X1, X 2 , X 3 , X 4 为来自总体 N(1, 2 ) ( 0) 的简单随机样本,则统计量
4
2 2
2
(10)
dy dx
xe
(ln
x 1)
xe
1 e
【分析】本题主要考查复合函数求表达式及复合函数求导数。先利用分析法得到
y f ( f (x)) 的表达式,再求导数,或直接根据分段函数的定义用复合函数求导法求导
2012年考研数学三答案(完整版)
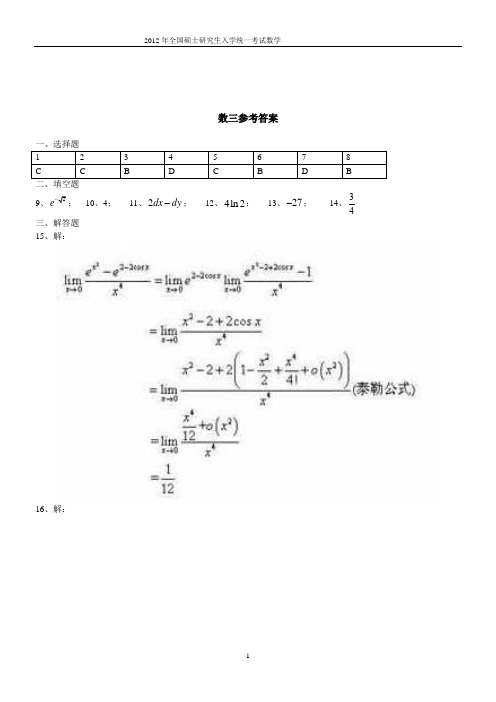
数三参考答案一、选择题二、填空题9、e; 10、4; 11、2dx dy -; 12、4ln 2; 13、27-; 14、34三、解答题 15、解:16、解:17、解:(I )(,)=20+2xx C x y ',对x 积分得:()2(,)204xC x y xD y =++再对y 求导有,()(,)6yC x yD y y ''==+ 再对y 积分有,()262yD y y c =++所以22(,)20642x y C x y x y c =++++,又(0,0)10000C =,所以10000c = 所以22(,)2061000042xyC x y x y =++++(II )x+y=50,把y=50-x 代入22(,)2061000042xyC x y x y =++++23()36115504x C x x =-+令23()361155004x C x x '⎛⎫'=-+= ⎪⎝⎭,得x=24,y=50-24=26, 这时总成本最小C (24,26)=11118万元(III )()24,26(,)32xC x y '=(万元/件) 经济意义:总产量为50件,当甲产品的产量为24时,每增加一件甲产品,则甲产品的成本增加32万元。
18、证明:令()21lncos 112x xf x x x x+=+---,()212lnsin 11x x f x x xxx+'=+----()00f '= ()()()222221411cos 1111xx f x x xxx -+''=++--+--()()222244cos 12011x x x =--≥->--所以()()00f x f ≥=即证得:()21ln cos 11112x xx x x x++≥+-<<-19、解:(I )'''()()2()0f x f x f x +-=对应的特征方程为220r r +-=,r=-2,r=1 所以()212xxf x C e C e -=+把()212xxf x C e C e -=+代入''()()2x f x f x e +=,得到()xf x e =(II )同理,当x<0时,0y ''<可知(0,0)点是曲线唯一的拐点。
2012年全国硕士研究生入学统一考试数学三试题及答案

4- x 222012 年全国硕士研究生入学统一考试数学三试题解析一、选择题:1~8 小题,每小题 4 分,共 32 分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答.题.纸.指定位置上. x 2 + x(1) 曲线 y =(A )0 (B )1(C )2(D )3【答案】: C【解析】: lim x →1x 2-1x 2 + xx 2 -1渐近线的条数为()=∞ ,所以 x = 1为垂直的lim x 2+ x = 1,所以 y = 1为水平的,没有斜渐近线 故两条选C x →∞ x 2 -1(2) 设函数 f (x ) = (e x -1)(e 2x - 2) (e nx - n ),其中n 为正整数,则 f ' (0) =(A ) (-1)n -1(n -1)!(B ) (-1)n (n -1)!(C ) (-1)n -1n !(D ) (-1)n n ! 【答案】:A【解析】: f ' (x ) = ex (e 2x - 2)所以 f '(0) = (-1)n -1(n -1)!π2(3) 设函数 f (t ) 连续,则二次积分⎰2 d θ ⎰ f (r 2 )rdr =()24- x222 2 22 cos θ(A ) ⎰0 dx⎰2 x - x2x (B ) ⎰0 dx⎰2 x - x2f (x + y f (x + y 2 + y 2 )dy)dy24- y 22222(C ) ⎰0dy⎰1+ 1- y 2x + y f (x + y )dx(e nx - n ) + (e x -1)(2e 2x - 2) (e nx - n ) + (e x -1)(e 2x - 2) (ne nx - n )4- y 2 x 2 + y 2 2x - x 2 2n n2n(D ) ⎰0dy⎰1+f (x 2 + y 2 )dx【答案】:(B )【解析】:由 x ≤ 解得 y 的下界为 ,由≤ 2 解得 y 的上界为.故排除答案(C )(D ). 将极坐标系下的二重积分化为 X -型区域的二重积分得到被积函数为 f (x 2 + y 2 ) ,故选(B ).∞n1 ∞ (-1) n(4)已知级数∑(-1)n =1 1 n sin α 绝对收敛, ∑ 2-α 条件收敛,则α 范围为( )i =1 (A ) 0 < α ≤21(B ) 2< α ≤ 13(C )1 < α ≤2 3(D ) 2< α < 2【答案】:(D )∞n1 【解析】:考察的知识点是绝对收敛和条件收敛的定义及常见的 p 级数的收敛性结论.∑(-1)i =1sinnα3∞ (-1) n绝对收敛可知α > ;∑ 2-α条件收敛可知α ≤ 2 ,故答案为(D )i =1⎛ 0 ⎫ ⎛ 0 ⎫ ⎛ 1 ⎫ ⎛ -1⎫ (5)设α = 0 ⎪,α = 1 ⎪,α = -1⎪, α = 1 ⎪ 其中c , c , c , c 为任意常数,则下列向量组线性相关1 ⎪2 ⎪3 ⎪4 ⎪ 1 2 3 4c ⎪ c ⎪ c ⎪ c ⎪ ⎝ 1 ⎭ ⎝ 2 ⎭ ⎝ 3 ⎭ ⎝ 4 ⎭的是()(A )α1,α2,α3(C )α1,α3,α4 【答案】:(C )【解析】:由于 (α ,α ,α (B )α1,α2,α4(D )α2,α3,α40 1 -1 )= 0 -1 1 = c 1 -1= 0 ,可知α ,α ,α 线性相关。
2012考研数学三模拟题2答案解析

参考答案一、选择题:1~8小题,每小题4分,共32分.在每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内.(1)设函数()f x 有二阶连续导数,且0()1lim1cos x f x x →-=-,()1lim1x f x →''-=,则(A)()f x 在点0x =处取极大值 (B)()f x 在点0x =处取极小值 (C)点(0,(0))f 是曲线()y f x =的拐点(D)点0x =不是()f x 的极值点,点(0,(0))f 也不是()y f x =的拐点 [ ]正确答案:B .解析:由()1lim1cos x f x x→-=-,0lim (1cos )0x x →-=,得0lim (()1)0x f x →-=,而由()f x ''连续知()f x 连续,所以lim ()(0)1x f x f →==.于是220()(0)()11cos (0)limlim 01cos x x f x f f x x xf xx x x →→---'==⋅⋅=-,所以0x =是()f x 的驻点.又由lim1x →''=,0lim 1)0x →=,得0lim (()1)(0)10x f x f →''''-=-=,即(0)10f ''=>,所以()f x 在点0x =处有(0)0f '=,(0)10f ''=>,故点0x =是()f x 的极小值.应选(B).(2)设函数(,)f x y 在全平面上都有(,)f x y x∂<∂,(,)f x y y∂>∂.则下列条件中能保证1122(,)(,)f x y f x y <的是(A) 1212,x x y y << (B)1212,x x y y <>(C)1212,x x y y >< (D)1212,x x y y >>正确答案:C .解析:由 (,)f x y x∂<∂,当固定y 时,(,)f x y 对x 单调下降,故对12x x >时,有1121(,)(,)f x y f x y <;又由(,)f x y y∂>∂,,当固定x 时,(,)f x y 对y 单调上升,故对12y y <时,有2122(,)(,)f x y f x y <;因此,当1212,x x y y ><时,有 112122(,)(,)(,)f x y f x y f x y <<.应选(C).[ ](3)累次积分cos 2(cos ,sin )d f r r rdrπθθθθ⎰⎰可以写成(A)1(,)dy f x y dx⎰⎰(B)1(,)dy f x y dx⎰⎰(C)11(,)dx f x y dy⎰⎰(D)1(,)dx f x y dy⎰[ ]正确答案:D .解析:由题设可知积分区域在极坐标系cos ,sin x r y r θθ==下是{(,)|0,0c o s }2D r r πθθθ=≤≤≤≤,D 的图形如图所示.它在直角坐标系下是{(,)|01,0D x y x y =≤≤≤≤或{(,)|01,D x y y =≤≤1122-≤+,因此,这个二重积分在直角坐标下化为累次积分应为1(,)dx f x y dy⎰或112102(,)dy f x y dx⎰⎰.由此可见(D )是正确的,应选(D ).(4)设01p <≤,级数11sin()1n pnn x dxx π∞+=+∑⎰(A)绝对收敛 (B)条件收敛 (C)发散 (D)敛散性与p 有关 [ ]正确答案:B .解析:当01p <≤时,由积分中值定理得11sin()12(1)sin()11(1)nn n pppnnnn x dx x dx x ππξπξ++-==+++⎰⎰,(,1)n n n ξ∈+,所以1sin()22||1(1)((1)1)n pppn n x dx x n ππξπ+=>++++⎰,(,1)n n n ξ∈+,而22~()((1)1)ppn n nππ→∞++,12pn nπ∞=∑发散,所以原级数非绝对收敛.又1sin()2||0()1(1)n ppnn x dx n x ππξ+=→→∞++⎰,而(,1)n n n ξ∈+,即1sin()||1n pnx dx x π++⎰单调减少.由莱布尼茨判别法知原级数收敛,故级数是条件收敛的,应选(B ). (5)设A ,B 是n 阶可逆矩阵,满足AB A B =+.则 ① ||||||A B A B +=; ② 111()AB A B---=;③()0A E X -=只有零解; ④B E -不可逆. 中正确的项数是(A )1 (B )2 (C )3 (D )4 [ ]正确答案:C .解析:因A ,B 满足AB A B =+.两边取行列式,显然有||||||||A B AB A B +==,(A )成立. 又AB A B =+,移项,提公因子得()AB A A B E B-=-=,()A B E B E E -=-+, ()()A E B E E --=.故A E -,B E -都是可逆阵,且互为逆矩阵,从而知方程组()0A E X -=只有零解,正确. B E -不可逆是错误的,又因()()A E B E E --=,故()()B E A E E --=, 从而有BA A B E E --+=,BA A B =+,得AB BA =,从而有1111()()AB BA A B----==成立.故(1)、(2)、(3)是正确的,应选(C ).(6)已知线性方程组12AX k ββ=+有解,其中111121111A -⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦,1213β⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,2131β⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,则k 等于(A )1 (B )-1 (C )2 (D )-2 [ ]正确答案:D . 解析:将12AX k ββ=+的增广矩阵作初等行变换,121112111121[|]121301034111310202k k A k k k k k ββ⎡-+⎤⎡-+⎤⎢⎥⎢⎥+=--+→-+⎢⎥⎢⎥⎢⎥⎢⎥-----⎣⎦⎣⎦1112101034000510k k k ⎡-+⎤⎢⎥→-+⎢⎥⎢⎥--⎣⎦,12AX k ββ=+有解⇔12()(|)r A r A k ββ=+,得2k =-,故应选(D ).(7)设A 、B 、C 为事件,()0P ABC >,如果(|)(|)(|)P AB C P A C P B C =,则 (A )(|)(|)P C AB P C A = (B )(|)(|)P C AB P C B = (C )(|)(|)P B AC P B A = (D )(|)(|)P B AC P B C = [ ]正确答案:D .解析:已知(|)(|)(|)P AB C P A C P B C =意指:“在C 发生的条件下,A 与B 独立”.所以“在C 发生的条件下,A 发生与否不影响B 发生的概率”,即(|)(|)P B AC P B C =,选择(D ).我们也可以通过计算来确定选项.事实上:(|)(|)(|)P AB C P A C P B C =⇔(|)(|)(|)(|)P A C P B AC P A C P B C = ⇔(|)(|)P B AC P B C =,选择(D ).选项(A )、(C )表示:在A 发生下,B 与C 独立;选项(B )表示:在B 发生下,A 与C 独立.注:条件()0P ABC >,除了保证各条件概率有意义外,还保证各项概率均不为零.(8)设12,,,nX X X 是总体(0,1)N 的简单随机样本,记11nii X X n==∑,2211()1nii S X X n ==--∑,2(1)(1)T X S =++,则()E T 的值为(A )0 (B )1 (C )2 (D )4 [ ]正确答案:C . 解析:()0E X =,2()1E S =,且X ,2S 相互独立.所以22()(1)(1)(1)(1)E T E X S E X E S =++=++1(11)2=⋅+=.二、填空题:9~14小题,每小题4分,共24分.把答案填在题中横线上.(9)2cos 0txedt -+=⎰⎰的实根个数是_____.正确答案:1. 解析:设2cos ()xtxf x edt-=+⎰⎰,则21(0)0tf edt -=<⎰,()02f π=>,由介值定理知,存在0(0,)2x π∈,使0()0f x =.又2cos ()sin xf x ex-'=⋅1>,2cos |sin |1xex -⋅≤,故()0f x '>,()f x 严格单调增加,()0f x =只有唯一的根0x.(10)设(,)f x y 存在一阶偏导数,且(1,1)1f =,(1,1)2x f '=,(1,1)1y f '=.又()(,(,(,)))x f x f x f x x ϕ=,则(1)ϕ'=_____. 正确答案:7.解析:由复合函数求导法则,逐层展开有121212()[()]x f f f f f f ϕ'''''''=+++,所以(1)21[21(21)]7ϕ'=+⋅+⋅+=.(11)设()y y x =是由sin()ln1x e xy y+=+确定的隐函数,则(0)________y '=.正确答案:4e e -.解析:在方程中令0x =可得0ln1(0)e y =+,2(0)y e=将方程两边对x 求导数,得1cos()()y xy y xy x ey ''+=-+将0x =,2(0)y e =代入,有221(0)y e ee'=-,即4(0)y e e'=-(12)幂级数1(2)3nnn x n ∞=-⋅∑的收敛域为____.正确答案:[1,5)- 解析:由公式,111(1)3l i m 133n n nn n +→∞+=所以3R =,收敛区间(23,23)-+,即(1,5)-.再考虑端点1,5x x =-=处.在1x =-处,原级数成为1(1)nn n∞=-∑,收敛;在5x =处.原级数成为11n n ∞=∑,发散.所以应填[1,5)-.(13)设A 是三阶矩阵,有特征值11λ=,21λ=-,32λ=.*A 是A的伴随矩阵,E 是三阶单位阵,则*0||_____.2A A E A ⎡⎤=⎢⎥-⎣⎦正确答案:112.解析:A 有特征值11λ=,21λ=-,32λ=,故31||2i i A λ==∏=-,*31||||4A A -==. 从而有*633*11||||(1)(2)||22A A A A E A ⎡⎤=-⋅-=⎢⎥-⎣⎦.(14)已知随机变量X 的概率分布为1{},(1,2,3)3P X k k ===,当X k =时随机变量Y 在(0,)k 上服从均匀分布,即0,0,{|},0,1,.y yP Y y X k y k kk y ≤⎧⎪⎪≤==<<⎨⎪≤⎪⎩则{ 2.5}____.P Y ≤=正确答案:1718.解析:由题设知31{}1k P Xk ===∑,1{}3P X k ==.根据全概率公式得31{ 2.5}{ 2.5,}k P Y P YX k =≤=≤=∑31{}{ 2.5|}k P Xk P Y X k ===≤=∑1 2.58.517[11]33918=++==.三、解答题:15~23小题,共94分.解答应写出文字说明、证明过程或演算步骤.(15)设函数()f x 在点0x =处二阶可导,且满足()231lim (3x fx xx→-+=.求'(0),(0)f f 与''(0)f .解析:由题设可知()()22311lim ()lim (x x fx fx x xxx→→--+=+⋅=,()()2lim (lim (x x fx fx x xxxx→→+=+⋅=,从而()011(0)lim ()lim (lim 11cos 2limlim0,x x x x x f f x fx xx xxx→→→→→--==+---=-=-=()()()()'20(0)limlim0lim (limlim1cos 2lim 12sin 2lim1,22x x x x x x x f x f f x f x xf x x xxxxxx x →→→→→→→-==-=+-=--=⋅=-=-()()()()()'''222023001(0)2lim2lim ()12lim (2lim ((162limx x x x x f x f fxfx f xxxfx xx xxx x→→→→→--==+=++---=+0226lim6lim 33x x x →→=+=+2200221)2sin 26[limlim]3x x x x xxx→→-=++21cos 26[lim lim]32cos 211cos 26[limlim]36.x x x x xx x x xxx→→→→-=+--=++=(16)计算二重积分(1)Dx y d σ+⎰⎰,其中积分区域D 由y轴与曲线y y ==.解析:引入极坐标(,)r θ满足cos ,sin x r y r θθ==,在极坐标(,)r θ中积分区域D 可表示为{(,)|0,2cos 2}2D r r πθθθ=≤≤≤≤,于是2202cos 22322202cos 02cos 4343220(1)cos (sin 1)cos sin cos 22cos sin [1cos ]cos [1cos ],43Dx y d d r r rdrd r dr d r drd d I J πθππθθππσθθθθθθθθθθθθθθθ+=+=+=-+-=+⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰由于41442002114cos sin [1cos ]4(1)4()4263I d t t dt πθθθθ=-=-=-=⎰⎰, 334222000288318cos [1cos ](cos cos )(1)33342232J d d d πππππθθθθθθθ⋅⋅=-=-=-=-⋅⋅⎰⎰⎰,故48(1)43322Dx y d I J ππσ+=+=+-=-⎰⎰.(17)设生产某种产品需投入甲、乙两种原料,x 和y 分别为甲、乙两种原料的投入量(单位:吨),Q 为产出量,且生产函数为Q kx y αβ=,其中常数0k >,0α>,0β>.已知甲种原料每吨的价格为1P (单位:万元),乙种原料每吨的价格为2P (单位:万吨).如果投入总价值为A (万元)的这两种原料,当每种原料各投入多少吨时,才能获得最大的产出量?解析:本题要求函数Q kx yαβ=在条件120P x P y A +-=下的最大值点.用拉格朗日系数法,构造拉格朗日函数12(,,)()F x y kx yP x P y A αβλλ=++-,为求函数(,,)F x y λ的驻点,令 111212000x y F k x y P F k x yP F P x P y A αβαβλαλβλ--⎧'=+=⎪⎪'=+=⎨⎪'=+-=⎪⎩①②③由①、②消去参数λ可得12P yxP αβ=,即12P x y P βα=,代入③不难计算出唯一驻点1()A x P ααβ=+,2()A y P βαβ=+.因驻点唯一,且实际问题必存在最大产量,所以计算结果表明,当投入总价值为A (万元)的甲、乙两种原料时,使产量Q 最大的甲、乙两种原料的投入量分别是1()A x P ααβ=+(吨)与2()A y P βαβ=+(吨).(18)设(,)f u v 具有连续偏导数,且(,)(,)sin()u vu v f u v f u v u v e +''+=+,求2()(,)xy x ef x x -=所满足的一阶微分方程,并求其通解.解析:由2()(,)xy x ef x x -=,有2212()2(,)[(,)(,)]xxy x e f x x ef x x f x x --'''=-++,在条件(,)(,)sin()u vu v f u v f u v u v e+''+=+,即12(,)(,)sin()u vf x x f x x u v e+''+=+,中令,u x v x==得212(,)(,)sin(2)xf x x f x x x e''+=,于是()y x 满足一阶线性微分方程()2()sin 2y x y x x '+=.通解为22()[sin 2]xxy x ex e dx c -=⋅+⎰,由分部积分公式,可得221sin 2(sin 2cos 2)4xxx e dx x x e⋅=-⎰,所以21()(sin 2cos 2)4xy x x x ce-=-+.注:也可由(,)f u v ,满足的偏微分方程,直接得到()y x 满足的常微分方程. 由(,)(,)sin()u vu v f u v f u v u v e+''+=+,令,u x v x ==,上式转化为常微分方程2(,)sin(2)xdf x x x edx=⋅,所以22(())sin(2)xxd y x ex edx=⋅,得()y x 满足的微分方程()2()sin 2y x y x x '+=.(19)设()f x 在区间[,]a b 上可导,且满足22()cos ()cos a b af b b f x xdxb a+⋅=⋅-⎰.求证至少存在一点(,)a b ξ∈,使得()()tan f f ξξξ'=⋅.证明:由于()f x 在[,]a b 上可导,知()f x 在[,]a b 上连续,从而()()c o s F x f x x =在[,]2a b a +上连续.由积分中值定理,知存在一点(,)2a b c a +∈使得22()()cos 2()()2()a b aF b f x xdx b aa b F c a b aF c +=⋅-+=⋅⋅--=⎰在[,]c b 上,由罗尔定理得至少存在一点(,)(,)c b a b ξ∈⊂使()()cos ()sin 0F f f ξξξξξ''=-=, 即()()tan f f ξξξ'=⋅,(,)a b ξ∈.(20)设四维向量组1(1,1,4,2)Tα=,2(1,1,2,)Tb α=--,3(3,1,,9)Ta α=---,(1,3,10,)Ta b β=+.问:(Ⅰ)当,a b 取何值时,β不能由123,,ααα线性表出;(Ⅱ)当,a b 取何值时,β能由123,,ααα线性表出,并写出此时的表达式.解析:设112233x x x αααβ++=,对增广矩阵123(,,|)A αααβ=作初等行变换得113111311113011142100060290524A a a ba b b a b ⎡-⎤⎡-⎤⎢⎥⎢⎥----⎢⎥⎢⎥=→⎢⎥⎢⎥-+⎢⎥⎢⎥-+-+-⎢⎥⎢⎥⎣⎦⎣⎦(Ⅰ)当6a ≠-且24a b +≠时, 113101110060024A a a b ⎡-⎤⎢⎥--⎢⎥→⎢⎥+⎢⎥+-⎢⎥⎣⎦ ()3r A =,()4r A =.方程组无解,β不能由123,,ααα线性表出.(Ⅱ)当6a =-时,11310111005210000A b b ⎡-⎤⎢⎥--⎢⎥→⎢⎥--⎢⎥⎢⎥⎣⎦若5b =,方程组有无穷多解. 令3x t=,得21x t =-,122x t =+,即123(22)(1)t t t βααα=++-+,t 为任意常数.若5b ≠,方程组有唯一解1236,1,2x x x ===,即12362βααα=++.(21)设二次型222123123121323(,,)33484T f x x x x Ax x ax x x x x x x x ==++---其中2-是二次型矩阵A 的一个特征值.(Ⅰ)试用正交变换将二次型f 化为标准形,并写出所用正交变换;(Ⅱ)求f 在条件2221231x x x ++=下的最小值,并求最小值点123(,,)x x x ;(Ⅲ)如果*A kE +是正定矩阵,求k 的取值.解析:(Ⅰ) 二次型f 的矩阵32422423A a --⎡⎤⎢⎥=--⎢⎥⎢⎥--⎣⎦由2λ=-是A 的特征值,有524|2|2229(6)0425E A a a ---=--=--=-得到6a =.由矩阵A 的特征多项式2324||22(7)(2)423E A a λλλλλλ--=-=-+-得到矩阵A 的特征值是127λλ==,32λ=-.对7λ=,解齐次方程组(7)0E A x -=得基础解系 1(1,2,0)Tα=-,2(1,0,1)Tα=-对2λ=-,解齐次方程组(2)0E A x --=得基础解系3(2,1,2)Tα=.因为12,αα不正交,故需Schmidt 正交化,有11120βα⎡⎤⎢⎥==-⎢⎥⎢⎥⎣⎦,2122111114()11022()55105αββαβββ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-=--=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦. 再单位化,得1120γ⎡⎤⎥=-⎥⎥⎦,2425γ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,321132γ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦那么令123231(,,)3203Q γγγ⎡⎤⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦,则在正交变换x Qy =下,有222123772TTx A x y y y y y =Λ=+-(Ⅱ) 条件2221231x x x ++=,即1Tx x =.而()()TTTTTx x Q y Q y y Q Q y y y===可知f 在条件2221231x x x ++=的极小值,即f 在条件2221231y y y ++=下的极小值.由于222222123123123(,,)7722()T T f x x x x Ax y y y y y y y y ==Λ=+-≥-++,所以2221231|2x xx f ++==-.而极小值点是123223302211033122033x x x ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=-=±⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥±⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦.(Ⅲ)因为矩阵A 的特征值:7,7,-2.所以||98A =-,那么*A 的特征值为:-14,-14,49.从而*A k E +的特征值为14k -,14k -,49k +.因此,14k >时,*A kE +正定.(22)设两随机变量(,)X Y 在区域D 上均匀分布,其中{(,):||||1}D x y x y =+≤.又设U X Y =+,V X Y =-,试求:(Ⅰ)U 与V 的概率密度()U f u 与()V f v ;(Ⅱ) U 与V 的协方差cov(,)U V 的相关系数U V ρ.解析:区域D 实际上是以(1,0),(1,0),(0,1),(0,1)--为顶点的正方形区域,D 的面积为2,(,)X Y 的联合密度为1,(,);(,)20,.x y D f x y ⎧∈⎪=⎨⎪⎩其他有了(,)f x y 就可以求()U f u 和()V f v ,特别可利用(,)f x y 的对称性.(Ⅰ) U X Y =+,(){}{}(,)U x y uF u P U u P X Y u f x y dxdy+≤=≤=+≤=⎰⎰.当1u <-时,()0U F u =;当11u -≤≤时,11()22U x y uu F u dxdy +≤+==⎰⎰;当1u >时,()1U F u =.1,11;()()20,U U u f u F u ⎧-≤≤⎪'==⎨⎪⎩其他. ~[1,1]U U -. V X Y =-,(){}{}(,)V x y vF v P V v P X Y u f x y dxdy-≤=≤=-≤=⎰⎰.当1v <-时,()0V F v =;当11v -≤≤时,11()22U x y vv F u dxdy -≤+==⎰⎰;当1v >时,()1V F v =.1,11;()()20,V V v f v F v ⎧-≤≤⎪'==⎨⎪⎩其他. ~[1,1]V U -. (Ⅱ)cov(,)()U V E UV EU EV =-⋅.显然0E U E V ==,而2222()()()()E U V E X Y X Y E X Y EXEY =+-=-=-,由于,X Y 的对称性得22EX EY =,所以cov(,)0U V =,UV ρ==.(23)设两随机变量(,)X Y 的概率密度为 (),01;(,)0,k x y y x f x y +<<<⎧=⎨⎩其它.求(Ⅰ)常数k 的值;(Ⅱ) (,)X Y 的边缘密度()X f x 和()Y f y ;(Ⅲ)条件密度|(|)Y X f y x 和|(|)X Y f x y ;(Ⅳ){1}P X Y +≤的值.解析:(Ⅰ)11221(,)()()122x Dk f x y dxdy dx k x y dy k x x dx =+=+==⎰⎰⎰⎰⎰,所以2k =.(Ⅱ)2202()3,01;()(,)0,X x y dy x x f x f x y dy +∞-∞⎧+=<<⎪==⎨⎪⎩⎰⎰其它.1212()123,01;()(,)0,yY x y dx y y y f y f x y dx +∞--∞⎧+=+-<<⎪==⎨⎪⎩⎰⎰其它.(Ⅲ)()0X f x ≠,即01x <<时,2|2(),0;(,)(|)3()0,Y X X x y y x f x y f y x x f x +⎧<<⎪==⎨⎪⎩其它.()0Y f y ≠,即01y <<时,2|2(),1;(,)123(|)()0,X Y Y x y y x f x y y yf x y f y +⎧<<⎪+-==⎨⎪⎩其它.(Ⅳ)1101{1}(,)2()x y x y y x P X Y f x y dxdy x y dxdy+≤+≤<<<+≤==+⎰⎰⎰⎰112012()3y ydy x y dx -=+=⎰⎰.。
2012考研数学三【解析版】【无水印】

f ′(1) f ( f (x))
ln
f (x), f (x) ≥ 1 ,而 f (x) ≥ 1 ⇔ x ≥ e2 ,
2 f (x) −1, f (x) < 1
f (x) < 1 ⇔ x < e2
所= 以 y
f ( f= (x))
ln
f (x), x ≥ e2 =
0 0 c3 + c4
−1 1 =(c3 + c4 ) 。 c4
由于 c1, c2 , c3, c4 为任意常数,所以α1,α3,α4 线性相关。故应选(C)。
(6)【答案】B
1 0 0
【分析】考查矩阵的运算。将
Q
用
P
表示,即
Q
=
P
1
1
0
,然后代入计算
0 0 1
即可。
1 0 【详解】由于 P = (α1,α2 ,α3 ) ,所以 Q = (α1 + α2 ,α2 ,α3 ) = P 1 1
±1 ,又因为 lim y x→1
=
lim
x→1
x2 + x x2 −1
=
∞,
= lim y x→−1
xl= →im−1 xx22 +−1x
1 ,所以该曲线只有一条铅直渐近线; 2
斜渐近线:
因= 为 lim y x→∞
lxi= →m∞ xx22 +−1x
1 ,所以该曲线没有斜渐近线。
故应选(C).
(2) 【答案】A
【分析】本题考查全微分的概念与多元函数连续的定义。
【详解】由于 lim f (x, y) − 2x + y − 2 = 0 ,,所以 lim[ f (x, y) − 2x + y − 2] =0
2012考研数学三真题与答案

2012年考研数学三真题一、选择题(18小题,每小题4分,共32分。
下列每题给出的四个选项中,只有一个选项是符合题目要求的。
)(1)曲线渐近线的条数为(A)0 (B)1(C)2 (D)3【答案】C。
【解析】由,得是曲线的一条水平渐近线且曲线没有斜渐近线;由得是曲线的一条垂直渐近线;由得不是曲线的渐近线;综上所述,本题正确答案是C【考点】高等数学—一元函数微分学—函数图形的凹凸、拐点及渐近线(2)设函数,其中为正整数,则(A) (B)(C) (D)【答案】A【解析】【方法1】令,则故应选A.【方法2】由于,由导数定义知.【方法3】排除法,令,则则(B)(C)(D)均不正确综上所述,本题正确答案是(A)【考点】高等数学—一元函数微分学—导数和微分的概念(3)设函数连续,则二次积分(A)(B)(C)(D)【答案】B。
【解析】令,则所对应的直角坐标方程为,所对应的直角坐标方程为。
由的积分区域得在直角坐标下的表示为所以综上所述,本题正确答案是(B)。
【考点】高等数学—多元函数微积分学—二重积分的概念、基本性质和计算(4)已知级数绝对收敛,级数条件收敛,则(A) (B)(C) (D)【答案】D。
【解析】由级数绝对收敛,且当时,故,即由级数条件收敛,知综上所述,本题正确答案是(D)【考点】高等数学—无穷级数—数项级数敛散性的判定(5)设,其中为任意常数,则下列向量组线性相关的为(A) (B)(C) (D)【答案】C。
【解析】个维向量相关显然所以必线性相关综上所述,本题正确答案是(C)。
【考点】线性代数—向量—向量组的线性相关和线性无关(6)设为3阶矩阵,为3阶可逆矩阵,且.若,则(A) (B)(C) (D)【答案】B。
【解析】由于经列变换(把第2列加至第1列)为,有那么=综上所述,本题正确答案是(B)。
【考点】线性代数—矩阵—矩阵运算、初等变换(7)设随机变量相互独立,且都服从区间上的均匀分布,则(A) (B)(C) (D)【答案】D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年考研数学模拟试题(数学三)参考答案一、选择题(本题共8小题,每小题4分,满分32分,在每小题给出的四个选项中,只有一项符合题目要求)(1) 设)(x y 是微分方程x e y x y x y =+'-+''2)1(的满足0)0(=y ,1)0(='y 的解,则2)(limx xx y x -→ ( ) (A )等于0. (B )等于1.(C )等于2. (D )不存在.解 2000()()1()1l i ml i m l i m (0)222x x x y x x y x y x y x x →→→'''--''===,将0x =代入方程,得2(0)(1)(0)(0)1y x y x y '''+-+=,又0)0(=y ,1)0(='y ,故(0)2y ''=,所以2()lim1x y x xx→-=,选择B. (2)设在全平面上有0),(<∂∂xy x f ,0),(>∂∂y y x f ,则保证不等式1122(,)(,)f x y f x y <成立的条件是( )(A )21x x >,21y y <. (B )21x x <,21y y <. (C )21x x >,21y y >.(D )21x x <,21y y >.解(,)0(,)f x y f x y x∂<⇒∂关于x 单调减少, (,)0(,)f x y f x y y∂>⇒∂关于y 单调增加, 当21x x >,21y y <时,112122(,)(,)(,)f x y f x y f x y <<,选择A.(3)设)(x f 在),(+∞-∞存在二阶导数,且)()(x f x f --=,当0<x 时有()0f x '<,()0f x ''>,则当0>x 时有( )(A )0)(,0)(>''<'x f x f . (B )0)(,0)(<''>'x f x f . (C )0)(,0)(>''>'x f x f . (D )0)(,0)(<''<'x f x f . 解 【利用数形结合】)(x f 为奇函数,当0<x 时,)(x f 的图形为递减的凹曲线,当0x >时,)(x f 的图形为递减的凸曲线,选择D.(4) 设函数)(x f 连续,且(0)0f '<,则存在0δ>,使得( ) (A )在(0,)δ内单调增加(B )在(,0)δ-内单调减少 (C )对任意的(0,)x δ∈,有()(0)f x f > (D )对任意的(,0)x δ∈-,有()(0)f x f >解 【利用导数的定义和极限的保号性】0()(0)(0)lim 0x f x f f x→-'=<,由极限的的保号性,(0,)U δ∃ ,在此邻域内,()(0)0f x f x-<,所以对任意的(,0)x δ∈-,有()(0)f x f >,选择D.(5)二次型222123123121323(,,)44448f x x x x x x x x x x x x =++-+-的规范型是( ). (A )222123f z z z =++. (B )222123f z z z =+-. (C )2212f z z =-. (D )21f z =. 解 二次型的规范型由它的正负惯性指数确定,二次型的矩阵122244244A -⎛⎫ ⎪=-- ⎪ ⎪-⎝⎭,其特征多项式212292224400(9)2440A E λλλλλλλλλ-----=---=-=----, 故A 的特征值为9,0,0,正惯性指数1p =,负惯性指数0q =,选择 D.(6)设1211121k A k k ⎛⎫ ⎪=+ ⎪ ⎪⎝⎭,B 是三阶非零矩阵,且AB O =,则( ).(A )当1k =时,()1r B = . (B )当3k =-时,()1r B =. (C )当1k =时,()2r B = . (D )当2k =-时,()2r B =.解 ()1B O r B ≠⇒≥,()()3()3()AB O r A r B r B r A =⇒+≤⇒≤-, 1()3()r B r A ≤≤-.当1k =时,()1r A =,1()2r B ≤≤,排除A ,C ,当2k =-时,122033111~111221003A --⎛⎫⎛⎫ ⎪ ⎪=-- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭,()3r A =,1()0r B ≤≤,矛盾,排除D ,选择B.(7)设随机变量X 与Y 分别服从12N -(,)和2N (1,),且X 与Y 不相关,1k X Y +与2X k Y +也不相关,则( ).(A )120k k +=. (B )120k k ==. (C )120k k +≠. (D )120k k +≠. 解 X 与Y 不相关(,)0Cov X Y ⇔=,1k X Y +与2X k Y +不相关121122(,)(,)(,)(,)(,)Cov k X Y X k Y k Cov X X k k Cov X Y Cov Y X k Cov Y Y ⇔++=+++ 1212122200k DX k DY k k k k =+=+=⇔+=,选择A.(8) 设12,,,(2)n X X X n ≥ 为来自总体(0,1)N 的简单随机样本,X 为样本均值,2S 为样本方差,则 ( )(A )~(0,1)nX N . (B )22~()nS n χ.(C ))1(~)1(--n t SX n . (D )2122(1)~(1,1)n i i n X F n X =--∑. 解 221()()D nX n D X n n n==⋅=,排除A , 2222(1)(1)~(1)n S n S n χσ-=--,排除B ,~(1)t n =-,排除C ,选择D.二、填空题(本题共6小题,每小题4分,满分24分,把答案填在题中横线上) (9)设)(1lim)(2212N n xbxax x x f nn n ∈+++=-∞→,若1lim ()x f x → 与1lim ()x f x →-都存在,那么a =________, ________b =.解 当1x <时,21222()lim 1n n n x ax bxf x ax bx x -→∞++==++, 当1x >时,23222111()lim1n n n n a bx x f x xx x--→∞++==+, 1lim ()x f x →存在11lim ()lim ()x x f x f x -+→→⇔=,即1a b +=, 1lim ()x f x →-存在11lim ()lim ()x x f x f x -+→-→-⇔=,即1a b -=-,解得0,1a b ==. (10)222222021limcos()xy r x y r e x y dxdy r π→+≤-⎰⎰________=.解 由积分中值定理知,存在(,)D ξη∈:2222x y r +≤,使得222222222200211lim cos()lim cos()22xy r r x y r ex y dxdy e r rrξηξηπππ→→+≤-=⋅-⋅=⎰⎰.(11)设(,)z z x y =由方程()()xy xf z yg z =+确定,且()()0xf z yg z ''+≠,则[()][()]________z zx g z y f z x y∂∂---=∂∂. 解 方程为(,,)()()0F x y z xf z yg z xy =+-=,()()()x z F z f z y x F xf z yg z ∂-=-=-''∂+,()()()y z F z g z xy F xf z yg z ∂-=-=-''∂+, [()][()]z z x g z y f z x y∂∂---∂∂ ()()[()][()]0()()()()y f z x g z x g z y f z xf z yg z xf z yg z --=---=''''++.(12) 设)()(x f x F 是的一个原函数,且1)0(=F x x f x F 2cos )()(,=,则dx x f ⎰π|)(|________=.解 ()()F x f x '=,2()()2cos 2F x f x dx xdx =⎰⎰,2()()2cos 2F x f x dx xdx =⎰⎰,2()sin 2F x x C =+,又(0)1F =,故1C =,2()sin 21F x x =+,()sin cos F x x x ==+, 22|cos 2||cos sin ||()|cos sin |()||cos sin |x x x f x x x F x x x -===-+,404|()|cos sin (cos sin )(sin cos )f x dx x x dx x x dx x x dx πππππ=-=-+-⎰⎰⎰⎰1)(1=+=(13)设矩阵2T A E αβ=+,其中,αβ是n 维列向量,且2T αβ=,则1______A -=. 解 22(2)44()T T T T A E E αβαβαβαβ=+=++126()65T E E A E A E αβ=+=+-=-,故256(6)E A A E A A =-=-,所以11(6)5AE A -=-. (14)设129,,,X X X 是来自正态总体X的简单随机样本,1161()6Y X X =++ 27891()3Y X X X =++,922271()2i i S X Y ==-∑,12)Y Y Z S-=,则统计量Z 服从______.解 设正态总体2~(,)X N μσ,12()0E Y Y -=,2221212()632D Y Y DY DY σσσ-=+=+=,212~(0,)2Y Y N σ-~(0,1)N ,2222~(2)S χσ,又12Y Y -,2S 独立,12)~(2)Y Y Z t S -==.三、解答题(15-23题,满分94分,解答应写出文字说明,证明过程或演算步骤) (15)(10分)设()f x 在(,0]-∞上连续,且满足222221()ln(1)12xx tf t x dt x x -=-++⎰,求()f x 及其极小值. 解 令22,2u t x du tdt =-=,202201()()2xx tf t x dt f u du --=⎰⎰,故2202211()ln(1)212x x f u du x x -=-++⎰, 再令2t x =-,011()ln(1)212t t f u du t t -=---⎰ 即2()ln(1)1ttf u du t t-=---⎰,对t 求导,得22211()(0)(1)1(1)tf t t t t t +=-=<---, 故21()(0)(1)xf x x x +=<-33()03(1)xf x x x +'==⇒=--, 当3x <-时,()0f x '<,当30x -<<时,()0f x '>,所以3x =-,()f x 取得极小值1(3)8f -=-. (16)(10分)设函数()f x 在[,]a b 上连续,在(,)a b 上二阶可导,且()0,()0,()0f a f b f a +'=><.证明:①在(,)a b 内至少存在一点ξ,使得()0f ξ=; ②在(,)a b 内至少存在一点η,使得()0f η''>. 证 ①()()()()lim lim 0x ax a f x f a f x f a x ax a +++→→-'==<--, 由极限的保号性知,存在0δ>,当(,)x a a δ∈+时,()0f x x a<-,()0f x <,取(,)c a a δ∈+,则()0f c <,()f x 在[,]c b 上连续,又()0f c <,()0f b >,由零点定理知,存在(,)(,)c b a b ξ∈⊂,使得()0f ξ=.②对()f x 在[,],[,]a c c b 上用拉格朗日定理,存在(,)r a c ∈,(,)s c b ∈使得()()()()0f c f a f c f r c a c a -'==<--,()()()0f b f c f s b c-'=>-,再对()f x '在[,]r s 上用拉格朗日定理,存在(,)(,)r s a b η∈⊂,使得()()()0f s f r f s rη''-''=>-.(17)(10分)求微分方程236xy y x '=-的一个解()y y x =,使得曲线()y y x =与直线1,0x y ==所围成的平面图形绕x 轴旋转一周所得旋转体体积最小. 解 方程236xy y x '=-化为36y y x x'-=-, 其通解为333323216e (6e )(6)()6dxdx xx y x dx C x dx C x C x Cx x x---⎰⎰=-+=-+=+=+⎰⎰,旋转体体积21232036(6)(2)75C V x Cx dx C ππ=+=++⎰, 2()(2)077C V C C π'=+=⇒=-,又2()07V C π''=>, 故7C =-,体积V 最小,所以2367y x x =-.(18)(10分)计算1DI d σ=,区域D由曲线y =x 轴围成.解 画出区域D 的图形,单位圆221x y +=将区域D 分成两部分,单位圆221x y +=内的部分记作1D ,单位圆221x y +=外的部分记作2D ,则121(11)DD D I d d d σσσ==+⎰⎰⎰⎰112cos 3203(1(1)(1)D d d r rdr d r rdr ππθπσθθ-=-+-⎰⎰⎰⎰⎰⎰23238(2cos cos )183d πππθθθ=+-⎰ 233188[sin sin sin ]18239πππθθθθ=++-+2239418π=+-22cos 311)(1)D d d r rdr πθσθ=-⎰⎰⎰⎰233081(2cos cos )36d πθθθ=--⎰33051885[sin 2sin sin ]1823918πθπθθθ=+-+=,故231218DI d πσ==-.(19)(10分)求幂级数21(1)n nn n x n ∞=+-∑的收敛域及和函数.解 收敛半径2211(1)limlim 1(1)(1)1nnn n n n n a n R n a n +→∞→∞++-===++-+, 当1x =时,级数21(1)n n n n ∞=+-∑发散,当1x =-时,级数21(1)(1)n n n n n ∞=+--∑发散,故幂级数21(1)n nn n x n ∞=+-∑的收敛域为(1,1)-.其和函数2111(1)(1)()n n n n nn n n n s x x nx x n n ∞∞∞===+--==+∑∑∑1101111(1)()[(1)]n x n n nn n n n n n x nxx x x x dx n ∞∞∞∞--====-'=+=+-∑∑∑∑⎰201()ln(1)11(1)x x xx dx x x x x -'=+=-+-+-⎰,(1,1)x ∈-.(20)(11分)设33A ⨯是实对称矩阵,12A =-,A 的三个特征值之和为1,且102T α=-(,,)是方程组(4)0A E x *-=的一个解向量. ①求矩阵A ;②求方程组(6)0A E x *+=的通解.解 ①102Tα=-(,,)是方程组(4)0A E x *-=的一个解向量(4)0A E α*⇒-=,即4A αα*=,又**12A A AA A E E ===-,故4123A A A A ααααα*==-⇒=-,所以102Tα=-(,,)是A 的对应特征值33λ=-的特征向量; 设A 的另外两个特征值为12λλ,,则123123112Aλλλλλλ++===-,,解得122λλ==,设122λλ==对应的特征向量为123,,)T x x x x =(,则它与102Tα=-(,,)正交,即1320x x -=,其基础解系为12010201T Tαα==(,,),(,,), 令12(,)P ααα=,,则1223P AP Λ-⎛⎫⎪== ⎪ ⎪-⎝⎭,所以1102020202A P P Λ-⎛⎫⎪== ⎪ ⎪-⎝⎭②(6)0(6)0(2)0A E x AA A x A E x **+=⇒+=⇒-=,1021022000~000204000A E --⎛⎫⎛⎫⎪ ⎪-= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭,同解方程组为1322332x x x x x x =⎧⎪=⎨⎪=⎩,通解为12010201T Tk k +(,,)(,,),其中12,k k 为任意常数. (21)(11分)设n 阶实对称矩阵A 的秩为r ,且满足2A A =,求 ①二次型Tx Ax 的标准形;②行列式||2n A A A E ++++ 的值,其中E 为单位矩阵.解 设(0)A αλαα=≠,则22A αλα=,又2A A ααλα==, 故22()01λαλαλλαλ=⇒-=⇒=或者0λ=.由n 阶实对称矩阵A 的秩为r 知,1λ=,0λ=分别为A 的r 重和n r -重特征值, 故存在正交矩阵P ,使得1rTE O P AP P AP OO -⎛⎫==⎪⎝⎭. ①经正交变换x Py =,二次型Tx Ax 的标准形为22212r y y y +++ . ②2A A =⇒2nA A A === ,故行列式1111||()(1)r E nA PP nP P P E n P P E n P E n n ΛΛΛΛ----+=++=+=+=+.(22)(11分)已知随机变量X 与Y 的联合概率分布为01011/31/3Y X αβ⎛⎫⎪ ⎪ ⎪⎝⎭①证明X 与Y 不相关的充分必要条件是事件{1}Y =与{1}X Y +=相互独立; ②若X 与Y 不相关,求X 与Y 的边缘分布. 解 由概率分布的性质知0.5αβ+=①X 与Y 不相关的充分必要条件是(,)0Cov X Y EXY EX EY =-⋅=,X 的概率分布为011133αβ⎛⎫⎪ ⎪++ ⎪⎝⎭,13EX β=+, Y 的概率分布为011233⎛⎫⎪ ⎪⎪⎝⎭,23EY =, XY 的概率分布为012133⎛⎫⎪ ⎪⎪⎝⎭,13EXY =, 121(,)()333Cov X Y β=-+,故X 与Y 不相关的充分必要条件是121()0333β-+=. 事件{1}Y =与{1}X Y +=相互独立的充分必要条件是{}{}{}1,111P Y X Y P Y P X Y =+===+={}{}11,11,03P Y X Y P Y X =+=====, {}{}2111()33P Y P X Y β=+==+, 故事件{1}Y =与{1}X Y +=相互独立的充分必要条件是121()333β=+, 所以X 与Y 不相关的充分必要条件是事件{1}Y =与{1}X Y +=相互独立. ②若X 与Y 不相关,则12111(),33366ββα=+⇒==,故X 的概率分布为011122⎛⎫ ⎪ ⎪⎝⎭, Y 的概率分布为011233⎛⎫ ⎪ ⎪ ⎪⎝⎭. (23)(11分)设总体),1(~θU X ,参数1>θ未知,n X X ,,1 是来自X 的简单随机样本. ①求θ的矩估计和极大似然估计量;②求上述两个估计量的数学期望.解 总体),1(~θU X ,其分布密度为⎪⎩⎪⎨⎧≤≤-=其它,01,11),(θθθx x f(1)由12X EX θ+==,解得21X θ=-,故θ的矩估计量为1ˆ21X θ=-; 似然函数1()(1)nL θθ=-,1()0(1)n n L θθ+-'=<- ,()L θ递减, 又1,,(1,)n X X θ∈ ,故θ的极大似然估计量为{}21ˆmax ,,nX X θ= . (2)11ˆ2121212E EX θθμθ+=-=-=⨯-=,而{}21ˆmax ,,nX X θ= 的分布函数 {}{}2ˆ21ˆ()()max ,,n F x P x P X X x θθ=≤=≤ {}{}11,,n n i i P X x X x P X x ==≤≤=≤∏ 0,11(),111,n z x z z θθθ<⎧⎪-⎪=≤<⎨-⎪≥⎪⎩221ˆˆ(1),1()()(1)0,n n n x x f x F x θθθθ-⎧-≤≤⎪'==-⎨⎪⎩其它 11211(1)(1)ˆ(11)(1)(1)n n n nn x n x E x dx x dx θθθθθ----=⋅=-+--⎰⎰ 111(1)(1)(1)(1)nn n n n x n x dx θθθθ---=+--⎰⎰ 111(1)(1)1(1)11(1)(1)11n nnnn x x n n n n n θθθθθθ+--+=+=-+=+--++.。
