山东省郯城县红花镇2018届中考数学专题复习 专题二(8)一元一次方程当堂达标题
郯城县红花镇2018届中考数学复习三(12-2)一次函数与一元一次方程及不等式教案

一次函数与一元一次方程及不等式一、【教材分析】教学目标知识技能1。
认识一次函数与一次方程、一元一次不等式之间的联系.会用函数观点解释方程和不等式及其解(解集)的意义;2。
经历用函数图象表示方程、不等式解的过程,进一步体会“以形表示数,以数解释形”的数形结合思想。
过程方法1。
经历探究一次函数与一元一次方程、一元一次不等式之间的联系的过程,体会数形结合、分类、类比、归纳等数学思想方法的运用,积累数学活动经验。
2。
通过自主探究、小组合作等活动,锻炼自学能力、归纳概括的能力,增强合作意识.情感态度1。
通过对一次函数、一次方程与一元一次不等式内在关系的探究,认识事物部分与整体的辩证统一关系,2.培养用联系的观点看待数学问题的意识。
教学重点体会一次函数与一元一次方程、一元一次不等式的内在联系。
教学难点掌握一次函数、一元一次方程、一元一次不等式在解决问题过程中的作用和联系。
二、【教学流程】教学环节教学问题设计师生活动二次备课知识回顾【回顾练习】探究一:1。
已知一次函数y=2x+1,求当函数值y=3,y=0,y=-1时,自变量x取值范围?探究二:2。
1)已知一次函数y=3x+2,求当函数值y>2,y<0,y<—1时,自变量x取值范围?2)这三个不等式有什么共同特点?你能从函数的角度对解这三个不等式进行解释吗?归纳:一次函数、一元一次方程、一元一次不等式有着紧密的联系。
已知一次函数的表达式,生课前独立完成,课上交流展示;分析:当y=3时,2x+1等于几?当y=0、y = —1时,2x+1又等于几呢?你能把它们写成一个方程的形式吗?引导学生根据题意得:3x+2>当其中一个变量的值确定时,可以由相应的一元一次方程确定另一个变量的值;当其中一个变量的取值范围确定时,可以由相应的一元一次不等式确定另一个变量的取值范围.2,3x+2<0,3x+2<—1。
就变成了一元一次不等式。
三个不等式的左边都是代数式,而右边分别是2,0,—1.它们可以看成y=3x+2 的函数值y大于2、小于0、小于—1时自变量x的取值范围。
山东省郯城县红花镇2018届中考数学专题复习 专题二 单元检测题(四)

单元检测题(四)一、选择题(每小题3分,共30分)在每小题给出的四个选项中, 只有一项是符合题目要求的.1. 一元二次方程x 2-2x =0的根是( ).A.x 1=0,x 2=-2B. x 1=1,x 2=2C. x 1=1,x 2=-2D. x 1=0,x 2=22. 已知一元二次方程22530x x -+=,则该方程根的情况是( ).A .有两个不相等的实数根B .有两个相等的实数根C .两个根都是自然数D .无实数根 3. 用配方法解方程2250x x --=时,原方程应变形为( ).A .2(1)6x +=B .2(2)9x +=C .2(1)6x -=D .2(2)9x -= 4. 一元二次方程x 2+px -2=0的一个根为2,则p 的值为( ).A .1B .2C .-1D .-2 5. 已知x 2-2x -3=0,则2x 2-4x 的值为( ).A . -6B . 6C . -2或6D . -2或306. 若关于x 的方程230x x a ++=有一个根为-1,则另一个根为( ).A .-2B .2C .4D .-37. 三角形的两边长分别为3和6,第三边是方程2680x x -+=的解,这个三角形的周长是( ).A.13B. 11C. 11或13D. 11和138. 某种花卉每盆的盈利与每盆的株数有一定的关系. 每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元. 要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x 株,则可以列出的方程是( ).A. ()()340.515x x ++=B. ()()140.515x x +-=C. ()()430.515x x +-=D. ()()340.515x x +-=(第10题图)9. 有两个一元二次方程:M :20ax bx c ++=,N :20cx bx a ++=,其中0a c +=,以下列四个结论中,错误的是( ).A .如果方程M 有两个不相等的实数根,那么方程N 也有两个不相等的实数根;B .如果方程M 有两根符号相同,那么方程N 的两根符号也相同;C .如果5是方程M 的一个根,那么15是方程N 的一个根; D .如果方程M 和方程N 有一个相同的根,那么这个根必是1x =10.如图,将长方形纸片ABCD 折叠,使边DC 落在对角线AC上,折痕为CE ,且D 点落在D ′ 处,若AB =3,AD =4,则ED 的长为( ). A.32 B. 3 C. 1 D. 43 二、填空题(每小题4分,共24分)请把答案填在题中横线上.11.方程(52)(7)9(7)x x x --=-的解是_________.12. 若关于x 的一元二次方程x 2+x +m =0有两个相等的实数根,则m =_______.13. 某小区2013年绿化面积为2000平方米,计划2015年绿化面积达到2880平方米,如果每年绿化面积的增长率相间,那么这个增长率是______.14. 关于x 的一元二次方程x 2-5x +k =0有两个不相等的实数根,则k 可能的最大整数为 .15. 若矩形ABCD 的两邻边长分别为一元二次方程x 2-7x +12=0的两个实数根,则矩形ABCD 的对角线长为__________ .16.一块矩形菜地的面积是120m 2,如果它的长减少2m ,那么菜地就变成正方形,则原菜地的长是 m .三、 解一解, 试试谁更棒(本大题共5小题,共46分)17.(6分)解方程:x 2-6x -4=0(第19题图)墙18.(8分)已知:关于x 的方程x 2+2mx +m 2-1=0(1)不解方程,判别方程的根的情况;(2)若方程有一个根为3,求m 的值.19.(10分)如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB 、BC 各为多少米?20.(10分)某商店准备进一批季节性小家电,单价40元,经市场预测,销售定价为52元时,可售出180个.定价每增加1元,销售量净减少10个;定价每减少1元,销售量净增加10个.因受库存的影响,每批次进货个数不得超过180个.商店若将准备获利2000元,则应进货多少个?定价多少元?21.(12分)菜农李伟种植的某蔬菜,计划以每千克5元的价格对外批发销售.由于部分菜农盲目扩大种植,造成该蔬菜滞销,李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克3.2元的价格对外批发销售.(1)求平均每次下调的百分率;(2)小华准备到李伟处购买5吨该蔬菜,因数量多,李伟决定再给予两种优惠方案以供选择:方案一,打九折销售;方案二,不打折,每吨优惠现金200元.试问小华选择哪种方案更优惠?请说明理由.九年级数学复习单元检测题答案(四)内容:一元二次方程一、选择题1.D2.A3.C4.C5.B6.A7.A8.D9.D 10.A二、填空题 11. 12117,5x x == 12. 1413. 20% 14. 6 15. 5 16. 12 三、 解答题17.解:(x -3)2=13,xx -x -3=∴x 1x 2=318.解:(1)∵b 2-4ac =(2m )2-4×1×(m 2-1)=4>0,∴方程有两个不相等的实数根;(2)将x =3代入原方程,得9+6m +m 2-1=0,解之,得m 1=-2,m 2=-4.19. 解:设AB =x 米,根据题意得:x (100—4x )=400,整理得x 2—25x +100=0,解得:x 1=20,x 2=5.当AB =20米时,BC =20米;当AB =5米时,BC =80米>25米,故舍去.答:羊圈的边长AB 、BC 都为20米.20.解:设商品的定价为x 元时,商店可获得2 000元利润,根据题意, 得(x -40)[180-10(x -52)]=2000解得150x =,260x =当x =50时,销量为180+2×10=200>180,故不合题意,舍去当x =60时,销量为180-(60-52)×10=100<180,符合题意.答:商店若准备获利2000元,应进货100件,定价为60元.21. 解:(1)设平均每次下调的百分率为x ,由题意,得5(1-x )2=3.2,解得2.01=x =20%,8.12=x (舍去)∴平均每次下调的百分率为20%;(2)小华选择方案一购买更优惠,理由如下:方案一所需费用为:3.2×0.9×5000=14400(元);方案二所需费用为:3.2×5000-200×5=15000(元),∵14400<15000,∴小华选择方案一购买更优惠.。
山东省郯城县红花镇2018届中考数学专题复习 专题二(10)一元一次不等式组学案

一元一次不等式组【学习目标】1.理解不等式,不等式的解等概念,会在数轴上表示不等式的解.2.理解不等式的基本性质,会应用不等式的基本性质进行简单的不等式变形,会解一元一次不等式;3.理解一元一次不等式组和它的解的概念,会解一元一次不等式组.4.能应用一元一次不等式(组)的知识分析和解决简单的数学问题和实际问题.【重点难点】重点:解一元一次不等式及不等式组.难点:1.通过探寻实际问题中的不等式关系,认识不等式2.根据实际问题建立合理的不等关系.【知识回顾】回顾练习1.设a <b ,用“<”或“>”填空:(1)a -5___b -5.(2)-3a ___-3b . (3)2a +5__2b +52.不等式2x -1<3的正整数解是___.3.不等式组201x x -<⎧⎨≥-⎩的解集在数轴上表示正确的是( )__.4.解不等式:2132x x -≤-5.解不等式组2(1)3253x x x x --≤⎧⎪+⎨>⎪⎩并把它的解集在数轴上表示出来.【综合运用】一.自主探究A B C D小红准备用50元钱买甲乙两种饮料共10瓶,已知甲饮料每瓶7元,乙饮料每瓶4元,则小红最多能买多少瓶甲饮料?二.组内交流求使方程组 {23654+=++=+m y x m y x 的解x 、y 都是正数的m 的取值范围三.成果展示 1.若不等式组0,122x a x x +⎧⎨->-⎩≥有解,则a 的取值范围是( ) A .1a >- B .1a -≥ C .1a ≤ D .1a <2.若关于x ,y 的二元一次方程组{13222-=+-=+k y x y x 的解满足x +y >1,求k 的取值范围【直击中考】 1.如果一元一次不等式组3x x a>⎧⎨>⎩的解集为3x >.则a 的取值范围是( )A .3a >B .a ≥3C .a ≤3D .3a < 2.在数轴上,点A 所表示的实数为3,点B 所表示的实数为a ,A 的半径为2.下列说法中不正确...的是( ) A .当5a <时,点B 在A 内 B .当15a <<时,点B 在A 内C .当1a <时,点B 在A 外D .当5a >时,点B 在A 外3.已知关于x 的方程5x -2m =3x -6m +1的解满足-3<x ≤2,求m 的整数值.一元一次不等式组复习学案答案【知识回顾】回顾练习1.(1)< (2)> (3)<2.13.B4. 解:去分母得2(2)36x x -≤- 去括号得2436x x -≤- 移项得2364x x -≤-+ 合并同类项得2x -≤- 系数化为1得2x ≥5.解:解不等式①得1x ≥- 解不等式②得5x <∴原不等式组的解集是1x -≤<【综合运用】一.自主探究解:设小红能买x 瓶甲饮料,根据题意:7x +4(10-x )≤50.解得x ≤313,所以最多买3瓶甲饮料.二.组内交流 解方程组得{752+-=-=m x m y .根据题意得{07052>+->-m m .解得25<m <7 三.成果展示 1.A 2.解:法一,这个方程组得{k x k y 21=--=.∵x +y >1 ∴2k -k -1>1 解得k >2. 法二,方程1加方程2得,3x+3y=3k-3.两边除以3得,x+y=k -1,∵x +y >1, ∴k -1>1 解得k >2.【直击中考】1.C2.A3.解:由5x -2m =3x -6m +1可解得: 122x m =-+ ∵32x -<≤,∴13222m -<-+≤. ∴73222m -<-≤ ∴3744m -≤< ∴m 的整数解为0、1。
山东省郯城县红花镇2018届中考数学专题复习专题一数与式分式分式方程教案
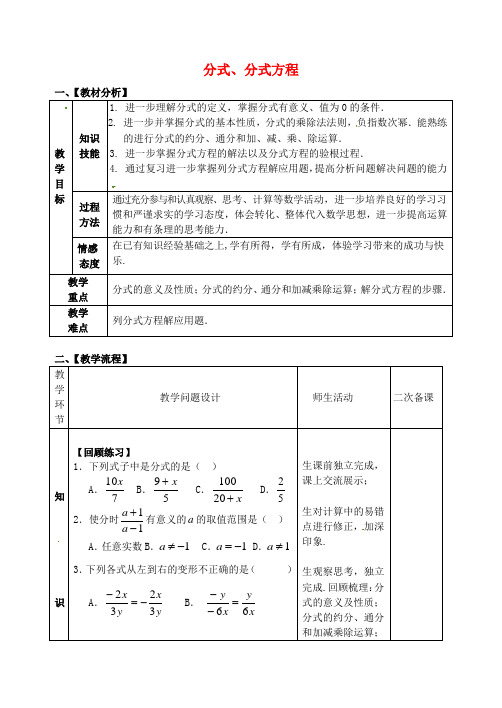
分式、分式方程一、【教材分析】教学目标知识技能1. 进一步理解分式的定义,掌握分式有意义、值为0的条件.2. 进一步并掌握分式的基本性质,分式的乘除法法则,负指数次幂.能熟练的进行分式的约分、通分和加、减、乘、除运算.3. 进一步掌握分式方程的解法以及分式方程的验根过程.4. 通过复习进一步掌握列分式方程解应用题,提高分析问题解决问题的能力.过程方法通过充分参与和认真观察、思考、计算等数学活动,进一步培养良好的学习习惯和严谨求实的学习态度,体会转化、整体代入数学思想,进一步提高运算能力和有条理的思考能力.情感态度在已有知识经验基础之上,学有所得,学有所成,体验学习带来的成功与快乐.教学重点分式的意义及性质;分式的约分、通分和加减乘除运算;解分式方程的步骤.教学难点列分式方程解应用题.二、【教学流程】教学环节教学问题设计师生活动二次备课知识【回顾练习】1.下列式子中是分式的是()A.710xB.59x+C.x+20100D.522.使分时11-+aa有意义的a的取值范围是()A.任意实数B.1-≠a C.1-=a D.1≠a3.下列各式从左到右的变形不正确的是()A.yxyx3232-=-B.xyxy66=--生课前独立完成,课上交流展示;生对计算中的易错点进行修正,加深印象.生观察思考,独立完成.回顾梳理:分式的意义及性质;分式的约分、通分和加减乘除运算;回顾C.yxyx3838-=-- D.yxyx4343-=-4.分式2134,,11m m m+-的最简公分母是____.5.①13(3)ab--=___________,②0.000 000 0407= ×10( ).6.化简:112223+----xxxxxx7.解分式方程:625+-=-xxxx8.甲.乙两地相距l9千米,某人从甲地去乙地,先步行7千米,然后改骑自行车,到达乙地一共用了2小时,已知此人骑自行车的速度筹于他步行速度的4倍,求此人步行的速度.【小结】解分式方程的一般步骤是什么?应该注意什么?解分式方程的步骤;负指数次幂运算.生展示并讲解第8题,师引导回顾分式方程应用题的解答过程和注意问题.通过回顾练习,生总结归纳所用知识点、方法及规律,然后组内交流,补充完善对问题的认识和方法.综【自主探究】1.若分式221x xx--+的值为零,那么x的值为()A.x=-1或x=2 B.x=0C.x=2 D.x=-12.下列各式正确的是()A.0x yx y+=+B.22y yx x=教师展现问题,学生独立思考完成,要求学生做题时注意知识点和方法的运用,做每一道题进行反思总结.解题过程中要求学合运用C.1x yx y-+=--D.11x y x y=--+-3.已知0,0,ab a b??则()111a b---+应等于()A.a b+B.1abC.aba b+D.a bab+4.将分式2221a aa a+++约分后得 .5.当x≠时,式子()()3211155x x xx x x+-+=++成立.6. 化简求值:222222484yxyxyx-+-,其中x=2,y=3.7. 甲.乙二人分别加工1500个零件.由于乙采用新技术,在同一时间内,乙加工的零件数是甲加工零件数的3倍,因此,乙比甲少用20小时加工完,问他们每小时各加工多少个零件?【组内交流】学生根据问题解决的思路和解题中所呈现的问题进行组内交流,归纳出方法、规律、技巧.生仔细认真,教师要有意识培养学生学习数学的严谨态度.引导学生体会转化、整体数学思想.学生全体参与,教师巡视指导.一生展示,其它小组补充完善,展示问题解决的方法、规律,注重一题多解及解题过程中的共性问题,教师注意总结问题的深度和广度.给学生充足的时间思考分析.通过学生思考梳理解分式方程步骤及验根的意义.其中a =﹣1. 6.已知312=-y x ,2=xy ,求 43342y x y x -的值.完 善整合1.1. 知识结构图 2.本课你收获了什么? 你 3.还有哪些待掌握之处?师生梳理本课的知识点及及注意问——归结本节课所复习的内容,梳理知识,构建思维导图,凸显数学思想方法.生反思总结本课中的难点、重点及易错点,并在错题中整理所产生的问题.针对性问题师板书.对内容的升华理解认识整式的加减复习四、【教后反思】作 业一.必做题: 1.解方程: ①2131x x x =++- ② 25231x x x x +=++ 2.先化简,再求值:11131332--+÷--x x x x x ,其中2=x .二.选做题:请根据所给方程6615x x +=+,联系生活实际,编写一道应用题(要求题目完整,题意清楚,不要求解方程)第一题学生课下独立完成,延续课堂. 第二题课下交流讨论有选择性完成.以生为本,正视学生学习能力、认知水平等个体差异,让不同的学生都能学有所得,学有所成,体验学习带来的成功与快乐. 易错点总结:知识结构。
山东省郯城县红花镇2018届中考数学专题复习 专题二 单元检测题(三)

单元检测题(三)内容:一元一次方程、二元一次方程(组)、一元一次不等式(组)一、选择题(每小题3分,共30分)在每小题给出的四个选项中, 只有一项是符合题1. 方程213x -=的解是( ).A . -1B .12C . 1D . 2 2. 若x y >,则下列式子错误的是( ).A .33x y ->-B .33x y ->-C .32x y +>+D .33x y > 3. 不等式3x +2>-1的解集是( ).A .x >-13 B .x <-13C .x >-1D .x <-1 4.已知35x y =⎧⎨=-⎩是方程22mx y +=-的一个解,那么m 为( ).A .83 B .83- C .4- D .855. 不等式组312840x x ->⎧⎨-⎩,≥的解集在数轴上表示为( ).6.已知a ,b 满足方程组51234a b a b +=⎧⎨-=⎩,则a +b 的值为( ).A .﹣2B .2C .﹣4D .4 7. 若关于x 的一元一次不等式组10,x x a -<⎧⎨->⎩无解,则a 的取值范围是( ).A .a ≥1B .a >1C .a ≤-1D .a <-18. 某种商品的进价为800元,出售标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则最多可打( ). A .6折 B .7折 C .8折 D .9折A .B .C .D .9. 若不等式组1,911123x a x x +<⎧⎪++⎨+-⎪⎩≥有解,则实数a 的取值范围是( ).A. 36a <-B. 36a -≤C. 36a >-D. 36a -≥10. 为了开展阳关体育活动,某班计划购买毽子和跳绳两种体育用品,共花费35元,毽子单价3元,跳绳单价5元,购买方案有( ).A . 1种B . 2种C . 3种D . 4种二、填空题(每小题4分,共24分)请把答案填在题中横线上.11.已知关于x 的方程2x +a -5=0的解是x =2,则a 的值为____________. 12. 不等式组2030x x -<⎧⎨+>⎩的解集为 .13. 已知x ,y 满足方程组⎩⎨⎧=+=+,42,52y x y x 则x y -的值为________.14. 王大爷用280元买了甲、乙两种药材,甲种药材每千克20元,乙种药材每千克60元,且甲种药材比乙种药材多买了2千克.则甲种药材买了______千克. 15. 若关于x 的不等式0721x m x -<⎧⎨-⎩≤的整数解共有4个,则m 的取值范围是 .16. 定义运算“*”,规定x *y =ax 2+by ,其中a ,b 为常数,且1*2=5,2*1=6,则2*3= .三、 解一解, 试试谁更棒(本大题共5小题,共46分)17.(6分)解方程组:⎪⎩⎪⎨⎧-=-=-)12(21152y x y x18.(8分)解不等式组:312(2)15233x xx x+<+⎧⎪⎨-≤+⎪⎩,并把其解集在数轴上表示出来.19.(10分)今年“春节”期间,某市外来与外出旅游的总人数为226万人,分别比去年同期增长30%和20%,去年同期外来旅游比外出旅游的人数多20万人.求该市今年外来和外出旅游的人数.20.(10分)某超市预购进A、B两种品牌的T恤共200件,已知两种T恤的进价如下表所示,设购进A种T恤x件,且所购进的两种T恤能全部卖出,获得的总利润为W元.(1)求W关于x的函数关系式.(2)如果购进两种T恤的总费用不超过9500元,那么超市如何进货才能获得最大利润?并求出最大利润.(提示:利润=售价-进价)21.(12分)为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设某工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m 3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作.租赁公司提供的挖掘机有关信息如下表所示:(1)若租用甲、乙两种型号的挖掘机共乙两种型号的挖掘机各需多少台?(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有那几种不同的租用方案?九年级数学复习单元检测题(三)内容:一元一次方程、二元一次方程(组)、一元一次不等式(组)一、选择题1.D2.B3.C4.A5.C6.D7.A8.B9.C 10.B 二、填空题11. 1 12. -3<x <2 13.1x y -= 14.515. 6<m ≤7 16. 10 三、 解答题17. 解:原方程组可化为25221y x x y =-⎧⎨-=⎩①②,将①代入②,得22(25)1x x --=,解得92x =,将92x =代入①,得4y =,所以方程组的解为924x y ⎧=⎪⎨⎪=⎩.18. 解:由不等式①得3x +1<2x +4,3x -2x <4-1,解得x <3;由不等式②得-x ≤5x +6,-x -5x ≤6,解得x ≥-1.故解集为-1≤x <3,数轴表示如下:19. 解:设该市去年外来人数为x 万人,外出旅游的人数为y 万人,由题意得,20(130%)(120%)226x y x y -=⎧⎨+++=⎩,解得:10080x y =⎧⎨=⎩,则今年外来人数为:100×(1+30%)=130(万人), 今年外出旅游人数为:80×(1+20%)=96(万人).答:该市今年外来人数为130万人,外出旅游的人数为96万人. 20. 解:(1)根据题意,得: W =(80-50)x +(65-40)(200-x ) 化简,得:W =5x +5000即W 与x 的函数关系式为W =5x +5000. (2)根据题意,得: 50x +40(200-x )≤9500 解得:x ≤150由(1)可知W 随x 的增大而增大,要使W 最大,则x 取最大值,即x =150. 200-x =50此时的最大利润为:5×150+5000=5750(元)即:超市应购进A 种品牌T 恤150件,B 种种品牌T 恤50件能获得最大利润,最大利润为5750元.21.(1)设租用甲型号的挖掘机x 台,乙型号的挖掘机共y 台,根据题意,得⎩⎨⎧=+=+.5408060,8y x y x 解得⎩⎨⎧==.3,5y x 答:甲、乙两种型号的挖掘机各需5台、3台.(2)设租用甲型号的挖掘机m 台,则租用乙型号的挖掘机8060540m-台,根据题意,得 100m +120×8060540m-≤850.解得m ≤4.又m 为非负整数,∴m =0,或1,或2,或3,或4.分别代入8060540m-,可知,只有当m =1时,8060540m-=6,为整数符合题意.∴符合条件的租用方案只有一种,即租用甲型号的挖掘机1台,乙型号的挖掘机共6台.。
山东省郯城县红花镇2018届中考数学专题复习专题八综合应用单元检测题(十五)

单元检测题(十五)内容:探索性问题一、填空题(每小题8分,共64分)请把答案填在题中横线上.1.一组按规律排列的式子:2a ,43a ,65a ,87a ,….则第n 个式子是________.2.如图,是用火柴棒拼成的图形,则第n 个图形需 2n+1 根火柴棒.3.在Rt △ABC 中,∠A =90°,有一个锐角为60°,BC =6. 若点P 在直线AC 上(不与点A ,C 重合),且∠ABP =30°,则CP 的长为________.4.已知在矩形ABCD 中,AB =3,BC =4,P 为对角线AC 上一点,过P 作BP 的垂线交直线AD 于点Q ,若△APQ 为等腰三角形,则AP 的长度为 或 .5.在如图所示的平面直角坐标系中,点P 是直线y =x 上的动点,A (1,0)、B (2,0)是x 轴上的两点,则PA +PB 的最小值 .6.平面坐标系中,正方形ABCD 的位置如图所示,点A 的坐标为(1,0),点D 的坐标为(0,2),延长CB 交x 轴于点A 1,作正方形A 1B 1C 1C ,延长C 1B 1交x 轴于点A 2,作正方形A 2B 2C 2C 1,…,按这样的规律进行下去,第2013个正方形的面积为 .7.如图,以扇形OAB 的顶点O 为原点,半径OB 所在的直线为x 轴,建立平面直角坐标系,点B 的坐标为(2,0),若(第7题图)(第2题图)(第6题图)(第5题图)抛物线k x y +=221与扇形OAB 的边界总有两个公共点,则实数k 的取值范围是 .8.如图,在Rt △ABC 中,∠BAC =90°,AB =AC =16cm ,AD 为BC 边上的高,动点P 从点A 出发,沿A →D 方向的速度向点D 运动.设△ABP 的面积为S 1,矩形PDFE 的面积为S 2,运动时间为t 秒(0≤t≤8),则t= 秒时,S 1=2S 2.三、解答题(本大题共3小题,共36分) 9.(本小题满分10分)如图,在四边形ABCD 中,AB =AD ,CB =CD ,E 是CD 上一点,BE 交AC 于F ,连接DF .(1) 证明:∠BAC =∠DAC ,∠AFD =∠CFE ; (2) 若AB ∥CD ,试证明四边形ABCD 是菱形; (3) 在(2)的条件下,试确定E 点的位置,使∠EFD =∠BCD ,并说明理由.(第8题图)EFABC(第9题图)(第10题图)10.(本小题满分12分)问题情境:(1)如图1,在正方形ABCD 中,点E ,H 分别在BC ,AB 上,若AE ⊥DH 于点O ,求证:AE =DH ;类比探究:(2)如图2,在正方形ABCD 中,点H ,E ,G ,F 分别在AB ,BC ,CD ,DA 上,若EF ⊥HG 于点O ,探究线段EF 与HG 的数量关系,并说明理由;综合运用:(3)在(2)问条件下,HF ∥GE ,如图3所示,已知BE =EC =2,EO =2FO ,求图中阴影部分的面积.(第11题图)11. (本小题满分14分)11.二次函数2y ax bx c =++的图象的一部分如图所示.已知它的顶点M 在第二象限,且经过点A (1,0)和点B (0,l).(1)试求a ,b 所满足的关系式;(2)设此二次函数的图象与x 轴的另一个交点为C ,当△AMC 的面积为△ABC 面积的54倍时,求a 的值; (3)是否存在实数a ,使得△ABC 为直角三角形.若存在,请求出a 的值;若不存在,请说明理由.九年级数学复习单元检测题(十五)内容:探索性问题一、填空题1.221n a n -(n 为正整数)2.2n+1 3.6 4. 3.6或15. 6.4024)23(5⨯ 7. -2<k <21 8. 6三、解答题9.解:(1) ∵AB=AD CB=CD AC=AC∴△ABC≌△ADC∴∠BAC =∠DAC∵ AB=AD ∠BAF =∠DAF AF=AF∴△ABF≌△ADF∴∠AFB=∠AFD又∵∠CFE =∠AFB∴∠AFD=∠CFE∴∠BAC=∠DAC ∠AFD=∠CFE(2) ∵AB∥CD∴∠BAC=∠ACD又∵∠BAC=∠DAC∴∠BAC=∠ACD∴∠DAC=∠ACD∴AD=CD∵ AB=AD ,CB=CD∴AB=CB=CD=AD∴四边形ABCD是菱形.(3)当BE⊥CD时,∠EFD=∠BCD理由:∵四边形ABCD为菱形∴BC=CD ∠BCF=∠DCF又∵CF为公共边∴△BCF≌△DCF∴∠CBF=∠CDF∵BE⊥CD∴∠BEC =∠DEF=90°∴∠EFD =∠BCD.10. 解:(1)∵四边形ABCD是正方形,∴AB=DA,∠ABE=∠DAH=90°.∴∠HAO+∠OAD=90°.∵AE⊥DH,∴∠ADO+∠OAD=90°.∴∠HAO=∠ADO.∴△ABE≌△DAH(ASA),图2∴AE =DH . (2)EF =GH .如图1,将FE 平移到AM 处,则AM ∥EF ,AM =EF . 将GH 平移到DN 处,则DN ∥GH ,DN =GH . ∵EF ⊥GH ,∴AM ⊥DN ,根据(1)的结论得AM =DN ,所以EF =GH ;……5分 (3)∵四边形ABCD 是正方形, ∴AB ∥CD ,∴∠AHO =∠CGO∵FH ∥EG ,∴∠FHO =∠EGO ,∴∠AHF =∠CGE ∴△AHF ∽△CGE ∴∵EC =2,∴AF =1如图2,过F 作FP ⊥BC 于P , 根据勾股定理得EF =,∵FH ∥EG ,∴根据(2)①知EF =GH ,∴FO =HO . ∴,,∴阴影部分面积为.11. 解:(1)将A (1,0),B (0,l )代入2y ax bx c =++得:⎩⎨⎧==++10c c b a ,可得:1-=+b a(2)由(1)可知:()112++-=x a ax y ,顶点M 的纵坐标为()()aa a a a 4141422--=+-, 因为ABC AMCS S ∆∆=45,由同底可知:()145412⨯=--a a ,整理得:0132=++a a ,得:32a -=由图象可知:0<a ,因为抛物线过点(0,1),顶点M 在第二象限,其对称轴x =102a a+<,∴01<<-a , ∴253--=a 舍去,从而a =(3)① 由图可知,A 为直角顶点不可能;② 若C 为直角顶点,此时与原点O 重合,不合题意;③ 若设B 为直角顶点,则可知222BC AB AC +=,令0=y ,可得:()0112=++-x a ax ,ax x 1,121== ∴2,11,1122=+=-=AB aBC a AC 2211(1)2(1)a a-=++.解得:1a =-,由-1<a <0,不合题意.所以不存在.综上所述:不存在.。
山东省郯城县红花镇2018届中考数学专题复习 专题二(11-1)一元二次方程的解法当堂达标题
一元二次方程的解法复习当堂达标题一、选择题1.在下列方程中,一元二次方程的个数是( ).①3x 2+7=0 ②ax 2+bx +c =0 ③(x -2)(x +5)=x 2-1 ④3x 2-5x=0 A .1个 B .2个 C .3个 D .4个2.一元二次方程x 2-ax +1=0的两实数根相等,则a 的值为( ).A .a =0B .a =2或a =-2C .a =2D .a =2或a =03.方程x 2-8x +5=0的左边配成完全平方式后所得的方程是( )A.(x -6)2=11B.(x-4)2=11C.(x -4)2=21D.以上答案都不对4.若关于x 的方程230x x a ++=有一个根为-1,则另一个根为( ).A .-2B .2C .4D .-3二、填空题5.用__________________法解方程(x-2)2=4比较简便.6.关于x 的方程(m -1)x 2+(m +1)x +3m -1=0,当m _________时,是一元一次方程;当m _________时,是一元二次方程.7.方程(2x -1)(x +1)=1化成一般形式是_______,其中二次项系数是______,一次项系数是______.8.关于x 的一元一次方程x 2–x +m =0没有实数根,则m 的取值范围是 .三、解答题9.选择合适的方法解方程(1)x 2+3=0 (2)(x -2) 2=(2x-3)2(3) 07522=--x x10.x 为何值时,代数式x 2-13x +12的值与代数式-4x 2+18的值相等?11.关于x 的一元二次方程 0322=-+m x x 有两个不相等的实数根,求m 的取值范围.12.已知1x 2—2x +c =0的一个根,求方程的另一个根及c 的值.答案一、选择题1.A2.B3.B4.A二、填空题5.因式分解法6.m =1 m ≠1.7. 0222=-+x x 2 1 .8. m >41 三、解答题 9. (1)321==x x (2)1,3521==x x (3)27,121=-=x x 10.解:根据题意得,x x x x 184121322+-=+-.解得3,5221=-=x x ,所以当52-=x 或3时,这两个代数式的值相等.11.由题知9)(2432>m -⨯⨯-=∆,解得89->m ,答:m 的取值范围是89->m 12.解:方程的另一个根是1+3,c 的值是-2.。
山东省郯城县红花镇2018届中考数学专题复习 专题一 数与式单元检测题(二)(因式分解、分式与分式方
九年级数学复习单元检测题(二)内容:因式分解、分式与分式方程一、选择题(每小题3分,共30分)在每小题给出的四个选项中, 只有一项是符合题目要求的.1.代数式21,,,13x x a x x x π+中,分式的个数是( ). A .1 B .2 C .3 D .42. 下列因式分解正确的是( ).A .22x -2=2(x +1)(x -1)B .2221x x x +-=(-1) C .221(1)x x +=+ D .22(1)2x x x x -+=-+. 3.把39x x -分解因式,结果正确的是( ).A .()29x x - B .()23x x - C .()23x x + D .()()33x x x +-4. 化简211x xx x+--的结果是( ). A .x +1B .x -1C . xD .-x5. 计算:221585-=( ).A .70B .700C .4900D .7000 6. 若m -n = -1,则(m -n )2-2m +2n 的值是( ). A .3 B .2 C .1 D .-17. 将下列多项式分解因式,结果中不含因式1-x 的是( ).A .12-xB .)2()2(x x x -+-C .122++x xD . 122+-x x8.若x =3是a 的值是( ). A .-5 B . 5 C .3 D . -39.某工厂计划生产210个零件,由于采用新技术,实际每天生产零件的数量是原计划的1.5倍,因此提前5天完成任务.设原计划每天生产零件x 个,依题意列方程为( ).A .2102101.5x x -=5 B .2102101.5x x --=5 C .2102101.5x x -+=5 D .2102101.55x=+ 10.如图,从边长为(4)a cm +的正方形纸片中剪去一个边长为()1a cm +的正方形(0)a >,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( ).A .22(25)cm a a +B .2(315)cm a +C .2(69)cm a + D .2(615)cm a +二、填空题(每小题4分,共24分)请把答案填在题中横线上. 11.若分式15x -有意义,则实数x 的取值范围是________. 12. 分解因式:2363a a -+-=. 13. 在实数范围内分解因式:36x x -= . 14. 已知),0,0(0322≠≠=++b a b ab a 则代数式baa b +的值等于________. 15. 若代数式12x -和321x +的值相等,则x =__________. 16. 一列数123,,,a a a ……n a ,其中11-=a ,1211a a -=,2311a a -=,……,111--=n n a a ,则321a a a +++……+2017a = .三、解答题(本大题共5小题,共46分)17.(6分)分解因式(a -b )(a -4b )+ab18. (8分)解方程13932=-+-x xx .19. (10分)先化简,再求值:222222()2a b a b a ab b b a a ab -+÷-+--,其中a ,b 满足|b =0.20. (10分)观察下列关于自然数的等式:32﹣4×12=5 ① 52﹣4×22=9 ② 72﹣4×32=13 ③… 根据上述规律解决下列问题:(1)完成第四个等式:92﹣4× 2= ;(2)写出你猜想的第n 个等式(用含n 的式子表示),并验证其正确性.21.(12分)某工厂计划在规定时间内生产24000个零件.若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.(1)求原计划每天生产的零件个数和规定的天数;(2)为了提前完成生产任务,工厂在安排原有工人按原计划生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%.按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.九年级数学复习单元检测题(二) 内容:因式分解、分式与分式方程一、选择题1. B2. A3.D4. C 5 D 6. A 7.C 8.B 9. A 10.D 二、填空题三、 解答题17.解: (a -b )(a -4b )+a b =a 2-5ab +4b 2+ab =a 2-4ab +4b 2=(a -2b )2.18.解:两边同乘以x 2-9得:3+x (x +3)=x 2-9化简得:3x =-12 解得:x =-4 检验:x =-4时,(x +3)(x -3)≠0, ∴x =-4是原分式方程的解.19.解:原式=22()()()[]()a b a b a a a b a b a b b -+----=2()b a a b a b b --=ab .≥0,|b +|b =0,∴a +1=0且b 0.∴a =-1,b=-. 20. (1)第四个等式:92﹣4×42=17;(2)第n 个等式为:(2n +1)2﹣4n 2=2(2n +1)﹣1, 左边=(2n +1)2﹣4n 2=4n 2+4n +1﹣4n 2=4n +1, 右边=2(2n +1)﹣1=4n +2﹣1=4n +1. 左边=右边∴(2n +1)2﹣4n 2=2(2n +1)﹣1.21.解:(1)设原计划每天生产零件x 个,由题意得240002400030030x x +=+. 解得x =2400,经检验,x =2400是原方程的根,且符合题意. ∴规定的天数为24000÷2400=10(天).答:原计划每天生产零件2400个,规定的天数是10天. (2)原计划安排的工人人数为y 人,由题意得2400[520(120%)2400](102)24000y⨯⨯+⨯+⨯-=, 解得y =480.经检验,y =480是原方程的根,且符合题意. 答:原计划安排的工人人数为480人.本文档仅供文库使用。
山东省郯城县红花镇2018届中考数学专题复习 专题二(11-2)一元二次方程的应用学案
一元二次方程的应用【学习目标】1.能根据具体问题中的数量关系列出一元二次方程,体会方程是刻画现实世界的一个有效地数学模型.2.能根据具体问题的实际意义,检验结果是否合理.【重点难点】重点:列出一元二次方程解决实际问题.难点:将实际问题抽象为代数问题,探索问题中的数量关系,并能运用一元二次方程解决实际问题.【知识回顾】一.回顾练习1.参加一次足球联赛的每两队之间都进行一场比赛,现有6个球队,共需安排_____场比赛.2.某种商品经过两次连续降价,每件售价由原来的90元降到了40元,求平均每次降价率是3.一件工程,甲独做2小时完成,乙独做3小时天完成,甲乙合作_____小时可以完成.4.一个两位数个位数字是a,十位数字是b,这个两位数是_______5.为了绿化学校,需移植草皮到操场,若矩形操场的长比宽多14米,面积是3200平方米则操场的长为米,宽为米.【综合运用】(一)面积问题如图,在长为10cm,宽为8cm的矩形的四个角上截去四个全等的正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,所截去的小正方形的边长是多少?(二)传播问题有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了多少个人?(三)平均增长率问题某种商品,原价50元,受金融危机影响,1月份降价10%,从2月份开始涨价,3月份的售价为64.8元,求2、3月份价格的平均增长率.(四)商品销售问题某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.现该商品要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?【直击中考】1..如图某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长18m),另三边用木栏围成,木栏长35m。
①鸡场的面积能达到150m2吗?②鸡场的面积能达到180m2吗?如果能,请你给出设计方案;如果不能,请说明理由.2.(2010年)(本小题满分7分)为落实素质教育要求,促进学生全面发展,我市某中学2009年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2011年投资18.59万元.(1)求该学校为新增电脑投资的年平均增长率;(2)从(2009年)到2011年,该中学三年为新增电脑共投资多少万元?一元二次方程的应用复习学案答案【知识回顾】回顾练习1.152.313. 56 4. 10b +a 5.64、50 【综合运用】(一)面积问题解:设截去小正方形的边长为xcm ,根据题意得,10×8×80%=10×8-42x ,解得2,221-==x x (舍去),所以小正方形的边长为2cm .(二)传播问题解:设每轮传播中平均每个人传染了x 个人,1+x +x (1+x )=121,解得x =10或x =-12(舍去)答:平均一个人传染了10个人.(三)平均增长率问题解:设两个月平均增长率是x , 50(1-10%)8.6412=+)(x ,解得2.01=x ,2.22-=x (舍去) 答:平均增长率是20%. (四)商品销售问题解:设每天应涨价x 元,(10+x )(500-20x )=6000,解得10,521==x x ,要顾客得到实惠,应取x =5.所以每千克水果应涨价5元.【直击中考】1.解:设垂直于墙的一面为xm , (1)x (35-2x )=150,解得5.7,1021==x x ,当x =7.5时,35-2x =20>18(舍去),当x =10时,35-2x =15.答:垂直于墙的一面为10m ,平行于墙的一面为15m 时面积是150.(2)x(35-2x)=180,01803522=+-x x ,Δ<0,方程无解.答:鸡场面积不能达到180平方米.2.解:(1)设投资的年平均增长率是x , 1195.1812=+)(x ,解得舍去)(3.2,3.021-==x x ,所以年平均增长率是30%.(2)三年共投资 11+11×(1+0.3)+18.59=43.893.本文档仅供文库使用。
学2018届九年级数学中考复习章节检测卷2:方程(组)与不等式(组)(附答案)
山东省郯城县红花镇中学2018届九年级数学中考复习章节检测卷2方程(组)与不等式(组)(建议时间:60分钟 总分:100分)一、选择题(本大题共9个小题,每小题3分,共27分)1.若关于x 的方程2x -m =x -2的解为x =3,则m 的值为( B )A .-5B .5C .-7D .72.用配方法解方程x 2+2x -1=0时,配方结果正确的是 ( B )A .(x +2)2=2B .(x +1)2=2C .(x +2)2=3D .(x +1)2=3 3.一元二次方程x 2-2x =0的根是 ( C )A .2B .0C .0和2D .14.分式方程1x =2x +3的解是( D ) A .-2 B .1 C .2 D .35.若关于x 的方程kx 2-3x -94=0有实数根,则实数k 的取值范围是( C ) A .k =0B .k ≥-1且k ≠0C .k ≥-1D .k >-16.若关于x 的不等式x -a 2<1的解集为x <1,则关于x 的一元二次方程x 2+ax +1=0根的情况是( C )A .有两个相等的实数根B .有两个不相等的实数根C .无实数根D .无法确定7.已知4<m <5,则关于x 的不等式组⎩⎪⎨⎪⎧x -m <0,4-2x <0的整数解共有( B ) A .1个 B .2个 C .3个 D .4个8.小明到商店购买“五四青年节”活动奖品,购买20支铅笔和10本笔记本共需110元,但购买30支铅笔和5本笔记本只需85元,设每支铅笔x 元,每本笔记本y 元,则可列方程组( B )A.⎩⎪⎨⎪⎧ 20x +30y =11010x +5y =85B.⎩⎪⎨⎪⎧20x +10y =11030x +5y =85C.⎩⎪⎨⎪⎧ 20x +5y =11030x +10y =85D.⎩⎪⎨⎪⎧5x +20y =11010x +30y =85 9.已知不等式组⎩⎪⎨⎪⎧x -a <-1,1-x 3≤1的解集如图所示(原点没标出),则a 的值为( D )A .-1B .0C .1D .2二、 填空题(本大题共7个小题,每小题3分,共21分)10.方程组⎩⎪⎨⎪⎧ x +y =1,3x -y =3的解是 ⎩⎪⎨⎪⎧x =1y =0 . 11.若关于x 的一元二次方程x 2-x +k +1=0有两个不相等的实数根,则k 的取值范围是 k <-34 . 12.若关于x 的方程ax +1x -1-1=0有增根,则a 的值为 -1 . 13.若方程3x 2-5x -2=0有一根是a ,则6a 2-10a = 4 .14.如果5a -3x 2+a >1是关于x 的一元一次不等式,则其解集为 x <-2 . 15.若关于x 的一元二次方程(k -1)x 2-4x -5=0没有实数根,则k 的取值范围是 k <15. 16.目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小琼步行12 000步与小博步行9 000步消耗的能量相同.若每消耗1千卡能量小琼行走的步数比小博多10步,求小博每消耗1千卡能量需要行走 30 步.三、解答题(本大题共6个小题,共52分)17.(7分)解不等式组⎩⎪⎨⎪⎧ 12x -1-x <2,并写出该不等式组的最大整数解.解:解不等式12(x -1)≤1,得x ≤3. 解不等式1-x <2,得x >-1.∴该不等式组的解集为-1<x ≤3,∴该不等式组的最大整数解为x =3.18.(9分)某校组织“大手拉小手,义卖献爱心”活动,购买了黑白两种颜色的文化衫共140件,进行手绘设计后出售,所获利润全部捐给山区困难孩子.每件文化衫的批发价和零售价如下表:解:设黑色文化衫x 件,白色文化衫y 件,根据题意,得⎩⎪⎨⎪⎧ x +y =140,-x +-y =1 860, 解得⎩⎪⎨⎪⎧x =60,y =80. 答:黑色文化衫60件,白色文化衫80件.19.(9分)已知关于x 的方程x 2-2mx +m 2+m -2=0有两个不相等的实数根.(1)求m 的取值范围;(2)当m 为正整数时,求方程的根.解:(1)根据题意,得Δ=(-2m )2-4(m 2+m -2)>0,解得m <2;(2)∵m 为正整数,∴m 的值为1,∴方程为x 2-2x =0,解得x 1=0,x 2=2.∴当m 为正整数时,方程的根为0或2.20.(9分)某商店分两次购进A ,B 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:(1)求A ,B (2)商场决定A 种商品以每件30元出售,B 种商品以每件100元出售.为满足市场需求,需购进A ,B 两种商品共1 000件,且A 种商品的数量不少于B 种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.解:(1)设A 种商品每件的进价为x 元,B 种商品每件的进价为y 元,根据题意,得⎩⎪⎨⎪⎧ 30x +40y =3 800,40x +30y =3 200,解得⎩⎪⎨⎪⎧x =20,y =80.答:A 种商品每件的进价为20元,B 种商品每件的进价为80元.(2)设购进B 种商品m 件,则购进A 种商品(1 000-m )件,获得的利润为w元,根据题意,得w =(30-20)(1 000-m )+(100-80)m=10m +10 000.∵A 种商品的数量不少于B 种商品数量的4倍,∴1 000-m ≥4m ,解得m ≤200.∵10>0,∴w 随m 的增大而增大,∴当m =200时,w 取得最大值10×200+10 000=12 000.答:当购进A 种商品800件,B 种商品200件时,销售利润最大,最大利润为12 000元.21.(9分)某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.(1)问实际每年绿化面积多少万平方米?(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?解:(1)设原计划每年绿化面积为x 万平方米,则实际每年绿化面积为1.6x万平方米,根据题意,得360x -3601.6x=4, 解得x =33.75.经检验,x =33.75是原分式方程的解,且符合题意.则1.6x =1.6×33.75=54(万平方米).答:实际每年绿化面积为54万平方米;(2)设实际平均每年绿化面积增加a 万平方米.根据题意,得54×3+2(54+a )≥360,解得a ≥45.答:实际平均每年绿化面积至少增加45万平方米.22.(9分)“春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已经连续三年全国第一.2016年全国谷子种植面积为 2 000万亩,年总产量为150万吨,我省谷子平均亩产量为160 kg ,国内其他地区谷子的平均亩产量为60 kg ,请解答下列问题:(1)求我省2016年谷子的种植面积是多少万亩;(2)2017年,若我省谷子的平均亩产量保持160 kg 不变,要使我省谷子的年 总产量不低于52万吨,那么,今年我省至少应再多种植多少万亩的谷子? 解:方法一:(1)设我省2016年谷子的种植面积为x 万亩,则国内其他地区 谷子的种植面积为(2 000-x )万亩.根据题意,得1601 000x +601 000(2 000-x )=150, 解得x =300.答:我省2016年谷子的种植面积是300万亩;(2)设我省今年应再多种植y 万亩谷子.根据题意,得1601 000(300+y )≥52, 解得y ≥25.答:我省今年至少应再多种植25万亩谷子.方法二:(1)设我省2016年谷子的种植面积为x 万亩,国内其他地区谷子的 种植面积为y 万亩,根据题意,得⎩⎪⎨⎪⎧ x +y =2 000,1601 000x +601 000y =150, 解得⎩⎪⎨⎪⎧x =300,y =1 700. 答:我省2016年谷子的种植面积是300万亩;(2)设我省今年应种植z 万亩谷子,根据题意,得1601 000z ≥52, 解得z ≥325.325-300=25.答:我省今年至少应再多种植25万亩谷子.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元一次方程
一、选择题
1.下列方程中,是一元一次方程的是( )
A.x 2-4x =3
B.3x -1=2x
C. x +2y =1
D.xy -3=5 2.若关于x 的方程2x +a -4=0的解是x =-2,则a 的值等于( )
A.-8
B.0
C.2
D.8
3.已知某商店有两个进价不同的计算器都卖了80元,其中一个盈利60%,另一个亏损20%, 这次买卖中,这家商店( )
A.不盈不亏
B.盈利10元
C.亏损10元
D.盈利50元
二、填空题
4.方程
423
2=-x 的解是_________________ 5.如果关于x 的方程37615=-x 与m x x 2214218++=-的解相同,那么m 的值是_____________
6.轮船沿江从A 港顺流行驶到B 港,比从B 港返回少用3h .若船速为26km/h ,水速为2km/h ,则A 港和B 港相距_______________km.
三、解答题
7.解方程
(1)2x +5=3(x -1) (2)3
2213415x x x --+=-
8.用白铁皮做罐头盒,每张白铁皮可制作盒身16个或盒底43个,一个盒身与两个盒底配成一个罐头盒.现有150张白铁皮,用多少张白铁皮制盒身、多少张白铁皮制盒底可以正好制成整套罐头盒而无余料?
9.为了拓展销路,商店对某种照相机的售价做了调整,按原价的8折出售,此时利润率为14%.若此种照相机的进价为1200元,该照相机的原售价是多少?
10.公园门票价格规定如下表:
购票张数1~50张51~100张100张以上
每张票的价格13元11元9元
某校七年级(1)(2)两个班共104人去游园,其中(1)班现有40多人,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1240元.问:
(1)两班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可省多少钱?
(3)如果七年级(1)班单独组织去游园,作为组织者的你将如何购票才最省钱?
答案
一、选择题
1.B
2.D
3.B
二、填空题
4. x =9
5. ±2 提示:由37615=-x ,得x =3,代入m x x 22
14218++=-,得m =2,所以m =±2. 6. 504. 提示:设A 港和B 港相距xkm ,列方程2263226-=++x x ,解得x =504
三、解答题
7. (1)x =8;(2)x =7
1- 8.解:设用x 张白铁皮制盒身,(150-x )张白铁皮制盒底,列方程
2×16x =43(150-x ),解得x =86,所以150-x =150-86=64
答:用86张白铁皮制盒身,64张白铁皮制盒底.
9.解:设该照相机的原售价为x 元,列方程 0.8x =1200(1+14%),解得x =1710 答:该照相机的原售价为1710元.
10.(1)解:设七年级(1)班有x 人,则七年级(2)班有(104-x )人,列方程13x +11(104-x )=1240 解得x =48,104-x =56.
答:七年级(1)班有48人,七年级(2)班有56人.
(2)1240-104×9=304,所以两个班联合起来,作为一个团体购票,可省304元钱.
(3)因为48×13=624,51×11=561,所以按照51张票购买比较省钱.。
