八年级上学期数学压轴几何题复习
八年级上册数学几何压轴大题

八年级上册数学几何压轴大题在数学几何的学习中,大题是测试学生对知识点掌握和解题能力的重要方式。
本文将为大家展示八年级上册数学几何压轴大题,帮助同学们更好地理解数学几何知识和提高解题能力。
大题一:平面图形的性质与判断1. 已知三角形ABC中,角A=90度,AB=5cm,BC=12cm,求角C的度数和边AC的长度。
解析:由已知条件可得三角形ABC为直角三角形。
根据直角三角形的性质,角C为90度,边AC可以通过勾股定理求得。
勾股定理表达式如下:AC² = AB² + BC²代入已知值,得:AC² = 5² + 12² = 25 + 144 = 169通过开方运算,可得:AC = √169 = 13因此,角C的度数为90度,边AC的长度为13cm。
2. 如果一个四边形的两条对角线相等,这个四边形是否一定是矩形?请给出理由。
解析:不一定。
对于四边形来说,两条对角线相等是矩形的充分条件,但并非必要条件。
除了矩形之外,还存在其他特殊的四边形,如菱形和正方形,它们的两条对角线也相等。
因此,只知道两条对角线相等无法准确判断四边形的类型,还需进一步观察其他条件。
大题二:空间几何图形的投影与旋转1. 一个正方体的边长为3cm,将它围绕其中一个顶点逆时针旋转90度,再向下投影到地面上,求投影图形的面积。
解析:首先我们可以通过观察得知,正方体的一个顶点以及连接这个顶点的3条边组成一个等边三角形,且边长为3cm。
这个等边三角形在投影到地面时会变为一个边长为3cm的正三角形。
正三角形的面积计算公式为:正三角形的面积 = 边长的平方× √3 / 4代入已知值,得:正三角形的面积= 3² × √3 / 4 = 9√3 / 4 ≈ 3.9cm²因此,投影图形的面积约为3.9cm²。
2. 一个圆锥的底面半径为6cm,高为8cm,将它绕底面的直径旋转一周,求旋转体的体积。
一次函数与几何压轴(十大题型)(解析版)—2024-2025学年八年级数学上册(浙教版)

一次函数与几何压轴(十大题型)【题型1 一函数中面积问题】【题型2 一次函数中等腰三角形的存在性问题】【题型3 次函数中直角三角形的存在性问题】【题型4 一次函数中等腰直角三角形的存在性问题】【题型5 一次函数中平行四边形存在性问题】【题型 6 一次函数中菱形的存在性问题】【题型7 一次函数中矩形的存在性问题】【题型8 一次函数中正方形的存在性问题】【题型9 一次函数与相等角/2倍角的问题】【题型10 一次函数中45°角问题】【技巧点睛1】铅锤法求三角形面积【技巧点睛2】处理与一次函数相关的面积问题,有三条主要的转化途径:①知底求高、转化线段;②图形割补、面积和差;③平行交轨、等积变换。
【技巧点睛3】处理线段问题(1)在平面直角坐标系中,若线段与y轴平行,线段的长度时端点纵坐标之差(上减下,不确定时相减后加绝对值),若线段与x轴平行,线段的长度时端点横坐标之差(右减左,不确定时相减后加绝对值);(2)线段相关计算注意使用”化斜为直”思想。
【技巧点睛4】角度问题(1)若有角度等量关系,不能直接用时,我们要学会角度转化,比如借助余角、补角、外角等相关角来表示,进行一些角度的和差和角度的代换等,直到转化为可用的角度关系。
(2)遇45°角要学会先构造等腰直角三角形,然后构造“三垂直”全等模型,一般情况下是以已知点作为等腰直角三角形的直角顶点【技巧点睛5】最值问题(1)求线段和最值,可以从“两点之间线段最短”“垂线段最短”“三角形两边之和大于第三边,两边之差小于第三边”的模型去考虑;(2)注意“转化思想”的运用,将不可用线段进行转化,变成我们熟悉的模型【技巧点睛6】特殊三角形存在问题等腰三角形存在性问题1、找点方法:①以AB 为半径,点A 为圆心做圆,此时,圆上的点(除 D 点外)与A、B构成以 A 为顶点的等腰三角形(原理:圆上半径相等)②以AB 为半径,点B 为圆心做圆,此时,圆上的点(除 E 点外)与A、B构成以 B 为顶点的等腰三角形(原理:圆上半径相等)③做AB 的垂直平分线,此时,直线上的点(除F 点外)与A、B 构成以C 为顶点的等腰三角形(原理:垂直平分线上的点到线段两端的距离相等)2、求点方法:二、直角三角形存在性问题若▲ABC是直角三角形,则分三种情况分类讨论:∠A=90°,∠B=90°,∠C=90°,然后利用勾股定理解题。
八上数学几何压轴题30道

八上数学几何压轴题30道当提到数学几何的压轴题,我们通常指的是那些考察学生对几何知识和解题能力的较难题目。
以下是30道八年级数学几何的压轴题示例:1. 计算一个正方形的对角线长度。
2. 证明三角形内角和为180度。
3. 判断一个四边形是否为平行四边形,并解释你的答案。
4. 计算一个圆的周长和面积。
5. 证明垂直平分线定理。
6. 证明等腰三角形的性质。
7. 计算一个梯形的面积。
8. 证明两条平行线被一条横截线所切割,对应角相等。
9. 计算一个正五边形的内角和外角。
10. 证明直角三角形的斜边长度与直角边长度的关系。
11. 解释相似三角形的性质。
12. 计算一个圆锥的体积。
13. 证明圆的直径与周长的关系。
14. 解释正交投影的原理。
15. 证明圆的切线与半径的垂直关系。
16. 计算一个正多边形的内角和外角。
17. 证明平行线的性质。
18. 解释三视图的绘制方法。
19. 计算一个球的表面积和体积。
20. 证明圆柱的体积公式。
21. 解释平行四边形的性质。
22. 计算一个椎体的体积。
23. 证明同位角与内错角的关系。
24. 解释棱台的性质。
25. 计算一个多面体的表面积和体积。
26. 证明圆锥的侧面积公式。
27. 解释圆的切线定理。
28. 计算一个圆环的面积。
29. 证明立体图形的展开图与表面积的关系。
30. 解释圆锥的性质。
以上是30道八年级数学几何的压轴题示例,这些题目涵盖了几何知识的各个方面,旨在考察学生的几何分析和解决问题的能力。
希望这些题目能够帮助你更好地理解数学几何的知识。
八上期末复习专题汇编——几何压轴题

八上期末复习专题汇编——几何压轴题一.倍长中线类(共2小题)1.阅读下面材料:数学课上,老师给出了如下问题:如图,AD 为ABC ∆中线,点E 在AC 上,BE 交AD 于点F ,AE EF =.求证:AC BF =.经过讨论,同学们得到以下两种思路: 思路一如图①,添加辅助线后依据SAS 可证得ADC GDB ∆≅∆,再利用AE EF =可以进一步证得G FAE AFE BFG ∠=∠=∠=∠,从而证明结论.思路二如图②,添加辅助线后并利用AE EF =可证得G BFG AFE FAE ∠=∠=∠=∠,再依据AAS 可以进一步证得ADC GDB ∆≅∆,从而证明结论.完成下面问题:(1)①思路一的辅助线的作法是:;②思路二的辅助线的作法是:.(2)请你给出一种不同于以上两种思路的证明方法(要求:只写出辅助线的作法,并画出相应的图形,不需要写出证明过程).2.已知ABC∆是等边三角形,点D在射线BC上(与点B,C不重合),点D关于直线AC 的对称点为点E,连接AD,AE,CE,DE.(1)如图1,当点D为线段BC的中点时,求证:ADE∆是等边三角形;(2)当点D在线段BC的延长线上时,连接BE,F为线段BE的中点,连接CF.根据题意在图2中补全图形,用等式表示线段AD与CF的数量关系,并证明.二.角平分线类(共4小题)3.在ABC∆的角平分线,点E是直线BC上的动点.∆中,AD为ABC(1)如图1,当点E在CB的延长线上时,连接AE,若48∠==,则ABC∠=︒,AE AD DCE的度数为.(2)如图2,AC AB+之间的大小+与AB CP>,点P在线段AD延长线上,比较AC BP关系,并证明.(3)连接AE,若90∠的度∠=︒,且满足AB AC EC+=,请求出ACBDAE∠=︒,24BAC数(要求:画图,写思路,求出度数).4.在ABC∆的两条角平分线,且BD,CE交于点∠=︒,BD,CE是ABC∆中,60AF.(1)如图1,用等式表示BE,BC,CD这三条线段之间的数量关系,并证明你的结论;小东通过观察、实验,提出猜想:BE CD BC=,+=.他发现先在BC上截取BM,使BM BE连接FM,再利用三角形全等的判定和性质证明CM CD=即可.①下面是小东证明该猜想的部分思路,请补充完整:ⅰ)在BC上截取BM,使BM BE∆与全等,判定它们=,连接FM,则可以证明BEF全等的依据是;ⅱ)由60∠=︒;∆的两条角平分线,可以得出EFB∠=︒,BD,CE是ABCA⋯②请直接利用ⅰ),ⅱ)已得到的结论,完成证明猜想BE CD BC+=的过程.(2)如图2,若40=.∠=︒,求证:BF CAABC5.课堂上,老师提出了这样一个问题:如图1,在ABC+=.∠交BC于点D,且AB BD AC∆中,AD平分BAC求证:2∠=∠.ABC ACB小明的方法是:如图2,在AC上截取AE,使AE AB=,连接DE,构造全等三角形来证明结论.(1)小天提出,如果把小明的方法叫做“截长法”,那么还可以用“补短法”通过延长线段AB构造全等三角形进行证明.辅助线的画法是:延长AB至F,使BF=,连接DF.请补全小天提出的辅助线的画法,并在图1中画出相应的辅助线;(2)小芸通过探究,将老师所给的问题做了进一步的拓展,给同学们提出了如下的问题:如图3,点D在ABC∠,且∠,ACB∠,ABC∆的内部,AD,BD,CD分别平分BAC∠=∠.ABC ACBAB BD AC+=.求证:2请你解答小芸提出的这个问题;(3)小东将老师所给问题中的一个条件和结论进行交换,得到的命题如下:如果在ABC+=,那么AD平分BAC ∠=∠,点D在边BC上,AB BD AC∠.ABC ACB∆中,2小东判断这个命题也是真命题,老师说小东的判断是正确的.请你利用图4对这个命题进行证明.6.在ABC∆,E为AC的中点,连接DE∆的外部作等边三角形ACD=,在ABC∆中,AB AC并延长交BC于点F,连接BD.(1)如图1,若100∠的度数;BAC∠=︒,求BDF(2)如图2,ACB∠的平分线交AB于点M,交EF于点N,连接BN.①补全图2;②若BN DN=.=,求证:MB MN三.等补模型类(共1小题)7.(1)老师在课上给出了这样一道题目:如图1,等边ABC∆边长为2,过AB边上一点P 作PE AC=,连接PQ交AC于D,求DE的⊥于E,Q为BC延长线上一点,且AP CQ长.小明同学经过认真思考后认为,可以通过过点P作平行线构造等边三角形的方法来解决这个问题.请根据小明同学的思路直接写出DE的长.(2)【类比探究】老师引导同学继续研究:1.等边ABC⊥的延长线于点E,Q为∆边长为2,当P为BA的延长线上一点时,作PE CA边BC上一点,且AP CQ=,连接PQ交AC于D.请你在图2中补全图形并求DE的长.2.已知等边ABC∆,当P为AB的延长线上一点时,作PE⊥射线AC于点E,Q为(①=,连接PQ交直线AC BC边上;②BC的延长线上;③CB的延长线上)一点,且AP CQ于点D,能使得DE的长度保持不变.(将答案的编号填在横线上)四.旋转类(共2小题)8.等腰ABC=,点E与∆中,AB AC∠>︒,点D为边AC上一点,满足BD BC=,60ACB点B位于直线AC的同侧,ADE∆是等边三角形.(1)①请在图1中将图形补充完整;②若点D 与点E 关于直线AB 轴对称,ACB ∠= ;(2)如图2所示,若80ACB ∠=︒,用等式表示线段BA 、BD 、BE 之间的数量关系,并说明理由.9.如图,过等边ABC ∆的顶点B 在ABC ∠内部作射线BP ,(060ABP αα∠=︒<<︒且30)α≠︒,点A 关于射线BP 的对称点为点D ,直线CD 交BP 于点E ,连接BD ,AE .(1)依据题意,补全图形;(2)在(060αα︒<<︒且30)α≠︒变化的过程中,AEB ∠的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请求出AEB ∠的大小;(3)连接AD 交BP 于点F ,用等式表示线段AE ,BF ,CE 之间的数量关系,并给予证明.五.轴对称类(共5小题)10.如图,在ABC ∆中,AB AC =,90BAC ∠=︒,点D 是边BC 上的动点,连接AD ,点C 关于直线AD 的对称点为点E ,射线BE 与射线AD 交于点F .(1)在图中,依题意补全图形;(2)记DAC α∠=(45α<︒),求ABF ∠ 的大小;(用含α 的式子表示)(3)若ACE ∆是等边三角形,猜想EF 和BC 的数量关系,并证明.11.如图1,在等腰直角三角形ABC中,AB AC∠=︒,点D在BC边上,连接AD,=,90BAC⊥,AE AD=,连接CE,DE.AE AD(1)求证:B ACE∠=∠;(2)点A关于直线CE的对称点为M,连接CM,EM.①补全图形并证明EMC BAD∠=∠;②利用备用图进行画图、试验、探究,找出当D,E,M三点恰好共线时点D的位置.请直接写出此时BAD∠的度数,并画出相应的图形.12.如图,CN是等边ABC∠内部的一条射线,点A关于CN的对称点为D,∆的外角ACM连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.(1)依题意补全图形;(2)若ACNα∠的大小(用含α的式子表示);∠=,求BDC(3)用等式表示线段PB,PC与PE之间的数量关系,并证明.13.已知C是线段AB垂直平分线m上一动点,连接AC,以AC为边作等边三角形ACD,点D在直线AB的上方,连接DB与直线m交于点E,连接BC,AE.(1)如图1,点C在线段AB上.①根据题意补全图1②求证:EAC EDC∠=∠;(2)如图2,点C在直线AB的上方,030︒<∠<︒,用等式表示线段BE,CE,DE之CAB间的数量关系,并证明.14.如图,在ABC>,D为AB的中点,E为CA延长线上一点,∠=︒,AC BC∆中,90C连接DE,过点D作DF DE⊥,交BC的延长线于点F,连接EF.作点B关于直线DF的对称点G,连接DG.(1)依题意补全图形;(2)若ADFα∠=;①求EDG∠的度数(用含α的式子表示);②请判断以线段AE,BF,EF为边的三角形的形状,并说明理由.八上期末复习专题汇编——几何压轴题参考答案一.倍长中线类(共2小题)1.延长AD至点G,使DG=AD,连接BG;作BG=BF交AD的延长线于点G;2.;二.角平分线类(共4小题)3.108°;4.△BMF;SAS;60;5.BD;6.;三.等补模型类(共1小题)7.②;四.旋转类(共2小题)8.75°;9.;五.轴对称类(共5小题)10.;11.;12.;13.;14.;。
八年级上学期数学压轴题复习总结
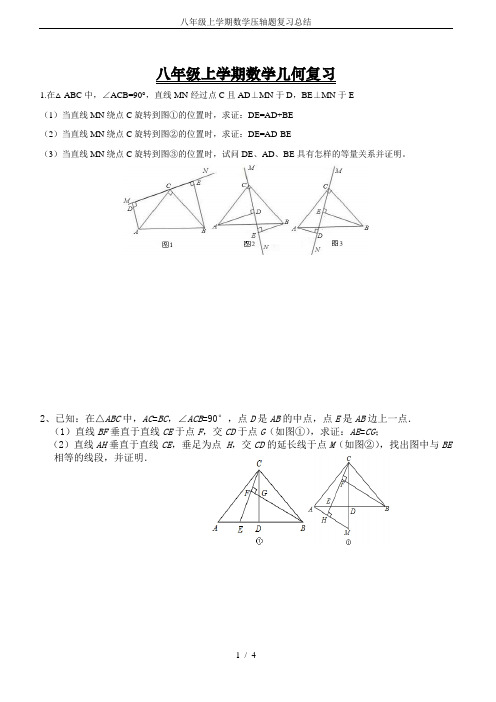
八年级上学期数学几何复习1.在△ABC中,∠ACB=90°,直线MN经过点C且AD⊥MN于D,BE⊥MN于E(1)当直线MN绕点C旋转到图①的位置时,求证:DE=AD+BE(2)当直线MN绕点C旋转到图②的位置时,求证:DE=AD-BE(3)当直线MN绕点C旋转到图③的位置时,试问DE、AD、BE具有怎样的等量关系并证明。
2、已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.(1)直线BF垂直于直线CE于点F,交CD于点G(如图①),求证:AE=CG;(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图②),找出图中与BE 相等的线段,并证明.3.(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.Ⅱ.如图④,当动点D在等边△边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.ABC D E MN4、(本小题8分)如图,△ABC 和△ADE 都是等腰直角三角形,CE 与BD 相交于点M,BD 交AC 于点N ,证明:(1)BD=CE. (2)BD ⊥CE.5.操作:如图①,△ABC是正三角形,△BDC 是顶角∠BDC=120°的等腰三角形,以D 为顶点作一个60°角,角两边分别交AB ,AC 边于M ,N 两点,连接MN .(1)探究线段BM 、MN 、NC 之间的关系,并加以证明(2)若点M 、N 分别是射线AB 、CA 上的点,其它条件不变,请你再探线段BM ,MN ,NC 之间的关系,在图④中画出图形,并说明理由.(3)求证:CN-BM=MN\图① 图② 图③图④6.(10分)如图,△ABC的∠B,∠C的外角的平分线交于点P.(1)若∠ABC=50°,∠A=70°,则∠P=_________°.(2)若∠ABC=48°,∠A=70°,则∠P=_________°.(3)若∠A=68°,则∠P=_________°.(4)根据以上计算,试写出∠P与∠A的数量关系:_________.7.(11分)如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A,B重合),BE⊥CD 于E,交直线AC于F.(1)点D在边AB上时,试探究线段BD,AB和AF的数量关系,并证明你的结论;(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请直接写出正确结论.。
八上期中几何压轴题

八上期中几何压轴题1、在平面直角坐标系中,A,P分别是x轴、y轴正半轴上的点,B是线段OA上一点,连接PB.(1)如图1,CA⊥x轴于点A,BC⊥PB,D是OP上一点,且∠BDO=∠PBO;①求证:∠DBO=∠CBA;②若OP=OA,求证:BD+BC=BP;(2)如图2,A(5,0),B(2,0),G是PB 的中点,连接AG,M是x轴负半轴上一点,PM=2AG,当点P在y轴正半轴上运动时,点M 的坐标是否会发生变化?若不变,求点M的坐标;若改变,求出其变化的范围.2、在等边△ABC中,AB=4,点D和点E分别在边AB,BC上,以DE为边向右侧作等边△DEF,连接CF.(1)如图1,当点D和点A重合时,试求∠ACF的度数;(2)当点D是边AB的中点时,①如图2,判断线段FE与FC的数量关系并证明;②如图3,在点E从点B沿BC运动到点C的过程中,请直接写出点F的运动轨迹的长度.3、如图,在平面直角坐标系中,已知三点A(0,a)(a>0),B(0,b)(b≤0),C(c,0)(c<0),且(a﹣b)2=c2.(1)试判断线段AB与OC的数量关系,并证明;(2)如图1,当b=0时,连接AC,点P是线段AC上一点,CQ⊥OP于Q,连接AQ.若∠AQP=45°,试探究CQ和OQ之间数量关系;(3)如图2,当b<0时,点D在x轴负半轴上,位于点C的左侧,且CD=OB,连接AD,射线BC交AD于点E.当点B在y轴负半轴上运动时,∠CED的度数是否为定值?如果是,请求出∠CED的度数;如果不是,请说明理由.4、如图,在平面直角坐标系中,点A坐标是(0,4),点B(﹣4,0)、C(4,0),点D在x 轴上,DE⊥AD且DE=AD.(1)在图1中,①若点D坐标为(2,0),则点E坐标为;②若点E的坐标为(3m﹣1,m﹣2),求点D的坐标;(2)在图2中,若点M在x轴上运动,点N在直线BE上运动,点F坐标为(0,3),当△FMN为等腰直角三角形时,请直接写出点M的坐标.5、在平面直角坐标系中,点A为y轴正半轴上一点,点B为x轴上一动点,以AB为腰作等腰Rt△ABC,∠BAC=90°.(1)如图1,点B在x轴负半轴上,点C的坐标是(2,﹣2);(2)如图2,点B在x轴负半轴上,AC交x轴于点D,且点C的纵坐标是﹣3,求线段BD 的长;(3)如图3,点B在x轴正半轴上,以BC为边在BC左侧作等边△BCE,CO,若∠COE =60°,求△AOC的面积.6、【问题背景】如图1,在△ABC与△ADE中,若AB=AC,AD=AE,∠BAC=∠DAE.求证:△ABD≌△ACE;【尝试运用】如图2,在△ABC和△DEC中,∠ACB=∠DCE=120°,AC=BC,CD=CE,∠ADC=90°,延长ED交AB于点F.求证:F为AB的中点;【拓展创新】如图3,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AC边上的高为√3,点M是直线BC上一动点,连接AM,在直线AM的右侧作等边△AMN,连接BN,则AN+BN的最小值=.7、如图,点A(a,0),B(0,b),满足(a﹣1)2+|2﹣2b|=0,若点P为射线OA上异于原点O和点A的一个动点.(1)如图1,①直接写出点A的坐标为,点B的坐标为;②当点P位于点O与点A之间时,连接PB,以线段PB为边作等腰直角△BPE(P为直角顶点,B,P,E按逆时针方向排列),连接AE.求证:AB⊥AE;(2)点D是直线AB上异于点A与点B的一点,使得∠BPO=∠APD,过点D作DF⊥BP交y轴于点F,探究BP,DP,DF之间的数量关系,并证明.。
初二上册几何压轴练习题

初二上册几何压轴练习题几何学是数学中的重要分支,它研究的是空间形状和相对位置的关系。
初中阶段是学习几何的关键时期,通过解决各种几何题目,可以提高学生的空间想象力和问题解决能力。
下面是几个初二上册的压轴几何练习题,希望能帮助同学们巩固所学的知识和技能。
1. 平行线与角度求解已知AB//CD,∠A=60°,∠D=110°,求∠B和∠C的度数。
解析:由于平行线AB和CD之间存在一对内错角,所以∠B = ∠C = 180° - (∠A + ∠D) = 180° - (60° + 110°) = 180° - 170° = 10°。
2. 等腰三角形的角度计算在三角形ABC中,AB = AC,∠B = 40°,求∠A和∠C的度数。
解析:由于AB = AC,所以∠B = ∠C。
又已知∠B = 40°,因此∠C = 40°。
由三角形的内角和为180°可知,∠A = 180° - 2∠C = 180° - 2 ×40° = 180° - 80° = 100°。
3. 三角形内角求解在三角形ABC中,∠A = 75°,∠B = 45°,求∠C的度数。
解析:由于三角形的内角和为180°,所以∠C = 180° - (∠A + ∠B) = 180° - (75° + 45°) = 180° - 120° = 60°。
4. 临角和补角问题已知∠A的补角是120°,求∠A的临角和补角的度数。
解析:补角是指两角相加等于90°的两个角,所以∠A + 120°= 90°。
解得∠A = 90° - 120° = -30°。
人教版八年级上册数学几何压轴题期末复习提高训练

人教版八年级数学数学几何压轴题期末复习提高练习题1、如图,在Rt△ABC 中,△ACB=90°,△A=40°,△ABC 的外角△CBD 的平分线BE 交AC 的延长线于点E . (1)求△CBE 的度数;(2)过点D 作DF ∥BE ,交AC 的延长线于点F ,求△F 的度数.2、如图,△ABC 中,AD ⊥BC ,EF 垂直平分AC ,交AC 于点F ,交BC 于点E ,且BD =DE .(1)若∠BAE =40°,求∠C 的度数;(2)若△ABC 周长13cm ,AC =6cm ,求DC 长.3、如图,在△ABC 中,△ABC=45°,CD△AB 于点D ,AC 的垂直平分线BE 与CD 交 于点F ,与AC 交于点E .(1)判断△DBC 的形状并证明你的结论. (2)求证:BF=AC . (3)试说明CE=21BF .4、如图,已知点B 、E 、C 、F 在同一直线上,AB =DE ,∠A =∠D ,AC ∥DF . 求证:(1)△ABC ≌△DEF ;(2)BE =CF .5、如图,设△ABC和△CDE都是等边三角形,并且∠EBD=90°,求证:(1) △ACE≌△BCD (2) 求∠AEB的度数6、如图,在△ABC中,AB=BC=CA,点D,E分别在边BC,AB上,且BD=AE,AD与CE 交于点F.(1)求证:AD=CE;(2)求∠DFC的度数。
7、如图,在△ABC中,∠ACB=90°,BC=6cm,AC=8cm,点O为AB的中点,连接CO.点M在CA边上,从点C以1cm/秒的速度沿CA向点A运动,设运动时间为t秒。
(1)当∠AMO=∠AOM时,求t的值;(2)当△COM是等腰三角形时,求t的值。
8、如图,已知△ABC 中,AB=AC,∠BAC=90°,点D 为BC 的中点,点E、F 分别在直线AB、AC 上运动,且始终保持AE=CF.(1)如图①,若点E、F 分别在线段AB,AC 上,求证:DE=DF 且DE⊥DF;(2)如图②,若点E、F 分别在线段AB,CA 的延长线上,(1)中的结论是否依然成立?说明理由.9、(1)已知,如图①,在△ABC中,∠BAC=90°,AB=AC,直线m 经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E, 求证:DE=BD+CE;(2)如图②,将(1)中的条件改为在△ABC中,AB=AC,D,A,E 三点都在直线m 上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角, 请问结论D E=BD+CE 是否成立?若成立,请你给出证明:若不成立, 请说明理由.10、如图,在Rt△ABC 中,∠ACB=90°,AC=BC=4,CD⊥AB 于D,P 是线段CD 上一个动点,以P 为直角顶点向下作等腰Rt△BPE,连接AE、DE.(1)∠BAE 的度数是否为定值?若是,求出∠BAE 的度数;若不是,说明理由.(2)直接写出DE 的最小值.11、概念学习:规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.理解概念(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,请写出图中两对“等角三角形”.概念应用(2)如图2,在△ABC中,CD为角平分线,∠A=40°,∠B=60°.求证:CD为△ABC的等角分割线.(3)在△ABC中,∠A=42°,CD是△ABC的等角分割线,直接写出∠ACB的度数.12、【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013八年级上学期数学几何复习
【图形的剪拼】
1.如图,有边长为1、3的两个连接的正方形纸片,用两刀裁剪成三块,然后拼成
一个正方形,如何拼?
2.如图,有一张长为5 ,宽为3的矩形纸片ABCD,要通过适当的剪拼,得到
一个与之面积相等的正方形
(1)正方形的边长为____________.(结果保留根号)
(2)现要求只能用两条裁剪线,请你设计出一种裁剪的方法,在图中画出裁
剪线,并简要说明剪拼过程_____________.
(天津市中考题)【三角形】
1.在△ABC中,∠ACB=90°,直线MN经过点C且AD⊥MN于D,BE⊥MN于E
(1)当直线MN绕点C旋转到图①的位置时,求证:DE=AD+BE
(2)当直线MN绕点C旋转到图②的位置时,求证:DE=AD-BE
(3)当直线MN绕点C旋转到图③的位置时,试问DE、AD、BE具有怎样的等量关系并证明。
2.如图,在平面直角坐标系中,点A的坐标为(2,0),以OA为边在第四象限做
等边△AOB,点C为x轴正半轴一动点(OC > 2),连接BC,以BC为边在第
四象限内作等边△CBD,直线DA交y轴于点E.
(1)试问△OBC与△ABD全等吗?并证明你的结论;
(2)随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求出点
E的坐标;若有变化,请说明理由.
3.如图,△ABC 中AB=AC ,∠ABC=36°,D 、C 为BC 上的点,且
∠BAD=∠DAE=∠EAC ,则图中的等腰三角形有( )个。
A. 2
B. 4
C. 6
D. 8
4.如图,在△ABC 中,∠BAC=90°,AB=AC=6,D 为BC 的中点.
(1)若E 、F 分别是AB 、AC 上的点,且AE=CF ,求证:△AED ≌△CFD ;
(2)当点F 、E 分别从C 、A 两点同时出发,以每秒1个单位长度的速度沿CA 、AB 运动,到点A 、B 时停止;设△DEF 的面积为y ,F 点运动的时间为x ,求y 与x 的函数关系式;
(3)在(2)的条件下,点F 、E 分别沿CA 、AB 的延长线继续运动,求此时y 与x 的函数关系式
(4)当x 的值为多少事,S △DEF 能最大化?
5.M
为△ABC 中BC 中点,AN 平分∠BAC ,BN ⊥AN ,已知AB=10,
BC=15,MN=3
(1)求证:BN=DN
(2)求△ABC 周长
6.在△ABC 中,∠ACB=90°,AC=BC
,DA=DB
,CD 为直角边作等腰直角
三角形CDE ,∠DCE=90°
(1)求证:△ACD ≌△BCE
(2)若AC=3cm ,则BE = ________ cm .
7.已知:△ABC 为等边三角形,ED=EC ,探究AE 与DB 的大小关系
图一 图二
8.如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为
AD延长线上一点,且CE=CA
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM.,求证:ME=BD.
9.如图,DE=BF,将平行四边形沿EF折叠,求证:(1)∠1=∠2 (2)DG=B’G
10.已知,△ABC为等边三角形,D为AC中点,CE=CD
(1)用尺规作图,过D作DM⊥PF,垂足为M
(2)求证:BM=EM
11.(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:
Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.
Ⅱ.如图④,当动点D在等边△边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
12.操作:如图①,△ABC 是正三角形,△BDC 是顶角∠BDC=120°的等腰三角形,以D 为顶点作一个
60°
角,
角两边分别交AB ,
AC 边于M ,N 两点,连接MN .
(1)探究线段BM 、MN 、NC 之间的关系,并加以证明
(2)若点M 、N 分别是射线AB 、CA 上的点,其它条件不变,请你再探线段BM ,MN ,NC 之间的关系,在图④中画出图形,并说明理由.
(3)求证:CN-BM=MN
13.如图,已知△ABC 和△ADC 是以AC 为公共底边的等腰三角形,E 、F
分别在AD 和CD 上,已知:∠ADC+∠ABC=180°,∠ABC=2∠EBF
(1)求证:EF=AE+FC
(2)若点E 、F 在直线AD 和BD 上,则是否有类似的结论? 图① 图② 图③
图④。
