物理化学相平衡资料
物理化学相平衡知识点
物理化学相平衡知识点相平衡一、主要概念组分数，自由度，相图，相点，露点，泡点，共熔点，(连)结线，三相线，步冷(冷却)曲线，低共熔混合物(固相完全不互溶)二、重要定律与公式本章主要要求掌握相律的使用条件和应用，单组分和双组分系统的各类典型相图特征、绘制方法和应用，利用杠杆规则进行有关计算。
1、相律： F = C - P + n, 其中：C=S-R-R’(1) 强度因素T，p可变时n=2(2) 对单组分系统：C=1, F=3-P(3) 对双组分系统：C=2，F=4-P；应用于平面相图时恒温或恒压，F=3-P。
2、相图(1)相图：相态与T，p，x的关系图，通常将有关的相变点联结而成。
(2)实验方法：实验主要是测定系统的相变点。
常用如下四种方法得到。
12对于气液平衡系统，常用方法蒸气压法和沸点法；液固(凝聚)系统，通常用热分析法和溶解度法。
3、单组分系统的典型相图对于单组分系统C =1，F =C -P +2=3-P 。
当相数P =1时，自由度数F =2最大，即为双变量系统，通常绘制蒸气压-温度(p-T )相图，见下图。
pTlBC AOsgC 'pTlBCA Os gFGD单斜硫pT液体硫BCAO正交硫硫蒸气(a) 正常相图 (b) 水的相图(c) 硫的相图图6-1 常见的单组分系统相图4、二组分系统的相图类型：恒压的t -x (y )和恒温的p -x (y )相图。
相态：气液相图和液-固(凝聚系统)相图。
(1)气液相图根据液态的互溶性分为完全互溶(细分为形3成理想混合物、最大正偏差和最大负偏差)、部分互溶(细分为有一低共溶点和有一转变温度的系统)和完全不溶(溶液完全分层)的相图。
可以作恒温下的p -x (压力-组成)图或恒压下的t -x (温度-组成)图，见图5-2和图5-3。
t = 常数液相线气相线g + llgB Apx B (y B )t = 常数g + l液相线气相线g + llgB Apx B (y B )g + lg + lt = 常数液相线气相线lgBApx B (y B )(a) 理想混合物 (b) 最大负偏差的混合物 (c) 最大正偏差的混合物 图6-2 二组分系统恒温下的典型气液p -x 相图p = 常数液相线或泡点线气相线或露点线g + llgBAtx B (y B )p = 常数g + l液相线或泡点线气相线或露点线g + llg BAtx B (y B )g + lp = 常数液相线或泡点线气相线或露点线g + llgBAtx B (y B )(a) 理想或偏差不大的混合物 (b) 具有最高恒沸点(大负偏差) (c) 具有最低恒沸点(大正偏差)B在A液层中的溶解度线A在B液层中的溶解度线最高会溶点l 1 + l 2p = 常数lBAtx B最低会溶点B在A液层中的溶解度线A在B液层中的溶解度线最高会溶点l 1 + l 2p = 常数lBAtx B DCGFOgg + l g + ll 1 + l 2p = 常数lBAtx B (y B )(d) 有最高会溶点的部分互溶系统 (e)有最高和最低会溶点的部分互溶系统 (f) 沸点与会溶点分离4x B (y B )三相线COD ( l 1 +g + l 2)l 1DC GFOgg + lg + l l 1 + l 2p = 常数l 2B Atx B (y B )三相线COD ( g + l 1 + l 2)g + l 1l 1DC GFOgg + l 2l 1 + l 2p = 常数l 2BAtg + B(l )三相线COD [ A(l ) +g + B(l ) ]DCGFOgg + A(l )A(l ) + B( l )p = 常数BAtx B (y B )(g) 液相部分互溶的典型系统 (h)液相有转沸点的部分互溶系统 (i) 液相完全不互溶的系统图6-3 二组分系统恒压下的典型气液相图(2)液-固系统相图： 通常忽略压力的影响而只考虑t -x 图。
物理化学 第五章 相平衡
一、基本概念和公式 （一）几个基本概念 1. 相和相数 （1）相 (phase) 系统内部物理和化学性质完全均匀的部分称为相。 特点 相与相之间在指定条件下有明显的界面， 在界面上宏观性质的改变是飞跃式的。 （2）相数 (number of phase) 系统中相的总数称为相数，用 表示。 气体:
（三）二组分系统的相图及应用
(3) 同时具有最高、最低会溶温度 （4） 不具有会溶温度
（三）二组分系统的相图及应用
4. 不互溶双液系 (1) 特点 如果A，B 两种液体彼此互溶程度极小，以致可忽略 不计。则A与B共存时，各组分的蒸气压与单独存在时一 样，液面上的总蒸气压等于两纯组分饱和蒸气压之和。 * * 即： p pA pB 当两种液体共存时，不管其相对数量如何，其 总蒸气压恒大于任一组分的蒸气压，而沸点则恒低 于任一组分的沸点。 (2) 水蒸气蒸馏
CaF2 ( A)
0 .6
0 .8
1 .0 CaCl2 ( B)
（三）二组分系统的相图及应用
(3) 相合熔点 A和B形成的化合物有确定的熔点，完全熔化时不 分解，在熔点时液相和固相的组成相同，所以稳定化 合物的熔点称为相合熔点。 (4) 不相合熔点 因为C没有自己的熔点，将C加热，到O点温 度时分解成 CaF2 (s) 和组成为B的熔液，所以将O点 的温度称为转熔温度（peritectic temperature）也 叫异成分熔点或不相合熔点。
（四）三组分系统的相图及其应用
(d) 如果代表两个三个组分 系统的D点和E点，混合成新 系统的物系点O必定落在DE 连线上。哪个物系含量多， O点就靠近哪个物系点。 O点的位置可用 杠杆规则求算。
mD OD mE OE
物理化学(第三版)第4章相平衡
R=1 NH4HCO3(s) ƒ NH3(g) CO2 (g) H2O(g) R＇=2 p(NH3)=p(CO2)
p(NH3)=p(H2O) p(CO2)=p(H2O) C＝4-1-2=1
练习 : ⑴ 将PCl3(g)和Cl2(g)放在一真空容器中，达平衡后， C=？
答：容器内有PCl5(g)=PCl3(g)+Cl2(g) S=3，R=1，R’=0，C=3– 1– 0=2。
冰水混合物 P=2
PCl5 (g) ƒ PCl3(g) Cl2 (g) P=1
CaCO3(s) ƒ CaO(s) CO2 (g)
P=3
NH4Cl(s) ƒ NH3(g) HCl(g)
P=2
水、冰和水蒸气组成的系统
P=3
2. 物种数(S)和组分数(C)
(1)物种数 系统中所包含的化学物质的种类数。用S表示 例如, 系统中含有PCl3、PCl5、和Cl2三种物质 S=3
均匀混合
P=1
分为两层
P=2
分为三层
P=3
液体：P=1，2， 3 (视其互溶程度而定)
（3）固体 P=1，2，…
固溶体（固体溶液）: P =1
铈锆固溶体
碳化钛-碳化钨固溶体粉末
固体:除固溶体之外，有几种物质就有几相 P=1,2…
注意：相数与数量无关，与破碎程度无关。 P =1
相和相数(P)
气体：P=1 无论包括多少中气体都是一相 液体：P=1,2, 3 (视其互溶程度而定) 固体：P=1，2，…，有几种物质就有几相（固溶体除外）
C(s)
1 2
O2
(
g)
ƒ
CO( g )
⑴
C(s) O2 (g) ƒ CO2 (g)
物理化学：相平衡
相平衡是热力学在化学领域中的重要应用之一。研究 多相体系的平衡在化学、化工的科研和生产中有重要的 意义，例如：溶化、蒸馏、重结晶、萃取、提纯及金相 分析等方面都要用到相平衡的知识。
一、基本概念
第一节 相律
1、 相（phase） 体系内部物理和化学性质完全均匀的 部分称为相。相与相之间在指定条件下有明显的界面， 在界面上宏观性质的改变是飞跃式的。体系中相的总数 称为相数，用Φ表示。
三、自由度数（f）
自由度: 确定平衡体系的状态所必须的独立强度变量的
数目称为自由度，用字母 f 表示。这些强度变量通常是
压力、温度和浓度等。
以水为例〔注意是商量平衡态〕∶ a. 当φ=1时，例如液态水的T、p可在肯定范围内改变， φ不变 ∴ f=2 b. 当φ=2时，例如气－液平衡，指定p外，则Tb确定； 而指定T，则水有确定的平衡蒸气压p，∴ f=1 c. 当φ=3时，即气－液－固三相平衡共存时〔三相点〕，T、 p是确定的〔273.16K、6.1×102Pa、由水的性质所决定〕， ∴ f=0，如果变化T或p，则不可能三相共存〔即φ≠3〕。
一、水的相图 水的相图是依据实验绘制的。图上有：
水 的 相 图
(1) 气、液、固单相区∶f=1－1＋2=2
(2) 两相平衡线∶
f=1－2＋2=1
OC线∶气－液平衡
T与液态水的饱和蒸气压p蒸气的关系
或沸点Tb与p外的关系
OA线∶液－固平衡 凝固点Tf与p外的关系
OB线∶气－固平衡
T与冰的饱和蒸气压p蒸气的关系
dp/dT=ΔHm / T·ΔVm 此方程适合于任何纯物质的两相平衡
2、对于气－液或气－固两相平衡体系 近似处理∶a. 假设蒸气遵守理想气体状态方程
物理化学6相平衡资料
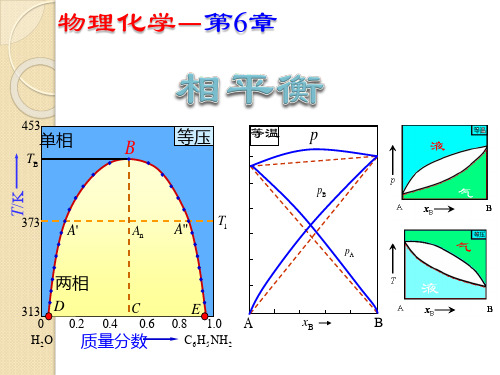
水的相图
p / Pa
C
水f
A
冰
P
610.62 D O
q
B
水蒸气
OC 是液-固两相平衡线
273.16
TC T / K
• OC线不能任意延长：当C点延长至压力大于2.07×108Pa时， 相图变得复杂，有不同结构的冰生成。
OA，OB，OC线 p / Pa 的斜率都可以用克-
E
超 临
C
水
界 水
F
A
f
克方程或克拉佩龙方
例如：对于没有气相存在的凝聚系统，可以忽略压力
f * f 1
多相系统平衡的一般条件――吉布斯相律
对具有 个相系统的热力学平衡，实际上包
含了如下四个平衡： (1) 热平衡
(2) 力学平衡 (3) 相平衡
(4) 化学平衡
某平衡系统中有 S 种不同的化学物种，有 个
相，需要多少独立强度变量（f）才能确定系统的状 态？
物种数（S）：系统中存在的化学物种数。 组分数（K）：构成平衡系统所需的最少物种数。
K=S- R- R′
R表示独立的化学反应数， R′表示独立的浓度限 制条件数。物质在不同相之间保持一定的数量关 系，不能算作浓度限制条件。
平衡系统 NH4Cl (s) ＝NH3 (g) + HCl (g)中， S = 3， R = 1， R′= 1，K=1
K=S- R- R′=5- 0- 1=4
若考虑可能析出固体，以K+、Na+、 SO42-、NO3-、H2O和K2SO4、Na2SO4、 KNO3、NaNO3为对象 S=9 R=4，4个独立的化学平衡 R′=1，溶液保持电中性
K=S- R- R′=9- 4- 1=4
物理化学之相平衡
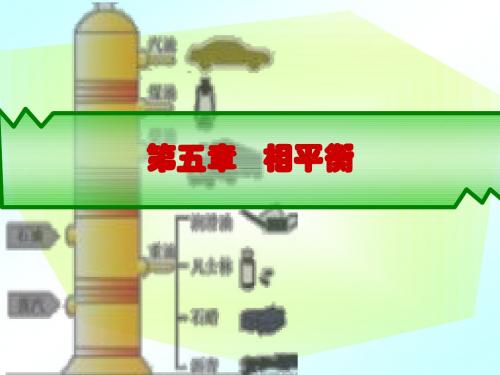
通过升华从冻结的样品中除去水份的方法。
E
f=2
B
冰
水
f=2 A
C
气
D
f=2
s+g, f=1，冷冻干燥
T
一、单组分系统的相图
f f=K- +2 水的相图
E
B
冰
水
p
610.6Pa
A:三相点
C
A
气
f=0
D
T
0.0098℃
一、单组分系统的相图
f=K-f+2 水的三相点：水的气、液、固三相平衡点。 f=0，T=273.16K ( 0.01℃)，p=610.6Pa 水的凝固点（冰点）：水的液、固二相平衡点。
↑
l+g, f=1
l+g, f=1 TB
l, f=2
T
A
xB →
B
T
二、杠杆规则
TA
↑
f f=K- +2 g, f=2
l+g, f=1 TB
l, f=2
A
xB →
B
T
二、杠杆规则
TA
↑
f f=K- +2 g, f=2
l+g, f=1 TB
l, f=2
A
xB →
B
T
二、杠杆规则
TA
↑
f=K-f+2 g, f=2
单位与相图一致
A
x1 x0
y1
B
二、杠杆规则
f=K-f+2 系统温度变化时，相如何变化？
n1L1= n2L2
TA
L1
L2
气
T0时，L1=0，得 n2=0
物理化学 第六章 相平衡
S = 6， R =2， R′= 2 C = S – R - R’ = 6 –2 -2 = 2 若 NaCl 溶解完，则只存在一个化学平衡 H2O = H+ + OH S = 5， R =1， R′= 2
C =S –R -R’ = 5 –1 -2 = 2
一、理想液态混合物的气—液平衡相图
1)蒸气压-组成图 因是理想液态混合物，任一组分都服从拉乌尔定律，即
p = pA*xA + pB*xB p = pA* ( 1- xB ) + pB*xB =pA* + ( pB* - pA* ) xB
即系统总压与液相组成xB 成线性关系，在p - x图中是一直线， 这是理想双液系相图的一个特点。
解：
(1) C = S - R - R´= 3 - 1 - 1=1
F=C-P +2= 1-2+2=1 (2) C = S - R - R´= 3 - 1 - 0 =2
F =C-P+2= 2-2+2=2
例2 (1) 仅由CaCO3(s)部分分解，建立如下反应平衡： CaCO3 (s) = CaO(s) + CO2(g) (2) 由任意量的 CaCO3 (s), CaO (s), CO2 (g)建立如下反应平衡：
2 相律（Phase rule)的推导
①系统中的变量总数 设系统中有 S 个物种，分布在 P 个相中，在温度T、压力p下 达到平衡。 在α 相中的变量为：T，p，xα 1，xα 2，…， xα S-1 在β 相中的变量为：T，p，xβ 1，xβ 2，…， xβ S-1 ………… 在P 相中的变量为：T，p，xP1，xP2，…， xPS-1
物理化学 第三章 相平衡
p实际 > p理想 →正偏差 ， p实际 < p理想 →负偏差
p
l
pB*
p
l
pB* g+ l
pA*
g
A
pA*
g
B A
xB→
xB→
B
一般正偏差系
一般负偏差系
pA* < p < pB*， yB > xB
( 实验结果 )
正偏差很大 负偏差很大
Tb - xB图
Tbmin
p - x B图 p max
液 气
p - x B图 p min
不定积分，可得
lnp/p0 = -△Hm/RT + C 率-△Hm/R求相变热△Hm 。
可用实验数据绘制lnp/p0～1/T曲线，由斜
(实验一)
实验：水的汽化热的测定 H m 1 ln p I ln p ～1/T关系图 R T
直线的斜率
10.8 10.6 10.4
H m 5.5819 R H m 5.5819 8.314 46.41 kJ mol1
求水的汽化热有什么用？ 联系克-克方程讨论一下。
y = -5.5819x + 26.561 2 R = 0.9959
lnp
10.2 10 9.8 9.6 9.4 9.2 2.8 2.85 2.9 2.95 3 3.05 3.1 3.15
0.66 p 40.67 103 1 1 ② ln ( ) p 8.314 373 T2
T2 361.5K 88.5 ℃
T1 = 373K p1 = pθ ΔHm=40.67 kJmol-1
2.32 p 40.67 103 1 1 ③ ln ( ) p 8.314 373 T2
物理化学 第六章 相平衡
例如:体系中含有C（s）、CO（g）、H2O （g）、CO2（g）、H2（g）五种物质，它 们之间存在以下三个反应
C H2O CO H2
C CO2 2CO
CO H2O CO2 H2 （1）—（2）=（3）
(1) (2) (3) R=2
R 3
浓度限制条件
若有S种物质，如果其中有几种物质存在在同 一相中，浓度总保持某种数量关系，那么，存 在的独立浓度关系式的数目叫~。
c．如果PCl3（g）,Cl2（g）之间存在着比例关系， 投料时按PCl3（g）,Cl2（g）按1：1加入或完全由 PCl5（g）分解而来 C=S-1-1=1
C与S之间的关系
C S R R'
R： 独立的化学反应数
R’: 同一相中的浓度限制条件。 （同一相中有多少个浓度关系式）
独立的化学反应
相平衡：宏观上这种迁移停止，称为相平衡
相率:解决相平衡问题运用的一个基本规律
§6—1 相率
一、基本概念
1．相和相数 相：宏观上物理性质和化学性质完全均匀一 致的部分称为一相，相与相之间有明显界面。 越过界面体系物理性质和化学性质发生突变。
相数：体系中所包含相的总数叫相数。
用“ ”表示。
同一体系外界条件不同，相数是不同的
解： S R R’ C φ f 31 1 1 1 2
2．若在上述体系中加入少量的NH3（g）
解： S R R’ C φ f
3．自由度和自由度数
自由度：确定平衡体系状态所需要的独立强度 变量。或在不引起旧相消失和新相生成的前提 下，可以在一定范围内自由变动的强度性质。 叫~。通常指T、p、各物质的浓度xB
自由度数：指定条件下，体系自由度的总数 （体系中总共有几个自由度，自由度数就为几） 自由度用 “f”表示
物理化学-第四章相平衡
所以 C＝1 单组分系统
例2. 碳在氧气中燃烧，有如下方程：
(1) C(s)+O2 (g)=CO2 (g)
(2)
C(s)+
1 2
O2
(g)=CO(g)
因为(3)＝(1) - (2) 所以 R＝2
1 (3) CO(g)+ 2 O2 (g)=CO2 (g)
S = 4， R’＝0， 则 C＝4－2＝2 二组分系统
面
两相平衡： P＝2 f=1 一个独立变量
线
三相平衡： P＝3 f=0 无变量
点
p
B
冰
水A
①三条线：OA, OB, OC
D
O气
C
水的局部相图示意
三个区：单相区
三相点(triple point)：
T O点：三相共存，f = 0,
0.0099℃, 610.6 Pa 与冰点不同
OA：g-l共存，水的饱和蒸汽压曲线
S = 3, R = 1, R’ = 0，则 C＝3 -1＝2
注意：对于浓度限制条件，是固定不变的浓度关系。
2. 自由度和自由度数（f） (the number of freedom degree)
如何描述一个相平衡系统的状态(平衡性质)?
p1
p2
H2O(l) T1
H2O(g)
H2O(l) T2
相平衡的一个重要性质是它与各相中物质的量无关。 一个多相系统的相平衡状态是由体系的强度性质决定 的。例如 pv , Tb , Tf , 溶解度等。
d
ln p /[ p] dT
gc d H m RT 2
(1) 条件：纯物质g-l（s) 平衡，
（近似：忽略Vm (cd)，理想气体） (2) 若近似gcdHm不随T变化，则
物化相平衡知识点总结
物化相平衡知识点总结一、相变的基本概念1. 相和相变相是物质的几何结构和微观结构的基本要素，包括固态、液态和气态。
当物质处于不同的相之间，会发生相变。
相变是指物质由一种相转化为另一种相的过程，包括凝固、融化、升华、凝聚等。
2. 相变的热力学描述相变是伴随着热量的吸收或释放的过程。
在相变过程中，物质的内能不发生改变，热量的吸收或释放表现为相变潜热。
相变的热力学描述可以用热力学参数如热力学势函数、熵等来描述。
3. 相变的动力学过程相变是一个动力学过程，通过固液相变作为例子，可以用凝固和融化作为相变的动态过程的例子来描述。
凝固是液体转变为固体的过程，而融化则是固体转变为液体的过程。
这些过程受到温度、压力和物质的性质等因素的影响。
二、相变的平衡条件与方向1. 平衡条件相变达到平衡时，涉及的热力学参数如化学势、温度、压力等达到平衡状态。
在等温等压条件下，固液平衡和液气平衡时的热力学条件可以用相图来描述。
2. 方向性相变的方向性取决于温度、压力等条件，以及物质的性质。
通过熔点和沸点来描述相变的方向性，其中熔点是固液相变的温度，而沸点则是液气相变的温度。
三、气液平衡及其相关知识1. 气液平衡的热力学描述气液平衡是指气体和液体达到平衡状态的过程。
这种平衡状态受温度和压力等条件的影响，可以用物理化学参数如亨利定律、拉瓦定律等来描述。
2. 气液平衡条件气液平衡的条件包括温度、压力以及物质的性质，控制这些条件可以改变气液平衡达到的状态。
3. 蒸馏和凝结蒸馏是利用液体和气体的不同沸点来实现分离的过程，而凝结则是将气体转变为液体的过程。
这些过程都是气液平衡的重要应用。
四、物化相平衡的应用1. 材料应用物化相平衡在材料科学领域有着重要应用，例如金属材料的固溶体和析出相平衡、陶瓷材料的烧结过程等，这些过程都是利用相变达到平衡状态的过程。
2. 化学反应在化学反应中，物质的相变也是一个重要的过程，例如气体的吸收和析出等。
控制相变的过程可以影响化学反应的进行。
物理化学-相平衡
3
组分数：定义为 K＝ S – R – R’
例如：金属Zn的冶炼
4
例如：金属Zn的冶炼 ZnS(矿石)
灼烧
ZnO(s)
用C还原 ～1200℃
Zn
Zn(g)+CO(g)+CO2(g)
ZnO
(s) C (s)
Φ=3
S=5
5
反应① ZnO+C → CO+Zn 反应② 2ZnO+C → CO2+2Zn ③=2①－②
p V (g) 等T下： T m
①
∴
p
pv↑
23
②
pV p
T
值很小，表明pV对p 不敏感
结论：液体蒸汽压pV与p有关，但影响很 小；但pV对T敏感。 如：蒸馏易加压操作。 凝聚系统对压强变化不敏感。
24
6－4 纯物质的相图 (Phase diagram for pure substance )
液相线：直线，p～xB(sln) 气相线：曲线，p-yB(g) 相区： 物系点和相点：定义；在 单相区，物系点与相点重 合；在两相区，物系点与 两个相点在同一条水平线 上。
38
pA*
xB→
B
二、 T-x -y图（沸点－组成图） (Boiling point-composition diagram)
Clausius - Clapeyron Equation （克－克方
19
2、s-g平衡
d ln{p} gs H m dT RT 2
克－克方程
描述固体蒸气压与温度的关系 3、s-l平衡
dp ls H m l dT TsVm
物理化学 第六章 相平衡
l +β(s)
β(s) α(s)+β(s)
不断析 出α相
α、β
同时析出
开始析 出β相
液相消失 固相降温
xB
B
α相：B溶于A中的固态溶液。 β相：A溶于B中的固态溶液。
S1LS2线： l 加冷热却(s) (s) ，F＝2-3+1＝0，温度不变。
2. 系统有一转变温度
T
基本概念 相律的推导 几点说明
一、基本概念
1. 相：体系中物理性质和化学性质完全相同的部分。
相与相之间有明显的界面，其物理性质、化学性质发生突 变。
（1）气相：因任何气体均可以无限地均匀混合，则无 论体系内有多少种气体，只能有一相。
（2）液相： 不同种类的液体相互间的溶解不同，因此 体系中可出现一个液相，也可以出现多个液相。
子、原子或离子大小相互
均匀混合的一种固相，则
此固相为固溶体。
A
xB
B
Tb
L2
P
a
l
Q
L1
S1
l+s
液相降温 开始析出固相
S2
s
液相消失
固相降温
A
xB
B
PL1L2Q线：液相线或凝固点曲线。表示液态混合物的凝固点 与其组成的关系。
PS1S2Q线：固相线或熔点曲线。表示固态混合物的熔点与其 组成的关系。
若有R个独立的化学平衡反应存在（每个反应不一定和 这S种物质全有关系）。
对化学平衡，有 vBB 0 B
共有R个方程式
（3）独立限制条件
若有 R/ 个浓度限制条件。
例：若反应
N2
(
g
)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
绪论
化学化工
在化学研究和化学生产过程的分离操作中， 经常会遇到各种相变化过程，如蒸发、冷凝、 升华、溶解、结晶和萃取等，这些过程涉及到 不同相之间的物质传递。相平衡研究是选择分 离方法、设计分离装置以及实现最佳操作的理
论基础。
绪论
材料科学
硅酸盐制品——制品中大多数是含有多种晶 相和玻璃相的多相系统，因此制品的性能必 然是与相组成、含量及生产过程有关。 无机材料——功能材料（特殊性能的材料） 是由多种物质构成的复杂系统，制备过程中 涉及相变化。 冶炼过程——相的变化，研究金属成分、结 构与性能的关系。
处于不同相态的同种化学物质，只能算一个
物种。如：液态水和水蒸气。
物种数和独立组分数
（2）独立组分数 （number of independent component ）
——足以确定平衡体系中的所有各相组成所 需要的最少数目的物质的数目，记作C。
S≥C C = S – R – R`
R是独立化学平衡数， R'是独立浓度关系数。
物种数和独立组分数
（A）对于独立化学平衡数，要注意“独立” 两个字。
例如：系统中含有C（s）、CO（g）、H2O（g）、 CO2（g）、H2（g）等五种物质，可能存在的反应有 （1） C（s）+H2O(g)＝CO（g）＋H2（g） （2） C（s）＋CO2（g）＝2CO（g） （3）CO（g）＋H2O（g）＝CO2（g）＋ H2（g）
xS =1- x1 – x2-xs-1 P个浓度关系式。 （3）独立化学平衡数为R，独立浓度关系数为R'。
F = P(S + 2) –(P–1) –(P–1) –S(P–1)- P – R –R'
= S – R – R` –P + 2 = C –P + 2
相律的推导
相律——是表述平衡体系中相数、组分、自 由度数和影响物质性质的外界因素(如温度、 压力、电场、磁场、重力场等)之间关系的 规律， 即 P＋F= C+n 或者 F＝C -P+n
F—自由度数， P—相数， C—组分数， n—表示能够影响体系平衡状态的外界因素 的个数。
相律的推导
(1)、冰水共存 C=1，P=2 (冰、水)， F = 1-2+2=1 (T或p)
(2)、NH4Cl(s)部分分解为NH3(g)和HCl(g)
S=3，R=1，R’=1，P=2 (NH4Cl固相、气相) F=3–1–1–2+2=1
绪论
相平衡研究就是要揭示多相平衡体系中各种强 度性质（温度T、压力P 和组成）与相变化过程的关 系，这种关系相平衡系统的独立变量数与相数、独立
组分数之间关系的规律。 2、相图(phase diagram)：
以T，P，x为坐标作图，称为相图，能直观
地表达多相系统的状态随温度、压力、组成等强度性 质变化而变化的图形。
第六章 相平衡
绪论 §6.1 相律 §6.2 杠杆规则 §6.3 单组分系统相图 §6.4 二组分理想液态混合物的气-液平衡相图 §6.5 二组份真实液态混合物的气-液平衡相图 §6.6 精馏原理 §6.7 二组分液态部分互溶系统及完全不互溶系统
的气-液平衡相图 §6.8 二组分固态互不相溶系统液-固平衡相图 §6.9 二组分固态互溶系统液-固平衡相图 §6.10 生成化合物的二组分凝聚系统相图 §6.11 三组分系统液-液平衡相图
如：
（1）液态水，在一定范围内改变T、p，仍可以保
持水为单相液态水，所以，在确定其状态时，必须
同时指定T、p，才能确定水的状态。则F = 2。
（2）水的气液平衡，体系的温度和压力之间具有 函数关系， 温度一定，压力也随之而定；反之， 亦然。所以，指定其状态时只需指定温度或压力即 可。此时，F = 1。
2.相律的推导
依据：自由度数＝总变量数－方程式数
设一个多相多组分系统中，有S种物质1、2、
3…S）分布在P个相（α、β、γ…φ）中 对 于其中任意一相α相，必须知道Tα、pα、
xα1、…、xαs，才能确定其状态。所以，决定
α相状态的变量共有（S + 2）个。系统中共有
P个相，则整个系统的变量数为 P（S + 2） 但这些变量不是完全独立的，相互之间有
(T、p、 x NH3或xHCl其中之一)
(3) 1000K下，NH3、H2、N2三气平衡
S=3，R=1 (2NH3=3H2+N2)，P=1 F= C-P+1=2 (p、xNH3、x H2或x N2其中之二)
3.物种数和独立组分数 （1）物种数
（ number of substance ） ——系统中所包含的可以单独分离出来、并能独 立存在的化学物质的数目，称为系统的“物种 数”，记作S。 如：NaCl的水溶液中，有Na+、Cl-、H+和OH- 但 只能算两种物质，S = 2。
§6.1 相律（Phase Rule ）
1. 自由度数 （number of degrees of freedom ）
能够维持系统原有相数而可以独立改变的 变量（可以是温度、压力和表示相组成的某些 物质的相对含量）的数目。记作F。
因为这些变量在一定范围内可以变动，则 在讨论系统的状态时，必须指定这些变量的值。 所以，自由度数就是描述相平衡状态所需的最 少独立变量数。
联系， F = P(S + 2)-平衡时变量间的关系式数
相律的推导
（1）系统处于热力学平衡态，有
热平衡 Tα= … = Tp （P-1）个等式
力平衡 pα = … = pp (P-1）个等式
相平衡 μα1 = … = μp1 S（P-1）个等式
┊
┊
μαs = … = μps （2）每个相中有S种物质，ΣxB = 1，
物理化学
第六章 相平衡
学习要求：
理解相律的推导，掌握自由度数的概念以及相律 的内容及其应用，掌握单组份系统相图的阅读。 对二组份系统的气—液相图，要求掌握相图中点 线面的意义，会应用相律分析相图，熟练运用杠 杆规则计算各相的量。 重点掌握二组份系统的液—固平衡相图，要求了 解如何用热分析法制作相图，掌握典型相图的点 线面的特点和任意组成熔体的步冷曲线的绘制及 特征，熟悉相律和杠杆规则的应用。 了解三组份液—液平衡相图。