第一课弦振动的研究
弦振动的研究

x实验2.5 弦振动的研究、实验目的1. 观察弦振动时形成的横驻波的特性.2. 通过不同途径,测量弦线上横波的传播速度,比较测得的结果.3. 研究弦振动时波长与张力的关系.、仪器设备WZB-4型驻波实验仪、弦线、天平.WZB-4型驻波实验仪如图2.5-1所示,该实验仪用金属导线作为弦线,由信号发生器提供低频信号(频率可以改变),在金属导线下面放一块磁铁,这样载流导 体在磁场中因受安培力的作用,按信号频率作横向振动而产生横波,再由入射波 和反射波相干而形成驻波.图中 AA 、BB 为连接弦线和信号发生器的两对接线 柱,A 和A ,B 和B'已经连接好.C 为定位杆,上有小孔,弦线穿过小孔,可以 定位弦线的位置.R 1、R 2为两块劈形滑块,用以调整弦线的振动区长度 I (简称弦长).D 为一测量标尺,用以测量金属滑块之间的距离. M 为磁铁,E 为滑轮,以图2.5-1 WZB-4型驻波实验仪的结构三、实验原理1. 驻波图2.5-2驻波形成示意图频率和传播速度都相同的两列相干波,在同一直线上沿相反挂钩连接砝码,每组有3个砝码:10克,20克,40克各1个.频率计]安培表IB'频率调节振幅调节接线柱 电源R ^ M "?DITR驻波是由振幅、为V 的简谐振动.当x =±(2K +1)t 时(其中K = 0,1,2……),这些点的振动幅度始终为零,4 称为波节.当x=±K 上时(K = 0,1,2……),这些点的振幅达到最大2A,称为2 波腹.相邻两波节(或波腹)之间的距离恰为 一。
因此在驻波实验中,只要测得2 相邻两波节(或波腹)间的距离,就可以确定其波长.2. 弦线上横波的传播速度11图2.5-3 实验装置图如图2.5-3所示,将弦线的一端穿过定位杆C 的小孔固定,另一端跨过滑轮E 系以方向传播时叠加而成的一种特殊形式的干涉现象.如图 2.5-2所示,设有两列频率相同、振幅相同、初相位为零的简谐波,分别沿 ox 轴正方向和ox 轴负方向传播,它们的波动方程分别为xy r = Acos2兀(vt -—)Ay 2 = Acos2 兀(vt + —)A(2.5-1 ) (2.5-2 )x x=Acos2 兀(vt —―) + Acos2 兀(vt +—)AAf2兀)(2.5-3 )这就是驻波的波函数,常称之为驻波方程,式中2AC0S 竺X 是各点的振幅,它只A与x 有关.上式表明,当形成驻波时,弦线上的各点作振幅为2兀2AC0S ——x,频率砝码W并接通正弦信号源.在磁铁M的作用下,通有电流的弦线就会受到与电流垂直的安培力的作用,当弦线上通有正弦交变电流时,安培力也随之呈正弦 变化.可认为磁铁 M 所在处对应的弦线为振源,振动向两边传播,在劈形滑块 R i和R 2两处反射后又沿着各自相反的方向传播而发生干涉.由于固定弦线的两端是 由劈形滑块R 和R 支撑的,故两端点为波节,只有当R i 和R 之间的距离(即弦长I ) 等于半波长的整数倍时,才能形成驻波,这就是均匀弦振动产生驻波的条件设正弦信号频率为V ,则波速为(2.5-4 )21若这个时候R 与Fb 之间有n 个半波长,则波长A =-,弦线上的波速为n2I V =v —n可以证明(见附录)在线密度(单位长度的质量)为 P ,张力F T 的弦线上, 横波的传播速度(2.5-6 )波长(2.5-7 )四、实验内容1. 测定弦线的线密度在天平上秤其质量 m 求出线密度P (或者由实验室预 先秤好给出).2. 观察弦线上的驻波(1)刮去漆包线两端的漆层,穿过定位杆 C 的小孔,接到接线柱 A .另一端跨 过滑轮E 系上砝码 W 然后再接到接线柱B',构成一个导电回路.系砝码时请注意,从砝码到接线柱 B'间的弦线要松些,不能紧绷.信号发生 器的输出端接接线柱A 和B.(2)将弦长I 设置为一定长度.在砝码钩上增减砝码,改变弦线的张力F T ,(2.5-5 )取约2米长的漆包线,仔细调节信号频率^^和信号强度,使弦线上产生若干个波形清晰、稳定的驻波.(3)选定一定的砝码质量和信号频率,仔细调节弦长I、使弦线上产生若干个波形清晰、稳定的驻波.3.测量弦线上横波的传播速度(1)弦线张力不变,弦长I也不变的条件下,调节振动频率V ,测量弦线上横波的传播速度.(2)弦线张力不变,振动频率^/也不变的条件下,调节弦长I,测量弦线上横波的传播速度.(3)改变张力,重复步骤(1)、(2)。
弦振动的实验研究

弦振动的实验研究弦振动的实验研究弦是指⼀段⼜细⼜柔软的弹性长线,⽐如⼆胡、吉它等乐器上所⽤的弦。
⽤薄⽚拨动或者⽤⼸在张紧的弦上拉动就可以使整个弦的振动,再通过⾳箱的共鸣,就会发出悦⽿的声⾳。
对弦乐器性能的研究与改进,离不开对弦振动的研究,对弦振动研究的意义远不只限于此,在⼯程技术上也有着极其重要的意义。
⽐如悬于两根⾼压电杆间的电⼒线、⼤跨度的桥梁等,在⼀定程度上也是⼀根“弦”,它们的振动所带来的后果可不象乐器上的弦的振动那样使我们们感到愉快。
对于弦振动的研究,有助于我们理解这些特殊“弦”的振动特点、机制,从⽽对其加以控制。
同时,弦的振动也提供了⼀个直观的振动与波的模型,对它的分析、研究是处理其它声与振动问题的基础。
欧拉最早提出了弦振动的⼆阶⽅程,⽽后达朗贝尔等⼈通过对弦振动的研究开创了偏微分⽅程论。
本实验意在通过对⼀段两端固定弦振动的研究,了解弦振动的特点和规律。
预备问题1.复习DF4320⽰波器的使⽤。
2.什么是驻波?它是如何形成的?3.什么是弦振动的模式?共振频率与哪些因素有关?4.张⼒对波速有何影响?试⽐较以基频和第⼀谐频共振时弦中的波速。
⼀、实验⽬的:1、了解驻波形成的条件,观察弦振动时形成的驻波;2、学会测量弦线上横波传播速度的⽅法:3、⽤作图法验证弦振动频率与弦长、频率与张⼒的关系。
⼆、实验原理⼀根两端固定并张紧的弦,静⽌时处于⽔平平衡位置,当在弦的垂直⽅向被拉离平衡位置后,弦会有回到平衡位置的趋势,在这种趋势和弦的惯性作⽤下,弦将在平衡位置附近振动。
令弦线长度⽅向为x 轴,弦被拉动的⽅向(与x 轴垂直的⽅向)为y 轴,如图1所⽰。
若设弦的长度为L ,线密度为ρ,弦上的张⼒为T ,对⼀⼩段弦线微元dl 进⾏受⼒分析,运⽤⽜顿第⼆定律定律,可得在y ⽅向的运动微分⽅程()2222tydx dx x y T ??=??ρ(1)若令ρ/2T v =,上式可写为222221tyv x y ??=?? (2)y 图1(2)式反映了弦的位移y 与位置x 、时间t 的关系,其中)/(ρT v =代表了在弦线上横波传播的波速。
弦振动的研究

弦振动的研究
弦振动是物理学中的一个重要研究课题,应用广泛,具有重要的理论和实际意义。
简言之,弦振动是指弦的运动,包括弦的振动频率、振动模式、振幅等。
弦振动的基本方程是弦波方程或量子力学中极小作用量原理,可以通过一些理论和数学工具来描述。
弦的运动包括纵波和横波,其振幅和频率与弦的材料、长度、张力等因素有关。
弦振动理论的研究对于解决许多问题,如乐器的制造、声波的传播、光学、电子学等都非常重要。
传统的弦乐器包括小提琴、大提琴、中提琴、吉他、二胡等都是利用弦的振动来发出美妙的音乐。
在传统的音乐制作中,乐器演奏者通过调整弦的长度、材料、张力和空气的共振效应来调节音高和音色。
在摇滚音乐中,弦乐器的音乐效果可以被电吉他、电贝斯和合成器等电子乐器所模拟。
这些电子乐器配备了内置的高级数字信号处理器,允许乐手模拟各种音效,并使用不同的音效修饰器来调节音色。
弦振动的研究也可以应用于声波传播的分析和量子场论的理论研究。
声波的传播在医学成像中应用广泛,如超声波的成像。
在物理学中,弦振动问题是量子场论中的一种简单的形式,弦理论和标准模型都对此进行了研究。
总之,弦振动是物理学中一个非常重要的研究课题,其理论和应用方面也非常广泛。
通过研究弦振动,我们可以更深入地理解自然界的规律,并为科学技术的发展做出贡献。
弦振动的研究实验报告

弦振动的研究实验报告实验目的:通过实验研究弦的振动特性,并分析弦振动时的动力学特点。
实验装置和材料:1. 弦:选用一根细长的弹性绳或细细的金属丝作为实验弦。
2. 振动源:使用一个固定在实验台上的振动源,可以通过电机或手动方式产生振动。
3. 能量传输装置:使用一个振动传输装置,将振动传输到实验弦上,如夹子、固定块等。
4. 振动探测器:使用一个合适的装置或传感器,用于测量弦的振动状态,如光电传感器、激光干涉仪等。
5. 数据采集设备:使用一个数据采集器,将振动数据进行记录和分析。
实验步骤:1. 将实验弦固定在实验台上,并将振动源固定在一端,确保弦能够自由振动。
2. 施加适量的拉力到弦上,以保证弦的紧绷度。
3. 使用振动源产生一定频率和振幅的振动,并将振动传输到实验弦上。
4. 启动数据采集设备记录弦的振动数据,包括振动频率、振幅和相位等。
5. 根据需要,可以改变振动源的频率和振幅,记录不同条件下的振动数据。
6. 对实验数据进行分析,绘制振动频率与振幅的关系图,并分析振动的谐波特性。
实验结果与分析:1. 实验数据表明,弦的振动频率与振幅呈正相关关系,即振动频率随着振幅的增加而增加。
2. 弦振动呈现出谐波特性,即振动状态可分解为基频振动和多个谐波振动的叠加。
3. 弦的振动模式与弦长度、拉力和材料特性有关,可以通过改变这些参数来调节振动频率和振幅。
结论:通过实验研究弦的振动特性,我们发现弦振动具有谐波特性,振动频率与振幅呈正相关关系。
弦的振动模式受到弦长度、拉力和材料特性的影响。
这些实验结果对于理解弦乐器的音色产生原理和振动系统的动力学特性具有重要意义。
弦振动的研究
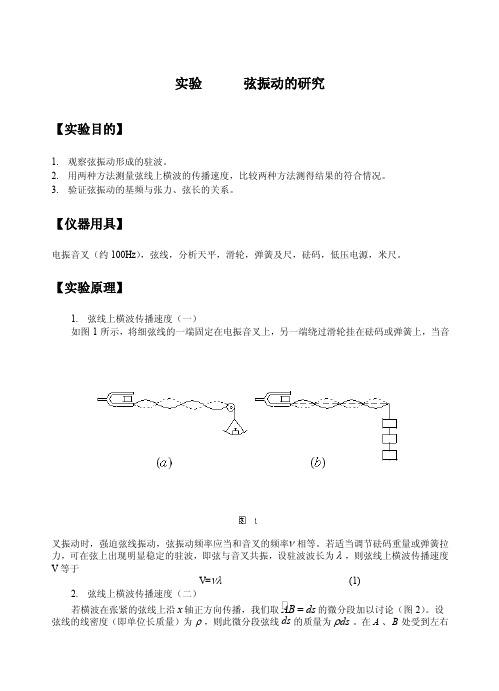
实验弦振动的研究【实验目的】1.观察弦振动形成的驻波。
2.用两种方法测量弦线上横波的传播速度,比较两种方法测得结果的符合情况。
3.验证弦振动的基频与张力、弦长的关系。
【仪器用具】电振音叉(约100Hz),弦线,分析天平,滑轮,弹簧及尺,砝码,低压电源,米尺。
【实验原理】1.弦线上横波传播速度(一)如图1所示,将细弦线的一端固定在电振音叉上,另一端绕过滑轮挂在砝码或弹簧上,当音叉振动时,强迫弦线振动,弦振动频率应当和音叉的频率ν相等。
若适当调节砝码重量或弹簧拉力,可在弦上出现明显稳定的驻波,即弦与音叉共振,设驻波波长为λ,则弦线上横波传播速度V等于V=νλ(1)2.弦线上横波传播速度(二)=的微分段加以讨论(图2)。
设若横波在张紧的弦线上沿x轴正方向传播,我们取 AB dsρ。
在A、B处受到左右弦线的线密度(即单位长质量)为ρ,则此微分段弦线ds的质量为ds邻段的张力分别为1T 、2T ,其方向为沿弦线的切线方向与x 轴交成1α、2α角。
由于弦线上传播的横波在x 方向无振动,所以作用在微分段ds 上的张力的x 分量应该为零,即2211cos cos 0T T αα-= (2)又根据牛顿第二定律,在y 方向微分段的运动方程为:222112sin sin d y T T ds dtααρ-= (3) 对于小的振动,可取ds dx ,而1α、2α都很小,所以1cos 1α ,2cos 1α ,11sin tg αα ,22sin tg αα 。
又从导数的几何意义可知1xdx tg dy α⎛⎫= ⎪⎝⎭,2x dx dy tg dx α+⎛⎫= ⎪⎝⎭,式(2)将成为210T T -=,即21T T T ==表示张力不随时间和地点而变,为一定值。
式(3)将成为22x dx xdy dy d y T T dx dx dx dt ρ+⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭。
(4) 将x dxdy dx +⎛⎫ ⎪⎝⎭按泰勒级数展开并略去二级微量,得 22x d x x xd y d y d y dx dx dx dx +⎛⎫⎛⎫⎛⎫=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭。
弦振动的研究教案

《弦振动的研究》教案实验方式:讲解与演示相结合(40-50分钟),学生实验(120-150分钟)实验要求:1、观察并研究弦上驻波的形成,加深对驻波特点的了解2、研究弦上横波的波长与弦所受的张力及弦的线密度的关系实验仪器:电动音叉、定滑轮、弦、,砝码、钢卷尺、弦线等。
讲解及演示主要内容:1、实验原理由波动理论可以证明,横波沿着一条拉紧的弦线传播时,波速v 与弦线的张力T 、线密度ρ(单位长度的质量)间的关系为ρT v = (1) 设f 为弦线的波动频率;λ为弦线上传播的横波波长,则根据v =f λ和(1)式得ρλT f 1= (2) 为了测定λ,采用在弦中形成驻波的方法。
两列频率相同、振幅相同、振动方向相同的平面简谐波,沿相反方向传播,干涉形成驻波。
振幅最大点称为波腹,振幅为零点静止不动,称为波节。
相邻波节之间距离为半波长,弦上驻波振幅最大且最稳定时,两端形成波节,弦线长度L 应满足下式L =n 2λ ( n =1,2,3,4,… 为弦上半波的个数) 2、实验内容A .观察驻波的形成和波形,波长的变化。
(1)安装调试实验装置。
接通电源后,调节螺钉,使音叉振动;(2)改变弦线长或砝码质量,使之产生振幅最大且稳定的驻波,改变数次,观察波形、波长的变化情况。
B .λ与T 的关系研究微调弦线长L ,不断改变砝码质量,测出振幅最大且稳定,让半波数n =5、4、3、2、1时所对应的张力T 、弦线长、波长λ。
3、操作中的注意事项(1)电音叉不起振或不使用时,应将触点断开。
(2)测量时应使驻波波形稳定,且波节清晰,砝码不要晃动,应保持静态。
(3)实验完毕,应立即将所有砝码取下防好。
4、数据处理(1)测弦线密度=弦线m (kg ) =弦线l (m )==l m弦线弦线ρ kg/m(2)数据表(3)取对数lg λ、lgT ,并作lg λ-lgT 图,以验证其线性关系及振动频率。
5、思考题A .调出稳定的驻波后,欲增加半波数的个数,应增加砝码还是减少砝码?是增长还是缩短弦线长?B .本实验中,改变音叉频率,会使波长变化还是波速变化?改变弦线长时,频率、波长、波速中那个量随之变化?改变砝码质量情况又怎样?。
实验弦振动的研究

福建农林大学 物理实验要求及原始数据表格1 实验 弦振动的研究专业___________________ 学号___________________ 姓名___________________一、预习要点1.了解振动,波动的含义; 2.掌握弦线振动,横波,纵波的含义; 3.掌握形成驻波的条件,并注意观察视频,实验时是如何调出驻波现象; 4. 在课前写好预习报告,上课时务必将预习报告和原始数据表格一并带来,否则扣分。
二、实验内容1. 验证横波的波长与弦线张力的关系(固定波源振动的频率Hz f 100=,改变砝码质量);固定一个波源振动的频率,在砝码盘上添加不同质量的砝码,以改变同一弦上的张力。
每改变一次张力(即增加一次砝码),均要左右移动可动滑轮的位置,使弦线出现振幅较大而稳定的驻波。
用实验平台上的标尺测量波节的位置,即可根据实验原理算出波长。
利用坐标纸作M ln ln -λ图,求其直线斜率1k ,并由1111ln ln ln C T k C M k '+=+=λ(1C 、1C '表示常数)说明λln 与T ln 的线性关系,验证横波的波长与弦线中的张力的关系。
2. 验证横波的波长与波源振动频率的关系(固定砝码质量M 225g =,改变波源振动的频率);在砝码盘上放上一定质量的砝码,以固定弦线上所受的张力,改变波源振动的频率,同样用驻波法即可算出各相应的波长。
利用坐标纸作ln ln f λ-图,求其直线斜率2k ,并由22ln ln k f C λ=+(2C 表示常数)说明λln 与ln f 的线性关系,验证横波的波长与波源振动频率的关系。
三、实验注意事项1. 注意砝码盘本身也有质量;2. 实验时要防止机械共振;①刚开机时出现的50Hz 就是易共振的频率,所以开机前先关小振幅,等开机后,调节好适当的频率,再把振幅调节到最大;②在验证横波的波长与弦线中的张力的关系实验中,加减砝码时,应把振幅调节到最小;3. 要准确求得驻波的波长,必须在弦线上调出振幅尽可能大且稳定的驻波。
弦振动研究实验报告

弦振动研究实验报告弦振动研究实验报告引言弦振动是物理学中一个重要的研究领域,对于理解声音、乐器演奏、结构工程等方面都具有重要意义。
本实验旨在通过实验观察和数据分析,探究弦振动的基本原理和特性。
实验目的1. 研究弦振动的基本原理和特性。
2. 通过实验观察和数据分析,验证弦振动的频率与弦长、张力和质量的关系。
3. 探究不同条件下弦振动的共振现象。
实验装置与方法本实验使用的装置包括弦线、定滑轮、振动发生器、频率计和质量块等。
具体实验步骤如下:1. 将弦线固定在两个支架上,并通过定滑轮使弦线保持水平。
2. 在弦线上固定一个质量块,调整张力。
3. 将振动发生器连接到弦线上,并调节频率。
4. 使用频率计测量弦线的频率。
5. 重复步骤2-4,改变质量块的质量、张力和弦长等条件。
实验结果与分析通过实验观察和数据分析,我们得到了以下结果:1. 频率与弦长的关系:在保持张力和质量不变的情况下,我们改变了弦长。
实验结果显示,随着弦长的增加,频率呈现出递减的趋势。
这与理论预测相符,即频率与弦长成反比关系。
2. 频率与张力的关系:在保持弦长和质量不变的情况下,我们改变了张力。
实验结果表明,随着张力的增加,频率也随之增加。
这符合理论预测,即频率与张力成正比关系。
3. 频率与质量的关系:在保持弦长和张力不变的情况下,我们改变了质量。
实验结果显示,随着质量的增加,频率呈现出递减的趋势。
这与理论预测相符,即频率与质量成反比关系。
4. 共振现象:我们在实验中发现了共振现象。
当振动发生器的频率与弦的固有频率相等时,弦会出现共振现象,振幅显著增大。
这说明共振频率与弦的固有频率相匹配。
结论通过本实验的观察和数据分析,我们得出以下结论:1. 弦振动的频率与弦长成反比关系,与张力和质量成正比关系。
2. 弦振动会出现共振现象,当振动发生器的频率与弦的固有频率相等时,振幅显著增大。
这些结论对于理解弦振动的基本原理和特性具有重要意义。
在实际应用中,我们可以根据这些关系来设计和调整乐器的音调,以及优化结构工程中的弦悬挂系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
力热学实验
1.观察驻波的形成,归纳驻波性质.
2.弦振动的研究:弦振动的波长与 弦张力之间的关系.
苏州大学物理实验教学中心
【实验原理】
力热学实验
振幅相同、频率相同、振动方向相同、周相差恒定的两 列波在同一直线上相向传播叠加而形成的一种看起来停驻不 前的波形,称为驻波。波的叠加引起的驻波是一种重要的振 动现象,它广泛存在于自然现象之中,管、弦、板、膜的振 动都可形成驻波。驻波在声学、无线电学和光学等领域都有 重要的应用。利用驻波可以测定波长,也可确定振动系统的 固有频率。
苏州大学物理实验教学中心
力热学实验
验证(2.8—3)式还可采用直观的图解法,对式 (2.8—3)取对数:
lgλ 1 lgT 1 lgρ lgf 22
因ρ、f均为确定值,故以lgλ对lgT作图应为直线, 且其斜率为1/2 如果ρ事先测得,则由直线的截距还可求得弦振动频 率值,并与音叉的频率比较是否一致。
苏州大学物理实验教学中心
【实验内容】
力热学实验
1、观察弦振动驻波的形成
(1)按图接好线路,弦线L的一端固定在音叉A的 一脚B,另一端跨过滑轮C悬一重物W. 音叉的 振动利用电磁铁来激发,电源E的一端接音叉, 另一端通过开关K、电磁铁B的线圈和可调螺丝 K’与音叉相接,调节K’使之与音叉相接触,则 电路接通,电磁铁吸引音叉. 音叉一被吸动后, 螺丝与音叉便不再接触,电流中断,电磁铁失 去吸引音叉的作用,音叉又回到原来的位置, 这样反复作用的结果,就使音叉按其固有频率 振动起来.
可记为
L
nλ 2
(n =1,2,…,为弦上半波个数)
可见形成驻波时可方便地测得波长λ。
苏州大学物理实验教学中心
力热学实验
本实验验证(2.8—3)式时测定λ,就是把弦振动调整 到驻波状态而进行的,弦线取适当长,在电动音叉带 动下,起振后适当调节张力(可先试以手按砝码盘) 即可看见驻波现象:某些点不振动为波节,波节中间 振幅最大处为波腹,应再细心调节注意观察,直至出 现波腹极大而且稳定,且仅限于y方向振动(没有z方 向的振动),这可在初选固定张力下慢慢移动支撑点 D的位置,细调弦长来获得。
弦振动可视作一维的波动,绷紧的弦线上一点作横向受迫振 动,会导致横波沿弦线传播并在其端点发生反射,前进波与 反射波干涉便产生驻波。
苏州大学物理实验教学中心
力热学实验
分析可知弦振动满足波动方程:
2 y t 2
T
2 y x 2
(2.8—1)
x为波动传播方向,y为振动位移方向,ρ为弦线的
线密度,T为弦线张力,弦上波速为
苏州大学物理实验教学中心
力热学实验
2、λ—T关系研究
(1)挂上适当的砝码,并使T一定,取n=1,微调弦长L (通过沿着弦线方向慢慢移动支撑点D),获得稳定、 最大的振幅,并且振动仅沿y方向(无z方向运动), 记下L、T求出λ。
(2) T不改变,再分别取n—2,3,4,5,重复上述细
调过程,记下相应的L、T .求出λ,并与λ 的理论值比较。
(2) 测量时应使驻波波形稳定,且波节清晰, 砝码不要晃动,应保持静态。
(3) 电振音叉不起振或不使用时,应将触点 断开。
(4) 实验完毕,应立即将所有砝码取下放好。
苏州大学物理实验教学中心
力热学实验
精品课件!
苏州大学物理实验教学中心
力热学实验
精品课件!
苏州大学物理实验教学中心
【思考题】
力热学实验
n=4
l4A l4B
l4
/cm /cm /cm
Hale Waihona Puke /m/s-1vf f
/m/s-1
lg f
lg T
f = Hz
苏州大学物理实验教学中心
力热学实验
(4)取对数lgλ、lgT,并作lgλ—lgT图,以验证其 线性关系及振动频率。
(5)对本实验进行误差分析
(6)写出各测量结果不确定度表示方式。即
n
(3)改变砝码值T,重复上述(1)(2)过程,求出相应的λ 值。
苏州大学物理实验教学中心
力热学实验
频率f不变,改变砝码(连托盘)质量m, 测定弦线中的横波波速vf
T =mg
n=1
l1A l1B
l1
/cm /cm /cm
n=2
l2A l2B
l2
/cm /cm /cm
n=3
l3A l3B
l3
/cm /cm /cm
υ
T ρ
(2.8—2)
按波动公式 u f,结合式(2.8—2)
可得弦振动波长与张力的关系为
λ
1 f
T ρ
(2.8—3)
苏州大学物理实验教学中心
力热学实验
从式(2.8—1)容易得出前进波、反射波都是波动方程的
解,当满足一定条件时弦振动方式为驻波,为简明起见,
设x=0及x=L处 y≡0,即视弦的两端为固定,则驻波条件
i
i i1
5
uc . i
S2 i
2
λi λi uc.λi ( cm)
Si
n
( i i )2
i 1
n( n 1)
0.2
3
苏州大学物理实验教学中心
【注意事项】
力热学实验
(1) 调节滑轮C高度,使弦线成水平,并使 弦线和音叉腿成一直线,不能是折线
(1)本实验是振动频率固定情况下的λ—T关系, 如果频率改变而波长不变则实验如何进行?
(2)弦在频率为f 的音叉策动下振动,当T为某 值时,若弦上出现m个半波区,则弦的基频应 为 f ,为什么?若频率不变,则应如何改变张力,
m
才会使弦上出现一个半波区?
苏州大学物理实验教学中心
苏州大学物理实验教学中心
力热学实验
弦线的张力
,
T mg W
m为砝码及砝码托的质量和.
(2)通电,调节振子螺钉(注意不可过紧)使音叉振动起 来,固定弦长约70cm左右,手按弦线以改变张力,观察 弦上形成不同半波个数时的驻波。取n =1,2,3,4,5, 可从手感觉张力T 的不同,并估计其大概数值。
