历年自主招生考试数学试题大全2017年上海复旦大学自主招生数学试题Word版
(完整)自主招生数学试题及答案,推荐文档

2017年自主招生数学试题(分值: 100分 时间:90分钟)一、选择题(本大题共6小题,每小题5分,共30分,在每小题给出的四个选项中,只有一个选项是正确的)1、若对于任意实数,关于的方程都有实数根,则实数的a x 0222=+--b a ax x b 取值范围是( )A ≤0B ≤C ≤D ≤-1b b 21-b 81-b 2、如图,D 、E 分别是△ABC 的边AB 、BC 上的点,且DE∥AC,已知S △BDE ∶S △CDE =1∶3,则S △DOE ∶S △AOC 的值为( )A .1∶3B .1∶4C .1∶9D .1∶163、某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高(如图所示)。
已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D 处测得电线杆顶端A 的仰角为300,在C 处测得电线杆顶端A 得仰角为450,斜坡与地面成600角,CD=4m ,则电线杆的高(AB)是( )A .mB .mC .mD .12m )344(+)434(-)326(+4、如图,矩形ABCD 中,AB=8,AD=3.点E 从D 向C 以每秒1个单位的速度运动,以AE 为一边在AE 的右下方作正方形AEFG .同时垂直于CD 的直线MN 也从C 向D 以每秒2个单位的速度运动,当经过( )秒时,直线MN 和正方形AEFG 开始有公共点。
A .53 B .12 C .43 D .23(第2题图) (第3题图) (第4题图)5、如图,在反比例函数的图象上有一动点A ,连接AO 并延长交图象的另一支于xy 2-=点B ,在第一象限内有一点C ,满足AC=BC ,当点A 运动时,点C 始终在函数的图xky =象上运动,若tan∠CAB=2,则k 的值为( )A. 2B. 4C. 6D. 86、如图,O 是等边三角形ABC 内一点,且OA=3,OB=4,OC=5.将线段OB 绕点B 逆时针旋转600得到线段O′B,则下列结论:①△AO′B 可以由△COB 绕点B 逆时针旋转600得到;②∠AOB=1500;③6AOBO'S =+四边形6AOB AOCS S +=△△是( )A.②③④B.①②④C.①④D.①②③O'OCB A(第5题图) (第6题图)二、填空题(本大题共6小题,每小题5分,共30分)7、已知方程组,且,则的取值范围是 。
复旦自主招生数学

一、选择题1.在(x 2−1x)10的展开式中系数最大的项是_____.A .第4、6项B .第5、6项C .第5、7项D .第6、7项 2.设函数y=ƒ (x)对一切实数x 均满足ƒ (5+x )=ƒ(5−x),且方程ƒ (x )=0恰好有6个不同的实根,那么这6个实根的和为____.A .10B .12C .18D .30 3.假设非空集合X={x |a +1≤x≤3a−5},Y={x |1≤x≤16},那么使得X ⊆X ∪Y 成立的所有a 的集合是_____.A .{a |0≤a≤7}B .{a |3≤a≤7}C .{a |a≤7}D .空集 4.设z 为复数,E={z |(z−1)2=|z−1|2},那么以下_ 是正确的A .E={纯虚数}B .E={实数}C .{实数}⊆E ⊆{复数}D .E={复数}5.把圆x 2+(y−1)2=1与椭圆x 2+2(1)9y +=1的公共点,用线段连接起来所得到的图形为_____.A .线段B .等边三角形C .不等边三角形D .四边形6.在正三棱柱ABC —A 1B 1C 1中,假设BB 1,那么AB 1与C 1B 所成的角的大小是___. A .60° B .75° C .90° D .105°7.某厂拟用集装箱托运甲乙两种货物,每箱的体积、重量、可获利润以及托运所受限制如在最合理的安排下,获得的最大利润是______百元.A .58B .60C .62D .648.假设向量a +3b 垂直于向量7a −5b ,并且向量a −4b 垂直于向量7a −2b ,那么向量a 与b 的夹角为___ ___.A .2π; B .3π; C .4π; D .6π. 9.复旦大学外语系某年级举行一次英语口语演讲比赛,共有十人参赛,其中一班有三位,二班有两位,其它班有五位.假设采用抽签的方式确定他们的演讲顺序,那么一班的三位同学恰好演讲序号相连.问二班的两位同学的演讲序号不相连的概率是____.A .120 B .140 C .160 D .19010.sin α,cos α是关于x 的方程x 2−tx+t=0的两个根,这里t ∈3sin α+3cos α=___.A .B .;C .−D .11.设z 1,z 2为一对共轭复数,如果|z 1−z 2且122z z 为实数,那么|z 1|=|z 2|=____. AB .2C .3 D12.假设四面体的一条棱长是x ,其余棱长都是1,体积是V(x),那么函数V(x)在其定义域上为____.A .增函数但无最大值B .增函数且有最大值C .不是增函数且无最大值D .不是增函数但有最大值 13.以下正确的不等式是____.A .16<1201k =; B .18<1201k =<19; C .20<1201k =; D .22<1201k =<23. 14.设{αn }是正数列,其前n 项和为S n ,满足:对一切n ∈Z +,αn 和2的等差中项等于S n 和2的等比中项,那么limnn n→∞α=______.A .0B .4C .12D .10015.x 1,x 2是方程x 2−(α−2)x+(α2+3α+5)=0(α为实数)的两个实根,那么x 12+x 22的最大值为______.A .18B .19C .20D .不存在 16=α.条件乙:sin2θ+cos 2θ=α.那么以下________是正确的. A .甲是乙的充分必要条件 B .甲是乙的必要条件C .甲是乙的充分条件D .甲不是乙的必要条件,也不是充分条件 17.函数ƒ(x)的定义域为(0,1),那么函数g(x)= ƒ(x+c)+ƒ(x−c)在0<c<12时的定义域为____. A .(−c,1+c); B .(1−c,c); C .(1+c,−c); D .(c,1−c); 18.函数____.A .y min =54-,y max =54; B .无最小值,y max =54; C .y min =54-,无最大值 D .既无最小值也无最大值19.等差数列{αn }中,α5<0,α6>0且α6>|α5|,S n 是前n 项之和,那么以下___是正确的.A .S 1,S 2,S 3均小于0,而S 4,S 5,…均大于0B .S 1,S 2,…,S 5均小于0,而S 6,S 7,…均大于0C .S 1,S 2,…,S 9均小于0,而S 10,S 11,…均大于0D .S 1,S 2,…,S 10均小于0,而S 11,S 12,…均大于0 20.角θ的顶点在原点,始边为x 轴正半轴,而终边经过点Q(,y),(y≠0),那么角θ的终边所在的象限为___.A .第一象限或第二象限B .第二象限或第三象限C .第三象限或第四象限D .第四象限或第一象限21.在平面直角坐标系中,三角形△ABC 的顶点坐标分别为A(3,4),B(6,0),C(−5,−2),那么∠A 的平分线所在直线的方程为_____.A .7x−y−17=0;B .2x+y+3=0;C .5x+y−6=0;D .x−6y=0. 22.对所有满足1≤n≤m≤5的m ,n ,极坐标方程11cos nm C θρ=-表示的不同双曲线条数为_____.A .6B .9C .12D .1523.设有三个函数,第一个是y=ƒ(x),它的反函数就是第二个函数,而第三个函数的图象与第二个函数的图象关于直线x+y=0对称,那么第三个函数是______.A .y=−ƒ(x);B .y=−ƒ(−x);C .y=−ƒ−1(x);D .y=−ƒ−1(−x);24∈[2,3]时,ƒ(x)=x ,那么当x ∈[−2,0]时,ƒ(x)的解析式为_____.A .x+4;B .2−x;C .3−|x+1|;D .2+|x+1|. 25.α,b 为实数,满足(α+b)59=−1,( α−b)60=1,那么α59+α60+b 59+b 60=_____.A .−2B .−1C .0D .1 26.设αn 是)n 的展开式中x 项的系数(n=2,3,4,…),那么极限2323222lim()nn n →∞+++ααα…=________. A .15 B .6 C .17 D .8 27.设x 1,x 2∈(0,2π),且x 1≠x 2,不等式成立的有 (1)12(tanx 1+tanx 2)>tan 122x x +; (2) 12(tanx 1+tanx 2)<tan 122x x +; (3)12(sinx 1+sinx 2)>sin 122x x +; (4) 12(sinx 1+sinx 2)<sin 122x x + A .(1),(3) B .(1),(4) C .(2),(3) D .(2),(4)28.如下图,半径为r 的四分之一的圆ABC 上,分别以AB 和AC 为直径作两个半圆,分别标有α的阴影局部面积和标有b 的阴影局部面积,那么这两局部面积α和b 有_____.A .α>bB .α<bC .α=bD .无法确定CBAba29.设a ,b PQ =2a +k b ,QR =a +b ,RS =2a −3b .假设P ,Q ,S 三点共线,那么k 的值为_____.A .−1;B .−3;C .43-;D .35-; ##Answer## 1.C 2.D 3.C 4.B 5.B6. 【简解】设BB 1=1,那么取AC 、BC 1的中点D 、O,DOC 1B 1A 1CBAOD ∥AB 1,∠BOD 即为所求;在△BOD 中,OD=OB 1=2,BD=2,∠BOD=90°。
2017年上海高考数学真题试卷(word解析版)

6 绝密★启用前2017 年普通高等学校招生全国统一考试(上海卷)数学试卷(满分 150 分,考试时间 120 分钟)1、考生注意2、1.本场考试时间 120 分钟,试卷共 4 页,满分 150 分,答题纸共 2 页.3、2.作答前,在答题纸正面填写姓名、准考证号,反面填写姓名,将核对后的条形码贴在答题纸指定位置.4、3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域,不得错位.在试卷上作答一律不得分. 5、4.用 2B 铅笔作答选择题,用黑色字迹钢笔、水笔或圆珠笔作答非选择题.一. 填空题(本大题共 12 题,满分 54 分,第 1~6 题每题 4 分,第 7~12 题每题 5 分) 1. 已知集合 A = {1, 2,3, 4},集合 B = {3, 4,5},则 AB =2. 若排列数P m= 6 ⨯ 5 ⨯ 4 ,则m =3. 不等式x -1> 1 的解集为 x4. 已知球的体积为36π ,则该球主视图的面积等于5. 已知复数 z 满足 z + 3= 0 ,则| z | =z 6. 设双曲线 x 9- y2 b 2 = 1 (b > 0) 的焦点为 F 1 、 F 2, P 为该双曲线上的一点,若| PF 1 | = 5 ,则| PF 2 | =7. 如图,以长方体 ABCD - A 1B 1C 1D 1 的顶点 D 为坐标原点,过 D 的三条棱所在的直线为坐标轴,建立空间直角坐标系,若 DB 1 的坐标为(4,3, 2) ,则 AC 1 的坐标为- ⎧⎪3x -1, x ≤ 08. 定义在(0, +∞) 上的函数 y = f (x ) 的反函数为 y = f 1(x ) ,若 g (x ) = ⎨ ⎪⎩ f (x ), 为 x > 0奇函数,则 f -1(x ) = 2 的解为119. 已知四个函数:① y = -x ;② y =- ;③ xy = x 3 ;④ y = x 2 . 从中任选 2 个,则事件“所选 2 个函数的图像有且仅有一个公共点”的概率为10. 已知数列{a } 和{b } ,其中a = n 2 , n ∈ N * ,{b } 的项是互不相等的正整数,若对于nnnn任意n ∈ N * ,{b } 的第a 项等于{a } 的第b 项,则lg(b 1b 4b 9b 16 ) =nnnnlg(b 1b 2b 3b 4 )2⎨2x + 3y = 4 n n 211. 设a 、 a ∈ R ,且1+1= 2 ,则| 10π - α - α |的最小值等于122 + sin α2 + sin(2α ) 121212. 如图,用 35 个单位正方形拼成一个矩形,点 P 1 、 P 2 、 P 3 、 P 4 以及四个标记为“#”的点在正方形的顶点处,设集合Ω = {P 1 , P 2 , P 3 , P 4 },点P ∈Ω,过 P 作直线l P ,使得不在l P 上的“#”的点分布在l P 的两侧. 用 D 1 (l P ) 和 D 2 (l P ) 分别表示l P 一侧和另一侧的“#”的点到l P 的距离之和. 若过 P 的直线l P 中有且只有一条满足 D 1 (l P ) = D 2 (l P ) ,则Ω 中 所有这样的 P 为二. 选择题(本大题共 4 题,每题 5 分,共 20 分)13. 关于 x 、 y 的二元一次方程组⎧x + 5y = 0 ⎩的系数行列式 D 为( )0 5 1 0 A.B. 4 32 4 1 5 6 0 C. D.2 35 414. 在数列{a } 中, a = (- 1)n , n ∈ N * ,则lim a ()n n2n →∞ n A. 等于- 1 2 B. 等于 0 C. 等于 12D. 不存在15. 已知a 、b 、c 为实常数,数列{x } 的通项 x = an 2+ bn + c ,n ∈ N * ,则“存在k ∈ N * ,使得 x 100+ k 、 x 200+ k 、 x 300+ k 成等差数列”的一个必要条件是( ) A. a ≥ 0B. b ≤ 0C. c = 0D. a - 2b + c = 0x 2y 2 16. 在平面直角坐标系 xOy 中,已知椭圆C 1 : 36 + 4= 1 和C : x 2 + y 9 = 1 . P 为C 1 上的动 点,Q 为C 2 上的动点, w 是OP ⋅ OQ 的最大值. 记Ω = {(P ,Q ) | P 在C 1 上,Q 在C 2 上,且OP ⋅ OQ = w },则Ω 中元素个数为() A. 2 个B. 4 个C. 8 个D. 无穷个三. 解答题(本大题共 5 题,共 14+14+14+16+18=76 分)17. 如图,直三棱柱 ABC - A 1B 1C 1 的底面为直角三角形,两直角边 AB 和 AC 的长分别为 4 和 2,侧棱 AA 1 的长为 5.(1) 求三棱柱 ABC - A 1B 1C 1 的体积; (2) 设 M 是 BC 中点,求直线 A 1M与平面 ABC 所成角的大小.219 2 ⎪⎩ny18. 已知函数 f (x ) = cos 2 x - sin 2 x + 1, x ∈ (0,π ) .2(1) 求 f (x ) 的单调递增区间;(2) 设△ABC 为锐角三角形,角 A 所对边a = ,角 B 所对边b = 5 ,若 f ( A ) = 0 ,求△ABC 的面积.19. 根据预测,某地第n (n ∈ N * ) 个月共享单车的投放量和损失量分别为a 和b (单位:辆),nn⎧⎪5n 4 +15, 1 ≤ n ≤ 3其中a n = ⎨-10n + 470, , b n = n + 5 ,第n 个月底的共享单车的保有量是前n 个月的 n ≥ 4 累计投放量与累计损失量的差.(1) 求该地区第 4 个月底的共享单车的保有量;(2) 已知该地共享单车停放点第n 个月底的单车容纳量 S = -4(n - 46)2 + 8800(单位:辆). 设在某月底,共享单车保有量达到最大,问该保有量是否超出了此时停放点的单车容纳量?20. 在平面直角坐标系 xOy 中,已知椭圆Γ : x 2 + 24= 1 , A 为Γ 的上顶点, P 为Γ 上异于 上、下顶点的动点, M 为 x 正半轴上的动点.(1)若 P 在第一象限,且| OP | = ,求 P 的坐标;8 3 P ( , ) 5 5,若以 A 、P 、M 为顶点的三角形是直角三角形,求 M 的横坐标;(3) 若| MA | = | MP | ,直线 AQ 与Γ 交于另一点 C ,且 AQ = 2 A C , PQ = 4PM ,求直线 AQ 的方程.21. 设定义在 R 上的函数 f (x 1) ≤ f (x 2 ) .f (x ) 满足: 对于任意的 x 1 、 x 2 ∈ R ,当 x 1 < x 2 时, 都有(2)设(1)若f (x) =ax3+1,求a 的取值范围;(2)若f (x) 为周期函数,证明:f (x) 是常值函数;(3)设f (x) 恒大于零,g(x) 是定义在R 上、恒大于零的周期函数,M 是g(x) 的最大值.函数h(x) =f (x)g(x) .证明:“h(x) 是周期函数”的充要条件是“ f (x) 是常值函数”.6 2 2017 年普通高等学校招生全国统一考试上海--数学试卷考生注意1. 本场考试时间 120 分钟,试卷共 4 页,满分 150 分,答题纸共 2 页.2. 作答前,在答题纸正面填写姓名、准考证号,反面填写姓名,将核对后的条形码贴在答题纸指定位置.3. 所有作答务必填涂或书写在答题纸上与试卷题号对应的区域,不得错位.在试卷上作答一律不得分.4. 用 2B 铅笔作答选择题,用黑色字迹钢笔、水笔或圆珠笔作答非选择题.一、填空题(本大题共有 12 题,满分 54 分,第 1-6 题每题 4 分,第 7-12 题每题 5 分)考生应在答题纸的相应位置直接填写结果.1. 已知集合 A ={1, 2, 3, 4}, B = {3, 4, 5} ,则 AB = .【解析】本题考查集合的运算,交集,属于基础题 【答案】{3, 4}2. 若排列数P m = 6⨯ 5⨯ 4 ,则m = . 【解析】本题考查排列的计算,属于基础题 【答案】3x -1 3. 不等式x> 1的解集为.【解析】本题考查分式不等式的解法,属于基础题 【答案】(-∞,0)4. 已知球的体积为36π ,则该球主视图的面积等于.【解析】本题考查球的体积公式和三视图的概念,4π R 3 = 36π ⇒ R = 3 ,3所以 S = π R 2 = 9π ,属于基础题【答案】9π5. 已知复数 z 满足 z +3 = 0 ,则 z = .z【解析】本题考查复数的四则运算和复数的模, z + 3= 0 ⇒ z 2 = -3 设 z = a + bi ,z则 a 2- b 2+ 2abi = -3 ⇒ a = 0, b = ± 3i ,z =,属于基础题【答案】6. 设双曲线x - y 29 b 2= 1(b > 0) 的焦点为 F 1、F 2 , P 为该双曲线上的一点.若 PF 1= 5 ,则 a 2 + b 2 34 PF 2 = .【 解 析 】 本 题 考 查 双 曲 线 的 定 义 和 性 质 ,PF 1 - PF 2 = 2a = 6 ( 舍 ),PF 2 - PF 1 = 2a = 6 ⇒ PF 2 = 11【答案】117. 如图,以长方体 ABCD - A 1B 1C 1D 1 的顶点 D 为坐标原点,过 D 的三条棱所在的直线为坐标轴,建立空间直角坐标系.若 DB 1 的坐标为(4, 3, 2) ,则 AC 1 的坐标是.【解析】本题考查空间向量,可得 A (4,0,0),C 1(0,3, 2) ⇒ AC 1 = (-4,3,2) ,属于基础题 【答案】(-4,3,2)8. 定义在(0, +∞) 上的函数 y =数,则 f -1(x )=2 的解为.⎧3x -1, x ≤ 0, f (x ) 的反函数 y = f -1(x ) .若 g (x ) = ⎨ ⎩ f (x ), x > 0 为奇函【解析】本题考查函数基本性质和互为反函数的两个函数之间的关系,属于中档题x > 0, -x < 0, g (-x ) = 3-x -1 = -g (x ) ⇒ g (x ) = 1- 1 3x,所以 f (x ) = 1- 1,3x 当 x = 2 时, f (x ) = 8,所以 f 9(8) = 29 【答案】 x = 89119. 已知四个函数:① y = - x ;② y =-;③ y = x 3;④ y = x 2.从中任选 2 个,则事件“所x选 2 个函数的图像有且仅有一个公共点”的概率为.【解析】本题考查事件的概率,幂函数的图像画法和特征,属于基础题总的情况有: C 2 = 6 种,符合题意的就两种:①和③,①和④-11 2 3 4 2 π nnnn1⎧ π ⎨ 1 【答案】310. 已知数列{a } 和{b } ,其中 a = n 2 , n ∈ N * ,{b } 的项是互不相等的正整数.若对于任意n ∈ N *,{b } 中的第 a 项等于{a } 中的第b 项,则 lg (b 1b 4b 9b 16 )= .nnn lg (b 1b 2b 3b 4 )【解析】本题考查数列概念的理解,对数的运算,属于中档题由题意可得: b = a ⇒ b = (b )2 ⇒ b = b 2 , b = b 2 , b = b 2 ,b = b 2 ,a nb nn 2n1 1 42 93 16 4lg (b 1b 4b 9b 16 ) lg (b 1b 2b 3b 4 ) lg (bb b b )2lg (b 1b 2b 3b 4 )【答案】211. 设α1,α2 ∈ R ,且12 + sin α+2 + sin(2α = 2 ,则 10π - α)1 - α2的最小值等于. 12【解析】考查三角函数的性质和值域,1∈ ⎡1 ,1⎤,1 ∈ ⎡1 ,1⎤2 + sin α1 ⎢⎣3 ⎥⎦ 2 + sin(2α2 ) ⎢⎣3 ⎥⎦ ,要使 1 + 1 = 2 ⎧ 1 =1 ⎪ 2 + sin α1 则⎨ α1 = - + 2k 1⎪ , k , k ∈ Z 2 + sin α 2 + sin(2α ) 1 π 1 2 1 2 ,⎪ =1 ⎪ α = - + k π ⎪⎩ 2 + sin(2α2 )⎪⎩ 2 4 2 10π -α -α= 10π + 3π - (2k + k )π = π 当2k + k =11时成立 1 2 minπ4 1 2 min4 , 【答案】 412. 如图,用 35 个单位正方形拼成一个矩形,点 P 1, P 2 , P 3 , P 4 以及四个标记为“▲”的点在正方形的顶点处.设集合Ω={P 1, P 2 , P 3 , P 4 } ,点 P ∈Ω .过 P 作直线l P ,使得不在l P 上的“▲” 的点分布在l P 的两侧.用 D 1 (l P ) 和 D 2 (l P ) 分别表示l P 一侧和另一侧的“▲”的点到l P 的距离之和.若过 P 的直线l P 中有且只有一条满足 D 1 (l P )=D 2 (l P ) ,则Ω 中所有这样的 P 为.⇒ n所以 = =21 2⎩ ⎨【解析】本题考查有向距离,以左下角的顶点为原点建立直角坐标系。
2017年上海高考数学真题试卷(word解析版)

绝密★启用前2017年普通高等学校招生全国统一考试(上海卷)数学试卷(满分150分,考试时间120分钟)1、考生注意2、1.本场考试时间120分钟,试卷共4页,满分150分,答题纸共2页.3、2.作答前,在答题纸正面填写姓名、准考证号,反面填写姓名,将核对后的条形码贴在答题纸指定位置.4、3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域,不得错位.在试卷上作答一律不得分.5、4.用2B 铅笔作答选择题目,用黑色字迹钢笔、水笔或圆珠笔作答非选择题目.一.填空题目(本大题共12题,满分54分,第1~6题每题4分,第7~12题每题5分)1.已知集合{1,2,3,4}A ,集合{3,4,5}B ,则A B ∩2.若排列数6654m P ,则m3.不等式11x x 的解集为4.已知球的体积为36 ,则该球主视图的面积等于5.已知复数z 满足30z z,则||z6.设双曲线22219x y b(0)b 的焦点为1F 、2F ,P 为该双曲线上的一点,若1||5PF ,则2||PF7.如图,以长方体1111ABCD A B C D 的顶点D 为坐标原点,过D 的三条棱所在的直线为坐标轴,建立空间直角坐标系,若1DB 的坐标为(4,3,2),则1AC的坐标为8.定义在(0,) 上的函数()y f x 的反函数为1()y f x ,若31,0()(),0x x g x f x x为奇函数,则1()2f x 的解为9.已知四个函数:①y x ;②1y x;③3y x ;④12y x .从中任选2个,则事件“所选2个函数的图像有且仅有一个公共点”的概率为10.已知数列{}n a 和{}n b ,其中2n a n ,*n N ,{}n b的项是互不相等的正整数,若对于任意*n N ,{}n b 的第na 项等于{}n a 的第nb 项,则149161234lg()lg()b b b b b b b b11.设1a 、2a R ,且121122sin 2sin(2) ,则12|10| 的最小值等于12.如图,用35个单位正方形拼成一个矩形,点1P、2P 、3P 、4P 以及四个标记为“”的点在正方形的顶点处,设集合1234{,,,}P P P P ,点P ,过P 作直线P l ,使得不在P l 上的“”的点分布在P l 的两侧.用1()P D l 和2()P D l 分别表示P l 一侧和另一侧的“”的点到P l 的距离之和.若过P 的直线P l 中有且只有一条满足12()()P P D l D l ,则 中所有这样的P 为二.选择题目(本大题共4题,每题5分,共20分)13.关于x 、y 的二元一次方程组50234x y x y的系数行列式D 为()A.0543 B.1024 C.1523 D.605414.在数列{}n a 中,1(2nn a ,*n N ,则lim n n a ()A.等于12B.等于0C.等于12D.不存在15.已知a 、b 、c 为实常数,数列{}n x 的通项2n x an bn c ,*n N ,则“存在*k N ,使得100kx 、200kx 、300kx 成等差数列”的一个必要条件是()A.0aB.0b C.0c D.20a b c 16.在平面直角坐标系xOy 中,已知椭圆221:1364x y C 和222:19y C x .P 为1C 上的动点,Q 为2C 上的动点,w 是OP OQ的最大值.记{(,)|P Q P 在1C 上,Q 在2C 上,且}OP OQ w,则 中元素个数为()A.2个B.4个C.8个D.无穷个三.解答题(本大题共5题,共14+14+14+16+18=76分)17.如图,直三棱柱111ABC A B C 的底面为直角三角形,两直角边AB 和AC 的长分别为4和2,侧棱1AA 的长为5.(1)求三棱柱111ABC A B C 的体积;(2)设M 是BC 中点,求直线1A M 与平面ABC 所成角的大小.18.已知函数221()cos sin 2f x x x,(0,)x .(1)求()f x 的单调递增区间;(2)设△ABC 为锐角三角形,角A所对边a ,角B 所对边5b ,若()0f A ,求△ABC 的面积.19.根据预测,某地第n *()n N 个月共享单车的投放量和损失量分别为n a 和n b (单位:辆),其中4515,1310470,4n n n a n n,5n b n ,第n 个月底的共享单车的保有量是前n 个月的累计投放量与累计损失量的差.(1)求该地区第4个月底的共享单车的保有量;(2)已知该地共享单车停放点第n 个月底的单车容纳量24(46)8800n S n (单位:辆).设在某月底,共享单车保有量达到最大,问该保有量是否超出了此时停放点的单车容纳量?20.在平面直角坐标系xOy 中,已知椭圆22:14x y ,A 为 的上顶点,P 为 上异于上、下顶点的动点,M 为x 正半轴上的动点.(1)若P在第一象限,且||OP ,求P的坐标;(2)设83(,)55P ,若以A 、P 、M 为顶点的三角形是直角三角形,求M 的横坐标;(3)若||||MA MP ,直线AQ 与 交于另一点C ,且2AQ AC ,4PQ PM ,求直线AQ 的方程.21.设定义在R 上的函数()f x 满足:对于任意的1x 、2x R ,当12x x 时,都有12()()f x f x .(1)若3()1f x ax ,求a 的取值范围;(2)若()f x 为周期函数,证明:()f x 是常值函数;(3)设()f x 恒大于零,()g x 是定义在R 上、恒大于零的周期函数,M 是()g x 的最大值.函数()()()h x f x g x .证明:“()h x 是周期函数”的充要条件是“()f x 是常值函数”.2017年普通高等学校招生全国统一考试上海--数学试卷考生注意1.本场考试时间120分钟,试卷共4页,满分150分,答题纸共2页.2.作答前,在答题纸正面填写姓名、准考证号,反面填写姓名,将核对后的条形码贴在答题纸指定位置.3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域,不得错位.在试卷上作答一律不得分.4.用2B 铅笔作答选择题目,用黑色字迹钢笔、水笔或圆珠笔作答非选择题目.一、填空题目(本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分)考生应在答题纸的相应位置直接填写结果.1.已知集合1,2,3,4,3,4,5A B ,则A B ∩.【解析】本题考查集合的运算,交集,属于基础题【答案】3,42.若排列数6P 654m ,则m .【解析】本题考查排列的计算,属于基础题【答案】33.不等式11x x 的解集为.【解析】本题考查分式不等式的解法,属于基础题【答案】,0 4.已知球的体积为36 ,则该球主视图的面积等于.【解析】本题考查球的体积公式和三视图的概念,343633R R ,所以29S R ,属于基础题【答案】95.已知复数z 满足30z z,则z .【解析】本题考查复数的四则运算和复数的模,2303z z z设z a bi ,则22230,a b abi a b,z【答案】6.设双曲线 222109x y b b 的焦点为12F F 、,P为该双曲线上的一点.若15PF ,则2PF.【解析】本题考查双曲线的定义和性质,1226PF PF a (舍),2122611PF PF a PF 【答案】117.如图,以长方体1111ABCD A B C D 的顶点D 为坐标原点,过D 的三条棱所在的直线为坐标轴,建立空间直角坐标系.若1DB 的坐标为(4,3,2),则1AC的坐标是.【解析】本题考查空间向量,可得11(400)(03,2)(432)A C AC,,,,,,,属于基础题【答案】(432) ,,8.定义在(0,) 上的函数()y f x 的反函数-1()y f x .若31,0,()(),0x x g x f x x 为奇函数,则-1()=2f x 的解为.【解析】本题考查函数基本性质和互为反函数的两个函数之间的关系,属于中档题10,0,()31()()13x x x x g x g x g x,所以1()13x f x,当2x 时,8()9f x,所以18(29f【答案】9x9.已知四个函数:①y x ;②1y x;③3y x ;④12y x .从中任选2个,则事件“所选2个函数的图像有且仅有一个公共点”的概率为.【解析】本题考查事件的概率,幂函数的图像画法和特征,属于基础题总的情况有:42C 6种,符合题意的就两种:①和③,①和④【答案】1310.已知数列na 和 nb ,其中2,N na n n , nb 的项是互不相等的正整数.若对于任意N n n b ,中的第n a 项等于 n a 中的第n b 项,则149161234lg lg b b b b b b b b.【解析】本题考查数列概念的理解,对数的运算,属于中档题由题意可得:222222114293164(),,,n n a b n n b a b b b b b b b b b b ,所以214916123412341234lg lg =2lg lg b b b b b b b b b b b b b b b b 【答案】211.设12R ,,且121122sin 2sin(2) ,则1210 的最小值等于.【解析】考查三角函数的性质和值域,121111,1,12sin 32sin(2)3,,要使121122sin 2sin(2) ,则111122221=122sin 2,,1=12sin(2)4k k k Z k1212min min31010(2)44k k,当122=11k k 时成立【答案】412.如图,用35个单位正方形拼成一个矩形,点1234,,,P P P P 以及四个标记为“▲”的点在正方形的顶点处.设集合1234=,,,P P P P ,点P .过P 作直线P l ,使得不在P l 上的“▲”的点分布在P l 的两侧.用1()P D l 和2()P D l 分别表示P l 一侧和另一侧的“▲”的点到P l 的距离之和.若过P 的直线P l 中有且只有一条满足12()=()P P D l D l ,则 中所有这样的P 为.【解析】本题考查有向距离,以左下角的顶点为原点建立直角坐标系。
历年自主招生考试数学试题大全2018年上海复旦大学自主招生数学试题Word版

2018年复旦大学自主招生考试数学试题选择题(每题5分,共150分,答对得5分,答错扣2分,不答得0分) 1.三边均为整数,且最大边长为11的三角形,共有 个. A .20B .26C .30D .362.若a>1,b>1且lg (a+b )=lga+lgb ,则lg (a −1)+lg (b −1)= . A .lg2B .1C .不是与a 、b 无关的常数D .03.已知z ∈C ,若∣z ∣=2-4i ,则z1的值是 . A .3+4i B .i 5453+ C .i 154153+ D .i 254253-4.已知函数f (x )=cos (x k 2316++π)+cos (x k 2316--)=23sin (x 23+π),其中x 为实数且k 为整数.则f (x )的最小正周期为 .A .3πB .2π C .πD .2π5.已知A ={(x ,y )∣y ≥x 2},B={(x ,y )∣x 2+(y −a )2≤1}.则使A∩B=B 成立的充分必要条件为 .A .a=45B .a≥45 C .0<a<1 D .a≥16.已知平面上三角形ABC 为等边三角形且每边边长为a ,在AB 和BC 上分别取D ,E 两点使得AD =BE =3a,连接A ,E 两点以及C ,D 两点.则AE 和CD 之间的最小夹角为 . A .9πa B .3πa C .3π D .以上均不对7.已知数列{a n }满足3a n+1+a n =4,(n≥1),且a 1=9, 其前n 项之和为S n ,则满足不等式∣S n −n −6∣<1251的最小整数是45. A .6B .7C .8D .98.将一个四棱锥的每个顶点染上一种颜色,并使用一条棱的两端点异色,若只有五种颜色可供使用,则不同的染色方法的总数为 .A .120B .260C .340D .4209.设甲乙两个袋子中装有若干个均匀白球和红球,且甲乙两个袋子中的球数比为1∶3.已知从甲袋中摸到红球的概率为31,而将甲乙两个袋子中的球装在一起后,从中摸到红球的概率为32.则从乙袋中摸到红球率为 . A .97 B . 4519C .3013D .4522 10.方程f (x )=543423322212321---------x x x x x x x x x =0 的实根的个数是 .A .1个B . 2个C .3个D .无实根11.已知a ,b 为实数,满足(a+b )59=−1,(a −b )60=1,则∑=-601)(n n nb a= .A .0121B .−49C .0D .2312.a=21是“直线(a+2)x +3a y +1=0与直线(a −2)x +(a+2)y −3=0相互垂直”的 . A .充分必要条件B .充分而不必要条件C .必要而不充分条件D .既不充分也不必要条件13.设函数y =f (x )对一切实数x 均满足f (2+x )=f (2−x ),且方程f (x )=0恰好有7个不同的实根,则这7个不同实根的和为 .A .0B .10C .12D .1414.已知α,β,γ分别为某三角形中的三个内角且满足tan 2βα+=sinγ,则下列四个表达式:(1)tanαtanβ=1 (2)0<sinα+sinβ≤2 (3)sin 2α+sin 2β=1 (4)cos 2α+cos 2β=sin 2γ中,恒成立的是 .A .(1)(3)B .(10(4)C .(2)(3)D .(2)(4)15.设S n =1+2+…+n,n ∈N .则∞→n lim1)32(2++n nS n nS = .A .2B .321C .161 D .6416.复数z =iia 212+-(a ∈R ,i=1-)在复平面上对应的点不可能位于 . A .第一象限B .第二象限C .第三象限D .第四象限17.已知f (x )=asin x +b 3x +4(a ,b 为实数)且f [lg (lg 310)]=5,则f [lg (lg3)]= .A .−5B .−3C .3D .随a ,b 取不同值而取不同值18.已知四棱锥P -ABCD ,底面ABCD 是菱形,∠DAB =3π,PD ⊥平面ABCD ,线段PD =AD ,点E 是AB 的中点,点F 是PD 的中点,则二面角P -AB -F 的平面角的余弦值= .A .21 B .552 C .1475D .1473 19.在(32-)50的展开式中有 项为有理数.A .10B .11C .12D .1320.棱长为a 的正方体内有两球互相外切,且两球各与正方体的三个面相切.则两球半径之和为为 .A .无法确定B .aC .a 233-D .a 255- 21.在集合{1,2,…11}中任选两个作为椭圆方程12222=+by a x 中的a 和b ,则能组成落在矩形区域{(x ,y )||x |<11,|y |<9}内的椭圆个数是 .A .70B .72C .80D .8822.设a ,b ,c 为非负实数,且满足方程02562684495495=+⨯-++++cb a cb a ,则a+b+c的最大值和最小值 .A .互为倒数B .其和为13C .其乘积为4D .均不存在23.给定正整数n 和正常数a ,对于满足不等式a 12+a n+12≤a 的所有等差数列a 1,a 2,a 3,…,和式∑++=1211n n i a的最大值= .A .)1(210+n aB .n a210 C .)1(25+n aD .n a 2524.设z 0(z 0≠0)为复平面上一定点,z 1为复平面上的动点,其轨迹方程为|z 1−z 0|=|z 1|,z 为复平面上另一个动点满足z 1z =−1.则z 在复平面上的轨迹形状是 .A .一条直线B .以01z -为圆心,01z 为半径的圆 C .焦距为012z 的双曲线 D .以上均不对25.一个球与正四面体的六条棱都相切,若正四面体的棱长为a ,则这个球的体积为 .A .3123a π B .343a π C .3242a π D .3243a π 26.已知函数f (x )的定义域为(0,2),则函数g (x )=f (x +c )+f (x −c ) 在 0<21时的定义域为 .A .(1−c ,2+c )B .(c ,2−c )C .(1−c ,2−c )D .(c ,2+c ) 27.设函数f (x )=sin (2x +ϕ),(−π<ϕ<0),y =f (x )图象的一条直线x =8π.则ϕ的值为 .A .4πB .43πC .-43πD .2π28.设f (x )是定义在实数集上的周期为2的周期函数,且是偶函数.已知当x ∈[2,3]时,f (x )=−x ,则当x ∈[-2,0]时,f (x )的表达式为 .A .−3+|x +1|B .2−|x +1|C .3−|x +1|D .2+|x +1|29.当a 和b 取遍所有实数时,则函数f (a ,b )=(a+5−3|cosb|)2+(a −2)|sinb|)2所能达到的最小值为 .A .1B .2C .3D .430.对任意实数x ,y ,定义运算x ºy 为x ºy =a x +b y +c xy ,其中a ,b ,c 为常数,且等式右端中的运算为通常的实数加法、乘法运算.已知1º2=3,2º3=4且有一个非零实数d ,使得对于任意实数x 均有x ºd=x ,则d= .A .-4B .-2C .1D .4历年自主招生考试数学试题大全专题下载链接:/a760682.html链接打开方法:1、按住ctrl键单击链接即可打开专题链接2、复制链接到网页。
复旦大学自主招生考试数学试题及答案
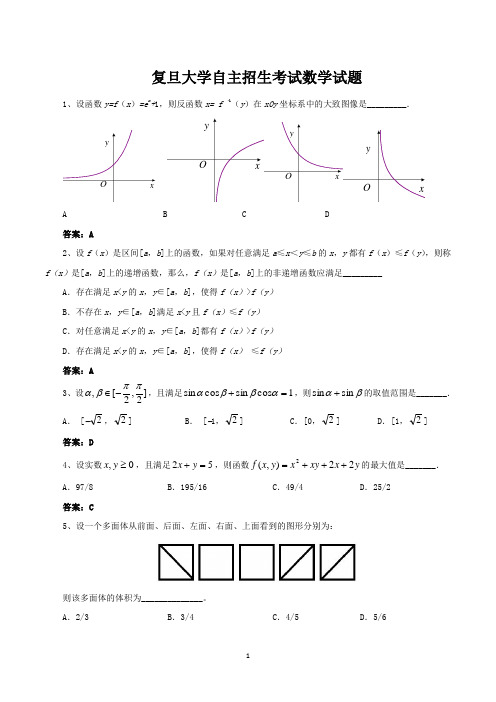
1、设函数y=f(x)=e x+1,则反函数OyxOyxO x答案:A2、设f(x)是区间[a,b]f(x)是[a,b]上的递增函数,那么,f(xA.存在满足x<y的x,y∈[a,b]B.不存在x,y∈[a,b]满足x<y且fC.对任意满足x<y的x,y∈[a,b]D.存在满足x<y的x,y∈[a,b]答案:A3、设]2,2[,ππβα-∈,且满足sinαA. [−2,2] B. [答案:D4、设实数0,≥yx,且满足2=+yxA.97/8 B.答案:C5则该多面体的体积为______________。
A.2/3 B.3/4答案:D6、在一个底面半径为1/2,高为1的圆柱内放入一个直径为1的实心球后,在圆柱内空余的地方放入和实心球、侧面以及两个底面之一都相切的小球,最多可以放入这样的小球个数是___________。
A .32个;B .30个;C .28个;D .26个答案:B7、给定平面向量(1,1),那么,平面向量(231-,231+)是将向量(1,1)经过________. A .顺时针旋转60°所得; B .顺时针旋转120°所得; C .逆时针旋转60°所得;D .逆时针旋转120°所得;答案:C8、在直角坐标系O xy 中已知点A 1(1,0),A 2(1/2,3/2),A 4(−1,0),A 5(−1/2,−3/2)和A6(1/2, −3/2).问在向量−−→−ji A A (i ,j=1,2,3,4,5,6,i≠j)中,不同向量的个数有_____. A .9个; B .15个; C .18个; D .30个答案:C9、对函数f:[0,1]→[0,1],定义f 1(x )=f (x ),……,f n(x ) =f (f n −1(x )),n=1,2,3,…….满足f n (x )=x 的点x ∈[0,1]称为f 的一个n −周期点.现设⎪⎪⎩⎪⎪⎨⎧≤≤-≤≤=121,22,210,2)(x x x x x f 问f 的n −周期点的个数是___________.A .2n 个;B .2n 2个;C .2n个;D .2(2n−1)个.答案:C10、已知复数z 1=1+3i ,z 2=−3+3i ,则复数z 1z 2的幅角__________. A .13π/12 B .11π/12 C .−π/4 D .−7π/12答案:A11、设复数βαβαcos sin ,sin cos i w i z +=+=满足z w =3/2,则sin (β−α)=______. A .±3/2B .3/2,−1/2C .±1/2D .1/2,−3/2答案:D12、已知常数k 1,k 2满足0<k 1<k 2,k 1k 2=1.设C 1和C 2分别是以y =±k 1(x −1)+1和y =±k 2(x −1)+1为渐近线且通过原点的双曲线.则C 1和C 2的离心率之比e 1/e 等于_______.A .222111k k ++ B .212211k k ++ C .1 D .k 1/k 2答案:C13、参数方程0,)cos 1()sin (>⎩⎨⎧-=-=a t a y t t a x 所表示的函数y=f (x )是____________.A .图像关于原点对称;B .图像关于直线x =π对称;C .周期为2a π的周期函数D .周期为2π的周期函数.答案:C14、将同时满足不等式x −k y −2≤0,2x +3y −6≥0,x +6y −10≤0 (k>0)的点(x ,y )组成集合D 称为可行域,将函数(y +1)/x 称为目标函数,所谓规划问题就是求解可行域中的点(x ,y )使目标函数达到在可行域上的最小值.如果这个规划问题有无穷多个解(x ,y ),则k 的取值为_____.A .k≥1;B .k≤2C .k=2D .k=1.答案:C15、某校有一个班级,设变量x 是该班同学的姓名,变量y 是该班同学的学号,变量z 是该班同学的身高,变量w 是该班同学某一门课程的考试成绩.则下列选项中正确的是________.A .y 是x 的函数;B .z 是y 的函数;C .w 是z 的函数;D .w 是x 的函数.答案:B16、对于原命题“单调函数不是周期函数”,下列陈述正确的是________. A .逆命题为“周期函数不是单调函数”; B .否命题为“单调函数是周期函数”; C .逆否命题为“周期函数是单调函数”; D .以上三者都不正确 答案:D17、设集合A={(x ,y )|log a x +log a y >0},B={(x ,y )|y +x <a}.如果A∩B=∅,则a 的取值范围是_______ A .∅ B .a>0,a≠1 C .0<a≤2, a≠1 D .1<a≤2答案:D18、设计和X 是实数集R 的子集,如果点x 0∈R 满足:对任意a>0,都存在x ∈X 使得0<|x −x 0|<a ,则称x 0为集合X 的聚点.用Z 表示整数集,则在下列集合(1){n/(n+1)|n ∈Z , n≥0}, (2) R\{0}, (3){1/n|n ∈Z , n≠0}, (4)整数集Z 中,以0为聚点的集合有_____. A .(2),(3)B .(1),(4)C .(1),(3)D .(1),(2),(4)答案:A19、已知点A (−2,0),B (1,0),C (0,1),如果直线kx y =将三角形△ABC 分割为两个部分,则当k =______时,这两个部分得面积之积最大?A .23-B .43-C .34-D .32-答案:A20、已知x x x x f 2cos 3cos sin )(+=,定义域⎥⎦⎤⎢⎣⎡=ππ127,121)(f D ,则=-)(1x f_____A .π12123arccos 21+⎪⎪⎭⎫ ⎝⎛-x B .π6123arccos 21-⎪⎪⎭⎫ ⎝⎛-x C .π12123arcsin 21+⎪⎪⎭⎫ ⎝⎛--x D .π6123arcsin 21-⎪⎪⎭⎫ ⎝⎛-x 答案:A21、设1l ,2l 是两条异面直线,则直线l 和1l ,2l 都垂直的必要不充分条件是______ A .l 是过点11l P ∈和点22l P ∈的直线,这里21P P 等于直线1l 和2l 间的距离 B .l 上的每一点到1l 和2l 的距离都相等 C .垂直于l 的平面平行于1l 和2lD .存在与1l 和2l 都相交的直线与l 平行 答案:D22、设ABC −A’B’C’是正三棱柱,底面边长和高都为1,P 是侧面ABB’A’的中心,则P 到侧面ACC’A’的对角线的距离是_____A .21B .43C .814D .823答案:C23、在一个球面上画一组三个互不相交的圆,成为球面上的一个三圆组.如果可以在球面上通过移动和缩放将一个三圆组移动到另外一个三圆组,并且在移动过程中三个圆保持互不相交,则称这两个三圆组有相同的位置关系,否则就称有不同的位置关系.那么,球面上具有不同的位置关系的三圆组有______A .2种B .3种C .4种D .5种 答案:A24、设非零向量()()()321321321,,,,,,,,c c c c b b b b a a a a ===为共面向量,),,(31x x x x x = 是未知向量,则满足0,0,0=⋅=⋅=⋅x c x b x a的向量x 的个数为_____A .1个B .无穷多个C .0个D .不能确定 答案:B25、在Oxy 坐标平面上给定点)1,2(),3,2(),2,1(C B A ,矩阵⎪⎪⎭⎫⎝⎛-112k 将向量OC OB OA ,,分别变换成向量,,,如果它们的终点',','C B A 连线构成直角三角形,斜边为''C B ,则k 的取值为______A .2±B .2C .0D .0,−2 答案:B26、设集合A ,B ,C ,D 是全集X 的子集,A∩B≠∅,A∩C≠∅.则下列选项中正确的是______. A .如果B D ⊂或C D ⊂,则D∩A≠∅; B .如果A D ⊂,则C x D∩B≠∅,C x D∩C≠∅; C .如果A D ⊃,则C x D∩B=∅,C x D∩C=∅; D .上述各项都不正确.27、已知数列{}n a 满足21=a 且n a n ⎧⎫⎨⎬⎩⎭是公比为2的等比数列,则∑==nk k a 1______A .221-+n nB .22)1(1+-+n n C .)1(22-+n n n D .n n n 22)1(+-28、复平面上圆周2211=+--iz z 的圆心是_______ A .3+i B .3−iC .1+iD .1−i29.已知C 是以O 为圆心、r 为半径的圆周,两点P 、P *在以O 为起点的射线上,且满足|OP|∙|OP *|=r 2,则称P 、P *关于圆周C 对称.那么,双曲线22x y -=1上的点P (x ,y )关于单位圆周C':x 2+y 2=1的对称点P *所满足的方程是(A )2244x y x y -=+(B )()22222x y x y-=+(C )()22442x y x y-=+(D )()222222x y x y-=+30、经过坐标变换⎩⎨⎧+-=+=θθθθcos sin 'sin cos 'y x y y x x 将二次曲线06532322=-+-y xy x 转化为形如1''2222=±b y a x 的标准方程,求θ的取值并判断二次曲线的类型_______ A .)(6Z k k ∈+=ππθ,为椭圆 B .)(62Z k k ∈+=ππθ,为椭圆C .)(6Z k k ∈-=ππθ,为双曲线D .)(62Z k k ∈-=ππθ,为双曲线31、设k , m , n 是整数,不定方程mx+ny=k 有整数解的必要条件是____________ A .m ,n 都整除kB .m ,n 的最大公因子整除kC .m ,n ,k 两两互素D .m ,n ,k 除1外没有其它共因子。
历年上海复旦大学自主招生试题汇总

⽆忧考为⼤家整理的历年上海复旦⼤学⾃主招⽣试题汇总,供⼤家参考。
2012年复旦⼤学⾃主招⽣千分考试题 据复旦招办预计,2012年通过千分考进⼊⾃主招⽣⾯试的学⽣⽐例将与2011年基本持平,成绩和⾯试⽅案将于⼀周内公布。
以下是中国教育在线为您整理的2012年复旦“千分考”部分考题。
选摘考题如下: 1.冷战以后,我国规模的⼀次撤侨是从哪个国家撤离的? 2.中国的13个船员是在哪条河遇难的? 3.在欧债危机中,有哪些国家的政权发⽣了更迭? 4.请从东到西排出“iPhone4S”第⼀批上市的⼏个国家。
5.“《社戏》、《藤野先⽣》、《从百草园到三味书屋》等是否都出⾃《朝花⼣拾》? 6.按照时间顺序排列鲁迅的四⼤名著《药》、《狂⼈⽇记》、《阿Q正传》、《祝福》。
7."五⽉渡泸,深⼊不⽑"出⾃哪⾥?” 8.清朝哪位⽂⼈将⽂体分为阴柔派和阳刚派? 9.以下哪个地⽅对柑橘的⽣长危险因素? 10.中国的四个卫星发射中⼼哪个耗能? 11.上海出租车在3公⾥以内收费14元,超过3公⾥10公⾥以内,是每公⾥2.4元,请计算要付的钱和公⾥数的函数关系。
12.伊丽莎⽩⼥王的权⼒受限是因为哪个法案? 13.根据⽔稻育种、播种的时间,请判断这是什么地区? 14.根据某地茶叶上市的时节来判断当地⽓候。
15.⼀个磁铁矿完全变成氯化铁矿,会有多少四氧化三铁的含量? 16.1M字节等于多少K字节? 17.如果⾦属钠失⽕,要⽤什么来扑灭? 18.中国有4个卫星发射中⼼,哪个发射中⼼的能耗? 19.把⼗元钱换成1元、5⾓、1⾓零钱,有⼏种不同的组合⽅法? 20.⼆进制1101011转化成⼗进制是多少? 21. 1M字节等于多少K字节?2011年复旦⼤学千分考试题选摘: 辨别莎⼠⽐亚作品台词; ⼼绞痛可以⽤何种药物治疗; 列举陀思妥耶夫斯基的代表作; 朝韩炮击事件是在哪⾥发⽣的; 去年联合国⽓候⼤会在哪⾥举⾏; 世界杯半决赛对阵的是哪四⽀球队; 《达·芬奇密码》是什么类型的⼩说; 《六书》中哪些是造字⽅法、哪些是⽤字⽅法; 辨别“⼲涸、征伐、蜡烛、多余”等繁体字正误; 说是⼀辆辆车⼦进站出站,考汽车进出站的顺序; 给出了⾜球世界杯中对阵的⼏组国家的名字,问哪组国家⽂化背景相似; 世博园中⼀位游客的⼿表显⽰6点,当时北京时间是7点,这位游客来⾃哪个时区2010年复旦⼤学⾃主招⽣试题 复旦⼤学⾃主招⽣笔试全是选择题,考查内容囊括语⽂、数学、外语、物理、化学、⽣物、政治、历史、地理和计算机⼗门学科。
9大高校自主招生考试真题汇总(2017年)

9大高校自主招生考试真题汇总(2017年)二、清华大学清华大学2017年自主招生测试主要分为笔试和面试,笔试依然采用机考的模式来进行据悉,2017年清华笔试在全国44个城市设有61考点,相比去年增加25个考点其中,每个城市还设有多个考点。
1、笔试题型理科:数学30题,物理20题,化学18题,一共68题,180分钟合在一起考的。
题。
2、笔试真题文科综合(文史)类笔试试题:考题有明清时的自然经济解、抗日战争、诗词等内容,不是考知识点记忆,主要考查阅读面、逻辑思维深度等,数学与逻辑难度较大。
今年的语文试题对语文基础知识与运用能力提出了更高要求,材料多出自社会热点或经典著作,注重对知识联系实际、学以致用能力的考查注重考查对经典或常识的精准理解,注重对独立思考与批判思维的考查化学试题成为新考查内容今年化学成为新考查内容。
刘震表示,新增化学试题注重对学科基础内容的考查综合多模块内容、加强化学学科的应用性、创新试题的设问模式,充分体现化学学科的学术价值,考查了考生的基础知识、综合能力、科学素养和创新精神,关注环境问题,讨论产生酸雨的原因及危害、食品中的增塑剂与人体健康等社会焦点问题。
物理试题注重基本概念的准确理解和灵活运用。
通过采用单选和多选题随机编排的方式,来考查学生构建正确、合理的物理模型,综合运用物理知识分析、解决实际问题的能力,同时増加了能力考查的区分度。
除了定量的分析和计算外,试题还设置了部分内容来考查学生运用物理学基本原理来定性和半定量分析题的能力3、面试模式复试中,领军人才选拔及自强计划考生需参加综合面试,自主招生考生及部分领军人オ选拔考生需参加学科专业面试。
清华大学2017年自主招生考核的特色有1.综合面试新增材料阋读环节综合面试在清华自主选中已开展多年,今年这一考察方式有了新变化新增了材料阅读环节。
考生在进入考场接受半结构化面试之前,在候场教室里将会得到一份阅读材料,经过半小时备考后进入考场、接受提问。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年复旦大学自主招生考试
数学试题
一、填空题(每题8分,共80分)
1.设842421(21)(1)x x x x ax +=+++,则a = .
2.已知|5x +3|+|5x −4|=7,则x 的取值范围是 .
3.椭圆22
1169
x y +=内接矩形的周长最大值是 . 4.12只手套(左右有区别)形成6双不同的搭配,要从中取出6只正好能形成2双,有 种取法.
5.已知等比数列{}n a 中a 1=3,且第l 项至第8项的几何平均数为9,则第3项为 . 6.若2
(1)0x a x a -++<的所有整数解之和为27,则实数a 的取值范围是 . 7.己知22
(4)149
x y -+=,则2249x y +的最大值为 . 8.设x 1、x 2是方程2x −x sin 35π+cos 35π=0的两个实数解,那么arctan x 1+
arctan x 2= .
9.方程3z z =的非零解是 .
10.方程112x
x y -+=的值域是 .
二、解答题(每题15分,共120分)
1.解方程:5log (3)1x x -=.
2.已知12sin(),13αβ+=
4sin(),5αβ-=-且0,0,,2παβαβ>>+<求tan 2α.
3.已知过两抛物线C 1:x +1=(y −1)2,及C 2: (y −1)2=−4x −a +11的一个交点的两条切线互相垂直,求a 的值.
4.若存在M ,使任意x ∈D (D 为函数f (x )的定义域),都有|f (x )|≤M.则称函数f (x )有界,函数f (x )=
11sin x x 在10,2x ⎛⎫∈ ⎪⎝⎭上是否有界?
5.求证:
3113n ++<.
6.已知E 是棱长为a 的正方体1111ABCD A B C D -的棱A B 的中点,求点B 到平面1A EC 的距离.
7.比较24log 25与25log 26的大小,并说明理由.
8.已知数列{}{},n n a b 满足12,n n n a a b +=--且166n n n b a b +=+,又12a =,14b =, 求:(1) ,,n n a b ;(2)1im lim n n n
a b →∞.。
