统计学第九章 时间序列分析课后答案
第九章+++时间数列分析与预测参考答案

第九章 时间数列分析与预测一、填空题9.1.1 时间数列一般由两个基本要素构成:一是现象所属的 时间 ,二是反映客观现象的 观察值 。
9.1.2 时间数列按其观察值具体表现形式不同可分为三种:绝对数时间数列、 相对数时间数列和 平均数时间 数列。
9.1.3 同一时间数列中,各期环比发展速度的连乘积等于相应的 定基发展速度 。
9.1.4 绝对数时间数列中, 时期 数列中,各期的指标值直接相加有意义。
9.1.5 某公司2007年的利额比2003年增长25%,2006年比2003年增长20%,则2007年比2006年增长 4.17% ,2004年至2007年平均每年增长 5.74% 。
9.1.6 某地2006年1季度的GDP 为100亿元,2006年3季度的GDP 为115亿元,则其年度化增长率为 32.25% 。
9.1.7 计算平均发展速度有两种方法,即 几何平均法 和 高次方程法 ,它们的数理依据、侧重点、计算方法和应用场合都不相同。
9.1.8 影响时间序列的因素主要有四种,它们是 长期趋势 、 季节变动 、 循环变动 和 不规则变动 。
9.1.9 时间数列变动的趋势有直线趋势和曲线趋势。
在建立模型之前,先要确定现象变动的形态。
判定趋势变动形态的方法常用的有两种,即 画散点图的方法 和 指标判别法 。
9.1.10 若时间数列的 逐期增减量 大致相等,则该现象的发展趋势近似于一条直线,可拟合一条直线趋势方程。
9.1.11 如果时间数列中各期二次逐期增减量大致相等,则应拟合 二次曲线 方程;如果各期环比发展速度大致相等,则应拟合 指数曲线 方程。
9.1.12 某些社会经济现象,随着季节的更换或社会因素的影响而引起的在年度内比较有规律性的变动称 季节变动 ,测定它的变动常用且最简便的方法是 同期平均法 。
9.1.13 客观社会经济现象在一个相当长的时间内,受某些基本因素的影响所呈现的一种基本发展趋势称 长期趋势 。
《统计学》第9章课后习题参考答案

第9章习题参考答案
9.1
解:(1)长度Y(厘米)与重量X(克)之间的散点图如下所示:
由Y与X的散点图可以大致推测长度Y关于重量X是线性相关,且二者呈正相关关系。
(2)首先,先分别求出平均重量和平均长度:
;;
其次,计算回归参数,其计算表如下:
表1:回归方程参数的计算表
(X-(Y-
最后,根据公式(9.6)计算相应的回归参数:
;
所以,Y关于X的一元线性回归方程为:
9.5
解:总变差,回归平方和,残差平方和的计算如下:
表2:总变差,回归平方和,残差平方和的计算表
∴残差平方和:;
回归平方和:
9.6
解:由表2得:
判定系数
又∵习题9.1的散点图显示Y与X是呈正相关关系
∴相关系数
显著性检验:
(1)回归方程的显著性检验:
原假设H0:该回归方程不显著;备择假设H1:该回归方程显著
计算F统计量:
∵在α=0.05的显著性水平下,有4454.79>F0.05(1,4)=7.71
∴拒绝原假设,认为该回归方程式显著的。
(2)回归参数的假设检验:
原假设H0:备择假设H1:
计算t统计量:;
[其中] ∵在α=0.05的显著性水平下,有15.98>t0.05(4)=2.776
∴拒绝原假设,即认为自变量X对因变量Y有显著性影响。
(3)相关关系的显著性检验:
原假设H0:ρ=0;备择假设H1:ρ
计算t统计量:;
∵在α=0.05的显著性水平下,有66.64> t0.05(4)=2.776
∴拒绝原假设,认为总体相关系数不为0。
第9章 习题参考答案

第九章静态时间序列模型课后习题参考答案1.遍历性、平稳性对时间序列回归有何意义?答:静态时间序列模型研究的是不同随机变量的时间序列之间体现出的静态(同期)结构关系,也称为结构型时间序列模型。
由第七章“时间序列回归的基本问题”可知,对于时间序列回归,如果假定TS.1-假定TS.6均成立,OLSE具有无偏性、有效性和正态性,不必考虑时间序列是否具有遍历性与平稳性问题。
然而,如果这些假定不完全满足,例如解释变量x仅为同期外生,为了保证OLSE具有良好的大样本性质(一致性),我们要求时间序列产生自遍历、平稳过程,即假定TS.4’。
常用统计推断方法的适用性对该假定是否成立非常敏感,当高度持久时间序列或非平稳序列用于回归时,我们无法借助于大数定律和中心极限定理进行统计推断,所以遍历性、平稳性对时间序列回归至关重要。
大多数情况下,时间序列建模之前,都须对时间序列的遍历、平稳性质进行研判,否则很可能造成回归方法的误用,产生伪回归问题,进而得出误导性的结论。
所以,应该重点关注非平稳遍历时间序列条件下建模特殊性问题。
本章讨论的静态时间序列建模过程中,就可能存在解释变量只是同期外生,这时时间序列的特殊性将x y都是产生自平稳、遍历过程,在大样本下OLSE仍然是一致的、给回归分析带来一些问题。
但如果,jt t渐进有效和渐进正态的,因此也可以按照经典回归分析的方法进行参数估计和统计推断。
对于非平稳、遍历时间序列,进行OLS回归之前需要通过去势(消除确定性趋势)和差分(消除随机趋势)等方法进行平稳化(遍历化)处理。
2.DF、ADF和PP检验分布适用于什么情况下的单位根检验?如何确定检验模型?答:由于真实DGP是未知的,我们可以通过一个时间序列(相当于一个样本)的特征,对DGP是否存在单位根进行推测,这个方法称为单位根检验(Unit Root)。
本章介绍三种常用的方法。
(1)Dickey-Fuller 检验(DF检验)Dickey和Fuller通过数值模拟,计算了对应不同DGP和序列长度T的DF分布百分位数,并编制了DF临界值表。
统计学第九章课后习题答案

9.1(1)设原假设为H:不同收入群体对某种特定商品的购买习惯相同:即不同收入群体对某种特定商品的购买习惯不完全相同H1(2)由SPSS计算可得χ2值为17.626(3)自由度=(3-1)×(4-1)=6,当α=0.1时,χ0.12(6)=10.64∵χ2=17.626>10.64=χ0.12(6)故拒绝原假设,即不同收入群体对某种特定商品的购买习惯不完全相同。
(4)由SPSS计算可得φ系数为0.183、c系数为0.180、V系数为0.1299.2解:设原假设为H0:现在情况与经验数据相比没有发生变化;H1:现在情况与经验数据相比发生了变化。
由已知条件可得χ2值为:χ2=(28−0.1×200)20.1×200+(56−0.2×200)20.2×200+(48−0.3×200)20.3×200+(36−0.2×200)20.2×200+(32−0.2×200)20.2×200=14P[χ2(5−1)>14]=0.007295<0.1=α,故拒绝原假设。
9.3设原假设为H0:π1=π2=π3=π4(即阅读习惯与文化程度无关)H1:π1,π2,π3,π4不完全相等(即阅读习惯与文化程度有关)表中各项的期望值:E11=n1×n1n=77×50254=15.16E12=n2×n1n=91×50254=17.91E13=n3×n1n=42×50254=8.27E14=n4×n1n=44×50254=8.66E21=n1×n2n=77×44254=13.34E22=n2×n2n=91×44254=15.76E23=n3×n2n=42×44254=7.28E24=n4×n2n=44×44254=7.62E31=n1×n3n=77×95254=28.80E32=n2×n3n=91×95254=34.04E33=n3×n3n=42×95254=15.71E34=n4×n3n=44×95254=16.46E41=n1×n4n=77×65254=19.70E42=n2×n4n=91×65254=23.29E43=n3×n4n=42×65254=10.75E44=n4×n4n=44×65254=11.26所以χ2=(6-15.16)2/15.16+(12-13.34)2/13.34+……+(13-11.26)2/11.26=31.86。
统计学第九章时间序列分析课后答案

第九章时间序列分析1、时间序列指标数值3、简单a -n- 间断 连续 间隔相等间隔不等 4、逐期累计报告期水平崔期水平逐期累计5、环比 定基报告期水平 - 环比 定基 环比基期水平6、水平法 累计法水平X “丨【X 或 X =n佟累计.a 。
23n 一aX X X Xa 。
7、 26 268、72、总量指标时间数列总量指标时间数列相对指标时间数列 平均指标时间数列9、y (y — ?) = 0(y — ?)2 为最小五、简答题(略) 六、计算题第一季度平均人数258 24 264 10 275 30 270 17 272 9,=268.1 (人)24 10 30 17 9第一季度平均库存额同理,第二季度平均库存额4-1上半年平均库存额a 2 +a 3 • 2 3f2 ■■2f1 + f2 + …+ fn4326 330330 335412 408 ,1 2 12 2 2 1::;,2 亠-亠 14620”、==385 (箱)1210、季节比率1200%400%1、 4月份平均库存320 5 250 12 370 8 300 5= 302 (辆)302、 3、 a 1-a2 ■■■ 2 a 二 n —1型 408 405 43424-12= 410 (万元)434426 438 聖82乙=430(万元)400 2408 405 434 426 438 418—=420 (万元)4、年平均增加的人数55、某酿酒厂成品库1998年的平均库存量7 -1410 430 “一、=420 (万兀)21656 1793 1726 1678 1629 十.= =1696.4 (万a 1 a 2a=^- a n J an2该柴油机厂全年的平均计划完成程度指标为25602496 2356 2= 77.2% 32003200 3100 - 2②第一季度平均职工人数 =265 265 275 = 268. 33 (人)3③ 第一季度工业总产值 =27.825 + 26.500 + 29.150 = 83.475 (万元) 第一季度平均每月工业总产值 =83.475 =27.825 (万元)3④第一季度劳动生产率 =834750 =3110.91 (元/人)268.333110 91第一季度平均月劳动生产率 = -------- =1036.97 (元/人)268.33 或=278250 =1036.97 (元 /人)268.3347747.4 34600.0=138.0%2250 2 3000 2(%) 定基 一 0.32 7.42 15.32 27.26 40.65第①、②与③的要求,计算结果直接在表中;2 52④平均增长量=竺 =0.504 (万吨)5⑤水平法计算的平均发展速度 =5 8.72 =5 1.4065 = 107.06%\6.20平均增长速度=107.06% -100%=7.06%10、以1991年为基期的总平均发展速度为63 2V 1.03 X1.05 X1.06= 104.16%11、每年应递增:5 2.35 =118.64%平均增长量为:- (万台)平均发展速度为:6 3.6556= 124.12% 平均增长速度为:124.12%-1= 24.12%按8 %的速度递增,约经过 11.9年该市的国民收入额可达到 200亿元。
《统计分析和SPSS的应用(第五版)》课后练习答案与解析(第9章)
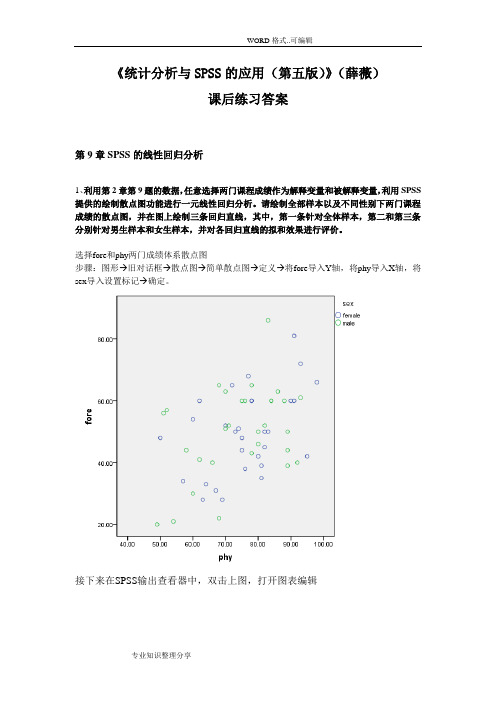
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第9章SPSS的线性回归分析1、利用第2章第9题的数据,任意选择两门课程成绩作为解释变量和被解释变量,利用SPSS 提供的绘制散点图功能进行一元线性回归分析。
请绘制全部样本以及不同性别下两门课程成绩的散点图,并在图上绘制三条回归直线,其中,第一条针对全体样本,第二和第三条分别针对男生样本和女生样本,并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩体系散点图步骤:图形→旧对话框→散点图→简单散点图→定义→将fore导入Y轴,将phy导入X轴,将sex导入设置标记→确定。
接下来在SPSS输出查看器中,双击上图,打开图表编辑在图表编辑器中,选择“元素”菜单→选择总计拟合线→选择线性→应用→再选择元素菜单→点击子组拟合线→选择线性→应用。
分析:如上图所示,通过散点图,被解释变量y(即:fore)与解释变量phy有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的?相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义。
如果在没有对变量之间是否相关以及相关方向和程度做出正确判断之前,就进行回归分析,很容易造成“虚假回归”。
与此同时,相关分析只研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况,因此,在具体应用过程中,只有把相关分析和回归分析结合起来,才能达到研究和分析的目的。
线性回归分析是相关性回归分析的一种,研究的是一个变量的增加或减少会不会引起另一个变量的增加或减少。
3、请说明为什么需要对线性回归方程进行统计检验?一般需要对哪些方面进行检验?检验其可信程度并找出哪些变量的影响显著、哪些不显著。
统计学习题答案 第9章 时间序列分析

第9章 时间序列分析——练习题●1. 某汽车制造厂2003年产量为30万辆。
(1)若规定2004—2006年年递增率不低于6%,其后年递增率不低于5%,2008年该厂汽车产量将达到多少?(2)若规定2013年汽车产量在2003年的基础上翻一番,而2004年的增长速度可望达到7.8%,问以后9年应以怎样的速度增长才能达到预定目标?(3)若规定2013年汽车产量在2003年的基础上翻一番,并要求每年保持7.4%的增长速度,问能提前多少时间达到预定目标?解:设i 年的环比发展水平为x i ,则由已知得:x 2003=30, (1)又知:320042005200620032004200516%x x x x x x ≥+(),2200720082006200715%x x x x ≥+(),求x 2008由上得32200820072008200320032007(16%)(15%)x x x x x x =≥++ 即为3220081.061.0530x ≥,从而2008年该厂汽车产量将达到 得 x 2008≥30× 31.06×21.05= 30×1.3131 = 39.393(万辆) 从而按假定计算,2008年该厂汽车产量将达到39.393万辆以上。
(2)规定201320032x x =,20042003x x =1+7.8%由上得=107.11%==可知,2004年以后9年应以7.11%的速度增长,才能达到2013年汽车产量在2003年的基础上翻一番的目标。
(3)设:按每年7.4%的增长速度n 年可翻一番, 则有 201320031.0742na a == 所以 1.074log 20.30103log 29.70939log1.0740.031004n ====(年)可知,按每年保持7.4%的增长速度,约9.71年汽车产量可达到在2003年基础上翻一番的预定目标。
原规定翻一番的时间从2003年到2013年为10年,故按每年保持7.4%的增长速度,能提前0.29年即3个月另14天达到翻一番的预定目标。
统计学:时间序列分析习题与答案

一、单选题1、根据季度数据测定季节比率时,各季节比率之和为()。
A.100%B.0C.400%D.1200%正确答案:C2、增长1%水平值的表达式是()。
A.报告期增长量/增长速度B.报告期发展水平/100C.基期发展水平/100D.基期发展水平/1%正确答案:C3、若报告期水平是基期水平的8倍,则我们称之为()。
A.翻了 3番B.翻了 8番C.发展速度为700%D.增长速度为800%正确答案:A4、若时间数列呈现出长时间围绕水平线的周期变化,这种现象属于()。
A.无长期趋势、有循环变动B.有长期趋势、有循环变动C.无长期趋势、无循环变动D.有长期趋势、无循环变动正确答案:B5、银行年末存款余额时间数列属于()。
A.平均指标数列B.时点数列C.时期数列D.相对指标数列正确答案:B6、某一时间数列,当时间变量t=1,2,3,...,n时,得到趋势方程为y=38+72t,那么,取t=0,2,4,6,8,...时,方程中的b将为()。
A.36B.34C.110D.144正确答案:A7、某企业2018年的产值比2014年增长了 200%,则年平均增长速度为()。
A.50%B.13.89%C.29.73%D.31.61%正确答案:D8、2010年某市年末人口为120万人,2020年年末达到153万人,则年平均增长量为()万人。
A. 3B.33C. 3.3D.30正确答案:C9、在测定长期趋势时,如果时间数列逐期增长量大体相等,则宜拟合()。
A.抛物线模型B.直线模型C.曲线模型D.指数曲线模型正确答案:B10、在测定长期趋势时,当时间数列的逐期增长速度基本不变时,宜拟合()。
A.逻辑曲线模型B.二次曲线模型C.直线模型D.指数曲线模型正确答案:D二、多选题1、编制时间数列的原则有()。
A.经济内容的一致性B.计算方法的一致性C.时间的一致性D.总体范围的一致性正确答案:A、B、C、D2、以下表述正确的有()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 时间序列分析一、单项选择题 1 2 3 4 5 6 7 8 9 10 B C A D A C D D C D 11 12 13 14 15 16 17 18 19 20 CACABBBDBB二、多项选择题1 2 3 4 5 BCDE ABC ABCD ABD ABCDE 6 7 8 9 10 ABCDE ABCDE ACE ABCE CE 11 12 13 14 15 ABCD BCDE ABCE ABCDE BCDE 16 17 18 19 20 BCD ABCDEBEABCDEBDE三、判断题 1 2 3 4 5 6 7 8 9 10 ××√××√√××√四、填空题1、时间序列 指标数值2、总量指标时间数列 相对指标时间数列 平均指标时间数列 总量指标时间数列3、简单 na a ∑=间断 连续 间隔相等 间隔不等4、逐期 累计 报告期水平–基期水平 逐期 累计5、环比 定基基期水平报告期水平环比 定基 环比6、水平法 累计法 水平 nx x ∏=或nna a x 0= 累计 032a a xx x x n∑=++++ 7、26 26 8、79、)-(y y ˆ∑= 0 )-(y y ˆ∑ 2为最小 10、季节比率 1200% 400% 五、简答题(略) 六、计算题1、4月份平均库存 = 3053008370122505320⨯+⨯+⨯+⨯= 302(辆)2、第一季度平均人数917301024927217270302751026424258++++⨯+⨯+⨯+⨯+⨯=268.1(人)3、第一季度平均库存额142434405408240012221-+++=-+++=n a a a a n = 410(万元) 同理,第二季度平均库存额1424184384262434-+++= 430(万元)上半年平均库存额1724184384264344054082400-++++++= 420(万元)或 2430410+= 420(万元)4、年平均增加的人数 =516291678172617931656++++= 1696.4(万人)5、某酿酒厂成品库1998年的平均库存量12111232121222---+++++++++=n n n n f f f f a a f a a f a a a=121124084122233533012330326+++⨯+++⨯++⨯+=124620= 385(箱)6、列计算表如下:季 度 一 二 三 四 合 计 计 划 产 值(万元) b 计划完成程度(%)c = a/b 实 际 产 值(万元)a = bc8000.0 130.0 10400.08870.0 147.0 13038.98750.0 129.0 11287.58980.0 145.0 13021.034600.0 138.0 47747.4该柴油机厂全年的平均计划完成程度指标为.346004.47747==∑∑b bc c = 138.0% 7、列计算表如下:日 期1月1日 2月1日 3月1日 4月1日 生 产 工 人 数(人) a 生产工人占全部人数比重(%)c = a/b 全 部 职 工 人 数(人) b = a/c2250 75 30002496 78 32002356 76 31002560 80 3200该企业第一季度生产工人数占全部职工人数比重232003100320023000225602356249622250++++++==b a c = 77.2% 8、①填写表中空格:月 份 1 2 3 4 月初职工人数(人) 月总产值(万元) 月平均人数(人) 月劳动生产率(元/人) 250 27.825 265 1050无资料 26.500 265 1000280 29.150 275 1060270 — — —②第一季度平均职工人数 =3275265265++= 268. 33(人)③第一季度工业总产值 = 27.825 + 26.500 + 29.150 = 83.475(万元) 第一季度平均每月工业总产值 =3475.83=27.825(万元) ④第一季度劳动生产率 =33.268834750=3110.91(元/人)第一季度平均月劳动生产率 =33.26891.3110=1036.97(元/人)或 =33.268278250=1036.97(元/人)9、煤产量动态指标计算表:年 份 1980 1981 1982 1983 1984 1985 原煤产量(万吨) 6.20 6.22 6.66 7.15 7.89 8.72 增长量 (万吨) 逐期 — 0.02 0.44 0.49 0.74 0.83 累计 — 0.02 0.46 0.95 1.69 2.52 发展速度 (%) 环比 — 100.32 107.07 107.36 110.35 110.52 定基 100.00 100.32 107.42 115.32 127.26 140.65 增长速度环比—0.327.077.3610.3510.52(%) 定基 — 0.32 7.42 15.32 27.26 40.65第①、②与③的要求,计算结果直接在表中; ④平均增长量=552.2= 0.504(万吨) ⑤水平法计算的平均发展速度=554065.120.672.8== 107.06% 平均增长速度= 107.06%-100%=7.06% 10、以1991年为基期的总平均发展速度为62306.105.103.1⨯⨯= 104.16%11、每年应递增:535.2=118.64%以后3年中平均每年应递增:355.135.2=114.88% 12、计算并填入表中空缺数字如下:(阴影部分为原数据) 年 份 销售量 (万台) 增长量(万台) 发展速度(%) 增长速度(%) 增长1%绝对值 逐 期 累 计 环 比 定 基 环 比 定 基 1987 1230.00 — — — 100.00 — — — 1988 1430.00 200.00 200.00 116.26 116.26 16.26 16.26 12.30 1989 1833.00 403.00 603.00 128.18 149.02 28.18 49.02 14.30 1990 2543.00 710.00 1313.00 138.73 206.75 38.73 106.75 18.33 1991 3019.65 476.65 1789.65 118.74 245.50 18.74 145.50 25.43 1992 3640.80 621.15 2410.80 120.57 296.00 20.57 196.00 30.20 19934496.39855.593266.39123.50365.5623.50265.5636.41平均增长量为:3266.39÷6 = 544.40(万台) 平均发展速度为:66556.3= 124.12% 平均增长速度为:124.12%-1= 24.12%13、设在80亿元的基础上,按8 %的速度递增,n 年后可达200亿元,即n80200= 108% → n 1log2.5 = log1.08 → n = 08.1log 5.2log = 11.9 按8 %的速度递增,约经过11.9年该市的国民收入额可达到200亿元。
14、①磷肥产量移动平均计算如下: 年 份 83 84 85 86 87 88 89 90 91 92 93 94 95 产量(万吨) 424650524846525060646264603年移动平均 — 46.0 49.3 50.0 48.7 48.7 49.3 54.0 58.0 62.0 63.0 62.0 —4年移动平均 47.5 49.0 49.0 49.5 49.0 52.0 56.5 58.5 62.5 62.54年移正平均— — 48.3 49.0 49.3 49.3 50.5 54.3 57.5 60.5 62.5 — —②分别以1982年和1989年为原点,列计算表如下: 年份 序号t 82年为0 产量y t 2ty 序号t ´ 89年为0t ´2 t ´y 1983 1 42 1 42 -6 36 -252 1984 2 46 4 92 -5 25 -230 1985 3 50 9 150 -4 16 -200 1986 4 52 16 208 -3 9 -156 1987 5 48 25 240 -2 4 -96 1988 6 46 36 276 -1 1 -46 1989 7 52 49 364 0 0 0 1990 8 50 64 400 1 1 50 1991 9 60 81 540 2 4 120 1992 10 64 100 640 3 9 192 1993 11 62 121 682 4 16 248 1994 12 64 144 768 5 25 320 1995 13 60 169 780 636 360 合计916968195182182310以82年为原点采用最小平方法建立直线方程: b =∑∑∑∑∑--22)(t t n y t ty n =2918191369691518213-⨯⨯-⨯=1.70 a =139170.113696⨯-=-∑∑nt b ny = 41.64得直线趋势方程 yˆ= 41.62 + 1.70 t 96年产量约为:yˆ= 41.64 + 14×1.70 = 65.44(万吨) 97年产量约为:yˆ= 41.64 + 15×1.70 = 67.14(万吨) 以89年为原点采用最小平方法建立直线方程: b =∑∑''2t y t = 182310=1.70a = 13696=∑ny = 53.54 得直线趋势方程 yˆ= 53.54 + 1.70 t ˊ 96年产量约为:yˆ= 53.54 + 7×1.70 = 65.44(万吨) 97年产量约为:yˆ= 53.54 + 8×1.70 = 67.14(万吨) 15、按月平均法计算表: 月份 1990 1991 1992 1993 1994 按月平均 季节比率% 1 80 150 240 280 345 219.00 176.83 2 60 90 150 140 210 130.00 104.97 3 20 40 60 80 90 58.00 46.83 4 10 25 40 30 45 30.00 24.22 5 6 10 20 12 10 11.60 9.37 6 4 8 11 9 9 8.20 6.62 7 8 12 32 37 18 21.40 17.28 8 12 20 40 48 32 30.40 24.55 9 20 35 70 83 65 54.60 44.09 10 50 85 150 140 180 121.00 97.70 11 210 340 420 470 450 378.00 305.21 12 250 350 480 510 530 424.00 342.35 总平均60.8397.08142.75153.25165.33123.85100.00趋势剔除法第一步:计算十二个月移动平均修匀值; 第二步:计算二项移正平均修匀值; (得以下表中计算结果)趋势剔除法修匀值计算表月份十二个月移动平均后再二项移正平均1990 1991 1992 1993 19941 —72.92 114.42 145.46 165.632 —73.42 116.09 146.00 164.173 —74.38 118.38 146.88 162.754 —76.46 122.54 147.00 163.675 —83.33 128.59 148.67 164.506 —92.92 137.34 152.00 164.507 63.75 100.83 144.42 155.96 —8 67.92 107.08 145.67 161.59 —9 70.00 110.42 146.09 164.92 —10 71.46 111.88 146.50 165.96 —11 72.25 112.92 145.75 166.50 —12 72.59 113.46 145.34 166.42 —第三步:用与第二步结果对应的实际值,分别除以第二步结果的修匀值(例如:90年7月份的8÷63.75 = 12.55 %);第四步:计算各年同月平均数;第五步:计算各年同月平均数总平均数;第六步:计算季节比率。
