初中中招二次函数和圆的综合体包含答案
二次函数和圆综合(压轴题+例题+巩固+答案解析)

【例1】.如图,点()40M ,,以点M 为圆心、2为半径的圆与x 轴交于点A B ,.已知抛物216y x bx c =++过点A 和B ,与y 轴交于点C .⑴ 求点C 的坐标,并画出抛物线的大致图象.⑵ 点()8Q m ,在抛物线216y x bx c =++上,点P 为此抛物线对称轴上一个动点,求PQ PB + 最小值. ⑶ CE 是过点C 的M ⊙的切线,点E 是切点,求OE 所在直线的解析式.【巩固】已知抛物线2y ax bx c =++与y 轴的交点为C ,顶点为M ,直线CM 的解析式2y x =-+并且线段CM 的长为(1)求抛物线的解析式。
(2)设抛物线与x 轴有两个交点A (X 1 ,0)、B (X 2 ,0),且点A 在B 的左侧,求线段AB 的长。
(3)若以AB 为直径作⊙N ,请你判断直线CM 与⊙N 的位置关系,并说明理由。
【例2】如图,在平面直角坐标系中,以点(04)C ,为圆心,半径为4的圆交y 轴正半轴于点A ,AB 是C ⊙的切线.动点P 从点A 开始沿AB 方向以每秒1个单位长度的速度运动,点Q 从O 点开始沿x 轴正方向以每秒4个单位长度的速度运动,且动点P 、Q 从点A 和点O 同时出发,设运动时间为t (秒).⑴当1t =时,得到1P 、1Q 两点,求经过A 、1P 、1Q 三点的抛物线解析式及对称轴l ;⑵当t 为何值时,直线PQ 与C ⊙相切?并写出此时点P 和点Q 的坐标;⑶在⑵的条件下,抛物线对称轴l 上存在一点N ,使NP NQ +最小,求出点N 的坐标并说明理由.提示:(1)先求出t=1时,AP 和OQ 的长,即可求得P 1,Q 1的坐标,然后用待定系数法即可得出抛物线的解析式.进而可求出对称轴l 的解析式.(2)当直线PQ 与圆C 相切时,连接CP ,CQ 则有Rt △CMP ∽Rt △QMC (M 为PG 与圆的切点),因此可设当t=a 秒时,PQ 与圆相切,然后用a 表示出AP ,OQ 的长即PM ,QM 的长(切线长定理).由此可求出a 的值.(3)本题的关键是确定N 的位置,先找出与P 点关于直线l 对称的点P ′的坐标,连接P ′Q ,那么P ′Q 与直线l 的交点即为所求的N 点,可先求出直线P ′Q 的解析式,进而可求出N 点的坐标.【巩固】已知二次函数图象的顶点在原点O ,对称轴为y 轴.一次函数1y kx =+的图象与 二次函数的图象交于A B ,两点(A 在B 的左侧),且A 点坐标为()44-,.平行于x 轴的直线l 过()01-,点.⑴ 求一次函数与二次函数的解析式;⑵ 判断以线段AB 为直径的圆与直线l 的位置关系,并给出证明;⑶ 把二次函数的图象向右平移2个单位,再向下平移t 个单位()0t >,二次函数的图象与x轴交于M N,,三点的圆的,两点,一次函数图象交y轴于F点.当t为何值时,过F M N面积最小?最小面积是多少?【例3】如图1,⊙O的半径为1,正方形ABCD顶点B坐标为(),,顶点D在⊙O上运动.50⑴当点D运动到与点A、O在同一条直线上时,试证明直线CD与⊙O相切;⑵当直线CD与⊙O相切时,求OD所在直线对应的函数关系式;⑶设点D的横坐标为x,正方形ABCD的面积为S,求S与x之间的函数关系式,并求出S 的最大值与最小值.【巩固】如图,已知点A 从()10,出发,以1个单位长度/秒的速度沿x 轴向正方向运动,以O A ,为顶点作菱形OABC ,使点B C ,在第一象限,且60AOC ∠=︒;以()03P ,为圆心,PC 为半径作圆.设点A 运动了t 秒,求: ⑴ 点C 的坐标(用含t 的代数式表示);⑵ 当点A 在运动过程中,所有使P 与菱形OABC 的边所在直线相切的t 的值.【例4】已知:如图,抛物线213y x m =+与x 轴交于A B ,两点,与y 轴交于C 点,90ACB ∠=︒⑴ 求m 的值及抛物线顶点坐标;⑵ 过A B C ,,的三点的M ⊙交y 轴于另一点D ,连结DM 并延长交M ⊙于点E ,过E 点的M ⊙的切线分别交x 轴、y 轴于点F G ,,求直线FG 的解析式;⑶ 在条件⑵下,设P 为CBD 上的动点(P 不与C D ,重合),连结PA 交y 轴于点H ,问是否存在一个常数k ,始终满足AH AP k ⋅=,如果存在,请写出求解过程;如果不存在,请说明理由.【巩固】如图,已知点A的坐标是(),,以AB为直径作O',90-,,点B的坐标是()10交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.⑴求抛物线的解析式;⑵点E是AC延长线上一点,BCE∠的平分线CD交O'于点D,连结BD,求直线BD的解析式;⑶在⑵的条件下,抛物线上是否存在点P,使得PDB CBD∠=∠?如果存在,请求出点P的坐标;如果不存在,请说明理由.DCEA yxBO O'课后作业:1.如图,直角坐标系中,已知两点()A,,点B在第一象限且OAB2000O,,()∆为正三角形,OAB∆的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D.⑴求B C,两点的坐标;⑵求直线CD的函数解析式;⑶设E F,分别是线段AB AD,上的两个动点,且EF平分四边形ABCD的周长.试探究:AEF∆的最大面积?参考答案例1【巩固】例2分析:(1)先求出t=1时,AP和OQ的长,即可求得P1,Q1的坐标,然后用待定系数法即可得出抛物线的解析式.进而可求出对称轴l的解析式.(2)当直线PQ与圆C相切时,连接CP,CQ则有Rt△CMP∽Rt△QMC(M为PG与圆的切点),因此可设当t=a秒时,PQ与圆相切,然后用a表示出AP,OQ的长即PM,QM的长(切线长定理).由此可求出a的值.(3)本题的关键是确定N的位置,先找出与P点关于直线l对称的点P′的坐标,连接P′Q,那么P′Q与直线l的交点即为所求的N点,可先求出直线P′Q的解析式,进而可求出N点的坐标.【巩固】例3【巩固】例4【巩固】作业。
中考数学专题复习二次函数的综合题及答案解析

中考数学专题复习二次函数的综合题及答案解析一、二次函数1.如图,对称轴为直线x 1=-的抛物线()2y ax bx c a 0=++≠与x 轴相交于A 、B 两点,其中A 点的坐标为(-3,0).(1)求点B 的坐标;(2)已知a 1=,C 为抛物线与y 轴的交点.①若点P 在抛物线上,且POC BOC S 4S ∆∆=,求点P 的坐标;②设点Q 是线段AC 上的动点,作QD ⊥x 轴交抛物线于点D ,求线段QD 长度的最大值.【答案】(1)点B 的坐标为(1,0).(2)①点P 的坐标为(4,21)或(-4,5).②线段QD 长度的最大值为94. 【解析】【分析】(1)由抛物线的对称性直接得点B 的坐标.(2)①用待定系数法求出抛物线的解析式,从而可得点C 的坐标,得到BOC S ∆,设出点P 的坐标,根据POC BOC S 4S ∆∆=列式求解即可求得点P 的坐标.②用待定系数法求出直线AC 的解析式,由点Q 在线段AC 上,可设点Q 的坐标为(q,-q-3),从而由QD ⊥x 轴交抛物线于点D ,得点D 的坐标为(q,q 2+2q-3),从而线段QD 等于两点纵坐标之差,列出函数关系式应用二次函数最值原理求解.【详解】解:(1)∵A 、B 两点关于对称轴x 1=-对称 ,且A 点的坐标为(-3,0), ∴点B 的坐标为(1,0).(2)①∵抛物线a 1=,对称轴为x 1=-,经过点A (-3,0), ∴2a 1b 12a 9a 3b c 0=⎧⎪⎪-=-⎨⎪-+=⎪⎩,解得a 1b 2c 3=⎧⎪=⎨⎪=-⎩.∴抛物线的解析式为2y x 2x 3=+-.∴B 点的坐标为(0,-3).∴OB=1,OC=3.∴BOC 13S 1322∆=⨯⨯=. 设点P 的坐标为(p,p 2+2p-3),则POC 13S 3p p 22∆=⨯⨯=. ∵POC BOC S 4S ∆∆=,∴3p 62=,解得p 4=±. 当p 4=时2p 2p 321+-=;当p 4=-时,2p 2p 35+-=,∴点P 的坐标为(4,21)或(-4,5).②设直线AC 的解析式为y kx b =+,将点A ,C 的坐标代入,得:3k b 0b 3-+=⎧⎨=-⎩,解得:k 1b 3=-⎧⎨=-⎩. ∴直线AC 的解析式为y x 3=--.∵点Q 在线段AC 上,∴设点Q 的坐标为(q,-q-3).又∵QD ⊥x 轴交抛物线于点D ,∴点D 的坐标为(q,q 2+2q-3).∴()22239QD q 3q 2q 3q 3q q 24⎛⎫=---+-=--=-++ ⎪⎝⎭. ∵a 10<=-,-3302<<-∴线段QD 长度的最大值为94.2.童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销该店决定降价销售,经市场调查发现:每降价1元,每星期可多卖10件,已知该款童装每件成本30元,设降价后该款童装每件售价x 元,每星期的销售量为y 件.(1)降价后,当某一星期的销售量是未降价前一星期销售量的3倍时,求这一星期中每件童装降价多少元?(2)当每件售价定为多少元时,一星期的销售利润最大,最大利润是多少?【答案】(1)这一星期中每件童装降价20元;(2)每件售价定为50元时,一星期的销售利润最大,最大利润4000元.【解析】【分析】(1)根据售量与售价x (元/件)之间的关系列方程即可得到结论.(2)设每星期利润为W 元,构建二次函数利用二次函数性质解决问题.【详解】解:(1)根据题意得,(60﹣x )×10+100=3×100,解得:x =40,60﹣40=20元,答:这一星期中每件童装降价20元;(2)设利润为w ,根据题意得,w =(x ﹣30)[(60﹣x )×10+100]=﹣10x 2+1000x ﹣21000=﹣10(x ﹣50)2+4000,答:每件售价定为50元时,一星期的销售利润最大,最大利润4000元.【点睛】本题考查二次函数的应用,一元二次不等式,解题的关键是构建二次函数解决最值问题,利用图象法解一元二次不等式,属于中考常考题型.3.如图,在平面直角坐标系中,二次函数2y ax bx c =++交x 轴于点()4,0A -、()2,0B ,交y 轴于点()0,6C ,在y 轴上有一点()0,2E -,连接AE .(1)求二次函数的表达式;(2)若点D 为抛物线在x 轴负半轴上方的一个动点,求ADE ∆面积的最大值; (3)抛物线对称轴上是否存在点P ,使AEP ∆为等腰三角形,若存在,请直接写出所有P 点的坐标,若不存在请说明理由.【答案】(1)二次函数的解析式为233642y x x =--+;(2)当23x =-时,ADE ∆的面积取得最大值503;(3)P 点的坐标为()1,1-,(1,11-,(1,219--. 【解析】分析:(1)把已知点坐标代入函数解析式,得出方程组求解即可;(2)根据函数解析式设出点D 坐标,过点D 作DG ⊥x 轴,交AE 于点F ,表示△ADE 的面积,运用二次函数分析最值即可;(3)设出点P 坐标,分PA =PE ,PA =AE ,PE =AE 三种情况讨论分析即可.详解:(1)∵二次函数y =ax 2+bx +c 经过点A (﹣4,0)、B (2,0),C (0,6), ∴16404206a b c a b c c -+=⎧⎪++=⎨⎪=⎩,解得:34326a b c ⎧=-⎪⎪⎪=-⎨⎪=⎪⎪⎩, 所以二次函数的解析式为:y =233642x x --+; (2)由A (﹣4,0),E (0,﹣2),可求AE 所在直线解析式为y =122x --, 过点D 作DN ⊥x 轴,交AE 于点F ,交x 轴于点G ,过点E 作EH ⊥DF ,垂足为H ,如图,设D (m ,233642m m --+),则点F (m ,122m --), ∴DF =233642m m --+﹣(122m --)=2384m m --+, ∴S △ADE =S △ADF +S △EDF =12×DF ×AG +12DF ×EH =12×DF ×AG +12×DF ×EH =12×4×DF =2×(2384m m --+) =23250233m -++(), ∴当m =23-时,△ADE 的面积取得最大值为503. (3)y =233642x x --+的对称轴为x =﹣1,设P (﹣1,n ),又E (0,﹣2),A (﹣4,0),可求PA 29n +PE 212n ++()AE 16425+=,分三种情况讨论:当PA =PE 时,29n +=212n ++(),解得:n =1,此时P (﹣1,1); 当PA =AE 时,29n +=16425+=,解得:n =11±,此时点P 坐标为(﹣1,11±);当PE =AE 时,212n ++()=16425+=,解得:n =﹣219±,此时点P 坐标为:(﹣1,﹣219±).综上所述:P 点的坐标为:(﹣1,1),(﹣1,11±),(﹣1,﹣219±).点睛:本题主要考查二次函数的综合问题,会求抛物线解析式,会运用二次函数分析三角形面积的最大值,会分类讨论解决等腰三角形的顶点的存在问题时解决此题的关键.4.二次函数y=x 2-2mx+3(m >)的图象与x 轴交于点A (a ,0)和点B (a+n ,0)(n >0且n 为整数),与y 轴交于C 点.(1)若a=1,①求二次函数关系式;②求△ABC 的面积;(2)求证:a=m-;(3)线段AB (包括A 、B )上有且只有三个点的横坐标是整数,求a 的值.【答案】(1)y=x 2-4x+3;3;(2)证明见解析;(3)a=1或a=−.【解析】试题分析:(1)①首先根据a=1求得A 的坐标,然后代入二次函数的解析式,求得m 的值即可确定二次函数的解析式;②根据解析式确定抛物线与坐标轴的交点坐标,从而确定三角形的面积;(2)将原二次函数配方后即可确定其对称轴为x=m ,然后根据A 、B 两点关于x=m 对称得到a+n-m=m-a ,从而确定a 、m 、n 之间的关系;(3)根据a=m-得到A (m-,0)代入y=(x-m )2-m 2+3得0=(m--m )2-m 2+3,求得m 的值即可确定a 的值.试题解析:(1)①∵a=1,∴A (1,0),代入y=x 2-2mx+3得1-2m+3=0,解得m=2,∴y=x 2-4x+3;②在y=x 2-4x+3中,当y=0时,有x 2-4x+3=0可得x=1或x=3,∴A (1,0)、B (3,0),∴AB=2再根据解析式求出C 点坐标为(0,3),∴OC=3,△ABC 的面积=×2×3=3;(2)∵y=x 2-2mx+3=(x-m )2-m 2+3,∴对称轴为直线x=m,∵二次函数y=x2-2mx+3的图象与x轴交于点A和点B∴点A和点B关于直线x=m对称,∴a+n-m=m-a,∴a=m-;(3)y=x2-2mx+3(m>)化为顶点式为y=(x-m)2-m2+3(m>)①当a为整数,因为n>0且n为整数所以a+n是整数,∵线段AB(包括A、B)上有且只有三个点的横坐标是整数,∴n=2,∴a=m-1,∴A(m-1,0)代入y=(x-m)2-m2+3得(x-m)2-m2+3=0,∴m2-4=0,∴m=2,m=-2(舍去),∴a=2-1=1,②当a不是整数,因为n>0且n为整数所以a+n不是整数,∵线段AB(包括A、B)上有且只有三个点的横坐标是整数,∴n=3,∴a=m-∴A(m-,0)代入y=(x-m)2-m2+3得0=(m--m)2-m2+3,∴m2=,∴m=,m=-(舍去),∴a=−,综上所述:a=1或a=−.考点:二次函数综合题.5.在平面直角坐标系xOy中,抛物线y=x2﹣2x+a﹣3,当a=0时,抛物线与y轴交于点A,将点A向右平移4个单位长度,得到点B.(1)求点B的坐标;(2)将抛物线在直线y=a上方的部分沿直线y=a翻折,图象的其他部分保持不变,得到一个新的图象,记为图形M,若图形M与线段AB恰有两个公共点,结合函数的图象,求a的取值范围.【答案】(1)A(0,﹣3),B(4,﹣3);(2)﹣3<a≤0;【解析】【分析】(1)由题意直接可求A,根据平移点的特点求B;(2)图形M与线段AB恰有两个公共点,y=a要在AB线段的上方,当函数经过点A时,AB与函数两个交点的临界点;【详解】解:(1)A(0,﹣3),B(4,﹣3);(2)当函数经过点A时,a=0,∵图形M与线段AB恰有两个公共点,∴y=a要在AB线段的上方,∴a>﹣3∴﹣3<a≤0;【点睛】本题二次函数的图象及性质;熟练掌握二次函数图象的特点,函数与线段相交的交点情况是解题的关键.6.(10分)(2015•佛山)如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=﹣x2+4x刻画,斜坡可以用一次函数y=x刻画.(1)请用配方法求二次函数图象的最高点P的坐标;(2)小球的落点是A,求点A的坐标;(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积.请直接写出点M的坐标.【答案】(1)(2,4);(2)(,);(3);(4)(,).【解析】试题分析:(1)利用配方法抛物线的一般式化为顶点式,即可求出二次函数图象的最高点P的坐标;(2)联立两解析式,可求出交点A的坐标;(3)作PQ⊥x轴于点Q,AB⊥x轴于点B.根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA,代入数值计算即可求解;(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,由于两平行线之间的距离相等,根据同底等高的两个三角形面积相等,可得△MOA的面积等于△POA的面积.设直线PM的解析式为y=x+b,将P(2,4)代入,求出直线PM的解析式为y=x+3.再与抛物线的解析式联立,得到方程组,解方程组即可求出点M的坐标.试题解析:(1)由题意得,y=﹣x2+4x=﹣(x﹣2)2+4,故二次函数图象的最高点P的坐标为(2,4);(2)联立两解析式可得:,解得:,或.故可得点A的坐标为(,);(3)如图,作PQ⊥x轴于点Q,AB⊥x轴于点B.S△POA=S△POQ+S△梯形PQBA﹣S△BOA=×2×4+×(+4)×(﹣2)﹣××=4+﹣=;(4)过P作OA的平行线,交抛物线于点M,连结OM、AM,则△MOA的面积等于△POA的面积.设直线PM的解析式为y=x+b,∵P的坐标为(2,4),∴4=×2+b,解得b=3,∴直线PM的解析式为y=x+3.由,解得,,∴点M的坐标为(,).考点:二次函数的综合题7.已知二次函数的图象以A(﹣1,4)为顶点,且过点B(2,﹣5)(1)求该函数的关系式;(2)求该函数图象与坐标轴的交点坐标;(3)将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.【答案】(1)y=﹣x2﹣2x+3;(2)抛物线与x轴的交点为:(﹣3,0),(1,0)(3)15.【解析】【分析】(1)已知了抛物线的顶点坐标,可用顶点式设该二次函数的解析式,然后将B 点坐标代入,即可求出二次函数的解析式;(2)根据函数解析式,令x=0,可求得抛物线与y轴的交点坐标;令y=0,可求得抛物线与x轴交点坐标;(3)由(2)可知:抛物线与x轴的交点分别在原点两侧,由此可求出当抛物线与x轴负半轴的交点平移到原点时,抛物线平移的单位,由此可求出A′、B′的坐标.由于△OA′B′不规则,可用面积割补法求出△OA′B′的面积.【详解】(1)设抛物线顶点式y=a(x+1)2+4,将B(2,﹣5)代入得:a=﹣1,∴该函数的解析式为:y=﹣(x+1)2+4=﹣x2﹣2x+3;(2)令x=0,得y=3,因此抛物线与y轴的交点为:(0,3),令y=0,﹣x2﹣2x+3=0,解得:x1=﹣3,x2=1,即抛物线与x轴的交点为:(﹣3,0),(1,0);(3)设抛物线与x轴的交点为M、N(M在N的左侧),由(2)知:M(﹣3,0),N(1,0),当函数图象向右平移经过原点时,M 与O 重合,因此抛物线向右平移了3个单位, 故A'(2,4),B'(5,﹣5),∴S △OA′B′=12×(2+5)×9﹣12×2×4﹣12×5×5=15.【点睛】本题考查了用待定系数法求抛物线解析式、函数图象与坐标轴交点、图形面积的求法等知识.熟练掌握待定系数法、函数图象与坐标轴的交点的求解方法、不规则图形的面积的求解方法等是解题的关键.8.如图,已知直线y kx 6=-与抛物线2y ax bx c =++相交于A ,B 两点,且点A (1,-4)为抛物线的顶点,点B 在x 轴上。
2019届中考数学专题二次函数和圆综合检测试卷含答案

2019 初三数学中考专题复习二次函数和圆专题综合检测1. 以下关系式中,属于二次函数的是(x 为自变量 )()1 221 4 4A.y =8x=-x -=x2=a x22 1 22. 抛物线 y=2x ,y=- 2x ,y=2x 的共同性质是 ( )A. 张口向上B.对称轴是y轴C.都有最高点随x的增大而增大3.若二次函数 y=(x -m)2-1,当 x≤1时, y 随 x 的增大而减小,则 m的取值范围是 ( )=>1≥1≤14.如图, AB是⊙ O的直径 . 若∠ BAC=35°,那么∠ ADC=( )°°°°5.在同圆中,以下四个命题:①圆心角是极点在圆心的角;②两个圆心角相等,它们所对的弦也相等;③两条弦相等,它们所对的弧也相等;④等弧所对的圆心角相等 . 此中真命题有 ()A.4 个个个个6.如图,CD是⊙ O的直径,弦 AB⊥CD于 E,连结 BC、BD.以下结论错误的选项是( )=BE B.C.OE =DE D. . ∠DBC=90°7.如图, AD、AE、CB均为⊙ O的切线, D、E、F 分别是切点, AD=8,则△ ABC的周长为 ()8. 假如二次函数y=ax2+bx+c 的图象以下图,那么一次函数y=bx+c 和反比b例函数 y=x在同一坐标系中的图象大概是( )9.如图,圆形薄铁片与直角三角尺、直尺紧靠在一同平放在桌面上 . 已知铁片的圆心为O,三角尺的直角极点 C 落在直尺的 10cm处,铁片与直尺的独一公共点 A 落在直尺的14cm处,铁片与三角尺的独一公共点为 B. 以下说法错误的选项是 ( )A. 圆形铁片的半径是 4cmB. 四边形 AOBC为正方形C. 弧 AB的长度为 4πcmD.扇形 OAB的面积是4πcm210.已知二次函数 y=ax2+bx+c(a ≠0) 的图象以下图,而且对于 x 的一元二次方程ax2+bx+c-m=0 有两个不相等的实数根,以下结论:①b2-4ac<0;②abc>0;③a-b+c<0;④ m>- 2,此中正确的个数有 ( )11. 如图,扇形 OAB的圆心角为 120°,半径为 3,则该扇形的弧长为( 结果保留π).2112. 已知抛物线 y=x - 4x 上有两点 P1(3 ,y1) 、P2( -2,y2) ,则 y1与 y2的大小关系为: y1y2( 填“>”“<”或“=”).13.如图,⊙ I 是△ ABC的内切圆, D、E、F 为三个切点,若∠ DEF=52°,则∠ A 的度数为.14.某软件商铺销售一种益智游戏软件,假如以每盘 50 元的售价销售,一个月能售出 500 盘,依据市场剖析,若销售单价每涨价 1 元,月销售量就减少10 盘,当每盘的售价涨x 元 (x取整数)时,该商铺月销售额y( 元) 与 x 的函数关系式为,自变量 x 的取值范围是.15.设 A、B、C三点挨次分别是抛物线 y=x2-2x- 5 与 y 轴的交点以及与 x 轴的两个交点,则△ ABC的面积是.16.已知二次函数 y=- x2+2x+m的部分图象以下图,则对于 x 的一元二次方程- x2+2x+m=0 的解为.25117.已知抛物线 y=2x +x-2.(1)用配方法求出它的极点坐标和对称轴;(2)若抛物线与 x 轴的两个交点为 A、B,求线段 AB的长 .18.如, AB是半 O的直径, C、D是半 O上的两点,且 OD∥BC,OD与 AC交于点E.(1)若∠ B=70°,求∠ CAD的度数;(2)若 AB=4,AC=3,求 DE的 .19.已知二次函数 y=ax2+bx+c 中,函数 y 与自量 x 的部分以下表:x⋯-101234⋯y⋯1052125⋯(1)求二次函数的关系式;(2)当 x 何, y 有最小,最小是多少?(3) 若 A(m,y1) 、B(m+1,y2) 两点都在函数的象上,比y1与 y2的大小 .420.如图,已知 AB是⊙ O的直径,点 C、D在⊙ O上,∠ D=60°且 AB=6,过 O 点作 OE⊥AC,垂足为 E.(1) 求 OE的长;(2) 若 OE的延伸线交⊙ O于点 F,求弦 AF、AC和围成的图形(暗影部分)的面积.21.某企业经销一种绿茶,每千克成本为 50 元,市场检查发现,在一段时间内,销售量 w(千克 ) 随销售单价 x( 元/ 千克 ) 的变化而变化,详细关系为 w=- 2x+240,且物价部门规定这类绿茶的销售单价不得高于90 元/ 千克 . 设这类绿茶在这段时间内的销售收益为y( 元) ,解答以下问题:(1)求 y 与 x 的函数关系式;(2)当 x 取何值时, y 的值最大?(3)假如企业想要在这段时间内获取 2250 元的销售收益,销售单价应定为多少元?22.如图,已知⊙ O是△ ABC的外接圆, AD是⊙ O的直径,且 BD=BC,延伸 AD到 E,且有∠ EBD=∠ CAB.(1)求证: BE是⊙ O的切线;(2)若 BC= 3,AC=5,求圆的直径 AD及切线 BE的长 .23.如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-3,0)、B(5,0)、C(0,5)三点,O为坐标原点 .(1)求此抛物线的分析式;13(2)若把抛物线 y=ax2+bx+c(a ≠0) 向下平移3个单位长度,再向右平移 n(n >0) 个单位长度获取新抛物线,若新抛物线的极点M在△ABC内,求 n 的取值范围;(3)设点 P 在 y 轴上,且知足∠ OPA+∠ OCA=∠ CBA,求 CP的长 .参照答案:1—10 ABCBB CCACB12.<13.76 °14.y=- 10x2+250000 ≤x≤50 且 x 为整数15.5616.x1=-1,x2=31217.解: (1)y =2(x + 1)-3,它的极点坐标为 ( -1,- 3),对称轴为 x=- 1;1(2)令 y=0,∴2(x +1) 2-3=0,∴x1=- 1+ 6,x2=- 1- 6,∴ AB=| -1+ 6 -( -1- 6)| =2 6.18.解:(1) ∵OD∥BC,∴∠ DOA=∠ B=70°,又∵ OA=OD,∴∠ DAO=∠ ADO=55°,∵AB是直径,∴∠ ACB=90°,∴∠ CAB=20°,∴∠ CAD=35°;BC77 (2) 在 Rt△ACB中,BC=7,O是 AB中点,OD∥BC,∴OE=2=2,∴DE=2-2 .19.解: (1) 依题意设 y=a(x -2) 2+1,把 (3,2) 代入得 a=1,∴ y=(x -2) 2+1;(2)当 x=2 时, y 有最小值,最小值为 1;(3)当 m≥2时, y2≥y1,当 m<1 时, y1>y2.20. 解:(1) 连结 OC,∵∠D和∠ AOC分别是所对的圆周角和圆心角,∠D=60°,1∴∠ AOC=2∠D=120°,∵ OE⊥AC,∴∠ AOE=∠ COE=2∠AOC=60°,∠OAE=1330°. ∵AB 是⊙O的直径, AB=6,∴ OA=3,∴ OE=2OA=2;1(2) ∵OE =2OA,∴EF = OE.∵OE⊥AC ,∴∠ AEF =∠CEO= 90°, AE =2CE.∴△ AEF≌△ CEO∴S.=S=60· π·3 3暗影=π.扇形 COF36028与x 的关系式为: y=- 2x2+340x-12000;(2)y =- 2x2+340x-12000=- 2(x -85) 2+2450,∴当 x=85 时, y 的值最大;(3) 当 y=2250 时,可得方程- 2(x -85) 2+2450=2250. 解这个方程,得x1= 75,x2=95,依据题意, x2=95 不合题意,应舍去 . ∴当销售单价为75 元/ 千克时,可获取销售收益2250 元.22.解:(1) 如图,连结 OB,∵BD= BC,∴∠ CAB=∠ BAD,∵∠ EBD=∠ CAB,∴∠ BAD =∠EBD,∵AD是⊙O的直径,∴∠ABD=90°,OA=BO,∴∠BAD=∠ABO,∴∠EBD =∠ABO,∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°,∵点 B 在⊙O上,∴ BE是⊙O的切线;(2)设圆的半径为 R,连结 CD,∵ AD为⊙O 的直径,∴∠ ACD=90°,∵ BC= BD,15∴OB⊥CD,∴ OB∥AC,∵ OA= OD,∴ OF=2AC=2,∵四边形 ACBD是圆内接四边形,∴∠ BDE=∠ ACB,∵∠ DBE=∠ CAB,∴△ DBE∽△ CAB,∴3DE3=,∴DE=,∵∠ OBE 53552R3,∵R>0,∴R= 3,∵BE是⊙O的切线,∴BE =∠ OFD=90°,∴DF∥BE,∴R=R+533311=DE×AE=5×2×3+5=5.23. 解: (1) 把 A、B、C三点的坐标代入函数分析式可得,抛物线分析式为y=-1 223x +3x+5;16(2) ∵抛物线极点坐标为(1 ,3 ) ,新抛物线的极点M 坐标为 (1 +n,1) ,设直线 BC95k+m=0,解得k=- 1分析式为 y=kx+m,把 B、C 两点坐标代入可得,m=5m=5∴直线 BC的分析式为 y=- x+5,令 y=1,代入可得 1=- x+5,解得 x=4,∵新抛物线的极点 M在△ ABC内,∴ 1+ n<4,且 n>0,解得 0<n<3,即 n 的取值范围为 0<n<3;(3)当点 P 在 y 轴负半轴上时,如图 1,过 P作 PD⊥AC,交 AC的延伸线于点 D,由题意可知 OB=OC=5,∴∠ CBA=45°,∴∠ PAD=∠ OPA+∠ OCA=∠ CBA=45°,∴AD= PD,在 Rt△OAC中,OA=3,OC=5,可求得 AC=34,设 PD=AD=m,则 CDCO AO = AC+AD=34+m,∵∠ ACO=∠ PCD,∠COA=∠ PDC,∴△ COA∽△ CDP,∴=CD PD3=AC533453334,∴33434,即==PC,由=可求得 m=22=PC,解得PC34+m m34+m mPC=17;可求得 PO=PC-OC=17-5=12,如图 2,在 y 轴正半轴上截取OP′= OP =12,连结 AP′,则∠ OP′A=∠ OPA,∴∠ OP′A+∠ OCA=∠ OPA+∠ OCA=∠ CBA,∴P′也知足题目条件,此时 P′C=OP′- OC=12-5=7,综上可知 PC 的长为 7或17.10。
二次函数和圆练习(含答案)

二次函数和圆一.解答题(共15小题)1.(2012•宜昌)如图,在平面直角坐标系中,直线y=x+1分别与两坐标轴交于B,A两点,C为该直线上的一动点,以每秒1个单位长度的速度从点A开始沿直线BA向上移动,作等边△CDE,点D和点E都在x轴上,以点C为顶点的抛物线y=a(x﹣m)2+n经过点E.⊙M与x轴、直线AB都相切,其半径为3(1﹣)a.(1)求点A的坐标和∠ABO的度数;(2)当点C与点A重合时,求a的值;(3)点C移动多少秒时,等边△CDE的边CE第一次与⊙M相切?OB===,∴的坐标是(﹣,(﹣﹣,∴﹣)﹣2﹣33,4﹣﹣a+4+3a+,2.(2012•盐城)在平面直角坐标系xOy中,已知二次函数y=的图象经过点A(2,0)和点B(1,﹣),直线l经过抛物线的顶点且与t轴垂直,垂足为Q.(1)求该二次函数的表达式;(2)设抛物线上有一动点P从点B处出发沿抛物线向上运动,其纵坐标y1随时间t(t≥0)的变化规律为y1=﹣+2t.现以线段OP为直径作⊙C.①当点P在起始位置点B处时,试判断直线l与⊙C的位置关系,并说明理由;在点P运动的过程中,直线l与⊙C 是否始终保持这种位置关系?请说明你的理由.②若在点P开始运动的同时,直线l也向上平行移动,且垂足Q的纵坐标y2随时间t的变化规律为y2=﹣1+3t,则当t在什么范围内变化时,直线l与⊙C相交?此时,若直线l被⊙C所截得的弦长为a,试求a2的最大值.,﹣,x+2t,,﹣+2t,﹣+t+t=t+(﹣OP=2t+OC=t+;上时,﹣+t=t=时,的距离:﹣﹣t+,时,﹣(﹣+t,<t+,<时,直线t=,=,直径a=时,圆心,t+t=.3.(2012•南充)如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB=,抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6).(1)求抛物线的函数解析式;(2)直线m与⊙C相切于点A,交y轴于点D.动点P在线段OB上,从点O出发向点B运动;同时动点Q在线段DA上,从点D出发向点A运动;点P的速度为每秒一个单位长,点Q的速度为每秒2个单位长,当PQ⊥AD 时,求运动时间t的值;(3)点R在抛物线位于x轴下方部分的图象上,当△ROB面积最大时,求点R的坐标.,解得xAOB=AOB=×=2.4×==1.8AOB=xx+b x+b,x=,即,x=(,4.(2012•荆门)如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=,A(3,0),D(﹣1,0),E(0,3).(1)求抛物线的解析式及顶点B的坐标;(2)求证:CB是△ABE外接圆的切线;(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.,即=3BE==.BAE==BAE=BAE=,BAE=DEO==tanBAE= =÷BAE=÷,;,﹣,解得.x=,∴(时,设,得(t﹣,当.即IV AQ=t..5.(2012•济南)如图1,抛物线y=ax2+bx+3与x轴相交于点A(﹣3,0),B(﹣1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.(1)求抛物线的解析式;(2)求cos∠CAB的值和⊙O1的半径;(3)如图2,抛物线的顶点为P,连接BP,CP,BD,M为弦BD中点,若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标.CAB==.B=.,)=BP=,PC=,即BN=MN=解之得,,,,)或(,)6.(2011•遵义)已知抛物线y=ax2+bx+3(a≠0)经过A(3,0),B(4,1)两点,且与y轴交于点C.(1)求抛物线y=ax2+bx+3(a≠0)的函数关系式及点C的坐标;(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求点E的坐标.x x+3 x x+3=x x+3==x=点坐标为()7.(2011•襄阳)如图,在平面直角坐标系xoy中,AB在x轴上,AB=10,以AB为直径的⊙O'与y轴正半轴交于点C,连接BC,AC.CD是⊙O'的切线,AD丄CD于点D,tan∠CAD=,抛物线y=ax2+bx+c过A,B,C三点.(1)求证:∠CAD=∠CAB;(2)①求抛物线的解析式;②判断抛物线的顶点E是否在直线CD上,并说明理由;(3)在抛物线上是否存在一点P,使四边形PBCA是直角梯形?若存在,直接写出点P的坐标(不写求解过程);若不存在,请说明理由.CAD=,则可求得CAD=由题意得:﹣﹣,x+4x x+4=(得顶点))代入直线×+4=x+4y=x+by=,解得(舍去)8.(2011•潍坊)如图,y关于x的二次函数y=﹣(x+m)(x﹣3m)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以AB为直径作圆,圆心为C.定点E的坐标为(﹣3,0),连接ED.(m>0)(1)写出A、B、D三点的坐标;(2)当m为何值时M点在直线ED上?判定此时直线与圆的位置关系;(3)当m变化时,用m表示△AED的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.,则﹣(m,k=mmx+(,y=m,AE OD=m+AE OD=m9.(2011•邵阳)如图所示,在平面直角坐标系Oxy中,已知点A(﹣,0),点C(0,3),点B是x轴上一点(位于点A的右侧),以AB为直径的圆恰好经过点C.(1)求∠ACB的度数;(2)已知抛物线y=ax2+bx+3经过A、B两点,求抛物线的解析式;(3)线段BC上是否存在点D,使△BOD为等腰三角形?若存在,则求出所有符合条件的点D的坐标;若不存在,请说明理由.(﹣,,三点坐标代入得,,=,==,,,DG=(,10.(2011•泉州)如图1,在第一象限内,直线y=mx与过点B(0,1)且平行于x轴的直线l相交于点A,半径为r的⊙Q与直线y=mx、x轴分别相切于点T、E,且与直线l分别交于不同的M、N两点.(1)当点A的坐标为(,p)时,①填空:p=1,m=,∠AOE=60°.②如图2,连接QT、QE,QE交MN于点F,当r=2时,试说明:以T、M、E、N为顶点的四边形是等腰梯形;(2)在图1中,连接EQ并延长交⊙Q于点D,试探索:对m、r的不同取值,经过M、D、N三点的抛物线y=ax2+bx+c,a的值会变化吗?若不变,求出a的值;若变化.请说明理由.,OA=,MN=(坐标为(;,,,=h+ MN=2MN=)11.(2011•黔西南州)如图,在平面直角坐标系中,点A的坐标为(﹣6,0),以点A为圆心的圆交x轴于O、B两点,直线y=x﹣3交x轴于点C,交y轴于点D,过A、C、D三点作一条抛物线.(1)求抛物线的解析式;(2)判断直线CD与⊙A的位置关系,并说明理由;(3)若点M以每秒4个单位长度的速度由点B沿x轴向点C运动,点N以每秒1个单位长度的速度由点C沿直线y=x﹣3向点D运动.设运动时间为t(t≤4),试问t为何值时△CMN与△CDB相似;(4)在抛物线上是否存在点P,使△APC的面积是△BCD面积的倍?若存在,请求出符合条件的所有点P的坐标;若不存在,请说明理由.时,,x xDCO==,===t===t=与t=秒时,=10h=×x xx x12.(2012•宁波)如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.(1)求二次函数的解析式;(2)点P在x轴正半轴上,且PA=PC,求OP的长;(3)点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.①若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标;②若⊙M的半径为,求点M的坐标.x=OP=,)的坐标代入,得k,x,×﹣,()== =,=,)或()13.(2012•长沙)如图半径分别为m,n(0<m<n)的两圆⊙O1和⊙O2相交于P,Q两点,且点P(4,1),两圆同时与两坐标轴相切,⊙O1与x轴,y轴分别切于点M,点N,⊙O2与x轴,y轴分别切于点R,点H.(1)求两圆的圆心O1,O2所在直线的解析式;(2)求两圆的圆心O1,O2之间的距离d;(3)令四边形PO1QO2的面积为S1,四边形RMO1O2的面积为S2.试探究:是否存在一条经过P,Q两点、开口向下,且在x轴上截得的线段长为的抛物线?若存在,请求出此抛物线的解析式;若不存在,请说明理由.,再代入计算得:,解得Q===m±n=5+=8PQ==PQ×8=(MR=(=,解得,=,)(14.(2011•来宾)如图,半径为1的⊙M经过直角坐标系的原点O,且分别与x轴正半轴、y轴正半轴交于点A、B,∠OMA=60°,过点B的切线交x轴负半轴于点C,抛物线过点A、B、C.(1)求点A、B的坐标;(2)求抛物线的函数关系式;(3)若点D为抛物线对称轴上的一个动点,问是否存在这样的点D,使得△BCD是等腰三角形?若存在,求出符合条件的点D的坐标;若不存在,请说明理由.,,,x x+=2±+=2,解得:,),﹣+)15.(2011•荆州)如图甲,分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA 所在直线为x轴、y轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在x轴上),抛物线y=经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.(1)求B点坐标;(2)求证:ME是⊙P的切线;(3)设直线AC与抛物线对称轴交于N,Q点是此对称轴上不与N点重合的一动点,①求△ACQ周长的最小值;②若FQ=t,S△ACQ=S,直接写出S与t之间的函数关系式.﹣x x+2=,FG=∵,,∴,∴△PEF∽△EMF,∴∠EPF=∠FEM,∴∠PEM=∠PEF+∠FEM=∠PEF+∠EPF=90°,∴ME是⊙P的切线;(3)解:①如图乙,延长AB交抛物线于A′,连CA′交对称轴x=3于Q,连AQ,则有AQ=A′Q,∴△ACQ周长的最小值为AC+A′C的长,∵A与A′关于直线x=3对称,∴A(0,2),A′(6,2),∴A′C==2,而AC==2,∴△ACQ周长的最小值为2+2;②当Q点在F点上方时,S=S梯形ACFK﹣S△AKQ﹣S△CFQ=×(3+1)×2﹣×(2﹣t)×3﹣×t×1=t+1,同理,可得:当Q点在线段FN上时,S=1﹣t,当Q点在N点下方时,S=t﹣1.。
(整理)初中中招二次函数和圆的综合体包含答案.

二次函数和圆【例题1】 (芜湖市) 已知圆P 的圆心在反比例函数ky x=(1)k >图象上,并与x 轴相交于A 、B 两点. 且始终与y 轴相切于定点C (0,1). (1) 求经过A 、B 、C 三点的二次函数图象的解析式;(2) 若二次函数图象的顶点为D ,问当k 为何值时,四边形ADBP 为菱形.【例题2】(湖南省韶关市) 25.如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线32y x =-+与坐标轴交于D 、E 。
设M 是AB 的中点,P 是线段DE 上的动点. (1)求M 、D 两点的坐标;(2)当P 在什么位置时,PA=PB ?求出此时P 点的坐标;(3)过P 作PH ⊥BC ,垂足为H ,当以PM 为直径的⊙F 与BC 相切于点N 时,求梯形PMBH 的面积.【例题3】(甘肃省白银等7市新课程)28. 在直角坐标系中,⊙A的半径为4,圆心A的坐标为(2,0),⊙A与x轴交于E、F两点,与y轴交于C、D两点,过点C作⊙A的切线BC,交x轴于点B.(1)求直线CB的解析式;(2)若抛物线y=ax2+b x+c的顶点在直线BC上,与x轴的交点恰为点E、F,求该抛物线的解析式;(3)试判断点C是否在抛物线上?(4)在抛物线上是否存在三个点,由它构成的三角形与△AOC相似?直接写出两组这样的点.【例题4】(绵阳市)25.如图,已知抛物线y = ax2 + bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为5.设⊙M与y轴交于D,抛物线的顶点为E.(1)求m的值及抛物线的解析式;(2)设∠DBC = α,∠CBE = β,求sin(α-β)的值;(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由.【例题5】(南充市)25.如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B.已知抛物线216y x bx c =++过点A 和B ,与y 轴交于点C . (1)求点C 的坐标,并画出抛物线的大致图象. (2)点Q (8,m )在抛物线216y x bx c =++上,点P 为此抛物线对称轴上一个动点,求PQ +PB 的最小值.(3)CE 是过点C 的⊙M 的切线,点E 是切点,求OE 所在直线的解析式.【例题6】(山西省临汾市)26. 如图所示,在平面直角坐标系中,M 经过原点O ,且与x 轴、y 轴分别相交于(60)(08)A B --,,,两点.(1)请求出直线AB 的函数表达式;(2)若有一抛物线的对称轴平行于y 轴且经过点M ,顶点C 在M 上,开口向下,且经过点B ,求此抛物线的函数表达式;(3)设(2)中的抛物线交x 轴于D E ,两点,在抛物线上是否存在点P ,使得115PDE ABC S S =△△?若存在,请求出点P 的坐标;若不存在,请说明理由. x例题1:例题2:例题3:例题4:例题5:例题6:。
专题62 二次函数与圆综合性问题(解析版)
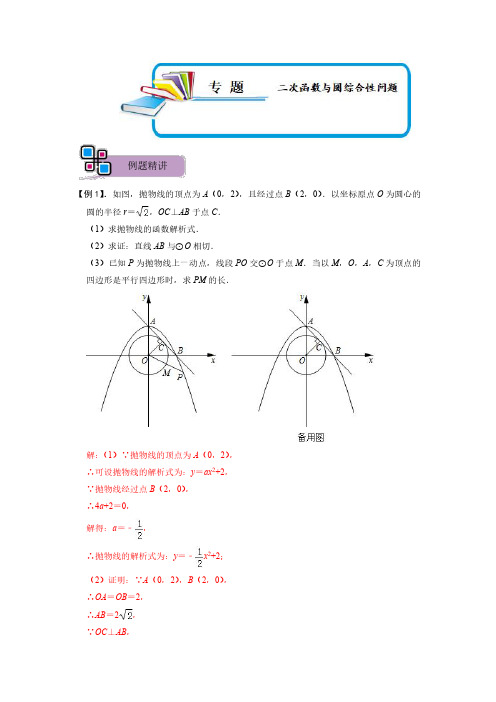
例题精讲【例1】.如图,抛物线的顶点为A(0,2),且经过点B(2,0).以坐标原点O为圆心的圆的半径r=,OC⊥AB于点C.(1)求抛物线的函数解析式.(2)求证:直线AB与⊙O相切.(3)已知P为抛物线上一动点,线段PO交⊙O于点M.当以M,O,A,C为顶点的四边形是平行四边形时,求PM的长.解:(1)∵抛物线的顶点为A(0,2),∴可设抛物线的解析式为:y=ax2+2,∵抛物线经过点B(2,0),∴4a+2=0,解得:a=﹣,∴抛物线的解析式为:y=﹣x2+2;(2)证明:∵A(0,2),B(2,0),∴OA=OB=2,∴AB=2,∵OC⊥AB,∴•OA•OB=•AB•OC,∴×2×2=×2•OC,解得:OC=,∵⊙O的半径r=,∴OC是⊙O的半径,∴直线AB与⊙O相切;(3)∵点P在抛物线y=﹣x2+2上,∴可设P(x,﹣x2+2),以M,O,A,C为顶点的四边形是平行四边形时,可得:AC=OM=,CM=OA=2,∵点C是AB的中点,∴C(1,1),M(1,﹣1),设直线OM的解析式为y=kx,将点M(1,﹣1)代入,得:k=﹣1,∴直线OM的解析式为y=﹣x,∵点P在OM上,∴﹣x2+2=﹣x,解得:x1=1+,x2=1﹣,∴y1=﹣1﹣,y2=﹣1+,∴P1(1+,﹣1﹣),P2(1﹣,﹣1+),如图,当点P位于P1位置时,OP1===(1+)=+,∴P1M=OP1﹣OM=+﹣=,当点P位于P2位置时,同理可得:OP2=﹣,∴P2M=OP2﹣OM=﹣﹣=﹣2;综上所述,PM的长是或﹣2.变式训练【变1-1】.如图,抛物线y=ax2+bx+2与直线AB相交于A(﹣1,0),B(3,2),与x轴交于另一点C.(1)求抛物线的解析式;(2)在y上是否存在一点E,使四边形ABCE为矩形,若存在,请求出点E的坐标;若不存在,请说明理由;(3)以C为圆心,1为半径作⊙O,D为⊙O上一动点,求DA+DB的最小值解:(1)把A(﹣1,0)、B(3,2)代入y=ax2+bx+2,得,解得,∴抛物线的解析式为y=x2+x+2.(2)存在.如图1,作AE⊥AB交y轴于点E,连结CE;作BF⊥x轴于点F,则F(3,0).当y=0时,由x2+x+2=0,得x1=1,x2=4,∴C(4,0),∴CF=AO=1,AF=3﹣(﹣1)=4;又∵BF=2,∴,∵∠BFC=∠AFB=90°,∴△BFC∽△AFB,∴∠CBF=∠BAF,∴∠ABC=∠CBF+∠ABF=∠BAF+∠ABF=90°,∴BC∥AE,∵∠BCF=90°﹣∠BAC=∠EAO,∠BFC=∠EOA=90°,∴△BCF≌△EAO(ASA),∴BC=EA,∴四边形ABCE是矩形;∵OE=FB=2,∴E(0,﹣2).(3)如图2,作FL⊥BC于点L,连结AL、CD.由(2)得∠BFC=90°,BF=2,CF=1,∴CF=CD,CB==.∵∠FLC=∠BFC=90°,∠FCL=∠BCF(公共角),∴△FCL∽△BCF,∴=,∴=,∵∠DCL=∠BCD(公共角),∴△DCL∽△BCD,∴=,∴LD=DB;∵DA+LD≥AL,∴当DA+LD=AL,即点D落在线段AL上时,DA+DB=DA+LD=AL最小.∵CL=CF=,∴BL==,∴BL2=()2=,又∵AB2=22+42=20,∴AL===,DA+DB的最小值为.【例2】.如图1,在平面直角坐标系中,抛物线与x轴分别交于A、B两点,与y轴交于点C(0,6),抛物线的顶点坐标为E(2,8),连结BC、BE、CE.(1)求抛物线的表达式;(2)判断△BCE的形状,并说明理由;(3)如图2,以C为圆心,为半径作⊙C,在⊙C上是否存在点P,使得BP+EP 的值最小,若存在,请求出最小值;若不存在,请说明理由.解:(1)∵抛物线的顶点坐标为E(2,8),∴设该抛物线的表达式为y=a(x﹣2)2+8,∵与y轴交于点C(0,6),∴把点C(0,6)代入得:a=﹣,∴该抛物线的表达式为y=x2+2x+6;(2)△BCE是直角三角形.理由如下:∵抛物线与x轴分别交于A、B两点,∴令y=0,则﹣(x﹣2)2+8=0,解得:x1=﹣2,x2=6,∴A(﹣2,0),B(6,0),∴BC2=62+62=72,CE2=(8﹣6)2+22=8,BE2=(6﹣2)2+82=80,∴BE2=BC2+CE2,∴∠BCE=90°,∴△BCE是直角三角形;(3)⊙C上存在点P,使得BP+EP的值最小且这个最小值为.理由如下:如图,在CE上截取CF=(即CF等于半径的一半),连结BF交⊙C于点P,连结EP,则BF的长即为所求.理由如下:连结CP,∵CP为半径,∴==,又∵∠FCP=∠PCE,∴△FCP∽△PCE,∴==,即FP=EP,∴BF=BP+EP,由“两点之间,线段最短”可得:BF的长即BP+EP为最小值.∵CF=CE,E(2,8),∴由比例性质,易得F(,),∴BF==.变式训练【变2-1】.在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是第四象限内抛物线上的一个动点.(1)求二次函数的解析式;(2)如图甲,当△ACP是以AC为直角边的直角三角形时,求点P的坐标;(3)如图乙,过A,B,P三点作⊙M,过点P作PE⊥x轴,垂足为D.交OM于点E.点P在运动过程中线段DE的长是否变化,若有变化,求出DE的取值范围;若不变,求DE的长.解:(1)把A(﹣2,0),B(4,0)代入y=x2+bx+c得:,解得,∴二次函数的解析式为y=x2﹣x﹣4;(2)如图:由y=x2﹣x﹣4可得C(0,﹣4),设P(x,x2﹣x﹣4),∴AC2=(﹣2﹣0)2+(0+4)2=20,CP2=x2+(x2﹣x)2,AP2=(x+2)2+(x2﹣x ﹣4)2,∵△ACP是以AC为直角边的直角三角形,∴AC2+CP2=AP2,即20+x2+(x2﹣x)2=(x+2)2+(x2﹣x﹣4)2,∴20+x2+(x2﹣x)2=x2+4x+4+(x2﹣x)2﹣8(x2﹣x)+16,解得x=0(与C重合,舍去)或x=3,∴P(3,﹣);(3)点P在运动过程中线段DE的长不变,理由如下:连接AP、BE,如图:∵=,=,∴∠APD=∠DBE,∠DAP=∠DEB,∴△ADP∽△EDB,∴=,∴DE=,设P(m,m2﹣m﹣4),则D(m,0),∵A(﹣2,0),B(4,0),C(0,﹣4),∴AD=m+2,BD=4﹣m,PD=﹣(m2﹣m﹣4)=﹣m2+m+4,∴DE===2,∴DE是定值2,∴点P在运动过程中线段DE的长不变,是定值2.1.如图,已知⊙P的半径为2,圆心P在抛物线y=x2﹣1上运动,当⊙P与坐标轴相切时,圆心P的坐标可以是(,2)或(﹣,2)或(2,1)或(﹣2,1).解:分两种情况:(1)当⊙P与x轴相切时,依题意,可设P(x,2)或P(x,﹣2).①当P的坐标是(x,2)时,将其代入y=x2﹣1,得2=x2﹣1,解得x=±,此时P(,2)或(﹣,2);②当P的坐标是(x,﹣2)时,将其代入y=x2﹣1,得﹣2=x2﹣1,无解.(2)当⊙P与y轴相切时,∵⊙P的半径为2,∴当⊙P与y轴相切时,点P到y轴的距离为2,∴P点的横坐标为2或﹣2,当x=2时,代入y=x2﹣1可得y=1,当x=﹣2时,代入y=x2﹣1可得y=1,∴点P的坐标为(2,1)或(﹣2,1),综上所述,符合条件的点P的坐标是(,2)或(﹣,2)或(2,1)或(﹣2,1);故答案为:(,2)或(﹣,2)或(2,1)或(﹣2,1).2.如图1,抛物线与x轴交于O、A两点,点B为抛物线的顶点,连接OB.(1)求∠AOB的度数;(2)如图2,以点A为圆心,4为半径作⊙A,点M在⊙A上.连接OM、BM,①当△OBM是以OB为底的等腰三角形时,求点M的坐标;②如图3,取OM的中点N,连接BN,当点M在⊙A上运动时,求线段BN长度的取值范围.解:(1)令y=0,则﹣2x=0,解得:x=0或8.∴A(8,0).∴OA=8.∵y=﹣2x=﹣4,∴B(4,﹣4).过点B作BD⊥OA于点D,如图,则OD=4,BD=4,∴OD=BD,∴∠AOB=∠OBD=45°;(2)①设⊙A与x轴交于点C,则C(4,0).连接BC,如图,∵B(4,﹣4),∴BC⊥OA.∵CO=CB=4,∴△CBO是以OB为底的等腰三角形.∴点M与点C重合时,△MBO是以OB为底的等腰三角形.此时点M(4,0);过点A作AM⊥x轴,交⊙A于点M,延长MA交⊙A于点E,连接BE,过点M作MF⊥y轴于点F,如图,则M(8,4),E(8,﹣4),F(,4).∴MF=ME=8.∵B(4,﹣4),∴BE∥x轴.∴BE⊥ME,BE=4.∴∠BEM=∠MFO=90°,BE=OF=4.在△MOF和△MBE中,,∴△MOF≌△MBE(SAS).∴MO=MB.∴△MBO是以OB为底的等腰三角形.此时点M(8,4);综上,当△OBM是以OB为底的等腰三角形时,点M的坐标为(4,0)或(8,4);②设⊙A与x轴交于点C,则C(4,0).连接BC,CN,AM,如图,∵A(8,0),∴点C是OA的中点.∵N为OM的中点,∴CN是△OMA的中位线.∴CN=AM=2.当点M在⊙A上运动时,由三角形的三边的关系定理可知:BC﹣CN≤BN≤BC+CN.∵BC=4,∴4﹣2≤BN≤4+2.∴线段BN长度的取值范围为:2≤BN≤6.3.如图,抛物线y=ax2﹣2ax﹣3a(a>0)与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,且OB=OC.(1)求抛物线的解析式;(2)如图1,若点P是线段BC(不与B,C重合)上一动点,过点P作x轴的垂线交抛物线于M点,连接CM,将△PCM沿CM对折,如果点P的对应点N恰好落在y轴上,求此时点P的坐标;(3)如图2,若第四象限有一动点E,满足BE=OB,过E作EF⊥x轴于点F,设F坐标为(t,0),0<t<3,△BEF的内心为I,连接CI,直接写出CI的最小值.解:(1)在y=ax2﹣2ax﹣3a(a>0)中,令y=0,得:ax2﹣2ax﹣3a=0,解得:x1=3,x2=﹣1,∴A(﹣1,0),B(3,0),∴OB=3,∵OB=OC,∴OC=3,∴C(0,﹣3),∴﹣3a=﹣3,∴a=1,∴抛物线解析式为:y=x2﹣2x﹣3.(2)设直线BC解析式为y=kx+b,∵B(3,0),C(0,﹣3),∴,解得:,∴直线BC解析式为:y=x﹣3,设M点坐标为(m,m2﹣2m﹣3),∵PM⊥x轴,∴P(m,m﹣3),∴PM=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m,∵OB=OC,∠BOC=90°,∴CB=OB,∴CP=m,∵△PCM沿CM对折,点P的对应点N恰好落在y轴上,∴∠PCM=∠NCM,∵PM∥y轴,∴∠NCM=∠PMC,∴∠PCM=∠PMC,∴PC=PM,∴m=﹣m2+3m,整理得:m2+(﹣3)m=0,解得:m1=0(舍去),m2=3﹣,∴当m=3﹣时,m﹣3=﹣,∴P(3﹣,﹣).(3)如图2,连接BI,OI,EI,作△OBI的外接圆⊙M,连接OM,BM,MI,CM,过M作MH⊥y轴于H,∵EF⊥x轴,∴∠BFE=90°,∴∠FBE+∠FEB=90°,∵△BEF的内心为I,∴BI,EI分别平分∠FBE,∠FEB,∴∠IBE=∠FBE,∠IEB=∠FEB,∴∠IBE+∠IEB=(∠FBE+∠FEB)=45°,∴∠BIE=135°,在△BIO和△BIE中,,∴△BIO≌△BIE(SAS),∴∠BIO=∠BIE=135°,∵⊙M是△OBI的外接圆,∴∠OMB=2×(180°﹣∠BIO)=90°,∴OM=BM=OB=,∴MI=OM=,∴∠MOB=∠MOH=45°,∵MH⊥y轴,∴∠HOM=∠HMO=45°,∴OH=HM=OM=,∴CH=OH+OC=+3=,∴CM==,∵CI≥CM﹣MI,当且仅当C、M、I三点共线时,CI取得最小值,∴CI的最小值为﹣.4.已知抛物线y=x2﹣(2m﹣1)x+4m﹣6.(1)试说明对于每一个实数m,抛物线都经过x轴上的一个定点;(2)设抛物线与x轴的两个交点A(x1,0)和B(x2,0)(x1<x2)分别在原点的两侧,且A、B两点间的距离小于6,求m的取值范围;(3)抛物线的对称轴与x轴交于点C,在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由.解:(1)由题意可知:y=(x﹣2)(x﹣2m+3),因此抛物线与x轴的两个交点坐标为:(2,0)(2m﹣3,0),因此无论m取何值,抛物线总与x轴交于(2,0)点;(2)令y=0,有:x2﹣(2m﹣1)x+4m﹣6=0,则:x1+x2=2m﹣1,x1x2=4m﹣6;∵AB<6∴x2﹣x1<6,即(x2﹣x1)2<36,(x1+x2)2﹣4x1x2<36,即(2m﹣1)2﹣4(4m﹣6)<36,解得﹣<x<.①根据A、B分别在原点两侧可知:x1x2<0,即4m﹣6<0,m<.②综合①②可得﹣<m<;(3)假设存在这样的m,设圆M与y轴的切点为D,过M作x轴的垂线设垂足为E.①当C点在x轴正半轴时,x=>0,因此<m<,∵弧BC=弧CD,因此BC=CD.OC=,CD=BC=OB﹣OC=2﹣=,EC=BC=,OE=MD=OC+CE=+=.易知:OD=ME,即OD2=ME2∴CD2﹣OC2=CM2﹣CE2,()2﹣()2=()2﹣()2;解得m=,符合m的取值范围.②当C点在x轴负半轴时,x=<0,因此﹣<m<,同①可求得OC=,CD=AC=,CE=,MD=OE=.同理有:CD2﹣OC2=MC2﹣CE2()2﹣()2=()2﹣()2化简得:m2=,∴m=±,均不符合m的取值范围,因此这种情况不成立.综上所述,存在符合条件的m,且m=.5.已知抛物线y=x2+mx﹣2m﹣4(m>0).(1)证明:该抛物线与x轴总有两个不同的交点;(2)设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.①试判断:不论m取任何正数,⊙P是否经过y轴上某个定点?若是,求出该定点的坐标;若不是,说明理由;②若点C关于直线x=﹣的对称点为点E,点D(0,1),连接BE,BD,DE,△BDE的周长记为l,⊙P的半径记为r,求的值.解:(1)令y=0,∴x2+mx﹣2m﹣4=0,∴△=m2﹣4[﹣2m﹣4]=m2+8m+16,∵m>0,∴Δ>0,∴该抛物线与x轴总有两个不同的交点;(2)令y=0,∴x2+mx﹣2m﹣4=0,∴(x﹣2)[x+(m+2)]=0,∴x=2或x=﹣(m+2),∴A(2,0),B(﹣(m+2),0),∴OA=2,OB=m+2,令x=0,∴y=﹣2(m+2),∴C(0,﹣2(m+2)),∴OC=2(m+2),①通过定点(0,1)理由:如图,∵点A,B,C在⊙P上,∴∠OCB=∠OAF,在Rt△BOC中,tan∠OCB===,在Rt△AOF中,tan∠OAF===,∴OF=1,∴点F的坐标为(0,1);②如图1,由①知,点F(0,1),∵D(0,1),∴点D在⊙P上,∵点E是点C关于抛物线的对称轴的对称点,∴∠DCE=90°,∵⊙P是△ABC的外接圆,∴点P在抛物线的对称轴上,∴点E在⊙P上,∴DE是⊙P的直径,∴∠DBE=90°,∵∠BED=∠OCB,∴tan∠BED=,设BD=n,在Rt△BDE中,tan∠BED===,∴BE=2n,根据勾股定理得,DE==n,∴l=BD+BE+DE=(3+)n,r=DE=n,∴==.6.如图所示,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y轴分别相交于M (4,0),N(0,3)两点.已知抛物线开口向上,与⊙C交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x轴于点D.(1)求线段CD的长及顶点P的坐标;(2)求抛物线的函数表达式;=8S△QAB,(3)设抛物线交x轴于A,B两点,在抛物线上是否存在点Q,使得S四边形OPMN 且△QAB∽△OBN成立?若存在,请求出Q点的坐标;若不存在,请说明理由.解:(1)如图,连接OC,∵M(4,0),N(0,3),∴OM=4,ON=3,∴MN=5,∴OC=MN=,∵CD为抛物线对称轴,∴OD=MD=2,在Rt△OCD中,由勾股定理可得CD===,∴PD=PC﹣CD=﹣=1,∴P(2,﹣1);(2)∵抛物线的顶点为P(2,﹣1),∴设抛物线的函数表达式为y=a(x﹣2)2﹣1,∵抛物线过N(0,3),∴3=a(0﹣2)2﹣1,解得a=1,∴抛物线的函数表达式为y=(x﹣2)2﹣1,即y=x2﹣4x+3;(3)在y=x2﹣4x+3中,令y=0可得0=x2﹣4x+3,解得x=1或x=3,∴A(1,0),B(3,0),∴AB=3﹣1=2,∵ON=3,OM=4,PD=1,=S△OMP+S△OMN=OM•PD+OM•ON=×4×1+×4×3=8=8S△QAB,∴S四边形OPMN=1,∴S△QAB设Q点纵坐标为y,则×2×|y|=1,解得y=1或y=﹣1,当y=1时,则△QAB为钝角三角形,而△OBN为直角三角形,不合题意,舍去,当y=﹣1时,可知P点即为所求的Q点,∵D为AB的中点,∴AD=BD=QD,∴△QAB为等腰直角三角形,∵ON=OB=3,∴△OBN为等腰直角三角形,∴△QAB∽△OBN,综上可知存在满足条件的点Q,其坐标为(2,﹣1).7.如图,已知二次函数的图象顶点在原点,且点(2,1)在二次函数的图象上,过点F(0,1)作x轴的平行线交二次函数的图象于M、N两点.(1)求二次函数的表达式;(2)P为平面内一点,当△PMN是等边三角形时,求点P的坐标;(3)在二次函数的图象上是否存在一点E,使得以点E为圆心的圆过点F和点N,且与直线y=﹣1相切.若存在,求出点E的坐标,并求⊙E的半径;若不存在,说明理由.解:(1)∵二次函数的图象顶点在原点,故设二次函数表达式为:y=ax2,将(2,1)代入上式并解得:a=,故二次函数表达式为:y=x2;(2)将y=1代入y=x2并解得:x=±2,故点M、N的坐标分别为(﹣2,1)、(2,1),则MN=4,∵△PMN是等边三角形,∴点P在y轴上且PM=4,∴PF=2;∵点F(0,1),∴点P的坐标为(0,1+2)或(0,1﹣2);(3)假设二次函数的图象上存在一点E满足条件,设点Q是FN的中点,则点Q(1,1),故点E在FN的中垂线上.∴点E是FN的中垂线与y=x2图象的交点,∴y=×12=,则点E(1,),EN==,同理EF==,点E到直线y=﹣1的距离为|﹣(﹣1)|=,故存在点E,使得以点E为圆心半径为的圆过点F,N且与直线y=﹣1相切.8.已知二次函数y=﹣x2+bx+c+1,①当b=1时,求这个二次函数的对称轴的方程;②若c=﹣b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?③若二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<x2,b>0,与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足=,求二次函数的表达式.解:①二次函数y=﹣x2+bx+c+1的对称轴为x=,当b=1时,=,∴当b=1时,求这个二次函数的对称轴的方程为x=.②二次函数y=﹣x2+bx+c+1的顶点坐标为(,),∵二次函数的图象与x轴相切且c=﹣b2﹣2b,∴,解得:b=,∴b为,二次函数的图象与x轴相切.③∵AB是半圆的直径,∴∠AMB=90°,∴∠OAM+∠OBM=90°,∵∠AOM=∠MOB=90°,∴∠OAM+∠OMA=90°,∴∠OMA=∠OBM,∴△OAM∽△OMB,∴,∴OM2=OA•OB,∵二次函数的图象与x轴交于点A(x1,0),B(x2,0),∴OA=﹣x1,OB=x2,x1+x2,=b,x1•x2=﹣(c+1),∵OM=c+1,∴(c+1)2=c+1,解得:c=0或c=﹣1(舍去),∴c=0,OM=1,∵二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足=,∴AD=BD,DF=4DE,DF∥OM,∴△BDE∽△BOM,△AOM∽△ADF,∴,,∴DE=,DF=,∴×4,∴OB=4OA,即x2=﹣4x1,∵x1•x2=﹣(c+1)=﹣1,∴,解得:,∴b=﹣+2=,∴二次函数的表达式为y=﹣x2+x+1.9.已知抛物线y=ax2+bx+c过点A(0,2).若该抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足;当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B,C,且△ABC 有一个内角为60°.①求抛物线的解析式;②若点P与点O关于点A对称,且O,M,N三点共线,求证:PA平分∠MPN.解:①当x1<x2<0时,x1﹣x2<0,∵(x1﹣x2)(y1﹣y2)>0,∴y1﹣y2<0,∴当x<0时,y随x的增大而增大,当0<x1<x2时,x1﹣x2<0,∵(x1﹣x2)(y1﹣y2)<0,∴y1﹣y2>0,∴当x>0时,y随x的增大而减小.∴抛物线关于y轴对称,∴b=0,∵抛物线y=ax2+bx+c过点A(0,2),∴c=2,如图,连接OB、OC,设BC y轴于点D.由对称性可知,△ABC为等腰三角形,又∵△ABC有一个内角为60°,∴△ABC是等边三角形,∴OD=OA=1,CD=OD=,∴B(﹣,﹣1),C(,﹣1),将C点坐标代入y=ax2+2可求得a=﹣1,∴抛物线的解析式为y=﹣x2+2.②设直线OM的解析式为y=k1x,∵O、M、N三点共线,∴x1≠0,x2≠0,且=,化为x1﹣x2=,∵x1≠x2,∴x1x2=﹣2,∴,∴,设点N关于y轴的对称点为N',则N'的坐标为,∵点P是点O关于点A的对称点,∴OP﹣2OA=4,即点P的坐标为(0,4),设直线PM的解析式为y=k2x+4,∵点M的坐标为,∴,∴,∴直线PM的解析式为x+4.∵,即N'在直线PM上,∴PA平分∠MPN.10.如图,在平面直角坐标系xOy中,O为坐标原点,点A(4,0),点B(0,4),△ABO 的中线AC与y轴交于点C,且⊙M经过O,A,C三点.(1)求圆心M的坐标;(2)若直线AD与⊙M相切于点A,交y轴于点D,求直线AD的函数表达式;(3)在(2)的条件下,在过点B且以圆心M为顶点的抛物线上有一动点P,过点P作PE∥y轴,交直线AD于点E.若以PE为半径的⊙P与直线AD相交于另一点F.当EF =4时,求点P的坐标.解:(1)点B(0,4),则点C(0,2),∵点A(4,0),则点M(2,1);(2)应该是圆M与直线AD相切,则∠CAD=90°,设:∠CAO=α,则∠CAO=∠ODA=∠PEH=α,tan∠CAO===tanα,则sinα=,cosα=,AC=,则CD==10,则点D(0,﹣8),将点A、D的坐标代入一次函数表达式:y=mx+n并解得:直线AD的表达式为:y=2x﹣8;(3)抛物线的表达式为:y=a(x﹣2)2+1,将点B坐标代入上式并解得:a=,故抛物线的表达式为:y=x2﹣3x+4,过点P作PH⊥EF,则EH=EF=2,cos∠PEH=,解得:PE=5,设点P(x,x2﹣3x+4),则点E(x,2x﹣8),则PE=x2﹣3x+4﹣2x+8=5,解得x=或2,则点P(,)或(2,1).11.如图,抛物线y=ax2+6ax(a为常数,a>0)与x轴交于O,A两点,点B为抛物线的顶点,点D的坐标为(t,0)(﹣3<t<0),连接BD并延长与过O,A,B三点的⊙P相交于点C.(1)求点A的坐标;(2)过点C作⊙P的切线CE交x轴于点E.①如图1,求证:CE=DE;②如图2,连接AC,BE,BO,当a=,∠CAE=∠OBE时,求﹣的值.解:(1)令ax2+6ax=0,ax(x+6)=0,∴A(﹣6,0);(2)①证明:如图,连接PC,连接PB,延长交x轴于点M,∵⊙P过O、A、B三点,B为顶点,∴PM⊥OA,∠PBC+∠BDM=90°,又∵PC=PB,∴∠PCB=∠PBC,∵CE为切线,∴∠PCB+∠ECD=90°,又∵∠BDM=∠CDE,∴∠ECD=∠CDE,∴CE=DE.②解:设OE=m,点D的坐标为(t,0),∵∠CAE=∠CBO,∠CAE=∠OBE,∴∠CBO=∠EBO,由角平分线成比例定理可得:,即:,∴,∴,∴,=,=.12.抛物线y=﹣x2+x﹣1与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,其顶点为D.将抛物线位于直线l:y=t(t<)上方的部分沿直线l向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象.(1)点B,D的坐标分别为(3,0),(,);(2)如图①,抛物线翻折后,点D落在点E处,当点E在△ABC内(含边界)时,求t的取值范围;(3)如图②,当t=0时,点Q是“M”形新图象上一动点.①直接写出“M”形图象AB段的函数关系式;②是否存在以CQ为直径的圆与x轴相切于点P?若存在,求出点P的坐标;若不存在,请说明理由.解:(1)令y=0,则﹣x2+x﹣1=0,解得x=3或x=,∴B(3,0),A(,0),令x=0,则y=﹣1,∴C(0,﹣1),∵y=﹣x2+x﹣1=﹣(x﹣)2+,∴顶点D(,),故答案为:(3,0),(,);(2)∵E与D关于直线y=t对称,∴E(,2t﹣),设直线BC的解析式为y=kx+b,将B(3,0),C(0,﹣1)代入,得,∴,∴y=x﹣1,当x=时,y=﹣,∵E点在△ABC内(含边界),∴2t﹣≥﹣,∴t≥,∵2t﹣≤0,∴t≤,∵t<,∴t的取值范围是≤t≤;(3)①当t=0时,y=﹣x2+x﹣1关于x轴对称的函数为y=x2﹣x+1,∴“M”形图象AB段的函数关系式为y=x2﹣x+1(≤x≤3);②存在点P,理由如下:设Q点的横坐标为m,∵以CQ为直径的圆与x轴相切于点P,∴P点的横坐标为m,当m>3或m<时,Q(m,﹣m2+m﹣1),∵△CPQ为直角三角形,∴CQ2=CP2+PQ2,即m2+(﹣m2+m)2=m2+1+m2+(﹣m2+m﹣1)2,解得m=或m=,∴P(,0)或P(,0);当≤m≤3时,Q(m,m2﹣m+1),∵△CPQ为直角三角形,∴CQ2=CP2+PQ2,即m2+(m2﹣m+2)2=m2+1+m2+(m2﹣m+1)2,解得m=2或m=,∴P(,0)或P(1,0);综上所述:存在以CQ为直径的圆与x轴相切于点P,P点坐标为(,0)或(,0)或(,0)或P(1,0).13.已知抛物线y=ax2+bx+c过点A(0,2).(1)若点(﹣,0)也在该抛物线上,求a,b满足的关系式;(2)若该抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为心,OA为半径的圆与抛物线的另两个交点为B,C,且△ABC有一个内角为60°.①求抛物线的解析式;②若点P与点O关于点A对称,且O,M,N三点共线,求证:PA平分∠MPN.解:(1)∵抛物线y=ax2+bx+c过点A(0,2),∴c=2.又∵点(﹣,0)也在该抛物线上,∴a(﹣)2+b(﹣)+c=0,∴2a﹣b+2=0(a≠0).(2)①∵当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0,∴x1﹣x2<0,y1﹣y2<0,∴当x<0时,y随x的增大而增大;同理:当x>0时,y随x的增大而减小,∴抛物线的对称轴为y轴,开口向下,∴b=0.∵OA为半径的圆与抛物线的另两个交点为B、C,∴△ABC为等腰三角形,又∵△ABC有一个内角为60°,∴△ABC为等边三角形.设线段BC与y轴交于点D,则BD=CD,且∠OCD=30°,又∵OB=OC=OA=2,∴CD=OC•cos30°=,OD=OC•sin30°=1.不妨设点C在y轴右侧,则点C的坐标为(,﹣1).∵点C在抛物线上,且c=2,b=0,∴3a+2=﹣1,∴a=﹣1,∴抛物线的解析式为y=﹣x2+2.②证明:由①可知,点M的坐标为(x1,﹣+2),点N的坐标为(x2,﹣+2).直线OM的解析式为y=k1x(k1≠0).∵O、M、N三点共线,∴x1≠0,x2≠0,且=,∴﹣x1+=﹣x2+,∴x1﹣x2=﹣,∴x1x2=﹣2,即x2=﹣,∴点N的坐标为(﹣,﹣+2).设点N关于y轴的对称点为点N′,则点N′的坐标为(,﹣+2).∵点P是点O关于点A的对称点,∴OP=2OA=4,∴点P的坐标为(0,4).设直线PM的解析式为y=k2x+4,∵点M的坐标为(x1,﹣+2),∴﹣+2=k2x1+4,∴k2=﹣,∴直线PM的解析式为y=﹣x+4.∵﹣•+4==﹣+2,∴点N′在直线PM上,∴PA平分∠MPN.14.如图,已知二次函数y=ax2+bx+3(a≠0)的图象经过点A(3,0),B(4,1),且与y 轴交于点C,连接AB、AC、BC.(1)求此二次函数的关系式;(2)判断△ABC的形状;若△ABC的外接圆记为⊙M,请直接写出圆心M的坐标;(3)若将抛物线沿射线BA方向平移,平移后点A、B、C的对应点分别记为点A1、B1、C1,△A1B1C1的外接圆记为⊙M1,是否存在某个位置,使⊙M1经过原点?若存在,求出此时抛物线的关系式;若不存在,请说明理由.解:(1)把点A(3,0),B(4,1)代入y=ax2+bx+3中,,解得:,所以所求函数关系式为:y=x2﹣x+3;(2)△ABC是直角三角形,过点B作BD⊥x轴于点D,易知点C坐标为:(0,3),所以OA=OC,所以∠OAC=45°,又∵点B坐标为:(4,1),∴AD=BD,∴∠DAB=45°,∴∠BAC=180°﹣45°﹣45°=90°,∴△ABC是直角三角形,圆心M的坐标为:(2,2);(3)存在取BC的中点M,过点M作ME⊥y轴于点E,∵M的坐标为:(2,2),∴MC==,OM=2,∴∠MOA=45°,又∵∠BAD=45°,∴OM∥AB,∴要使抛物线沿射线BA方向平移,且使⊙M1经过原点,则平移的长度为:2﹣或2+;∵∠BAD=45°,∴抛物线的顶点向左、向下均分别平移=个单位长度或=个单位长度,∵y=x2﹣x+3=(x﹣)2﹣,∴平移后抛物线的关系式为:y=(x﹣+)2﹣﹣,即y=(x﹣)2﹣,或y=(x﹣+)2﹣﹣,即y=(x﹣)2﹣.综上所述,存在一个位置,使⊙M1经过原点,此时抛物线的关系式为:y=(x﹣)2﹣或y=(x﹣)2﹣.15.已知抛物线C1:y=ax2过点(2,2)(1)直接写出抛物线的解析式y=x2;(2)如图,△ABC的三个顶点都在抛物线C1上,且边AC所在的直线解析式为y=x+b,若AC边上的中线BD平行于y轴,求的值;(3)如图,点P的坐标为(0,2),点Q为抛物线上C1上一动点,以PQ为直径作⊙M,直线y=t与⊙M相交于H、K两点是否存在实数t,使得HK的长度为定值?若存在,求出HK的长度;若不存在,请说明理由.解:(1)把点(2,2)坐标代入y=ax2,解得:a=,∴抛物线的解析式为y=x2;(2)把y=x+b和y=x2得:x2﹣2x﹣2b=0,设A、C两点的坐标为(x1,y1)、(x2,y2),则:x1+x2=2,x1•x2=﹣2b,点D坐标为(,),即;D(1,1+b),B坐标为(1,),AC2=[(x2﹣x1)]2=16b+8BD=+b,∴=16;(3)设点Q坐标为(a,a2),点P的坐标为(0,2),由P、Q坐标得点M的坐标为(,a2+1),设圆的半径为r,由P(0,2)、M两点坐标可以求出r2=+(a2﹣1)2=a4﹣a2+1,设点M到直线y=t的距离为d,则d2=(a2+1﹣t)2=a4+a2+1+t2﹣2t﹣a2t,则HK=2=2,当t﹣=0时,HK为常数,t=,HK=.16.定义:平面直角坐标系xOy中,过二次函数图象与坐标轴交点的圆,称为该二次函数的坐标圆.(1)已知点P(2,2),以P为圆心,为半径作圆.请判断⊙P是不是二次函数y=x2﹣4x+3的坐标圆,并说明理由;(2)如图1,已知二次函数y=x2﹣4x+4图象的顶点为A,坐标圆的圆心为P,求△POA 周长的最小值;(3)如图2,已知二次函数y=ax2﹣4x+4(0<a<1)图象交x轴于点A,B,交y轴于点C,与坐标圆的第四个交点为D,连结PC,PD.若∠CPD=120°,求a的值.解:(1)对于二次函数y=x2﹣4x+3,当x=0时,y=3;当y=0时,解得x=1或x=3,∴二次函数图象与x轴交点为A(1,0),B(3,0),与y轴交点为C(0,3),∵点P(2,2),∴PA=PB=PC=,∴⊙P是二次函数y=x2﹣4x+3的坐标圆.(2)如图1,连接PH,∵二次函数y=x2﹣4x+4图象的顶点为A,坐标圆的圆心为P,∴A(2,0),与y轴的交点H(0,4),∴△POA周长=PO+PA+OA=PO+PH+2≥OH+2=6,∴△POA周长的最小值为6.(3)如图2,连接CD,PA,设二次函数y=ax2﹣4x+4图象的对称轴l与CD交于点E,与x轴交于点F,由对称性知,对称轴l经过点P,且l⊥CD,∵AB=,∴AF=BF=,∵∠CPD=120°,PC=PD,C(0,4),∴∠PCD=∠PDC=30°,设PE=m,则PA=PC=2m,CE=m,PF=4﹣m,∵二次函数y=ax2﹣4x+4图象的对称轴l为,∴,即,在Rt△PAF中,PA2=PF2+AF2,∴,即,化简,得,解得,∴.17.如图,在平面直角坐标系中,抛物线y=x2﹣bx﹣c交x轴于点A,B,点B的坐标为(4,0),与y轴于交于点C(0,﹣2).(1)求此抛物线的解析式;(2)在抛物线上取点D,若点D的横坐标为5,求点D的坐标及∠ADB的度数;(3)在(2)的条件下,设抛物线对称轴l交x轴于点H,△ABD的外接圆圆心为M(如图1),过点B作⊙M的切线交于点P(如图2),设Q为⊙M上一动点,则在点运动过程中的值是否变化?若不变,求出其值;若变化,请说明理由.解:(1)将点B、C的坐标代入抛物线表达式得:,解得:,∴抛物线的解析式为y=x2﹣x﹣2;(2)当x=5时,y=x2﹣x﹣2=3,故D的坐标为(5,3),令y=0,则x=4(舍去)或﹣1,故点A(﹣1,0),如图,连接BD,作BN⊥AD于N,∵A(﹣1,0),B(4,0),C(0,﹣2),∴AD=3,BD=,AB=5,==,∵S△ABD∴BN=,∴sin∠BDN===,∴∠BDN=45°,∴∠ADB=∠BDN=45°;(3)不变.如图,连接MQ,MB,∵过点B作⊙M的切线交1于点P,∴∠MBP=90°,∵∠MBO=45°,∴∠PBH=45°,∴PH=HB=2.5,∵==,==,∵∠HMQ=∠QMP,∴△HMQ∽△QMP,∴==,∴在点Q运动过程中的值不变,其值为.18.如图,抛物线y=ax2+bx+c(a≠0),与x轴交于A(4,0)、O两点,点D(2,﹣2)为抛物线的顶点.(1)求该抛物线的解析式;(2)点E为AO的中点,以点E为圆心、以1为半径作⊙E,交x轴于B、C两点,点M为⊙E上一点.①射线BM交抛物线于点P,设点P的横坐标为m,当tan∠MBC=2时,求m的值;②如图2,连接OM,取OM的中点N,连接DN,则线段DN的长度是否存在最大值或最小值?若存在,请求出DN的最值;若不存在,请说明理由.解:(1)由抛物线顶点式表达式得:y=a(x﹣2)2﹣2,将点A的坐标代入上式并解得:a=,故抛物线的表达式为:y=(x﹣2)2﹣2=x2﹣2x①;(2)①点E是OA的中点,则点E(2,0),圆的半径为1,则点B(1,0),当点P在x轴下方时,如图1,∵tan∠MBC=2,故设直线BP的表达式为:y=﹣2x+s,将点B(1,0)的坐标代入上式并解得:s=2,故直线BP的表达式为:y=﹣2x+2②,联立①②并解得:x=±2(舍去﹣2),故m=2;当点P在x轴上方时,同理可得:m=4±2(舍去4﹣2);故m=2或4+2;②存在,理由:连接BN、BD、EM,则BN是△OEM的中位线,故BN=EM=,而BD==,在△BND中,BD﹣BN≤ND≤BD+BN,即﹣0.5≤ND≤+0.5,故线段DN的长度最小值和最大值分别为﹣0.5和+0.5.19.如图,在平面直角坐标系上,一条抛物线y=ax2+bx+c(a≠0)经过A(1,0)、B(3,0)、C(0,3)三点,连接BC并延长.(1)求抛物线的解析式;(2)点M是直线BC在第一象限部分上的一个动点,过M作MN∥y轴交抛物线于点N.1°求线段MN的最大值;2°当MN取最大值时,在线段MN右侧的抛物线上有一个动点P,连接PM、PN,当△PMN的外接圆圆心Q在△PMN的边上时,求点P的坐标.解:(1)把A、B、C三点的坐标代入抛物线y=ax2+bx+c(a≠0)中,得,解得,,∴抛物线的解析式为:y =x 2﹣4x +3;(2)1°设直线BC 的解析式为y =mx +n (m ≠0),则,解得,,∴直线BC 的解析式为:y =﹣x +3,设M (t ,﹣t +3)(0<t <3),则N (t ,t 2﹣4t +3),∴MN =﹣t 2+3t =﹣,∴当t =时,MN 的值最大,其最大值为;2°∵△PMN 的外接圆圆心Q 在△PMN 的边上,∴△PMN 为直角三角形,由1°知,当MN 取最大值时,M (),N (),①当∠PMN =90°时,PM ∥x 轴,则P 点与M 点的纵坐标相等,∴P 点的纵坐标为,当y =时,y =x 2﹣4x +3=,解得,x =,或x =(舍去),∴P ();②当∠PNM =90°时,PN ∥x 轴,则P 点与N 点的纵坐标相等,∴P 点的纵坐标为﹣,当y =﹣时,y =x 2﹣4x +3=﹣,解得,x =,或x =(舍去),∴P (,);③当∠MPN =90°时,则MN 为△PMN 的外接圆的直径,∴△PMN的外接圆的圆心Q为MN的中点,∴Q(),半径为,过Q作QK∥x轴,与在MN右边的抛物线图象交于点K,如图②,令y=,得y=x2﹣4x+3=,解得,x=<(舍),或x=,∴K(,),∴QK=>,即K点在以MN为直径的⊙Q外,设抛物线y=x2﹣4x+3的顶点为点L,则l(2,﹣1),连接LK,如图②,则L到QK的距离为,LK=,设Q点到LK的距离为h,则,∴=,∴直线LK下方的抛物线与⊙Q没有公共点,∵抛物线中NL部分(除N点外)在过N点与x轴平行的直线下方,∴抛物线中NL部分(除N点外)与⊙Q没有公共点,∵抛物线K点右边部分,在过K点与y轴平行的直线的右边,∴抛物线K点右边部分与⊙Q没有公共点,综上,⊙Q与MN右边的抛物线没有交点,∴在线段MN右侧的抛物线上不存在点P,使△PMN的外接圆圆心Q在MN边上;综上,点P的坐标为()或().20.如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴分别相交于A、B两点,与y轴相交于点C,下表给出了这条抛物线上部分点(x,y)的坐标值:x…﹣10123…y…03430…(1)求出这条抛物线的解析式;(2)如图1,直线y=kx+1(k<0)与抛物线交于P,Q两点,交抛物线的对称轴于点T,若△QMT的面积是△PMT面积的两倍,求k的值;(3)如图2,点D是第四象限内抛物线上一动点,过点D作DF⊥x轴,垂足为F,△ABD的外接圆与DF相交于点E.试问:线段EF的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.解:(1)根据表格可得出A(﹣1,0),B(3,0),C(0,3),设抛物线解析式为y=a(x+1)(x﹣3),将C(0,3)代入,得:3=a(0+1)(0﹣3),解得:a=﹣1,∴y=﹣(x+1)(x﹣3)=﹣x2+2x+3,∴该抛物线解析式为y=﹣x2+2x+3;(2)设P(x1,y1),Q(x2,y2),令y=kx+1=﹣x2+2x+3,整理得:x2+(k﹣2)x﹣2=0,∴x1+x2=2﹣k,x1x2=﹣2①,∵△QMT的面积是△PMT面积的两倍,∴MT•(x2﹣1)=2×MT•(1﹣x1),∴2x1+x2=3,即x2=3﹣2x1②,将②代入①得:2x12﹣3x1﹣2=0,解得:x1=2或,∴或,∴k=1或,∵k<0,∴k=﹣;(3)线段EF的长为定值1,如图,连接BE,设D(t,﹣t2+2t+3),且t>3,∵EF⊥x轴,∴DF=﹣(﹣t2+2t+3)=t2﹣2t﹣3,∵F(t,0),∴BF=OF﹣OB=t﹣3,AF=t﹣(﹣1)=t+1,∵四边形ABED是圆内接四边形,∴∠DAF+∠BED=180°,∵∠BEF+∠BED=180°,∴∠DAF=∠BEF,∵∠AFD=∠EFB=90°,∴△AFD∽△EFB,∴,∴,∴EF===1,∴线段EF的长为定值1.21.如图,抛物线y=﹣x2+2x+3与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.(1)直接写出A、B、C三点的坐标和抛物线的对称轴.(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?②△BCF的面积为S,求S与m的函数关系式,并求出S的最大值.(3)现有一个以原点O为圆心,长为半径的圆沿y轴正半轴方向向上以每秒1个单位的速度运动,问几秒后⊙O与直线AC相切?解:(1)设0=﹣x2+2x+3,解得:x=﹣1或3,∵抛物线y=﹣x2+2x+3与x相交于AB(点A点B左侧),∴A(﹣1,0),B(3,0),∵抛物线与y轴相交于点C,∴C(0,3),∴抛物线的对称轴是:直线x=1.(2)①设直线BC的函数关系式为y=kx+b,把B(3,0),C(0,3)分别代入,得,解得:k=﹣1,b=3∴直线BC的函数关系式为y=﹣x+3.当x=1时,y=﹣1+3=2,∴E(1.2).当x=m时,y=﹣m+3,∴P(m,﹣m+3)在y=﹣x2+2x+3中,当x=1时,y=4,∴D(1,4).当x=m时,y=﹣m2+2m+3,∴F(m,﹣m2+2m+3),∴线段DE=4﹣2=2,线段PF=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,∵PF∥DE∴当PF=DE时,四边形PEDF为平行四边形.由﹣m2+3m=2,解得m=2或m=1(不合题意,舍去).因此,当m=2时,四边形PEDF为平行四边形.②设直线PF与x轴交于点M,由B(3,0),O(0,0),可得OB=OM+MB=3.+S△CPF,∵S=S△EPF即S=PF•BM+PF•OM=PF(BM+OM)=PF•OB,∴S=×3(﹣m2+3m)=﹣m2+m(0≤m≤3)∴当m=﹣=时S最大值=;。
二次函数与圆综合训练(含解析)
二次函数与圆综合提高(压轴题)1、如图,在等边△ABC中,AB=3,D、E分别是AB、AC上的点,且DE∥BC,将△ADE沿DE 翻折,与梯形BCED重叠的部分记作图形L.(1)求△ABC的面积;(2)设AD=x,图形L的面积为y,求y关于x的函数解析式;∴MO=OE,∠MOE=120°,∴∠OME=30°,∴∠DME=90°,∴DE是直径,S⊙O=π×12=π.2、(2013•压轴题)如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(﹣4,0),点P在射线AB上运动,连结CP与y轴交于点D,连结BD.过P,D,B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q于点F,连结EF,BF.(1)求直线AB的函数解析式;(2)当点P在线段AB(不包括A,B两点)上时.①求证:∠BDE=∠ADP;②设DE=x,DF=y.请求出y关于x的函数解析式;(3)请你探究:点P在运动过程中,是否存在以B,D,F为顶点的直角三角形,满足两条直角边之比为2:1?如果存在,求出此时点P的坐标:如果不存在,请说明理由.解:(1)设直线AB的函数解析式为y=kx+4,代入(4,0)得:4k+4=0,解得:k=﹣1,则直线AB的函数解析式为y=﹣x+4;(2)①由已知得:OB=OC,∠BOD=∠COD=90°,又∵OD=OD,∴△BOD≌△COD,∴∠BOD=∠CDO,∵∠CDO=∠ADP,∴∠BDE=∠ADP,②连结PE,∵∠ADP是△DPE的一个外角,∴∠ADP=∠DEP+∠DPE,∵∠BDE是△ABD的一个外角,∴∠BDE=∠ABD+∠OAB,∵∠ADP=∠BDE,∠DEP=∠ABD,∴∠DPE=∠OAB,∵OA=OB=4,∠AOB=90°,OD=43, ∴点D 的坐标为(0,﹣43), 直线CD 的解析式为:y=﹣13x ﹣43, 由得:,∴点P 的坐标为(8,﹣4),综上所述,点P 的坐标为(2,2)或(8,﹣4).3、抛物线y=x ²-bx-3b+3过A 、B 两点(点A 在点B 的左边),交y轴于点C ,且经过点(b -2,2b 2-5b -1).(1)求这条抛物线的解析式;(2)⊙M 过A 、B 、C 三点,交y 轴于另一点D ,求点M 的坐标;(3)连接AM 、DM ,将∠AMD 绕点M 顺时针旋转,两边MA 、MD 与x轴、y 轴分别交于点E 、F ,若△DMF 为等腰三角形,求点E 的坐标.解析:(1)把点(b -2,2b 2-5b -1)代入解析式,得2b 2-5b -1=(b -2)2+b (b -2)-3b +3, ……………1′解得b =2.∴抛物线的解析式为y =x 2+2x -3. ……………2′(2)由x 2+2x -3=0,得x =-3或x=1.∴A (-3,0)、B (1,0)、C (0,-3).抛物线的对称轴是直线x =-1,圆心M 在直线x =-1上. ……………3′∴设M (-1,n ),作MG ⊥x 轴于G ,MH ⊥y 轴于H ,连接MC 、MB .∴MH =1,BG =2. ……………4′∵MB =MC ,∴BG 2+MG 2=MH 2+CH 2,即4+n 2=1+(3+n )2,解得n=-1,∴点M (-1,-1) ……………5′(3)如图,由M (-1,-1),得MG =MH .∵MA =MD ,∴Rt △AMG ≌RtDMH ,∴∠1=∠2.由旋转可知∠3=∠4. ∴△AME ≌△DMF .若△DMF 为等腰三角形,则△AME 为等腰三角形. ……………6′设E (x ,0),△AME 为等腰三角形,分三种情况:①AE =AM =5,则x=5-3,∴E (5-3,0);②∵M 在AB 的垂直平分线上,∴MA =ME =MB ,∴E (1,0) ……………7′③点E 在AM 的垂直平分线上,则AE =ME .AE =x +3,ME 2=MG 2+EG 2=1+(-1-x )2,∴(x +3)2=1+(-1-x )2,解得x =47-,∴E (47-,0). ∴所求点E 的坐标为(5-3,0),(1,0),(47-,0) ……………8′4、(2013•压轴题)如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=.(1)求抛物线的解析式;(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA 面积的最大值;(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.:解:(1)如答图1所示,过点D作DE⊥x轴于点E,则DE=3,OE=2.∵tan∠DBA==,∴BE=6,∴OB=BE﹣OE=4,∴B(﹣4,0).∵点B(﹣4,0)、D(2,3)在抛物线y=ax2+bx﹣2(a≠0)上,∴,解得,∴抛物线的解析式为:y=x2+x﹣2.(2)抛物线的解析式为:y=x2+x﹣2,令x=0,得y=﹣2,∴C(0,﹣2),令y=0,得x=﹣4或1,∴A(1,0).设点M坐标为(m,n)(m<0,n<0),如答图1所示,过点M作MF⊥x轴于点F,则MF=﹣n,OF=﹣m,BF=4+m.S四边形BMCA=S△BMF+S梯形MFOC+S△AOC=BF•MF+(MF+OC)•OF+OA•OC=(4+m)×(﹣n)+(﹣n+2)×(﹣m)+×1×2=﹣2n﹣m+1∵点M(m,n)在抛物线y=x2+x﹣2上,∴n=m2+m﹣2,代入上式得:S四边形BMCA=﹣m2﹣4m+5=﹣(m+2)2+9,∴当m=﹣2时,四边形BMCA面积有最大值,最大值为9.(3)假设存在这样的⊙Q.如答图2所示,设直线x=﹣2与x轴交于点G,与直线AC交于点F.设直线AC的解析式为y=kx+b,将A(1,0)、C(0,﹣2)代入得:,解得:k=2,b=﹣2,∴直线AC解析式为:y=2x﹣2,令x=﹣2,得y=﹣6,∴F(﹣2,﹣6),GF=6.在Rt△AGF中,由勾股定理得:AF===3.设Q(﹣2,n),则在Rt△AGF中,由勾股定理得:OQ==.设⊙Q与直线AC相切于点E,则QE=OQ=.坐标为(﹣1,0),以AB的中点P为圆心,AB为直径作⊙P的正半轴交于点C.(1)求经过A、B、C三点的抛物线所对应的函数解析式;(2)设M为(1)中抛物线的顶点,求直线MC对应的函数解析式;∴MC与⊙P的位置关系是相切.6、(2013•压轴题)如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,二次函数y=ax2+bx+c的图象经过点A,B,与x轴分别交于点E,F,且点E的坐标为(﹣23,0),以0C为直径作半圆,圆心为D.(1)求二次函数的解析式;(2)求证:直线BE是⊙D的切线;(3)若直线BE与抛物线的对称轴交点为P,M是线段CB上的一个动点(点M与点B,C 不重合),过点M作MN∥BE交x轴与点N,连结PM,PN,设CM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值围.S是否存在着最大值?若存在,求出最大值;若不存在,请说明理由.解答:解:(1)由题意,得A(0,2),B(2,2),E的坐标为(﹣23,0),则,解得,,∴该二次函数的解析式为:y=﹣98x2+94x+2;(2)如图,过点D作DG⊥BE于点G.由题意,得ED=+1=,EC=2+=,BC=2,∴BE==.∵∠BEC=∠DEG,∠EGD=∠ECB=90°,∴△EGD∽△ECB,∴=,∴DG=1.∵⊙D的半径是1,且DG⊥BE,∴BE是⊙D的切线;(3)由题意,得E(﹣23,0),B(2,2).设直线BE为y=kx+h(k≠0).则,解得,,∴直线BE为:y=34x+12.∵直线BE与抛物线的对称轴交点为P,对称轴直线为x=1,∴点P的纵坐标y=54,即P(1,54).∵MN∥BE, ∴∠MNC=∠BEC.∵∠C=∠C=90°,∴△MNC∽△BEC,∴=,∴=2t ,则CN=43t , ∴DN=t﹣1,∴S △PND =12DN•PD=5568t -. S △MNC =12CN•CM=23t 2. S 梯形PDCM =(12PD+CM )•CD=5182t +. ∵S=S △PND +S 梯形PDCM ﹣S △MNC =﹣+t (0<t <2).∵抛物线S=﹣+t (0<t <2)的开口方向向下,∴S 存在最大值.当t=1时,S 最大=23. 7、(2013•)已知:一元二次方程x +kx+k ﹣=0.(1)求证:不论k 为何实数时,此方程总有两个实数根;(2)设k <0,当二次函数y=x 2+kx+k ﹣的图象与x 轴的两个交点A 、B 间的距离为4时,求此二次函数的解析式;(3)在(2)的条件下,若抛物线的顶点为C ,过y 轴上一点M (0,m )作y 轴的垂线l ,当m 为何值时,直线l 与△ABC 的外接圆有公共点?(1)证明:∵△=k 2﹣4××(k ﹣)=k 2﹣2k+1=(k ﹣1)2≥0,∴关于x 的一元二次方程x 2+kx+k ﹣=0,不论k 为何实数时,此方程总有两个实数根;(2)令y=0,则x 2+kx+k ﹣=0.∵x A +x B =﹣2k ,x A •x B =2k ﹣1,∴|x A ﹣x B |===2|k ﹣1|=4,即|k ﹣1|=2,解得k=3(不合题意,舍去),或k=﹣1.∴此二次函数的解析式是y=x 2﹣x ﹣;(3)由(2)知,抛物线的解析式是y=x 2﹣x ﹣.易求A (﹣1,0),B (3,0),C (1,﹣2),∴AB=4,AC=2,BC=2.显然AC 2+BC 2=AB 2,得△ABC 是等腰直角三角形.AB 为斜边,∴外接圆的直径为AB=4,∴﹣2≤m≤2.8、(2013•压轴题)如图,已知抛物线y=ax +bx+c (a≠0)的顶点坐标为(4,﹣),且与y轴交于点C (0,2),与x 轴交于A ,B 两点(点A 在点B 的左边).(1)求抛物线的解析式及A ,B 两点的坐标;(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP 的最小值,若不存在,请说明理由;(3)在以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.解:(1)由题意,设抛物线的解析式为y=a(x﹣4)2﹣(a≠0)∵抛物线经过(0,2)∴a(0﹣4)2﹣=2解得:a=∴y=(x﹣4)2﹣即:y=x2﹣x+2当y=0时,x2﹣x+2=0解得:x=2或x=6∴A(2,0),B(6,0);(2)存在,如图2,由(1)知:抛物线的对称轴l为x=4,因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小∵B(6,0),C(0,2)∴OB=6,OC=2∴BC=2,∴AP+CP=BC=2∴AP+CP的最小值为2;(3)如图3,连接ME∵CE是⊙M的切线∴ME⊥CE,∠CEM=90°由题意,得OC=ME=2,∠ODC=∠MDE∵在△COD与△MED中∴△COD≌△MED(AAS),∴OD=DE,DC=DM设OD=x则CD=DM=OM﹣OD=4﹣x则RT△COD中,OD2+OC2=CD2,∴x2+22=(4﹣x)2∴x=∴D(,0)设直线CE的解析式为y=kx+b∵直线CE过C(0,2),D(,0)两点,则解得:∴直线CE的解析式为y=﹣+2;圆的圆心坐标为C (2,0),B 是第一象限圆弧上的一点,且BC ⊥AC ,抛物线c bx x y ++-=221经过C 、B 两点,与x 轴的另一交点为D 。
专题16 巧解二次函数与圆综合题(含答案)
专题16 巧解二次函数与圆综合题知识解读二次函数与圆结合的问题,是灵活运用数学思想方法解决类似以抛物线为主线,以圆为背景的函数综合题,这类题难度大,考查知识点多.对于在抛物线上架构圆的这类题型,不仅要求对抛物线和圆的相关知识能熟练掌握,还要挖掘其中隐含的等量关系,同时注意分类讨论所有可能的情况,避免遗漏;在抛物线中求圆问题时,要将点的坐标转化为所有图形边的长度.二次函数与圆的综合应用是初中阶段的重点题型,是知识覆盖面广、数学方法运用较多的试题,因而综合能力要求比较高,解决这类问题时应从多角度、多方面去分析,灵活运用多种数学方法和数学思想.解题中常用的数学思想方法有:方程和函数思想,数形结合思想,分类讨论思想.培优学案典例示范例1 如图161,抛物线2y ax bx c (,,a b c 是常数,0a)的对称轴为y 轴,且经过(0,0)和1(,)16a 两点,点p 在该抛物线上运动,以点P 为圆心的p 总经过定点(0,2)A .(1)求,,a b c 的值;(2)求证:在点P 运动的过程中,p 始终与x 轴相交;(3)设p 与x 轴相交于1212(,0),(,0)()M x N x x x 两点,当AMN △为等腰三角形时,求圆心P 的纵坐标.【提示】(1)根据题意得出二次函数一般形式进而将已知点代入求出,,a b c 的值即可;(2)设(,)P x y ,表示出p 的半径r ,进而与214x 比较得出答案即可;(3)分别表示出,AM AN 的长,进而分别利用当AM AN 时,当AMMN 时,当1ANMN 时,求出x 的值,进而得出圆心P 的纵坐标即可。
第(2)题综合程度高,难度加大,主要考查了直线与圆的位置关系,解决的方法是利用函数、圆的性质及勾股定理的有关知识进行计算并比较圆心到直线的距离与半径的大小关系;第(3)题主要是运用分类讨论的数学思想进行探究,是动态问题,计算量大。
在探讨动态问题时,首先要对运动过程做一个全面的分析,弄清楚运动过程中的变量和常量,变量反映了运动变化关系,常量则是问题求解的重要依据.其次,要分清运动过程中不同的变化关系.【解答】跟踪训练如图16-2,在平面直角坐标系中,O 为坐标原点,抛物线c bx ax y ++=2(0≠a )过O 、B 、C 三点,B 、C 坐标分别为(10,0)和(524,518-),以OB 为直径的⊙A 经过C 点,直线l 垂直x 轴于B 点。
-圆与二次函数综合题精练(带答案)
圆与二次函数综合题1、已知:二次函数y=x2-kx+k+4的图象与y轴交于点c,且与x轴的正半轴交于A、B两点(点A 在点B左侧)。
若A、B两点的横坐标为整数。
(1)确定这个二次函数的解析式并求它的顶点坐标;(2)若点D的坐标是(0,6),点P(t,0)是线段AB上的一个动点,它可与点A重合,但不与点B重合。
设四边形PBCD的面积为S,求S与t的函数关系式;(3)若点P与点A重合,得到四边形ABCD,以四边形ABCD的一边为边,画一个三角形,使它的面积等于四边形ABCD的面积,并注明三角形高线的长。
再利用“等底等高的三角形面积相等”的知识,画一个三角形,使它的面积等于四边形ABCD的面积(画示意图,不写计算和证明过程)。
2、(1)已知:关于x、y的方程组有两个实数解,求m的取值范围;(2)在(1)的条件下,若抛物线y=-(m-1)x2+(m-5)x+6与x轴交于A、B两点,与y轴交于点C,且△ABC的面积等于12,确定此抛物线及直线y=(m+1)x-2的解析式;(3)你能将(2)中所得的抛物线平移,使其顶点在(2)中所得的直线上吗?请写出一种平移方法。
3、已知:二次函数y=x2-2(m-1)x+m2-2m-3,其中m为实数。
(1)求证:不论m取何实数,这个二次函数的图像与x轴必有两个交点;(2)设这个二次函数的图像与x轴交于点A(x1,0)、B(x2,0),且x1、x2的倒数和为,求这个二次函数的解析式。
4、已知二次函数y1=x2-2x-3. (1)结合函数y1的图像,确定当x取什么值时,y1>0,y1=0,y1<0;(2)根据(1)的结论,确定函数y2= (|y1|-y1)关于x的解析式;(3)若一次函数y=kx+b(k 0)的图像与函数y2的图像交于三个不同的点,试确定实数k与b应满足的条件。
5、已知:如图,直线y= x+ 与x轴、y轴分别交于A、B两点,⊙M经过原点O及A、B两点。
2020中考数学 二次函数培优专题:二次函数与圆综合(含答案)
2020中考数学 培优专题:二次函数与圆综合(含答案)例题1. 在平面直角坐标系xOy 中,抛物线2y ax bx c =++与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,点A 的坐标为(3,0)-,若将经过A 、C 两点的直线y kx+b =沿y 轴向下平移3个单位后恰好经过原点,且抛物线的对称轴是直线2x =-. (1)求直线AC 及抛物线的函数表达式;(2)如果P 是线段AC 上的一点,设三角形ABP 、三角形BPC 的面积分别为ABP S △、BPC S △,且2:3ABP BPC S S =△△:,求点P 的坐标;(3)设Q 的半径为1,圆心Q 在抛物线上运动,则在运动的过程中是否存在Q 与坐标轴相切的情况?若存在,求出圆心Q 的坐标;若不存在,请说明理由.并探究:若设Q 的半径为r ,圆心Q 在抛物线上运动,则当r 取何值时,Q 与两坐标轴同时相切?【答案】(1)因为y kx+b =沿y 轴向下平移3个单位后恰好经过原点, 所以3b =,(0,3)C ,将(3,0)A -代入3y kx =+, 得330k -+=,解得1k =.所以直线AC 为:3y x+= 因为抛物线的对称轴是直线2x =-,所以930222a b c c b a ⎧⎪-+=⎪=⎨⎪⎪-=-⎩,解得143a b c =⎧⎪=⎨⎪=⎩. 所以抛物线的函数表达式为:243y x x =++.(2)如图,过点B 作BD AC ⊥于点D .因为:2:3ABP BPC S S =△△,所以:2:3AP PC =. 过点P 作PE x ⊥轴于点E ,则PE//CO ,所以APE ACO △∽△. 所以25PE AP CO AC ==. 所以2655PE OC ==. 所以635=x +,解得95x =-. 所以点P 的坐标为96,55⎛⎫- ⎪⎝⎭.(3)存在,设点Q 的坐标为00(,)x y ①当Q 与y 轴相切时,有01x =,即01x =±.11yxO当01x =-时,得20(1)4(1)30y =-+⨯-+=,所以1(1,0)Q -. 当01x =时,得2014138y =+⨯+=,所以2(1,8)Q , ②当Q 与x 轴相切时,有01y =,即01y =±, 当01y =-时,得200143x x -=++,即200440x x ++=,解得02x =-,所以3(2,1)Q -- 当01y =时,得200143x x =++,即200420x x ++=,解得02x =-±,所以4(2Q -,5(2Q -+综上所述,存在符合条件的Q ,其圆心Q 的坐标分别为1(1,0)Q -,2(1,8)Q ,3(2,1)Q --,4(2Q -,5(2Q -探究:设点Q 的坐标为00(,)x y .当Q 与两坐标同时轴相切时,有00y x =±.①当00y x =时,得200043x x x ++=,即200330x x ++=, 此时0<△,所以次方程无解.②当00y x =-时,得200043x x x ++=-,即200530x x ++=.解得0x =. ∴当Q的半径为0r x ===Q 与两坐标同时轴相切.例题2. 在平面直角坐标系中,抛物线经过(0,0)O 、(4,0)A、3,B ⎛ ⎝⎭三点. (1)求此抛物线的解析式;(2)以OA 的中点M 为圆心,OM 的长为半径作M ,在(1)中的抛物线上是否存在这样的点P ,过点P 作M 的切线l ,且l 与x 轴的夹角为30︒?若存在,请求出此时点P 的坐标;若不存在,请说明理由.(注意:本题中的结果保留根号)【答案】(1)设抛物线的解析式为2y ax bx c =++,11Oyx由题意,得0164093c a b c a b c ⎧⎪=⎪⎪++=⎨⎪⎪++=⎪⎩,解得0a b c ⎧=⎪⎪⎪⎪=⎨⎪=⎪⎪⎪⎩.所以抛物线的解析式为2y x =. (2)存在,抛物线222)y x x ==-所以抛物线的顶点为2,⎛ ⎝⎭,作抛物线和M (如图) 设满足条件的切线l 与x 轴交于点B ,与M 相切于点C . 连接MC ,过点C 作CD x ⊥轴于点D .因为2MC OM ==,30CBM ∠=︒,CM BC ⊥, 所以90BCM ∠=︒,60BMC ∠=︒,24BM CM ==. 所以2OB =,所以(2,0)B -.在Rt CDM △中,9030DCM CMD ∠=︒-∠=︒,2CM =. 所以1DM =,CD .所以C . 设切线l 的解析式为y=kx+b ,则可得20k b k b ⎧+=⎪⎨-+=⎪⎩,解得k b ⎧=⎪⎪⎨⎪=⎪⎩. 所以切线BC的解析式为.由题意2y ⎧=⎪⎪⎨⎪⎪⎩,解得1112x y ⎧=-⎪⎪⎨⎪=⎪⎩226x y =⎧⎪⎨=⎪⎩.所以点P的坐标为112P ⎛- ⎝⎭、2P ⎛ ⎝⎭. 因为抛物线和M 都关于直线2x =对称,则存在切线l 关于2x =对称的直线'l 也满足条件.同样得到满足的点P 关于1P 和2P对称,则得到392P ⎛ ⎝⎭、4P ⎛- ⎝⎭. 综上所述,这样的点P 共有4个,112P ⎛- ⎝⎭、2P ⎛ ⎝⎭、392P ⎛ ⎝⎭、4P ⎛- ⎝⎭.例题3. 如图,抛物线2134y x x =-++与x 轴交于点A 、B ,与y 轴交于点C ,顶点为点D ,对称轴l 与直线BC 交于点E ,与x 轴交于点F . (1)求直线BC 的解析式.(2)设点P 为该抛物线上的一个动点,以点P 为圆心、r 为半径作P ⊙. ①当点P 运动到点D 时,若P ⊙与直线BC 相交,求r 的取值范围;②若r =,是否存在点P 使P ⊙与直线BC相切?若存在,请求出点P 的坐标;若不存在,请说明理由.【答案】(1)抛物线2134y x x =-++中,令0y =,得21034x x =-++,解得12x =-,26x =;令0x =,得3y =;∴(2,0)A -,(6,0)B ,(0,3)C ;设直线BC 的解析式为y kx b =+,则有:603k b b +=⎧⎨=⎩,解得123k b ⎧=-⎪⎨⎪=⎩,∴直线BC 的解析式为:132y x =-+;(2)(2,4)D ,(2,2)E ;∴2EF DE ==,4BF =; ①过D 作DG BC ⊥于G ,则DEG BEF △∽△; ∴::2:1DE GE BF EF ==,即2DG GE =; Rt DGE △中,设GE x =,则2DG x =, 由勾股定理,得:222GE DG DE +=,即:2244x x +=,解得x;∴2DG x ==故D 、P 重合时,若P ⊙与直线BC 相交,则r DG >,即r >; ②存在符合条件的P 点,且P 点坐标为:1(2,4)P ,2(4,3)P,33P ⎛+ ⎝⎭,43P ⎛ ⎝⎭;过点F 作FM BC ⊥于M ; ∵2DE EF ==,则Rt Rt DGE FME △≌△;∴FM DG r == 分别过D 、F 作直线m 、n 平行于直线BC ,则直线m 与直线BC 、直线n 与直线BC 之间的距离都等于x ;所以P 点必为直线m 、n 与抛物线的交点; 设直线m 的解析式为:y ax h =+,由于直线m 与直线m 与直线BC 平行,则12a =-;∴1242h -⨯+=,5h =,即直线m 的解析式为152y x =-+;同理可求得直线x 的解析式为:112y x =-+;联立直线m 与抛物线的解析式,得:2134152y x xy x⎧=-++⎪⎪⎨⎪=-+⎪⎩,解得24xy=⎧⎨=⎩,43xy=⎧⎨=⎩;∴1(2,4)P,2(4,3)P;同理,联立直线n与抛物线的解析式可求得:33P⎛+⎝⎭,43P⎛-⎝⎭;故存在符合条件的P点,且坐标为:1(2,4)P,2(4,3)P,33P⎛+⎝⎭,43P⎛⎝⎭.例题4. 已知,如图4-1,抛物线2y ax bx c=++经过点1(,0)A x,2(,0)B x,(0,2)C-,其顶点为D.以AB为直径的M交y轴于点E、F,过点E作M的切线交x轴于点N.30ONE∠=︒,12||8x x-=.(1)求抛物线的解析式及顶点D的坐标;(2)如图4-2,点Q为EBF上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH AQ⋅是否为定值?若是,请求出这个定值;若不是,请说明理由.【答案】(1)圆的半径12||84222x xABr-====.连接ME,∵NE是切线,∴ME NE⊥.在Rt MNE△中,30ONE∠=︒,4MA ME==.∴60EMN∠=︒,8MN=,∴2OM=.∴2OA=,6OB=.∴点A、B的坐标分别为(2,0)-、(6,0).∵抛物线过A、B两点,所以可设抛物线解析式为:图(a)图(b)(2)(6)y a x x =+-,又∵抛物线过点(0,2C -,∴2(02)(06)a -=+-,解得:16a =. ∴抛物线解析为:2112(2)(6)2663y x x x x =+-=--,∴当232126x -=-=⨯时,128422633y =⨯-⨯-=-.即抛物线顶点D 的坐标为82,3⎛⎫- ⎪⎝⎭.(2)连接AF 、QF , 在AQF △和AFH △中, 由垂径定理易知:AE AF =.∴AQF AFH ∠=∠,又QAF HAF ∠=∠,∴AQF AFH △∽△,∴AF AHAQ AF =,∴2AH AQ AF ⋅= 在Rt AOF △中,22222216AF AO OF =+=+= (或利用22816AF AO AB =⋅=⨯=) ∴16AH AQ ⋅=即:AH AQ ⋅为定值.例题5. 如图,已知点A 的坐标是(1,0)-,点B 的坐标是,0(9),以AB 为直径作'O ,交y 轴的负半轴于点C ,连接AC ,BC ,过A ,B ,C 三点作抛物线. (1)求抛物线的解析式;(2)点E 是AC 延长线上一点,BCE ∠的平分线CD 交'O 于点D ,连接BD ,求直线BD 的解析式;(3)在(2)的条件下,抛物线上是否存在点P ,使得PDB CBD ∠=∠?如果存在,请求出点P 的坐标;如果不存在,请说明理由.【答案】(1)连接'O C ,因为(1,0)A -,(9,0)B ,所以1'''52O A O B O C AB ====,1OA =,''4OO O A OA =-=,由勾股定理,得3OC =,所以(0,3)C -, 设抛物线的解析式为2y ax bx c =++,则038190a b c c a b c -+=⎧⎪=-⎨⎪++=⎩,解得13833a b c ⎧=⎪⎪⎪=-⎨⎪=-⎪⎪⎩,所以抛物线的解析式为218333y x x =--;(2)连接'O D ,则由圆周角定理,90ACB BCE ∠=∠=︒,又CD 平分BCE ∠,所以45BCD ∠=︒,'290BO D BCD ∠=∠=︒,所以可以得到(4,5)D -,又(9,0)B ,所以直线BD 的解析式为:9y x =-.(3)存在,①当1//DP CB 时,能使PDB CBD ∠=∠,又可得13BC k =, 所以113DP k =,且点(4,5)D -,所以直线1DP 的解析式为11933y x =-,则 由题意21193318333y x y x x ⎧=-⎪⎪⎨⎪=--⎪⎩,解得11x y ⎧=⎪⎪⎨⎪=⎪⎩22x y ⎧=⎪⎪⎨⎪=⎪⎩(舍去)所以此时点1P ⎝⎭. ②过点C 作BD 的平行线,交'O 于点G , 此时有,GDB GCB ∠=∠CBD =∠.又可得1BD k =,1CG k =,所以直线CG 的解析式为:3y x =-, 设点(,3)G m m -,作GH x ⊥轴交x 轴于点H ,连接'O G ,则在Rt 'O GH △中,由勾股定理可得,7m =,所以此时(7,4)G , 所以直线DG 的解析式为:317y x =-,则由题意231718333y x y x x =-⎧⎪⎨=--⎪⎩,解得111425x y =⎧⎨=⎩或2238x y =⎧⎨=-⎩(舍去), 所以此时点2(14,25)P .综上所述,1P ⎝⎭,2(14,25)P .例题6. 如图所示,抛物线与x 轴交于点(1,0)A -、(3,0)B 两点,与y 轴交于点(0,3)C -.以AB 为直径作M ,过抛物线上一点P 作M 的切线PD ,切点为D ,并与M 的切线AE 相交于点E ,连结DM 并延长交M 于点N ,连结AN 、AD . (1)求抛物线所对应的函数关系式及抛物线的顶点坐标;(2)若四边形EAMD的面积为,求直线PD 的函数关系式;(3)抛物线上是否存在点P ,使得四边形EAMD 的面积等于DAN △的面积?若存在,求出点P 的坐标;若不存在,说明理由.【答案】(1)因为抛物线与轴交于点(1,0)A -,(3,0)B 两点, 设抛物线的函数关系式为:(1)(3)y a x x =+-, ∵抛物线与y 轴交于点(0,3)C -, ∴3(01)(03)a -=+-, ∴1a =所以,抛物线的函数关系式为:223y x x =--, 又2(1)4y x =--,因此,抛物线的顶点坐标为(1,4)-.(2)连结EM ,∵EA 、ED 是M 的两条切线,x∴∴, 又四边形EAMD 的面积为∴∴又2AM =,∴AE =,因此,点E的坐标为1(1,E -或2(1,E --. 当E 点在第二象限时,切点D 在第一象限.在直角三角形EAM 中,∴∴, 过切点D 作垂足为点F , ∴1MF =,DF =因此,切点D的坐标为(2,,设直线PD 的函数关系式为y kx b =+,将(1,E -、(2,D 的坐标代入得 解之,得 所以,直线PD 的函数关系式为 当E 点在第三象限时,切点D 在第四象限.同理可求:切点D的坐标为(2,,直线PD 的函数关系式为 因此,直线PD 的函数关系式为(3)若四边形EAMD 的面积等于DAN △的面积 又 ∴∴E 、D 两点到x轴的距离相等,∵PD 与M 相切,∴点D 与点E 在x 轴同侧, ∴切线PD 与x 轴平行,此时切线PD 的函数关系式为或当时,由得, 当时,由得,故满足条件的点P 的位置有4个,分别是1(12)P +、2(12)P 、3(12)P -、4(12)P -.EA ED EA AM ED MN =⊥⊥,,,EAM EDM △≌△EAM S =△12AM AE =⋅tan EA EMA AM ==∠60EMA =∠,°60DMB =∠°DF AB ⊥2k b k b +-+⎪⎩k b ⎧=⎪⎪⎨⎪⎪⎩y =y =y =y 22EAM DAN AMD EAMD S S S S ==△△△四边形,AMD EAM S S =△△2y = 2.y =-2y =223y x x =--1x =2y =-223y x x =--1x =例题7. 如图,在直角坐标系中,以点(3,0)A 为圆心,以23为半径的圆与x 轴交于B 、C 两点,与y 轴交于D 、E 两点. (1)写出B 、C 、D 三点的坐标; (2)若B 、C 、D 三点在抛物线析式; 2y ax bx c =++上,求这个抛物线的解(3)若圆A 的切线交x 轴正半轴于点M ,交y 轴负半轴于点N ,切点为P 且30OMN ∠=︒,试判断直线MN 是否经过所求抛物线的顶点?说明理由. 【答案】(1)(3,0)B -,(33,0)C ,(0,3)D -(2)由题意得,330273303a b c a b c c ⎧-+=⎪⎪++=⎨⎪=-⎪⎩,解得13233a b c ⎧=⎪⎪⎪=-⎨⎪=-⎪⎪⎩,所以抛物线的解析式为212333y x x =--,(3)连接AP ,则23AP =,在Rt APM △中,30AMP ∠=︒,则43AM =,所以(53,0)M ,所以直线MN 解析式为35y x =-, 又(2)得抛物线2212313(3)433y x x x =--=--,所以抛物线的顶点为(3,4)-,将顶点代入直线MN 验证, 得顶点在直线MN 上.例题8. 已知抛物线2y ax bx c =++与y 轴的交点为C ,顶点为M ,直线CM 的解析式为2y x =-+,并且线段CM 的长为22;(1)求抛物线的解析式;(2)设抛物线与x 轴有两个交点1(,0)A x 、2(,0)B x ,且点A 在B 的左侧,求线段AB 的长; (3)若以AB 为直径作N ,请判断直线CM 与N 的位置关系,并说明理由.【答案】(1)因为直线CM 的解析式为2y x =-+,所以(0,2)C ,又线段CM 的长为22,所以(2,0)M或(2,4)M -,所以抛物线的解析式可得21222y x x =-+或21222y x x =-++. (2)因为抛物线和x 轴有两个交点1(,0)A x 、2(,0)B x ,所以此时抛物线为21222y x x =-++,令0y =,得1x 和2x 是方程212202x x =-++的两根,且12x x <, 则由韦达定理得,124x x +=,124x x ⋅=-,所以22211212()()432x x x x x x -=+-⋅⋅=,所以21AB x x =-=(3)相切,由题意抛物线的对称轴应为2x =-,所以(2,0)N -,作NP CM ⊥于点P ,设直线CM 与x 轴相交于点D ,则45NPD ∠=︒,且(2,0)D ,4DN =,所以得NP =AB 为N 的直径,且AB =N 点到直线CM 的距离等于N 的半径,所以直线CM 与N相切.例题9. 如图,在平面直角坐标系中,已知抛物线2y ax bx c =++交x 轴于(2,0)A ,(6,0)B 两点,交y 轴于点(0,23)C . (1)求此抛物线的解析式; (2)若此抛物线的对称轴与直线2y x =交于点D ,作D 与x 轴相切,D 交y 轴于点E 、F 两点,求劣弧EF 所对圆心角的度数;(3)P 为此抛物线在第二象限图像上的一点,PG 垂直于x 轴,垂足为点G ,试确定P 点的位置,使得PGA △的面积被直线AC 分为1:2两部分.【答案】(1)由题意,得420366023a b c a b c c ⎧++=⎪++=⎨⎪=⎩,解得34323a b c ⎧=⎪⎪⎪⎪=-⎨⎪⎪=⎪⎪⎩ 所以抛物线的解析式为:234323y x x =-+. (2)由(1)得22343323234)y x x x =-+=--(, 所以它的对称轴为4x =,所以得(4,8)D ,所以D 的半径为8,作DH EF ⊥于点H ,连接EH 、FH ,则8DE DF ==,4DH =,且EDH FDH ∠=∠,在Rt DEH △中,8DE =,4DH =,1cos 2DH EDH DE ∠==, 所以60EDH ∠=︒,2120EDF EDH ∠=∠=︒,所以劣弧EF 所对圆心角的度数为120︒.(3)设AC 交PG 于点Q ,则由题可知PGA △被直线AC 分为AQP △和AQG △,故:2:1AQP AQG S S =△△或1:2,所以11:2:122PQ AG QG AG ⎛⎫⎛⎫⋅⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭或1:2, 所以:2:1PQ QG =或1:2,由题,(2,0)A ,(0,23)C ,所以直线AC 为323y x =-+,因为P 点为抛物线第二象限上的一个点,设2343,23P t t t ⎛⎫-+ ⎪ ⎪⎝,0t <, 则(,323)Q t t -+,(,0)G t ,所以223433323(323)PQ t t t t t =-+--+=-,323QG t =-+, ①当:2:1PQ QG =时,得2332(323)t t t -=-+, 解得12t =-,(2t =舍去),此时(12,423)P -,②当:2:1PQ QG =21(2=+,解得3t =-,(2t =舍去),此时P ⎛- ⎝,综上所述,(12,P -或P ⎛- ⎝。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数和圆
【例题1】 (芜湖市) 已知圆P 的圆心在反比例函数k
y x
=
(1)k >图象上,并与x 轴相交于A 、B 两点. 且始终与y 轴相切于定点C (0,1). (1) 求经过A 、B 、C 三点的二
次函数图象的解析式;
(2) 若二次函数图象的顶点为D ,
问当k 为何值时,四边形ADBP 为菱形.
【例题2】(湖南省韶关市) 25.如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线32
y x =-+
与坐标轴交于D 、E 。
设M 是AB 的中点,P 是线段DE 上的动点. (1)求M 、D 两点的坐标;
(2)当P 在什么位置时,PA=PB ?求出此时P 点的坐标;
(3)过P 作PH ⊥BC ,垂足为H ,当以PM 为直径的⊙F 与BC 相切于点N 时,求梯形PMBH 的面积.
【例题3】(甘肃省白银等7市新课程)28. 在直角坐标系中,⊙A的半径为4,圆心A的坐标为(2,0),⊙A与x轴交于E、F两点,与y轴交于C、D两点,过点C作⊙A的切线BC,交x轴于点B.
(1)求直线CB的解析式;
(2)若抛物线y=ax2+b x+c的顶点在直线BC上,与x
轴的交点恰为点E、F,求该抛物线的解析式;
(3)试判断点C是否在抛物线上?
(4)在抛物线上是否存在三个点,由它构成的三角形与
△AOC相似?直接写出两组这样的点.
【例题4】(绵阳市)25.如图,已知抛物线y = ax2 + bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为5.设⊙M与y轴交于D,抛物线的顶点为E.
(1)求m的值及抛物线的解析式;
(2)设∠DBC = α,∠CBE = β,求sin(α-β)的值;
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
【例题5】(南充市)25.如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B.已
知抛物线2
16
y x bx c =
++过点A 和B ,与y 轴交于点C . (1)求点C 的坐标,并画出抛物线的大致图象. (2)点Q (8,m )在抛物线2
16
y x bx c =
++上,点P 为此抛物线对称轴上一个动点,求PQ +PB 的最小值.
(3)CE 是过点C 的⊙M 的切线,点E 是切点,求OE 所在直线的解析式.
【例题6】(山西省临汾市)26. 如图所示,在平面直角坐标系中,
M 经过原点O ,且与x 轴、y 轴分
别相交于(60)(08)A B --,,
,两点. (1)请求出直线AB 的函数表达式;
(2)若有一抛物线的对称轴平行于y 轴且经过点M ,顶点C 在M 上,开口向下,且经过点B ,求此抛物线的函数表达式;
(3)设(2)中的抛物线交x 轴于D E ,两点,在抛物线上是否存在点P ,使得1
15
PDE ABC S S =△△?若存在,请求出点P 的坐标;若不存在,请说明理由.
例题1:
x
例题2:
例题3:
例题4:
例题5:
例题6:。
