弦切角定理及其逆定理PPT课件
合集下载
广东省广州市白云区汇侨中学九年级数学《弦切角定理》课件
小结：
你掌握了吗？
3、定理的证明
4、应用与推论
一般情况下，弦切角、圆周角、圆心角都是 通过它们夹的（或对的）同一条弧（或等弧）联 系起来，因此，当已知有切线时常添线构建弦切 角或添切点处的半径应用切线的性质。
作业
• 1、课课练 /P.84 • 2、预习“弦切角”（2）
∵ AB是⊙O的切线，
∴
∠BAC＝90°
︵∵∠BAC＝180°－∠DAC
又∵ AmC 是半圆，
∴ ∠P＝90° ∠P＝180°－∠Q
∴ ∠BAC＝∠P
∠DAC＝∠Q
∴ ∠BAC＝∠P
课堂练习：
1、已知AB是⊙O的切线A为切点,由图填空：
30º
O 70º
2
1
A
B
O
O 80º
4
A
B
∠1= 30º ；∠2= 70º ；∠3= 65º ； ∠4= 40º 。 弦切角等于它所夹的弧对的圆心角的一半.
径，AC是弦，直线CE和⊙O切于
点C，AD⊥CE于D。
B
O
求证：(1)AC平分∠BAD
(2)AC2=2AD·AO
A
你还能用其他方法解答 吗？试试看！
E
C
D
有弦切角，常连结弦切角 所夹弧所对的圆周角。
例题解析(思路2)
例1: 如图，已知AB是⊙O的直径，AC是弦，直 线CE和⊙O切于点C，AD⊥CE，垂足是D，求证： AC平分∠BAD.
QC
P
O
P
m
A
B
弦切角等于所夹弧对的圆周角。
( 1 ) 圆心O在∠BAC的外部 作⊙O的直径AQ，连结CQ
∵∠BAQ＝∠ACQ＝90°
九年级上数学《弦切角定理》课件
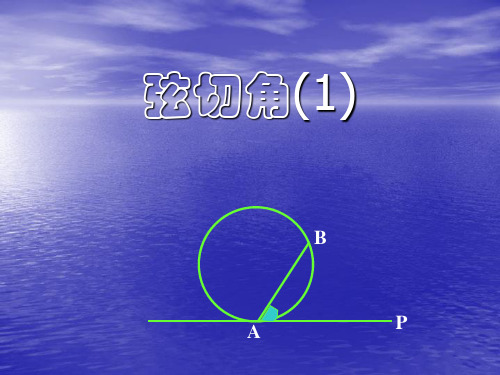
B
一边与圆相交，
另一边与圆相切 的角叫做弦切角
A
AmB 是弦切角∠PAB所夹的弧。
m
P
顶点在圆上，一边与圆相交，另一边 与圆相切的角叫做弦切角。 下面五个图中的∠BAC是不是弦切角？
C B A C C A
×
B
×
C
B
A
×
B
B C
×
A
A
√
从数学的角度看，弦切角能分成几大类？ C C C .O .O .O P P P D A B A A B D
BAC为直角， 圆心在AC上。 BAC为锐角， 圆心在角外。
B
BAC为钝角， 圆心在角内。
上图中BAC所夹的弧分别是：半圆、劣弧、优弧。
猜想：弦切角BAC与圆周角APC的关系 现在分别作出他们所对的圆周角APC, 如上图
︵ 已知：AC是⊙O的弦，AB是⊙O的切线，AmC 是弦切角∠BAC所 ︵ 夹的弧，∠P是AmC所对的圆周角。 求证：∠BAC＝∠P Q C
课堂练习：
1、已知AB是⊙O的切线A为切点,由图填空：
30º
O
70º
1 3
O
25º
O
2
80º 4 A ； B
A ∠1= 30º ∠4= 40º
B
A
B
；∠2= 70º ；∠3= 65º 。 弦切角等于它所夹的弧对的圆心角的一半.
2、选择： AB为⊙O直径，PC为⊙O的切线，C为切点， 若∠BPC=30°，则∠BCP=（ A ）。 A、 30°B、 60°C、 15°D、22. 5°
如图，DE切⊙O于点A，AB、AC是 ⊙O的弦，若 AB=AC，那么∠DAB 与∠EAC是否相等？为什么？
2020届一轮复习人教A版 弦切角定理 课件(22张)
即 BC2=BE·CD.
1234 5
5.如图,AB是半圆O的直径,C是圆周上一点(异于点A,B),过点C作圆 O的切线l,过点A作直线l的垂线AD,垂足为点D.AD交半圆于点E.求 证:CB=CE.
分析转化为证明∠CBE=∠CEB.
题型一 题型二 题型三
证明连接BD,如图.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
又∠BCD=∠BAD,∠CBD=∠CAD,
∴∠BCD=∠CBD.∴BD=CD.
又BE为☉O的切线,
∴∠EBD=∠BAD,∠EBD=∠BCD.
故在△BED和△CEB中,
∠EBD=∠ECB,∠BED=∠CEB,
∴△BED∽△CEB.
题型一 题型二 题型三
题型二 线段成比例问题
【例2】 如图,已知△ABC内接于☉O,∠BAC的平分线交☉O于点 D,CD的延长线交过点B的切线于点E.
求证:������������������������22 = ������������������������.
分析直接证明此等式有一定的难度,可以考虑把它分解成两个比 例式的形式,然后借助相似三角形的性质得出结论.
又∠ACB=80°,
∴∠D=∠ACB-∠DAC=80°-35°=45°.
答案:A
对弦切角的理解 剖析弦切角的特点:(1)顶点在圆上;(2)一边与圆相交;(3)另一边与 圆相切.
弦切角定义中的三个条件缺一不可.如图①②③④中的角都不是 弦切角.图①中,缺少“顶点在圆上”的条件;图②中,缺少“一边和圆相 交”的条件;图③中,缺少“一边和圆相切”的条件;图④中,缺少“顶点
在圆上”和“另一边和圆相切”两个条件.
题型一 题型二 题型三
题型一
1234 5
5.如图,AB是半圆O的直径,C是圆周上一点(异于点A,B),过点C作圆 O的切线l,过点A作直线l的垂线AD,垂足为点D.AD交半圆于点E.求 证:CB=CE.
分析转化为证明∠CBE=∠CEB.
题型一 题型二 题型三
证明连接BD,如图.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
又∠BCD=∠BAD,∠CBD=∠CAD,
∴∠BCD=∠CBD.∴BD=CD.
又BE为☉O的切线,
∴∠EBD=∠BAD,∠EBD=∠BCD.
故在△BED和△CEB中,
∠EBD=∠ECB,∠BED=∠CEB,
∴△BED∽△CEB.
题型一 题型二 题型三
题型二 线段成比例问题
【例2】 如图,已知△ABC内接于☉O,∠BAC的平分线交☉O于点 D,CD的延长线交过点B的切线于点E.
求证:������������������������22 = ������������������������.
分析直接证明此等式有一定的难度,可以考虑把它分解成两个比 例式的形式,然后借助相似三角形的性质得出结论.
又∠ACB=80°,
∴∠D=∠ACB-∠DAC=80°-35°=45°.
答案:A
对弦切角的理解 剖析弦切角的特点:(1)顶点在圆上;(2)一边与圆相交;(3)另一边与 圆相切.
弦切角定义中的三个条件缺一不可.如图①②③④中的角都不是 弦切角.图①中,缺少“顶点在圆上”的条件;图②中,缺少“一边和圆相 交”的条件;图③中,缺少“一边和圆相切”的条件;图④中,缺少“顶点
在圆上”和“另一边和圆相切”两个条件.
题型一 题型二 题型三
题型一
弦切角定理及推论
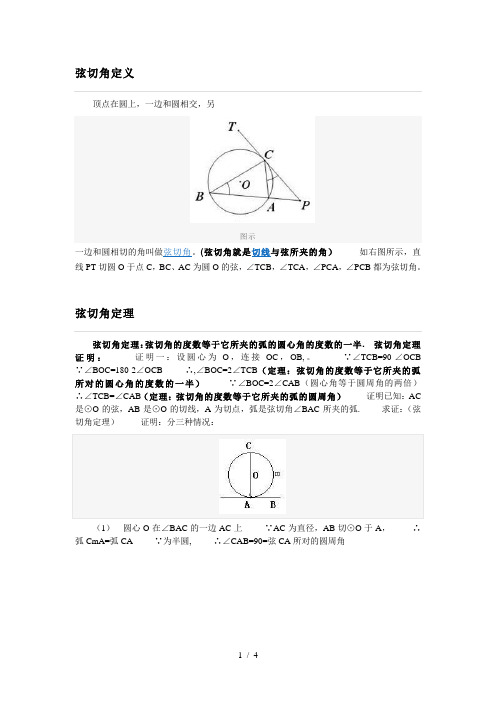
弦切角定义顶点在圆上，一边和圆相交，另图示一边和圆相切的角叫做弦切角。
(弦切角就是切线与弦所夹的角）如右图所示，直线PT切圆O于点C，BC、AC为圆O的弦，∠TCB，∠TCA，∠PCA，∠PCB都为弦切角。
弦切角定理弦切角定理：弦切角的度数等于它所夹的弧的圆心角的度数的一半.弦切角定理证明：证明一：设圆心为O，连接OC，OB,。
∵∠TCB=90-∠OCB ∵∠BOC=180-2∠OCB ∴,∠BOC=2∠TCB（定理：弦切角的度数等于它所夹的弧所对的圆心角的度数的一半）∵∠BOC=2∠CAB（圆心角等于圆周角的两倍）∴∠TCB=∠CAB（定理：弦切角的度数等于它所夹的弧的圆周角）证明已知：AC 是⊙O的弦，AB是⊙O的切线，A为切点，弧是弦切角∠BAC所夹的弧. 求证：（弦切角定理）证明：分三种情况：（1）圆心O在∠BAC的一边AC上∵AC为直径，AB切⊙O于A，∴弧CmA=弧CA ∵为半圆, ∴∠CAB=90=弦CA所对的圆周角B点应在A点左侧（2）圆心O在∠BAC的内部. 过A作直径AD交⊙O于D, 若在优弧m所对的劣弧上有一点E 那么，连接EC、ED、EA 则有：∠CED=∠CAD、∠DEA=∠DAB ∴∠CEA=∠CAB ∴（弦切角定理）（3）圆心O在∠BAC的外部, 过A作直径AD交⊙O于 D 那么∠CDA+∠CAD=∠CAB+∠CAD=90 ∴∠CDA=∠CAB ∴（弦切角定理）弦切角推论推论内容若两弦切角所夹的弧相等，则这两个弦切角也相等应用举例例1：如图，在Rt△ABC中，∠C=90，以AB为弦的⊙O与AC相切于点A，∠CBA=60° , AB=a 求BC长. 解：连结OA，OB. ∵在Rt△ABC中, ∠C=90 ∴∠BAC=30°∴BC=1/2a(RT△中30°角所对边等于斜边的一半）例2：如图，AD是ΔABC中∠BAC的平分线，经过点A的⊙O与BC切于点D，与AB，AC分别相交于E，F. 求证：EF∥BC. 证明：连DF. AD是∠BAC的平分线∠BAD=∠DAC ∠EFD=∠BAD ∠EFD=∠DAC ⊙O切BC于 D ∠FDC=∠DAC ∠EFD=∠FDC EF∥BC例3：如图，ΔABC内接于⊙O，AB是⊙O直径，CD⊥AB于D，MN切⊙O于C，求证：AC平分∠MCD，BC平分∠NCD. 证明：∵AB是⊙O直径∴∠ACB=90 ∵CD⊥AB ∴∠ACD=∠B，∵MN切⊙O于 C ∴∠MCA=∠B，∴∠MCA=∠ACD，即AC平分∠MCD，同理：BC平分∠NCD.。
弦切角PPT课件
2
教学重点、难点
重
1、弦切角的概念和定理的证明。
点
2、弦切角定理的运用。
难 点
3、通过作辅助线把“一般情况”
转化为“特殊情况”。
2020年10月2日
3
教学方法
在复习圆心角、圆周角的概念的 基础上，通过几何画板的动画演 示，由学生通过观察动画，抽象 总结出弦切角的定义，并揭示出 弦切角与圆周角的关系，然后引 导学生观察思考、阅读教材、分 析议论得到弦切角定理。
2020年10月2日
4
教学过程
复习引入 探求新知 例题选讲
课堂练习 小结
2020年10月2日
5ห้องสมุดไป่ตู้
复习引入
复习 1、在贺 1、
我们已学过了两个与圆有
关的角，即圆心角和圆周角，那么怎样的角 是圆心角、圆周角？
2. 引入
2020年10月2日
6
弦切角定理教学
探求定理
演示及证明过程
2020年10月2日
7
演讲完毕，谢谢观看！
汇报人：XXX 汇报日期：20XX年10月10日
8
教学目的 教学重点、难点
教学方法 教学过程
2020年10月2日
1
教学目的
1、使学生理解弦切角的定义，掌握弦切角定理 并能初步加以运用。
2、运用运动的观点进行概念教学，逐步培养学 生探讨问题从感性认识上升到理性认识的抽 象思维能力求。
3、通过对定理的证明，训练学生认识事物由特 殊到一般的思想方法。
2020年10月2日
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
弦切角精品PPT教学课件
教学目的 教学重点、难点
教学方法 教学过程
2020/12/6
1
教学目的
1、使学生理解弦切角的定义，掌握弦切角定理 并能初步加以运用。
2、运用运动的观点进行概念教学，逐步培养学 生探讨问题从感性认识上升到理性认识的抽 象思维能力求。
3、通过对定理的证明，训练学生认识事物由特 殊到一般的思想方法。
2020/12/6
2020/12/6
4
教学过程
复习引入 探求新知 例题选讲
课堂练习 小结
2020/12/6
5
复习引入
复习 1、在贺 1、
我们已学过了两个与圆有
关的角，即圆心角和圆周角，那么怎样的角 是圆心角、圆周角？
2. 引入
2020/12/6
6
弦切角定理教学
探求定理
2020/12/6
演示及证明过程
7
感谢你的阅览
Thank you for reading
温馨提示：本文内容皆为可修改式文档，下载后，可根据读者的需求 作修改、删除以及打印，感谢各位小主的阅览和下载
日期：
演讲者：蒝味的薇笑巨蟹
2
教学重点、难点
重
1、弦切角的概念和定理的证明。
点
2、过作辅助线把“一般情况”
转化为“特殊情况”。
2020/12/6
3
教学方法
在复习圆心角、圆周角的概念的 基础上，通过几何画板的动画演 示，由学生通过观察动画，抽象 总结出弦切角的定义，并揭示出 弦切角与圆周角的关系，然后引 导学生观察思考、阅读教材、分 析议论得到弦切角定理。
教学方法 教学过程
2020/12/6
1
教学目的
1、使学生理解弦切角的定义，掌握弦切角定理 并能初步加以运用。
2、运用运动的观点进行概念教学，逐步培养学 生探讨问题从感性认识上升到理性认识的抽 象思维能力求。
3、通过对定理的证明，训练学生认识事物由特 殊到一般的思想方法。
2020/12/6
2020/12/6
4
教学过程
复习引入 探求新知 例题选讲
课堂练习 小结
2020/12/6
5
复习引入
复习 1、在贺 1、
我们已学过了两个与圆有
关的角，即圆心角和圆周角，那么怎样的角 是圆心角、圆周角？
2. 引入
2020/12/6
6
弦切角定理教学
探求定理
2020/12/6
演示及证明过程
7
感谢你的阅览
Thank you for reading
温馨提示：本文内容皆为可修改式文档，下载后，可根据读者的需求 作修改、删除以及打印，感谢各位小主的阅览和下载
日期：
演讲者：蒝味的薇笑巨蟹
2
教学重点、难点
重
1、弦切角的概念和定理的证明。
点
2、过作辅助线把“一般情况”
转化为“特殊情况”。
2020/12/6
3
教学方法
在复习圆心角、圆周角的概念的 基础上，通过几何画板的动画演 示，由学生通过观察动画，抽象 总结出弦切角的定义，并揭示出 弦切角与圆周角的关系，然后引 导学生观察思考、阅读教材、分 析议论得到弦切角定理。
【人教版】九年级上册数学《弦切角》ppt教学课件
连结OC,由切线性质, 可得OC∥AD,于是 有∠2=∠3,又由于 B ∠1=∠3,可证得 ∠1=∠2
E
·O 1A 32 CD
小结：
1、概念的引入
顶点在圆上，一边与圆相交，另一边与圆相 切的角叫做弦切角。
2、定理的发现
弦切角定理：弦切角等于它所夹的弧对的圆周角。
推论：两个弦切角所夹的弧相等，
那么这两个弦切角相等。
的度数是（ B ）。
A、38°B、52° C、68° D、42°
O
A
B
38°
M
C
D N
弦切角定理：弦切角等于它所夹的弧对的圆周角。 推论：两个弦切角所夹的弧相等， 那么这两个弦切角相等。
如图，DE切⊙O于点A，AB、AC是 ⊙O的弦，若 AB=AC，那么∠DAB 与∠EAC是否相等？为什么？
∠ DAB＝ ∠EAC
C
B O
E
A
D
例题解析
例1：如图：已知AB是⊙O的直
径，AC是弦，直线CE和⊙O切于
点C，AD⊥CE于D。
B
O
求证：(1)AC平分∠BAD
(2)AC2=2AD·AO
A
你还能用其他方法解答 吗？试试看！
E
C
D
有弦切角，常连结弦切角 所夹弧所对的圆周角。
例题解析(思路2)
例1: 如图，已知AB是⊙O的直径，AC是弦，直 线CE和⊙O切于点C，AD⊥CE，垂足是D，求证： AC平分∠BAD.
4
A
B
∠1= 30º ；∠2= 70º ；∠3= 65º ； ∠4= 40º 。 弦切角等于它所夹的弧对的圆心角的一半.
2、选择： AB为⊙O直径，PC为⊙O的切线，C为切点，
高中数学 1.2.3弦切角定理课件 北师大版选修41
3.正确使用弦切角定理 剖析:要正确使用弦切角定理,第一步要找到弦切角,弦切角的特点是:(1)顶点在 圆上;(2)一边与圆相交;(3)一边与圆相切,这三个条件缺一不可,第二步要准确找到 弦切角所夹的弧,再看这段弧上的圆周角,然后用弦切角定理解题,如果没有圆周角, 有这段弧所对的圆心角也可以.
M Z Z 目标导航 UBIAODAOHANG
Байду номын сангаас
A.∠ADB
B.∠AOB
C.∠ABC D.∠BAO
解析:∠ADB 是圆周角,∠AOB 是圆心角,∠ABC 是弦切角,∠BAO 不是
弦切角.
答案:C
M Z Z 目标导航 UBIAODAOHANG
知识梳理
HISHI SHULI
重难聚焦
HONGNAN JVJIAO
D S 典例透析 IANLI TOUXI
圆相切”两个条件.
M Z Z 目标导航 UBIAODAOHANG
知识梳理
HISHI SHULI
重难聚焦
HONGNAN JVJIAO
D S 典例透析 IANLI TOUXI
随堂演练
UITANGYANLIAN
2.圆心角、圆周角、弦切角的比较 剖析:如下表所示.
圆心角
圆周角
顶点在圆心的 定义
角
顶点在圆上,两边和 圆相交
知识梳理
HISHI SHULI
重难聚焦
HONGNAN JVJIAO
D S 典例透析 IANLI TOUXI
随堂演练
UITANGYANLIAN
12
1.弦切角 顶点在圆上,一边和圆相交,另一边和圆相切的角称为弦切角.
名师点拨弦切角可分为三类:(1)圆心在角的外部,如图①所示;(2)圆心在 角的一边上,如图②所示;(3)圆心在角的内部,如图③所示.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
汇报人：XXX 汇报日期：20XX年10月10日
2020年9月28日
9
2020年9月28O于A、B两点，AE是⊙O的
直径，点C为⊙O上一点，且AC平分∠PAE，过C作 CD⊥PA于D. （1）求证：CD为⊙O的切线； （2）若DC+DA=6，⊙O的直径为10，求AB的长.
2020年9月28日
4
提高练习
练3.已知直线l切△ABC外接圆于点C， AD⊥BC于点D，BE⊥AC于点E，EG⊥l于点G ，DF⊥l于点F. 求证：EG=DF.
回味无穷
2020年9月28日
7
课后作业
《优等生数学》九年级 P66-67 T1、 T2 、T3、T4 写在作业本上. 预习《优等生数学》九年级的第29、30节
2020年9月28日
8
演讲完毕，谢谢观看！
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
XUSUHUA
第二十七章 圆
27.16 弦切角定理及其逆定理
2020年9月28日
1
经典例题
例. 如图，从圆上一点A作直径BC的垂线AD，
过A作圆的切线MN. 证明：AB、AC分别平分
MN与AD的夹角.
2020年9月28日
2
巩固练习
练1. 如图，四边形ABCD内接于圆O，AD是圆O 的直径，直线MN切圆O于B点，∠MBA=40°， 求∠BCD.
2020年9月28日
5
挑战自己 练3. （牛顿定理3）圆的外切四边形的对角线的 交点和以切点为顶点的四边形对角线交点重合 .
牛顿定理1：四边形两条对边的延长线的交点所连线段的中点 和两条对角线的中点，三点共线. 这条直线叫做这个四边形的牛顿线. 牛202顿0年定9月2理8日2：圆外切四边形的两条对角线的中点，及该圆的圆6 心，三点共线.
2020年9月28日
9
2020年9月28O于A、B两点，AE是⊙O的
直径，点C为⊙O上一点，且AC平分∠PAE，过C作 CD⊥PA于D. （1）求证：CD为⊙O的切线； （2）若DC+DA=6，⊙O的直径为10，求AB的长.
2020年9月28日
4
提高练习
练3.已知直线l切△ABC外接圆于点C， AD⊥BC于点D，BE⊥AC于点E，EG⊥l于点G ，DF⊥l于点F. 求证：EG=DF.
回味无穷
2020年9月28日
7
课后作业
《优等生数学》九年级 P66-67 T1、 T2 、T3、T4 写在作业本上. 预习《优等生数学》九年级的第29、30节
2020年9月28日
8
演讲完毕，谢谢观看！
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
XUSUHUA
第二十七章 圆
27.16 弦切角定理及其逆定理
2020年9月28日
1
经典例题
例. 如图，从圆上一点A作直径BC的垂线AD，
过A作圆的切线MN. 证明：AB、AC分别平分
MN与AD的夹角.
2020年9月28日
2
巩固练习
练1. 如图，四边形ABCD内接于圆O，AD是圆O 的直径，直线MN切圆O于B点，∠MBA=40°， 求∠BCD.
2020年9月28日
5
挑战自己 练3. （牛顿定理3）圆的外切四边形的对角线的 交点和以切点为顶点的四边形对角线交点重合 .
牛顿定理1：四边形两条对边的延长线的交点所连线段的中点 和两条对角线的中点，三点共线. 这条直线叫做这个四边形的牛顿线. 牛202顿0年定9月2理8日2：圆外切四边形的两条对角线的中点，及该圆的圆6 心，三点共线.