2018年春湘教版九年级数学下2.5.3切线长定理ppt公开课优质教学课件
合集下载
九年级数学下册 第2章 圆 2.5 直线与圆的位置关系 2.5.3 切线长定理课件 (新版)湘教版

2.5.3 切线长定理
反思
如图 2-5-16,PA,PB,CD 分别切⊙O 于点 A,B,E,
CD 交 PA,PB 于 C,D 两点,若∠P=40°,则∠PAE+∠PBE
的度数为( )
A.140° B.62°
C.66° D.70°
答案:A
图 2-5-16
以上答案是否正确?若不正确,请给出正确答案.
图 2-5-15
2.5.3 切线长定理
解:(1)∵PA,PB,EF 是⊙O 的切线, ∴PA=PB,EA=EQ,FQ=FB,
∴△PEF 的周长=PE+PF+EQ+FQ=PA+PB=24(cm).
(2)连接 OA,OB,OQ.∵PA,PB,EF 是⊙O 的切线, ∴PA⊥OA,PB⊥OB,EF⊥OQ, ∠AEO=∠QEO,∠QFO=∠BFO, ∴∠AOE=∠QOE,∠BOF=∠QOF. 又∠AOB=180°-∠P=110°,
∴∠CAE=12∠PCD,∠DBE=21∠PDC, 即∠PAE=12∠PCD,∠PBE=21∠PDC. ∵∠P=40°, ∴∠PAE+∠PBE=12∠PCD+21∠PDC=12(∠PCD+∠PDC)=12(180°-∠P)=70°.
故选 D.
1 ∴∠EOF=2∠AOB=55°.
2.5.3 切线长定理
【归纳总结】运用切线长定理解决有关问题: (1)在解决有关圆的切线长问题时,往往需要构建基本图形: ①连接圆心和切点; ②连接两个切点; ③连接圆心和两切线的交点.
2.5.3 切线长定理
(2)在运用切线长定理解决问题时,要注意分解、提炼出切线 长定理的基本图形,挖掘图形中的常见几何关系:
第2章 圆
2.5.3 切线长定理
第2章 圆
2.5.3 切线长定理
九年级数学《切线长定理》课件

PB,切点分别是A、B.
求证: AP=BP, ∠OPA=∠OPB
证明:连接OA,OB
A
∵PA,PB与⊙O相切,
点A,B是切点
∴OA⊥PA,OB⊥PB
即 ∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
B
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB
切线长定理
从圆外一点可以引圆的两条切线,它们的切线长 相等,这一点和圆心的连线平分两条切线的夹角
AD、BE、CF C
A D
O
C B
PF
A
E
O B
D
24.4.3 切线长定理
平面内任取一点P,作圆O的切线, 你能作几条?怎么作?
O
概念辨析
切线长:切线上一点与切点之间的线段 长叫做这点到圆的切线长
思考:切线和切线长有何区别和联系?
(1)切线是一条与圆相切的直线,不能度量.
(2)切线长是一条线段的长,它是一个数量,
可以度量.
A
B
已知:从⊙O外的一点P引两条切线PA,
(2)若∠APB=60°,则∠AOB= ,PA= ;
连接AB,则AB=
;
在A、B之间弧上任取
A
一点C,则∠ACB= .
4 30°
2
B
3、如左图,PA、PB、DE是圆O的三条切线,
∆PCD的周长为8,则PA=
.
4、如图,∆ABC的内切圆O与AB、BC、AC相
切于点D、E、F,且AB=5,BC=9,AC=6,求
符号语言:
A
∵PA、PB分别切⊙O于点A、B
∴PA = PB;∠OPA=∠OPB
课时九切线长定理课件.ppt
半径为_斜__边__的__一__半__.
2.直角三角形内切圆的圆心(内心)在_三__角__形__内__部_, 半径r=____a+_b_-c_____.
2
知识拓展 4.Rt△ABC中,∠C=90°,a=3,b=4,则内切圆的半 径是____1___. 5.直角三角形的外接圆半径为5cm,内切圆半径为 1cm,则此三角形的周长是_2_2_c_m___.
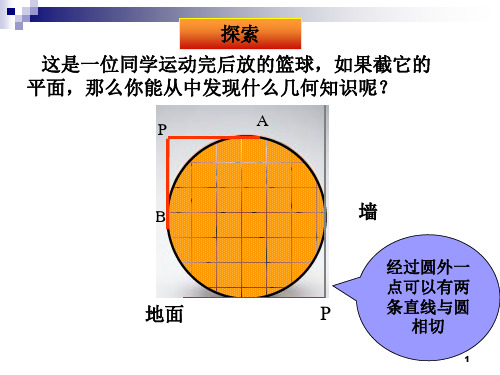
探索
这是一位同学运动完后放的篮球,如果截它的 平面,那么你能从中发现什么几何知识呢?
P
A
B
地面
墙
经过圆外一
点可以有两
P
条直线与圆 相切
1
问题2、经过圆外一点P,如何作已知⊙O的
切线?
A
。
P
O
B
思考:假设切线PA已作出,A为切点,
则∠OAP=90°,连接OP,可知A在怎样
的圆上?
2
过⊙O外一点作⊙O的切线
依据。必须掌握并能灵活应用。
13
数学探究 三角形的内切圆: 与三角形各边都相切的圆叫做三角形的内切圆
三角形的内心: 三角形的内切圆的圆心叫 做三角形的内心
三角形的内心是三角形三 条角平分线的交点,它到 三角形三边的距离相等。 B
A
D
O
F
E
C
14
练习四 已知:△ABC是⊙O外切三角形,切点
为D,E,F。若BC=14 cm ,AC=9cm,AB=
例1.如图所示PA、PB分别切圆O于A、B, 并与圆O的切线分别相交于C、D, 已知 PA=7cm, (1)求△PCD的周长. (2) 如果∠P=46°,求∠COD的度数
A D
P
·O
E
九年级数学下册 2.5 切线的性质(第2课时)课件 (新版)湘教版

精品课件
8
8.(4 分)如图所示,△ABC 中,AB=AC,∠BAC =120°,⊙A 与 BC 相切于点 D,与 BA 相交于点 E, 则∠ADE=__60°__.
精品课件
9
9.(8 分)如图,⊙O 的直径 AB=8 cm,过点 C 的
切线交 AB 的延长线于点 P,∠P=30°,求点 C 到 AB
精品课件
6
6.(4 分)如图,AB 是⊙O 的直径,O 是圆心,BC 与⊙O 相切于 B 点,CO 交⊙O 于点 D,且 BC=8, CD=4,那么⊙O 的半径是__6__.
精品课件
7
7.(4 分)(2015·湖州)如图,以点 O 为圆心的两个 圆中,大圆的弦 AB 切小圆于点 C,OA 交小圆于点 D, 若 OD=2,tan∠OAB=12,则 AB 的长是__8__.
的距离.
解:连接 OC,过 C 作 CD⊥PO 于 D,∵PC 切
⊙O 于 C,∴∠PCO=90°,∵∠P=30°,∴PO=
2OC=AB=8 cm,PC= PO2-OC2= 82-42=4 3,
S△PCO=12·OP·CD=12PC·OC,∴OP·CD=PC·OC, 8CD=4 3×4,CD=2 3,∴点 C 到 AB 的距离为 2 3
∠AOB=90°-∠A=90°-30°=60°,∵OB=
OC,∴∠ACB=∠OBC,而∠ACB+∠OBC=∠AOB
=60°,∴∠ACB=30°=∠A,∴AB=BC (2)连接
OD,∵B︵D=C︵D,∴∠BOD=∠COD,∵∠AOB=
60°,∴∠BOC=120°,∴∠BOD=∠COD=60°,
又 OB=OD=OC,∴△BOD 与△DOC 都是等边三角
精品课件
2.5.3-切线长定理

B
CA=CB
。
P
C
O
A 证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB 又∴ PC=PC
∴ △PCA ≌ △PCB ∴AC=BC
第10页,共18页。
例1.PA、PB是⊙O的两条切线,A
典例赏析 、B为切点,直线OP交于⊙O于点D
、E,交AB于C。
(1)写出图中所有的垂直关系
∴ PA = PB
∠OPA=∠OPB
第6页,共18页。
试用文字语 言叙述你所 发现的结论
二、切线长定理 从圆外一点引圆的两条切线, 它们的切线长相等,圆心和这一点的连线平分两 条切线的夹角。
B
。
P
O
几何语言: PA、PB分别切⊙O于A、B
A PA = PB
∠OPA=∠OPB
反思:切线长定理为证明线段相等、 角相等提 供了新的方法
C E
D
F
A
·O
B
C E
D
A
·O
B
第15页,共18页。
课堂小结
1.切线长定理 从圆外一点引圆的两条切线,它们的切线长相
等,圆心和这一点的连线平分两条切线的夹角。
B
∵PA、PB分别切⊙O于A、B
∴PA = PB ,∠OPA=∠OPB
。
E
O CD
P
OP垂直平分AB
切线长定理为证明线段相等,角相等
A
,弧相等,垂直关系提供了理论依据。必须 掌握并能灵活应用。
第8页,共18页。
若连结两切点A、B,AB交OP于点M.你又能得出什 么新的结论?并给出证明.
B
OP垂直平分AB
。
CA=CB
。
P
C
O
A 证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB 又∴ PC=PC
∴ △PCA ≌ △PCB ∴AC=BC
第10页,共18页。
例1.PA、PB是⊙O的两条切线,A
典例赏析 、B为切点,直线OP交于⊙O于点D
、E,交AB于C。
(1)写出图中所有的垂直关系
∴ PA = PB
∠OPA=∠OPB
第6页,共18页。
试用文字语 言叙述你所 发现的结论
二、切线长定理 从圆外一点引圆的两条切线, 它们的切线长相等,圆心和这一点的连线平分两 条切线的夹角。
B
。
P
O
几何语言: PA、PB分别切⊙O于A、B
A PA = PB
∠OPA=∠OPB
反思:切线长定理为证明线段相等、 角相等提 供了新的方法
C E
D
F
A
·O
B
C E
D
A
·O
B
第15页,共18页。
课堂小结
1.切线长定理 从圆外一点引圆的两条切线,它们的切线长相
等,圆心和这一点的连线平分两条切线的夹角。
B
∵PA、PB分别切⊙O于A、B
∴PA = PB ,∠OPA=∠OPB
。
E
O CD
P
OP垂直平分AB
切线长定理为证明线段相等,角相等
A
,弧相等,垂直关系提供了理论依据。必须 掌握并能灵活应用。
第8页,共18页。
若连结两切点A、B,AB交OP于点M.你又能得出什 么新的结论?并给出证明.
B
OP垂直平分AB
。
精选-九年级数学下册第2章圆2.5直线与圆的位置关系2.5.3切线长定理课件新版湘教版

精选中小学课件
15
仅供学习交流!!!
2.5.3 切线长定理
反思
如图 2-5-16,PA,PB,CD 分别切⊙O 于点 A,B,E,
CD 交 PA,PB 于 C,D 两点,若∠P=40°,则∠PAE+∠PBE
的度数为( )
A.140° B.62°
C.66° D.70°
答案:A
图 2-5-16
2021/2/以5 上答案是否正确?若不精正选中确小学,课件请给出正确答案.
[备选例题] 已知:如图所示,在△ABC 中,∠ABC=90°, O 是 AB 上一点,以点 O 为圆心,OB 长为半径的圆与 AB 交于 点 E,与 AC 相切于点 D.
求证:DE∥OC.
2021/2/5
精选中小学课件
12
2.5.3 切线长定理
证明: 如图,连接 BD.
∵∠ABC=90°,OB 为⊙O 的半径,
2021/2/5
精选中小学课件
10
2.5.3 切线长定理
(2)在运用切线长定理解决问题时,要注意分解、提炼出切线 长定理的基本图形,挖掘图形中的常见几何关系:
①线段相等、弧相等; ②角相等、角的互余关系; ③线段的垂直关系; ④全等三角形与相似三角形.
2021/2/5
精选中小学课件
11
2.5.3 切线长定理
∴CB 是⊙O 的切线.
∵AC 是⊙O 的切线,D 是切点,
∴CD=CB,∠1=∠2,
∴OC⊥BD.∵BE 是⊙O 的直径,
∴DE⊥BD,∴DE∥OC.
2021/2/5
精选中小学课件
13
2.5.3 切线长定理
总结反思
小结 知识点 切线长的概念与切线长定理
