最新浙教版九年级数学下册2.2切线长定理公开课优质PPT课件(2)
新浙教版九年级数学下册第二章《切线长定理》公开课课件.ppt

O
p
B
作业
一:作业本2.2 二补充:
已知:如图,PA ,PB 分别B切AC⊙1OA于PBA、B,AC 为直径。2 求证:
P
A
O
B
C
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/192020/12/19Saturday, December 19, 2020
CA、AB A
切于点D、
E、F。若 BC=a ,
AC=
F
EO
CD
B
b,AB=c
幻灯片 17
小结
1、本节学习了切线长的定义,注意和切线比较。学习了
切线长定理 从圆外一点引圆的两条切线,它们的切线长相等, 圆心和这一点的连线平分两条切线的夹角。
2、记住圆外切四边形的性质,并比较圆内接四边形
3、希望同学们在以后的学习中要勇于探索和实践,养成科 学的学习态度。同时还要注意总结作辅助线的方法,和解题 时要注意运用“数形结合”的思想方法。
对于较复杂的图 形为了解题我们 可以用数形结合
的方法
已知:四边形ABCD的边 AB,BC,CD,DA和圆O分别 相切于L,M,N,P。
探索圆外切四边形边的关系。
(1)找出图中所有相等的线段
D N C DN=DP,AP=AL,BL=BM,CN=CM
P OM
A
L B (2)填空:AB+CD = AD+BC(>,<,=)
A
O
P
B
(2)如图,Δ ABC的内切圆分别和BC,AC,AB切于D,E,
F;如果AF=2cm,BD=7cm,CE=4cm,则BC=11 cm,AC= 6cm
浙教版数学九年级下册《2.2 切线长定理》教学设计2

浙教版数学九年级下册《2.2 切线长定理》教学设计2一. 教材分析《2.2 切线长定理》是浙教版数学九年级下册中的一章,主要讲述了切线长定理的内容及其应用。
本章内容在学生的数学知识体系中占据重要地位,为后续学习圆的性质和方程奠定了基础。
二. 学情分析九年级的学生已经掌握了相似三角形的性质、锐角三角函数等知识,具备了一定的逻辑思维能力和空间想象能力。
但他们对切线长定理的理解还需要通过具体实例和实际操作来加深。
三. 教学目标1.理解切线长定理的定义及其内涵。
2.学会运用切线长定理解决实际问题。
3.培养学生的空间想象能力、逻辑思维能力和动手操作能力。
四. 教学重难点1.重点:切线长定理的理解和应用。
2.难点:切线长定理的证明和灵活运用。
五. 教学方法1.采用问题驱动法,引导学生探究切线长定理。
2.利用实物模型和几何画板软件,直观展示切线长定理的应用。
3.采用小组合作学习,培养学生的团队协作能力。
六. 教学准备1.准备相关的实物模型和图片,用于展示和讲解。
2.准备几何画板软件,用于动态展示切线长定理。
3.准备练习题和拓展题,用于巩固和提高学生的理解。
七. 教学过程1.导入(5分钟)通过展示生活中的实例,如自行车轮子、滑滑板等,引导学生思考这些实例中是否存在切线长定理的应用。
让学生意识到本节课的重要性,激发学生的学习兴趣。
2.呈现(10分钟)利用实物模型和几何画板软件,呈现切线长定理的定义和证明过程。
让学生直观地理解切线长定理,并学会如何应用它解决实际问题。
3.操练(10分钟)让学生分组讨论,每组选择一个实例,运用切线长定理进行解答。
教师巡回指导,解答学生的疑问。
4.巩固(10分钟)出示一组练习题,让学生独立完成。
题目要求运用切线长定理解决问题。
完成后,教师进行讲评,指出解题的关键点和易错点。
5.拓展(10分钟)出示一组拓展题,让学生小组合作,探讨解题方法。
题目要求运用切线长定理解决生活中的实际问题。
教师巡回指导,解答学生的疑问。
++2.2切线长定理++课件+2023--2024学年浙教版九年级数学下册

A.4
B.8
C.4
D.8
课 堂 练 习 【知识技能类作业】必做题:
3.如图,P为⊙O外一点,PA,PB分别切⊙O于点A,B,CD切⊙O于点E,分
10
别交PA,PB于点C,D,若PA=5,则△PCD的周长为______.
4.如图,PA,PB分别是⊙O的切线,A,B为切点,AC是⊙O的直径,已知
典例精析
例2 如图,⊙O表示皮带传动装置的一个轮子,传动皮带MA,NB分别切⊙O
于点A,B. 延长MA,NB,相交于点P.已知∠APB=60°,AP=24cm,求两切
Ⴃ
点间的距离和的长(结果精确到1cm).
解:如图,连结AB,OA,OB,OP .
M
∵MP,NP分别切⊙O于点A ,B,
∴OA⊥AP,OB⊥BP , AP=BP.
课堂练习
【综合拓展类作业】
解:(1)连接CD,
∵BC为直径,
∴∠ADC=∠BDC=90°,
∵AC⊥BC,
∴EC是⊙O的切线,
∵ED是⊙O的切线,
∴ED=EC,
∴∠EDC=∠ECD,
∵∠EDC+∠ADE=∠ECD+∠A=90°,
∴∠A=∠ADE
课堂练习
【综合拓展类作业】
解:(2)如图,连结CD.
∵∠ADE=∠A,
70°
∠BAC=35°,则∠P的度数为________.
课 堂 练 习 【知识技能类作业】选做题:
5.如图,四边形ABCD的边AB、BC、CD、DA和⊙O分别
相切于点L、M、N、P,
求证:AD+BC=AB+CD.
D
浙教版初中数学九年级下册 2.2 切线长定理1 课件

论?并给出证明.
OP垂直平分AB
OM
P
A
证明:∵PA,PB是⊙O的切线,点A,B是切点
∴PA = PB ∠OPA=∠OPB
∴△PAB是等腰三角形,PM为顶角的平分线
∴OP垂直平分AB
若延长PO交⊙O于点C,连结CA、CB, 你又能得出什么新的结论?并给出B证明.
CA=CB C
。
O
P
A
证明:∵PA,PB是⊙O的切线,点A,B是切点 ∴PA = PB ∠OPA=∠OPB ∴PC=PC ∴ △PCA ≌ △PCB ∴AC=BC
画一画
1、如何过⊙O外一点P画出⊙O的切线? 如下左图,借助三角板,我们可以画出 PA是⊙O的切线。 2、这样的切线能画出几条? 3、如果∠P=50°,求∠AOB的度数
130° 50°
如何用圆规和直尺作出这两条切线呢?
A
P O。
B 思考:已画出切线PA、PB,A、B为切点,则
∠OAP= °,连接9O0P,可知A、B 除了在⊙O
∴周长为24cm
Q
P
B F
探究:PA、PB是⊙O的两条切
线,A、B为切点,直线OP交于⊙O 于点D、E,交AB于C。
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB AB⊥OP
A EO
B
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
(3)写出图中所有的全等三角形
D
P
C
△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP
P ∴PA = PB ,∠OPA=∠OPB
OP垂直平分AB
切线长定理为证明线段相等,角相等,弧相等,垂 直关系提供了理论依据。必须掌握并能灵活应用。
2.2切线长定理-2020春浙教版九年级数学下册习题课件(共25张PPT)

上一页 返回导航 下一页
数学·九年级·配浙教
17
解:连结 OA,OB,OP,延长 BO 交切线 PA 于点 F.∵PA, PB 切⊙O 于 A,B 两点,CD 切⊙O 于点 E,∴∠OAF=∠PBF =90°,CA=CE,DB=DE,PA=PB.∵△PCD 的周长=PC +CE+DE+PD=PC+CA+PD+DB=PA+PB=3r,∴PA =PB=32r.在△OAF 和△PBF 中,∵∠FAO=∠FBP,∠OFA =∠PFB,∴△OAF∽△PBF,
第2章 直线与圆的位置关系
上一页 返回导航 下一页
数学·九年级·配浙教
4
【典例】 如图,PA,PB分别切⊙O于A,B两点,⊙O的半径是,∠APB= 60°,求PO,PA,AB的长.
分析:连结OB,OA,由切线及切线长的性质可得△APB是等边三角形,在△PAO 中,运用30°角所对的直角边是斜边的一半及勾股定理可求得PO,PA的长,由等边 三角形的性质求得AB的长.
第2章 直线与圆的位置关系
上一页 返回导航 下一页
第2章 直线与圆的位置关系
数学·九年级·配浙教
上一页 返回导航 下一页
第2章 直线与圆的位置关系
上一页 返回导航 下一页
数学·九年级·配浙教
24
(3)解:在 Rt△AOQ 中,OA =OQ·cos α=15×45=12,∴AQ= OQ2-OA2= 152-122=9,BQ=OB+OQ=OA+OQ=12+15=27.由(2)知△QPB∽ΔQOA,∴OPBA =QQAB,即P1B2 =297,解得 PB=36.由(1)中△AOP≌△BPO,易得 PO⊥AB,∴AB=2AC, PO= PB2+OB2= 362+122=12 10.根据△AOP 面积之间的关系,得 PA·OA= PO·AC,即 36×12=12 10·AC,解得 AC=18510,∴AB=2AC=36510.
浙教版数学九年级下册2.2 切线长定理
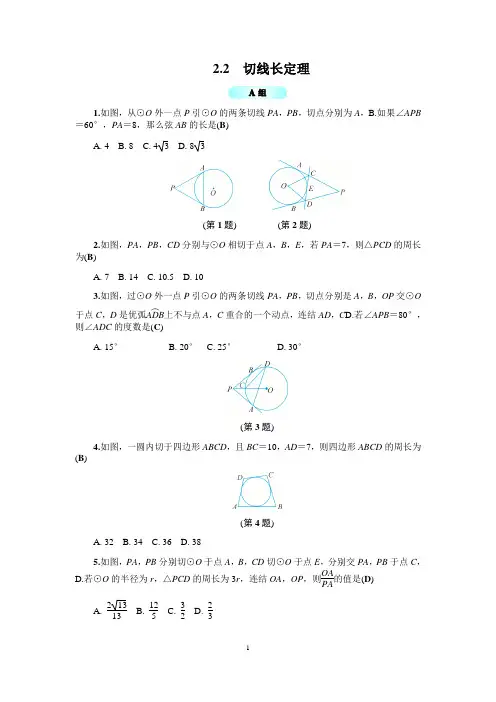
2.2 切线长定理1.如图,从⊙O 外一点P 引⊙O 的两条切线PA ,PB ,切点分别为A ,B.如果∠APB =60°,PA =8,那么弦AB 的长是(B )A. 4B. 8C. 4 3D. 8 3(第1题) (第2题)2.如图,PA ,PB ,CD 分别与⊙O 相切于点A ,B ,E ,若PA =7,则△PCD 的周长为(B )A. 7B. 14C. 10.5D. 103.如图,过⊙O 外一点P 引⊙O 的两条切线PA ,PB ,切点分别是A ,B ,OP 交⊙O于点C ,D 是优弧ADB ︵上不与点A ,C 重合的一个动点,连结AD ,C D.若∠APB =80°,则∠ADC 的度数是(C )A. 15°B. 20°C. 25°D. 30°(第3题)4.如图,一圆内切于四边形ABCD ,且BC =10,AD =7,则四边形ABCD 的周长为(B )(第4题)A. 32B. 34C. 36D. 385.如图,PA ,PB 分别切⊙O 于点A ,B ,CD 切⊙O 于点E ,分别交PA ,PB 于点C ,D.若⊙O 的半径为r ,△PCD 的周长为3r ,连结OA ,OP ,则OAPA 的值是(D )A. 21313B. 125C. 32D. 23(第5题)(第6题)6.如图,⊙O与△ABC中AB,AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,则⊙O的半径是2.(第7题)7.如图,PA,PB分别切⊙O于点A,B,连结OP与⊙O交于点C,连结AC,B C.求证:AC=B C.【解】∵PA,PB分别切⊙O于点A,B,∴PA=PB,∠APC=∠BP C.又∵PC=PC,∴△APC≌△BP C.∴AC=B C.(第8题)8.如图,已知正方形ABCD的边长为2,M是BC的中点,P是线段MC上的一个动点(不与点M,C重合),以AB为直径作⊙O,过点P作⊙O的切线交AD于点F,切点为E.求四边形CDFP的周长.【解】∵四边形ABCD是正方形,∴∠A=∠B=90°,即OA⊥AD,OB⊥B C.∵OA,OB是半径,∴AF,BP是⊙O的切线.又∵PF是⊙O的切线,∴FE =FA ,PE =PB ,∴四边形CDFP 的周长为DC +PC +DF +FP =DC +PC +DF +FE +PE =DC +PC +DF +FA +PB =DC +AD +CB =2+2+2=6.9.如图,在直角梯形ABCD 中,以AD 为直径的半圆O 与BC 相切于点E ,BO 交半圆O 于点F ,DF 的延长线交AB 于点P ,连结DE .有下列结论:①DE ∥OF ;②AB +CD =BC ;③PB =PF ;④AD 2=4AB ·D C.其中正确的结论是(C )(第9题)A. ①②③④B. ①②C. ①②④D. ③④ 【解】 连结AE .∵四边形ABCD 是直角梯形, ∴CD ⊥AD ,AB ⊥A D.∵AD 是半圆O 的直径,∴CD ,AB 是半圆O 的切线. ∵BC 是半圆O 的切线,∴BO 是∠ABE 的平分线,CD =CE ,AB =BE , ∴OB ⊥AE ,AB +CD =BC ,故②正确. ∵点E 在半圆O 上,∴DE ⊥AE ,∴DE ∥OF ,故①正确. 连结O C.易得△OAB ∽△CDO ,∴OA CD =ABDO ,即OA ·OD =AB ·CD , ∴AD 2=4AB ·DC ,故④正确. ③无法证明,故正确的结论是①②④.(第10题)10.如图,⊙D 的半径为3,A 是⊙D 外一点,且AD =5,AB ,AC 分别与⊙D 相切于B ,C 两点,G 是BC ︵上任意一点,过点G 作⊙D 的切线,交AB 于点E ,交AC 于点F .(1)△AEF 的周长是 8 .(2)当G 为线段AD 与⊙D 的交点时,连结CD ,则五边形DBEFC 的面积是 9 . 【解】 (1)∵AB ,AC 分别与⊙D 相切于点B ,C , ∴AB =AC ,∠ABD =∠ACD =90°. 又∵BD =3,AD =5, ∴AB =AD 2-BD 2=4.∵EF 切⊙O 于点G , ∴BE =EG ,FG =F C.∴△AEF 的周长=AE +EG +FG +AF =AB +AC =8.(第10题解)(2)如解图,AG =AD -DG =5-3=2. 在△AEG 和△ADB 中, ∵∠AGE =∠ABD =90°, ∠GAE =∠BAD , ∴△AEG ∽△ADB ,∴S △AEG S △ADB =⎝⎛⎭⎫AG AB 2=⎝⎛⎭⎫242=14. 又∵S △ADB =12AB ·BD =12×4×3=6, ∴S △AEG =32.同理,S △ACD =6,S △AFG =32.∴S 五边形DBEFC =S △ABD +S △ACD -S △AEG -S △AFG =6+6-32-32=9.11.如图,在△ABC 中,∠ACB =90°,以AC 为直径的⊙O 交AB 于点D ,过点D 作⊙O 的切线交BC 于点E ,EF ⊥AB ,垂足为F .(第11题)(1)求证:DE =12B C.(2)若AC =6,BC =8,求S △ACD ∶S △EDF 的值. 【解】 (1)由题意,得EC ,ED 都是⊙O 的切线, ∴EC =ED ,∠ECD =∠ED C.∵AC 为⊙O 的直径,∴∠ADC =90°, ∴∠EDC +∠EDB =90°,∠ECD +∠B =90°, ∴∠EDB =∠B ,∴ED =BE . ∴DE =BE =E C.∴DE =12B C.(2)在Rt △ABC 中,∵AC =6,BC =8,∴AB =10. 易知△ADC ∽△ACB ,∴AD AC =ACAB , ∴AD =AC 2÷AB =3.6, ∴BD =AB -AD =6.4,∴S△ACD∶S△BCD=AD∶BD=9∶16.∵ED=EB,EF⊥BD,∴S△EDF=12S△EB D.同理可得S△EBD =12S△BCD,∴S△EDF=14S△BCD,∴S△ACD∶S△EDF=94.12.如图,O是△ABC内一点,⊙O与BC相交于F,G两点,且与AB,AC分别相切于点D,E,DE∥BC,连结DF,EG.(1)求证:AB=A C.(2)若AB=10,BC=12,求当四边形DFGE是矩形时⊙O的半径.(第12题)【解】(1)∵⊙O与AB,AC分别相切于点D,E,∴AD=AE,∴∠ADE=∠AE D.∵DE∥BC,∴∠B=∠ADE,∠C=∠AED,∴∠B=∠C,∴AB=A C.(2)如解图,连结AO,交DE于点M,延长AO交BC于点N,连结OE,DG.(第12题解)设⊙O的半径为r.∵四边形DFGE是矩形,∴∠DFG=90°.∴DG是⊙O的直径.∵⊙O与AB,AC分别相切于点D,E,∴OD ⊥AB ,OE ⊥A C.又∵OD =OE ,∴AN 平分∠BA C. ∵AB =AC ,∴AN ⊥BC ,BN =12BC =6, ∴AN =AB 2-BN 2=102-62=8.∵OD ⊥AB ,AN ⊥BC ,∴∠ADO =∠ANB =90°. 又∵∠OAD =∠BAN ,∴△AOD ∽△ABN , ∴OD BN =AD AN ,即r 6=AD 8.∴AD =43r .∴BD =AB -AD =10-43r . ∵OD ⊥AB ,∴∠GDB =∠ANB =90°. 又∵∠B =∠B ,∴△GBD ∽△ABN , ∴BD BN =GD AN ,即10-43r6=2r 8,∴r =6017.∴当四边形DFGE 是矩形时,⊙O 的半径为6017.13.如图,在△ABC 中,AC =BC ,∠CAB =α(定值),⊙O 的圆心O 在AB 上,并分别与AC ,BC 相切于点P ,Q .(第13题)(1)求∠POQ 的度数(用含α的代数式表示).(2)设D 是CA 延长线上的一个动点,DE 与⊙O 相切于点M ,点E 在CB 的延长线上,试判断∠DOE 的度数是否保持不变,并说明理由.(3)在(2)的条件下,如果AB =m(m 为已知数),cos α=35,设AD =x ,DE =y ,求y 关于x 的函数表达式(并指出自变量x 的取值范围).【解】 (1)∵AC =BC , ∴∠OBQ =∠OAP =α.∵⊙O 分别与AC ,BC 相切于点P ,Q , ∴∠OPA =∠OQB =90°, ∴∠AOP =∠BOQ =90°-α, ∴∠POQ =180°-2(90°-α)=2α. (2)∠DOE 的度数保持不变.理由如下: 连结OM .由切线长定理,得EM =EQ . 又∵OM =OQ ,OE =OE , ∴△OEM ≌△OEQ . ∴∠MOE =∠QOE .同理,∠MOD =∠PO D.∴∠DOE =12(∠POM +∠QOM )=12(360°-∠POQ )=180°-α.∵α为定值,∴∠DOE 的度数保持不变.(3)∵OP =OQ ,∠APO =∠BQO =90°,∠PAO =∠QBO , ∴△APO ≌△BQO .∴OA =O B. ∵AB =m ,∴OA =OB =12AB =m2, ∴BQ =AP =AO ·cos α=310m , ∴DM =DP =310m +x .∵∠ADO +∠AOD =∠OAP =α,∠BOE+∠AOD=180°-∠DOE=α,∴∠ADO=∠BOE.又∵∠DAO=∠OBE=180°-α,∴△ADO∽△BOE,∴ADAO=BOBE,∴BE=OA·OBAD=m24x.∴ME=QE=BQ+BE=310m+m2 4x.∴DE=DM+ME=310m+x+310m+m24x=x+m24x+35m.因此所求的函数表达式为y=x+m24x+35m(x>0).初中数学试卷金戈铁骑制作。
新浙教版九年级数学下册第二章《切线长定理(第2课时)》公开课课件
证明: 两个同心圆.连接OA,OB OA=OB
∴△OAB为等腰三角形 C为切点,OC⊥AB 即OC为△ABO的高, ∴OC为△ABO的中线
∴C为AB的中点
O· A C· B
2.证明:圆心到圆的割线的距离小于半径.
3.画一个圆O,在圆O上任取一点A,过点A画圆O的切线.
作法: ⑴连结OA;
⑵过点A作直线l与OA垂直.
O·
·
l
直线 l 就是所求作的切线,如图 A
再见
•不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另 一眼睛看到纸的背面。2022年3月29日星期二2022/3/292022/3/292022/3/29 •书籍是屹立在时间的汪洋大海中的灯塔。2022年3月2022/3/292022/3/292022/3/293/29/2022 •正确的略读可使人用很少的时间接触大量的文献,并挑选出有意义的部分。2022/3/292022/3/29March 29, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。
从第⑵点的结论得出:
O·
l A
切线的性质定理 圆的切线垂直于过点的半径.
例3
如图, 直线l是圆O的切线, 切点为A, ∠OBA=40°,求∠AOB.
解: 由于线段OA是过切点的半径,
因此 OA ⊥l,从而∠OAB=90°,
于是∠AOB=90°-40°
·O
=50°
40°
B
浙教版数学九年级下册2.2切线长定理.doc
2.2切线长定理一、选择题1. 如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A=70°,则∠BOC的度数为()A.130°B.120°C.110°D.100°2. 如图,P A、PB分别切⊙O于A、B两点,如果∠P=60°,P A=2,那么AB的长为()A.1 B.2 C.3 D.43. 如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为()A.50 B.52 C.54 D.564. 如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是()A.9 B.10 C.12 D.145. 如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB、BC、AC于D、E、F,则AF的长为()A.5 B.10 C.7.5 D.46. 如图,从圆O外一点P引圆O的两条切线P A,PB,切点分别为A,B.如果∠APB=60°,P A=8,那么弦AB的长是()A .4B .8C .34D .38二、填空题7. 如图,⊙O 的半径为3cm ,点P 到圆心的距离为6cm ,经过点P 引⊙O 的两条切线,这两条切线的夹角为 .8. 如图,⊙O 与△ABC 中AB 、AC 的延长线及BC 边相切,且∠ACB =90°,∠A ,∠B ,∠C 所对的边长依次为3,4,5,则⊙O 的半径是 .9. 如图:EB 、EC 是⊙O 的两条切线,B 、C 是切点,A 、D 是⊙O 上两点,如果∠E =46°,∠DCF =32°,则∠A 的度数是 °.10. 如图,⊙O 的半径为3cm ,点P 到圆心的距离为6cm ,经过点P 引⊙O 的两条切线,则∠APO =°.11. 如图,P A 、PB 分别切⊙O 于A 、B .P A =5,在劣弧AB 上取点C ,过C 作⊙O 的切线,分别交P A ,PB 于D ,E ,则△PDE 的周长等于 .12.如图,已知PA,PB分别切⊙O于A、B,CD切⊙O于E,PO=13,AO=5,则△PCD周长为 .三、解答题13.已知:⊙O的半径为3cm,点P和圆心O的距离为6cm,经过点P和⊙O的两条切线,求这两条切线的夹角及切线长.参考答案2.2切线长定理一、选择题1.C2.B3.B4.D5.A6.B二、填空题7.60度8.29.9910.3011.1012.24三、解答题13.初中数学试卷鼎尚图文**整理制作。
浙教版九年级数学下册电子课本课件【全册】
1.1锐角三角函数
浙教版九年级数Biblioteka 下册电子课本课 件【全册】1.2锐角三角函数的计算
浙教版九年级数学下册电子课本课 件【全册】
1.3解直角三角形
浙教版九年级数学下册电子课本课 件【全册】
第2章 直线与圆的位置关系
浙教版九年级数学下册电子课本课 件【全册】
浙教版九年级数学下册电子课本 课件【全册】目录
0002页 0042页 0118页 0137页 0213页 0258页 0324页
第1章 解直角三角形 1.2锐角三角函数的计算 第2章 直线与圆的位置关系 2.2切线长定理 第3章 投影与三视图 3.2简单几何体的三视图 3.4简单几何体的表面展开图
第1章 解直角三角形
初中九年级下册数学《切线长定理》PPT精品课件
2020/11/20
1
A
O
P
2020/11/20
B
过圆外一点作圆的切线,这点 和切点之间的线段的长,叫做这点 到圆的切线长。
2
A
O
P
B
• 切线是直线,不能度量;
• 切线长是线段的长,这条线段的两个端 点分别是圆外一点和切点,可以度量。
2020/11/20
3
A
1
O
M的两条切线,
内切圆圆心:三角形三个 内角平分线的交点。
内切圆的半径:交点到三 角形任意一边的垂直距离。
2020/11/20
9
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
谢谢大家!本文档为精心编制而成,您可以在下载后自由修改和打印,希望下载对您有帮助!
2020/11/20
10
有什么关系? 又OA=OB,OP=OP, 地理课件:
历史课件:
∴Rt△AOP≌Rt△BOP(HL)
∴PA=PB,∠1=∠2
2020/11/20
4
A
O
P
B
• 切线长定理:
• 从圆外一点引圆的两条切线,它们的切线 长相等,这一点和圆心的连线平分两条切 线的夹角。
2020/11/20
5
切线长定理的拓展
A
D
O HC
P
B
(1)写出图中所有的垂直关系
(2)图中有哪些线段相等(除半径 外)、弧相等?
2020/11/20
6
2020/11/20
7
o.
o.
2020/11/20
8
三角形外接圆
C
