自考概率论与数理统计2009年10月真题及详解答案
2009-1010概率统计期末考试试卷A卷(3学时)
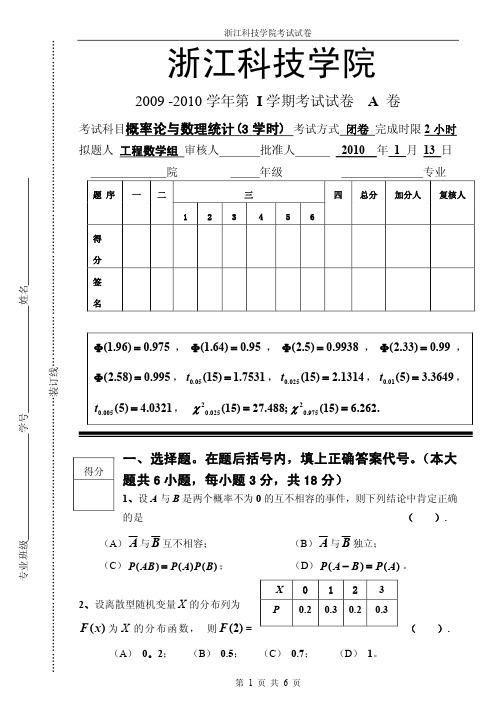
浙江科技学院2009 2010 学年第 I 学期考试试卷 A 卷考试科目概率论与数理统计(3 学时) 考试方式 闭卷 完成时限2 小时 拟题人 工程数学组 审核人批准人 2010 年 1 月 13 日院年级专业三题 序一二123 456四总分加分人复核人得分签名(1.96)0.975 F = , (1.64)0.95 F = , (2.5)0.9938 F = , (2.33)0.99 F = , (2.58)0.995 F = , 0.05 (15) 1.7531 t = , 0.025 (15) 2.1314 t = , 0.01 (5) 3.3649 t = , 0.005 (5) 4.0321t = , 2 0.025 (15)27.488; c = 2 0.975 (15) 6.262. c = 一、选择题。
在题后括号内,填上正确答案代号。
(本大题共 6 小题,每小题 3 分,共 18 分)1、设 A 与 B 是两个概率不为 0 的互不相容的事件,则下列结论中肯定正确 的是().(A ) A 与B 互不相容; (B ) A 与B 独立; (C ) ()()() P AB P A P B = ;(D ) ()() P A B P A -= 。
2、设离散型随机变量X 的分布列为() F x 为 X 的分布函数, 则 (2) F =(). (A ) 0。
2;(B ) 0.5; (C ) 0.7;(D ) 1。
得分X0 123 P 0.20.3 0.20.3专业班级学号姓名………………………………………………………………………装订线……………………………………………………………………………………3、设两个随机变量 X 与Y 相互独立且同分布, {1}{1}1/2 P X P Y =-==-= ,{1}{1}1/2 P X P Y ==== ,则下列式子成立的是( ).(A ) {}1/2 P X Y == ; (B ) {}1 P X Y == ;(C ) {0}1/4 P X Y +== ;(D ) {1}1/4 P XY == 。
09-10概率统计试题答案

北京工业大学2009—2010年度第一学期 概率论与数理统计考试试卷(工类,A 卷)学号 姓名 得分一. 填空题(每空两分,共30分)1. 已知P(A )=0.5,P(A ∪B )=0.8,且A 与B 相互独立,则P(A-B )= 0.2 , P(A B ⋃)= 0.8 。
2. 设随机变量X 服从参数是λ的泊松分布,且P(X=3)=2P(X=4),则λ= 2 ,P(X >1)= 1-3e -2。
3. 设连续型随机变量X 的概率密度函数为:⎩⎨⎧≤≤=其它,010,4)(3x x x f ,且P (X >a )=P (X <a ),则a= 2-1/4。
4. 若随机变量X 和Y 相互独立,且有相同的概率分布则随机变量Z=max{X,Y}的概率分布V=min{X ,Y}的概率分布 U=XY 的概率分布5. 设随机变量X ~B (n ,p ),已知E (X )=3,Var (X )=2.4,则n= 15 ,p= 0.2 。
6. 设X 1,X 2,…,X n 为独立同分布的随机变量,且X 1~N (0,1),则∑=ni i X 12~2n χ。
E21n i i X =⎛⎫ ⎪⎝⎭∑= n 。
Var 21n i i X =⎛⎫⎪⎝⎭∑= 2n 。
7. 设X 1,X 2,X 3是正态总体2(,)N μσ的随机样本,其中μ已知,2σ未知,在)(1),,,max(,2),(3121222123211321X X X X X X X X X X +++++σμ中,是统计量的有 ),,,max(,2),(313211321X X X X X X X μ+++8. 已知一批零件的长度X (单位:cm )服从正态分布N (μ,1),从中随机抽取16个零件,得到长度的平均值为40cm ,则μ的置信系数为0.95的置信区间为2ασZ nX。
二、计算题(每题14分)注意:每题要写出计算过程,无过程的不得分!1. 钥匙掉了,掉在宿舍里、掉在教室里、掉在路上的概率分别是40%、35%和25%。
全国2009年10月自学考试高等数学(工本)试题.

全国2009年10月自学考试高等数学(工本)试题课程代码:00023一、单项选择题(本大题共5小题,每小题3分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1. 向量a ={-1,-3,4}与x 轴正向的夹角α满足( )A. 0<1<α<2πB. α=2π C. 2π<α<π D. α=π2. 设函数f (x , y )=x +y, 则点(0,0)是f (x ,y )的( )A. 极值点B. 连续点C. 间断点D. 驻点3. 设积分区域D :x 2+y 2≤1, x ≥0, 则二重积分⎰⎰D ydxdy 的值( ) A. 小于零B. 等于零C. 大于零D. 不是常数 4. 微分方程xy ′+y =x +3是( )A. 可分离变量的微分方程B. 齐次微分方程C. 一阶线性齐次微分方程D. 一阶线性非齐次微分方程 5. 设无穷级数∑∞=1n p n收敛,则在下列数值中p 的取值为( )A. -2B. -1C. 1D. 2二、填空题(本大题共5小题,每小题2分,共10分)请在每小题的空格中填上正确答案。
错填、不填均无分。
6. 已知向量a ={3,0,-1}和b ={1,-2,1} 则a -3b =___________.7. 设函数z =2x 2+y 2,则全微分dz=___________.8. 设积分区域D 由y =x , x =1及y =0所围成,将二重积分⎰⎰Ddxdy y x f ),(化为直角坐标下的二次积分为___________.9. 微分方程y ″+3y =6x 的一个特解y *=___________.10. 无穷级数14332232323232+++++n n+…的和为___________. 三、计算题(本大题共12小题,每小题5分,共60分)11. 求过点(-1,-2,3)并且与直线223-=-=z y x 垂直的平面方程. 12. 求曲线x =t , y =t 2, z =t 3在点(1,1,1)处的切线方程.13. 求函数f (x , y , z )=xy 2+yz 2+zx 2在点P (1,2,1)处的梯度.14. 设方程e z -x 2y +z =3确定函数z =z (x , y ), 求xz ∂∂. 15. 计算二重积分⎰⎰--Dy x dxdy e 22,其中积分区域D :x 2+y 2≤2. 16. 计算三重积分⎰⎰⎰Ωxdxdydz ,其中积分区域Ω是由x =0, y =0, z =0及x +y +z =1所围成.17. 计算对坐标的曲线积分⎰++C dy x y xdx )(, 其中C 为从点(1,0)到点(2,1)的直线段.18. 计算对面积的曲面积分⎰⎰∑xyzdS ,其中∑为球面x 2+y 2+z 2=a 2(a >0).19. 求微分方程(1+x )dx -(1+y )dy =0的通解.20. 求微分方程y ″+ y ′-12y =0的通解.21. 判断级数∑∞=+⋅13)1(2n n n n 的敛散性. 22. 求幂级数∑∞=12n n n x 的收敛区间. 四、综合题(本大题共3小题,每小题5分,共15分)23. 求函数f (x , y )=x 3+3xy 2-15x -12y 的极值点.24. 求曲面z=22y x +(0≤z ≤1)的面积.25. 将函数f (x )=ln(1+x )展开为x 的幂级数.。
2009概率论与数理统计(A卷)试卷解答1

0102461911811313XY华南农业大学期末考试试卷(A 卷)2009学年第一学期 考试科目:考试类型:(闭卷) 考试时间:120分钟学号 姓名 年级专业一、 填空题(每小题3分,共3⨯5=15分)1、设随机变量X 服从二项分布()10,B p ,若X 的方差是52,则12p =2、设随机变量X 、Y 均服从正态分布()2,0.2N 且相互独立,则随机变量21Z X Y =-+的概率密度函数为()211z +-()()~1,1Y N -3、设二维离散型随机变量X 、Y 的联合分布律为: 则联合分布函数值()1,3F =5184、设总体X 服从参数为λ的指数分布,12,,...,n x x x 是它的一组样本值,作λ的极大似然估计时所用的似然函数()12,,...,;n L x x x λ=1nii x neλλ=-∑。
5、作单因素方差分析,假定因素有r 个水平,共作了n 次试验,当H 0为真时, 统计量~A A E ESS df F SS df =()1,F r n r --二、单项选择题(每小题3分,共3⨯5=15分) 1、设A ,B 是两个互斥的随机事件,则必有( A )()()()()()()()()A P A B P A P B B P A B P A P B =+-=- ()()()()()()()1C P AB P A P B D P A P B ==-2、设A ,B 是两个随机事件,()()()245,,556P A P B P B A ===,则( C )()()()()()()()()1351224825A P AB B P A BC P A BD P A B ====3、设X ,Y 为相互独立的两个随机变量,则下列不正确的结论是( D )()()()()()()()()A E X Y E X E Y B E XY E X E Y ±=±= ()()()()()()()()C D XY D X D YD D XY D X D Y ±=+=4、作单因素方差分析,假定因素有三个水平,具有共同方差2σ。
山东农业大学200910(1)概率统计含试卷A含参考答案与评分标准

⼭东农业⼤学200910(1)概率统计含试卷A含参考答案与评分标准2009 – 2010学年第⼀学期《概率统计》试卷A_参考答案与评分标准课程代码BB103001 考试⽅式闭卷考试时长100分钟题号⼀⼆三四五六七⼋合计满分15 18 12 15 13 15 12 100 得分阅卷⼈考⽣须知:1、姓名、学号、专业班级均要填在密封线以内,否则试卷作废。
2、答题请在题后空⽩区域,在草稿纸上答题⽆效。
3、试卷上不准做任何标记,否则按作弊论处。
4、考试期间,试卷不准拆开,否则按作弊处理。
(注:不⽤计算器)⼀、填空题(每⼩题3分,共15分)1.设B-=,则()0.8P A BP A=, ()0.3A,为随机事件,()0.5P AB.=2. 设随机变量X 的分布列为 01234560.10.150.20.30.120.10.03X P ,则{4}0.87≤=P X .3. 设随机变量X 的密度函数为2, 1()0, 1cx f x x x ?≥?=??c .4. 设~(1,2)X N ,~(3,4)Y N ,且X 和Y 相互独⽴,则(3)22-=D X Y .5. 设随机变量~()X P λ,且已知[(1)]3E X X +=,则λ1=.⼆、选择题(每⼩题3分,共18分)1.有8件零件,其中5件为正品,3件为次品.从中任取4件,取出的零件中有2件正品2件次品的概率为 C .()A17; ()B 27; ()C 37; ()D 47. 2. 在0H 为原假设,1H 为备择假设的假设检验中,若显著性⽔平为α,则 C .()00(|)A P H H α=接受成⽴; ()11(|)B P H H α=接受成⽴;()10(|)C P H H α=接受成⽴; ()01(|)D P H H α=接受成⽴.3. 设12(,,,)(1)n X X X n >L 为总体2~(,)X N µσ的⼀个样本,X 为样本均值,2S 为样本⽅差,则有 C .()A2~(,)X N µσ; ()B 2~(,)nX N µσ;()C~(1)/X t n S nµ--; ()D /~(1)X S t n -.4. 设随机变量X 的⽅差为2,由切⽐雪夫不等式得{|()|2}-≥≤P X E X A .()A12; ()B 13; ()C 14; ()D 15.5. 对总体),(~2σµN X 的均值µ作区间估计,得到置信度为95%的置信区间,其意是指这个区间 B .()A 平均含总体95%的值; ()B 有95%的机会含µ的值; ()C 有95%的机会含样本的值; ()D 平均含样本95%的值.6. 设12,,,n X X X L 独⽴同分布,它们的期望与⽅差分别为2,µσ,若令1nkk n Xn Y n µσ=-=∑,则n Y 近似服从 D .()A 2()n χ; ()B ()t n ; ()C (1,)F n ; ()D (0,1)N .三、计算题(12分)设随机变量X 服从区间(1,6)上的均匀分布,求⼀元⼆次⽅程210t X t ++=有实根的概率.解:依题意知,X 密度函数为1/5,16()0,x f x <⽅程有实根的条件为X 2-4≥0,即X ≤-2 或 X ≥2,从⽽,P {t 2+Xt +1=0有实根}= P {X ≤-2}+ P {X ≥2} = P {X ≤-2}+1-P {X <2} ……………………………………………………… 6分得分=22()1()--∞-∞+-=?f x dx f x dx 21141.55=-=?dx ………………………………… 2分四、计算题(15分)设⼆维随机变量(,)X Y 的联合分布列(律)如右表,试求解以下问题(要求:计算要有主要过程):① X 的边缘分布为 ……………… 3分② Y 的边缘分布为 ……………… 3分③ ),(Y X Cov =()()()E XY E X E Y -= ……………… 3分Y X0 1 2 3 0 1/6 1/12 4 1/6 1/6 1/6 5 1/121/60 1 2 1/4 1/2 1/4Y P3 4 5 1/4 1/2 1/4X P得分④ XY ρ=(,)()()Cov X Y D X D Y = ……………… 3分⑤ X ,Y 是否相互独⽴?因为{3,0}{3}{0}P X Y P X P Y ==≠==,所以X ,Y 不相互独⽴. … 3分五、计算题(13分)设国际市场上每年对我国某种出⼝农产品的需求量X (单位:t )是随机变量,它服从[1200,3000]上的均匀分布.若售出这种农产品1t ,可赚2万元,但若销售不出去,则每吨需付仓库保管费1万元,问每年应准备多少吨产品才可得到最⼤利润?解: 设每年准备该种商品a 吨,年利润为Y ,则利润为 ………… 1分2,3000()2(),1200a a X Y g X X a X X a≤≤?==?--≤12003000()18000?≤≤?=x f x ,,其它, ……………… 2分得到平均利润为300012001()()d 1800=?E Y g x x …………………………………… 2分 300012001[(3)2]1800d d a a x a x a x =-+?? …………………………………… 2分213(72002160000)18002a a =-+-. …………………………………… 2分求极值过程,略. 当a = 2400时,()E Y 取到最⼤值,故每年准备此种商品2400 t ,可使平均利润达到最⼤. ………………………………………… 2分六、参数估计题(15分)设总体X 的密度函数为 <<=-其它,010,),(1x x x f θθθ,其中0θ>未知,12,,,n X X X L 为⼀组简单随机样本,试求θ的矩估计与极⼤似然估计.解:①因X 1, X 2,…,X n 为来⾃总体的⼀组样本, ………………… 1分由矩估计原理得 ?()E XX =,计算得 ()()E X xf x dx +∞-∞=?110x x dx θθ-=?1θθ=+, ………………… 3分解得θ的矩估计量为 ?1XXθ=- . ……………………………… 1分②设x 1, x 2,…,x n 为样本的⼀组观测值, …………………………… 1分则似然函数为11)(-=?=∏θθθi ni n x L ,…………………………………… 3分取对数得 1ln ()ln()(1)ln()nii L n x θθθ==+-∑, …………………………… 1分求导数得1ln ()ln()ni i d L n x d θθθ==+∑, …………………………………… 1分令 0)(ln =θθd L d ,得似然⽅程 1ln()0ni i n x θ=+=∑, …………………… 1分解得θ的极⼤似然估计值为 1ln()nii nx θ==-∑, …………………… 3分因此得θ的极⼤似然估计量为 1ln()nii nX θ==-∑ . (⽆此步,不扣分)七、假设检验题(12分)⼀般情况下667m 2粮⾷产量服从正态分布. 某县在秋收时随机抽查了25个村的667m 2产量,得平均产量x =1050kg ,标准差s =50kg ,试问该县已达到吨粮县的结论是否成⽴?(= 0.05),其中:0.050.0250.050.0250.050.025(25) 1.7081,(25) 2.0595;(24) 1.7109,(24) 2.0639;1.645, 1.96.t t t t u u ======解:属σ2未知的参数µ的左单侧检验问题.依题意有 H 0: µ=1000;H 1: µ<1000 , ……………………………… 4分选取统计量 ~(1)/µ-==-X t t n S n, …………………………………… 2分查表得 0.05(24) 1.7109t =,拒绝域为 t <-1.7109 , …………………… 2分计算统计量的值得 105010005/50/25µ--===x t s n , …………………… 2分由于t 不在拒绝域内,所以接受H 0, ………………………………………… 1分认为该县已经达到了吨粮县的标准. ………………………………………… 1分。
2009-2010学年概率论与数理统计B甲(答案)

安徽工业大学2009-2010学年概率论与数理统计B 期末考试卷(甲卷)参考答案0. 6 0. 6 ----- 0.750.6 0.6 亠 0.4 0.31 1 1 7. & — 9. 0.62 10.2 4 e 1 (z_2)2111. e 18 , -::::Z :: ::. 12. 3、壬7 2010 、选择题(本题共6小题,每小题3分,共18分) 1. B 2. D 3. B 4. C 5.A6. D、填空题(本题共6小题,每小题3分,共18分) 三、判断题(本题共5小题,每小题2分,共10分) 13.X 14. V 15. X 16. X 17. V 四、解答题(本题共7小题,满分54分,解答应写出演算步骤.) 18.解:设事件A ={作弊被监视器发现}; B ={作弊被监考教师发现} 则由题意有 p(A)=0.6 , p(B)=0.4, p(AB)=0.2 —— (4 分)故作弊考生被发现的概率为 P (A B) = p(A) p(B)-p(AB) =0. 6 0. 4 0.=2 0 即作弊考生被发现的概率为 0.8 (8 分)佃.解:由题意知: 13 1 1八—亠—亠—亠A 亠——亠B =1 ——(1) ……(3分)8812 24 若X 与Y 独立,应有: PX=1,Y=2 二 PX=1 PY=2 -1 A -2M V 12 丿(6分)即该同学若重考超过了 80分,他第一次考试就超过80分的概率为0.75。
------- (8 分)22 23 241 1 综合(1)(2)有:A =- B - 4 8 (8 分)20 (8分)【解】 (I ) EZ =3EX 2 -2E XY EY 2- 2 =3 DX +(EX f 丨—2 EX 莊Y + P XY + DY +(EY 「-2 =69 (3 分) (4分) (II ) DW =4DX DY 2Cov(2X,-Y) =4 4 9 -4Cov(X,Y) =25-4 匚丫 ' DX 、DY -------- (7 分)= 37. .................................. (8 分) 21. (8分)解:记事件 A ={第一次考试超过 80分},事件B = {重考超过80 分},则由题意条件知: P(A 尸 0. ,6 P(B|A) =0.6,P(A)=0.4, P(B|A)=0.3 .............. (3 分)而所求事件的概率应为P(A| B)=P(A)P(B|台) P(A)P(B| A)P(A)P(B| A)------ (6 分)(8分)解:由已知条件有 X 的分布密度函数为「1/4, 1兰 X 乞5;f(T 0,令Y 表示三次独立观测中观测值大于丫3 二 B(3,p)else2的次数,则其中p 为故有(8 分) 解:5p= p{X 3}=(1/4)dx 二 1/2PM 勺心片一;)w(2 分)(4分)(6 分)(8 分)n1j1 (1)因为 E(X)二 xf (x)dx= 0(r 1)x dx—22EX -1 2X_12EX2=1为所求的矩估计量1 — X(2)似然函数为令:ln L胡(4分)L(%, ,X n ,T )二(二 1)n (X 1叮1 ln(x 1 小0ln(X1…X n )「为所求的极大似然估计星(6分)解: 设X 为n 次掷硬币正面出现的次数,则1X ~ B(n, p),其中 p 二2XnF , 0 人 1 ,(8 分)(1)由切比雪夫不等式知P 0.4辽 X ^o du P | X 一0.5卜 0.1 丄 P 1| x - 0.5n# 0.1n1 I. n J[ n J_1 一 D(X )2=1_(0.1n)n 兀丄 n4.252 — I —,0.01 n n令 1 一兰 H 90%.n则得 n- 250(3 分)(2)由中心极限定理, X P{0.4 0.6} = P{0.4n 乞 X < 0.6n}n得:p{0.4n 「0.5n X 「0.5n0.6n 「0.5ni 0.25n 0.25n0.25n0 1ny n2 :」( )-1= 2〉( )-1— 90%0.引 n 5=」()-0.95.5从而有厶1.605即沦644沦655 ,(6 分)。
2009年10月全国自考(教育学)真题试卷(题后含答案及解析)

2009年10月全国自考(教育学)真题试卷(题后含答案及解析)题型有:1. 单项选择题 2. 名词解释题 3. 简答题 4. 论述题 5. 案例分析题单项选择题每小题2分,在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.首次把“教育学”作为一门独立科学提出来的学者是A.夸美纽斯B.培根C.康德D.赫尔巴特正确答案:B2.在世界教育学史上,被公认为第一本现代教育学的著作是A.《康德论教育》B.《大教学论》C.《普通教育学》D.《学记》正确答案:C3.世界上最早颁布义务教育法的国家是A.普鲁士B.奥地利C.英国D.美国正确答案:A4.“人类之所以千差万别,就是由于教育之故”,洛克的这一观点属于A.遗传决定论B.教育万能论C.辐和论D.主体活动论正确答案:B5.形成学校文化的最重要的因素是A.学生B.校长C.教师D.家长正确答案:C6.体育活动可以提高学生对自然环境的适应能力,这说明体育具有A.健体功能B.教育功能C.价值功能D.娱乐功能正确答案:A7.涂尔干说:“教育在于使青年社会化()在我们每一个人之中,造成一个社会的我。
这便是教育的目的。
”这种观点属于A.神学教育目的论B.社会本位教育目的论C.个人本位教育目的论D.教育无目的论正确答案:B8.在课程的各种理论基础中,对课程影响最为长久、最为深刻的是A.心理学B.社会学C.教学论D.哲学正确答案:D9.从发达国家的经验来看,小班教学通常采取的方式是A.分科任教B.走班授课C.教师包班D.分层教学正确答案:C10.迄今为止,在世界范围内应用最广泛、最普遍的教学方法是A.讲授法B.谈话法C.讨论法D.练习法正确答案:A11.班主任工作的首要任务是A.树立明确的共同目标B.建设学生干部队伍C.培养健康的集体舆论D.组织建立良好的班集体正确答案:D12.我国普通中小学进行教育教学活动的基本单位是A.班集体B.少先队C.共青团D.班委会正确答案:A13.在学校咨询与辅导中,属于着重训练行为的方法是A.鼓励表达B.深入共感C.身体放松D.系统脱敏正确答案:D14.一个测验能测到预先想测的知识和能力的程度,指的是A.测验的实用性B.测验的可信度C.测验的有效性D.测验的难度正确答案:C15.当前我国教育法规定的法律责任是一种A.民事法律责任B.行政法律责任C.刑事法律责任D.经济法律责任正确答案:B名词解释题每小题3分16.学校绩效正确答案:是指学校功能发挥所产生的实际效果,是管理有效性的重要标志。
2009概率论与数理统计试题及答案——同济

1 n X i 是已知的,个体(总体)的 E( X i ) 未知,矩估计: X ,完成了一个从样本到 n i 1
1
总体的推断过程。
二、做题的 18 个口诀(概率 15 个,统计 3 个) 1、概率
(1)题干中出现“如果” 、 “当” 、 “已知”的,是条件概率。 例 7:5 把钥匙,只有一把能打开,如果某次打不开就扔掉,问第二次打开的概率? (2)时间上分两个阶段的,用“全概公式”或者“贝叶斯公式” 。 例 8:玻璃杯成箱出售,每箱 20 只,设各箱含 0,1,2 只残次品的概率分别为 0.8, 0.1 和 0.1。一顾客欲购买一 箱玻璃杯,由售货员任取一箱,而顾客开箱随机地察看 4 只;若无残次品,则买下该箱玻璃杯,否则退回。试求: (1)顾客买此箱玻璃杯的概率; (2)在顾客买的此箱玻璃杯中,确实没有残次品的概率。 (3) “只知次数,不知位置”是“二项分布” 。 例 9:抛 5 次硬币,其中有 3 次正面朝上的概率?
Hale Waihona Puke 2 、 F 分布取面积对称的分位数。
3
三、选择题常考的 5 个混淆概念 1、乘法公式和条件概率
例 24:100 个学生,60 个男生,40 个女生,棕色头发 30 个,棕色头发的男生 10 个,任取一个学生,是棕色头发 的男生的概率?已知取了一个男生,是棕色头发的概率?
P( AB) P( A) P( B / A)
(10)均匀分布用“几何概型”计算。
0 x 1,0 y x,
试求 U=X-Y 的分布密度。
其他. 0 x 1,0 y x,
,试求 P(X+Y>1)。
2 例 17:设随机变量(X,Y)的分布密度为: ( x, y ) 0,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙04183# 概率论与数理统计(经管类)试卷 第 1 页 共 10 页
全国2009年10月高等教育自学考试
概率论与数理统计(经管类)试题
课程代码:04183
一、单项选择题(本大题共10小题,每小题2分,共20分)
在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.某射手向一目标射击两次,A i 表示事件“第i 次射击命中目标”,i =1,2,B 表示事件“仅第一次射击命中目标”,则B =( B ) A .A 1A 2 B .21A A C .21A A
D .21A A
2.某人每次射击命中目标的概率为p (0<p <1),他向目标连续射击,则第一次未中第二次命中的概率为( D ) A .p 2 B .(1-p )2 C .1-2p
D .p (1-p )
3.已知P (A )=0.4,P (B )=0.5,且A ⊂B ,则P (A |B )=( C ) A .0 B .0.4 C .0.8
D .1
解:(P14)∵A ⊂B ,∴()()P AB P A =,()()()()()0.40.80.5
P AB P A P A B P B P B ====。
4.一批产品中有5%不合格品,而合格品中一等品占60%,从这批产品中任取一件,则该件产品是一等品的概率为( D ) A .0.20 B .0.30 C .0.38
D .0.57
解:(P14)设A 为取到不合格品的事件,B 为取到一等品的事件; 则A 为取到合格品的事件,∴()()
()5%,195%P A P A P A ==-= 合格品中一等品概率为:()60%P B A =,显然,()
0P B A =
浙04183# 概率论与数理统计(经管类)试卷 第 2 页 共 10 页
由全概率公式得:()()()()()
5%095%60%57%P B P A P B A P A P B A =+=⨯+⨯= 5.设随机变量X 的分布律为
,则P {X <1}=( C )
A .0
B .0.2
C .0.3
D .0.5
解(P?):
6.下列函数中可作为某随机变量的概率密度的是( A )
A .⎪⎩⎪⎨⎧≤>100,
0,100,1002x x x
B .⎪⎩⎪⎨⎧≤>0,0,0,10
x x x
C .⎩⎨⎧≤≤-其他,0,
20,1x D .⎪⎩⎪⎨⎧≤≤其他,
0,232121x ,
解:(P39)∵
()1f x dx +∞
-∞
=⎰
∴(A)
()210010010010010001100f x dx dx x x +∞
+∞
+∞
-∞
⎛⎫
==-=--= ⎪⎝⎭
⎰
⎰; (B)
()0
10
10ln 1f x dx dx x x
+∞
+∞+∞-∞
==≠⎰
⎰
;
(D)
()332
2112
2
1113111
12222222
f x dx dx x +∞
-∞
===⨯-⨯=≠⎰
⎰
; 7.设随机变量X 与Y 相互独立,X 服从参数为2的指数分布,Y ~B (6,
2
1
),则E(X-Y)= ( A )
A .2
5- B .
2
1 C .2
D .5
解:(P ?)∵()12E X =
,()1632E Y =⨯=,()()()15322
E X Y E X E Y -=-=-=-。
