理论力学第三章习题解析
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解
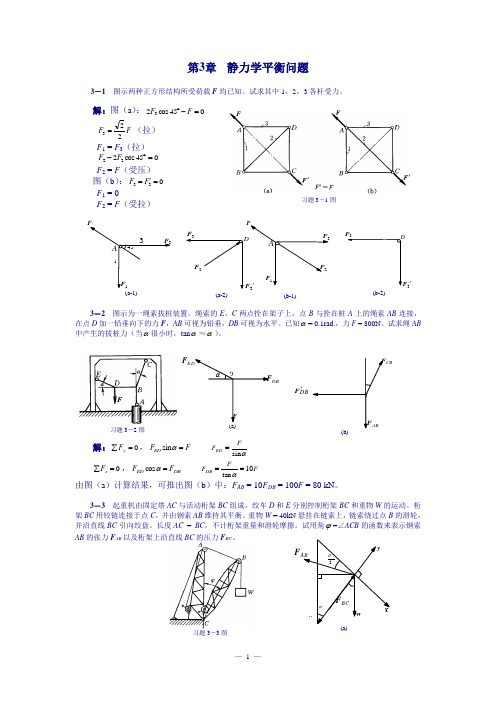
F DBCBDBF '习题3-3图第3章 静力学平衡问题3-1 图示两种正方形结构所受荷载F 均已知。
试求其中1,2,3各杆受力。
解:图(a ):045cos 23=-︒F FF F 223=(拉) F 1 = F 3(拉) 045cos 232=︒-F F F 2 = F (受压) 图(b ):033='=F F F 1 = 0F 2 = F (受拉)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αs i nFF ED = 0=∑x F ,DB ED F F =αcos F FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN 。
3-3 起重机由固定塔AC 与活动桁架BC 组成,绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ,并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上,链索绕过点B 的滑轮,并沿直线BC 引向绞盘。
长度AC = BC ,不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3-1图(a-1)(a-2)'3(b-2)习题3-2图F习题3-5图习题3-4图 解:图(a ):0=∑x F ,0sin 2cos=-ϕϕW F AB ,2sin2ϕW F AB =0=∑y F ,02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3-4 杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
胡汉才编著《理论力学》课后习题答案第3章习题解答(精编文档).doc

【最新整理,下载后即可编辑】3-3在图示刚架中,已知kN/m3=mq,26=F kN,mkN10⋅=M,不计刚架自重。
求固定端A处的约束力。
mkN12kN60⋅===AAyAxMFF,,3-4杆AB及其两端滚子的整体重心在G点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
对于给定的θ角,试求平衡时的β角。
Aθ3lGβGθBBFARF32lO解:解法一:AB为三力汇交平衡,如图所示ΔAOG中βsinlAO=,θ-︒=∠90AOG,β-︒=∠90OAG,βθ+=∠AGO由正弦定理:)90sin(3)sin(sinθβθβ-︒=+ll,)cos31)sin(sinθβθβ=+l即βθβθθβsincoscossincossin3+=即θβtantan2=)tan21arctan(θβ=解法二::=∑xF,0sinR=-θGF A(1)=∑yF,0cosR=-θGF B(2))(=∑F A M ,0sin )sin(3R =++-ββθl F lG B (3)解(1)、(2)、(3)联立,得)tan 21arctan(θβ=3-5 由AC 和CD 构成的组合梁通过铰链C 连接。
支承和受力如图所示。
已知均布载荷强度kN/m 10=q ,力偶矩m kN 40⋅=M ,不计梁重。
kN 15kN 5kN 40kN 15===-=D C B A F F F F ;;;解:取CD 段为研究对象,受力如图所示。
0)(=∑F C M ,024=--q M F D ;kN 15=D F 取图整体为研究对象,受力如图所示。
0)(=∑F A M ,01682=--+q M F F D B ;kN 40=B F 0=∑y F ,04=+-+D B Ay F q F F ;kN 15-=Ay F 0=∑x F ,0=Ax F3-6如图所示,组合梁由AC 和DC 两段铰接构成,起重机放在梁上。
已知起重机重P1 = 50kN ,重心在铅直线EC 上,起重载荷P2 = 10kN 。
理论力学课后习题第三章解答

理论力学课后习题第三章解答3.1解 如题3.1.1图。
均质棒受到碗的弹力分别为,棒自身重力为。
棒与水平方向的夹角为。
设棒的长度为。
由于棒处于平衡状态,所以棒沿轴和轴的和外力为零。
沿过点且与轴平行的合力矩为0。
即:①②③ 由①②③式得:④ 又由于即⑤ 将⑤代入④得:图题1.3.11N ,2N G θl x y A z 0sin 2cos 21=-=∑θθN N F x0cos 2sin 21=-+=∑G N N Fyθθ0cos 22=-=∑θlG c N M i ()θθ22cos 1cos 22-=c l ,cos 2c r =θrc 2cos =θ3.2解 如题3.2.1图所示,均质棒分别受到光滑墙的弹力,光滑棱角的弹力,及重力。
由于棒处于平衡状态,所以沿方向的合力矩为零。
即①由①②式得:所以()cr c l 2224-=o图题1.3.21N 2N G y 0cos 2=-=∑G N Fyθ0cos 22cos 2=-=∑θθlG d N M z ld=θ3cos 31arccos ⎪⎭⎫ ⎝⎛=l d θ3.3解 如题3.3.1图所示。
棒受到重力。
棒受到的重力。
设均质棒的线密度为。
由题意可知,整个均质棒沿轴方向的合力矩为零。
3.4解 如题3.4.1图。
轴竖直向下,相同的球、、互切,、切于点。
设球的重力大小图题1.3.32AB i G ag ρ=1i G bgρ=2ρz ()BH BF G OD G M z --⋅=∑21sin θ=0sin cos 2sin 2=⎪⎭⎫ ⎝⎛--θθρθρa b gb a ga aba b 2tan 22+=θ图题1.3.4Ox A B C B C D为,半径为,则对、、三个球构成的系统来说,在轴方向的合力应为零。
即:①对于球,它相对于过点与轴平行的轴的合力矩等于零。
即:②由式得:3.5解 如题3.5.1图。
梯子受到地面和墙的弹力分别为,,受地面和墙的摩擦力分别为,。
理论力学第三章题解

理论力学题解第三章 思考题3.1. 仅(4)式正确.3.2. 甲正确. 乙错在角度不可以定义为从动线指向定线.3.3. 乙的方程正确. 甲错在空气阻力亦应为yk -,y 取负值,y k -取正值. 3.4. 仅对固定方向才有动量守恒的分量形式. 径向和横向均不是空间固定方向.3.5. (1)对;(2)错.3.6. 一质点动量守恒,则对空间任一固定点角动量守恒. 质点对空间某一固定点角动量守恒,其动量不一定守恒.3.7. 质点作匀速直线运动时,其动量和角动量均守恒.3.8. 动能定理是标量方程,不可能投影而得出分量方程. 但x F mv x x d )21(d 2=是正确的.仿照动能定理的导出,用x t v x d d =乘牛顿第二定律的x 分量方程x xF tv m =d d 即可证明.第三章 习题3.1. 力为时间的函数,积分两次可得)cos(200ϕωω+++=t m eE t V X x ,其中ϕωcos 2000m eE x X -=,ϕωsin 000m eE v V +=. 3.2. 以地心O 为原点,建立x 轴经抛出点竖直向上. 质点受万有引力沿x 轴负方向. 所以2x GMm xm -= . 因为2RGMm mg =,故g R GM 2=. 故有 22xg R x -= . 做变换)2(d d d d d d d d 2x x x xx t x x x x ===,则x x gR x d )2(d 222-= . 积分并用0=t 时R x =,0v x= 定积分常数,得到 )11()(212202Rx g R v x -=- . 质点达最大高度时H R x +=,0=x,可求出12020)21(2--=Rgv g v H .三点讨论:(1)令∞=H ,对应Rg v 20=为第二宇宙速度.(2)若Rg v 220<<,则回到重力场模型所得结果.(3)题中不考虑地球自转及空气阻力,均不大合理,试进一步讨论之.3.3. 质点运动微分方程为(Oy 轴竖直向上);上升阶段22y g mk mg ym --=,下降阶段22y g mk mg ym +-=. 3.4. 可参见例题3. 令meB=ω,电子运动微分方程为 y x ω-=, (1) meEx y-= ω, (2) 0=z. (3) 对(2)式求导,利用(1)式得02=+y yω,解出)sin(αω+=t A y . 0=t 时0=y 故0=α,由t A y ωωcos =,且0=t 时m eBv Ee y 0+-= ,故BBv E A 0+-=,则t B Bv E yωsin 0+-= . 积分得)cos 1()(20t m eBeB Bv E m y -+-=. 代入(1)式积分可得t m eB eB Bv E m t B E x sin )(20--=. 3.5. (旋轮线是如图圆轮在直线AB 上作无滑滚动时P 点的轨迹,曲线上P 点切线方向即为轮上P 点速度方向. 因无滑,0P 为瞬心,故P 点切线与P P 0垂直,因此可知P 点切线与x 轴夹角为2ϕ. ) 以曲线最低点(0=ϕ)为自然坐标原点,弧长正方向与t e一致. 质点运动微分方程为2sinϕmg s m -= .对曲线参数方程求微分,得ϕϕd )cos 1(d +=a x 和ϕϕd sin d a y =,所以ϕϕd 2cos2d d d 22a y x s =+=,积分并用0=ϕ时0=s 定积分常数,得2sin 4ϕa s =. 代入质点运动微分方程消去ϕ,得到04=+s a gs ,s 作简谐振动而具有等时性. 其解为)cos(0αω+=t A s ,ag 40=ω与振幅无关.3.6. 小球运动微分方程为T F r r m -=-)(2θ , (1) 0)2(=+θθr r m , (2) a r-= . (3) 由(3)式求出at R r -=,代入(2)式求出)/(0at R t v -=θ,再由(1)式求出3220)(--=at R R mv F T .3.7. 珠子的运动微分方程为2b 2n d d N N F F tv m+-=μ, (1) n 2/N F mv =ρ, (2) mg F N -=b 0, (3)R =ρ(约束方程). (4)把(2)、(3)、(4)式代入(1)式,作变换s v t v d /)21(d d d 2=,可求出]/)ln[()2/(224020Rg g R v v R s ++=μ.3.8. 以椭圆最低点为自然坐标原点O ,弧长正方向指向小球初始位置,θ为切向与水平方向的夹角,小球的运动微分方程为θsin mg vm -= , (1) θρcos /2mg F mv N -=. (2)Oy 竖直向上,将s y d /d sin =θ代入(1)式得s y g s v v d /d d /d -=,积分可求出小球达最低点时gb v 22=. 由轨道方程22x a aby --=求出当0=x 时0='y ,2/a b y ='',由公式可求出22/32)1(1a by y ='+''=ρ. 再由(2)式求出0=θ时)/21(/cos 222a b mg mv mg F N +=+=ρθ.3.9. 11bF M x =,11aF M y -=,01=z M ,2222/b a bcF M x +=,2222/b a acF M y +-=,02=z M .3.10. 由运动学方程求出→v ,根据定义即可求出→→→→→→++--=⨯=k r m j t t t r km i t t t r km v r m L ωωωωωωω200000000)sin (cos )cos (sin ,)]cos ()sin )([(]cos )()sin ([000000),,(a t r k t r c kt m m t r c kt b t r k l m L n m l -+-----=ωωωωωω)sin cos (00200t br t ar r n m ωωωωω--+.3.11. 由对21O O 轴的角动量定理ωαωm l ml t-=)(d d2,积分可得l t /0e αωω-=,求出α/)2ln (l t =. 将角动量定理化为l /d d θαω-=,积分可以求得αωαωθπ4/)rad (2/00l l ==(圈).3.12. (1)由动能定理)(4121212222122b a mk mv mv W -=-=. (2)用曲线积分算⎰⎰+=⋅=→→2121)d d (y ym x x m r d F W ,把轨道参数方程kt b y kt a x sin ,cos ==代入,则曲线积分化为对t 的积分,可得同样结果.3.13. 珠子的动能定理为s F F mv N N d )21(d 2b 2n 2+-=μ,参见3.7提示. 3.14. 因机械能守恒,小球动能不变,因此0v v =.过O 点作z 轴竖直向上(垂直纸面向外),质点对z 轴的角动量δcos rmv L z =. 质点所受对z 轴力矩δsin N z rF M -=. 由对z 轴的角动量定理得δδsin )cos (d d0N rF rmv t-=. 由于θθθθθ ar ar t r rv a r -=-===-e d d d d 0,θθr v =. 故a v v r =-=θδtan . 将它代入角动量定理方程,得到N N arF rF rmv -=-=δtan 0 . 而δδsin sin 0v v v rr -=-== ,所以θδδδa N ar mv a r mv armv ar mv F e 11tan 1tan sin 2020220222020+=+=+==. 3.15. 当0=⨯∇→F 时势能存在,要求311332232112,,a a a a a a ===. 以原点为势能零点,则)444(21132312233222211xz a zy a xy a z a y a x a V +++++-=. 3.16. )/cos (d d d )d d (d 2r pq r F r F e r e r F r F r r θθθθθ-=+=+⋅=⋅→→→→→,故为有势场. 3.17. y ky x kx y ky ky x b x k b x k r F d 2d 2d )(d )]()([d --=--+--+-=⋅→→)](d [22y x k +-=.故势能存在. 以O 为势能零点,则)(22y x k V +=. 3.18. 根据机械能守恒定律,以椭圆弧最低点为势能零点,mgb mv =221,可知gb v 2=,参见3.8提示. 3.19. 3.20. 3.21.。
理论力学(胡运康)第三章作业答案

11
3-26 已知:M1=10kN,求FBx 、 FBy 、MB 、FAC 、 FEx 、 FEy 解: 1、整体:
∑M
∑F
MB
FBx FBy
x
B
= 0 ⇒ MB
= 0 ⇒ FBx = 0
= 0 ⇒ FBy
∑F
y
2、AB: FD
A
FEy
E
∑M
FEx
B
E
= 0 ⇒ FD
∑F
∑F
x
= 0 ⇒ FEx
= 0 ⇒ FEy
3-42 已知:q1=4kN/m , q2=2kN/m ,F =2 kN ,M=2 kN.m 。求 A、B处受力;销钉C所受的力。
F1 F2
F B FB FC1y C FC2y
C FC2y 1m
4/3 m
q 解: 1、BC: F1 = 1 ⋅ 2 = 4kN, 2
F2 =
1 q1 ⋅ ⋅ 2 = 2kN 2 2
M1 B
FE
Aቤተ መጻሕፍቲ ባይዱ
∑M
2、DC:
M2
FC
x
A
= 0, ⇒ FE
F'E
D
FE= F'E
C FCy
∑M
C
= 0, ⇒ M 2
8
3-17 求 机构平衡时力偶M1、M2的关系。
FAx FAy
A
FD F'D D
B
M1
FD= F'D
FCx
M2
C FCy
解: 1、AB: ∑ M A = 0, FD ⋅ d − M 1 = 0, ⇒ FD = M 1
2
3-3
几何法
理论力学答案第三章

《理论力学》第三章作业参考答案习题3-9解:力F在x 、y 坐标轴上的投影分别为:)(03.169100050301010222N F x =⨯++=)(09.507100050301030222N F y =⨯++=力F作用点的坐标为1500.15x m m m =-=-,(10050)0.15y mm m =+=。
所以,0.15507.090.15169.09101.4(.)Z y x M xF yF N m =-=-⨯-⨯≈-答: 力F对z 轴的力矩为-101.4Nm .习题3-11解:力F在x 、y 、z 坐标轴上的投影分别为:00cos 60cos 304x F F F ==1cos 60sin 304y F F F=-=-FF F Z 2360sin 0-=-=力F的作用点C 的坐标为1sin 302o x r r==,cos 302o y r ==,z h =。
所以,()Fr h F h F r zF yF My z X341412323-=⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=-=()F r h F r F h xF zF Mz x y+=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛=-=4323243rF F r F r yF xF Mxy Z214323412-=⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=-=答:力F对x 、y 、z 轴的矩分别为:()134h r F -,)4h r F +,12rF-。
习题3-12解:以整个支架为研究对象。
由于各杆为二力杆,球铰链A 、B 、C 处的约束力A F 、B F 、C F 沿杆件连线汇交于D 端球铰链,与物块的重力P构成一空间汇交力系,其受力情况如图所示。
以O 为原点建立坐标系,列平衡方程,我们有⎪⎪⎩⎪⎪⎨⎧===∑∑∑000z y x F F F⎪⎩⎪⎨⎧=-++=++=-015sin 30sin 45sin 30sin 45sin 015cos 30cos 45sin 30cos 45sin 045cos 45cos 000000000000P F F F F F F F F C B A C B A B A 解之得:()()()cos1526.39()2sin 45sin 3015cos1526.39()2sin 45sin 3015cos 3033.46()sin 3015o A o o ooB o o ooC o o P F kN P F kN F P kN ⎧⎪==-⎪⎪⎪==⎨-⎪⎪⎪=-=-⎪-⎩答:铰链A 、B 的约束力均等于26.39kN ,方向与图示相同,即为压力,铰链C 的约束力等于-33.46 kN ,方向与图示相反,即为拉力。
《理论力学》第三章-受力分析试题及答案

理论力学3章作业题解
3-1 作下列指定物体的示力图。
物体重量除图上已注明者外,均略去不计。
假设接触处都是光滑的。
题2-1 附图
解答:(a) A 、B 处为光滑接触,产生法向约束力。
(b) A 处为固定铰,能产生水平和竖向约束力;B 处为活动较,产生法向约束力。
(c) A 、C 处为光滑接触,产生法向约束力。
A
B C
D
轮
(d) O 处为固定铰,BC 简化为连杆约束。
(e) A 处为固定铰,B 处为绳子约束,产生拉力。
(f) A 处为固定铰,BC 为连杆约束。
(g) A 处为固定铰;B 、D 处为连杆约束;C 处为铰链接,此处销钉约定放在某个物体上,所以要满足作用与反作用定律。
(h) A 、B 处为光滑接触,产生法向约束力; C 处为铰链接,此处销钉约定放在某个物体上,所以要满足作用与反作用定律;DE 为绳子约束。
(f)
(d)
(a)
(b)
C
(c)
(g) F
A
F (h)
(i) B 处为固定铰;AC 为连杆; C 处为铰链接,销钉约定放在轮子上;E 处为绳子约束。
3-3 试作图示刚架及ACB 部分的示力图。
A
C
q
C
q
F F F F Cy
Cx
整体
ABC 部分
F 1。
理论力学课外作业加答案解析详解
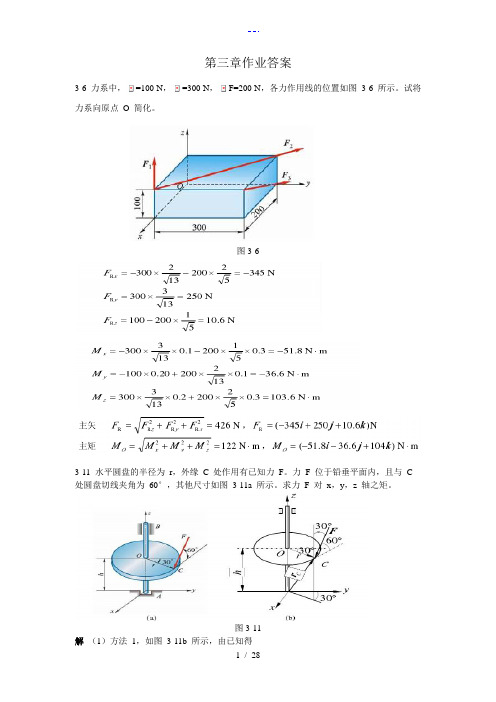
第三章作业答案3-6 力系中,=100 N,=300 N,F=200 N,各力作用线的位置如图3-6 所示。
试将力系向原点O 简化。
图3-63-11 水平圆盘的半径为r,外缘C 处作用有已知力F。
力F 位于铅垂平面内,且与C 处圆盘切线夹角为60°,其他尺寸如图3-11a 所示。
求力F 对x,y,z 轴之矩。
图3-11解(1)方法1,如图3-11b 所示,由已知得(2)方法23-14 图3-14a 所示空间桁架由杆1,2,3,4,5 和6 构成。
在节点A 上作用1 个力F,此力在矩形ABDC 平面内,且与铅直线成45°角。
ΔEAK =ΔFBM。
等腰三角形EAK,FBM和NDB 在顶点A,B 和D 处均为直角,又EC=CK=FD=DM。
若F=10 kN,求各杆的内力。
图3-14解(1) 节点 A 为研究对象,受力及坐标如图3-14b 所示(2)节点B 为研究对象,受力如图3-14b 所示3-19 图3-19a 所示6 杆支撑1 水平板,在板角处受铅直力F 作用。
设板和杆自重不计,求各杆的内力。
图3-19解截开6 根杆,取有板的部分为研究对象,受力如图3-19b 所示。
3-22 杆系由球铰连接,位于正方体的边和对角线上,如图3-22a 所示。
在节点D 沿对角线LD 方向作用力。
在节点C 沿CH 边铅直向下作用F。
如球铰B,L 和H 是固定的,杆重不计,求各杆的内力。
图3-22解(1)节点D 为研究对象,受力如图3-22b 所示(2)节点C 为研究对象,受力如图3-22b 所示3-25 工字钢截面尺寸如图3-25a 所示,求此截面的几何中心。
图3-25解把图形的对称轴作轴x,如图3-25b 所示,图形的形心C 在对称轴x 上,即第五章作业答案5-3 如图5-3 所示,半圆形凸轮以等速= 0.01m/s沿水平方向向左运动,而使活塞杆AB 沿铅直方向运动。
当运动开始时,活塞杆A 端在凸轮的最高点上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章习题( 3.1;3.6;3.7;3.9;3.10;3.12;3.13;3.20;3.21,3.22)3.1 半径为r 的光滑半球形碗,固定在水平面上。
一均质棒斜靠在碗缘,一端在碗内,一端则在碗外,在碗内的长度为c ,试证棒的全长为()cr c 2224-3.1解 如题3.1.1图。
图题1.3.1均质棒受到碗的弹力分别为1N ,,2N 棒自身重力为G 。
棒与水平方向的夹角为θ。
设棒的长度为l 。
由于棒处于平衡状态,所以棒沿x 轴和y 轴的和外力为零。
沿过A 点且与z 轴平行的合力矩为0。
即:0sin 2cos 21=-=∑θθN N F x① 0cos 2sin 21=-+=∑G N N F yθθ②0cos 22=-=∑θlG c N M i ③由①②③式得:()θθ22cos 1cos 22-=c l ④ 又由于,cos 2c r =θ即rc 2cos =θ⑤将⑤代入④得:()cr c l 2224-=3.6把分子看作相互间距离不变的质点组,试决定以下两种情况下分子的中心主转动惯量:()a 二原子分子。
它们的质量是1m ,2m ,距离是l 。
()b 形状为等腰三角形的三原子分子,三角形的高是h ,底边的长度为a 。
底边上两个原子的质量为1m ,顶点上的为2m 。
∙Cx yha1m 2m 1m 第3.6(b)题图3.6解 (a )取二原子的连线为x 轴,而y 轴与z 轴通过质心。
O 为质心,则Ox ,Oy ,Oz 轴即为中心惯量主轴。
设1m 、2m 的坐标为()()0,0,,0,0,21l l ,因为O 为质心(如题3.6.2图)故02211=+l m l m ①且l l l =-12 ②由①②得21122121,m m lm l m m l m l +=+-=所以中心惯量主轴:()0221=+=∑i i i z y m I()22121222l m m m m x z m I i i i +=+=∑()22121223l m m m m y x m I i i i +=+=∑(b )如题3.6.3图所示,图题3.6.3该原子由A 、B 、D 三个原子构成。
C 为三个原子分子的质心。
由对称性可知,图中Cx 、Cy 、Cz 轴即为中心惯量主轴。
设A 、B 、D 三原子的坐标分别为()0,,0A y ,⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-0,,2,0,,2D B y a y a 因为C 为分子的质心。
所以DB A DD B B A A C m m m y m y m y m y ++++==0112112=++++m m m y m y m y m DB A ①又由于DB y y =②h y y B A =-③由①②③得:2122112.22m m h m y y m m h m y D B A +-==+=故该分子的中心主转动惯量()()D B A i h m m m m z y m I i i i ,,2222121221=+=+=∑()()D B A i am x z m I i i i ,,221222==+=∑()()D B A i am h m m m m y x m I i i i ,,2222122121223=++=+=∑3.7如椭球方程为1222222=++c z b y a x 试求此椭球绕其三个中心主轴转动时的中心主转动惯量。
设此椭球的质量为m ,并且密度ρ是常数。
3.7解 如题3.7.1图所示。
沿y 轴平行于Oxy 平切椭球得切面为一椭圆,则该椭圆方程为:11122222222=⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-b y c z b y a x可求该切面的面积()⎪⎪⎭⎫ ⎝⎛-=221b y ac S y π 故积分()c ab dy b y ac y dy S y dm y bb bb y 3222221541πρρπρ=⎪⎪⎭⎫ ⎝⎛-=⋅=⎰⎰⎰-- 同理可求,15432bc a dm x πρ=⎰32154abcdm z πρ=⎰故中心主转动惯量:()()22221154c b abc dm z y I +=+=⎰πρ()()22222154c a abc dm z x I +=+=⎰πρ()()22223154b a abc dm y x I +=+=⎰πρ又由于椭球体积()abc dy b y ac dy S V bb bb y ππ34122=⎪⎪⎭⎫ ⎝⎛-==⎰⎰-- 故abcmV m πρ43==将ρ代入321,,I I I 得:()22151c b m I +=()22251c a m I += ()22351b a m I +=3.9立方体绕其对角线转动时的回转半径为23d k =试证明之。
式中d 为对角线的长度。
3.9解 如题3.9.1图所示Oxyz 坐标系。
图题1.9.3O 为正方体中心。
Ox 、Oy 、Oz 分别与正方体的边平行。
由对称性可知,Ox 、Oy 、Oz 轴就是正方体的中心惯量主轴。
设正方体的边长为a 。
设为平行于轴的一小方条的体积,则正方体绕轴的转动惯量()22222226am dydz z y a I a a a a xx =+=⎰⎰--ρ根据对称性得26a m I I I xxzz yy === 易求正方体的对角线与Ox 、Oy 、Oz 轴的夹角都为θ。
且31cos =θ故正方体绕对角线的转动惯量22226cos cos cos am I I I I zz yy xx ====θθθ①又由于ad 3=②绕对角线的回转半径mI k =③由①②③得23d k =3.10一均质圆盘,半径为a ,放在粗糙水平桌上,绕通过其中心的竖直轴转动,开始时的角速度为0ω。
已知圆盘与桌面的摩擦系数为μ,问经过多少时间后盘将静止?3.10解 如题3.10.1图。
图题1.3.10z 轴过O 点垂直纸面向外。
均质圆盘的密度为ρ。
设盘沿顺时针转动,则沿z 的方向有z zM dtdI = 即z z M I =ω① I 为转盘绕z 轴的转动惯量:221ma I =(m 为盘的质量), ωω-=z ②(ω为盘转动的角频率,负号因为规定顺时针转动)320232a g dr d r g M az ρμπθρμπ==⎰⎰=()232a m ma g πρρμ=③由①②③得ag 34μω-= 又因为(),00ωω=故()tag t 340μωω-=所以(),0=t ω得ga t μω430=3.12矩形均质薄片ABCD ,边长为a 与b ,重为mg ,绕竖直轴AB 以初角速0ω转动。
此时薄片的每一部分均受到空气的阻力,其方向垂直与薄片的平面,其量值与面积及速度平方成正比,比例系数为k 。
问经过多少时间后,薄片的角速减为初角速的一半?CDb第3.12题图3.12解 如题3.12.1图,第3.12.1图坐标Oxyz 与薄片固连,则沿z 轴方向有: ① 且现取如图阴影部分的小区域 ,该区域受到的阻力df 对z 轴的力矩所以zz dJ M dt=z zM I ω=22d d d ()z f k sv kb y y ω==23d d d z z M f y kb y yω=-⋅=-d d s b y=②又薄片对轴的转动惯量()ab m ma bdy y dm y I aaρρ====⎰⎰202231③由①②③得:()21431ωω+=t m b ka t z当()2ωω=t z 时,234ωb ka mt =3.13一段半径R 为已知的均质圆弧,绕通过弧线垂直的轴线摆动。
求其作微振动时的周期。
3.13解 如题3.13.1图所示,图题1.3.13坐标系Oxyz 的原点位于圆弧最顶点。
设圆弧平衡时,质心c 的坐标为()0,,0l c -。
如图所示圆弧偏离平衡位置一小角度θ,则θ满足微分方程θθ I mgl =-sin I 为圆弧相对于Oz 轴的转动惯量。
当θ很小时,θθ≈sin ,代入上式得:0=+θθImgl ①圆弧上对应转角为θ的一小段圆弧的坐标为()0,cos ,sin R R R -θθ质心c 的纵坐标()R R Rd R R R d y csin cos 0θθθρθθρθθθθ+-=-=⎰⎰--上式中ρ为圆弧的线密度R R l 0sin θθ-= ②又()()[]θθθρθθd R R R R I ⎰-+-=022sin cos ⎪⎪⎭⎫ ⎝⎛-=002sin 12θθmR ③其中02θρR m =,将②③代入①得02=+θθRg ④解④式得通解()⎪⎪⎭⎫⎝⎛+=ϕθt R g A t 2cos 微振动周期g R RgT 2222ππ==3.20质量为M 半径为r 的均质圆柱体放在粗糙水平面上。
柱的外面绕有轻绳,绳子跨过一个很轻的滑轮,并悬挂一质量为m 的物体。
设圆柱体只滚不滑,并且圆柱体与滑轮间的绳子是水平的。
求圆柱体质心的加速度1a ,物体的加速度2a 及绳中张力T 。
m第3.20题图3.20解 如题3.20.1图,题3.20.1图'm设圆柱体的转动角速度为k ωω-=,设它受到地面的摩擦力为f ,由动量定理和动量矩定理知:1a M x M f T F c x ∑==+= ① ∑-=+-=ω 221Mr fr Tr M z②对于滑块。
由动量定理知:③又无滑滚动条件:ωr xc =两边对时间求导:ω r xa c ==1④ 以C 为基点:r a a Ax ω+=1 假设绳不可拉伸。
则2a a Ax =。
故r a a ω+=12⑤ 由①②③④⑤解得:mM mMgT m M mg a m M mg a 833,838,83421+=+=+=3.21一飞轮有一半径为r 的杆轴。
飞轮及杆轴对于转动轴的总转动惯量为I 。
在杆轴上绕有细而轻的绳子,绳子的另一端挂一质量为m 的重物。
如飞轮受到阻尼力矩G 的作用,求飞轮的角加速度。
若飞轮转过θ角后,绳子与杆轴脱离,并再转过ϕ角后,飞轮停止转动,求飞轮所受到的阻尼力矩的量值。
第3.21题图2y FT mg myma =-==-∑3.21解 (1)如题3.21.1图。
题3.21.1图设z 轴过O 点垂直纸面向外。
绳子上的弹力为T 。
对于飞轮,根据动量矩定理,在z 轴方向:∑=-=ωI G Tr Mz① maT mg =-②a 为物块下落的加速度。
因为物块的加速度应与A 点加速度一样大小,故r a ω= ③由①②③解得:2mrI Gmgr +-=ω(2)假若飞轮受到的阻尼力矩为G 的话,由(1)问知,飞轮的角加速度2mrI Gmgr +-=ω 。
现在来求绳子脱落以后飞轮的角加速度ω' 。
同样根据动量矩,在z轴方向:IG G I -='-='ωω可以证明:类似于位移、加速度、初速度和末速度之间的关系式as v v t2202=-。
