2014年春季新版新人教版七年级数学下学期第5章、相交线与平行线单元复习学案1
人教版七年级数学下册《第五章相交线和平行线复习》教学设计

《第五章相交线与平行线复习》教学设计一、教学内容人教版七年级数学下册《第五章相交线与平行线》复习课。
二、学情分析学生在学完本单元知识后,对某些知识可能还存在一些不同程度的问题。
比如,基础知识似懂非懂、不能在解题中准确应用所学知识等等。
问题比较集中的可能会是垂线的存在、唯一性及平行公理的限制条件的理解、平行线的判定定理和性质定理的区分及综合应用等方面,教师应注意学生出现问题比较集中的知识点,教学中作重点突破。
三、教学目标知识与能力:了解本单元的知识点及其之间的关系;复习巩固相交线与平行线的有关概念和性质,使学生会用这些概念和性质进行简单的推理或计算;能用直尺、三角板画垂线和平行线;加深理解推理证明,提高学生分析问题、解决问题的能力。
过程与方法:在参与猜想、观察、实验、综合实践等活动的过程中,形成从特殊到一般的思维方式,了解数学知识是来源于实践,应用于实践的,了解数形结合思想,数学建模思想.情感态度与价值观:认识数学严谨、抽象和应用广泛的特点,体会数学的应用价值,激发学习图形与几何的兴趣.四、教学重点:对本单元的知识结构进行梳理,使学生掌握本单元的知识体系,理解各知识点之间的关联,会利用相交线和平行线的有关知识解决问题。
五、教学难点:会灵活应用本单元知识解决综合性问题;证明题会分析、推理,会写出严谨的解答推理过程。
六、教学方法:引导启发法、讨论交流法七、教学准备:任务单、幻灯片、知识卡片八、教学过程(一)、本章知识点梳理(1、用八开纸书写本章知识思维导图,利用投影仪展示书写优秀的作品。
2、利用知识贴片将本章知识点进行系统归纳,由教师动手归纳操作,其他学生注意观察,并及时提出质疑。
)教师活动:展示优秀作品,引导学生将本章知识以思维导图的形式进行梳理。
启发、引导学生探索,自然导入新课。
学生活动:学生欣赏优秀作品,积极思考并参与知识系统归纳。
设计意图:利用投影仪展示自己的作品,调动学生的兴趣,采用知识贴片激发学生的思维,为复习旧知识及本节课的学习做铺垫。
人教版七年级下册第五章 相交线与平行线章末复习教案(3课时)
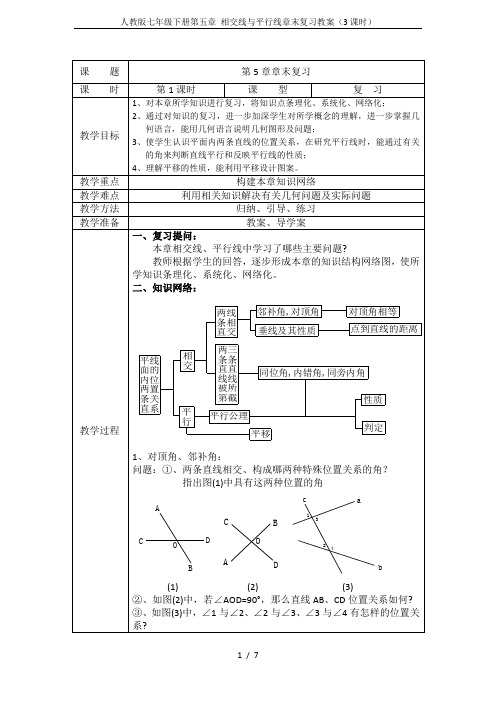
对顶角有什么性质? (对顶角相等)
如果两个对顶角互补或邻补角相等,你得到什么结论?
让学生明确:对顶角总是相等,邻补角一定互补;但加上其他条件如对顶角或邻补角相等后,那么问题中每个角的度数就随之确定为90°角,这时两条直线互相垂直.
2、垂线及其性质:
(5)(6)
(6)如图:已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
学生先尝试完成,然后教师就学生完成情况酌情讲评。
三、课时小结:
今天我们主要对本章相关题目进行了总结性的大扫荡,本章中的相关题目我们基本上做完了也讲完了。同时,我希望同学们通过这些练习能很好地掌握解题方法,能灵活运用本章是知识来解决一些相关的数学问题和实际问题。
③点到直线的距离、两条平行线的距离.
初中阶级学习了三种距离。
共同点:距离都是线段的长度;
区别:两点间距离是连接这两点的线段的长度;点到直线的距离是直线外一点引已知直线的垂线段的长度;平行线间距离是某条直线上一点到另一点平行线的距离。
练习:①如图(6)四边形ABCD,AD∥BC,AB∥CD,过A作AE⊥BC,过A作AF⊥CD,垂足分别是E、F,量出点A到BC的距离和AB、CD平行线间的距离。
4、理解平移的性质,能利用平移设计图案。
教学重点
构建本章知识网络
教学难点
利用相关知识解决有关几何问题及实际问题
教学方法
归纳、引导、练习
教学准备
教案、导学案
教学过程
一、复习提问:
本章相交线、平行线中学习了哪些主要问题?
教师根据学生的回答,逐步形成本章的知识结构网络图,使所学知识条理化、系统化、网络化。
2014年春季新版新人教版七年级数学下学期第5章、相交线与平行线单元复习学案7

课案(学生用)相交线平行线复习2(复习课)【学习目标】1.知识技能(1)通过对基本概念的复习了解直线、射线、线段的联系和区别.(2)通过了解方位角,理解角的定义,掌握度、分、秒之间的换算,掌握余角和补角的定义及其性质.(3)通过理解中点、角平分线的定义,利用中点、角平分线的性质进行简单的计算.2.解决问题掌握“两点确定一条直线”、“两点之间线段最短”,并能够利用它们解决实际问题. 3.数学思考(1)通过角的第二定义的教学,来进一步认识几何图形中的运动、变化的情况.(2)初步会用运动、变化的观点看待几何图形,初步形成辩证唯物主义观点.4.情感态度通过探索古希腊的“几何作图三大难题”,使求知欲望得到激发,通过应用自己所学知识解决身边的问题,提高学习数学的兴趣。
【学习重难点】 1. 重点:(1)直线、射线、线段的概念(2)角的概念及两个定义和角的表示法是本节的重点也是难点.(3)角的两种比较方法、角的和、差、倍、分的作法和计算、角的平2. 难点:(1)角的概念及两个定义和角的表示法(2)角平分线定义的各种数学表达式课前延伸1.已知:如图,E 、A 、F 在一条直线上,且EF ∥BC ,试说明∠B +∠C +∠BAC =180°.2.如图,已知AB ∥CD ,MP 平分∠BMN ,且∠PMN =∠PNM ,求∠NPM 的度数.课内探究例1 下列说法是否正确?请说明理由.(1)连结A 、C 两点的线段叫做A 、C 两点之间的距离. (2)射线AB 与射线BA 表示同一条射线.(3)已知线段AB 和点C ,如果AC =BC ,那么点C 是线段AB 的中点.EAFBC(4)如果∠A+∠B+∠C=90°,那么∠A、∠B、∠C互余.(5)货船在岛屿O的南偏东30°的A处,则岛屿O在货船的北偏西60°方向上.例2 一个角是另一个角的3倍,且小角的余角与大角的补角之差为21°10′,求这两个角的度数.例3 如图,在平原上有A、B、C、D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池,不考虑其他因素,请你画图确定水池的位置,使它与四个村庄的距离之和最小.D●A●B●●C例4 怎样正确量出跳远的成绩?例5 在同一平面内不在同一直线上的3个点,过任意2个点作一条直线,则可作直线的条数为___________.例6 如图1,直线AB,CD相交于点O,OE⊥AB于O,∠COE=55°,则∠BOD的度数是()A .40°B .45C .30°D .35°例7 如图2,已知AB ∥CD ,∠C =35°,BC 平分∠ABE ,试求∠ABE 的度数。
2014年春季新版新人教版七年级数学下学期第5章、相交线与平行线单元复习学案3

课案(学生用)5.1.1 相交线(新授课)【学习目标】1.知识技能(1)了解对顶角与邻补角的概念,能从图中辨认对顶角与邻补角. (2)知道“对顶角相等”.(3)了解“对顶角相等”的说理过程. 2.解决问题通过小组学习等活动经历得出对顶角相等的过程,进一步提高学生应用已有知识解决数学问题的能力.3.数学思考(1)经历探究对顶角、邻补角的位置关系的过程,建立空间观念.(2)通过分析具体图形得到对顶角、邻补角的概念,发展学生的抽象概括能力. 4.情感态度(1)通过对对顶角的探究,使学生初步认识数学与现实生活的密切联系.(2)通过师生的共同活动,促使学生在学习活动中培养良好的情感、合作交流、主动参与的意识,在独立思考的同时能够认同他人. 【学习重难点】1.重点:对顶角的概念,“对顶角相等”的性质. 2.难点:“对顶角相等”的探究过程. 【课时安排】一课时 【教学设计】课前延伸【知识梳理】1.下列说法中,正确的是( )A .有公共顶点的角是对顶角B .相等的角是对顶角C .对顶角一定相等D .不是对顶角的角不相等 2.如图所示,∠1和∠2是对顶角的图形有( )12121221A .1个B .2个C .3个D .4个 3.如图,所示,AB 与CD 相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___. 4.如图,所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.34D CBA 12自学本课内容后,你有哪些疑难之处?课内探究一、课堂探究1(问题探究,自主学习)(1)直线a、b相交,∠1 = 40°,求∠2、∠3、∠4的度数.(2)∠1等于90°时,∠2、∠3、∠4等于多少度?(3)如图是一个对顶角量角器.你能说明它度量角度的原理吗?二、课堂探究2(分组讨论,合作探究)找出图中∠AOE的对顶角及邻补角.若没有请画出.CDEABO1234Oab三、反馈训练1.如图所示,三条直线AB ,CD ,EF 相交于一点O ,则∠AOE +∠DOB +∠COF 等于( • ) A ..150° B.180° C .210° D.120°第1题 第3题 第4题 2.下列说法正确的有( )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A.1个B.2个C.3个D.4个 3.如图所示,直线AB 和CD 相交于点O ,若∠AOD 与∠BOC 的和为236°,则∠AOC •的度数为( )A.62°B.118°C.72°D.59°4.如图所示,直线L 1,L 2,L 3相交于一点,则下列答案中,全对的一组是( ) A.∠1=90°,∠2=30°,∠3=∠4=60° B.∠1=∠3=90°,∠2=∠4=30C.∠1=∠3=90°,∠2=∠4=60°D.∠1=∠3=90°,∠2=60°,∠4=30° 5.如图所示,直线AB ,CD ,EF 相交于点O ,则∠AOD 的对顶角是_____,∠AOC 的邻补角是_______;若∠AOC =50°,则∠BOD =______,∠COB =_______.6.如图所示,已知直线AB ,CD 相交于O ,OA 平分∠EOC ,∠EOC =70°,则∠BOD =•______.第5题 第6题 第7题 第8题 7.如图所示,直线AB ,CD 相交于点O ,若∠1-∠2=70,则∠BOD =_____,∠2=____.8.如图,直线AB 、CD 、EF 相交于点O ,∠AOE =30°,∠BOC =2∠AOC ,求∠DOF 的度数.四、布置作业:1.必做题:教科书第8页习题5.1第1、2、7题 2.选做题:①如图,三条直线相交于一点,求∠1+∠2+∠3的度数.②如图所示,AB ,CD ,EF 交于点O ,∠1=20°,∠BOC =80°,求∠2的度数. ③如图所示,L 1,L 2,L 3交于点O ,∠1=∠2,∠3:∠1=8:1,求∠4的度数.60 ︒ 30︒ 3 4L 1 1 2 L 2L 3ODCBAOFED CBAOF ED C B A OE D C B A O D C BA 1 2 OF CBA12第①题 第②题 第③题3.预习题;(1)下列说法中,不正确的是( )A .经过一点能画一条直线和已知线段垂直B .一条直线可以有无数条垂线C .过射线的端点与该射线垂直的直线只有一条D .过直线外一点并过直线上一点可画一条直线与该直线垂直 (2)下列说法正确的有( )①两条直线相交,交点叫垂足;②在同一平面内,过一点有且只有一条直线与已知直线垂直;③在同一平面内,一条直线有且只有一条垂线;④在同一平面内,一条线段有无数条垂线;⑤过一点不可能向一条射线或线段所在的直线作垂线;⑥若1l ⊥2l ,则1l 是2l 的垂线,2l 不是垂线.A .2个B .3个C .4个D .5个 (3)过一条线段外一点,画这条线段的垂线,垂足在( ) A . 这条线段上 B .这条线段的端点 C . 这条线段的延长线上 D .以上都有可能 (4) 如图,直线AB 与直线CD 的位置关系是__________,记作__________,此时,∠AOD =∠________=∠________=∠________=90°.(5) 如图,直线AB 、CD 相交于点O ,OE 为射线,若∠1=35°,∠2=55°,则OE 与AB _____(填“垂直”或“不垂直”).第4题 第5题课后提升3 4 L 3 L 2L 11 2 A D O B CE12 O AB CD一、课后练习题及答案:1.如图3,直线AB 、CD 相交于点O ,∠AOC =34°,∠DOE =56°.则: (1)∠BOD =________,∠BOC =__________,∠AOE =___________. (2)写出表示下列各对角关系的名称:∠BOD 和∠EOD ____________;∠BOD 和∠AOC ____________; ∠BOD 和∠AOD ____________;∠AOC 和∠DOE ____________.2.如图4,AOE 是一条直线,OB ⊥AE ,OC ⊥OD ,则图中互补的角有_____对.第1题 第2题3.如图,直线AB 、CD 相交于点O ,OE 平分∠BOD ,OF 平分∠COE ,∠AOD ∶∠BOE =4∶1,求∠AOF 的度数.F C D E OBA4.如图,直线AB 交CD 于点O ,由点O 引射线OG 、OE 、OF ,使OC 平分∠EOG ,∠AOG =∠FOE ,∠BOD =56°,求∠FOC .5.观察下列图形,寻找对顶角(不含平角). (1)两条直线相交(如图1),图中共有______对对顶角; (2)三条直线相交于一点(如图2),图中共有______对对顶角; (3)四条直线相交于一点(如图3),图中共有______对对顶角; ……(4)n 条直线相交于一点,则可构成_______对对角角; (5)2006条直线相交于一点,则可构成_______对对顶角.(1) (2) (3)。
七年级数学下册第五章 相交线与平行线复习学案.doc0
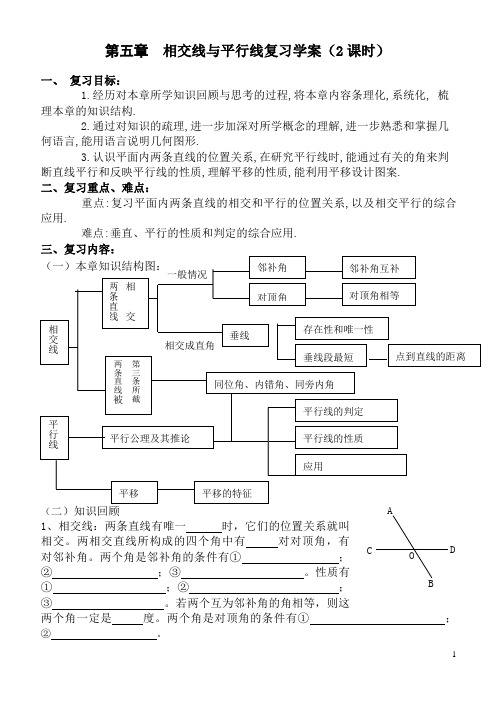
第五章 相交线与平行线复习学案(2课时)一、 复习目标:1.经历对本章所学知识回顾与思考的过程,将本章内容条理化,系统化, 梳理本章的知识结构.2.通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形.3.认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质,理解平移的性质,能利用平移设计图案. 二、复习重点、难点:重点:复习平面内两条直线的相交和平行的位置关系,以及相交平行的综合应用. 难点:垂直、平行的性质和判定的综合应用.(1、相交线:两条直线有唯一 时,它们的位置关系就叫相交。
两相交直线所构成的四个角中有 对对顶角,有对邻补角。
两个角是邻补角的条件有① ;② ;③ 。
性质有① ;② ;③ 。
若两个互为邻补角的角相等,则这两个角一定是 度。
两个角是对顶角的条件有① ;② 。
性质有 。
指出右图中具有这两种位置的O D C B A角:。
2、垂线:⑴如果两条直线相交所构成的角中有一个角是角,就叫这两条直线互相垂直,其中一条就是另一条的垂线。
过一点...(包括线上和线外两种情况)作已知直线的垂线条。
回忆并操作:如何过三角形(特别是钝角三角形)(O叫),所以∠ =的顶点作对边的垂线。
如图0,因为直线AB⊥CD于O,∠ =∠ =∠ = °。
反之,因为∠AOC= °(或或或),所以AB⊥CD。
⑵连接直线外一点与直线上各点的所有线段中,最短,简称成为。
举例:跳远成绩的测量、从河流引水的水渠的挖掘等。
3、三线八角:两条直线被第三条直线所截,必将构成八个角,其中两个角之间的位置关系分为三种情况:同位角:,内错角:,同旁内角:。
每一种角之间必须要有平行线为前提才有相等或互补的数量关系,否则其数量关系并不成立。
如找出图1、图3中的三线八角,能否确定它们之间的相等或互补的数4、平行线⑴同一平面内,两条永不相交(即没有交点)的直线的位置关系叫互相平行,其中一条叫另一条的平行线。
2014年春季新版新人教版七年级数学下学期第5章、相交线与平行线单元复习教案2

辽宁省瓦房店市第八初级中学七年级数学下册 第五章 相交线与平行线-垂直教学设计 新人教版(一)·垂直定义忆一忆 同一平面内的两条直线有哪些位置关系?相交(斜交)(垂直相交)平行a ba ba b1·看看周围(教室、书本等)哪些线是互相垂直的?2·你是怎样理解垂直的?教师根据学生回答画出图形。
学生尝试下定义教师总结如果两条直线相交成直角,那么这两条直线互相垂直。
两条线段互相垂直是指这两条线段所在的直线互相垂直。
另外,强调直线与线段(射线)垂直就是与线段(射线)所在直线垂直,并画图说明。
(二)垂直画法1·你会在方格纸上画两条直线垂直吗?2·你能利用三角尺作出两条互相垂直的直线吗?3·思考:如何判断你所作的两条直线互相垂直?(三)垂直表示方法互相垂直的两条直线的交点叫做垂足(教师在黑板上画图讲解).直线AB与直线CD垂直,记作AB⊥CD于点o如果用 l,m 表示这两条直线,那么直线 l 与 m 垂直,记作 l ⊥ m 于点o (四)探究性质性质1探究(使学生再操作活动中探索、体验经过一点有且只有一条直线和已知直线垂直)1·议一议(1)你是用何工具如何画垂线的?过程:1、靠2、过3、画(2)你画出的垂线有何特点?(互相垂直的两条直线形成的四个角有什么特征?为什么?)2·画一画在下面两个图中,分别过点A作l的垂线,您能作出来吗?每个图中您能作几条?。
A 。
A从中,您得到了什么结论?说说看!性质:平面内,过一点有且只有一条直线与已知直线垂直。
性质2探究:(使学生从生活中感知“垂线段最短”,并了解点到直线的距离)1、如何测量跳远成绩?2、过马路怎样走最短?3、测量图形中PA、PB、PC、PD的长,比较哪条线段最短?(其中PA是垂线段)PB AC D4你能得到什么启发?直线外一点与直线上各点连接的所有线段中,垂线段最短。
5、你觉得如何规定点到直线的距离比较合理?总结:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
人教版初中数学七年级下册第五章《相交线与平行线》复习教案

第五章相交线与平行线复习三维目标1.理解本章学过的关于描述图形形状和位置关系的语句,•会用语句描述简单的图形,会根据描述的语句画出图形,能结合一些具体内容进行说理,初步养成言之有据的习惯. 2.注意观察实物、模型和图形,通过观察、归纳、对比来寻找图形的位置、•关系和数量关系,从而发现图形的性质.3.在观察、操作、想象、说理、交流的过程中,发展空间观念,•初步形成积极参与数学活动,与他人合作交流的意识,激发学习空间与图形的兴趣.教学重点:回顾、思考本章的重点内容.教学难点:建立本章的知识结构框架图.导入新课活动1.1.在平面内,不重合的两条直线的位置关系有两种:相交、平行.•在研究平行线时,常常是通过有关的角来判断直线平行和反映平行线的性质的.下面是本章学到的一些数学名词,你能用自己的语言给它们一个简短的描述吗?你能画出一个图形来表示它们吗?对顶角、邻补角、垂直、平行、同位角、内错角、同旁内角、平移.2.对顶角有什么性质?你会度量点到直线的距离和两条平行线的距离吗?3.怎样识别两条直线是否平行?平行线有什么特征?•对比平行线的性质和直线平行的条件,它们有什么异同?4.图形平移时,连接各对应点的线段有什么关系?•你能利用平移设计一些图案吗? 5.学习本章时,要注意观察实物、模型和图形,通过观察、归纳、•对比来寻找图形中的位置关系和数量关系,从而发现图形的性质.推进新课建立本章的知识框架图活动2.在充分思考和交流的基础上,逐渐建立本章的知识结构图.设计意图:在反思和交流的过程中,逐渐建立知识体系.完善自己的知识结构,反思自己的学习过程.师生行为:可鼓励学生自己梳理全章的内容,使学生明白所学知识的系统性.教师引导学生完成本章知识结构图例题讲解导入新课活动1.1.在平面内,不重合的两条直线的位置关系有两种:相交、平行.•在研究平行线时,常常是通过有关的角来判断直线平行和反映平行线的性质的.下面是本章学到的一些数学名词,你能用自己的语言给它们一个简短的描述吗?你能画出一个图形来表示它们吗?对顶角、邻补角、垂直、平行、同位角、内错角、同旁内角、平移.2.对顶角有什么性质?你会度量点到直线的距离和两条平行线的距离吗?3.怎样识别两条直线是否平行?平行线有什么特征?•对比平行线的性质和直线平行的条件,它们有什么异同?4.图形平移时,连接各对应点的线段有什么关系?•你能利用平移设计一些图案吗? 5.学习本章时,要注意观察实物、模型和图形,通过观察、归纳、•对比来寻找图形中的位置关系和数量关系,从而发现图形的性质.推进新课建立本章的知识框架图活动2.在充分思考和交流的基础上,逐渐建立本章的知识结构图.设计意图:在反思和交流的过程中,逐渐建立知识体系.完善自己的知识结构,反思自己的学习过程.师生行为:可鼓励学生自己梳理全章的内容,使学生明白所学知识的系统性.教师引导学生完成本章知识结构图例题讲解例1:如图1所示,选择恰当的方向击打白球,可以使白球反弹后将红球撞入袋中,此时:∠1=∠2,并且∠2+∠3=90°,如果∠3=30°,那么∠1应等于多少度,才能保证红球能直接入袋?解:因为∠2+∠3=90°,∠3=30°,所以∠2=60°.所以∠1=∠2=60°.则∠1等于60°,才能保证红球直接入袋.例2:如图2,直线b与直线c平行吗?说说你的理由.解:直线b与直线c平行.因为b⊥a,c⊥a,所以∠1=90°,∠2=90°.因此∠1=∠2.由“同位角相等,两直线平行”,得b∥c.•(也可由内错角相等或同旁内角互补来说理由)例3:如图3所示,如果∠B与∠C互补,那么哪两条直线平行?∠A与哪个角互补,可以保证AD∥BC?答:如果∠B与∠C互补,那么线段AB与线段DC平行;∠A与∠B互补,•可保证AD•∥BC.理由都是:同旁内角互补,两直线平行.例4:如图4,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是北偏东42°,甲、乙两地同时开工,若干天后公路准确接通.乙地所修公路的走向是南偏西多少度?为什么?答:乙地所修公路的走向是南偏西42°.因为:两直线平行,内错角相等.例5:如图5,(1)如果a∥b,找出图中各角之间的等量关系.(2)如果c∥d,那么需要哪两个角相等?答:(1)a∥b,则图中各角之间的等量关系是:∠1=∠2,∠2=∠3,∠3=∠1,∠1+∠4=180°,∠2+∠4=180°,∠3+∠4=180°,∠5+∠6=180°.(2)c∥d,那么需要∠3=∠5或者∠4=∠6.课堂小结这节课我们共同复习回顾了本章的内容.大家要掌握直线平行的条件和平行线的特征,并会用自己的语言来表达理由.布置作业复习题5 2、3.活动与探究如图6,已知CD∥OB,EF∥AO,则∠1与∠O相等吗?为什么?[过程]让学生在活动过程中,寻找多种方法,这样能激发学生的思维.利用综合法分析:由CD∥OB,可推得:①∠1=∠2,②∠1与∠3互补,③∠O=∠4,④∠O=∠5,⑤∠O与∠6互补,由EF•∥AO,又推出:⑥∠1=∠5,⑦∠1=∠4,⑧∠1与∠6互补,⑨∠O=∠2,⑩∠O与∠3互补.由①与⑨,②与⑩,③与⑦,④与⑥,⑤与⑧均可推得∠1=∠O,从而得出五种不同证法.利用分析法分析:假如:∠1=∠O,由CD∥OB得∠1=∠2,所以只需有∠O=∠2即可.由EF∥OA可得,同理分析可有其他证法.[结果]∠1与∠O相等.证法一:因为CD∥OB,所以∠1=∠2(两直线平行,内错角相等).因为EF∥AO(已知),所以∠O=∠2(两直线平行,同位角相等),所以∠1=∠O.证法二://13//3CD OBEF OA O⇒∠∠⎫⇒⎬⇒∠∠⎭与互补与互补∠1=∠O.证法三://4//14CD OB OEF OA⇒∠=∠⎫⇒⎬⇒∠=∠⎭∠1=∠O.证法四://5//15CD OB OOA EF⇒∠=∠⎫⇒⎬⇒∠=∠⎭∠1=∠O.证法五://6180//16180CD OB OEF OA⇒∠+∠=︒⎫⇒⎬⇒∠+∠=︒⎭∠1=∠O.。
人教版七年级数学下册第五章相交线和平行线复习教学设计

七年级下册《相交线与平行线复习课》教案设计【教学目标】1.能够熟练运用平行线的性质、判定,会在平行线拐点问题中作辅助线。
2.会用几何语言进行推理。
3.提高应用和创新知识,积极参加教学活动,在教学活动过程中充分利用所学知识,发挥想象力,合作交流,体验获得成功与学习数学的乐趣。
【教学重点】重点:能够熟练运用平行线的性质、判定,会在平行线拐点问题中作辅助线。
【教学难点】难点:在平行线拐点问题中作辅助线。
【教学准备】教师准备:多媒体课件、白板、几何画板。
学生准备:练习本、尺子。
【教学方法】讲授法、练习法、问答法、合作探究法。
【教学过程】一.复习在此阶段的信息技术利用:(1)白板的幕布功能,展示本节课题目。
(2)超链接功能,回顾相交线与平行线知识点。
(3)2位同学利用白板的区域截图形式,展示下面题目的答案。
如图所示,按要求填空(1)若∠1=∠2,则_____//_____(2)若∠1=∠4,则_____//_____(3)若∠1+∠3=180°,则_____//_____(4)若AB//CD,则可以得到的结论有哪些?依据分别是什么?二.讲授知识点在此阶段的信息技术利用:(1)利用几何画板展示题目(2)利用白板模式下的几何画板,进行构造辅助线,书写简要过程。
例1.若AB//EF,则∠BAC+∠ACE+∠CEF的度数是多少?合作探究在此阶段的信息技术利用:(2)利用几何画板展示题目。
(2)利用白板模式下的几何画板,进行构造辅助线、动点的移动情况等,书写简要过程。
例2.若AB//EF,点C在直线MN上运动(点C不与点G、点H重合),直线MN分别与直线AB、EF相交于点G、H,则∠BAC,∠ACE,∠CEF 之间的数量关系有几种情况?并给予证明。
三.小结本节课有什么收获?四.作业在此阶段的信息技术利用:、利用几何画板展示题目若AB//EF,点C在直线MN上运动(点C不与点G、点H重合),直线MN分别与直线AB、EF相交于点G、H,则∠BAC,∠ACE,∠CEF之间的数量关系有几种情况?并给予证明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省洛阳市第二外国语学校2012-2013学年七年级数学下册《第五
章 相交线与平行线》学案(无答案) 新人教版
【知识网】
【合作探究】
1.对顶角、邻补角。
①两条直线相交、构成哪两种特殊位置关系的角?指出图(1) 中具有这两种位置的角
.
②如图(2)中,若∠AOD=90°,那么直线AB,CD 的位置关系如何?
③如图(3)中,∠1与∠2,∠2与∠3,∠3与∠4是怎么位置关系的角? 2.垂线及其性质.
①如图(4),直线AB 、CD 、EF 相交于点O,CD⊥EF,∠1=35°,求∠2的度数.
F
E
2
1
D
C
B
A
l
C B
A
D
C
B
A
(4) (5) (6)
②如图(5),AB⊥L,BC⊥L,B 为重足,那么A 、B 、C 三点在同一条直线上吗?为什么?
③如图(6),四边形ABCD,AD∥BC,AB∥CD,过A 作AE⊥BC,过A 作AF⊥CD,垂足分别是E 、F,量出点A 到BC 的距离和AB 、CD 平行线间的距离.
④请归纳一下与垂直有关的知识中,有哪些重要结论? 3.同位角、内错角、同旁内角.
如图(7),找出∠1、∠2、∠3中哪两个是同位角、内错角、同旁内角? 4.平行线判定与性质
学生练习:①填空:如图(8),当_______时,a∥c, 理由是________;当______时,b∥c,理由是_________;当a∥b, b∥c 时,______∥______,理由是_________.
c
b
d
a 4
32
1 D
C B A
B '
D
C
B
A
(8) (9) (10) ②如图(9),AB∥CD,∠A=∠C,试判断AD 与BC 的位置关系?为什么? 5.关于平移,让学生思考:
(1)图形平移时,连接对应点有什么关系?
(2)如何确定图形平移的方向和平移的距离?
练习:如图(10),平移四边形ABCD,使点B 移动到点B′,画出平移后的四边形A′B′C′D′. 【展示提升】
1.如图所示,直线L 1∥L 2,AB ⊥L 1,垂足为点O ,BC 与L 2相交于点E ,若∠1=43°,则∠2=____
2.如图,直线a ∥b ,点B 在直线b 上,且AB ⊥BC ,∠1=55°,则∠2=_____ 3.把一副三角板按如图所示的方式摆放,则两条斜边所成的钝角x 为_______ 4.如图,已知∠1=∠2,∠DAB=∠CBA ,且DE ⊥AC ,BF ⊥AC ,
问:(1)AD ∥BC 吗?(2)AB ∥CD 吗?为什么?
5.如图,在四边形BFCD 中,点E 、A 两点在FC 上,已知∠1=∠2,∠3=∠4,∠5=∠6,试
判断ED 与FB 的位置关系,并说明为什么?
第五章 相交线与平行线练习 一、填空题
1.a 、b 、c 是直线,且a∥b,b⊥c,则a 与c 的位置关系是________.
2.如图(11),MN⊥AB,垂足为M 点,MN 交CD 于N,过M 点作MG⊥CD,垂足为G,EF 过点N 点,且EF∥AB,交MG 于H 点,其中线段GM 的长度是________到________的距离, 线段MN 的长度是________到________的距离,又是_______的距离,点N 到直线MG 的距离是___.
G H N
M
F E
D
C B
A
F
E
O
D
C
B
A
(11) (12)
3.如图(12),AD∥BC,EF∥BC,BD 平分∠ABC,图中与∠ADO 相等的角有_______ 个,分别是___________.
4.因为AB∥CD,EF∥AB,根据_________,所以_____________.
5.命题“等角的补角相等”的题设__________,结论是__________.
6.如图(13),给出下列论断:①AD∥BC:②AB∥CD;③∠A=∠C.
以上其中两个作为题设,另一个作为结论,用“如果……,那么……”形式,写出一个你认为正确的命题是___________.
D
C
B
A
F
E
O D C B
A
c
l
N
M
b a
2
1
(13) (14) (15)
7.如图(14),直线AB、CD、EF相交于同一点O,而且∠BOC=2
3
∠AOC,∠DOF=
1
3
∠AOD,那么
∠FOC=______度.
8.如图(15),直线a、b被C所截,a⊥L于M,b⊥L于N,∠1=66°,则∠2=________.
三、选择题.
1.下列语句错误的是( )
A.连接两点的线段的长度叫做两点间的距离
B.两条直线平行,同旁内角互补
C.若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角
D.平移变换中,各组对应点连成两线段平行且相等
2.如图(16),如果AB∥CD,那么图中相等的内错角是( )
A.∠1与∠5,∠2与∠6;
B.∠3与∠7,∠4与∠8;
C.∠5与∠1,∠4与∠8;
D.∠2与∠6,∠7与∠3
3.下列语句:①三条直线只有两个交点,则其中两条直线互相平行; ②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直; ③过一点有且只有一条直线与已知直线平行,其中( )
A.①、②是正确的命题
B.②、③是正确命题
C.①、③是正确命题
D.以上结论皆错
4.下列与垂直相交的洗法:①平面内,垂直于同一条直线的两条直线互相平行; ②一条直线如果它与两条平行线中的一条垂直,那么它与另一条也垂直;③平行内, 一条直线不可能
与两条相交直线都垂直,其中说法错误个数有( )
A.3个
B.2个
C.1个
D.0个
四、解答题
1.如图(17),是一条河,C河边AB外一点:
(1)过点C要修一条与河平行的绿化带,请作出正确的示意图.
(2)现欲用水管从河边AB,将水引到C处,请在图上测量并计算出水管至少要多少?(本图比例尺为1:2000)
2.如图(18),ABA⊥BD,CD⊥MN,垂足分别是B、D点,∠FDC=∠EBA.
(1)判断CD与AB的位置关系;
(2)BE与DE平行吗?为什么?
3、已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4。
求证:AD∥BE。
证明:∵AB∥CD(已知)
∴∠4=∠()
∵∠3=∠4(已知)
∴∠3=∠()
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF()
即∠=∠
∴∠3=∠()
∴AD∥BE()
4.在方格纸上,利用平移画出长方形ABCD的立体图,其中点D′是D的对应点.(要求在立体图中,看不到的线条用虚线表示)。
