大学物理:1波粒二象性
大学物理教案:量子力学基础知识

大学物理教案:量子力学基础知识简介量子力学是现代物理学的重要分支,它描述了微观世界中的粒子行为,并解释了许多奇特的现象。
本教案旨在向大学物理学生介绍量子力学的基础知识,包括波粒二象性、不确定性原理、波函数等核心概念。
目标•理解波粒二象性的概念及其实验观测•掌握不确定性原理及其与经典物理的区别•熟悉波函数的表示和应用教学内容1. 波粒二象性•定义:波粒二象性指微观粒子既具有粒子性质又具有波动性质。
•实验观测:通过双缝干涉实验、康普顿散射实验证明波粒二象性。
•特征:粒子表现出波动行为,如干涉和衍射;波动表现出离散行为,如能级和量子跳跃。
2. 不确定性原理•定义:不确定性原理是由海森堡提出的一个基本原理,它指出在某些物理量之间存在固有的不确定关系。
•区别于经典物理:经典物理中,粒子的位置和动量可以同时被准确测量;而在量子力学中,由于波粒二象性,位置和动量不能同时被准确确定。
•数学表述:∆x * ∆p ≥ h/4π,其中∆x表示位置的不确定性,∆p表示动量的不确定性,h为普朗克常数。
3. 波函数•定义:波函数是描述微观粒子状态及其演化的数学函数。
在薛定谔方程下演化。
•形式:一维情况下可用复数函数表示ψ(x),三维情况下可用复数函数表示ψ(x, y, z)。
•解释与应用:波函数的平方模值|ψ|^2 表征了粒子在空间中存在的概率分布。
波函数可以描述能级、态叠加等现象。
教学方法与活动建议1.通过实验演示双缝干涉实验,让学生亲身体验波粒二象性。
2.运用黑板或幻灯片展示不确定性原理的公式推导过程,并举例说明其应用。
3.利用计算机模拟软件绘制波函数的图像,让学生观察不同态的波函数变化。
4.在课堂上进行小组讨论和问题解答,加深学生对概念和原理的理解。
总结通过本教案,学生将能够初步了解量子力学中重要的基础知识。
这些核心概念对于理解量子物理现象以及后续相关课程的学习都具有重要意义。
在教学过程中,鼓励学生积极思考并提出问题,以促进他们对量子力学的兴趣和深入理解。
大学物理基础知识波粒二象性与不确定性原理

大学物理基础知识波粒二象性与不确定性原理波粒二象性与不确定性原理是物理学中的重要概念,揭示了微观世界的奇妙行为和限制。
通过波粒二象性,物质既可呈现波动性又可呈现粒子性,而不确定性原理则限制了我们对粒子的同时准确了解其位置和动量。
本文将详细介绍波粒二象性与不确定性原理,并探讨其在量子力学和实际应用中的重要性。
一、波粒二象性波粒二象性是指微观粒子既可表现出波动性,又可表现出粒子性。
在具体描述波粒二象性之前,我们先来了解一下波动性和粒子性。
1. 波动性波动性是指物质表现出波动行为的特性。
根据波动性的性质,波动可以分为机械波和电磁波。
机械波需要通过物质的振动来传播,如声波和水波;而电磁波则是由振荡的电场和磁场构成,如光波和无线电波。
2. 粒子性粒子性是指物质表现出粒子行为的特性。
粒子性的代表是粒子,例如原子、分子和电子等。
粒子具有确定的质量和位置,可以在空间中运动,并与其他粒子相互作用。
在20世纪初,由于物理学实验中的一系列现象无法仅通过光的波动模型来解释,科学家们开始思考微观粒子的真实本质。
在此背景下,波粒二象性的概念应运而生。
波粒二象性告诉我们,微观粒子既可以像波一样传播和干涉,也可以像粒子一样定位和计数。
著名的物理学家德布罗意(Louis de Broglie)提出了波粒二象性的概念,他认为一个运动的微观粒子具有与其动量相关的波长。
这意味着微观粒子不仅具有粒子性质,还具有波动性质。
二、不确定性原理不确定性原理是由物理学家海森堡(Werner Heisenberg)在1927年提出的,它表明了我们在同时准确测量一个粒子的位置和动量时所面临的困难。
根据不确定性原理,我们无法同时确定一个粒子的位置和动量,更准确地说是不能将它们的不确定度降低到零。
当我们试图通过测量来确定粒子的位置时,其动量的测量结果将会变得不确定;相反,当我们试图测量粒子的动量时,其位置的测量结果将会变得不确定。
不确定性原理的表达式为:Δx * Δp ≥ h/4π其中,Δx表示位置的不确定度,Δp表示动量的不确定度,h为普朗克常数。
大学物理15 量子物理基础1

m
o
0.1A
(2) 若使其质量为m=0.1g的小球以与粒子相同的 速率运动,求其波长
若 m=0.1g 的小球速率 vm v
vm
v
q BR m
则 :m
h m vm
h m
1 v
h m
m q BR
h q BR
m m
6.64 10 27 0.1 10 3
6.641034
m
px x h
考虑到在两个一级极小值之外还有电子出现,
运动,则其波长为多少? (粒子质量为ma =6.64ⅹ10-27kg)(05.08…)
解:
(1)
求粒子德布罗意波长 h h
p m v
先求:m v ?
而:q vB
m
v2 R
m v q BR
h m v
h q BR
6.63 10 34 1.601019 0.025 0.083102
1.001011
( x,t ) 0 区别于经典波动
(
x,
t)
e i 2
0
(t x
)
自由粒子沿x方向运动时对应的单色平面波波函数
设运动的实物粒子的能量为E、动量为 p,与之相 关联的频率为 、波长为,将德布罗意关系式代入:
考虑到自由粒子沿三维方向的传播
式中的 、E 和 p 体现了微观粒子的波粒二象性
2、概率密度——波函数的统计解释 根据玻恩对德布罗意波的统计解释,物质波波
p mv h
德布罗意公式(或假设)
与实物粒子相联系的波称为德布罗意波(或物质波)
h h h
p mv m0v
1
v2 c2
如果v c,则 h
m0v
大学物理-波粒二象性
1 2
mv
2 m
h
A
A:逸出功
光子打出光电子是瞬时发生的(109 s) I N 单位时间打出光电子多 im
h > A 时才能产生光电效应,当 <A/h时,
不发生光电效应,所以存在:
红限频率
0
A h
光量子假设解释了光电效应的全部实验规律!
但是光量子理论在当时并未被物理学界接受, 普朗克在推荐爱因斯坦为柏林科学院院士时说
2h 3
M (T ) c2 eh kT 1
普朗克常量:h 6.626 1034 J s 4.1361015eV s
在全波段与实验曲线惊人地符合!
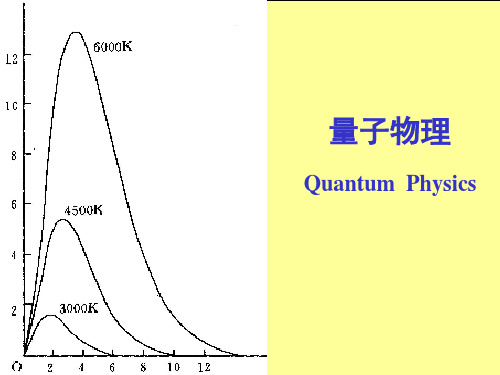
M (10 - 9 W/(m2 Hz))
2000K
(1900)M
(T
)
2
c2
2
kT
实验曲线
普朗克黑体辐射公式
M
(T )
2h
c2
3
e h kT
1
1926 年 , 薛 定 谔 (E.Schrodinger) 提出了非相对论粒子(能量远小于 静能)的运动方程—薛定谔方程, 由此方程出发的量子力学称为波动 力学。
同年,狄拉克(P.A.M. Dirac)提出了电子 的相对论性运动方程—狄拉克方程,把狭义相 对论引入薛定谔方程,统一了量子论和相对论 ,为研究粒子物理的量子场论奠定了基础。
光电流 电子电量
单位时间到达光电子数
25
﹡实验规律
(1) 饱和电流
im2
加速电势差增大时光电 im1
流增大,当加速电势差
增大到一定量值时,光
电流达到饱和值。
-Uc
(2) 光电子的最大初动能∝v入 , Uc/V
大学物理中的波粒二象性问题

大学物理中的波粒二象性问题波粒二象性是指光和其他微观粒子既可以表现出波动性,也可以表现出粒子性的现象。
这种二象性对于理解物理世界的一些基本原理和现象至关重要。
本文将重点讨论大学物理中的波粒二象性问题。
一、光的波粒二象性问题在物理学中,光既可以进行干涉和衍射等波动现象,也可以表现出光的能量是以光量子的形式传递的粒子性。
这种波粒二象性的问题成为光的波粒二象性问题。
波动理论认为,光是由电磁波组成的。
光的干涉和衍射现象可以得到很好的解释。
然而,对于特定实验现象,如光电效应和康普顿散射等,光的粒子性解释更为合理。
这就导致了波粒二象性的存在。
二、粒子的波粒二象性问题对于微观粒子,如电子、中子等,在一些实验中也可以观察到波动现象,如动态干涉和衍射。
例如,电子双缝干涉实验。
当电子通过双缝时,它们会形成干涉条纹,展示出波动性。
这一实验结果表明,尽管电子具有质量和电荷,它们也具有波动性质。
三、波粒二象性解释在20世纪初,普朗克提出了能量量子化的概念,为解释黑体辐射实验结果做出了贡献。
随后,爱因斯坦利用光电效应实验的结果,进一步提出了光的粒子性,并称之为光的能量子。
德布罗意假设是对波粒二象性的一种解释。
德布罗意假设认为,微观粒子具有波动性,其波长与动量呈反比关系。
这一假设通过实验得到了验证,奠定了波粒二象性的理论基础。
四、波粒二象性应用波粒二象性的研究不仅对于理解光和微观粒子的性质有重要意义,也在物理学的其他领域有广泛的应用。
在能谱分析中,波粒二象性可以解释光谱线的产生原理。
在原子物理学中,通过波粒二象性来解释电子在原子轨道中的分布和电子云的性质。
在量子力学中,波粒二象性为物质的波函数理论提供了基础。
此外,波粒二象性被应用于现代技术,如激光、光导纤维通信等。
五、波粒二象性的影响和挑战波粒二象性的存在给物理学家们提出了一些困惑。
到目前为止,波粒二象性的真正本质尚未完全揭示。
这也是量子力学领域仍然存在的挑战之一。
同时,波粒二象性的研究也推动了许多新理论的提出和实验的发展。
大学物理:18-5 德布罗意波 波粒二象性

L.V.de Broglie 1892 ——1987
整个世纪以来,在辐射理论上, 比起波动的研究方法来,是过于忽 视了粒子的研究方法;在实物理论 上,是否发生了相反的错误呢?是 不是我们关于粒子图象想得太多, 而过分地忽略了波的图象呢?
---德布罗意
回顾:光的本性的两个不同侧面
波动性: 表现在传播过程中(干涉、衍射)
对物质波的描述 E = mc2 = hν
p = mv = h
ν = E = mc2
λ
hh
λ=h= h = h
p mv m0v
1
−
v c
2 2
德布罗意公式
如果 v << c ,那么 λ = h
m0v
简洁地把对粒子描述手段 E, p
和对波的描述手段
ν , λ 联系到一起
与光子比较 光子 E = mc 2 = h ν
mv
宏观物质λ均太小,难以觉察其波动特性
2. 戴维孙-革末实验
1923年 : 用电子散射实验研究镍原子结构 1925年 : 偶然事件后实验曲线反常,出现 若干峰值,当时未和衍射联系起来。
φ
1926年: 了解德布罗意物质波假设
1927年: 有意识寻求电子波实验依据, 2~3 个月出成果,观察到电子衍射现象。
粒子性: 表现在与物质相互作用中 (光电效应、康普顿效应)
无法用经典语言(波动或粒子)准确建立光的模型。
光的量子理论模型-光子
E = h ν = hc = mc 2 λ
p
=
mc
=
h
λ
m
=
E c2
=
h
cλ
具有“波粒二象性”
借用经典“波”和“粒 子”术语,但既不是经 典波,又不是经典粒子
大学物理学习指导 第10章 光与物质的相互作用

第10章 光与物质的相互作用10.1 内容提要(一)光的波粒二象性 1.普朗克量子假设(1)一个频率为v 的谐振子只能处于一系列不连续的分立状态,在这些状态中,谐振子的能量只能是某一最小能量ε= hv 的整数倍,即hv ,2hv ,3hv ,…,nhv其中n 为正整数,h 是普朗克常量,ε=hv 称为能量子。
(2)当谐振子从一个量子态跃迁到另一个量子态时,谐振子将发射或吸收以能量子(现称为光子)为单位的电磁能。
一个光量子的能量就是两个相邻量子态之间的能量差,即Thh E ==ν (10.1) 而当谐振子停留在原来的量子态时,它将不发射或吸收任何能量。
普朗克的量子假设突破了经典物理学的观念,第一次提出了微观粒子具有分立的能量值,即振子的能量是按量子数做阶梯式分布,后来人们把振子处于某些能量状态,形象地称为处于某个能级。
2.爱因斯坦的光量子学说(1)光电效应:当光照到某些金属的表面时,金属内部的自由电子会逸出金属表面,这种光致电子发射现象叫做光电效应。
(2)爱因斯坦的光量子假设:光束可以看成是由微粒构成的粒子流,这些粒子叫光量子,也叫光子。
光子以光速运动,对于频率为v 的光束,光子的能量为νεh = (10.2)按照爱因斯坦的光子假设,频率为v 的光束可以看作是由许多能量均等于hv 的光子所构成;频率越高,光子的能量越大;对给定频率的光束来说,光的强度越大,就表示光子的数目越多。
(3)爱因斯坦的光电效应方程:0221A m h m +=v ν (10.3) 式(10.3)中A 0为逸出功,221m m v 为电子的初动能。
3.光的波粒二象性(1)光子的能量: λνhch E == (10.4)(2)光子的质量: λνhch m ==2(10.5)(3)光子的动量: λhmc p == (10.6)(二)光的吸收 散射 色散 1.光的吸收(1)朗伯定律:当一束单色光透过一定厚度的介质时,透射光的强度就会降低,并且产生吸收光谱。
大学物理有哪些内容

引言概述:大学物理作为一门重要的基础学科,涵盖了丰富而广泛的知识体系。
本文将继续讨论大学物理的内容,并详细阐述其五个主要领域,包括经典力学、电磁学、热学、光学和量子力学。
通过深入探讨每个领域的五至九个小点,我们将进一步了解大学物理的核心知识和重要概念,为我们构建牢固的物理学基础提供帮助。
正文内容:一、经典力学1.牛顿力学:牛顿定律、运动方程等基本理论。
2.质点运动:质点的直线运动、曲线运动和圆周运动等。
3.常见力学问题:例如摩擦力、弹性力和重力等。
4.动量和能量:动量和能量守恒定律等。
5.刚体力学:刚体运动、静力学和动力学等。
二、电磁学1.静电学:电场、电势和电荷等基本概念。
2.电场和电势:电场线、库仑定律和电势能等。
3.电磁感应:法拉第定律、电磁感应现象和感应电动势等。
4.交流电路:交流电路中的电阻、电感和电容等。
5.电磁波:电磁波的概念、性质和传播等。
三、热学1.温度和热量:温度的测量、热传递和热量计算等。
2.热力学定律:热力学第一定律和第二定律等。
3.状态方程:理想气体状态方程和非理想气体状态方程等。
4.热力学过程:等温过程、绝热过程和等压过程等。
5.热机和制冷:卡诺循环、制冷系统和热机效率等。
四、光学1.几何光学:反射、折射和光的成像等。
2.光的衍射和干涉:衍射和干涉现象的基本原理和应用。
3.光的波动性:光的波粒二象性和光的偏振等。
4.光的色散:光的色散现象和光的波长测量等。
5.现代光学:激光、光纤和光学器件等。
五、量子力学1.波粒二象性:波动方程和波粒二象性的基本理论。
2.波函数和薛定谔方程:波函数的性质和薛定谔方程的解析等。
3.粒子在势场中的运动:一维势场和三维势场中的粒子运动等。
4.量子力学中的算符:算符的定义、本征值和本征函数等。
5.微扰理论和矩阵力学:微扰理论的应用和矩阵力学的基本原理等。
总结:大学物理作为一门重要的学科,囊括了经典力学、电磁学、热学、光学和量子力学等多个领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1925年,海森伯(W.Heisenberg)放 弃电子轨道等经典概念,用实验上 可观测到的光谱线的频率和强度描 述原子过程,奠定了量子力学的一 种形式—矩阵力学的基础。
Байду номын сангаас
§1.1黑体辐射(Black-body radiation)
一、热辐射的基本概念 1、热辐射(thermal radiation) 物体由大量原子组成,热运动引起原子碰撞 使原子激发而辐射电磁波。原子的动能越大, 通过碰撞引起原子激发的能量就越高,从而辐 射电磁波的波长就越短。
热运动是混乱的,原子的动能与温度有关, 因而辐射电磁波的能量也与温度有关。
例如:加热铁块, 温度,铁块颜色由看
不出发光 暗红 橙色 黄白色 蓝白色
这种与温度有关的电磁辐射,称为热辐射。 并不是所有发光现象都是热辐射,例如: 激光 、 日光灯发光就不是热辐射。 任何物体在任何温度下都有热辐射,波长自 远红外区连续延伸到紫外区(连续谱)。 温度 辐射中短波长的电磁波的比例
【演示】黑体模型
2、基尔霍夫(Kirchhoff)辐射定律
在平衡热辐射时
T
黑
1
3
M 1 M 2 I(T , ) 1 2 I(T , )-与材料无关的普适函数
黑体 1
M 1
1
M 2
2
M 黑 体
I(T , )
黑体的光谱辐出度最大,与构成黑体的材料
无关。利用黑体可撇开材料的具体性质,普遍
几种温度下辐射最强的电磁波颜色
800K 1000K 1200K 1400K
低温物体(例如人体)也有热辐射,但辐射 较弱,并且主要成分是波长较长的红外线。
头部的红外照片(热的地方显白色,冷的显黑色)
中国第一张红外照片(熊大缜于1935年在清华 大学气象台顶上拍摄的北京西山夜景)
鸟的羽毛的颜色 是不是热辐射?
1926 年 , 薛 定 谔 (E.Schrodinger) 提出了非相对论粒子(能量远小于 静能)的运动方程—薛定谔方程, 由此方程出发的量子力学称为波动 力学。
同年,狄拉克(P.A.M. Dirac)提 出了电子的相对论性运动方程—狄拉 克方程,把狭义相对论引入薛定谔方 程,统一了量子论和相对论,为研究 粒子物理的量子场论奠定了基础。
研究热辐射本身的规律。
好的辐射体也是好的吸收体
1100K,自身辐射光
首先介绍揭示波粒二象性的实验规律,它们 不但是建立量子力学的实验基础,而且在现代 科学技术中也有广泛的应用。然后简要介绍量 子力学中的一些最基本的概念和规律。
第1章 波粒二象性
Wave-particle duality
§1.1黑体辐射 △ §1.2光电效应(自学)
§1.3光子、光的二象性 §1.4 康普顿效应 §1.5 实物粒子的波动性 §1.6 概率波与概率幅 §1.7不确定关系
矩阵力学和波动力学是等价的,前者偏重 于物质的粒子性,后者偏重于物质的波动性, 它们是量子力学的两种不同描述方式。薛定谔 方程是微分方程,数学工具人们比较熟悉,我 们只简要介绍波动力学。
量子物理的理论基础独立于经典力学,同我 们的日常感受格格不入。对于生活在宏观世界 又比较熟悉经典力学的人们来说,学习量子物 理确有一定难度。初学者往往试图用经典的概 念去理解量子物理,这将使学习陷入困境。
物理学是基于实验事实的信仰,对于量子物 理来说尤其是这样。合理的假定总是有些道理 可讲的,但它不能由更基本的假定或理论推导 出来,其正确性只能用实验来检验。相信这些 基本假定,并自觉应用它们去分析和解决问题, 是学习和理解量子物理的第一步。
强烈建议做好预习,带着问题来上课,否则 你会觉得被动和郁闷。
2、平衡热辐射 加热一物体,若物体所吸收的能量等于在
同一时间内辐射的能量,则物体的温度恒定。
这种温度不变的热辐射称为平衡热辐射。
3、光谱辐出度(单色辐出度)M monochromatic energy density of radiation
M —单位时间内,从物体单位表面发出的频
率在 附近单位频率间隔内的电磁波的能量。
1900年,普朗克(M.Pulanck)提出能量子, 即能量量子化的概念,这对经典物理理论是 一个极大的冲击,因为能量的连续性在经典 物理中是“天经地义”的事情。在物理学上, 能量子概念的提出具有划时代的意义,它标 志了量子力学的诞生。
1905年,为解释光电效应,爱因斯坦提出光 量子(光子)的概念,指出光具有波粒二象性。 1923年,德布罗意(P.L.de Broglie)提出实物 粒子也具有波动性的假设。波粒二象性的假设, 为物质世界建立了一个统一的模型。物质具有 波粒二象性是建立量子力学的一个基本出发点。
(T )
d d
E (吸收) E (入射)
二、黑体(black body)
1、黑体:能完全吸收各种波长电磁波而无反射
的物体,即 1的 物 体。黑体是理想化模型, 即使是煤黑,对太阳光的 也小于 99%。
维恩设计的黑体: 不透明介质空腔开一 小孔,电磁波射入小孔 后,很难再从小孔中射 出。小孔表面是黑体。
量子物理
Quantum Physics
2005年秋季学期
目录 第1章 波粒二象性 第2章 薛定谔方程 第3章 原子中的电子 第4章 固体中的电子 第5章 核物理和粒子物理简介
量子力学是研究原子、分子和凝聚态物质的 结构和性质的理论基础,在化学、生物、信息、 激光、能源和新材料等方面的科学研究和技术 开发中,发挥越来越重要的作用。
T
d E ( d() 单位时间内)
单位面积
M
d E (T )
d
M 取决于T、 和材
料种类和表面情况
4、(总)辐出度(总发射本领)M(T) radiant exitance
M(T ) M (T )d 单位:w/m2
0
5、单色吸收比(率) (T)
monochromatic absorptance
