高一数学必修一必修二难题
高中数学必修一第二章一元二次函数方程和不等式典型例题(带答案)

高中数学必修一第二章一元二次函数方程和不等式典型例题单选题1、已知x >0,则下列说法正确的是( ) A .x +1x −2有最大值0B .x +1x −2有最小值为0 C .x +1x−2有最大值为-4D .x +1x−2有最小值为-4答案:B分析:由均值不等式可得x +1x ≥2√x ×1x =2,分析即得解 由题意,x >0,由均值不等式x +1x≥2√x ×1x=2,当且仅当x =1x,即x =1时等号成立故x +1x −2≥0,有最小值0 故选:B2、不等式x (2x +7)≥−3的解集为( ) A .(−∞,−3]∪[−12,+∞)B .[−3,−12] C .(−∞,−2]∪[−13,+∞)D .[−2,−13] 答案:A分析:解一元二次不等式即可.x (2x +7)≥−3可变形为2x 2+7x +3≥0, 令2x 2+7x +3=0,得x 1=−3,x 2=−12,所以x ≤−3或x ≥−12,即不等式的解集为(−∞,−3]∪[−12,+∞).故选:A.3、已知命题“∀x ∈R ,4x 2+(a −2)x +14>0”是假命题,则实数a 的取值范围为( ) A .(−∞,0]∪[4,+∞)B .[0,4] C .[4,+∞)D .(0,4)答案:A分析:先求出命题为真时实数a的取值范围,即可求出命题为假时实数a的取值范围.若“∀x∈R,4x2+(a−2)x+14>0”是真命题,即判别式Δ=(a−2)2−4×4×14<0,解得:0<a<4,所以命题“∀x∈R,4x2+(a−2)x+14>0”是假命题,则实数a的取值范围为:(−∞,0]∪[4,+∞).故选:A.4、设a>b>c>0,则2a2+1ab +1a(a−b)−10ac+25c2取得最小值时,a的值为()A.√2B.2C.4D.2√5答案:A解析:转化条件为原式=1ab +ab+1a(a−b)+a(a−b)+(a−5c)2,结合基本不等式即可得解.2a2+1ab+1a(a−b)−10ac+25c2=1ab+ab+1a(a−b)+a(a−b)−ab−a(a−b)+2a2−10ac+25c2 =1ab+ab+1a(a−b)+a(a−b)+a2−10ac+25c2=1ab+ab+1a(a−b)+a(a−b)+(a−5c)2≥2√1ab ⋅ab+2√1a(a−b)⋅a(a−b)+0=4,当且仅当{ab=1a(a−b)=1a=5c,即a=√2,b=√22,c=√25时,等号成立.故选:A.小提示:易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:(1)“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.5、若“﹣2<x <3”是“x 2+mx ﹣2m 2<0(m >0)”的充分不必要条件,则实数m 的取值范围是( ) A .m ≥1B .m ≥2C .m ≥3D .m ≥4 答案:C分析:x 2+mx ﹣2m 2<0(m >0),解得﹣2m <x <m .根据“﹣2<x <3”是“x 2+mx ﹣2m 2<0(m >0)”的充分不必要条件,可得﹣2m ≤﹣2,3≤m ,m >0.解出即可得出. 解:x 2+mx ﹣2m 2<0(m >0),解得﹣2m <x <m .∵“﹣2<x <3”是“x 2+mx ﹣2m 2<0(m >0)”的充分不必要条件,∴﹣2m ≤﹣2,3≤m ,(两个等号不同时取)m >0. 解得m ≥3.则实数m 的取值范围是[3,+∞). 故选:C.6、关于x 的不等式ax 2−(a 2+1)x +a <0的解集为{x|x 1<x <x 2},且x 2−x 1=1,则a 2+a −2=( ) A .3B .32C .2D .23答案:A分析:根据一元二次不等式与解集之间的关系可得x 1+x 2=a +1a 、x 1x 2=1,结合 (x 2−x 1)2=(x 1+x 2)2−4x 1x 2计算即可.由不等式ax 2−(a 2+1)x +a <0的解集为{x |x 1<x <x 2}, 得a >0,不等式对应的一元二次方程为ax 2−(a 2+1)x +a =0, 方程的解为x 1、x 2,由韦达定理,得x 1+x 2=a 2+1a=a +1a ,x 1x 2=1,因为x 2−x 1=1,所以(x 2−x 1)2=(x 1+x 2)2−4x 1x 2=1, 即(a +1a )2−4=1,整理,得a 2+a −2=3. 故选:A7、已知关于x 的不等式ax 2+bx +c <0的解集为{x|x <−1或x >4},则下列说法正确的是( )A.a>0B.不等式ax2+cx+b>0的解集为{x|2−√7<x<2+√7}C.a+b+c<0D.不等式ax+b>0的解集为{x|x>3}答案:B分析:根据解集形式确定选项A错误;化不等式为x2−4x−3<0,即可判断选项B正确;设f(x)=ax2+ bx+c,则f(1)>0,判断选项C错误;解不等式可判断选项D错误.解:因为关于x的不等式ax2+bx+c<0的解集为{x|x<−1或x>4},所以a<0,所以选项A错误;由题得{a<0−1+4=−ba−1×4=ca,∴b=−3a,c=−4a,所以ax2+cx+b>0为x2−4x−3<0,∴2−√7<x<2+√7.所以选项B正确;设f(x)=ax2+bx+c,则f(1)=a+b+c>0,所以选项C错误;不等式ax+b>0为ax−3a>0,∴x<3,所以选项D错误.故选:B8、不等式1+x1−x≥0的解集为()A.{x|x≥1或x≤−1}B.{x∣−1≤x≤1} C.{x|x≥1或x<−1}D.{x|−1≤x<1}答案:D分析:不等式等价于x+1x−1≤0,即(x+1)(x−1)≤0,且x−1≠0,由此求得不等式的解集.不等式等价于x+1x−1≤0,即(x+1)(x−1)≤0,且x−1≠0,解得−1≤x<1,故不等式的解集为{x|−1≤x<1},故选:D.多选题9、已知关于x的不等式ax2+bx+c>0解集为{x|−2<x<3},则()A.a>0B.不等式ax+c>0的解集为{x|x<6}C.a+b+c>0D.不等式cx2−bx+a<0的解集为{x|−13<x<12}答案:BCD解析:根据已知条件得−2和3是方程ax2+bx+c=0的两个实根,且a<0,根据韦达定理可得b=−a,c=−6a,根据b=−a,c=−6a且a<0,对四个选项逐个求解或判断可得解.因为关于x的不等式ax2+bx+c>0解集为{x|−2<x<3},所以−2和3是方程ax2+bx+c=0的两个实根,且a<0,故A错误;所以−2+3=−ba ,−2×3=ca,所以b=−a,c=−6a,所以不等式ax+c>0可化为ax−6a>0,因为a<0,所以x<6,故B正确;因为a+b+c=a−a−6a=−6a,又a<0,所以a+b+c>0,故C正确;不等式cx2−bx+a<0可化为−6ax2+ax+a<0,又a<0,所以−6x2+x+1>0,即6x2−x−1<0,即(3x+1)(2x−1)<0,解得−13<x<12,故D正确.故选:BCD.小提示:利用一元二次不等式的解集求出参数a,b,c的关系是解题关键.本题根据韦达定理可得所要求的关系,属于中档题.10、设0<b<a<1,则下列不等式不成立的是()A.ab<b2<1B.√a<√b<1C.1<1a <1bD.a2<ab<1答案:ABD分析:对于ABD举例判断即可,对于C,利用不等式的性质判断对于A,取a=12,b=13,则ab=16>b2=19,所以A错误,对于B,取a=14,b=19,则√a=12>√b=13,所以B错误,对于C,因为0<b<a<1,所以1ab >0,所以b⋅1ab<a⋅1ab,即1a<1b,因为0<a<1,所以0<a⋅1a <1×1a,即1<1a,综上1<1a<1b,所以C正确,对于D,取a=12,b=13,则ab=16<a2=14,所以D错误,故选:ABD11、下面所给关于x的不等式,其中一定为一元二次不等式的是()A.3x+4<0B.x2+mx-1>0C.ax2+4x-7>0D.x2<0答案:BD分析:利用一元二次不等式的定义和特征对选项逐一判断即可.选项A是一元一次不等式,故错误;选项B,D,不等式的最高次是二次,二次项系数不为0,故正确;当a=0时,选项C是一元一次不等式,故不一定是一元二次不等式,即错误.故选:BD.填空题12、若x>0,y>0,xy=10,则2x +5y的最小值为_____.答案:2分析:化简2x +5y=2x+102y=2x+xy2y=2x+x2,结合基本不等式,即可求解.由x>0,y>0,xy=10,则2x +5y=2x+102y=2x+xy2y=2x+x2≥2√2x×x2=2,当且仅当x=2时取“=”,即2x +5y的最小值为2.所以答案是:2.13、已知x,y为正数,且12+x +4y=1,则x+y的最小值为________.答案:7解析:由题设等式有x+y+2=5+y2+x +4(x+2)y,利用基本不等式可求x+y+2的最小值,从而可得x+y的最小值.x+y+2=[(x+2)+y]×(1x+2+4y)=5+y2+x+4(x+2)y,由基本不等式有y2+x +4(x+2)y≥4,当且仅当x=1,y=6时等号成立,故x+y+2的最小值为9即x+y的最小值为7.所以答案是:7.小提示:应用基本不等式求最值时,需遵循“一正二定三相等”,如果原代数式中没有积为定值或和为定值,则需要对给定的代数变形以产生和为定值或积为定值的局部结构.求最值时要关注取等条件的验证.14、已知函数f(x)=√mx2+mx+1的定义域是R,则m的取值范围为______.答案:[0,4]分析:根据函数的定义域为R可得mx2+mx+1≥0对x∈R恒成立,对参数m的取值范围分类讨论,分别求出对应m 的范围,进而得出结果.因为函数f(x)=√mx2+mx+1的定义域为R,所以mx2+mx+1≥0对x∈R恒成立,当m=0时,mx2+mx+1=1>0,符合题意;当m>0时,由Δ=m2-4m≤0,解得0<m≤4;当m<0时,显然mx2+mx+1不恒大于或等于0.综上所述,m的取值范围是[0,4].所以答案是:[0,4].解答题15、设a,b,c∈R,a+b+c=0,abc=1.(1)证明:ab+bc+ca<0;(2)用max{a,b,c}表示a,b,c中的最大值,证明:max{a,b,c}≥√43.答案:(1)证明见解析(2)证明见解析.分析:(1)方法一:由(a+b+c)2=a2+b2+c2+2ab+2ac+2bc=0结合不等式的性质,即可得出证明;(2)方法一:不妨设max{a,b,c}=a,因为a+b+c=0,abc=1,所以a>0,b<0,c<0,a=(−b)+(−c)≥2√bc=2√1a ,则a3≥4,a≥√43.故原不等式成立.(1)[方法一]【最优解】:通性通法∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc=0,∴ab+bc+ca=−12(a2+b2+c2).∵abc=1,∴a,b,c均不为0,则a2+b2+c2>0,∴ab+bc+ca=−12(a2+b2+c2)<0.[方法二]:消元法由a+b+c=0得b=−(a+c),则ab+bc+ca=b(a+c)+ca=−(a+c)2+ac=−(a2+ac+c2)=−(a +c 2)2−34c 2≤0,当且仅当a =b =c =0时取等号,又abc =1,所以ab +bc +ca <0. [方法三]:放缩法方式1:由题意知a ≠0, a +b +c =0, a =−(c +b ), a 2=(c +b )2=c 2+b 2+2cb ≥4bc ,又ab +bc +ca =a (b +c )+bc =−a 2+bc ≤−a 2+a 24=−3a 24<0,故结论得证.方式2:因为a +b +c =0,所以0=(a +b +c )2=a 2+b 2+c 2+2ab +2bc +2ca=12[(a 2+b 2)+(b 2+c 2)+(c 2+a 2)]+2ab +2bc +2ca ≥12(2ab +2bc +2ca )+2ab +2bc +2ca =3(ab +bc +ca ).即ab +bc +ca ≤0,当且仅当a =b =c =0时取等号, 又abc =1,所以ab +bc +ca <0. [方法四]:因为a +b +c =0,abc =1,所以a ,b ,c 必有两个负数和一个正数,不妨设a ≤b <0<c,则a =−(b +c ), ∴ab +bc +ca =bc +a (c +b )=bc −a 2<0. [方法五]:利用函数的性质方式1:6b =−(a +c ),令f (c )=ab +bc +ca =−c 2−ac −a 2, 二次函数对应的图像开口向下,又abc =1,所以a ≠0, 判别式Δ=a 2−4a 2=−3a 2<0,无根, 所以f (c )<0,即ab +bc +ca <0.方式2:设f (x )=(x −a )(x −b )(x −c )=x 3+(ab +bc +ca )x −1, 则f (x )有a ,b ,c 三个零点,若ab +bc +ca ≥0, 则f (x )为R 上的增函数,不可能有三个零点, 所以ab +bc +ca <0.(2)[方法一]【最优解】:通性通法不妨设max {a,b,c }=a ,因为a +b +c =0,abc =1,所以a >0, b <0, c <0, a =(−b )+(−c )≥2√bc =2√1a,则a 3≥4,a ≥√43.故原不等式成立. [方法二]:不妨设max {a,b,c }=a ,因为a +b +c =0,abc =1,所以a >0,且{b +c =−a,bc =1a , 则关于x 的方程x 2+ax +1a =0有两根,其判别式Δ=a 2−4a ≥0,即a ≥√43. 故原不等式成立. [方法三]:不妨设max {a,b,c }=a ,则a >0, b =−(a +c ), abc =1, −(a +c )ac =1, ac 2+a 2c +1=0,关于c 的方程有解,判别式Δ=(a 2)2−4a ≥0,则a 3≥4,a ≥√43.故原不等式成立. [方法四]:反证法假设max {a,b,c }<√43,不妨令a ≤b <0<√43,则ab =1c >√43,−a −b =c <√43,又√43>−a −b ≥2√ab >√√43=21−13=√43,矛盾,故假设不成立.即max {a,b,c }≥√43,命题得证.【整体点评】(1)方法一:利用三项平方和的展开公式结合非零平方为正数即可证出,证法常规,为本题的通性通法,也是最优解法;方法二:利用消元法结合一元二次函数的性质即可证出;方法三:利用放缩法证出;方法四:利用符号法则结合不等式性质即可证出;方法五:利用函数的性质证出. (2)方法一:利用基本不等式直接证出,是本题的通性通法,也是最优解;方法二:利用一元二次方程根与系数的关系以及方程有解的条件即可证出;方法三:利用消元法以及一元二次方程有解的条件即可证出;方法四:利用反证法以及基本不等式即可证出.。
(word完整版)高一数学必修一必修二难题
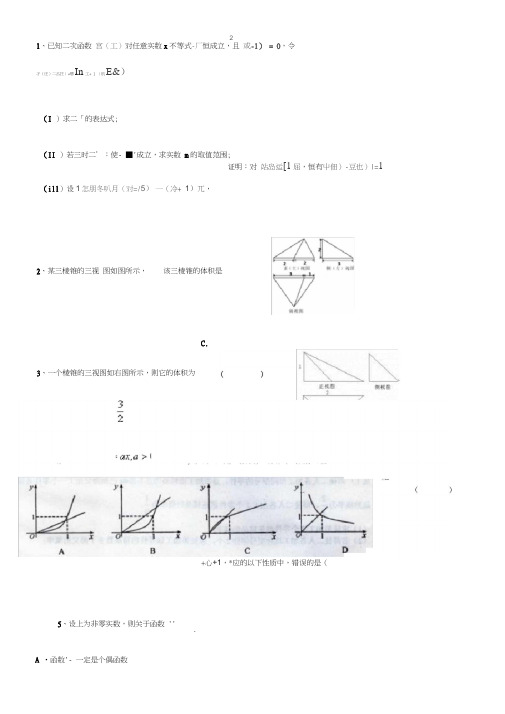
21、已知二次函数宫(工)对任意实数x不等式-厂恒成立,且或-1) = 0,令孑(庄)二呂拄)+唧In工+ ] (肌E&)(I )求二「的表达式;(II )若三时二’:使- ■'成立,求实数m的取值范围;证明:对站岛运[1屈,恒有屮佃)-豆也)|=1(ill)设1怎朋冬叭月(对=/5)一(冷+ 1)兀,2、某三棱锥的三视图如图所示,该三棱锥的体积是C.3、一个棱锥的三视图如右图所示,则它的体积为+心+1,*应的以下性质中,错误的是(5、设上为非零实数,则关于函数 '''A •函数'- 一定是个偶函数B . 一定没有最大值C •区间[叽+00) —定是/(尿)的单调递增区间D •函数1 -不可能有三个零点「,当x ― .时,均有'''1 ,则实数-;的取值范围是(7、如图,四棱锥 P-^BCD 中,底面 ABC [为平行四边形,P 从底面 ABCD M 是棱PD 的中点,且 PA = AB = AC =2 , 眈=2葩. (I )求证:CDL 平面PAC(H)求二面角-----的大小;西 AN_(皿)如果 N 是棱AB 上一点,且直线 CN 与平面MA 断成角的正弦值为,求丄主‘的值. 8、已知幕函数-?1< :1; ' '' 1?"- " 「为偶函数,且在区间' ':'上是单调递增函数。
(I)求函数-的解析式;6、已知-;:> 0,且』孑., =.V A.「IBD(H)设;,若二」能取遍W'内的所有实数,求实数 二的取值范围./空、=——1 ----------------9、已知定义域为 丘的函数. 是奇函数.(1)求实数匚」的值; (2)判断并证明.’「在:上的单调性;(3 )若1 -对任意•【一-恒成立,求匕的取值范围.参考答案一、计算题1、解(])设 ” {一 I ..•••屮-恒成立.•.丄「一 ■.二.;一和L,^....恒成立f(x)=呂学)+叨Ln x+— 肿已氏,工n 0) (II 厂 一 11 3 ,=—2T +W21n X 2 a -b^-c =a +<7f (疋)二A + —工当;,「时,「八的值域为R/(JC)= 1^ >0StVx>0, f(x)>o当;一「时,恒成立当朋吒o时,令y(x)—o x—J-也,(町心==-等+朋In上云这时若三「「使成立则只须-「「丄「厂"一,综上所述,实数m的取值范围= -'-1■ ■ ' 丁^^1所」「"单减屮佃)Fg)护⑴一二冷一胡n珂一|于是- -1 . 1 1| //(丙)一/f (叼j |<1<= —觀him——cl <=>,啊—In 也- h (?K)=—m—In m+ -— (1 <.懑壬劭记’' :' ,则. 1 1 331 1,1 n' '2 強2莎Tm y3—<0 Im所以函数'’- 〔是单增函数M I沐、誉1 3 〔根一刃& + 1)nc 血隹)二一一1一——= -------------------------------------- < 0所以'故命题成立.、选择题2、D3、A4、B5、C6、C三、简答题7、证明:(I)连结AC因为为在中,血"—2 BC=2^2所以所以■-因为AB/ CD所以又因为匸上一地面ABCD所以一空因为’所以「匸—平面PAC(II)如图建立空间直角坐标系,则丄.丄:一因为M是棱PD的中点,所以为平面MAB的法向量, 所以莎=(-1丄1),耳(2皿令丁=1,则2所以平面MAB的法向量一■ ■-因为F上一平面ABCD所以心:人、二是平面ABC的一个法向量. 所以设直线CN 与平面MAB 所成角为 ,因为平面MAB 勺法向量 ,AN d-- =1 解得・:一 1,即 0 - 1, ^ --,所以賈 .8、(I )T J 八为幕函数 •••2m - n = \又丿」■'在区间-'上是单调递增函数 •込'J - ■] .:■ . 2分 贝0 7 二丨「;-•)- 吃三三 .•.:◎=〕或[或 2 3分因为二面角 ”一」匸'一 -J 为锐二面角,71所以二面角3/ L -U'」的大小为4 .(ill)因为 N 是棱AB 上一点,所以设 , 」虛;:' ;所以2-J2 x J”十匚当玄二〔时,-'「’ - ''为奇函数,不合题意,舍去当卫二1时为偶函数,符合题意当■ ■-:时,」_ '为奇函数,不合题意,舍去f (对二工①当二:时,」-,则- -.单调递增,其值域为 R ,满足题意②当•小时,由得•;— 1:..,则」一在单调递减,在; ■.•.或叽加二呂㈠卫)二冷"加-2,则其值域为[皿+少-2他)•••二「-能取遍丁内的所有实数 .只需则N 「在-■--单调递增又宀 -.•.In 2^2 - 2 < 0 » 卩(总) < 卩(1) O 0 < 1 四、综合题r/(o )=o 29、解:(1) M-帖一了⑴ “-市门,经检验成立。
2019高一数学函数难题汇编(含解析)

高一数学必修一(难)一.选择题(共12小题)1.已知定义在R上的偶函数f(x)满足f(x+1)=﹣f(x),且当x∈[﹣1,0]时,,函数,则关于x的不等式f(x)<g(x)的解集为()A.(﹣2,﹣1)∪(﹣1,0)B.C.D.2.已知定义在R上的奇函数f(x)满足:当x≥0时,f(x)=x3,若不等式f(﹣4t)>f(2m+mt2)对任意实数t恒成立,则实数m的取值范围是()A.(﹣∞,﹣) B.(﹣,0)C.(﹣∞,0)∪(,+∞)D.(﹣∞,﹣)∪(,+∞)3.定义域为R的函数f(x)满足:f(x+2)=2f(x),当x∈[0,2)时,,若x∈[﹣4,﹣2)时,恒成立,则实数t的取值范围是()A.B.C.(0,1]D.(0,2]4.对于函数f(x),若∀a,b,c∈R,f(a),f(b),f(c)为某一三角形的三边长,则称f(x)为”可构造三角形函数“,已知函数f(x)=(0<x<)是“可构造三角形函数”,则实数t的取值范围是()A.[1,4]B.[1,2]C.[,2] D.[0,+∞)5.已知函数f(x)是定义在R上的奇函数,当x≤0时,f(x)=x(1﹣x),若数列{a n}满足a1=,且a n+1=,则f(a2015)+f(a2016)=()A.﹣8 B.8 C.﹣4 D.46.函数f(x)=,若x>0时,不等式f(x)≤恒成立,则实数m的取值范围为()A.[4,+∞)B.[3,+∞)C.[2,+∞)D.[,+∞)7.已知x>0,y>0,若不等式a(x+y)≥x+恒成立,则a的最小值为()A.B. C.+2 D.+8.已知函数f(x)=若函数g(x)=f[f(x)]﹣2的零点个数为()A.3 B.4 C.5 D.69.已知定义在R上的偶函数g(x)满足g(x)+g(2﹣x)=0,函数f(x)=的图象是g(x)的图象的一部分.若关于x的方程g2(x)=a(x+1)2有3个不同的实数根,则实数a的取值范围为()A.(,+∞)B.(,)C.(,+∞)D.(2,3)10.已知函数f(x)定义域为[0,+∞),当x∈[0,1]时,f(x)=sinπx,当x∈[n,n+1]时,f(x)=,其中n∈N,若函数f(x)的图象与直线y=b有且仅有2016个交点,则b的取值范围是()A.(0,1) B.(,)C.(,)D.(,)11.已知函数:,,设函数F(x)=f(x+3)•g(x﹣5),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b﹣a的最小值为()A.8 B.9 C.10 D.1112.已知函数,其中m>0,且函数f(x)=f(x+4),若方程3f(x)﹣x=0恰有5个根,则实数m的取值范围是()A.B. C.D.二.填空题(共7小题)13.设函数f(x)=2ax2+2bx,若存在实数x0∈(0,t),使得对任意不为零的实数a,b均有f(x0)=a+b成立,则t的取值范围是.14.若正数x,y满足=1,则的最小值为.15.已知集合{φ|f(x)=sin[(x﹣2φ)π]+cos[(x﹣2φ)π]为奇函数,且|log aφ|<1}的子集个数为4,则a的取值范围为.16.已知函数y=f(x)是定义在R上的奇函数,对∀x∈R都有f(x﹣3)=f(x ﹣1)成立,当,x∈(0,1]且x1≠x2时,有<0,给出下列命题:(1)f(x)在[﹣2,2]上有5个零点(2)点(2016,0)是函数y=f(x)的一个对称中心(3)直线x=2016是函数y=f(x)图象的一条对称轴(4)f(9.2)<f(π)则正确的是.17.已知函数f(x)=e x,对于实数m、n、p有f(m+n)=f(m)+f(n),f(m+n+p)=f(m)+f(n)+f(p),则p的最大值等于.18.定义在R上的单调函数f(x)满足:f(x+y)=f(x)+f(y),若F(x)=f(asinx)+f(sinx+cos2x﹣3)在(0,π)上有零点,则a的取值范围是.19.已知函数f(x)=,g(x)=(k>0),对任意p∈(1,+∞),总存在实数m,n满足m<0<n<p,使得f(p)=f(m)=g(n),则整数k的最大值为.三.解答题(共11小题)20.已知f(x)=log a是奇函数(其中a>1)(1)求m的值;(2)判断f(x)在(2,+∞)上的单调性并证明;(3)当x∈(r,a﹣2)时,f(x)的取值范围恰为(1,+∞),求a与r的值.21.已知向量=(cos,sin),=(cos,﹣sin),函数f(x)=•﹣m|+|+1,x∈[﹣,],m∈R.(1)当m=0时,求f()的值;(2)若f(x)的最小值为﹣1,求实数m的值;(3)是否存在实数m,使函数g(x)=f(x)+m2,x∈[﹣,]有四个不同的零点?若存在,求出m的取值范围;若不存在,说明理由.22.已知二次函数f(x)=ax2+bx+c.(1)若a=c>0,f(1)=1,对任意x∈|[﹣2,2],f(x)的最大值与最小值之和为g(a),求g(a)的表达式;(2)若a,b,c为正整数,函数f(x)在(﹣,)上有两个不同零点,求a+b+c的最小值.23.已知函数f(x)=.(1)求f(f());(2)若x0满足f(f(x0))=x0,且f(x0)≠x0,则称x0为f(x)的二阶不动点,求函数f(x)的二阶不动点的个数.24.已知a∈R,函数.(1)当a=0时,解不等式f(x)>1;(2)当a>0时,求函数y=2f(x)﹣f(2x)的零点个数;(3)设a<0,若对于t∈R,函数在区间[t,t+1]上的最大值与最小值之差都不超过1,求实数a的取值范围.25.已知a∈R,函数f(x)=.(1)若f(2)=﹣3,求实数a的值;(2)若关于x的方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一个元素,求a的取值范围.(3)设a>0,若对任意t∈[,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.26.设a∈R,函数f(x)=x|x﹣a|+2x.(1)若a=3,求函数f(x)在区间[0,4]上的最大值;(2)若存在a∈(2,4],使得关于x的方程f(x)=t•f(a)有三个不相等的实数解,求实数t的取值范围.27.如图,在半径为,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上,设矩形PNMQ的面积为y,∠P OB=θ.(Ⅰ)将y表示成θ的函数关系式,并写出定义域;(Ⅱ)求矩形PNMQ的面积取得最大值时•的值;(Ⅲ)求矩形PNMQ的面积y≥的概率.28.已知函数f(x)=x|x﹣a|,a∈R,g(x)=x2﹣1.(1)当a=1时,解不等式f(x)≥g(x);(2)记函数f(x)在区间[0,2]上的最大值为F(a),求F(a)的表达式.29.已知函数g(x)=,且函数f(x)=log a g(x)(a>0,a≠1)奇函数而非偶函数.(1)写出f(x)在(a,+∞)上的单调性(不必证明);(2)当x∈(r,a﹣3)时,f(x)的取值范围恰为(1,+∞),求a与r的值;(3)设h(x)=﹣m(x+2)﹣2是否得在实数m使得函数y=h(x)有零点?若存在,求出实数m的取值范围,若不存在,请说明理由.30.已知函数f(x)=1+log2x,g(x)=2x.(1)若F(x)=f(g(x))•g(f(x)),求函数F(x)在x∈[1,4]的值域;(2)令G(x)=f(8x2)f()﹣kf(x),已知函数G(x)在区间[1,4]有零点,求实数k的取值范围;(3)若H(x)=,求H()+H()+H()+…+H()的值.2018高一数学必修一(难)参考答案与试题解析一.选择题(共12小题)1.(2016秋•渝中区校级期末)已知定义在R上的偶函数f(x)满足f(x+1)=﹣f(x),且当x∈[﹣1,0]时,,函数,则关于x的不等式f(x)<g(x)的解集为()A.(﹣2,﹣1)∪(﹣1,0)B.C.D.【解答】解:由题意知,f(x+1)=﹣f(x),∴f(x+2)=﹣f(x+1)=f(x),即函数f(x)是周期为2的周期函数.若x∈[0,1]时,﹣x∈[﹣1,0],∵当x∈[﹣1,0]时,,∴当x∈[0,1]时,,∵f(x)是偶函数,∴f(x)=,即f(x)=.∵函数,∴g(x)=,作出函数f(x)和g(x)的图象如图:当﹣1<x<0时,由=,则,由选项验证解得x=,即此时不等式式f(x)<g(|x+1|)的解为﹣1<x<,∵函数g(x)关于x=﹣1对称,∴不等式式f(x)<g(x)的解为﹣1<x<或<x<﹣1,即不等式的解集为(,﹣1)∪(﹣1,),故选:D.2.(2016秋•通渭县期末)已知定义在R上的奇函数f(x)满足:当x≥0时,f (x)=x3,若不等式f(﹣4t)>f(2m+mt2)对任意实数t恒成立,则实数m的取值范围是()A.(﹣∞,﹣) B.(﹣,0)C.(﹣∞,0)∪(,+∞)D.(﹣∞,﹣)∪(,+∞)【解答】解:∵当x≥0时,f(x)=x3,①∴当x<0时,﹣x>0,f(﹣x)=(﹣x)3=﹣x3,又f(x)为定义在R上的奇函数,∴﹣f(x)=﹣x3,∴f(x)=x3(x<0),②综合①②知,f(x)=x3,x∈R.又f′(x)=3x2≥0,∴f(x)=x3为R上的增函数,∴不等式f(﹣4t)>f(2m+mt2)对任意实数t恒成立⇔﹣4t>2m+mt2对任意实数t恒成立,即mt2+4t+2m<0对任意实数t恒成立,∴,解得:m<﹣.故选:A.3.(2016秋•宜春期末)定义域为R的函数f(x)满足:f(x+2)=2f(x),当x ∈[0,2)时,,若x∈[﹣4,﹣2)时,恒成立,则实数t的取值范围是()A.B.C.(0,1]D.(0,2]【解答】解:当x∈[0,2)时,∈[﹣,0]∪[﹣1,﹣],∴当x∈[0,2)时,f(x)的最小值为f()=﹣1,又∵函数f(x)满足f(x+2)=2f(x),∴f(x)=f(x+2),当x∈[﹣2,0)时,f(x)的最小值为f(﹣)=f()=﹣,当x∈[﹣4,﹣2)时,f(x)的最小值为f(﹣)=f(﹣)=﹣若x∈[﹣4,﹣2]时,恒成立,∴﹣≥恒成立.即≤0,则0<t≤1,故选:C.4.(2016春•琅琊区校级期末)对于函数f(x),若∀a,b,c∈R,f(a),f(b),f(c)为某一三角形的三边长,则称f(x)为”可构造三角形函数“,已知函数f (x)=(0<x<)是“可构造三角形函数”,则实数t的取值范围是()A.[1,4]B.[1,2]C.[,2] D.[0,+∞)【解答】解:f(x)===2+,①若t=2,则f(x)=2,此时f(x)构成边长为2的等边三角形,满足条件,设m=tanx,则m=tanx>0,则函数f(x)等价为g(m)=2+,②若t﹣2>0即t>2,此时函数g(m)在(0,+∞)上是减函数,则2<f(a)<2+t﹣2=t,同理2<f(b)<t,2<f(c)<t,则4<f(a)+f(b)<2t,2<f(c)<t,由f(a)+f(b)>f(c),可得4≥t,解得2<t≤4.③当t﹣2<0,f(x)在R上是增函数,t<f(a)<2,同理t<f(b)<2,t<f(c)<2,则2t<f(a)+f(b)<4,t<f(c)<2,由f(a)+f(b)>f(c),可得2t≥2,解得1≤t<2.综上可得,1≤t≤4,故实数t的取值范围是[1,4];故选:A5.(2015秋•菏泽期末)已知函数f(x)是定义在R上的奇函数,当x≤0时,f (x)=x(1﹣x),若数列{a n}满足a1=,且a n+1=,则f(a2015)+f(a2016)=()A.﹣8 B.8 C.﹣4 D.4【解答】解:设x>0,则﹣x<0;∵f(x)是定义在R上的奇函数;∴f(x)=﹣f(﹣x)=﹣[﹣x(1+x)]=x(1+x);由,且得:,,,…;∴数列{a n}是以3为周期的周期数列;∴a2015=a671×3+2=a2=2,a2016=a671×3+3=a3=﹣1;∴f(a2015)+f(a2016)=f(2)+f(﹣1)=2(1+2)+(﹣1)(1+1)=4.故选:D.6.(2015秋•吉安期末)函数f(x)=,若x>0时,不等式f(x)≤恒成立,则实数m的取值范围为()A.[4,+∞)B.[3,+∞)C.[2,+∞)D.[,+∞)【解答】解:当0≤x≤4时,函数f(x)在[0,2]上为增函数,则[2,4]上为减函数,则当x=2时,函数f(x)取得最大值f(2)=,当4≤x≤8时,0≤x﹣4≤4,即f(x)=f(x﹣4)=,此时的最大值为f(6)=,当8≤x≤12时,4≤x﹣4≤8,即f(x)=f(x﹣4)=,此时的最大值为f(10)=,作出函数f(x)的图象如图,要使当x>0时,不等式f(x)≤恒成立,则m>0,设g(x)=,则满足,即,即,即m≥3,故选:B.7.(2015秋•杭州校级期末)已知x>0,y>0,若不等式a(x+y)≥x+恒成立,则a的最小值为()A.B. C.+2 D.+【解答】解:∵x>0,y>0,∴不等式a(x+y)≥x+等价为a≥=,令,∴a≥,令u=,∴u′=令u′=0,∴t=﹣(负值舍去)∴函数在(0,)上单调增,在(,+∞)上单调减∴t=时,函数u=取得最大值为∴a≥∴实数a的最小值为故选:A8.(2016秋•沙市区校级期末)已知函数f(x)=若函数g(x)=f[f(x)]﹣2的零点个数为()A.3 B.4 C.5 D.6【解答】解:∵函数f(x)=,∴f(x)=.∴x∈(﹣∞,log23)时,f(f(x))=∈[0,3],令f(f(x))=2,解得x=log2(1+log23).同理可得:x∈[log23,2)时,=2,解得x=.x∈时,=2,解得x=.时,=2,解得x=1+.综上可得:函数g(x)=f[f(x)]﹣2的x零点个数为4.故选:B.9.(2016春•重庆校级期末)已知定义在R上的偶函数g(x)满足g(x)+g(2﹣x)=0,函数f(x)=的图象是g(x)的图象的一部分.若关于x的方程g2(x)=a(x+1)2有3个不同的实数根,则实数a的取值范围为()A.(,+∞)B.(,)C.(,+∞)D.(2,3)【解答】解:∵定义在R上的偶函数g(x)满足g(x)+g(2﹣x)=0,∴g(x)=﹣g(2﹣x)=﹣g(x﹣2),则g(x+2)=﹣g(x),即g(x+4)=﹣g(x+2)=﹣(﹣g(x))=g(x),则函数g(x)是周期为4的周期函数,函数f(x)=的定义域为[﹣1,1],若1≤x≤2,则﹣2≤﹣x≤﹣1,则0≤2﹣x≤1,此时g(x)=﹣g(2﹣x)=﹣,当﹣2≤x≤﹣1,则1≤﹣x≤2,则g(x)=g(﹣x)=﹣则由g2(x)=a(x+1)2得,当﹣2≤x≤﹣1时,1﹣(x+2)2=a(x+1)2,作出函数g(x)的图象如图:若方程g2(x)=a(x+1)2有3个不同的实数根,则当a≤0时,不满足条件.则当a>0时,方程等价为g(x)=±=|x+1|,则当x=﹣1时,方程g(x)=|x+1|恒成立,此时恒有一解,当直线y=﹣(x+1)与g(x)在(﹣4,﹣3)相切时,此时方程g(x)=|x+1|有6个交点,不满足条件.当y=﹣(x+1)与g(x)在(﹣4,﹣3)不相切时,满足方程g(x)=|x+1|有三个交点,此时直线方程为x+y+=0,满足圆心(﹣4,0)到直线x+y+=0,的距离d=>1,即>1,即3>,平方得9a>a+1,得8a>1,则a>,故选:A10.(2016秋•荆门期末)已知函数f(x)定义域为[0,+∞),当x∈[0,1]时,f(x)=sinπx,当x∈[n,n+1]时,f(x)=,其中n∈N,若函数f(x)的图象与直线y=b有且仅有2016个交点,则b的取值范围是()A.(0,1) B.(,)C.(,)D.(,)【解答】解:根据题意,x∈[0,1]时,f(x)=sinπx,x∈[n,n+1]时,f(x)=,其中n∈N,∴f(n)=sinnπ=0,f()=sin=1,f()===,f()===,…;画出图形如图所示;当b∈(,1)时,函数f(x)的图象与直线y=b有2个交点;当b∈(,)时,函数f(x)的图象与直线y=b有4个交点;当b∈(,)时,函数f(x)的图象与直线y=b有6个交点;…;当b∈(,)时,函数f(x)的图象与直线y=b有2016个交点.故选:D.11.(2015秋•汕头校级期末)已知函数:,,设函数F(x)=f(x+3)•g(x﹣5),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b﹣a的最小值为()A.8 B.9 C.10 D.11【解答】解:∵f(0)=1>0,f(﹣1)=1﹣1﹣+﹣…+<0,∴函数f(x)在区间(﹣1,0)内有零点;当x∈(﹣1,0)时,f′(x)=>0,∴函数f(x)在区间(﹣1,0)上单调递增,故函数f(x)有唯一零点x∈(﹣1,0);∵g(1)=1﹣1+﹣+…﹣>0,g(2)=1﹣2+﹣+…+﹣<0.当x∈(1,2)时,g′(x)=﹣1+x﹣x2+x3﹣…+x2013﹣x2014=>0,∴函数g(x)在区间(1,2)上单调递增,故函数g(x)有唯一零点x∈(1,2);∵F(x)=f(x+3)•g(x﹣4),且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,∴f(x+3)的零点在(﹣4,﹣3)内,g(x﹣4)的零点在(5,6)内,因此F(x)=f(x+3)•g(x﹣3)的零点均在区间[﹣4,6]内,∴b﹣a的最小值为10.故选:C.12.(2015秋•衡水校级期末)已知函数,其中m >0,且函数f(x)=f(x+4),若方程3f(x)﹣x=0恰有5个根,则实数m的取值范围是()A.B. C.D.【解答】解:∵当x∈(﹣1,1]时,将函数化为方程x2+=1(y≥0),∴实质上为一个半椭圆,其图象如图所示,∵函数f(x)=f(x+4),∴函数的周期是4,同时在坐标系中作出当x∈(1,3]得图象,再根据周期性作出函数其它部分的图象,若方程3f(x)﹣x=0恰有5个根,则等价为f(x)=恰有5个根,由图易知直线y=与第二个椭圆(x﹣4)2+=1(y≥0)相交,而与第三个半椭圆(x﹣8)2+=1 (y≥0)无公共点时,方程恰有5个实数解,将y=代入(x﹣4)2+=1 (y≥0)得,(9m2+1)x2﹣72m2x+135m2=0,令t=9m2(t>0),则(t+1)x2﹣8tx+15t=0,由△=(8t)2﹣4×15t (t+1)>0,得t>15,由9m2>15,且m>0得m,同样由y=与第三个椭圆(x﹣8)2+=1 (y≥0)由△<0可计算得m<,综上可知m∈(,),故选:A.二.填空题(共7小题)13.(2017春•杭州期末)设函数f(x)=2ax2+2bx,若存在实数x0∈(0,t),使得对任意不为零的实数a,b均有f(x0)=a+b成立,则t的取值范围是(1,+∞).【解答】解:f(x)=a+b成立等价于(2x﹣1)b=(1﹣2x2)a,当x=时,左边=0,右边≠0,不成立,当x≠时,(2x﹣1)b=(1﹣2x2)a等价于=,设k=2x﹣1,则x=,则===(﹣k﹣2),∵x∈(0,t),(t<),或x∈(0,)∪(,t),(t>),∴k∈(﹣1,2t﹣1),(t<),或k∈(﹣1,0)∪(0,2t﹣1),(t>),(*)∵∀a,b∈R,∴=(﹣k﹣2),在(*)上有解,∴(﹣k﹣2),在(*)上的值域为R,设g(k)=(﹣k)﹣1,则g(k)在(﹣∞,0),(0,+∞)上单调递减,∴,解得t>1,故答案为:(1,+∞)14.(2016春•沙坪坝区校级期末)若正数x,y满足=1,则的最小值为2.【解答】解:∵正数x,y满足+=1,∴=1﹣=,∴(y>1),∴x﹣1=(x>1).则+=(y﹣1)+≥2=2,当且仅当y﹣1=,即y ﹣1=时取等号.∴的最小值为2.故答案为:215.(2016秋•武昌区校级期末)已知集合{φ|f(x)=sin[(x﹣2φ)π]+cos[(x ﹣2φ)π]为奇函数,且|log aφ|<1}的子集个数为4,则a的取值范围为()∪().【解答】解:∵集合{φ|f(x)=sin[(x﹣2φ)π]+cos[(x﹣2φ)π]为奇函数,∴f(0)=sin(﹣2φπ)+cos(﹣2φπ)=cos2φπ﹣sin2φπ=0,∴cos2φπ=sin2φπ,即tan2φπ=1,∴2φπ=kπ+,则φ=+,k∈Z.验证φ=+,k∈Z时,f(x)=sin[(x﹣2φ)π]+cos[(x﹣2φ)π]=sin[(x﹣k﹣)π]+cos[(x﹣k﹣)π]=sin(πx﹣)+cos()=为奇函数.∴φ=+,k∈Z.∵集合{φ|f(x)=sin[(x﹣2φ)π]+cos[(x﹣2φ)π]为奇函数,且|log aφ|<1}的子集个数为4,∴满足|log aφ|<1的φ有2个,即满足﹣1<log aφ<1的φ有2个.分别取k=0,1,2,3,得到φ=,,,,若0<a<1,可得a∈()时,满足﹣1<log aφ<1的φ有2个;若a>1,可得a∈()时,满足﹣1<log aφ<1的φ有2个.则a的取值范围为()∪().故答案为:()∪().16.(2016秋•清城区期末)已知函数y=f(x)是定义在R上的奇函数,对∀x∈R都有f(x﹣3)=f(x﹣1)成立,当,x∈(0,1]且x1≠x2时,有<0,给出下列命题:(1)f(x)在[﹣2,2]上有5个零点(2)点(2016,0)是函数y=f(x)的一个对称中心(3)直线x=2016是函数y=f(x)图象的一条对称轴(4)f(9.2)<f(π)则正确的是(1)(2)(4).【解答】解:对于(1),∵函数y=f(x)是定义在R上的奇函数,∴f(0)=0,又f(x﹣3)=f(x﹣1),∴函数y=f(x)是以2为周期的函数,且f(1﹣3)=f(1﹣1),即f(﹣2)=f(0)=0,又f(2)=﹣f(﹣2),∴f(2)=0;同理可得,f(1)=f(﹣1)=0,又当x∈(0,1]且x1≠x2时,有<0,即奇函数y=f(x)在区间(0,1]上单调递减,故函数y=f(x)在区间[﹣1,0)上也单调递减,由函数y=f(x)是以2为周期的函数可知函数y=f(x)在区间(﹣2,﹣1]、[1,2)上单调递减,∴f(x)在区间[﹣2,2]上有±1、0、±2共5个零点,故(1)正确;对于(2),∵函数y=f(x)是定义在R上的奇函数,∴(0,0)为其对称中心,又函数y=f(x)的是以2为周期的函数,∴点(2016,0)是函数y=f(x)的一个对称中心,故(2)正确;对于(3),作出函数y=f(x)的图象如下:(3)直线x=2016不是函数y=f(x)图象的一条对称轴,故(3)错误;对于(4),∵函数y=f(x)的是以2为周期的函数且在区间[1,2)上为减函数,∴f(9.2)=f(1.2)<f(π﹣2)=f(π),故(4)正确.综上所述,正确的是:(1)(2)(4),故答案为:(1)(2)(4).17.(2016春•扬州期末)已知函数f(x)=e x,对于实数m、n、p有f(m+n)=f(m)+f(n),f(m+n+p)=f(m)+f(n)+f(p),则p的最大值等于2ln2﹣ln3.【解答】解:由f(x)=e x得:f(m+n)=f(m)f(n),∵f(m+n)=f(m)+f(n),∴f(m)f(n)=f(m)+f(n),设f(m)f(n)=f(m)+f(n)=t,则f(m)、f(n)是x2﹣tx+t=0的解,∵△=t2﹣4t≥0,∴t≥4或t≤0(舍去).又f(m+n+p)=f(m)f(n)f(p)=f(m)+f(n)+f(p),∴tf(p)=t+f(p),∴f(p)==1+(t≥4),显然t越大,f(p)越小,∴当t=4时,f(p)取最大值,又f(p)=e p,∴f(p)取到最大值时,p也取到最大值,即p max=ln=2ln2﹣ln3.故答案为:2ln2﹣ln3.18.(2016秋•江岸区校级期末)定义在R上的单调函数f(x)满足:f(x+y)=f (x)+f(y),若F(x)=f(asinx)+f(sinx+cos2x﹣3)在(0,π)上有零点,则a的取值范围是[2,+∞).【解答】解:①令x=y=0,则f(0)=2f(0),则f(0)=0;再令y=﹣x,则f(x﹣x)=f(x)+f(﹣x)=0,且f(x)定义域为R,关于原点对称.∴f(x)是奇函数.②F(x)=f(asinx)+f(sinx+cos2x﹣3)在(0,π)上有零点.∴f(asinx)+f(sinx+cos2x﹣3)=0在(0,π)上有解;∴f(asinx)=﹣f(sinx+cos2x﹣3)=f(﹣sinx﹣cos2x+3)在(0,π)上有解;又∵函数f(x)是R上的单调函数,∴asinx=﹣sinx﹣cos2x+3在(0,π)上有解.∵x∈(0,π),∴sinx≠0;∴a==sinx+﹣1;令t=sinx,t∈(0,1];则a=t+﹣1;∵y=t+,<0,因此函数y在(0,1]上单调递减,∴a≥2.故答案为:[2,+∞).19.(2016春•盐城期末)已知函数f(x)=,g(x)=(k>0),对任意p∈(1,+∞),总存在实数m,n满足m<0<n<p,使得f(p)=f(m)=g(n),则整数k的最大值为7.【解答】解:显然g(x)=(k>0),在区间(1,+∞)上为减函数,于是g(n)>g(p),若f(p)=g(n),则对任意p>1,有f(p)>g(p).当x>1时,>,∴k<,设t=x﹣1(t>0),则==2(t++2)≥8,∴k<8∴k≤7.下面证明:当k=7时,对0<x<1,有f(x)<g(x).当0<x<1时,f(x)<g(x)⇔﹣ln(1﹣x)>0.令ψ(x)=﹣ln(1﹣x)(0<x<1),则ψ′(x)=﹣+<0,故ψ(x)在(0,1)上为减函数,于是ψ(x)>0.同时,当x∈(0,+∞)时,g(x)=∈(0,+∞).当x∈(0,1)时,f(x)∈R;当x∈(1,+∞)时,f(x)∈(0,+∞).结合函数的图象可知,对任意的正数p,存在实数m、n满足0<m<n<p,使得f(p)=f(m)=g(n).综上所述,正整数k的最大值为7.故答案为:7.三.解答题(共11小题)20.(2016秋•惠来县校级期末)已知f(x)=log a是奇函数(其中a>1)(1)求m的值;(2)判断f(x)在(2,+∞)上的单调性并证明;(3)当x∈(r,a﹣2)时,f(x)的取值范围恰为(1,+∞),求a与r的值.【解答】解:(1)由题意:f(x)是奇函数,则f(﹣x)+f(x)=0,即log a+=0∴,解得:m=±1,当m=﹣1时,f(x)无意义,所以,故得m的值为1.(2)由(1)得,设2<x1<x2,则f(x2)﹣f(x1)=﹣=∴2<x1<x2,∴0<2x1x2+2(x1﹣x2)﹣4<x1x2﹣(x1﹣x2)﹣4,∵a>1,∴f(x2)<f(x1)所以:函数f(x)在(2,+∞)上的单调减函数.(3)由(1)得,∴得,函数f(x)的定义域为(﹣∞,﹣2)∪(2,+∞)又∵,得f(x)∈(﹣∞,0)∪(0,+∞)令f(x)=1,则=,解得:.所以:f()=1当a>1时,>2,此时f(x)在在(2,+∞)上的单调减函数.所以:当x∈(2,)时,得f(x)∈1,+∞);由题意:r=2,那么a﹣2=,解得:a=5.所以:当x∈(r,a﹣2),f(x)的取值范围恰为(1,+∞)时,a和r的值分别为5和2.21.(2016秋•无锡期末)已知向量=(cos,sin),=(cos,﹣sin),函数f(x)=•﹣m|+|+1,x∈[﹣,],m∈R.(1)当m=0时,求f()的值;(2)若f(x)的最小值为﹣1,求实数m的值;(3)是否存在实数m,使函数g(x)=f(x)+m2,x∈[﹣,]有四个不同的零点?若存在,求出m的取值范围;若不存在,说明理由.【解答】解:(1)•=(cos,sin)•(cos,﹣sin)=cos cos﹣sin sin=cos(+)=cos2x,当m=0时,f(x)=•+1=cos2x+1,则f()=cos(2×)+1=cos+1=;(2)∵x∈[﹣,],∴|+|===2cosx,则f(x)=•﹣m|+|+1=cos2x﹣2mcosx+1=2cos2x﹣2mcosx,令t=cosx,则≤t≤1,则y=2t2﹣2mt,对称轴t=,①当<,即m<1时,当t=时,函数取得最小值此时最小值y=﹣m=﹣1,得m=(舍),②当≤≤1,即m<1时,当t=时,函数取得最小值此时最小值y=﹣=﹣1,得m=,③当>1,即m>2时,当t=1时,函数取得最小值此时最小值y=2﹣2m=﹣1,得m=(舍),综上若f(x)的最小值为﹣1,则实数m=.(3)令g(x)=2cos2x﹣2mcosx+m2=0,得cosx=或,∴方程cosx=或在x∈[﹣,]上有四个不同的实根,则,得,则≤m<,即实数m的取值范围是≤m<.22.(2016秋•义乌市期末)已知二次函数f(x)=ax2+bx+c.(1)若a=c>0,f(1)=1,对任意x∈|[﹣2,2],f(x)的最大值与最小值之和为g(a),求g(a)的表达式;(2)若a,b,c为正整数,函数f(x)在(﹣,)上有两个不同零点,求a+b+c的最小值.【解答】解:(1)a=c>0,f(1)=1,则a+b+a=1,b=1﹣2a,∴f(x))=ax2+(1﹣2a)x+a=a+,当1﹣≤﹣2,即0<a≤时,g(a)=f(﹣2)+f(2)=10a;当﹣2<1﹣≤0,即<a≤时,g(a)=f(1﹣)+f(2)=a﹣+3,当a>时,g(a)=f(1﹣)+f(﹣2)=9a﹣﹣1,综上所述,g(a)=;(2)函数f(x)在(﹣,)上有两个不同零点x1,x2,则x1+x2=﹣<0,>x1x2=>0∴a>16c,由根的分布可知f(﹣)=a﹣b+c>0,即a+16c>4b,∵a,b,c为正整数,∴a+16c≥4b+1f(0)=c>0,△>0,b,∴a+16c>8+1,可得()2>1,∵a>16c,∴>1,∴,∴a>25,∴a≥26,∴b≥,∴b≥11,c≥1.f(x)=26x2+11x+1,经检验符合题意,故a+b+c的最小值为38.23.(2016秋•佛山期末)已知函数f(x)=.(1)求f(f());(2)若x0满足f(f(x0))=x0,且f(x0)≠x0,则称x0为f(x)的二阶不动点,求函数f(x)的二阶不动点的个数.【解答】解:(1)∵f(x)=.∴f())=ln=,∴f(f())=f()=2﹣2×=1;(2)函数f(x)=.x∈[0,),f(x)=2﹣2x∈(1,2],x∈[,1),f(x)=2﹣2x∈(0,1],x∈[1,e],f(x)=lnx∈(0,1),∴f(f(x))=,若x0满足f(f(x0))=x0,且f(x0)≠x0,则称x0为f(x)的二阶不动点,所以:x0∈[0,),ln(2﹣2x0)=x0,由y=ln(2﹣x0),y=x0,图象可知:存在满足题意的不动点.x0∈[,1),﹣2+4x0=x0,解得x0=,满足题意.x0∈[1,e],2﹣2lnx0=x0,即2﹣x0=2lnx0,由y=2﹣x0,y=2lnx0,图象可知:存在满足题意的不动点.函数f(x)的二阶不动点的个数为:3个.24.(2016秋•海安县校级期末)已知a∈R,函数.(1)当a=0时,解不等式f(x)>1;(2)当a>0时,求函数y=2f(x)﹣f(2x)的零点个数;(3)设a<0,若对于t∈R,函数在区间[t,t+1]上的最大值与最小值之差都不超过1,求实数a的取值范围.【解答】解:(1)a=0时,f(x)=,∵f(x)>1,即>1,∴0<2x<1,解得x<0.(2)y=2f(x)﹣f(2x)=,∴函数y=2f(x)﹣f(2x)的定义域为{x|x≠log2a,且x≠log2a}.令y=0得22x+1﹣2x﹣a=0,令t=2x(t>0,且t≠a,t),方程为2t2﹣t﹣a=0,△=1+8a>0,若a=1,t=1或﹣,方程无解,即函数y=2f(x)﹣f(2x)的零点个数为0若0<a<1或a>1,方程有两个不相等的解,即函数y=2f(x)﹣f(2x)的零点个数为2;(3)函数f(x)在区间[t,t+1]上单调递减,由题意得f(t)﹣f(t+1)≤1,即﹣≤1,∴22t+1﹣(3a+1)•2t+a2≥0,设x=2t(x>0),则2x2﹣(3a+1)x+a2≥0,∴△≤0或,∴a≤﹣.25.(2016秋•西陵区校级期末)已知a∈R,函数f(x)=.(1)若f(2)=﹣3,求实数a的值;(2)若关于x的方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一个元素,求a的取值范围.(3)设a>0,若对任意t∈[,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.【解答】解:(1)f(2)=﹣3,∴log2(+a)=﹣3=log2,∴+a=,解得a=﹣(2)由f(x)﹣log2[(a﹣4)x+2a﹣5]=0得log2(+a)﹣log2[(a﹣4)x+2a ﹣5]=0.即log2(+a)=log2[(a﹣4)x+2a﹣5],即+a=(a﹣4)x+2a﹣5>0,①则(a﹣4)x2+(a﹣5)x﹣1=0,即(x+1)[(a﹣4)x﹣1]=0,②,当a=4时,方程②的解为x=﹣1,代入①,成立当a=3时,方程②的解为x=﹣1,代入①,成立当a≠4且a≠3时,方程②的解为x=﹣1或x=,若x=﹣1是方程①的解,则+a=a﹣1>0,即a>1,若x=是方程①的解,则+a=2a﹣4>0,即a>2,则要使方程①有且仅有一个解,则1<a≤2.综上,若方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一个元素,则a 的取值范围是1<a≤2,或a=3或a=4.(3)函数f(x)在区间[t,t+1]上单调递减,由题意得f(t)﹣f(t+1)≤1,即log2(+a)﹣log2(+a)≤1,即+a≤2(+a),即a≥﹣=设1﹣t=r,则0≤r≤,==,当r=0时,=0,当0<r≤时,=,∵y=r+在(0,)上递减,∴r+≥+4=,∴=≤=,∴实数a的取值范围是a≥26.(2016秋•徐汇区期末)设a∈R,函数f(x)=x|x﹣a|+2x.(1)若a=3,求函数f(x)在区间[0,4]上的最大值;(2)若存在a∈(2,4],使得关于x的方程f(x)=t•f(a)有三个不相等的实数解,求实数t的取值范围.【解答】解:(1)当a=3,x∈[0,4]时,f(x)=x|x﹣3|+2x=,可知函数f(x)在区间[0,]递增,在(,3]上是减函数,在[3,4]递增,则f()=,f(4)=12,所以f(x)在区间[0,4]上的最大值为f(4)=12.(2)f(x)=,①当x≥a时,因为a>2,所以<a.所以f(x)在[a,+∞)上单调递增.②当x<a时,因为a>2,所以<a.所以f(x)在(﹣∞,)上单调递增,在[,a]上单调递减.当2<a≤4时,知f(x)在(﹣∞,]和[a,+∞)上分别是增函数,在[,a]上是减函数,当且仅当2a<t•f(a)<时,方程f(x)=t•f(a)有三个不相等的实数解.即1<t<=(a++4).令g(a)=a+,g(a)在a∈(2,4]时是增函数,故g(a)max=5.∴实数t的取值范围是(1,).27.(2016春•信阳期末)如图,在半径为,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上,设矩形PNMQ的面积为y,∠POB=θ.(Ⅰ)将y表示成θ的函数关系式,并写出定义域;(Ⅱ)求矩形PNMQ的面积取得最大值时•的值;(Ⅲ)求矩形PNMQ的面积y≥的概率.【解答】解:(Ⅰ)在Rt△PON中,∠PNO=90°,∠POB=θ,,所以,,在Rt△QMO中,∠QMO=90°,∠QON=60°,QM=PN=所以OM=所以:MN=ON﹣OM=所以y=即:y=3sinθcosθ﹣sin2θ,()(Ⅱ)由(Ⅰ)得y=3sinθcosθ﹣sin2θ=﹣=)﹣=∵θ∈(0,)∴∴sin()∈∴,即时,y的最大值为.此时ON=cos==,则•=||•||cos=×=.(Ⅲ)若矩形PNMQ的面积y≥,则≥,即sin()≥,则sin()≥,∵∴≤≤,即≤θ≤,则对应的概率P==28.(2016春•苏州期末)已知函数f(x)=x|x﹣a|,a∈R,g(x)=x2﹣1.(1)当a=1时,解不等式f(x)≥g(x);(2)记函数f(x)在区间[0,2]上的最大值为F(a),求F(a)的表达式.【解答】解:f(x)≥g(x),a=1时,即解不等式x|x﹣1|≥x2﹣1,…(1分)当x≥1时,不等式为x2﹣x≥x2﹣1,解得x≤1,所以x=1;…(3分)当x<1时,不等式为x﹣x2≥x2﹣1,解得,所以;…(5分)综上,x∈.…(6分)(2)因为x∈[0,2],当a≤0时,f(x)=x2﹣ax,则f(x)在区间[0,2]上是增函数,所以F(a)=f(2)=4﹣2a;…(7分)当0<a<2时,,则f(x)在区间上是增函数,在区间上是减函数,在区间[a,2]上是增函数,所以F(a)=max{f(),f(2)},…(9分)而,f(2)=4﹣2a,令即,解得,所以当时,F(a)=4﹣2a;…(11分)令即,解得或,所以当时,;…(12分)当a≥2时,f(x)=﹣x2+ax,当即2≤a<4时,f(x)在间上是增函数,在上是减函数,则;…(13分)当,即a≥4时,f(x)在间[0,2]上是增函数,则F(a)=f(2)=2a﹣4;…(14分)所以,,…(16分)29.(2015秋•黄浦区校级期末)已知函数g(x)=,且函数f(x)=log a g(x)(a>0,a≠1)奇函数而非偶函数.(1)写出f(x)在(a,+∞)上的单调性(不必证明);(2)当x∈(r,a﹣3)时,f(x)的取值范围恰为(1,+∞),求a与r的值;(3)设h(x)=﹣m(x+2)﹣2是否得在实数m使得函数y=h(x)有零点?若存在,求出实数m的取值范围,若不存在,请说明理由.【解答】解:(1)函数g(x)=,且函数f(x)=log a g(x)(a>0,a≠1)奇函数而非偶函数,可得f(﹣x)=﹣f(x),即log a=﹣log a,可得•=1,即p2﹣x2=4﹣x2,即p2=4,解得p=2(﹣2舍去),即有f(x)=log a,当a>1时,f(x)在(2,+∞),(﹣∞,﹣2)递减;当0<a<1时,f(x)在(2,+∞),(﹣∞,﹣2)递增.(2)由(1)得f(x)=log a,函数f(x)的定义域为(﹣∞,﹣2)∪(2,+∞)又≠1,得f(x)∈(﹣∞,0)∪(0,+∞),令f(x)=1,则log a=1,解得x=.所以:f()=1,当a>1时,>2,此时f(x)在(2,+∞)上的单调减函数.所以:当x∈(2,)时,得f(x)∈1,+∞);由题意:r=2,那么a﹣3=,解得:a=3+2.所以:当x∈(r,a﹣3),f(x)的取值范围恰为(1,+∞)时,a和r的值分别为3+2和2;(3)假设h(x)=﹣m(x+2)﹣2即h(x)=﹣m(x+2)﹣2,存在实数m使得函数y=h(x)有零点.由题意可知,方程=m(x+2)+2在{x|x≥﹣2且x≠2}中有实数解,令=t,则t≥0且t≠2,问题转化为关于t的方程mt2﹣t+2=0①,有非负且不等于2的实数根.若t=0,则①为2=0,显然不成立,故t≠0,方程①可变形为m=﹣2()2+,问题进一步转化为求关于t的函数(t≥0且t≠2)的值域,因为t≥0且t≠2,所以>0且≠,所以m=﹣2()2+∈(﹣∞,0)∪(0,],所以实数m的取值范围是(﹣∞,0)∪(0,].30.(2015秋•无锡校级期末)已知函数f(x)=1+log2x,g(x)=2x.(1)若F(x)=f(g(x))•g(f(x)),求函数F(x)在x∈[1,4]的值域;(2)令G(x)=f(8x2)f()﹣kf(x),已知函数G(x)在区间[1,4]有零点,求实数k的取值范围;(3)若H(x)=,求H()+H()+H()+…+H()的值.【解答】解:(1)若F(x)=f(g(x))•g(f(x))=(1+log22x)•=(1+x)•2×=2x(1+x)=2x2+2x=2(x+)2﹣当x∈[1,4]上函数F(x)为增函数,则函数的最大值为F(4)=40,函数的最小值为F(1)=4,则函数的值域为[4,40].(2)令G(x)=f(8x2)f()﹣kf(x)=(1+log28x2)(1+log2)﹣k(1+log2x)=(1+og28+log2x2))(1+log2x)﹣k(1+log2x)=(4+2log2x))(1+log2x)﹣k(1+log2x)=(log2x)2+4log2x+4﹣k﹣klog2x=(log2x)2+(4﹣k)log2x+4﹣k,设t=log2x,当x∈[1,4],则t∈[0,2],则函数等价为y=h(t)=t2+(4﹣k)t+4﹣k若函数G(x)在区间[1,4]有零点,则等价为y=h(t)=t2+(4﹣k)t+4﹣k在t∈[0,2]上有零点,即h(t)=t2+(4﹣k)t+4﹣k=0在t∈[0,2]上有解,即t2+4t+4﹣k(1+t)=0在t∈[0,2]上有解,即k===t+1++2,设m=t+1,则m∈[1,3],则k=m++2,则k=m++2在m∈[1,3]上递增,则当m=1时,k=1+1+2=4,当m=3时,k=3++2=,∴4≤m++2≤,即4≤k≤,即实数k的取值范围是4≤k≤;(3)若H(x)=,则H(x)==,则H(x)+H(1﹣x)=+=+=+=1,设H()+H()+H()+…+H()=S,H()+H()+…H()+H()=S,两式相加得2015[H()+H()]=2S,即2S=2015,则S=.。
高一数学知识点难题及解答

高一数学知识点难题及解答随着高中学习的深入,数学作为一门理科学科,对于学生来说常常是最令人头疼的。
特别是在高一这个阶段,新的数学知识点和难题不断涌现。
本文将围绕高一数学知识点中的几个难题展开讲述,并提供相应的解答。
一、平方根的处理问题高一数学中,平方根的处理经常会对学生造成困扰。
在计算平方根时,首先需要明确一个原则:不能直接对负数开平方。
因此,当题目中出现像√(-16)这样的表达时,我们首先要做的是将其转化成复数的形式。
通过定义我们知道,√(a × b) = √a × √b。
因此,我们可以将√(-16)转化为√(-1) × √16。
根据定义√(-1) = i,其中i是虚数单位。
所以√(-16) = i × 4 = 4i。
二、函数的复合问题在高一数学中,函数的复合也是一个常见的难点。
当两个函数进行复合运算时,很多学生容易弄混运算的顺序。
以f(x) = 2x + 1和g(x) = x^2为例,我们可以先求f(g(x))。
首先将g(x)代入f(x)的表达式中,得到f(g(x)) = 2(g(x)) + 1 = 2(x^2) + 1。
类似地,我们也可以求g(f(x))。
将f(x)代入g(x)的表达式中,得到g(f(x)) = (f(x))^2 = (2x + 1)^2 = 4x^2 + 4x + 1。
通过这个例子,我们可以看到函数的复合运算顺序的影响。
因此,在解题过程中,要注意先执行内层函数的运算,再执行外层函数的运算。
三、不等式的求解问题在高一数学中,不等式的求解是一个需要注意的难点。
首先,我们要掌握不等式的性质:等号两边同时加(减)一个数时,不等号不变;等号两边同时乘(除)一个正数时,不等号不变;等号两边同时乘(除)一个负数时,不等号反向。
以2x - 5 > 3为例,我们首先将不等式转化成等价的形式:2x -5 - 3 > 0,即2x - 8 > 0。
高中数学必修一第二章一元二次函数方程和不等式经典大题例题(带答案)

高中数学必修一第二章一元二次函数方程和不等式经典大题例题单选题1、实数a,b满足a>b,则下列不等式成立的是()A.a+b<ab B.a2>b2C.a3>b3D.√a2+b2<a+b答案:C分析:利用不等式的性质逐一判断即可.A,若a=1,b=0,则a+b>ab,故A错误;B,若a=1,b=−2,则a2<b2,故B错误;C,若a>b,则a3−b3=(a−b)(a2+ab+b2)=(a−b)[(a+b2)2+3b24]>0,所以a3>b3,故C正确;D,若a=1,b=−2,则√a2+b2>a+b,故D错误.故选:C2、将进货价为每个80元的商品按90元一个出售时,能卖出400个,每涨价1元,销售量就减少20个,为了使商家利润有所增加,则售价a(元/个)的取值范围应是()A.90<a<100B.90<a<110C.100<a<110D.80<a<100答案:A分析:首先设每个涨价x元,涨价后的利润与原利润之差为y元,结合条件列式,根据y>0,求x的取值范围,即可得到a的取值范围.设每个涨价x元,涨价后的利润与原利润之差为y元,则a=x+90,y=(10+x)⋅(400−20x)−10×400=−20x2+200x.要使商家利润有所增加,则必须使y>0,即x2−10x<0,得0<x<10,∴90<x+90<100,所以a的取值为90<a<100.故选:A3、已知y=(x−m)(x−n)+2022(n>m),且α,β(α<β)是方程y=0的两实数根,则α,β,m,n的大小关系是()A.α<m<n<βB.m<α<n<βC.m<α<β<n D.α<m<β<n答案:C分析:根据二次函数图像特点,结合图像平移变换即可得到答案.∵α,β为方程y=0的两实数根,∴α,β为函数y=(x−m)(x−n)+2022的图像与x轴交点的横坐标,令y1=(x−m)(x−n),∴m,n为函数y1=(x−m)(x−n)的图像与x轴交点的横坐标,易知函数y= (x−m)(x−n)+2022的图像可由y1=(x−m)(x−n)的图像向上平移2022个单位长度得到,所以m<α<β<n.故选:C.4、关于x的不等式ax2−|x|+2a≥0的解集是(−∞,+∞),则实数a的取值范围为()A.[√24,+∞)B.(−∞,√24]C.[−√24,√24]D.(−∞,−√24]∪[√24,+∞)答案:A分析:不等式ax2−|x|+2a≥0的解集是(−∞,+∞),即对于∀x∈R,ax2−|x|+2a≥0恒成立,即a≥|x|x2+2,分x=0和a≠0两种情况讨论,结合基本不等式即可得出答案.解:不等式ax2−|x|+2a≥0的解集是(−∞,+∞),即对于∀x∈R,ax2−|x|+2a≥0恒成立,即a≥|x|x2+2,当x=0时,a≥0,当a≠0时,a≥|x|x2+2=1|x|+2|x|,因为1|x|+2|x|≤2√|x|⋅2|x|=√24,所以a≥√24,综上所述a∈[√24,+∞). 故选:A.5、不等式1+5x −6x 2>0的解集为( )A .{x|x >1或x <−16}B .{x |−16<x <1 }C .{x|x >1或x <−3}D .{x |−3<x <2 } 答案:B分析:解一元二次不等式,首先确保二次项系数为正,两边同时乘−1,再利用十字相乘法,可得答案, 法一:原不等式即为6x 2−5x −1<0,即(6x +1)(x −1)<0,解得−16<x <1,故原不等式的解集为{x |−16<x <1 }.法二:当x =2时,不等式不成立,排除A ,C ;当x =1时,不等式不成立,排除D . 故选:B .6、已知正实数a ,b 满足a +1b=2,则2ab +1a的最小值是( )A .52B .3C .92D .2√2+1 答案:A分析:由已知得, a =2−1b 代入得2ab +1a =2(2b −1)+b2b−1,令2b −1=t ,根据基本不等式可求得答案. 解:因为a +1b=2,所以a =2−1b>0,所以0<b <2 ,所以2ab +1a =2(2−1b )b +b 2b−1=2(2b −1)+b2b−1, 令2b −1=t ,则b =t +12,且−1<t <3 ,所以2ab +1a =2t +t +12t=2t +12t +12≥2√2t ⋅12t +12=52,当且仅当2t =12t ,即t =12,b =34,a =23时,取等号,所以2ab +1a 的最小值是52. 故选:A.7、已知−1≤x +y ≤1,1≤x −y ≤5,则3x −2y 的取值范围是( ) A .[2,13]B .[3,13]C .[2,10]D .[5,10] 答案:A分析:设3x −2y =m (x +y )−n (x −y )=(m −n )x +(m +n )y ,求出m,n 的值,根据x +y,x −y 的范围,即可求出答案.设3x −2y =m (x +y )−n (x −y )=(m −n )x +(m +n )y ,所以{m −n =3m +n =−2,解得:{m =12n =−52,3x −2y =12(x +y )+52(x −y ), , 因为−1≤x +y ≤1,1≤x −y ≤5,所以3x −2y =12(x +y )+52(x −y )∈[2,13], 故选:A.8、已知a >b >0,下列不等式中正确的是( ) A .ca >cb B .ab <b 2C .a −b +1a−b ≥2D .1a−1<1b−1 答案:C分析:由a >b >0,结合不等式的性质及基本不等式即可判断出结论. 解:对于选项A ,因为a >b >0,0<1a<1b,而c 的正负不确定,故A 错误;对于选项B ,因为a >b >0,所以ab >b 2,故B 错误;对于选项C ,依题意a >b >0,所以a −b >0,1a−b >0,所以a −b +1a−b ≥2√(a −b )×1a−b =2,故C 正确; 对于选项D ,因为a >b >0,a −1>b −1>−1,1a−1与1b−1正负不确定,故大小不确定,故D 错误;故选:C. 多选题9、已知函数y =ax 2+bx -3,则下列结论正确的是( ) A .关于x 的不等式ax 2+bx -3<0的解集可以是{x |x >3 } B .关于x 的不等式ax 2+bx -3>0的解集可以是∅C .函数y =ax 2+bx -3的图象与x 轴正半轴可以有两个交点D .“关于x 的方程ax 2+bx -3=0有一个正根和一个负根”的充要条件是“a >0” 答案:BCD分析:根据不等式的解集求出a 、b ,再解不等式ax 2+bx -3<0可判断A ;取a =-1,b =0,解不等式-x 2-3>0可判断B ;取a =-1,b =4可判断C ;根据根的分布、充要条件的定义可判断D . 若不等式ax 2+bx -3<0的解集是{x |x >3},则a =0且3b -3=0,得b =1,而当a =0,b =1时,不等式ax 2+bx -3<0,即x -3<0,得x <3,与x >3矛盾,故A 错误; 取a =-1,b =0,此时不等式-x 2-3>0的解集为∅,故B 正确;函数y =ax 2+bx -3的图象与x 轴正半轴可以有两个交点,即ax 2+bx -3=0可以有2个正根,取a =-1,b =4,则由y =-x 2+4x -3=0,得x =1或3,故C 正确;若关于x 的方程ax 2+bx -3=0有一个正根和一个负根,则{a ≠0,−3a<0,得a >0,若a >0,则Δ=b 2+12a >0,故关于x 的方程ax 2+bx -3=0有两个不等的实根x 1,x 2, 且x 1x 2=-3a <0,即关于x 的方程ax 2+bx -3=0有一个正根和一个负根.因此“关于x 的方程ax 2+bx -3=0有一个正根和一个负根”的充要条件是“a >0”,故D 正确. 故选:BCD .10、已知x ,y 是正实数,则下列选项正确的是( ) A .若x +y =2,则1x+1y 有最小值2B .若x +y =3,则x(y +1)有最大值5C .若4x +y =1,则2√x +√y 有最大值√2D .x4+y 2x+1y有最小值94答案:AC分析:将已知转化,再利用基本不等式可判断ABC 选项;利用特值法判断选项D 。
高一数学最难试题及答案

高一数学最难试题及答案一、选择题:(每题5分,共20分)1. 已知函数f(x)=x^2-4x+3,若f(a)=0,则a的值为()。
A. 1B. 3C. -1D. 02. 集合A={1,2,3},集合B={2,3,4},则A∩B等于()。
A. {1}B. {2,3}C. {3,4}D. {1,2,3}3. 若直线y=2x+3与直线y=-x+4相交,则交点的坐标为()。
A. (1,5)B. (-1,5)C. (1,-1)D. (-1,-1)4. 函数f(x)=x^3-3x^2+4x-2的导数f'(x)为()。
A. 3x^2-6x+4B. x^2-6x+4C. 3x^2-6x+2D. x^2-3x+4二、填空题:(每题5分,共20分)5. 已知等差数列{an}的前三项分别为2,5,8,则该数列的通项公式为an=______。
6. 函数y=x^2-6x+8的顶点坐标为(______,______)。
7. 圆x^2+y^2-6x+8y-24=0的圆心坐标为(______,______)。
8. 已知函数f(x)=x^3-3x^2+2x+1,若f'(x)=0,则x的值为______。
三、解答题:(每题15分,共30分)9. 已知函数f(x)=x^3-6x^2+11x-6,求证:该函数在区间[1,2]上单调递增。
10. 已知三角形ABC的顶点坐标分别为A(1,2),B(4,6),C(7,2),求三角形ABC的面积。
四、综合题:(每题30分,共30分)11. 已知函数f(x)=x^4-4x^3+6x^2-2x+1,求函数的极值点,并讨论函数在这些极值点处的性质。
答案:一、选择题:1. B2. B3. A4. A二、填空题:5. an=3n-16. (3,-1)7. (3,-4)8. 1或2三、解答题:9. 证明:首先求导f'(x)=3x^2-12x+11,令f'(x)=0,解得x=1或x=3。
高一数学必修一必修二难题

精心整理1、已知二次函数对任意实数x不等式恒成立,且,令.(I)求的表达式;(II)若使成立,求实数m的取值范围;(III)设,恒有2A.??????????3A..?4、函数,在同一直角坐标系第一象限中的图像可能是)5、设为非零实数,则关于函数,A.函数一定是个偶函数B.C.区间一定是的单调递增区间???????D.函数不可能有三个零点6、已知>0,且,=,当x∈时,均有,则实数的取值范围是(???)A .?????????B .??C .?D .7、如图,四棱锥中,底面ABCD 为平行四边形,PA ⊥底面ABCD ,M 是棱PD 的中点,且PA =AB =AC =2,. (I )求证:CD ⊥平面PAC ; 所成角的正弦值为,求的值.8为偶函数,且在区间上是单调递增函数。
(Ⅱ)设,若能取遍内的所有实数,求实数9的函数是奇函数.(1)求实数的值;(3)若对任意恒成立,求参考答案一、计算题1、解(I )设由题意令得??∴∴得∵恒成立∴和恒成立得∴(II)当当时,恒成立当时,令这时若使成立则只须,综上所述,实数m的取值范围(III)∵,所以单减于是记,则所以函数所以2、D3、A4、B5、C?6、C7因为为在中,,,所以,所以.因为AB//CD,所以.又因为地面ABCD,所以因为所以?(II)则.因为M所以所以,.设为平面MAB的法向量,所以,即,令,则,所以平面MAB的法向量.因为所以所以的大小为..,所以.解得,即,,所以.8、(Ⅰ)∵为幂函数?∴??????????????????????????????????????????1分???????又在区间上是单调递增函数?∴?????????????????2分???????则?∵?∴或或???????????????3分???????当时,为奇函数,不合题意,舍去???????当时,为偶函数,符合题意???????为奇函数,不合题意,舍去???????????????????????????????????????????????????????????????????5??①当单调递增,其值域为,满足题意?????时,由得,则在单调递减,在,则其值域为???????∵能取遍内的所有实数?????????????9 ???????令?单调递增???????又?∴????????????????11分??????综合①②知,实数的取值范围为??????????????????????????????????12分四、综合题9、解:(1),经检验成立。
高中数学必修一难题个人整理的,里面有详细答案的,供大家看看推荐一下吧!

三、解答题1. 判断一次函数,b kx y +=反比例函数xk y =,二次函数c bx ax y ++=2的 单调性.2. 已知函数()f x 的定义域为()1,1-,且同时满足下列条件:(1)()f x 是奇函数; (2)()f x 在定义域上单调递减;(3)2(1)(1)0,f a f a -+-<求a 的取值范围.3. 利用函数的单调性求函数x x y 21++=的值域;4. 已知函数[]2()22,5,5f x x ax x =++∈-.① 当1a =-时,求函数的最大值和最小值;② 求实数a 的取值范围,使()y f x =在区间[]5,5-上是单调函数.1. 解:当0k >,y kx b =+在R 是增函数,当0k <,y kx b =+在R 是减函数;当0k >,ky x =在(,0),(0,)-∞+∞是减函数, 当0k <,ky x=在(,0),(0,)-∞+∞是增函数;当0a >,2y ax bx c =++在(,]2b a -∞-是减函数,在[,)2b a -+∞是增函数,当0a <,2y ax bx c =++在(,]2b a -∞-是增函数,在[,)2b a -+∞是减函数.2. 解:22(1)(1)(1)f a f a f a -<--=-,则2211111111a a a a -<-<⎧⎪-<-<⎨⎪->-⎩,∴01a <<3. 解:1210,2x x +≥≥-,显然y 是x 的增函数,12x =-,min 1,2y =- 1[,)2y ∴∈-+∞ 4. 解:2(1)1,()22,a f x x x =-=-+对称轴min max 1,()(1)1,()(5)37x f x f f x f =====∴max m ()37,()1in f x f x ==(2)对称轴,x a =-当5a -≤-或5a -≥时,()f x 在[]5,5-上单调 ∴5a ≥或5a ≤-.17. 已知函数f(x)=x 2+2ax+2, x []5,5-∈.(1)当a=-1时,求函数的最大值和最小值;(2) 若y=f(x)在区间[]5,5- 上是单调 函数,求实数 a 的取值范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、已知二次函数对任意实数x不等式恒成立,且,令
.
(I)求的表达式;
(II)若使成立,求实数m的取值范围;
(III)设,,证明:对,恒有
2、某三棱锥的三视图如图所示,该三棱锥的体积是
A. B.C.2D.4
3、一个棱锥的三视图如右图所示,则它的体积为( )
A. B. C.1 D.
4、函数,在同一直角坐标系第一象限中的图像可能
是
()
5、设为非零实数,则关于函数,的以下性质中,错误的是()
A.函数一定是个偶函数
B.一定没有最大值
C.区间一定是的单调递增区间
D.函数不可能有三个零点
6、已知>0,且, =,当x∈时,均有, 则实数的取值范围是( ) A. B. C. D.
7、如图,四棱锥中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA =AB =AC =2,
.
(I)求证:CD⊥平面PAC;
(Ⅱ)求二面角的大小;
(Ⅲ)如果N是棱AB上一点,且直线CN与平面MAB所成角的正弦值为,求的值.
8、已知幂函数为偶函数,且在区间上是单调递增函数。
(Ⅰ)求函数的解析式;
(Ⅱ)设,若能取遍内的所有实数,求实数的取值范围.
9、已知定义域为的函数是奇函数.
(1)求实数的值;(2)判断并证明在上的单调性;
(3)若对任意恒成立,求的取值范围.
参考答案
一、计算题
1、解(I)设
由题意令得∴
∴得
∵恒成立
∴和恒成立
得
∴
(II)
当时,的值域为R
当时,恒成立
当时,令
-0 +
↘极小↗
这时
若使成立则只须,
综上所述,实数m的取值范围
(III)∵,所以单减于是
记,则
所以函数是单增函数
所以
故命题成立.
二、选择题
2、D
3、A
4、B
5、C
6、C
三、简答题
7、证明:(I)连结AC.
因为为在中,
,,
所以,
所以.
因为AB//CD,
所以.
又因为地面ABCD,
所以.
因为,
所以平面PAC.
(II)如图建立空间直角坐标系,
则.
因为M是棱PD的中点,
所以.
所以,.
设为平面MAB的法向量,所以,
即,
令,则,
所以平面MAB的法向量.
因为平面ABCD,
所以是平面ABC的一个法向量.
所以.
因为二面角为锐二面角,
所以二面角的大小为.
(III)因为N是棱AB上一点,所以设,.
设直线CN与平面MAB所成角为,
因为平面MAB的法向量,
所以.
解得,即,,所以.
8、(Ⅰ)∵为幂函数∴
1分又在区间上是单调递增函数∴
2分
则∵∴或或
3分
当时,为奇函数,不合题意,舍去
当时,为偶函数,符合题意
当时,为奇函数,不合题意,舍去
故
5分
(Ⅱ)由(Ⅰ)知,
①当时,,则单调递增,其值域为,满足题意 7分
②当时,由得,则在单调递减,在单调递增,∴,则其值域为
∵能取遍内的所有实数∴只需
9分
令则在单调递增
又∴
11分
综合①②知,实数的取值范围为
12分
四、综合题
9、解:(1),经检验成立。
—————————4分
(2)证明:设任意
,,
在上是减函数—————————————————————— 8分
(3)
对任意恒成立
设在上增时,——12。
