第二类换元法
第二类换元法三角代换

第二类换元法三角代换第二类换元法三角代换是高等数学中的一种重要的求解方法,它可以将一些复杂的三角函数积分转化为简单的代数函数积分,从而简化计算过程,提高求解效率。
本文将详细介绍第二类换元法三角代换的原理、步骤和应用。
一、原理第二类换元法三角代换的原理是将三角函数中的自变量用一个新的三角函数代替,从而将原积分式子转化为一个更简单的形式。
具体来说,设原积分式为:∫f(sin x,cos x)dx则进行第二类换元法三角代换,令:t=tan(x/2)则有:sin x=2t/(1+t^2)cos x=(1-t^2)/(1+t^2)dx=2dt/(1+t^2)将上述代换带入原积分式中,得到:∫f(2t/(1+t^2),(1-t^2)/(1+t^2))×2dt/(1+t^2)这样,原积分式就被转化为了一个只含有代数函数的积分式,可以通过代数方法求解。
二、步骤进行第二类换元法三角代换的步骤如下:1.观察原积分式,确定是否适合进行第二类换元法三角代换。
2.令t=tan(x/2),将sin x和cos x用t表示。
3.将dx用dt表示。
4.将代换后的式子带入原积分式中,得到只含有代数函数的积分式。
5.通过代数方法求解积分式。
三、应用第二类换元法三角代换在求解三角函数积分中有着广泛的应用。
例如,对于以下积分式:∫sin^3 x cos^2 x dx可以通过第二类换元法三角代换来简化计算。
具体来说,令t=tan(x/2),则有:sin x=2t/(1+t^2)cos x=(1-t^2)/(1+t^2)dx=2dt/(1+t^2)将上述代换带入原积分式中,得到:∫(2t/(1+t^2))^3((1-t^2)/(1+t^2))^2×2dt/(1+t^2)化简后得到:∫(16t^3-24t^5+10t^7-1)/(16t^2+16)dt这样,原积分式就被转化为了一个只含有代数函数的积分式,可以通过代数方法求解。
微积分第二类换元法

凑微分法
说明(2)
积分中为了化掉根式是否一定采用三角 代换并不是绝对的,需根据被积函数的情况 来定,但目的还是要去根号.
例4 求
1 dx . x 1 e
解 令 t 1 e x e x t 2 1,
2t x lnt 1, dx 2 dt , t 1 1 1 2 1 dx 2 dt dt x 1 e t 1 t 1 t 1
a2 x2 a x
2 2
可令 x a sin t ; t (
x2 a2
, ); 2 2 可令 x a tant; t ( , ); 2 2 可令 x a sec t ; t (0, ). 2
思考
1. x x a dx
2 2
2.
ax dx ax
解(二) 令 u x ,
dv cos xdx d (sin x),
x cos xdx xd (sin x) x sin x sin xdx
x sin x cos x C .
udv uv vdu
利用分部积分法求不定积分的关键是:合 理地选择u(x) 选择u(x)的有效方法:FDMSZ选择法
作业:P133 第3,4题
二、分部积分法 x 问题 xe dx ?
解决思路 利用两个函数乘积的求导法则.
设函数u u( x ) 和v v ( x )具有连续导数,
uv uv uv,
uv uv , uv
或d (uv) udv vdu, 所以得udv=d(uv)-vdu
例2 求
1 dx (a 0). 2 2 x a
不定积分第二类换元法题目

不定积分第二类换元法题目换元法是积分学中使用最广泛的一种方法,它的本质是利用两种形式的变量之间的关系来求解不定积分的问题。
作为一类特殊的不定积分,称为不定积分第二类,第二类换元法就是应用这种不定积分解题的手段。
一般来说,在第二类换元法求解不定积分问题时,首先要把待求积分式转换为一阶微分式,其次把微分式中的自变量更换为另外一种形式,即换元式,最后求解换元式,从而解出不定积分式的解析解。
以下是一个典型的第二类换元法解题例子:求解:$$int frac{sin x}{1+cos x}dx$$解:将不定积分式转换为一阶微分式:$$frac{d(1+cos x)}{dx}=sin x$$引入另外一种形式的自变量替换:$$cos x=t,~dx=-frac{dt}{sin x}$$把原式换元:$$begin{aligned}int frac{sin x}{1+cos x}dx&=-int frac{dt}{t+1}&=-ln|t+1|+Cend{aligned}$$将换元式中变量替换回原来的形式:$$ln|1+cos x|+C$$以上便是利用第二类换元法解题的具体过程,可以看出,第二类换元法可以有效地解决不定积分类问题,其实在积分学中,还有其他一些方法可以用来求解更复杂的不定积分问题,比如积分变换、积分可分离和换元法等。
之所以把换元法分为不同的类别,是因为它的应用范围是不一样的;当某一类问题中存在多种解法时,也会根据其具体情况进行划分类别。
比如,第一类换元法是用来求解同角变换不定积分,而第二类换元法则是利用不同余弦变换解不定积分。
此外,第二类换元法还可以用来解决一些复杂的不同余弦变换的不定积分问题,比如:$$int sqrt{1+cos x+cos^2 x}dx$$由前面的变换可得:$$1+cos x +cos^2 x=frac{1+t}{1-t}$$由此,可以把这个式子以$ t=cos x $的形式变为:$$begin{aligned}int sqrt{frac{1+t}{1-t}}dt&=int frac{1+t}{sqrt{1-t^2}}dt &=frac{1}{2}ln|1-t^2|+Cend{aligned}$$将变量替换为原式中的形式,即$$frac{1}{2}ln|1-(cos x)^2|+C$$以上便是第二类换元法解题的过程,可以看出,换元法确实是一种有效的解题方法,它可以在不定积分的解题中发挥重要作用,但还有一些其他的解题方法,比如积分可分离和积分变换也是解决不定积分类问题中不可或缺的一种手段。
《微积分》第二节 不定积分的第二类换元积分法

dx a sec t tan t d t
∴ 原式
a sect tan t a tan t
dt
sect d t
ln sec t tan t C1
t
ln
x a
x2 a2 a
C1
x2 a2
(C C1 ln a)
当x a 时 , 令 x u , 则 u a , 于是
du u 2 a2 ln u
2
,
2
sec tdt ln| sect tan t | C1
ln
x a
ln( x
x2 a
a2
C1
x2 a2 ) C.
x2 a2
x
t a
(C C1 ln a)
例4. 求
解:
当x
a时,
令
x
a sec t
,
t
(0,
π 2
)
,
则
x2 a2 a2 sec2 t a2 a tan t
x5 dx
1 x2
t2 1 2
t tdt
t 4 2t 2 1 dt
1 t5 2 t3 t C 1 (8 4x2 3x4 ) 1 x2 C.
53
15
例6 求
1 dx. 1 ex
解 令 t 1 e x e x t 2 1,
x lnt2 1,
dx
t
2t 2
是单调可导函数 , 且
具有原函数 , 则有换元公式
其中 t 1( x) 是 x (t)的反函数 .
证: 设 f [ (t)] (t)的原函数为 (t) , 令 F ( x) [ 1( x) ] (t) f [ (t)] (t)
则
换元法第二类换元法
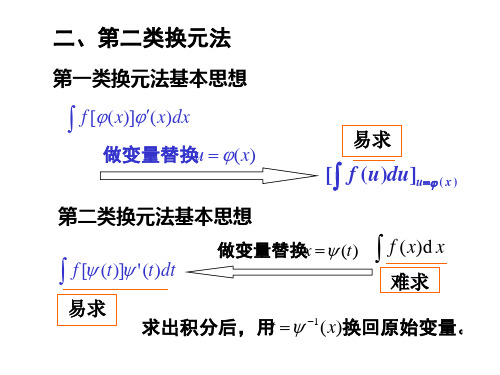
1 a
arctan
x a
C;
(21)
x2
1
a
2
dx
1 2a
ln
xa xa
C;
(22)
1 dx arcsin x C;
a2 x2
a
(23)
1 dx ln x x2 a2 C.
x2 a2
(24)
1 dx ln x x2 a2 C.
x2 a2
说明: 当遇到
时, 先将
2
2
例7. 求
解:
I
1 2
d (2x) 1 ln 2x (2x)2 32 2
4x2 9 C
(P203 公式 (23) )
例8. 求
解: 原式
dx
ex d x
ex 1 e2x
1 e2x
d ex arcsin ex C 1 e2x (P203 公式 (22) )
例9. 求 解: 原式 =
ln
a2 x x2 a2
C1
(C C1 2ln a)
2 倒代换
当分母的阶较高时, 可采用倒代换 x 1.
1
t
例4
求
x(
x7
dx 2)
解
令
x
1 t
dx
1 t2
dt ,
x(
1 x7
dx 2)
1
t 7
2
1 t2
dt
1
t
6
2t
7
dt
t
1 ln | 1 2t 7 | C 1 ln | 2 x7 | 1 ln | x | C.
(2) a2 x2 (3) x2 a2
可令x a tant; 可令x a sec t.
定积分换元积分法的不同换元方法

一、定积分的换元积分法概述定积分的换元积分法是计算定积分的一种重要方法,其主要思想是通过变量替换的方式将原积分转化为一个更容易求解的形式。
这种方法在解决复杂的定积分问题时具有较大的实用价值,因此对于不同的换元方法的掌握和熟练应用显得尤为重要。
二、常见的换元方法在定积分的换元积分法中,常见的换元方法包括但不限于以下几种:1. 第一类换元法:直接代入法直接代入法是指直接将被积函数中的某一个部分用一个变量表示并进行代入的方法。
通常适用于被积函数较简单的情况,能够将原积分转化为一个更容易处理的形式。
2. 第二类换元法:三角代换法三角代换法是指通过选取合适的三角函数来进行变量替换,将原积分转化为三角函数的积分形式。
这种方法通常适用于出现平方根和平方项时的情形,通过选择合适的三角函数可以使原积分变得更加简单。
3. 第三类换元法:指数代换法指数代换法是指通过选取适当的指数函数进行变量替换,将原积分转化为指数函数的积分形式。
这种方法通常适用于出现指数函数和对数函数时的情形,能够将原积分化为更容易处理的形式。
4. 第四类换元法:倒代换法倒代换法是指通过选取合适的变量倒数进行变量替换,将原积分从一个区间转化为另一个区间或者将原积分中的除法项转化为乘法项。
这种方法通常适用于变量之间的换元关系为倒数关系的情形,能够简化原积分的形式。
三、不同换元方法的选用原则在实际应用中,选择合适的换元方法是十分重要的。
一般而言,可以根据以下原则进行选择:1. 根据被积函数的形式选择当被积函数具有特定的形式时,可以根据不同的形式选择对应的换元方法。
如当被积函数中出现三角函数时,可以考虑使用三角代换法;当被积函数中出现指数函数时,可以考虑使用指数代换法。
2. 根据逆变换的便捷性选择在选择换元方法时,通常也要考虑逆变换的便捷性。
换元后新的积分形式是否容易转化回原来的变量,这将影响到最终的计算复杂程度。
3. 根据积分区间的选择当积分区间发生变化时,可以考虑使用倒代换法将原积分转化为更便于处理的形式,从而简化计算过程。
第二类换元法

不定积分 不定积分的第二类换元法
定理 设
是单调可导函数, 且
具有原函数, 则有换元公式
其中 t 1( x)是 x (t)的反函数.
证 设 f [ (t)] (t)的原函数为(t), 令F ( x) [ 1( x)]
则
F ( x)
d dt d t dx
f [ (t)] (t)
1((tt))
a
0
f
(t)d t
a
0
f (x)dx
a
0 [ f ( x) f (x)]dx
令 x t
当 f ( x) f ( x)时
当 f ( x) f ( x)时
暨南大学珠海学院苏保河主讲
例4 填空
2
sin 5x cos 7 x d x
2
0.
例5 填空
d dx
x
0
sin100
(
x
t)
d
t
_s_in__10_0_x__
2. 常用基本积分公式的补充 (P203)
暨南大学珠海学院苏保河主讲
例6
求
xd x d x. 3x2 4
解
原式
1 6
d(3 x 2 3x2
4) 4
1 3
3x2 4 C.
例7 求
解
I
1 2
d (2x) 1 ln 2x (2x)2 32 2
4x2 9 C.
暨南大学珠海学院苏保河主讲
x
a
时,
t
2
.
y
∴
原式 = a2
2 cos2 t d t
0
y a2 x2
a2 2
2 0
(1
第二类换元积分法分部积分法

ln 2 x2 x C
2
2
2
辅助三角形ຫໍສະໝຸດ ln 2 x2 x C1 C1 C ln 2
公式 dx ln x a2 x2 C
a2 x2
例3 求不定积分
dx 4x2 3
解 令 x 3 sec u, 则 dx 3 secu tan udu
2
2
原式 1 secudu 2 1 ln secu tan u C 2
原式
u
u 2
1
2udu
u2 11
2 u2 1 du
直接令根式为u, 化根式为有理式
2
(1
1
u2
)du 1
2u
arctan
u
C
2( x 1 arctan x 1) C
dx
例2 求不定积分 3 x 1
直接令根式为u, 化根式为有理式
解 令 u 3 x , 则 x u3, dx 3u2du
例2 求不定积分 xaxdx
udv uv vdu
解 令 u x, dv axdx
则 du dx,
a
a
dx arcsin x C(a 0)
a2 x2
a
dx ln | x x2 a2 | C x2 a2
dx ln | x x2 a2 | C x2 a2
◆公式的直接应用
例1
dx 1
d( 3x)
1 arcsin 3x C
5 3x2 3 ( 5)2 ( 3x)2 3
原式 xsin x sin xdx
xsin x cos x C
u 与 dv 的选择原则
v 1、 可求;
2、 vdu 可求,
或较易求
若令 u cos x, dv xdx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x 1 2
目录
C
下页 返回 结束
机动
上页
2. 求不定积分
2sin x cos x 1 sin x dx 2 2 sin x
2
解: 利用 凑微分法, 得 原式 =
1 sin 2 x 2 2 sin x
d(1 sin x )
2
令 t 1 sin2 x
2t 2 1 d t 2 (1 )d t 2 2 1 t 1 t
2 2 ,
), 则
x 2 a 2 a 2 tan2 t a 2 a sec t
dx a sec2 t d t
∴ 原式
a sec2 t
a sec t
d t sec t d t
ln sec t tan t C1
x2 a2 x ) ln( a a
机动 目录 上页 下页 返回 结束
例17.求
解:令 x a sin t , t (
a 2 x 2 dx (a 0)
,
a x dx a cos t d t t 2 2 ∴ 原式 a cos t a cos t d t a cos t d t 2 2 a x t sin 2t 2 a C 2 4 x a2 x2 sin 2t 2sin t cos t 2 a a x 1 a2 2 2 arcsin x a x C a 2 2
2)
2x 3 1 2 x x2
2 3 x 1 C 3 (2 2 x ) 5 dx dx 2
1 2x x
d(1 2 x x 2 ) 1 2 x x2
2
5
d( x 1) 2 ( x 1)2
2 1 2 x x 5arcsin
二、第二类换元法
第一类换元法解决的问题
f [ ( x )] ( x )dx f (u)du
难求 易求 若所求积分
u ( x)
f [ ( x )] ( x )dx
则得第二类换元积分法. 常用的第二类换元法有
f (u)du 难求,
易求,
三角代换,倒代换,根式代换
机动 目录 上页 下页 返回 结束
t
也可令 x a tan t ( t (
,0) (0, )), 2 2
a 2t 2 1
dt
1 d(a 2 t 2 1) 2 2a a 2t 2 1
1 2 a 2t 2 1 C a
当 x < 0 时, 类似可得同样结果.
机动 目录 上页 下页 返回 结束
t4 1 原式 2 2a
2 2 2 2 d( a t 1) ( a t 1)
3 2
1 2
(a 2 t 2 1) C 2 3a
当 x < 0 时, 类似可得同样结果.
机动 目录 上页 下页 返回 结束
例21.求
1 解:令 x ( x 0), 得 t
原式
2
1 2
2
机动
目录
上页
下页
返回
结束
dt
a tan t x2 a2 ln sec t tan t C1 t x x2 a2 ln C1 a a (C C1 ln a )
机动 目录 上页 下页 返回 结束
sec t d t
当 x a 时, 令
x u,
du u a
2 2
(1)
(2)
f ( x , n ax b )dx, 令 t n ax b
ax b ax b n f (x , n )dx , 令 t cx d cx d
2 2
第 四 节 讲
(3)
(4)
f (x ,
a x )dx ,令 x a sin t 或 x a cos t
例22
1 1 e
x
dx
解: 令 1 e x =t 1, 则 1 e x=t 2 ,
2t 从而 dx 2 dt , t 1 2 原式 2 dt t 1 t 1 ln | | C t 1
ln | 1 ex 1 1 e 1
x
| C
小结:
1. 第二类换元法常见类型:
2 2 2 2 2 2 2 a x a a sin t a cos t
), 则
机动
目录
上页
下页
返回
结束
例18.求 解: 当 x a 时 , 令 x a sec t , t ( 0,2 2 2 2 2 Nhomakorabea
2
), 则
∴ 原式
x a a sec t a a tan t d x a sec t tan t d t a sec t tan t
定理 2.设
是单调可导函数, 且 具有原函数, 则有换元公式
其中 t 1 ( x) 是 x (t )的反函数.
证: 设 f [ (t )] (t )的原函数为 ( t ), 令
F ( x ) [ ( x )]
1
(t ) f [ (t )] (t )
则
F ( x )
f ( x)dx F ( x ) C [
1 d dt f ( x) f [ ( t )] ( t ) (t ) dt dx
1
( x )] C
1 1 f[t ] [ (tC )] )d t t x) t(t ( x()
x2 a2
C1
t a
x
(C C1 ln a )
机动 目录 上页 下页 返回 结束
a2 x2 例20.求 dx 4 x 也可令 x a sin t (t ( , 0) (0, )), 2 2 1 解: 令 x , 则 t 1 2 a 2 1 1 t dt 2 2 2 原式 ( a t 1) t dt 2 1 t
f ( x , a 2 x 2 )dx , 令 x a tan t 或 x a sh t
(5)
f ( x , x 2 a 2 )dx , 令 x a sec t 或 x a ch t
机动 目录 上页 下页 返回 结束
(6) 分母中因子次数较高时, 可试用 倒代换
2. 基本积分公式 (二)
则 u a , 于是
2 2
ln u u a
C1
ln x x 2 a 2 C1
ln a2 x x2 a2 C1
(C C1 2ln a )
机动 目录 上页 下页 返回 结束
例19.求
解:令 x a tan t , t (
机动
目录
上页
下页
返回
结束
下页
例23.求 解:原式
1 d x 1) d ( x 2 ( x 1) ( 2 2 )2
1 2
arctan
x1 2
C
机动
目录
上页
下页
返回
结束
例24.求
解:原式 =
d(
2
1 x 2)
( 5 )2 ( x 1 )2
2
例25.求 解:原式
2( t arctan t ) C
2 1 sin 2 x arctan 1 sin 2 x C
机动 目录 上页 下页 返回 结束
3. 求不定积分
解: 令 x sin t , 1 x 2 1 sin2 t , d x cos t d t 原式 分子分母同除以 cos t
dx e 2 x (1 e 2 x )
e x d x 1 e 2 x
de x 1 e 2 x
arcsin e x C
机动 目录 上页 下页 返回 结束
备用题 1.求下列积分:
1)
x
2
1 dx 3 x3 1
1
1 x 1
3
d( x 3 1)
