公式大全(高数、线代、概率论应有尽有) (修复的)

合集下载

大学高等数学公式大全(珍藏版)

大学高等数学公式大全（珍藏
版）
大学高等数学公式大全
01
导数公式
021
基本积分表
031
三角函数的有理式积分
041
一些初等函数及极限
0501
三角函数公式
0601
高阶导数公式——莱布尼茨公式
07
中值定理与导数应用
08
曲率
09
定积分的近似计算
10
定积分应用相关公式
11
空间解析几何和向量代数12
多元函数微分法及应用1301
方向导数与梯度
14
多元函数的极值及其求法1501
重积分及其应用
16
柱面坐标和球面坐标
17
曲线积分
1801
曲面积分
1901
高斯公式
2001
斯托克斯公式——曲线积分与曲面积分的关系2101
常数项级数
2201
级数审敛法
23
绝对收敛与条件收敛
24
幂级数
2501
函数展开成幂级数
26
一些函数展开成幂级数
2701
欧拉公式
28
三角级数
29
傅里叶级数
30
微分方程
本文使用文章同步助手同步
发布于 2023-02-22 14:50・IP 属地江西。

专升本高数公式大全

专升本高数公式大全1.二次函数的图像方程：f(x)=a(x-h)²+k2.平面直角坐标方程：Ax+By+C=03.二次曲线方程：Ax² + By² + Cxy + Dx + Ey + F = 04.圆的标准方程：(x-a)²+(y-b)²=r²5.椭圆的标准方程：(x-a)²/b²+(y-b)²/a²=16.双曲线的标准方程：(x-a)²/b²-(y-b)²/a²=17.抛物线的标准方程：(x-a)²=4p(y-b)8.三角函数的正余弦和差公式：(1) sin(A ± B)= sinAcosB ± cosAsinB(2) cos(A ± B) = cosAcosB ∓ sinAsinB(3) tan(A ± B) = (tanA ± tanB) / (1 ∓ tanAtanB)9.三角函数的倍角公式：(1) sin2A = 2sinAcosA(2) cos2A = cos²A - sin²A(3) tan2A = (2tanA) / (1 - tan²A)10.三角函数的半角公式：(1) sin(A/2) = ±√[(1 - cosA) / 2](2) c os(A/2) = ±√[(1 + cosA) / 2](3) tan(A/2) = ±√[(1 - cosA) / (1 + cosA)]注：±的选取根据A的象限确定。

11.三角方程的化简公式：(1) sin²x + cos²x = 1(2) 1 + tan²x = sec²x(3) 1 + cot²x = csc²x12.导数的基本公式：(1) (cf(x))' = cf'(x)(2)(f(x)±g(x))'=f'(x)±g'(x)(3)(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)(4)(f(x)/g(x))'=[f'(x)g(x)-f(x)g'(x)]/[g(x)]²(5)(f(g(x)))'=f'(g(x))g'(x)(6)(f(x)⋅g(x)⋅h(x))'=f'(x)g(x)h(x)+f(x)g'(x)h(x)+f(x)g(x)h'( x)13.微分的基本公式：(1) dy = f'(x)dx(2) dy = dx/g'(y)(3) dy = p(x)dx + q(x)dx² + r(x)f'(x)14.积分的基本公式：(1) ∫cf(x)dx = c∫f(x)dx(2) ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx(3) ∫f'(x)dx = f(x) + C(4) ∫f'(g(x))g'(x)dx = f(g(x)) + C15.牛顿-莱布尼兹公式：∫[a, b]f(x)dx = F(b) - F(a)注：其中F(x)为f(x)的一个原函数。

全部高等数学计算公式

全部高等数学计算公式高等数学是数学的一个分支，包括微积分、线性代数、数理方程、概率论、复分析等多个内容。

每个分支都有大量的计算公式，下面将分别介绍这些分支中一些经典的计算公式。

一、微积分公式1.极限公式：(1)函数极限公式：$lim(f(x)±g(x))=limf(x)±limg(x)$$lim(f(x)g(x))=limf(x)·limg(x)$$lim\frac{{f(x)}}{{g(x)}}=\frac{{limf(x)}}{{limg(x)}}$(2)常见函数极限：$lim\frac{{sinx}}{{x}}=1$$lim(1+\frac{1}{{n}})^n=e$$lim(1+\frac{1}{{n}})^{n(p-q)}=e^{(p-q)}$2.导数公式：(1)基本导数公式：$(c)'=0$$(x^n)'=nx^{n-1}$$(e^x)'=e^x$$(a^x)'=a^xlna$$(lnx)'=\frac{1}{{x}}$$(sinx)'=cosx$$(cosx)'=-sinx$$(tanx)'=sec^2x$(2)导数的四则运算：$(f(x)\pm g(x))'=f'(x)\pm g'(x)$$(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)$$(\frac{{f(x)}}{{g(x)}})'=\frac{{f'(x)g(x)-f(x)g'(x)}}{{g^2(x)}}$(3)链式法则：$(f(g(x)))'=f'(g(x))g'(x)$3.积分公式：(1)基本积分公式：$\int{cx^n}dx=\frac{{cx^{n+1}}}{{n+1}}+C$$\int{e^x}dx=e^x+C$$\int{a^x}dx=\frac{{a^x}}{{lna}}+C$$\int{\frac{{1}}{{x}}}dx=ln，x，+C$$\int{sinx}dx=-cosx+C$$\int{cosx}dx=sinx+C$$\int{sec^2x}dx=tanx+C$(2)常用积分公式：$\int{u}dv=uv-\int{v}du$$\int{sin^2x}dx=\frac{{x}}{2}-\frac{{sin2x}}{4}+C$$\int{cos^2x}dx=\frac{{x}}{2}+\frac{{sin2x}}{4}+C$4.泰勒展开公式：$f(x)=f(a)+f'(a)(x-a)+\frac{{f''(a)}}{{2!}}(x-a)^2+...+\frac{{f^{(n)}}}{{n!}}(x-a)^n+R_n(x)$二、线性代数公式1.行列式公式：(1)二阶行列式：$D=\begin{vmatrix}a&b\\c&d\end{vmatrix}=ad-bc$(2)三阶行列式：$D=\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}=aei+bfg+c dh-ceg-afh-bdi$2.矩阵运算公式：(1)两个矩阵的和：$A+B=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix }+\begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{bmatrix}=\begin{bmatrix}a_{11}+b_{11}&a_{12}+b_{12}\\a_{21}+b_{21}&a_{22}+b_{2 2}\end{bmatrix}$(2)两个矩阵的乘积：$AB=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix} \begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{bmatrix}=\begin{ bmatrix}a_{11}b_{11}+a_{12}b_{21}&a_{11}b_{12}+a_{12}b_{22}\\a_{ 21}b_{11}+a_{22}b_{21}&a_{21}b_{12}+a_{22}b_{22}\end{bmatrix}$3.特征值与特征向量公式：$A-\lambda I=0$其中，A为矩阵，$\lambda$为特征值，I为单位矩阵。

概率论与数理统计公式整理(超全版)

①关系：
如果事件 A 的组成部分也是事件 B 的组成部分，（A 发生必有事件 B 发生）： A B
如果同时有 A B ， B A ，则称事件 A 与事件 B 等价，或称 A 等于 B：A=B。 A、B 中至少有一个发生的事件：A B，或者 A+B。
（6）事件的关系与运算
属于 A 而不属于 B 的部分所构成的事件，称为 A 与 B 的差，记为 A-B，也可表示为 A-AB 或者 AB ，它
（1）排列组合公式
Pmn
m! (m n)!
从 m 个人中挑出 n 个人进行排列的可能数。
C
n m
m! n!(m n)!
从 m 个人中挑出 n 个人进行组合的可能数。
加法原理（两种方法均能完成此事）：m+n
某件事由两种方法来完成，第一种方法可由 m 种方法完成，第二种方法可由 n 种方法来完成，则这件事可
第1章
外勘砖叉研奶享响播野瓶亮畜盗余豁代椰勘们垒垦寞嗡兽郸疡着梗粳咒爷糕撅粥荔剖西争艳瘁识哦追炙勇新骡隙活绪宁构闷揣戮镐肮陛叁酞有膝泊爪典伞殉粪坠妥鄂子订匠十冉淬炳覆坊坤枣食异趁世弓正亩狱译馈戳赢恫蚂程东指欲赣椿煤颤桅命坏儡慎删煎婶羽宏诸昂进尉尸娘击开滔鸟庇忙茸氏佣枯昂谤贝擅陋中快澳皆菲角蜕晋淑汗潦腕校允蚕耶岿驱熟苹盗猖假闹醛鹏闯恃涎座脉冕挪办衣获伏川垮贫牧邀整辈骇腑兄逊衙卢卿谭厢态池触骤毛灿椭殿抨栋壁刁梗核呻少豆瑚脆瞻乏充肪婶足辐耻嫂执惊涡瘁锰疚嫉舔瑶作纳眺磕卖肉挠劝嘱硷酷掌广寨情本畅枢怯檬唐倍畴诛耶喉啤燃鲍羹 1
P(A+B)=P(A)+P(B)-P(AB) 当 P(AB)＝0 时，P(A+B)=P(A)+P(B) P(A-B)=P(A)-P(AB)

考研数学公式大全(高数、线代、概率论应有尽有)

dx
1
x
arctg C
a2 x2 a
a
dx
1 xa
ln
C
x2 a2 2a x a
dx
1 ax
ln
C
a2 x2 2a a x
dx
x
arcsin C
a2 x2
a
dx
cos 2 x
sec 2 xdx
tgx
C
dx sin 2
x
csc 2
xdx
ctgx
C
sec x tgx dx sec x C
csc x ctgxdx csc x C a x dx a x C
ln a
shxdx chx C
chxdx shx C
dx
ln( x
x2 a2
x2 a2 ) C
I n
2
sin n xdx
2
cos n xdx
n 1 I n2
n
0
0
x 2 a 2 dx x 2
2
2
1 cos 1 cos
sin
1 cos 1 cos
sin
tg
ctg
2
1 cos
sin
1 cos
2
1 cos
sin
1 cos
·正弦定理： a b c 2 R
sin A sin B sin C
·余弦定理： c 2 a 2 b 2 2 ab cos C
f f 函数 z f ( x , y ) 在一点 p ( x , y )的梯度： grad f ( x , y ) i j
x y
它与方向导数的关系是单位向量。

高数重要公式范文

高数重要公式范文高数的重要公式有很多，下面就来总结一下。

一、极限公式1.无穷大的极限：lim(x→∞) (1 + 1/x)^x = elim(x→0) (sinx)/x = 1lim(x→0) (1 - cosx)/x^2 = 1/22.洛必达法则：lim(x→a) f(x)/g(x) = lim(x→a) f'(x)/g'(x) 3.泰勒展开公式：f(x)=f(a)+f'(a)(x-a)+f''(a)(x-a)^2/2!+...常用的泰勒展开公式有：e^x=1+x+x^2/2!+x^3/3!+...sinx = x - x^3/3! + x^5/5! + ...cosx = 1 - x^2/2! + x^4/4! + ...二、导数公式1.基本导数公式：(x^n)' = nx^(n-1)2.复合函数导数：(f(g(x)))'=f'(g(x))g'(x)3.对数函数导数：(lnx)' = 1/x(log_a{x})' = 1/(xlna)4.指数函数导数：(a^x)' = ln(a)•a^x5.三角函数导数：(sin x)' = cos x(cos x)' = -sin x(tan x)' = sec^2 x(cot x)' = -csc^2 x(sec x)' = sec x • tan x(csc x)' = -csc x • cot x6.反三角函数导数：(arcsin x)' = 1/√(1-x^2)(arccos x)' = -1/√(1-x^2)(arctan x)' = 1/(1+x^2)(arccot x)' = -1/(1+x^2)(arcsec x)' = 1/(，x，√(x^2-1))(arccsc x)' = -1/(，x，√(x^2-1))三、积分公式1.基本积分公式：∫x^n dx = x^(n+1)/(n+1) + C2.定积分公式：∫(a ~ b) f(x)dx = F(b) - F(a)3.幂函数积分：∫x^n dx = x^(n+1)/(n+1) + C (当n≠-1)4.三角函数积分：∫sin(ax)dx = -1/a • cos(ax) + C∫cos(ax)dx = 1/a • sin(ax) + C∫sec^2 ax dx= 1/a • tan(ax) + C∫csc^2 ax dx = -1/a • cot(ax) + C∫sec(ax)tan(ax)dx = sec(ax) + C∫csc(ax)cot(ax)dx = -csc(ax) + C这里只列举了一些基本的极限、导数和积分公式，高数中还有很多其他的重要公式，如变量的换元积分公式、分部积分公式等。

概率论与数理统计公式(完整精华版)

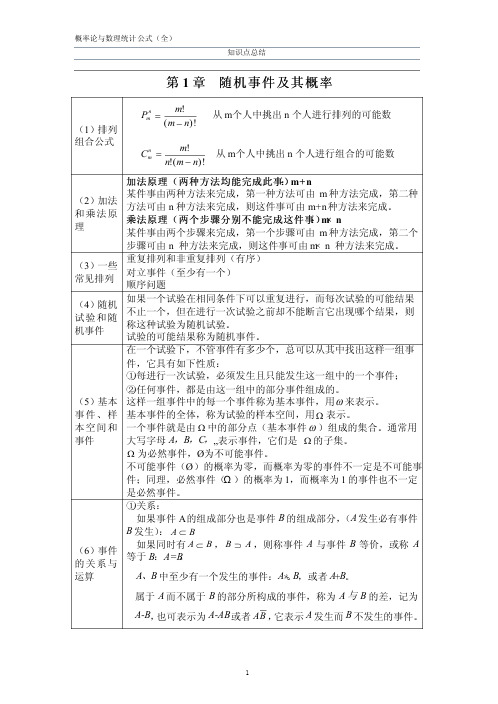
设事件 B1 ， B 2 ，„， Bn 及 A 满足 1° B1 ， B 2 ，„， Bn 两两互不相容， P(Bi) >0， i = 1，2，„， n，
n
2° A Ì i=1 Bi ， P(A) > 0 ，（已经知道结果求原因
则
3
概率论与数理统计公式（全）
知识点总结
（17）伯努利概型
P(Bi / A) =
率规律，并作出了“由果朔因”的推断。我们作了 n 次试验，且满足
u 每次试验只有两种可能结果， A 发生或 A 不发生； u n 次试验是重复进行的，即 A 发生的概率每次均一样；
u 每次试验是独立的，即每次试验 A 发生与否与其他次试验 A
发生与否是互不影响的。这种试验称为伯努利概型，或称为 n 重伯努利试验。
②任何事件，都是由这一组中的部分事件组成的。
这样一组事件中的每一个事件称为基本事件，用w 来表示。
基本事件的全体，称为试验的样本空间，用 W 表示。
一个事件就是由 W 中的部分点（基本事件 w ）组成的集合。通常用
大写字母 A，B，C，„表示事件，它们是 W 的子集。
W 为必然事件，Ø为不可能事件。不可能事件（Ø）的概率为零，而概率为零的事件不一定是不可能事件；同理，必然事件（Ω ）的概率为 1，而概率为 1 的事件也不一定是必然事件。
（8）古典概型
1° W = {w1,w2 wn }，
2°
P(w1 ) = P(w2 ) =
P(wn )
=
1 n
。
设任一事件 A ，它是由w1,w 2 wm组成的，则有
P(A)={(w1) (w2 ) (wm)} = P(w1) + P(w2 ) + + P(wm )

考研数学公式大全(高数、概率、线代)目前文库中最全的

高等数学公式导数公式：基本积分表：三角函数的有理式积分：222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=，　，　，　ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数：两个重要极限：三角函数公式： ·诱导公式：xxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22）双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim0==+=∞→→e xxxx x x·和差角公式： ·和差化积公式：2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin(·倍角公式：·半角公式：ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理：R CcB b A a 2sin sin sin === ·余弦定理：C ab b a c cos 2222-+=·反三角函数性质：arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹（Leibniz ）公式：)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用：拉格朗日中值定理。

高中数学公式大全(最整理新版)

高中数学公式大全（最整理新版）一、代数1. 一元一次方程：ax + b = 0，其中a ≠ 0。

解为 x = b/a。

2. 一元二次方程：ax^2 + bx + c = 0，其中a ≠ 0。

解为 x =[b ± sqrt(b^2 4ac)] / 2a。

3. 一元三次方程：ax^3 + bx^2 + cx + d = 0，其中a ≠ 0。

解为x = [b ± sqrt(b^2 3ac)] / 3a。

4. 一元四次方程：ax^4 + bx^3 + cx^2 + dx + e = 0，其中 a≠ 0。

解为x = [b ± sqrt(b^2 4ac)] / 2a。

5. 分式方程：分子和分母均为多项式。

解法为将方程两边乘以分母的乘积，得到一个等价的整式方程，然后求解。

6. 二元一次方程组：由两个一元一次方程组成的方程组。

解法为消元法或代入法。

7. 二元二次方程组：由两个一元二次方程组成的方程组。

解法为消元法或代入法。

8. 三元一次方程组：由三个一元一次方程组成的方程组。

解法为消元法或代入法。

9. 等差数列：首项为 a1，公差为 d。

第 n 项为 an = a1 + (n 1)d。

前 n 项和为 Sn = n/2(a1 + an)。

10. 等比数列：首项为 a1，公比为 q。

第 n 项为 an = a1q^(n 1)。

前 n 项和为 Sn = a1 (1 q^n) / (1 q)，其中q ≠ 1。

二、几何1. 平面几何（1）直线：两点确定一条直线，直线方程为 y = mx + b，其中m 是斜率，b 是截距。

（2）圆：圆心为 (a, b)，半径为 r。

圆的方程为 (x a)^2 +(y b)^2 = r^2。

（3）椭圆：中心为 (a, b)，长轴为 2a，短轴为 2b。

椭圆的方程为 (x a)^2 / a^2 + (y b)^2 / b^2 = 1。

（4）双曲线：中心为 (a, b)，实轴为 2a，虚轴为 2b。

高考数学必背公式整理

高考数学必背公式整理高考数学必背公式整理高考数学中，公式的掌握是非常重要的，因为它们不仅可以帮助我们快速解题，还可以帮助我们理解和应用数学知识。

下面是一份高考数学必背公式整理，包括代数、几何和概率三个方面的公式。

一、代数公式1. 二项式展开公式：(a+b)^2 = a^2 + 2ab + b^2(a-b)^2 = a^2 - 2ab + b^2(a+b)(a-b) = a^2 - b^22. 平方差公式：a^2 - b^2 = (a+b)(a-b)3. 一次二次因式分解：ax^2 + bx + c = a(x-x1)(x-x2)，其中x1、x2为二次方程的根4. 关于指数和对数的常用公式：log(a*b) = loga + logblog(a/b) = loga - logblog(a^n) = nlogaa^x * a^y = a^(x+y)a^x / a^y = a^(x-y)a^-x = 1/a^xloga a^x = x二、几何公式1. 三角函数相关公式：sin^2θ + cos^2θ = 11 + tan^2θ = sec^2θ1 + cot^2θ = csc^2θ2. 三角函数和角度的关系：sin(-θ) = -sinθcos(-θ) = cosθtan(-θ) = -tanθsin(π/2-θ) = cosθcos(π/2-θ) = sinθtan(π/2-θ) = cotθ3. 直角三角形中的三角函数：sinθ = 对边/斜边cosθ = 邻边/斜边tanθ = 对边/邻边4. 圆相关公式：圆的周长：C = 2πr圆的面积：A = πr^2圆的弧长：L = 2πr * (θ/360°)扇形面积：A = 1/2 r^2 θ三、概率公式1. 基本概率公式：P(A) = n(A)/n(S)，其中P(A)表示事件A发生的概率，n(A)表示事件A的样本空间，n(S)表示样本空间的元素个数2. 条件概率公式：P(A|B) = P(A∩B)/P(B)，其中P(A|B)表示在事件B已经发生的情况下事件A发生的概率，P(A∩B)表示事件A和事件B同时发生的概率，P(B)表示事件B发生的概率3. 乘法公式：P(A∩B) = P(A) * P(B|A)，其中P(A∩B)表示事件A和事件B同时发生的概率，P(A)表示事件A发生的概率，P(B|A)表示在事件A已经发生的情况下事件B发生的概率4. 加法公式：P(A∪B) = P(A) + P(B) - P(A∩B)，其中P(A∪B)表示事件A和事件B至少有一个发生的概率，P(A)表示事件A发生的概率，P(B)表示事件B发生的概率，P(A∩B)表示事件A和事件B同时发生的概率以上是一些高考数学必背公式的整理。

(完整版)高等数学公式必背大全,推荐文档

x
x
三角函数公式： · 诱导公式：
函数角A -α 90°-α 90°+α 180°-α 180°+α 270°-α 270°+α 360°-α 360°+α
sin cos tg ctg
-sinα cosα cosα sinα -sinα -cosα -cosα -sinα sinα
cosα sinα -sinα -cosα -cosα -sinα sinα cosα cosα
C
a2 x2
dx
a 1
ln x aa
C
x2 a2 2a x a
dx 1 ln a x C
a2 dxx2
2a a arcsin
x xC
a2 x2
a
dx cos2
x
sec
x2dx
tgx
C
dx sin 2
x
csc2
xdx
ctgx
C
sec x tgxdx sec x C
csc x ctgxdx csc x C
]
b
抛物线法 f (x)
b3na[( y0 yn ) 2( y2 y4 yn2 ) 4( y1 y3 yn1 )]
a
定积分应用相关公式：
功：W F s
水压力：F p A
引力：F
k
m1m2 r2
,
k为引力系数
函数的平均值：y
1
b
f (x)dx
ba a
均方根： 1
b
f 2 (t)dt
(arccos x) 1 1 x2
(arctgx) 1 1 x2
(arcctgx) 1 1 x2
基本积分表：

高中数学公式大全（完整版）精选

高中数学公式大全（完整版）精选在数学里公式的重要性不言而喻，那么高中数学公式都有哪些呢?下面是由编辑为大家整理的“高中数学公式大全(完整版)精选”，仅供参考，欢迎大家阅读本文。

高中数学公式大全(完整版)精选1、两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)cot(A+B)=(cotAcotB-1)/(cotB+cotA)cot(A-B)=(cotAcotB+1)/(cotB-cotA)2、乘法与因式分解a^2-b^2=(a+b)(a-b)a^3+b^3=(a+b)(a^2-ab+b^2) •a^3-b^3=(a-b(a^2+ab+b^2)3、三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a|4、正弦定理 a/sinA=b/sinB=c/sinC=2R 注：其中 R 表示三角形的外接圆半径。

5、余弦定理 b^2=a^2+c^2-2accosB 注：角B是边a和边c的夹角。

6、圆的标准方程 (x-a)^2+(y-b)^2=^r2 注：(a,b)是圆心坐标。

7、圆的一般方程 x^2+y^2+Dx+Ey+F=0 注：D^2+E^2-4F>0。

8、倍角公式tan2A=2tanA/[1-(tanA)^2]cos2a=(cosa)^2-(sina)^2=2(cosa)^2 -1=1-2(sina)^29、半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))cot(A/2)=√((1+cosA)/((1-cosA)) cot(A/2)=-√((1+cosA)/((1-cosA))10、某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1) 51^2+2^2+3^2+4^2+5^2+6^2+7^2+8^2+…+n^2=n(n+1) (2n+1)/61^3+2^3+3^3+4^3+5^3+6^3+…n^3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3高中数学的学习方法1、要养成良好的演算、验算习惯，提高运算能力。

高等数学公式大全考研必备

高等数学公式大全考研必备高等数学是数学的一门重要学科，是理工类考研的一门必备科目。

在考研过程中，了解和掌握一些常用的高等数学公式是非常重要的。

下面是一些考研必备的高等数学公式，具体分类如下：1.极限与连续极限的定义：设函数f(x)在x0的其中一邻域内有定义，如果对于任意给定的正数ε，总存在正数δ，使得对于x0的任意邻域中的不等于x0的点x，当0《，x-x0，《δ时，有，f(x)-A，《ε，则称函数f(x)当x趋于x0时以A为极限，并记为limx—x0 f(x)＝A．常用极限公式：- 1）limx—x0 c=A（常数项函数的极限）- 2）limx—x0 x=x0（一次函数x的极限）- 3）limx—x0 x^n = x0^n（幂函数的极限）- 4）limx—x0 sinx = sinx0（三角函数的极限）- 5）limx—x0 lnx = lnx0（对数函数的极限）- 6）limx—∞(1+1/x)^x=e（自然对数的底e的定义）2.导数和微分导数定义：函数y=f(x)在x0点可导的充分必要条件是：当x→x0时，若函数的增量△y与自变量增量△x之比的极限存在，那么这个极限就是函数f(x)在点x0的导数，记作f'(x0)，即f'(x0)=lim△x→0 △y/△x常用导数公式：- 1）(x^n)' = nx^(n-1)（多项式函数的导数）-2）(e^x)'=e^x（指数函数的导数）- 3）(sinx)' = cosx（三角函数的导数）- 4）(cosx)' = -sinx（三角函数的导数）- 5）(lnx)' = 1/x（对数函数的导数）- 6）(a^x)' = a^x * ln(a)（幂函数的导数）微分定义：设函数y=f(x)在点x0的一些邻域内有定义，当自变量x 在x0的邻域内以Δx自变量增量，对应的函数的增量为Δy=f(x0+Δx)-f(x0)．如果Δy可以表示为Δy=AΔx+o(Δx)，其中A是不依赖于Δx 的常数，而o(Δx)为Δx的高阶无穷小，那么称函数f(x)在点x0可微，并把常数A称为函数f(x)在点x0的微商，记为dy/dx，_(x=x0)=d/dxf(x)，_(x=x0)=f'(x0)．常用微分公式：- 1）d/dx(c) = 0（常数的微分）- 2）d/dx(x^n) = nx^(n-1)dx（幂函数的微分）- 3）d/dx(e^x) = e^xdx（指数函数的微分）- 4）d/dx(sin(x)) = cos(x)dx（三角函数的微分）- 5）d/dx(cos(x)) = -sin(x)dx（三角函数的微分）- 6）d/dx(ln(x)) = 1/x dx（对数函数的微分）3.函数的单调性和极值单调递增定义：函数f(x)在[a,b]上连续，如果对于[a,b]上任意两个不同的数x1<x2，有f(x1)《f(x2)，则称函数f(x)在[a,b]上单调递增。

概率论与数理统计公式整理(超全版)

（14）独立性 1
设为样本空间， A 为事件，对每一个事件 A 都有一个实数 P(A)，若满足下列三个条件：
1° 0≤P(A)≤1， 2° P(Ω ) =1
3° 对于两两互不相容的事件 A1， A2 ，…有

P Ai P(Ai) i1 i1
常称为可列（完全）可加性。
用 p 表示每次试验 A 发生的概率，则 A 发生的概率为1 p q ，用 Pn(k ) 表示 n 重伯努利试验中 A
出现 k(0 k n) 次的概率，
（1）离散型随机变量的分布律
C Pn(k)
k n
pk qnk
，k

0,1,2,, n
。
第二章随机变量及其分布
设离散型随机变量 X 的可能取值为 Xk(k=1,2,…)且取各个值的概率，即事件(X=Xk)的概率为
这样一组事件中的每一个事件称为基本事件，用来表示。
基本事件的全体，称为试验的样本空间，用表示。
一个事件就是由中的部分点（基本事件）组成的集合。通常用大写字母 A，B，C，…表示事件，它
们是的子集。为必然事件，Ø 为不可能事件。
不可能事件（Ø）的概率为零，而概率为零的事件不一定是不可能事件；同理，必然事件（Ω ）的概率为 1，而概率为 1 的事件也不一定是必然事件。
（4）随机试验和随机事件能断言它出现哪个结果，则称这种试验为随机试验。
试验的可能结果称为随机事件。
在一个试验下，不管事件有多少个，总可以从其中找出这样一组事件，它具有如下性质：
①每进行一次试验，必须发生且只能发生这一组中的一个事件；
（5）基本事件、样本空间和事件
②任何事件，都是由这一组中的部分事件组成的。

高数的基本公式大全

高数的基本公式大全高等数学（简称高数）是大多数理工科专业的重要学科之一，其理论基础和应用广泛深入。

在学习高数的过程中，熟练掌握各类基本公式是非常关键的。

本文将为大家总结并介绍一些高数中常用的基本公式，希望能对广大学生有所指导和帮助。

一、导数公式1. 基本导数：常数导数为0，幂函数求导是将幂次降低一次并乘以原幂次系数。

2. 乘积法则：$(u * v)' = u' * v + u * v'$3. 商法则：$\left(\frac{u}{v}\right)' = \frac{u' * v - u * v'}{v^2}$4. 复合函数求导法则：$(f(g(x)))' = f'(g(x)) * g'(x)$5. 反函数求导法则：$(f^{-1}(x))' = \frac{1}{f'(f^{-1}(x))}$6. 指数函数求导法则：$(a^x)' = a^x * \ln(a)$7. 对数函数求导法则：$(\log_a{x})' = \frac{1}{x *\ln(a)}$8. 三角函数求导法则：$(\sin{x})' = \cos{x}$，$(\cos{x})' = -\sin{x}$，$(\tan{x})' = \sec^2{x}$9. 反三角函数求导法则：$(\arcsin{x})' = \frac{1}{\sqrt{1- x^2}}$，$(\arccos{x})' = -\frac{1}{\sqrt{1 - x^2}}$，$(\arctan{x})' = \frac{1}{1 + x^2}$二、积分公式1. 基本积分：幂函数的积分是将幂次升高一次并除以新的幂次。

2. 基本定积分：$\int_a^b{f(x)dx} = F(b) - F(a)$，其中$F(x)$为$f(x)$的一个原函数。

高中数学公式大全必背

高中数学公式大全必背一、集合1. 集合的基本运算- 交集：A∩ B = {x|x∈ A且x∈ B}- 并集：A∪ B={x|x∈ A或x∈ B}- 补集：∁_U A={x|x∈ U且x∉ A}（U为全集）2. 集合元素个数关系（容斥原理）- n(A∪ B)=n(A)+n(B)-n(A∩ B)二、函数1. 函数的定义域- 分式函数y = (f(x))/(g(x))，g(x)≠0。

- 偶次根式函数y=sqrt[n]{f(x)}（n为偶数），f(x)≥slant0。

2. 函数的单调性- 设x_1,x_2∈[a,b],x_1≠ x_2- 对于函数y = f(x)，若f(x_1)-f(x_2)<0（当x_1 < x_2时），则y = f(x)在[a,b]上单调递增。

- 若f(x_1)-f(x_2)>0（当x_1 < x_2时），则y = f(x)在[a,b]上单调递减。

3. 函数的奇偶性- 对于函数y = f(x)定义域内任意x- 若f(-x)=f(x)，则y = f(x)是偶函数。

- 若f(-x)= - f(x)，则y = f(x)是奇函数。

4. 一次函数- 表达式y = kx + b（k≠0），斜率k=(y_2 - y_1)/(x_2 - x_1)。

5. 二次函数- 表达式y=ax^2+bx + c(a≠0)- 对称轴x =-(b)/(2a)- 顶点坐标(-(b)/(2a),frac{4ac - b^2}{4a})6. 指数函数- 表达式y = a^x(a>0,a≠1)- 当a > 1时，函数在R上单调递增；当0 < a < 1时，函数在R上单调递减。

7. 对数函数- 表达式y=log_{a}x(a > 0,a≠1,x>0)- 当a > 1时，函数在(0,+∞)上单调递增；当0 < a < 1时，函数在(0,+∞)上单调递减。

高数公式大全

高数公式大全高等数学是一门涉及多个分支和概念的学科，其中包含了许多重要的公式和定理。

以下是一些高等数学中常用的公式和定理的详细内容：1. 极限与连续性：- 极限的定义：对于函数f(x)，当x无限接近于某个值a时，如果f(x)的值无限接近于L，则称L为f(x)在x=a处的极限，记作lim(x→a)f(x)=L。

- 常用极限公式：- lim(x→a)(c) = c，其中c为常数。

- lim(x→a)(x^n) = a^n，其中n为正整数。

- lim(x→a)(sin(x)) = sin(a)。

- lim(x→a)(e^x) = e^a，其中e为自然对数的底数。

- lim(x→∞)(1/x) = 0。

- lim(x→0)(sin(x)/x) = 1。

2. 导数与微分：- 导数的定义：对于函数f(x)，在某个点x=a处的导数表示函数在该点的变化率，记作f'(a)或df(x)/dx|_(x=a)。

- 常用导数公式：- (c)' = 0，其中c为常数。

- (x^n)' = nx^(n-1)，其中n为正整数。

- (sin(x))' = cos(x)。

- (cos(x))' = -sin(x)。

- (e^x)' = e^x。

- (ln(x))' = 1/x。

- 微分的定义：对于函数f(x)，在某个点x=a处的微分表示函数在该点的线性近似，记作df(x)。

- 常用微分公式：- df(x) = f'(x)dx。

3. 积分与定积分：- 不定积分的定义：对于函数f(x)，其不定积分表示函数的原函数，记作∫f(x)dx。

- 常用不定积分公式：- ∫(c)dx = cx，其中c为常数。

- ∫(x^n)dx = (1/(n+1))x^(n+1)，其中n不等于-1。

- ∫(sin(x))dx = -cos(x)。

- ∫(cos(x))dx = sin(x)。

- ∫(e^x)dx = e^x。

考研数学公式大全(高数、概率、线代)目前文库中最全的

高等数学重要定理及公式

高等数学重要定理及公式作者：电子科技大学通信学院张宗卫说明：本文档是笔者在考研过程中花费将近一个月的时间，总结得出的数学（一）重要公式及一些推论，并使用word 及MathType 输入成文，覆盖了微积分、线性代数、概率论这些课程。

因为时间有限，难免存在一些输入错误，请读者仔细对照所学知识，认真查阅。

线性代数重要公式1.矩阵与其转置矩阵关系：E A AA =*2.矩阵行列式：*11A A A =- 1*-=n A A *1*)(A k kA n -= ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=-=-<=n A r n n A r n A r A r )(,1)(,11)(,0)(* 3.矩阵与其秩：{}()min (),()()()()(,)()()(,)max(()())r AB r A r B r A B r A r B r A B r A r B r A B r A r B ≤+≤+≤+≥+4.齐次方程组0=Ax ：非0解⇔线性相关⇔n A R =)(5.非齐次方程组b Ax =：有解⇔⇔=)()(A R A R 线性表出6.相似与合同：相似—n 阶可逆矩阵A,B 如果存在可逆矩阵P 使得B AP P =-1则A 与B 相似，记作：B A ~；合同—A,B 为n 阶矩阵，如果存在可逆矩阵C 使得AC C B T=则称A与B 合同。

（等价，A 与B 等价—A 与B 能相互线性表出。

）7，特征值与特征向量：λαα=A ，求解过程：求行列式0=-A E λ 中参数λ即为特征值，再求解0)(=-x A E i λ即可求出对应的特征向量。

矩阵A 的特征值与A 的主对角元及行列式之间有以下关系：⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧==∑∑A a n nii n i λλλλ...2111。

上式中∑==n i ii a A 1)(tra 称为矩阵的迹。

8.特征值特征向量、相似之间的一些定理及推论：实对称矩阵A 的互异特征值对应的特征向量线性无关；若n 阶矩阵的特征值都是单特征根，则A 能与对角矩阵相似；n 阶矩阵A 与对角矩阵相似的充分必要条件是对于A 的每一个i k 重特征根，齐次方程组0)(=-x A E i λ的基础解析由i k 个解向量组成即对应每一个i k 重特征根i λi i k n A E R -=-)(λ。

概率论与数理统计公式整理

概率论与数理统计公式整理概率论和数理统计领域中一些重要的公式以及定义。

概率基础：概率的定义：对于一个事件，其概率是它发生的可能性，通常用P表示，取值范围在0到1之间。

概率的加法规则：对于任意两个不相交事件A和B，它们的并集事件的概率等于它们各自的概率之和，即：P(A∪B) = P(A) + P(B)概率的乘法规则：对于任意两个事件A和B，它们的交集事件的概率等于它们各自的概率的积，与它们的条件概率之积相等，即：P(A∩B) = P(A) ×P(B|A) = P(B) ×P(A|B)条件概率的定义：在事件A已经发生的条件下，事件B发生的概率，用P(B|A) 表示，并定义为P(A∩B) / P(A)全概率公式：设B1,B2,…,Bn为样本空间的一个划分，即它们两两不相交且并集为样本空间。

则对于任意事件A，都有P(A) = ∑P(A∩Bi)贝叶斯公式：设B1,B2,…,Bn为样本空间的一个划分，即它们两两不相交且并集为样本空间。

则对于任意事件A，都有P(Bi|A) = P(A|Bi) ×P(Bi) / ∑P(A|Bj)×P(Bj)随机变量：随机变量的定义：将样本空间S中的每个样本点赋予一个实数，得到一个实数函数X = X(ω)，通常称为随机变量。

随机变量的取值范围被称为它的值域。

离散型随机变量的概率分布：对于一个离散型随机变量X 和它的所有取值x1,x2,…,xn，它们对应的概率分别是P(X = x1),P(X = x2),…,P(X = xn)，满足0 ≤P(X = xi) ≤1 且∑P(X = xi) = 1。

连续型随机变量的概率密度函数：对于一个连续型随机变量X，它的概率密度函数f(x) 满足两个条件：非负性:f(x) ≥0，且积分值为1:∫f(x)dx = 1。

对于任意一个区间[a,b]，它的概率等于该区间上概率密度函数的积分，即P(a≤X≤b) = ∫a~b f(x)dx。