苏教版数学高二-《新学案》 选修1-1教学案 1.3.2含有一个量词的命题的否定
苏教版数学高二-《新学案》 选修1-1教学案 常见函数的导数

3.2.3常见函数的导数教学过程一、问题情境前面我们用割线逼近切线的方法引入了导数的概念,那么,如何求函数的导数呢?二、数学建构问题1回顾前面所学内容,能否归纳出求导数的一般步骤?解给定函数y=f(x),计算=,当Δx→0时,→A(x),则f'(x)=A(x).问题2根据求导数的一般步骤,求下列函数的导数.①f(x)=kx+b(k,b为常数).解因为===k,当Δx→0时,→k,所以f'(x)=k.特别地,当k=0时,有f'(x)=0;当k=1,b=0时,有f'(x)=1.②f(x)=x2.解因为===2x+Δx,当Δx→0时,→2x,所以f'(x)=2x.③f(x)=x3.解因为===3x2+3x(Δx)+(Δx)2,当Δx→0时,→3x2,所以f'(x)=3x2.④f(x)=.解因为===,当Δx→0时,→-,所以f'(x)=-.⑤f(x)=.解因为===,当Δx→0时,→,所以f'(x)= .问题3你能根据问题2中的①~⑤发现什么结论?几个常用函数的导数:(kx+b)'=k(k,b为常数);C'=0(C为常数);x'=1;(x2)'=2x;(x3)'=3x2;'=-;()'=.对于基本初等函数,有下面的求导公式(教师直接给出):(xα)'=αxα-1(α为常数);(a x)'=a x lna(a>0,且a≠1);(lo x)'=log a e=(a>0,且a≠1);(e x)'=e x;(ln x)'= ;(sinx)'=cosx;(cosx)'=-sinx.三、数学运用【例1】求曲线y=cosx在点处切线的方程.(见学生用书P52)利用基本初等函数的求导公式求出在该点处的切线斜率,再利用点斜式求出切线方程.解y'=-sinx,所以在点处切线的斜率k=-sin=-,即切线方程为x+2y-π-1=0.求一些常见函数的导数可直接利用公式.变式求曲线y=在点处的切线的方程.y'=-,故点处的切线斜率为-,则切线方程为y-=-(x-2),即x+4y-4=0.【例2】若直线y=4x+b是函数y=x2图象上的一条切线,求b及切点坐标.(见学生用书P52) 设出切点坐标,利用导数的几何意义解题.解设切点坐标为(x0,).由f'(x0)=2x0=4,得x0=2,所以切点坐标为(2,4),故b=-4.本题应抓住切点的双重性:点既在曲线上也在切线上.变式若直线y=3x+1是曲线y=ax3的切线,求a的值.解设切点坐标为(x 0,a).由f'(x0)=3a=3,得a=1.又因为点(x0,a)满足切线方程,所以a=3x 0+1,将a=1代入,解得x0=-,则a=4.【例3】在函数y=2x的图象上求一点,使过此点的切线平行于直线xln4-y+3=0.(见学生用书P52) 利用常见函数的求导公式及导数的几何意义求出切线的斜率,再利用两平行直线之间斜率相等建构等式.解设切点坐标为(x 0,),由f'(x0)=ln2=ln4,得x0=1,即该点坐标为(1,2).过一点有切线,但该点不一定是切点;但本题有其特殊性,切线只可能与曲线有一个交点,所以对于本题,这个点即为切点.变式在抛物线y=x2上求一点P,使点P到直线x-y-1=0的距离最短,并求出这个最短距离.解设切点P的坐标为(x 0,).由f'(x0)=2x0=1,得x0=,则曲线在点P处切线方程为4x-4y-1=0,所以它与已知直线的距离d==,所以点P的坐标为,d=.四、课堂练习1. 已知四个命题:①曲线y=x3在原点处没有切线;②若函数f(x)=,则f'(x)=0;③速度是动点位移函数S(t)对时间t的导数;④函数y=x5的导数值恒非负.其中正确的命题是③④.(填序号)提示根据导数的概念及常见函数的导数公式解答.2. 设f(x)=sinx,则f'(x)=cosx,f'= .提示利用常见函数的导数公式求解.3. 若质点的运动方程是S=(S的单位为m,t的单位为s),则质点在t=3时的速度为-m/s.提示速度是动点位移函数S(t)对时间t的导数,所以v(t)=-4t-5,则质点在t=3时的瞬时速度为-m/s.五、课堂小结1. 熟记常见函数导数公式.2. 灵活应用导数解决相关问题.。
(新)高中数学1_3_2含有一个量词的命题的否定导学案无答案苏教版选修1-1

1.3.2含有一个量词的命题的否定(一) 问题引入1.思考1:对于下列命题,试判断其是存在性命题还是全称命题.(1)所有的人都喝水;(2)存在有理数x ,使022=-x ;(3)对所有的实数a ,都有0||≥a .2.思考2:我们学过命题的的非(否定),你能写出这三个命题的否定吗?3.思考3:这三个命题和它们的否定在形式上有什么变化?(二) 学生活动命题(1)的否定_______________________________________________________;命题(2)的否定_______________________________________________________;命题(3)的否定_______________________________________________________.从形式上发现:全称命题的否定都变成___________,存在性命题的否定都变成_________.(三) 知识建构1.一般地,对于含有一个量词的全称命题的否定,全称命题p :“)(,x p M x ∈∀”, 它的否定⌝p :_________________________.2.一般地,对于含有一个量词的存在性命题的否定,存在性命题p :“)(,x p M x ∈∃”, 它的否定⌝p :__________________________.(四)学习交流、问题探讨例1.写出下列命题的否定:(1) 所有人都晨练; 章节与课题 含有一个量词的命题的否定 课时安排 1课时使用人 使用日期或周次本课时学习目标或学习任务 1.通过生活和数学中的实例,理解对含有一个量词的命题的否定的意义; 2.能正确地对含有一个量词的命题的否定;3.进一步提高用全称量词与存在量词准确,简洁地叙述数学内容的能力. 本课时重点难点或学习建议对含有一个量词的命题进行否定,准确地应用全称量词与存在量词. 本课时教学资源的使用 导学案学 习 过 程(2) 2,10x R x x ∀∈++>;(3) 平行四边形的对边相等;(4)2,10x R x x ∃∈-+=.变式1:写出下列命题的否定,并判断真假:(1) 所有的菱形都是正方形;(2)21,04x R x x ∀∈-+≥;(3) 2,220x R x x ∃∈++≤;(4)至少有一个实数x ,使310x +=.例2.已知命题“⎥⎦⎤⎢⎣⎡∈∃2,0πx ,cos 23sin 21x x k +=+”为假命题,求实数k 的范围.(五)练习检测与提升1.写出下列命题的否定,并判断其真假:(1)211,132x Q x x ∀∈++是有理数;(2),sin()sin sin R αβαβαβ∃∈+=+,使;(3),,x y Z ∃∈使3x-4y=20;(4) {}110210x x ∀∈-+>,,,.2.若命题“2,(1)10x R x a x ∃∈+-+<使得”是假命题,则实数a 的取值范围是 .(六)课后作业1.写出下列命题的否定,并判断命题的否定的真假:①所有的有理数是实数;②有的三角形是直角三角形;③每个二次函数的图象都与y 轴相交;④2,20x R x x ∀∈->.2.已知命题p :2,230x R ax x ∀∈++>,如果命题p ⌝是真命题,求实数a 的取值范围.。
苏教版数学高二-《新学案》 选修1-1教学案 3.2.4函数的和、差、积、商的导数

3.2.4函数的和、差、积、商的导数教学过程一、问题情境1. 分别求下列函数的导数.(1) y=x2;(2) y=x;(3) y=x2+x.你能从以上计算结果中发现什么结论?解前两个函数的和(即第三个函数)的导数,等于这两个函数导数的和.2. 你能证明上述结论吗?解因为==2x+Δx+1,当Δx→0时,→2x+1,所以y'=2x+1.3. 两个函数的差的导数,等于这两个函数导数的差吗?从具体函数入手,利用导数的定义求出两个函数和的导数,在此基础上,作出猜想,给出两个函数和、差的求导法则,学生容易理解.两个函数的和的求导法则的推导,不要求学生掌握,可指导学生课外探究.二、数学建构问题1已知f'(x),g'(x),则解一般地,函数和的求导法则:'=f'(x)+g'(x).即两个函数的和的导数,等于这两个函数的导数的和.问题2可以怎么验证大家呈现的结论是否正确呢?问题4已知f'(x),g'(x),则',等于什么?函数的和(差)的求导法则两个函数的和(或差)的导数,等于这两个函数的导数的和(或差),即'=f'(x)±g'(x).函数的积的求导法则两个函数的积的导数,等于第一个函数的导数乘以第二个函数,加上第一个函数乘以第二个函数的导数,即'=f'(x)g(x)+f(x)g'(x).函数的商的求导法则两个函数的商的导数,等于分子的导数与分母的积,减去分母的导数与分子的积,再除以分母的平方,即=(g(x)≠0).对法则的理解:(1) 法则适用于两个可导函数的和、差、积、商;两个不可导函数的和、差、积、商不一定不可导.(2) '=Cf'(x)(C为常数).(3) 求导法则的证明不作要求.三、数学运用【例1】(教材第83页例2)求下列函数的导数:(1) f(x)=x2+sinx;(2) g(x)=x3-x2-6x+2. (见学生用书P53)先由学生写出解题过程,让其他学生点评.教师在学生的交流中,了解学生的思维过程,投影学生的解题过程,纠正出现的错误,同时强调书写格式的规范.解(1) f'(x)=(x2+sinx)'=(x2)'+(sinx)'=2x+cosx.(2) g'(x)==3x2-3x-6.根据函数的和(差)求导法则的一般步骤:先用求导法则转化为求基本函数的导数,再用导数公式进行运算.变式求y=2x3-3x2+5x-4的导数.解y'=(2x3-2x2+5x-4)'=6x2-6x+5.【例2】(教材第83页例3)求下列函数的导数:(1) h(x)=xsinx;(2) S(t)=. (见学生用书P54)解(1) h'(x)=(xsinx)'=x'sinx+x(sinx)'=sinx+xcosx.(2) S'(t)====.例2中的第(2)题还有其他解法:S'(t)==1-.例2第二种解法可由学生的探究活动产生,教师作适当的点拨.归纳根据函数的积商的求导法则求导的一般步骤,同时注意说明解法不唯一.要求学生正确运用公式.变式1用两种方法求y=(2x2+3)(3x-2)的导数.解法一y'=(2x2+3)'(3x-2)+(2x2+3)(3x-2)'=4x(3x-2)+(2x2+3)·3=18x2-8x+9.解法二y=6x3-4x2+9x-6,y'=18x2-8x+9.变式2求y=的导数.解y'===.变式3求y=xlnx的导数.解y'=x' ln x+x(ln x)'=ln x+1.变式4求y=在点x=3处的导数.解y'====,所以y'===-.【例3】已知函数f(x)的导数是f'(x),则函数2的导数为2f'(x).这个结论对吗?(见学生用书P54)2看作f(x)·f(x),再利用函数积的求导法则求解{'=f'(x)f(x)+f(x)f'(x)=2f(x)f'(x)≠2f'(x),所以上述结论错误.本题的实质是复合函数的求导,有兴趣的同学可以研究一下复合函数求导的规律.四、课堂练习1. 函数y=x2cosx的导数y'=2xcosx-x2sinx.2. 函数y=的导数y'=.3. 若曲线y=2ax2+1过点(,3),则此曲线在该点的切线方程是4x-y-1=0.4. 若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则a=1,b=1.五、课堂小结1. 函数的和、差、积、商的求导法则.2. 法则适用于两个可导函数的和、差、积、商;两个不可导函数和、差、积、商不一定不可导.3. 求导法则的证明不作要求.。
苏教版高中数学高二选修2-1课件 1.3.2含有一个量词的命题的否定

1234
2.对下列命题的否定说法错误的是________. ①p:能被2整除的数是偶数;綈p:存在一个能被2整除的 数不是偶数; ②p:有些矩形是正方形;綈p:所有的矩形都不是正方形; ③p:有的三角形为正三角形;綈p:所有的三角形不都是 正三角形; ④p:∃x∈R,x2+x+2≤0;綈p:∀x∈R,x2+x+2>0.
要点二 存在性命题的否定 例2 写出下列存在性命题的否定. (1)p:∃x>1,使x2-2x-3=0; 解 綈p:∀x>1,x2-2x-3≠0. (2)p:有的实数没有平方根; 解 綈p:所有的实数都有平方根. (3)p:我们班上有的学生不会用电脑. 解 綈p:我们班上所有的学生都会用电脑.
规律方法 存在性命题的否定是全称命题,写命题的否 定时要分别改变其中的量词和判断词.即p:∃x∈M,p(x) 成立⇒綈p:∀x∈M,綈p(x)成立.
挑战自我,点点落实 重点难点,个个击破 当堂训练,体验成功
[知识链接]
你能尝试写出下面含有一个量词的命题的否定吗? (1)所有矩形都是平行四边形; (2)每一个素数都是奇数; (3)∀x∈R,x2-2x+1≥0.
答:(1)存在一个矩形不是平行四边形; (2)存在一个素数不是奇数; (3)∃x0∈R,x20-2x0+1<0.
(2)数列{1,2,3,4,5}中的每一项都是偶数; 解 是全称命题, 其否定:数列{1,2,3,4,5}中至少有一项不是偶数. (3)∀a,b∈R,方程ax=b都有惟一解; 解 是全称命题, 其否定:∃a,b∈R,使方程ax=b的解不惟一或不存在.
(4)可以被5整除的整数,末位是0. 解 是全称命题, 其否定:存在被5整除的整数,末位不是0.
1.3.2 含有一个量词的命题的否定
苏教版数学高二-《新学案》 选修1-1教学案 极大值与极小值(2)

3.3.2极大值与极小值(2)教学过程一、问题情境引例已知f(x)=x3-3x2-9x+11.(1) 写出函数f(x)的单调区间;(2) 讨论函数f(x)的极值.解f'(x)=3(x+1)(x-3).令f'(x)=0,得x1=-1,x2=3.列表:x (-∞,-1) -1 (-1,3) 3 (3,+∞)f'(x) + 0 - 0 +f(x) ↗极大值f(-1) ↘极小值f(3)↗(1) 单调减区间为(-1,3),单调增区间为(-∞,-1),(3,+∞).(2) 极大值为f(-1)=16,极小值为f(3)=-16.二、数学建构问题1你能作出函数f(x)=x3-3x2-9x+11的草图吗?问题2你能从图上看出函数的哪些性质?问题3你能对引例进行变式,得到新的问题吗?三、数学运用【例1】已知f(x)=x3-3x2-9x+11,函数g(x)=f(x)+a,根据下列条件分别求出实数a的取值范围:(1) 有一个交点;(2) 恰有两个交点;(3) 有三个交点. (见学生用书P59)通过图象理解三次函数与x轴交点的情况.解f'(x)=3(x+1)(x-3).令f'(x)=0,得x1=-1,x2=3.列表:x (-∞,-1) -1 (-1,3) 3 (3,+∞)f'(x) + 0 —0 +高中数学f(x) ↗极大值f(-1) ↘极小值f(3)↗极大值为f(-1)=16,极小值为f(3)=-16.(1) 曲线y=g(x)与x轴仅有一个交点,即g(x)极小值>0或g(x)极大值<0,所以-16+a>0或16+a<0,即a>16或a<-16.(2) 曲线y=g(x)与x轴恰有两个交点,即g(x)极小值=0或g(x)极大值=0,所以-16+a=0或16+a=0,即a=±16.(3) 曲线y=g(x)与x轴有三个交点,即g(x)极小值<0且g(x)极大值>0,所以-16+a<0且16+a>0,即-16<a<16.有效利用图形语言,并注意解题的规范性.【例2】已知函数f(x)=x 3-3x2-9x+11,根据下列条件分别求实数t的取值范围.(1) f(x)在区间(t,t+2)上单调递减;(2) f(x)在区间(t,t+2)上单调递增. (见学生用书P60)先由学生口答,教师在学生中交流,了解学生的思考过程,投影学生的解题过程,纠正出现的错误.解(1) 由引例知所以-1≤t≤1.(2) 由引例知t≥3或t+2≤-1,即t≤-3或t≥3.若函数f(x)=x3-3x2-9x+11在区间(t,t+2)上不单调,你能否求出实数t的取值范围?【例3】已知x=1是函数f(x)=mx3-3(m+1)x2+nx+1的一个极值点,其中m,n∈R,m≠0.(1) 求m与n的关系表达式;(2) 求f(x)的单调区间.解(1) f'(x)=3mx2-6(m+1)x+n,由f'(1)=0得n=3m+6.(2) 由(1)得f'(x)=3mx2-6(m+1)x+3m+6=3m(x-1).当m>0时,单调增区间为(-∞,1)和,单调减区间为.当m<0时,单调增区间为,单调减区间为和(1,+∞).此题是逆向思维题,已知极值求参数的值,解题时充分利用f'(x)=0,同时注意单调性对极值的限制.用导数解决函数的单调性和极值问题,具有一般性,解题时强调解题的规范性.【例4】探究函数g(x)=-ax(x>0)的单调性和极值.解g'(x)=-a,x>0.当a≤0时,g'(x)>0,单调递增区间为(0,+∞),函数无极值.当a>0时,令g'(x)>0,即-a>0,解得0<x<;令g'(x)<0,即-a<0,解得x>.单调增区间为,高中数学单调减区间为,函数极大值为f=.四、课堂练习1. 设a∈R,若函数y=e x+ax(x∈R)有大于0的极值点,则实数a的取值范围为(-∞,-1).2. 若函数f(x)=-x3+ax2+1(a∈R)在(-2,3)内有两个不同的极值点,求实数a的取值范围.解f'(x)=-3x2+2ax.由题意知f'(x)在(-2,3)上有两个不同的实数解,解得a∈(-3,0)∪.五、课堂小结1. 用导数处理函数极值中的参数讨论问题,主要有两类运用:一是对导数等于0的根的讨论;二是单调区间的判断的问题.2. 注意领会分类讨论的思想、数形结合的思想、函数与方程的思想在解题中的灵活运用.高中数学。
苏教版数学高二-《新学案》 选修1-1教学案 1.3.1量词

1.3.1量词教学过程一、问题情境在日常生活和学习中,我们经常遇到这样的命题:(1)所有中国公民的合法权利都受到中华人民共和国宪法的保护;(2)对于任意实数x,都有x2≥0;(3)存在有理数x,使x2-2=0.二、数学建构问题1上述命题与以前学过的命题有何不同?问题2能说出上面3句话中的含义吗?解命题(1):只要是“中国公民”,其合法权利都受到中华人民共和国宪法的保护.命题(2):对每一个实数x,必有x2≥0,即没有使x2≥0不成立的实数x存在.命题(3):至少可以找到一个有理数x,使x2-2=0成立.1.全称量词“所有”“任意”“每一个”等表示全体的量词在逻辑中称为全称量词,通常用符号“∀x”表示“对任意x”.2.存在量词“有一个”“有些”“存在一个”等表示部分的量词在逻辑中称为存在量词,通常用符号“∃x”表示“存在x”.3.全称命题与存在性命题(1)含有全称量词的命题称为全称命题,含有存在量词的命题称为存在性命题.(2)全称命题与存在性命题的一般形式:全称命题:∀x∈M,p(x);存在性命题:∃x∈M,p(x).其中M为给定的集合,p(x)是一个关于x的命题.三、数学运用【例1】判断下列命题是全称命题还是存在性命题:(1)有一个实数a,a不能取对数;(2)所有不等式的解集A,都有A⊆R;(3)三角函数都是周期函数;(4)有的向量方向不定;(5)自然数的平方是正数. (见学生用书P9)引导学生说出每一个命题中的量词,再结合全称命题和存在性命题的定义得到答案.解(1)存在性命题;(2)全称命题;(3)全称命题;(4)存在性命题;(5)全称命题.(1) 判断一个语句是全称命题还是存在性命题,应先判断它是否为命题;(2) 判断命题是全称命题还是存在性命题,主要是看命题中是否含有全称量词或存在量词,要注意的是有些全称命题中并不含有全称量词(如“对顶角相等”),这时我们就要根据命题的意义去判断.【例2】(教材第14页例1)判断下列命题的真假:(1)∃x∈R,x2>x;(2)∀x∈R,x2>x;(3)∃x∈Q,x2-8=0;(4)∀x∈R,x2+2>0. (见学生用书P10)师生共同分析,找出判断全称命题和存在性命题真假的一般方法.解(1) 因为当x=2时,x2>x成立,所以“∃x∈R,x2>x”是真命题.(2)因为当x=0时,x2>x不成立,所以“∀x∈R,x2>x”是假命题.(3)因为使x2-8=0成立的数只有x=2与x=-2,但它们都不是有理数,所以“∃x∈Q,x2-8=0”是假命题.(4)因为对于任意实数x,都有x2+2>0成立,所以“∀x∈R,x2+2>0”是真命题.(1) 要判定一个存在性命题为真命题,只要在给定的集合中,找到一个元素x,使命题p(x)为真命题,否则命题为假命题.(2) 要判定一个全称命题为真命题,必须对给定的集合的每一个元素x,p(x)都为真命题;但要判定一个全称命题为假命题,只要在给定的集合内找出一个x0,p(x0)为假命题.【例3】用量词符号“∀”“∃”表达下列命题:(1)实数都能写成小数形式;(2)凸n边形的外角和等于2π;(3)任一个实数乘以-1都等于它的相反数;(4)存在实数x,使得x3>x2;(5)对任意角α,都有sin2α+cos2α=1.先找到命题中的全称量词或存在量词.解(1)∀x∈R,x能写成小数形式;(2)∀x∈{x|x是凸n边形},x的外角和等于2π;(3)∀x∈R,x·(-1)=-x;(4)∃x∈R,x3>x2;(5)∀α∈{角},sin2α+cos2α=1.正确认识存在量词和全称量词的符号表示.四、课堂练习1.判断下列命题是全称命题还是存在性命题:(1)所有能被2整除的整数都是偶数;(2)有的函数是偶函数;(3)圆周上任意一点到圆心的距离都等于圆的半径;(4)三角形有且仅有一个外接圆.解(1) 全称命题;(2)存在性命题;(3)全称命题;(4)全称命题.2.指出下列命题中的量词,并判断命题的真假.(1)任意一个正方形都是矩形;(2)所有的一元二次方程都有实数根;(3)至少存在一个锐角α,使得sinα=.解(1)任意;真命题.(2)所有;假命题.(3)存在;真命题.五、课堂小结1.全称命题和存在性命题的含义.2.判断全称命题和存在性命题真假的方法.。
2019-2020学年苏教版高中数学选修1-1学案:1.3.1量词
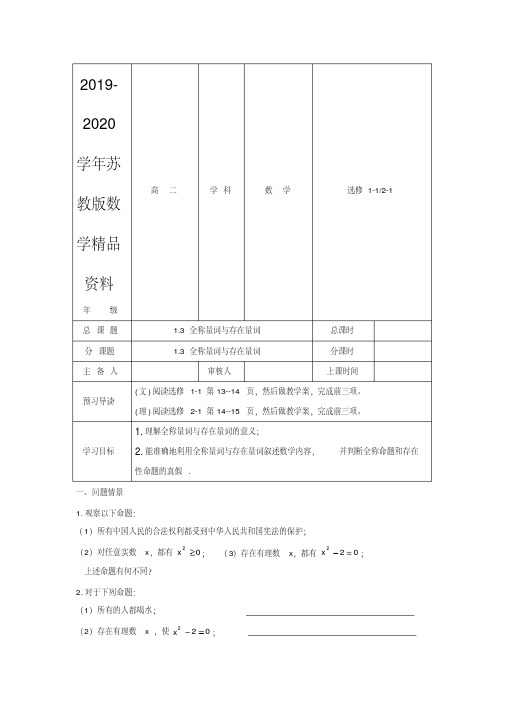
2019-2020学年苏教版数学精品资料年级高二学科数学选修1-1/2-1总课题 1.3全称量词与存在量词总课时分课题 1.3全称量词与存在量词分课时主备人审核人上课时间预习导读(文)阅读选修1-1第13--14页,然后做教学案,完成前三项。
(理)阅读选修2-1第14--15页,然后做教学案,完成前三项。
学习目标1.理解全称量词与存在量词的意义;2.能准确地利用全称量词与存在量词叙述数学内容,并判断全称命题和存在性命题的真假.一、问题情景1.观察以下命题:(1)所有中国人民的合法权利都受到中华人民共和国宪法的保护;(2)对任意实数x ,都有02x;(3)存在有理数x ,都有022x;上述命题有何不同?2.对于下列命题:(1)所有的人都喝水;(2)存在有理数x ,使022x;(3)对所有实数 a ,都有0||a 。
对上述命题进行否定,能发现什么规律?二、建构数学1.“所有”、“任意”、“每一个”等表示全体的量词在逻辑中称为全称量词,通常用符号表示“对任意x ”。
“有一个”、“有些”、“存在一个”等表示部分的量词在逻辑中称为存在量词,通常用符号表示“存在x ”。
2.含有全称量词的命题成为全称命题,含有存在量词的命题成为存在性命题。
它们的一般形式为:全称命题:存在性命题:其中,M 为给定的集合,)(x p 是一个关于x 的命题。
3.⑴要判定全称命题“x ∈M,p(x) ”是真命题,需要对集合M 中每个元素x, 证明p(x)成立;如果在集合M 中找到一个元素0x ,使得p(0x )不成立,那么这个全称命题就是假命题⑵要判定存在性命题“x ∈M, p(x)”是真命题,只需在集合M 中找到一个元素0x ,使p(0x )成立即可,如果在集合M 中,使p(x)成立的元素x 不存在,则存在性命题是假命题4.对含有全称量词的命题进行否定,全称量词变为存在量词;对含有存在量词的命题进行否定,存在量词变为全称量词。
一般地,我们有:“)(,x p M x ”的否定为“)(,x p M x”的否定为5.正面词语= > <是都是至多有一个至少有一个至多有n 个反面词语例1.判断下列命题的真假(1)x x R x 2,命题(2)x x R x 2,命题(3)08,2xQ x命题(4)2,2xR x命题例2.写出下列命题的否定⑴所有人都晨练;⑵01,2x xR x;⑶平行四边形的对边相等;⑶01,2x xR x例3.已知函数12)2(24)(22p p xp x x f 在区间]1,1[上至少存在一个实数c ,使0)(c f ,求实数p 的取值范围例4.已知命题“2,0x ,cos 23sin 21x x k ”为真命题,求实数k 的范围例5(理).⑴已知命题“01,2ax xR x”为真命题,则实数a 的取值范围是________ ⑵已知命题“01,2axaxR x”为真命题,则实数a 的取值范围是_______一、基础题1.命题“每一个等腰三角形的两个底角相等”,“过直线外一点存在惟一的一条直线与该直线平行”中,使用的全称量词是,存在量词是.2.下列全称命题或存在性命题中,真命题是:.(写出所有真命题的序号)(1)至少存在一个锐角,使得1sin2;(2)2,10x x R ;(3)1,2x xxR ;(4)2,230x x x R ;(5)至少有一个xR ,能使212x x ;(6)存在四个面都是直角三角形的四面体.3.指出下列命题是全称命题还是存在性命题,并判断真假:(1)所有的素数都是奇数;(2)有一个实数x ,使2230xx成立;(3)x R ,211x;(4)对每一个无理数x ,2x 也是无理数;(5)存在两个相交平面垂直同一条直线;(6)有些整数只有两个正因数.4.下列命题中真命题的个数是.(1)x R ,0x ;(2)至少有一个整数,它既不是合数,也不是素数;(3)末位是0的整数,可以被2整除;(4)角平分线上的点到这个角的两边的距离相等;(5)正四面体中两侧面的夹角相等.5.命题p :存在实数m ,使方程210xmx 有实数根,则“非p ”形式的命题是____________________________________________________________.6.已知:对5,x a xxR 恒成立,则a 的取值范围是.7.写出下列命题的否定:(1)有些质数是奇数;(2)若0m,则20x x m 有实数根;(3)可以被5整除的整数,末位是0;(4)x R ,sin 1x ;(5)2,1,0,1,2x,22x .二、提高题1.设函数f x 的定义域为R ,则下列三个命题中,真命题是.(1)若存在常数M ,使得对任意xR ,有f x M ,则M 是函数f x 的最大值;(2)若存在0x R ,使得对任意xR ,且0xx ,有0f xf x ,则0f x 是函数f x 的最大值;(3)若存在0x R ,使得对任意x R ,有0f xf x ,则0f x 是函数f x 的最大值.2.若函数2743kx ykxkx的定义域为R ,则k3. 已知命题“01,,02ax xx”为真命题,则实数a 的取值范围是4.“01,2ax x R x ”为假命题,则实数a 的取值范围是_______5.已知命题“01,,02ax x x”为真命题,则实数a 的取值范围是三、能力题1、已知:对xR ,方程2cos sin 30xx a有解,求a 的取值范围.2.若不等式)1(122xm x 对满足2m 的所有m 都成立,求x 的取值范围3.在平面直角坐标系xOy 中,已知圆221:314C x y 和圆222:454C x y .设P 为平面上的点,满足:存在过点P 的无穷多对互相垂直的直线1l 和2l ,它们分别与圆1C 和圆2C 相交,且直线1l 被圆1C 截得的弦长与直线2l 被圆2C 截得的弦长相等,试求所有满足条件的点P 的坐标.。
苏教版数学高一-苏教版高中数学选修1-1第一章1.3.2《含有一个量词的命题的否定》导学案

含有一个量词的命题的否定一、学习目标1.能正确地对含有一个量词的命题进行否定;2.能利用命题及其否定之间的真假关系解决相关问题。
二、自我构建1.全称命题的否定全称命题p:∀x∈M,p(x),它的否定¬p:____________,2.存在性命题的否定一般地,对于含有一个量词的存在性命题的否定,有下面的结论:存在性命题p:∃x∈M,p(x),它的否定¬p:________________。
三、学以致用例1写出下列命题的否定:(1)所有人都晨练;(2)∀x∈R,x2+x+1>0 ;(3)平行四边形的对边相等;(4)∃x∈R,x2-x+1=0.例2 指出下列命题中哪些是全称命题,哪些是存在性命题,并判断真假:(1)若a>0,且a≠1,则对任意实数x,a x>0;(2)对任意实数x1,x2,若x1<x2,则tan x1<tan x2;(3)∃T∈R,使sin(x+T)=|sin x|;(4)∃x∈R,使x2+1<0.四、总结提高1.全称命题的否定是;要证明一个全称命题是假命题,只需举一个反例即可.有些全称命题省略了量词,这种情况下对其否定时应加上存在量词。
2.存在性命题的否定是;要证明一个存在性命题是真命题,只需举出一例即可.有些存在性命题省略了量词,这种情况下对其否定时应加上全称量词.五、同步反馈1.“菱形的对角线互相垂直”的否定是_.2.命题“∀x∈R,x2≠x”的否定是_________________3.已知命题p:∀x>0,总有(x+1)e x>1,则¬p为______.4.“二次函数的图像与x轴有公共点”的否定是___________.5.写出下列命题的否定,并判断其真假:(1)三角形的内角和是1800;(2)所有的等边三角形都全等;(3)实系数一元二次方程有实数解;(4)有的实数没有平方根.6.已知p:x2-8x-20≤0,q:x2-2x+1-m2≤0 (m>0),若¬p是¬q的充分而不必要条件,求实数m的取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.3.2含有一个量词的命题的否定
教学过程
一、问题情境
对于下列命题:
(1)所有的人都喝水;
(2)存在有理数x,使x2-2=0;
(3)对所有实数a,都有|a|≥0.
问题1上述命题属于什么命题?
解都是含有量词的命题,(1)(3)是全称命题,(2)是存在性命题.
问题2试对上述命题进行否定,你发现有何规律?
解命题(1)的否定为“并非所有的人都喝水”,换言之为“有的人不喝水”.命题否定后,全称量词变为存在量词,“肯定”变为“否定”.
命题(2)的否定为“并非存在有理数x,使x2-2=0”,即“对所有的有理数x,x2-2≠0”.命题否定后,存在量词变为全称量词,“肯定”变为“否定”.
命题(3)的否定为“并非对所有的实数a,都有|a|≥0”,即“存在实数a,使|a|<0”.
二、数学建构
一般地,“∀x∈M,p(x)”的否定为“∃x∈M, p(x)”,
“∃x∈M,p(x)”的否定为“∀x∈M, p(x)”.
三、数学运用
【例1】(教材第15页例1)写出下列命题的否定:
(1)所有人都晨练;
(2)∀x∈R,x2+x+1>0;
(3)平行四边形的对边相等;
(4)∃x∈R,x2-x+1=0.(见学生用书P11)
允许学生写出不同的否定形式,但最后要求学生统一到常见的格式.
解(1)“所有人都晨练”的否定是“有的人不晨练”;
(2)“∀x∈R,x2+x+1>0”的否定是“∃x∈R,x2+x+1≤0”;
(3)“平行四边形的对边相等”是指任意一个平行四边形的对边相等,它的否定是“存在平行四边形,
它的对边不相等”;
(4)“∃x∈R,x2-x+1=0”的否定是“∀x∈R,x2-x+1≠0”.
含有量词的命题的否定应该有统一的形式.
【例2】写出下列命题的否定:
(1)实数的绝对值是正数;
(2)矩形的对角线互相垂直. (见学生用书P12)
引导学生首先将命题写成含有量词的形式.
解(1) 命题“实数的绝对值是正数”可改写成“所有实数的绝对值都是正数”,此命题是全称命题,所以此命题的否定为“存在一个实数的绝对值不是正数”.
(2)命题“矩形的对角线互相垂直”可改写成“所有矩形的对角线都互相垂直”,此命题是全称命题,所以此命题的否定为“存在一个矩形,它的对角线不互相垂直”.
对表面上不含有量词的命题的否定,首先根据命题中所叙述的对象的特征,挖掘其隐含的量词,确定它是全称命题还是存在性命题.
【例3】写出下列命题的否定:
(1)若xy=0,则x=0或y=0;
(2)若x2+y2=0,则x=0,y=0. (见学生用书P12)
由学生列出所有可能情况,理解命题的否定的写法.
解(1) 命题“若xy=0,则x=0或y=0”的否定为“若xy=0,则x≠0且y≠0”;
(2)命题“若x2+y2=0,则x=0,y=0” 的否定为“若x2+y2=0,则x≠0或y≠0”.
“或”的否定是“且”,“且”的否定是“或”.
【例4】(1) 写出命题p“偶数能被4整除”的否定形式“ p”,并判断“ p”的真假;
(2)将命题“偶数能被4整除”改写成“如果……那么……”的形式,然后再写出它的否命题,并判断否命题的真假.
注意“命题的否定”和“否命题”是两个不同的概念.
解(1) 命题p“偶数能被4整除”可写成“所有的偶数都能被4整除”,此命题是全称命题,所以此命题的否定“ p”为“存在一个偶数不能被4整除”,它是真命题.
(2)命题“偶数能被4整除” 可写成“如果一个数是偶数,那么它能被4整除”,所以此命题的否命题为“如果一个数不是偶数,那么它不能被4整除”,它是真命题.
“命题的否定”是原命题的矛盾命题,两者的真假性必然是一真一假;而否命题和原命题可能同真同假,也可能一真一假.
四、课堂练习
1.写出下列命题的否定:
(1) ∃x∈R,使得2x2-1<0;
(2) 有的三角形的外心在三角形外部;
(3) 有一个素数是偶数;
(4) 在实数范围内,有些一元二次方程无解.
解(1) ∀x∈R,都有2x2-1≥0;
(2) 任意一个三角形的外心都在三角形内部;
(3) 每一个素数都不是偶数;
(4) 在实数范围内,所有的一元二次方程都有解.
2.写出下列命题的否定:
(1) ∀x∈Z,x2的个位数字不等于3;
(2) 三角形的两边之和大于第三边;
(3) 存在实数x,使lgx<1;
(4) 和为0的两个实数互为相反数.
解(1) ∃x∈Z,x2的个位数字等于3;
(2) 存在这样的三角形,它的两边之和不大于第三边;
(3) 对任意的实数x,都有lgx≥1;
(4) 存在和为0的两个实数不互为相反数.
五、课堂小结
1.全称命题的否定:全称量词变存在量词,肯定变否定.
2.存在性命题否定:存在量词变全称量词,肯定变否定.。
