哈尔滨师大附中2020~2021学年高一上学期期中考试数学试卷及答案

合集下载

黑龙江省哈尔滨市师范大学附中2019-2020学年高一上学期期中数学试题

绝密★启用前黑龙江省哈尔滨市师范大学附中2019-2020学年高一上学期期中数学试题试卷副标题注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题)请点击修改第I 卷的文字说明一、单选题1．集合{}0M x x =≥，{}24xN x =<，则M N ⋂（） A.[]0,2B.()0,2C.[)02，D.(]0,2 2．对于0,1a a >≠，下列说法中，正确的是（） A.若M N =，则log log a a M N =B.若22M N =，则M N =C.若22log log a a M N =，则M N =D.若M N =，则1122MN--=3．下列函数中，在区间()2,+∞上为增函数的是（） A.3x y =-B.12log y x =C.()22y x =--D.12y x=- 4．若函数()log (1)(0,1)a f x x a a =->≠ 的图象恒过定点，则定点的坐标为（） A.()1,0B.()2,0C.()1,1D.()2,15．已知13241log 3log 72a b c ⎛⎫=== ⎪⎝⎭,，，则,,a b c 的大小关系为（）A.a c b <<B.b a c <<C.c a b <<D.a b c <<6．函数()2lg 2y x x =+-的单调递增区间是（）A ．1,⎛⎫-∞-B ．1,⎛⎫-+∞C ．(,2)-∞-D ．(1,)+∞………装…………请※※不※※要※※在※※装※………装…………7．已知函数g(x)＝1－2x，f[g(x)]＝221xx-(x≠0)，则f(12)等于( )A．1 B．3 C．15 D．308．已知函数()f x、()g x分别是定义在R上的奇函数、偶函数，且满足()()3xf xg x+=，则（）A.()33x xf x-=- B.33()2x xf x--= C.()33x xf x-=- D.33()2x xf x--=9．若函数()f x是定义在R上的偶函数，在(],0-∞上是减函数，且(2)0f=，则()()f x f xx+-<的解集为（）A.()2,2- B.()(),22,-∞-+∞C.()()2,02,-+∞ D.()(),20,2-∞-10．函数()1lnf x xx⎛⎫=-⎪⎝⎭的图象是( )A. B.C. D.11．函数y=的定义域为R，则实数k的取值范围是（）A.02k<< B.04k≤≤ C.04k≤< D.04k<<12．已知函数21,0()ln,0x xf xx x+≤⎧=⎨>⎩,则方程[]()3f f x=的实数根的个数是（）A.2B.3C.4D.5第II卷（非选择题)请点击修改第II卷的文字说明二、填空题13．若不等式23x<-的解集为,A则A=Rð___________．14．若4log3a=，则22a a-+=．15．幂函数()2531my m m x-=-+在()0+∞，上为减函数，则m的值为_______．16．已知函数()223f x x x a=-+，()21g xx=-．若对任意[]10,3x∈，总存在[]22,3x∈，使得()()12f xg x≤成立，则实数a的值为____．三、解答题17．已知集合{}{}{}22,1,3,3,21,1,3A a aB a a a A B=+-=--+=-.（Ⅰ）求实数a的值；（Ⅱ）求满足()()A B M A B⊆⊆的集合M的个数．18．计算：（Ⅰ）ln43lg4lg25log3e++-；（Ⅱ）)14230.2501648201949-⎛⎫-⨯-⎪⎝⎭.19．已知函数11()142x xf x⎛⎫⎛⎫=-+⎪ ⎪⎝⎭⎝⎭.（Ⅰ）求满足()3f x=的实数x的值；（Ⅱ）求[]2,3x∈-时函数()f x的值域．20．已知1a>，函数()131log1log222a af x x x⎛⎫⎛⎫=++-⎪ ⎪⎝⎭⎝⎭.（1）求()f x的定义域；（2）若()f x在51,2⎡⎤-⎢⎥⎣⎦上的最小值为2-，求a的值.21．定义域为R 的函数()f x 满足：对于任意的实数,x y 都有()()()f x y f x f y +=+ 成立，且当0x >时，()0f x <．（Ⅰ）判断函数()f x 的奇偶性，并证明你的结论；（Ⅱ）证明()f x 在R 上为减函数；（Ⅲ）若(1)(13)0f a f a -+-<，求实数a 的取值范围.22．已知定义在R 上的奇函数13()3x x af x b+-+=+.（Ⅰ）求,a b 的值；（Ⅱ）若存在t R ∈，使不等式22(2)(2)f t t f t k -<-有解，求实数k 的取值范围；（Ⅲ）已知函数()g x 满足[]1()()2(33)(0)3x xf xg x x -+=-≠，且规定(0)2g =，若对任意x ∈R ，不等式(2)()11g x m g x ≥⋅-恒成立，求实数m 的最大值.参考答案1．C 【解析】【分析】根据题意先求出集合N ，然后根据交集的定义求解即可. 【详解】解：{}{}24|2xN x x x =<=<，又{}0M x x =≥，所以{}|02M N x x ⋂=≤<.故选：C. 【点睛】本题考查集合交集的运算，指数不等式求解，属于基础题. 2．B 【解析】【分析】对数函数真数大于0，所以A 不成立；平方相等，M 、N 不一定相等，所以C 不成立；当M N=0≤时，12x -没有意义，所以D 不对；指数函数单调且定义域为R ，则B 成立，从而得出结果. 【详解】解：A ：当0M N =≤时，对数无意义，故A 不正确；B ：因为指数函数单调且定义域为R ，所以若22M N =，则M N =成立，故B 正确；C ：比如当 ()22222=-2M N =，,时，有22log log a a M N =，但M N ¹；故C 不正确；D ：当M N =0≤时，12x -没有意义，故D 不正确.故选：B. 【点睛】本题考查指对函数的定义域和运算性质，解题的关键是熟练掌握指对函数的基础知识，属于基础题. 3．D 【解析】【分析】根据指对函数的性质可排除A 、B ，根据二次函数的性质可排除C ，从而得出结果.【详解】解：A ：3x y =-在R 上单调递减，故A 不正确；B ：12log y x =定义域为()0,∞+且单调递减，故B 不正确；C ：()22y x =--对称轴为2x =，且开口向下，在()2,+∞上单调递减，故C 不正确；D ：12y x=-在()2,+∞上单调递增，故D 正确. 故选：D. 【点睛】本题考查函数单调性的判断，解题的关键是牢记基本初等函数的单调性，属于基础题. 4．B 【解析】【分析】因为对数函数恒过定点()1,0，所以函数()log (1)(0,1)a f x x a a =->≠可以看成由函数()log a f x x =向右平移一个单位得到，故而得到答案.【详解】解：因为函数log ay x =的图像恒过定点()1,0，所以函数()log (1)(0,1)a f x x a a =->≠可以看成由函数()log a f x x =向右平移一个单位得到，所以函数()log (1)(0,1)a f x x a a =->≠的图像恒过定点()2,0. 故选：B. 【点睛】本题考查了对数函数的图像与性质，以及函数图像间的平移变换，属于基础题. 5．A 【解析】【分析】容易得出01,a <<12,12b c <<<<，再根据对数函数的性质将b 化为与c 同底的对数，即可比较出大小. 【详解】解：1312a ⎛⎫= ⎪⎝⎭，01a ∴<<，244log 3log 9log 71b c ==>=>，所以b c a >>.故选：A. 【点睛】本题考查指数与对数大小的比较，考查对数换底公式以及对数函数的单调性，属于基础题. 6．D 【解析】【分析】首先考虑对数的真数取值大于0；其次将函数22lg xx y +-=拆成外层函数lg uy =和内层函数22u x x =+-，根据求复合函数单调性的法则：同増异减，判断出单调增区间；最后即可求得()2lg 2y x x =+-的单调增区间. 【详解】由220x x +->可得2x <-或1x >∵22u x x =+-在(1,)+∞单调递增，而lg y u =是增函数，由复合函数的同增异减的法则可得，函数()2lg 2y x x =+-的单调递增区间是(1,)+∞，故选D. 【点睛】复合函数单调性的判断方法：同増异减.（同：内外层函数单调性相同时，整个函数为增函数；异：内外层函数单调性不同时，整个函数为减函数）. 7．C【解析】令1－2x ＝12，得x ＝14，∴f(12)＝1116116-＝15，故选C. 8．D 【解析】【分析】函数()f x 、()g x 分别是定义在R 上的奇函数、偶函数，且满足()()3xf xg x +=，可得()()3x f x g x --+-=，即()()3xf xg x --+=，与()()3x f x g x +=联立求解即可解出()f x .【详解】解：因为函数()f x 、()g x 分别是定义在R 上的奇函数、偶函数，所以()()()()3xf xg x f x g x --+-=-+=，即：()()3()()3xxf xg x f x g x -⎧-+=⎨+=⎩ ，解得：()33()2332x x x xf xg x --⎧-=⎪⎪⎨+⎪=⎪⎩. 故选：D. 【点睛】本题考查了函数的奇偶性，考查了学生的推理能力与计算能力，属于中档题. 9．D 【解析】【分析】根据题意，由函数()f x 是定义在R 上的偶函数，又()f x 在(],0-∞上是减函数可得()f x 在()0,∞+上是增函数，因为(2)0f =，所以(2)0f -=，结合函数的单调性可知()0f x <的解为()2,2-；()0f x >的解为()(),22,-∞-+∞，()()0f x f x x +-<等价于()00x f x <⎧⎨>⎩或()00x f x >⎧⎨<⎩，结合分析可得出结果.【详解】解：函数()f x 是定义在R 上的偶函数，又()f x 在(],0-∞上是减函数，则()f x 在()0,∞+上是增函数，且(2)0f =，所以有(2)0f -=，所以()0f x <的解为()2,2-；()0f x >的解为()(),22,-∞-+∞.()()0f x f x x +-<等价于2()0f x x <，等价于()00x f x <⎧⎨>⎩或()00x f x >⎧⎨<⎩所以不等式的解集为：()(),20,2-∞-.故选：D. 【点睛】本题考查函数的单调性和奇偶性的综合应用，解题的关键是利用函数的单调性和奇偶性分析出函数的符号，属于中档题. 10．B 【解析】【分析】首先根据对数函数的性质，求出函数的定义域，再很据复合函数的单调性求出f （x ）的单调性，问题得以解决．【详解】因为x ﹣1x＞0，解得x ＞1或﹣1＜x ＜0，所以函数f （x ）=ln （x ﹣1x）的定义域为：（﹣1，0）∪（1，+∞）．所以选项A 、D 不正确．当x ∈（﹣1，0）时，g （x ）=x ﹣1x是增函数，因为y=lnx 是增函数，所以函数f （x ）=ln （x+1x）是增函数．故选：B ．【点睛】函数图象的辨识可从以下方面入手：（1）从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置；（2）从函数的单调性，判断图象的变化趋势；（3）从函数的奇偶性，判断图象的对称性；（4）从函数的特征点，排除不合要求的图象. 11．D 【解析】【分析】函数y =的定义域为R ，等价于210kx kx ++>恒成立.该函数为二次型的函数，考虑0k =和0k ≠两种情况，∆<0，分情况求解即可求出结果. 【详解】解：因为函数y =的定义域为R ，所以210kx kx ++>恒成立.令()21g x kx kx =++，当0k =时，()10g x =>恒成立，符合题意.当0k ≠时，00k >⎧⎨∆<⎩，即2040k k k >⎧⎨-<⎩解得：04k <<.故选：D. 【点睛】本题考查函数定义域为R 的问题，考查分类讨论的思想和二次函数的性质，属于基础题. 12．D 【解析】【分析】函数21,0()ln ,0x x f x x x +≤⎧=⎨>⎩,则方程[]()3f f x =等价于()213f x +=，()3f x e =或()3f x e -=.再根据21,0()ln ,0x x f x x x +≤⎧=⎨>⎩分析函数的单调性和值域，分析每一段上的解的个数，进而得出结果. 【详解】解：因为函数21,0()ln ,0x x f x x x +≤⎧=⎨>⎩, 当()0f x ≤时，[]()()213f f x f x =+=，即()1f x =不符合()0f x ≤，舍去；当()0f x >时，方程[]()3f f x =等价于()|ln |3f x =，解得：()3f x e =或()3f x e -=，0x ≤，211x ∴+≤，又()ln f x x =在()0,1上单调递减，且()[)0,f x ∈+∞；在()1,+∞上单调递增，且()[)0,f x ∈+∞.若()3f x e =1>，则321x e +=无解，3ln x e =有两个解；若()3f x e -=，则321x e -+=有一解，3ln x e -=有两解，所以共有5解.故选：D. 【点睛】本题考查函数与方程的应用，考查学生的分析与计算求解能力，解题的关键是对函数分段讨论求解，属于中档题. 13．5,34⎡⎤⎢⎥⎣⎦【解析】【分析】对不等式移项、通分、化简、得到4503x x-<-，求解不等式然后对解集求补集即可得到答案. 【详解】解：2123x x +<-等价于2121624520333x x x x x x x++-+--==<---，即()()4530x x -->，解得：3x >或54x <，则A =R ð5,34⎡⎤⎢⎥⎣⎦. 故答案为：5,34⎡⎤⎢⎥⎣⎦.【点睛】本题考查分式不等式求解集，以及补集的运算，解题的关键是对不等式进行正确的变形，属于基础题.14 【解析】【详解】∵4log 3a =，∴432a a =⇒=∴222a-+==考点：对数的计算 15．0 【解析】【分析】根据幂函数的定义可知211m m -+=，又函数在()0+∞，上为减函数，可知530m -<，对m 求解即可.【详解】解：因为函数()2531m y m m x-=-+为幂函数，所以211m m -+=，解得：0m =或1m =.又53m y x -=在()0+∞，上为减函数，所以530m -<，即35m <，所以0m =. 故答案为：0. 【点睛】本题考查根据幂函数的定义和单调性求参数，解题的关键是熟记幂函数的定义和单调性，属于基础题. 16．13- 【解析】【分析】将问题转化为()()max max f x g x ≤，根据二次函数和分式的单调性可求得()f x 在[]0,3上的最小值和最大值及()g x 在[]2,3上的最大值；分别讨论()f x 最大值小于零、最小值小于零且最大值大于零、最小值大于零三种情况，得到()f x 每种情况下的最大值，从而得到不等式，解不等式求得结果. 【详解】不等式()()12f x g x ≤恒成立可转化为：()()max max f x g x ≤ 当[]0,3x ∈时，()()min 113f x f a ==-+，()()max 333f x f a ==+ 当[]2,3x ∈时，()()max 22g x g ==①若330a +≤，即1a ≤-时，()max 1313f x a a =-+=-132a ∴-≤，解得：13a ≥-（舍）②若13033a a -+≤<+，即113a -<≤时，()()(){}max max 1,3f x f f =- 又()113f a -=-，()333f a =+ 当1333a a ->+，即113a -<<-时，()max 13f x a =- 132a ∴-≤，解得：13a ≥-（舍）当1333a a -≤+，即1133a -≤≤时，()max 33f x a =+ 332a ∴+≤，解得：13a ≤- 13a ∴=-③若130a -+>，即13a >时，()max 3333f x a a =+=+332a ∴+≤，解得：13a ≤-（舍）综上所述：13a =-本题正确结果：13-【点睛】本题考查恒成立和能成立综合应用的问题，关键是能够将不等式转化为两个函数最值之间的大小关系，从而根据函数的单调性求得函数的最值，通过最值的比较构造不等式求得结果. 17．（Ⅰ）1-；（Ⅱ）16个. 【解析】【分析】（Ⅰ）{}3,3AB B =-∴-∈，逐个分析集合B 中的元素求解a ，然后代入检验即可. （Ⅱ）因为{}3A B =-I ，{}4,3,0,1,2A B =--，()()A B M A B ⊆⊆，所以集合M 中必有-3，只需考虑剩余4个元素即可得到答案. 【详解】（Ⅰ）{}3,3A B B =-∴-∈显然213a +≠-,若33,a -=-则0a =，{}3,1A B ∴=-，不符合题意,若213,a -=-则1a =-，{}3A B ∴=-，满足题意,所以1a =- .（Ⅱ）{}3A B =-I ，{}4,3,0,1,2AB =--，因为()()A B M A B ⊆⊆，所以集合M 中必有-3，剩余4个元素：-4,0,1,2都有在与不在两种情况，所以个数为42=16个. 【点睛】本题考查了交集、并集的定义和运算，元素与集合的关系，考查了子集的定义，子集个数的求法，属于基础题.18．（Ⅰ）32-；（Ⅱ）8- . 【解析】【分析】（Ⅰ）根据对数和指数的运算性质和运算律化简计算即可. （Ⅱ）根据指数的运算性质和运算律化简即可得出结果. 【详解】解：（Ⅰ）ln 43lg 4lg 25log 3e ++- =323lg100log 314+--=3252+- =32-. （Ⅱ）)14230.2501648201949-⎛⎫-⨯- ⎪⎝⎭.=34237414⋅-⨯=271-=2721--- =8- 【点睛】本题考查指数、对数的运算性质和运算律，考查学生的计算能力，属于基础题. 19．（Ⅰ）1-；（Ⅱ）3,134⎡⎤⎢⎥⎣⎦.【解析】【分析】（Ⅰ）将12x ⎛⎫ ⎪⎝⎭看成一个整体，对()3f x =进行化简得到1121022x x ⎡⎤⎡⎤⎛⎫⎛⎫-⋅+=⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦先求解12x⎛⎫ ⎪⎝⎭的值，再根据对数的运算解x 即可. （Ⅱ）12xt ⎛⎫= ⎪⎝⎭，可知1,48t ⎡⎤∈⎢⎥⎣⎦，化简()f x 可得21y t t =-+，然后配方即可求出21y t t =-+在1,48t ⎡⎤∈⎢⎥⎣⎦的最大最小值，进而求得值域.【详解】（Ⅰ）11()1342x xf x ⎛⎫⎛⎫=-+= ⎪ ⎪⎝⎭⎝⎭,112042x x ⎛⎫⎛⎫∴--= ⎪ ⎪⎝⎭⎝⎭，1121022x x ⎡⎤⎡⎤⎛⎫⎛⎫∴-⋅+=⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦,122x ⎛⎫∴= ⎪⎝⎭或112x ⎛⎫=- ⎪⎝⎭（舍）122x⎛⎫∴= ⎪⎝⎭, 1x ∴=- .（Ⅱ）12x t ⎛⎫= ⎪⎝⎭令12xt ⎛⎫= ⎪⎝⎭，[]12,3,,48x t ⎡⎤∈-∴∈⎢⎥⎣⎦. 则2213124y t t t ⎛⎫=-+=-+ ⎪⎝⎭当12t =时，min 34y =；当4t =时，max 13y =, 所以()f x 的值域为3,134⎡⎤⎢⎥⎣⎦.【点睛】本题考查二次型函数已知值求自变量，以及二次函数已知自变量的范围求值域，考查了换元法的应用以及二次函数配方法求值域，考查了学生的计算能力，属于基础题. 20．（1）()2,3- ；（2）43. 【解析】【分析】（1）由题意，函数()f x 的解析式有意义，列出不等式组，即可求解函数的定义域；（2）由题意，化简得()()21log 64af x x x =-++，设()2164u x x =-++，根据复合函数的性质，分类讨论得到函数()f x 的单调性，得出函数最值的表达式，即可求解。

2022-2023学年黑龙江省哈尔滨师大附中数学高一上期末教学质量检测试题含解析

A. b c a
B. c b a
C. c a b
D. b a c
3．已知全集U {1, 2,3, 4,5}，集合 A {2, 4} ， B {3, 4} ，则 A U B （）
A.{2，3，4}
B.{1，2，4，5}
C.{2，5}
D.{2}
4．要证明命题“所有实数的平方都是正数”是假命题，只需（）
（1）写一个满足条件的 f (x) ；
（2）证明 f (x) 是奇函数；
（3）解不等式 1 f x2 f (x) 1 f (3x)
2
2
参考答案
一、选择题：本大题共 10 小题，每小题 5 分，共 50 分。在每个小题给出的四个选项中，恰有一项是符合题目要求的 1、B
【解析】根据对数函数的性质即可确定 a 的范围.
5 6
,0
a
1
a
，因此选 A
u(3) 0 9a 9 9 7 0
点睛:1．复合函数单调性的规则
若两个简单函数的单调性相同，则它们的复合函数为增函数；若两个简单函数的单调性相反，则它们的复合函数为减
函数．即“同增异减”
函数单调性的性质
(1)若 f(x)，g(x)均为区间 A 上的增(减)函数，则 f(x)＋g(x)也是区间 A 上的增(减)函数，更进一步，即增＋增＝增，
[( x
1) 1]2 ( x 1)2
sin( x 1
1)
，
f
(x
2)
f
(x)
[( x
2
1) 1]2 sin( x (x 2 1)2 1
2 1)
[( x
1) 1]2 sin( x ( x 1)2 1
1)

数学丨黑龙江省哈尔滨市师范大学附属中学2025届高三上学期11月期中考试数学试卷及答案

哈师大附中2024—2025学年度高三上学期期中考试数学试题考试说明：本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，满分150分．考试时间为120分钟．1．答题前，考生先将自己的姓名、准考证号码填写清楚．2．选择题必须使用2B 铅笔填涂，非选择题必须使用0.5毫米黑色字迹签字笔书写，字体工整，字迹清楚．3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效，在草稿纸、试题卷上答题无效．4．保持卡面清洁，不得折叠、不要弄破、弄皱，不准使用涂改液、刮纸刀．第I 卷(选择题,共58分)一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{}2|230A x x x =-+≤，(){}2ln 2B x y x==-，则A B = （）A ．()13，B．3⎡-⎣C．⎡⎤⎣⎦D．(⎤⎦2．复数2025z=2025i -在复平面内对应的点所在的象限为（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3.函数()2cos f x x x =+在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值为（）A.2πB .2C.6π+ D.13π+4．已知a 是单位向量，则“||||1a b b +-= 是“a b∥”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件5.已知函数()()e 1x a xf x -⎛⎫= ⎪⎝⎭在区间()1,0-上单调递增，则a 的取值范围是（）A ．[)0,+∞B ．[)2,-+∞C ．(],0-∞D ．(],2-∞-6.已知等比数列{}n a 的前n 项和为n S ，若3614S S =，则1236SS S =+（）A.43B.8C.9D.167.菱形ABCD 边长为2，P 为平面ABCD 内一动点，则()()PA PB PC PD +⋅+的最小值为()A.0B.2- C.2D.4-8.已知函数()f x 为偶函数，且满足(13)(13)f x f x -=+，当(0,1)x ∈，()31xf x =-，则323(log )f 的值为（）A.31B.5932C.4932D.21132二、多选题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分．9.函数()2sin(1)3f x x πωω=+≤的图象如图所示，则下列说法中正确的是（）A ．1ω=B ．函数的图象关于点,03π⎛⎫⎪⎝⎭对称C ．将()y f x =向左平移3π个单位长度，得到函数()2cos(6g x x π=+D ．若方程(2)f x m =在0,2π⎡⎤⎢⎥⎣⎦上有2个不相等的实数根，则m的取值范围是2⎤⎦10．设正实数,m n 满足1m n +=，则（）A ．1m nm+的最小值为3B+C的最小值为12D ．33m n +的最小值为1411.已知函数1()(0)xf x x x =>,则下列说法中正确的是（）A.方程1()(f x f x=有一个解B.若()()g x f x m =-有两个零点，则10em e<<C.若21()(log ())2a h x x f x =-存在极小值和极大值，则(1,e)a ∈D.若()0f xb -=有两个不同零点，2(())()0f x b x cx d --+≤恒成立，则2ln b c <<第Ⅱ卷(非选择题,共92分)三、填空题：本大题共3小题，每小题5分，共15分．将答案填在答题卡相应的位置上．12.中国冶炼块铁的起始年代虽然迟至公元前6世纪，约比西方晚900年，但是冶炼铸铁的技术却比欧洲早2000年.现将一个轴截面为正方形且侧面积为π36的实心圆柱铁锭冶炼熔化后，浇铸成一个底面积为π81的圆锥，则该圆锥的高度为.13．已知某种科技产品的利润率为P ，预计5年内与时间(t 月)满足函数关系式(t P ab =其中a b 、为非零常数).若经过12个月，利润率为10%，经过24个月，利润率为20%，那么当利润率达到50%以上，至少需要经过________________个月(用整数作答，参考数据：lg 20.3010)≈14.已知b 为单位向量，,a c 满足42a b c b ⋅=-= ，则12a c -的最小值为四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤.15．（本小题13分）在△ABC 中，a b c 、、分别为角A B C 、、所对的边，且22()b a a c c -=-(1)求角B .(2)若b =△ABC 周长的最大值.16.（本小题15分）已知数列{}n a 满足*3212122,N 22n n a a a n a n -++++=∈ (1)求{}n a 的通项公式；(2)在n a 和1n a +之间插入n 个数，使得这2n +个数依次构成公差为n d 的等差数列，求数列1n d ⎧⎫⎨⎬⎩⎭的前n 项和n T ．17．（本小题15分）行列式在数学中是一个函数，无论是在线性代数、多项式理论，还是在微积分学中（比如说换元积分法中），行列式作为基本的数学工具，都有着重要的应用．将形如11122122a a a a 的符号称二阶行列式，并规定二阶的行列式计算如下：1112112212212122a a a a a a a a =-，设函数22sin sin ()()π26cos()x xf x x x =∈+R ．(1)求()f x 的对称轴方程及在[0,]π上的单调递增区间；(2)在锐角ABC ∆中，已知()32f A =-,2133AD AB AC =+，cos B =，求tan BAD ∠18.（本小题17分）已知数列}{n a 满足111,,333,n n na n n a a a n n +⎧+⎪==⎨⎪-⎩为奇数为偶数（*∈N n ）.(1)记232-=n n a b （*∈N n ），证明：数列}{n b 为等比数列，并求}{n b 的通项公式；(2)求数列}{n a 的前n 2项和n S 2；(3)设12121--=+n n n b b c （*∈N n ），且数列}{n c 的前n 项和为n T ，求证：1133ln --<-n n n n T （*∈N n ）.19.（本小题17分）已知函数ln ()sin ,(0,)x a f x e x x -=-∈+∞.(1)当a e =时，求()y f x =在(0,(0))f 处的切线方程；(2)若32(())(())ln(1())0f x f x f x -++≥恒成立，求a 的范围；(3)若()f x 在(0,)π内有两个不同零点12,x x ，求证：122x x ππ<+<2024—2025学年度上学期高三学年期中考试数学答案一、单选题1.D 2.D 3.A 4.A 5.D 6.B7.D8.C二、多选题9.AC 10.ABD 11.ACD 三、填空题12.213.4014.1四、解答题15.（1）22()b a a c c -=-即222b a c ac =+-∵2222cos b a c ac B =+-∴1cos 2B =，又(0,)B π∈∴3B π=（2）由sin sin a c AC =可得，2sin a A =，2sin c C=2sin 2sin l a b c A C =++=+∵2+3A C π=∴23C Ap =-∴22sin 2sin()3l a b c A A π=++=+-3sin A A =)6A π=+∵203A π<<∴l的最大值为16.(1)321212222nn na a a a -++++= 当2n ≥时，312122)2222(1n n a a a n a --++++=- 两式相减，得122nn a -=，即2n n a =.又当1n =时，12a =符合题意，所以2n n a =.(2)由（1）得2n n a =，所以11222111n n nn n n b b d n n n ++--===+++，则112nn n d +=，所以()123111123412222nn T n ⎛⎫⎛⎫⎛⎫⎛⎫=⋅+⋅+⋅+⋅⋅⋅++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭()12341111112341222222nn n T n n +⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=⋅+⋅+⋅+⋅⋅⋅+++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭两式相减得：()()112111111111113342211112222222212n n n nn n n T n n ++++⎛⎫- ⎪+⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎝⎭=⋅++⋅⋅⋅+-+=+-+=- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭-，所以332n nn T +=-．17.（1）221()2sin cos()2sin 2sin (cos sin )2sin 226f x x x x x x x xπ=+-=--23323sin sin 2(1cos 2)sin(2)22232x x x x x π=---+-，由22,32x k k πππ+=+∈Z ，得,12x k k ππ=+∈Z ，所以()f x 的对称轴为ππ()122kx k =+∈Z .由222,232k x k k πππππ-+<+<+∈Z ，[]0,x π∈，所以单调递增区间为701212πππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦，，，（2）由（1）知，33())322f A A π=+-=-，则πsin(2)03A +=，由02A π<<，得ππ4π2333A <+<，则π23A π+=，解得π3A =，因为ABC V中，cos B =，则B 为锐角，所以sin 3B ===，因为π3A =，πA B C ++=，所以2π3C B =-，所以2π2π2π11sin sin sin cos cos sin 333232326C B B B ⎛⎫=-=-=⨯+⨯=+⎪⎝⎭，设BADθ∠=，则π3 CADθ∠=-，在ABD△和ACD中，由正弦定理得sin sinBD ADBθ==πsinsin3CD ADCθ=⎛⎫-⎪⎝⎭因为2CD BD=(π3sin3θθ⎛⎫-=+⎪⎝⎭，(1cos sin3sin22θθθ⎫-=+⎪⎪⎭(2sinθθ=+，所以tan tanBADθ∠==18.（1）证明：2123123)1231(231212221-+=-++=-=++++nanaabnnnnnnnnbaanna31)23(312131212)6(31222=-=-=-+-=，又212313123121=-+=-=aab，所以，数列}{nb为以21为首项，31为公比的等比数列.（2）由（1）可知13121-⎪⎭⎫⎝⎛=nnb，又232-=nnab，23312112+⎪⎭⎫⎝⎛=∴-nna.设nnaaaP242++=，则nnPnnn233143432331131121+⎪⎭⎫⎝⎛-=+-⎪⎭⎫⎝⎛-⋅=，设1231-++=nnaaaQ ，1231122-+=-naann，2312)121(31nQnnQPnnn+=-+⋅+=∴，233nPQnn-=∴，故21223631334nnnPQPSnnnnn-+⎪⎭⎫⎝⎛-=-=+=-.（3）nnnnnnnc321132113331311311-<--=--=-⎪⎭⎫⎝⎛-⎪⎭⎫⎝⎛=-，n n n n n n n T 311311()313131(22+-=--=+++-<∴ ，所以欲证1133ln --<-n n n n T ，只需证)311ln(313ln 133ln 31n n n n n n --=--=-<，即证n n 31311ln(-<-.设)0,1(),1ln()(-∈+-=x x x x f ，01)(<+='∴x xx f ，故)(x f 在)0,1(-上单调递减，0)0()(=>f x f ，)0,1(-∈∴x 时，)1ln(x x +>.)0,31[31-∈-n ，n n 31311ln(-<-∴得证.19.1) =s =K1−sins 0=−1,n =K1−coss n 0=−1−1∴−−1=−1−12）3−2+ln 1+≥0.令=s 3−2+ln 1+≥0(1)t >-令=3−2+ln 1+,n =32−2+1r1=33+2−2r1r1，当≥0,'≥0∴在0,+∞单调递增，当()32322(0,1),ln 1(1)0t t t t t t t t t t ∈+++<++=++<∴≥0解集为≥0∴≥0>0,sins1≥sin=ℎ. ℎ' = cosKsin =, ∴ 在单调递增, (4,54)单调递减,当>54时,ℎ<154∴ℎ=224∴1≥224,0<≤243）ℎ=sin ∴sin=1有两个根1,2。

黑龙江省哈尔滨师范大学附中2020-2021学年高一入学考试数学试题答案和解析

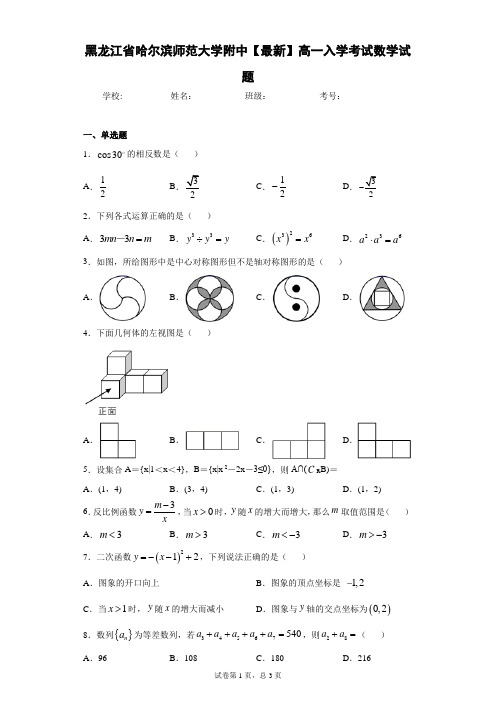
黑龙江省哈尔滨师范大学附中【最新】高一入学考试数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．cos30的相反数是（）A ．12BC ．12-D ． 2．下列各式运算正确的是（）A ．33mn n m =－B ．33y y y ÷=C ．()236x x =D ．236a a a ⋅= 3．如图，所给图形中是中心对称图形但不是轴对称图形的是（）A ．B ．C ．D ． 4．下面几何体的左视图是（）A ．B ．C ．D ． 5．设集合A ＝{x|1＜x ＜4}，B ＝{x|x 2－2x －3≤0}，则A∩(C R B)＝A ．(1，4)B ．(3，4)C ．(1，3)D ．(1，2) 6．反比例函数3m y x -=，当0x >时，y 随x 的增大而增大，那么m 取值范围是（） A ．3m < B ．3m >C ．3m <-D ．3m >- 7．二次函数()212y x =--+，下列说法正确的是（）A ．图象的开口向上B ．图象的顶点坐标是1,2C ．当1x >时，y 随x 的增大而减小D ．图象与y 轴的交点坐标为()0,2 8．数列{}n a 为等差数列，若34567540a a a a a ++++=，则28a a +=（）9．设()2|1|2,||11,||11x x f x x x --≤⎧⎪=⎨>⎪+⎩，则12f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦（） A ．12 B ．413 C ．95- D ．254110．“龟兔首次赛跑”之后，输了比赛的兔子总结惨痛教训后，决定和乌龟再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事（x 表示乌龟从起点出发所行的时间，1y 表示乌龟所行的路程，2y 表示兔子所行的路程）下列说法中正确的有（）个①“龟兔再次赛跑”的路程为1000米；②兔子和乌龟同时从起点出发；③乌龟在途中休息了10分钟；④兔子在途中750米处追上乌龟.A ．1B ．2C ．3D ．4二、填空题11．在函数y =中，自变量x 的取值范围是__________. 12．不等式组1221(1)0x x -⎧<⎪⎨⎪--<⎩的解是___________.13．把多项式22412x ax a --分解因式的结果是___________.14．在一个不透明的口袋中装有3个红球、1个黑球，这些球除颜色外其他都相同，在看不到球的条件下，随机地从这个袋子中摸出两个球，摸到的两个球都是红球的概率是___________.15．定义域为R 的奇函数()f x 为增函数，偶函数()g x 在区间[]0,∞上的图象与()f x 的图象重合，设0a b >>，给出下列不等式：（1）()()()()f b f a g a g b -->--（2）()()()()f b f a g a g b --<--（3）()()()()f a f b g b g a -->--（4）()()()()f a f b g b g a --<--其中成立的序号是___________.三、双空题16．在等比数列{}n a 中，若45a =，86a =，则210a a ⋅=______，6a =______；四、解答题17．先化简，再求值.221111121x x x x x +⎛⎫-÷ ⎪+-++⎝⎭，其中3tan 3045x =︒︒ 18．已知一次函数1y x b =+（b 为常数）的图像与反比例函数2k y x=（k 为常数，且0k ≠）的图像相交于点()3,1P .（1）求这两个函数的解析式；（2）当3x >时，试判断1y 与2y 的大小，并说明理由.19．已知集合{}34A x x =-≤≤，{}211B x m x m =-<<+，且B A ⊆，求实数m 的取值范围.20．已知二次函数2y ax bx =+，当2x =时0y =，并且方程2ax bx x +=有两个相等实数根.（1）求二次函数2y ax bx =+的表达式；（2）是否存在实数(),m n m n <使得当m x n ≤≤时，y 有最小值2m ，最大值2n .如果存在，求出m ，n ；如不存在说明理由.21．已知抛物线2111:12C y x x =-+，点()1,1F . （1）求抛物线1C 的顶点坐标；（2）若抛物线1C 与y 轴的交点为A ，连接AF ，并延长交抛物线1C 于点B ，求证：112AF BF+=；（3）将抛物线1C 作适当的平移，得抛物线()2221:2C y x h =-，若2x m <≤时，2y x ≤恒成立，求m 得最大值.参考答案1．D【解析】【分析】求出cos30︒，由相反数定义得结论．【详解】cos30=°，其相反数是．故选：D.【点睛】本题考查锐角的三角函数值，考查相反数概念，属于基础题．2．C【分析】根据幂的运算法则判断．【详解】A中是相减不是相除，错；B中指数相减为0，即为0y，错；由幂和乘方知C正确；由同底数相乘法则知D错误．故选：C.【点睛】本题考查幂的运算法则，属于基础题．3．C【分析】由中心对称图形和轴对称图形的定义判断．【详解】A，D都不是中心对称图形，B，C都是中心对称图形，B还是轴对称图形，C不是轴对称图形．故选：C.【点睛】本题考查中心对称图形和轴对称图形，掌握中心对称图形和轴对称图形的定义是解题关键．4．A【分析】根据三视图的概念判断．【详解】从左边投影，只看到三个小正方形，左侧是上下各一个，下方是左右各一个，只有A 符合．故选：A.【点睛】本题考查三视图，掌握三视图的概念是解题基础．5．B【解析】由题意B={x|x 2-2x-3≤0}={x|-1≤x≤3}，故∁R B={x|x ＜-1或x ＞3}，又集合A={x|1＜x ＜4}，∴A∩（∁R B ）=（3，4）故选B6．A【分析】由反比例函数性质求解．【详解】反比例函数中k y x=中，0k >，在0x >时，y 随x 的增大而减少，k 0<时，在0x >时，y 随x 的增大而增大，所以由题意30m -<，3m <．故选：A.【点睛】本题考查反比例函数的性质，属于基础题．7．C【分析】由二次函数性质判断．【详解】二次函数()212y x =--+中，二次项系数为1-，开口方向向下，顶点坐标是(1,2)，0x =时，1y =，即与y 交点为(0,1)，A ，B ，D 均错．对称轴是1x =，因此在1x >时，y 随x 的增大而减小，C 正确．故选：C.【点睛】本题考查二次函数的图象与性质，属于基础题．8．D【分析】由等差数列的性质计算．【详解】∵数列{}n a 为等差数列，∴34567374655()()5540a a a a a a a a a a a ++++=++++==，5108a =，∴2852216a a a +==．故选：D.【点睛】本题考查等差数列的性质，即等差数列{}n a 中，正整数,,,m n k l ，则m n k l m n k l a a a a +=+⇔+=+．9．B【分析】先计算1()2f ，再计算1[()]2f f ．【详解】由题意113()12222f =--=-，2314()32131()2f -==+-．故选：B.【点睛】本题考查分段函数，求值时要注意自变量的范围不同，选取的表达式可能就不相同． 10．C【分析】观察图象，由路程与时间的关系作答．【详解】从图象看两个的路程都是1000米，但不是同时从起点出发的，乌龟在走了30分钟的时候开始休息了10分钟然后再行走的，相遇点路程是750米，因此①③④正确，故选：C.【点睛】本题考查函数的图象的识别，理解函数的意义是解题关键．11．5x <；【分析】由分母不为0，二次根式下被开方数不小于0.求解【详解】由题意50x ->，5x <．故答案为：5x <．【点睛】本题考查函数定义域，属于基础题．12．25x <<；【分析】分别解不等式，然后求两个不等式解集的公共部分．【详解】由122x -<得5x <，由1(1)0x --<得2x >，所以原不等式组的解集是25x <<.故答案为：25x <<.【点睛】本题考查解不等式组，可分别解组成不等式组的不等式，然后求解集的公共部分即得． 13．()()62x a x a -+；【分析】利用十字相乘法分解．【详解】22412x ax a --(2)(6)x a x a =+-．故答案为：()()62x a x a -+【点睛】本题考查因式分解，掌握因式分解的方法是解题基础．14．12；【分析】可编号后用列举法列出各种可能，求出任意摸两个球的方法数，再求出两球都是红球的方法数，然后可计算概率．【详解】3个红球编号为,,a b c ，1 个黑球编号为B ，任取两球有如下可能：,,,,,ab ac aB bc bB cB 共6种，其中两个都是红球的有,,ab ac bc 三个，所以概率为3162=．故答案为：12．【点睛】本题考查古典概型，用列举法可列出所有基本事件，从而计算出概率．15．（1）与（3）；【分析】由奇偶性化简变形，再由单调性确定不等式是否正确．【详解】由题意 ()()()()f b f a g a g b -->--化为()()()()()()f b f a g a g b f a f b +>-=-，即()()f b f b >-()f b =-，由()f x 是增函数，()()f b f b >-正确，∴（1）正确，（2）错误；()()()()f a f b g b g a -->--化为()()()()()()f a f b g b g a f b f a +>-=-，()()()f a f a f a >-=-，由()f x 是增函数，()()f a f a >-正确，∴（3）正确，（4）错误．故答案为：（1）（3）．【点睛】本题考查函数的奇偶性与单调性，掌握奇偶性与单调性的定义是解题基础．16．30【分析】由等比数列的性质求解．【详解】由题意210485630a a a a ==⨯=，2210630a a a ==，∵等比数列中偶数项同号，∴6a =故答案为：30【点睛】本题考查等比数列的性质．掌握等比数列的性质是解题关键．等比数列{}n a 中，正整数,,,m n k l ，则m n k l m n k l a a a a +=+⇔⋅=⋅．17．21x x --【分析】按分式运算的法则化简，同时化简x 并代入计算．【详解】原式22211(1)(2)(1)2(1)(1)1(1)(1)1x x x x x x x x x x x --+-+-=⨯==+-+-+-3132x =⨯+=33==．【点睛】本题考查代数式的化简求值．因此需先化简再代入求值，可减少计算量，易于正确． 18．（1）12y x =-，23y x =；（2）12y y >．【分析】（1）把P 点坐标代入可求得解析式；（2）作差后与0比较可得．【详解】（1）∵次函数1y x b =+（b 为常数）的图像与反比例函数2k y x=（k 为常数，且0k ≠）的图像相交于点()3,1P . ∴13b =+⇒2b =-，13k =⇒3k =， ∴解析式为12y x =-，23y x =；（2）3x >时，212323(1)(3)20x x x x y y x x x x--+--=--==>，∴12y y >．【点睛】本题考查求函数解析式，考查实数的比较大小．比较大小通常用作差法，即两数的差与0比较后可得它们的大小关系．19．{|1}m m ≥-【分析】B A ⊆时，要分类讨论，分B =∅和B ≠∅讨论．【详解】∵B A ⊆，∴当B =∅时，211m m -≥+，即2m ≥，当B ≠∅时，213142m m m -≥-⎧⎪+≤⎨⎪<⎩，解得12m -≤<，综上所述，m 的取值范围是{|1}m m ≥-．【点睛】本题考查集合的包含关系，解题时要注意空集是任何集合的子集．因此需分类讨论． 20．（1）21()2f x x x =-+；（2）存在满足题意的,m n ，2,0m n =-=．【分析】（1）根据已知条件列出关于,a b 的两个方程联立可解,a b ，即得函数解析式．（2）由函数式，求出对称轴，根据对称轴分类讨论求函数值域．【详解】（1）由题意2420(1)0a b b +=⎧⎨-=⎩，解得121a b ⎧=-⎪⎨⎪=⎩． ∴21()2f x x x =-+；（2）假设存在满足题意的,m n ．由（1）22111()(1)222f x x x x =-+=--+，对称轴是1x =， ①1n ≤时，()f x 在[,]m n 是单调递增，∴()2()2f m m f n n=⎧⎨=⎩， ∴,m n 是方程()2f x x =的两个不等实根．()2f x x =为2122x x x -+=，解得120,2x x ==-，∴2,0m n =-⎧⎨=⎩． ②当1m n ≤≤时，max 1()(1)2f x f ==，则122n =，14n =，不合题意； ③当1m ≤时，()f x 在[,]m n 是单调递减，则221()221()22f m m m n f n n n m ⎧=-+=⎪⎪⎨⎪=-+=⎪⎩，无实解．综上，存在满足题意的,m n ，2,0m n =-=．【点睛】本题考查二次函数的解析式，考查二次函数的值域问题，解题关键是求出对称轴，由对称轴与已知区间的关系，分类讨论函数的最大值和最小值．21．（1）1(1,)2；（2）见解析；（3）8.【分析】（1）配方后可得顶点坐标；（2）求出A 点坐标，得到直线AF 的方程，与抛物线方程联立可解得B 点坐标，求出,AF BF 后可证结论成立；（3）令3y x =，求得其与2C 的一个交点的坐标，进而求得2C 解析式，再求得另一交点坐标即可得．【详解】（1）2211111(1)222y x x x =-+=-+，∴其顶点坐标为1(1,)2；（2）在21112y x x =-+中令0x =得1y =，所以(0,1)A ，此时直线AF 方程为1y =，由21112y y x x =⎧⎪⎨=-+⎪⎩，解得01x y =⎧⎨=⎩或21x y =⎧⎨=⎩，所以(2,1)B ， ∴1,1AF BF ==，所以112AF BF+=；（3）如图所示，设3y x =，设其与抛物线2C 交点的横坐标为01,x x ，且01x x <，根据题意要使m 最大，0x 也尽可能的大，因此02x =，则32y =，将(2,2)代入抛物线2C 方程得212(2)2h =-，解得14h =，20h =（舍去），∴221(4)2y x =-，令21(4)2x x =-，解得02x =，18x =，故m 的最大值是8.【点睛】本题考查二次函数的图象与性质，掌握二次函数的图象与性质是解题关键．解题关键是作出函数图象，利用数形结合思想求解．。

2020-2021学年黑龙江省哈师大附中高二下学期期中数学复习卷(2)(含解析)

2020-2021学年黑龙江省哈师大附中高二下学期期中数学复习卷(2)一、单选题（本大题共12小题，共60.0分）1.若复数(a∈R,i是虚数单位)是纯虚数，则a的值为()A. −2B. 2C. 1D. −12.设0<a<b，则下列不等式中正确的是()A. a<b<<B. a<<<bC. a<<b<D. <a<<b3.设α，β是两个不同的平面，直线m⊂α，则“m⊥β”是“α⊥β”的()条件A. 充分而不必要B. 必要而不充分C. 充分必要D. 既不充分也不必要4.当时，复数在复平面内对应的点位于：A. 第一象限B. 第二象限C. 第三象限D. 第四象限5.下列结论正确的是()A. 当且时，B. 当时，C. 当时，的最小值为2D. 当时，无最大值6.已知函数，则的值为()A. B. C. D.7.设函数f(x)是定义在R上周期为2的可导函数，若f(2)=2，且f′(2)=−4，则曲线y=f(x)在点(0,f(0))处切线方程是()x+2A. y=−2x+2B. y=−4x+2C. y=4x+2D. y=−128.秦九韶是我国南宋时期的数学家，普州(现四川省安岳县)人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图是实现该算法的程序框图，执行程序框图，若输入的a为2，2，5，x与n均为2，则输出的s等于()A. 34B. 17C. 12D. 79.执行如图所示的程序框图，输出的a值为()A. 3B. 5C. 7D. 910.过椭圆中心的直线与椭圆交于A、B两点，右焦点为(c,0)，则的最大面积是()A. AbB. bcC. AcD.11.下列有关命题的说法正确的是()A. 命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1”B. 命题“∃x∈R使得x2+x+1<0”的否定是：“γx∈R，均有x2+x+1<0”C. 在△ABC中，“A>B”是“cos2A<cos2B”的充要条件D. “x≠2或y≠1”是“x+y≠3”的非充分非必要条件12.已知双曲线的离心率为，若抛物线的焦点到双曲线的渐近线的距离为，则抛物线的方程为()．A. B. C. D.二、单空题（本大题共4小题，共20.0分）13.函数f(x)=x−√x，则f′(1)=______ ．14.华罗庚数学小组的同学们在图书馆发现一块古代楔形文字泥板的图片，同学们猜测它是一种乘法表的记录，请你根据这个猜测，判定表示______？(如图)15.计算机中常用的十六进制是逢16进1的记数制，采用数字0～9和字母A～F共16个记数符号，这些符号与十进制的数对应关系如下表：十六进制0123456789A B C D E F十进制0123456789101112131415例如，用十六进制表示：E+D=1B，则用十六进制表示：B×C=______ ．16.在下图所示的三角形数阵中，用a i,j(i≥j)表示第i行第j个数(i,j∈N∗),已知a i,1=a i,i=1−1(i∈N∗),且当i≥3时，每行中的其他各数均等于其“肩膀”上的两个数之和，即a i,j= 2i−1a i−1,j−1+a i−1,j(2≤j≤i−1),若a m,2>100,则正整数m的最小值为______________．三、解答题（本大题共6小题，共70.0分）17.选做题22.(本小题满分10分)如图设为圆的内接三角形，为圆的弦，且，过点作圆的切线与DB的延长线交于点E，AD与BC交于点F。

黑龙江省哈尔滨市哈师大附中2024届高三上学期期中数学试题(解析版)

哈师大附中2021级高三第三次调研考试数学试题（满分150分，考试时间120分钟）一、选择题（共8个小题，每题只有一个选项，每题5分，满分40分）1.已知复数2i z =-，则()iz z -的虚部为（）A.2- B.1- C.6D.2【答案】A 【解析】【分析】根据共轭复数的概念可得z ，根据复数的乘法运算求出()i z z -，即可得答案.【详解】复数2i z =-，则2i z =+则()(2i)(2i i)=42i i z z =---+-，则()i z z -的虚部为-2，故选：A2.下列函数中，在定义域上既是奇函数又是减函数的为（）A.sin 1y x =+B.1y x=C.[]()31,2y x x =-∈- D.y x x=-【答案】D 【解析】【分析】利用定义域关于原点对称，()f x -与()f x -关系，判断函数的奇偶性.【详解】A 选项：令()()sin 1R f x x x =+∈，则()()sin 1sin 1f x x x -=-+=-+，()f x 不具有奇偶性，所以不符合题意；B 选项：令()()10f x x x =≠，则()1f x x-=-，()()f x f x -=-，所以函数()f x 为奇函数，但在定义域内不具有单调性，所以不符合题意；C 选项：令()[]()31,2f x x x =-∈-，因为[]1,2x ∈-定义域不关于坐标原点对称，所以()f x 不具有奇偶性，所以不符合题意；D 选项：令()()R f x x x x =-∈，()()f x x x x x -=---=，即()()f x f x -=-，所以函数()f x 为奇函数，又()22,0,0x x f x x x ⎧-≥=⎨<⎩，所以0x ≥时，()f x 单调递减，0x <时，()f x 单调递减，满足题意.故选：D3.设a ，b 是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（）A.若//αβ，a α⊂，b β⊂，则//a bB.//a b ，a c ⊥则b c⊥C.若αβ⊥，a α⊂，b β⊂，则a b⊥r rD.若a αβ⋂=，//b a ，则//b α【答案】B 【解析】【分析】利用长方体模型，举例说明排除ACD ，B 结合异面直线所成角即可判断..【详解】在长方体1111ABCD A B C D -，令平面ABCD 是平面α，对于A ，若平面1111D C B A 为平面β，直线BC 为直线a ，直线11A B 为直线b ，显然//αβ，a α⊂，b β⊂，此时直线,a b 是异面直线，,a b 不平行，故A 错误；对B ，//a b ，a c ⊥，则直线a 与直线c 的夹角为π2，由异面直线所成角的定义知直线b 与直线c 的夹角也为π2，故b c ⊥，B 正确；对于C ，若平面11CDD C 为平面β，直线AB 为直线a ，直线DC 为直线b ，显然αβ⊥，a α⊂，b β⊂，此时直线,a b 平行，,a b 不垂直，故C 错误；对于D ，若平面11CDD C 为平面β，则DC αβ⋂=，直线DC 为直线a ，直线AB 为直线b ，显然//a b ，但b α⊂，此时直线b 不与平面α平行，故D 错误；故选：B.4.在数列{}n a 中，若11a =，22a =，21n n n a a a ++=-，则2024a =（）A.1-B.2- C.2D.1【答案】C 【解析】【分析】根据数列递推式求出数列的前面一些项，推出数列的周期，由此即可求得答案.【详解】由题意知数列{}n a 中，若11a =，22a =，21n n n a a a ++=-，故3211a a a =-=，4321a a a =-=-，5432a a a =-=-，6541a a a =-=-，7658761,2a a a a a a =-==-=，则{}n a 为周期为6的周期数列，故20243376222a a a ⨯+===，5.已知向量a ，b 的夹角为π3，且1a = ，2b = ，则向量a 在向量b 上的投影向量为（）A.bB.12bC.13b r D.14b【答案】D 【解析】【分析】根据投影向量的定义即可求得向量a 在向量b 上的投影向量为14b.【详解】易知πcos 13a b a b ⋅== ，由投影向量的定义可得向量a 在向量b上的投影向量为12241a b bb b b b =⋅⋅⋅=.故选：D.6.已知两个非零向量a 与b ，定义sin a b a b θ⋅⨯=⋅ ，其中θ为a 与b的夹角，若(2,3)a =- ，(1,1)b = ，则a b ⨯的值为（）A.5B.7C.2D.【答案】A 【解析】【分析】先利用平面向量夹角余弦的坐标表示求得cos θ，从而求得sin θ，进而利用定义即可得解.【详解】因为(2,3)a =- ，(1,1)b =，则|||a b ==21311a b ⋅=-⨯+⨯=，则,c s ||o ||a b a b a b ===⋅⋅，又[0,π]θ∈，则sin θ===5，则||a b ⨯==55.故选：A7.已知正项等比数列{}n a 中，320224a a =，则212222024log log log a a a ++⋅⋅⋅+=（）A.1012B.2024C.10122 D.20242【解析】【分析】根据等比数列的性质，结合对数的运算，即可求得答案.【详解】由题意知正项等比数列{}n a 中，320224a a =，则1120131202420230124a a a a a a =⋅⋅===⋅，故()()10122122220242122024232022log log log log log a a a a a a a a ++⋅⋅⋅+=⋅⋅⋅⋅⋅=1012202422log lo 4g 4202===，故选：B8.如图正方体的棱长为1，A ，B 分别为所在棱的中点，则四棱锥S ABCD -的外接球的表面积为（）A.16πB.32πC.41π16D.414π【答案】C 【解析】【分析】建立空间直角坐标系，求出相关点坐标，设外接球球心为(,,)x y z ，列方程组求解球心，验证后可得外接球半径，即可求得答案.【详解】以C 为坐标原点，以,CD CS 所在直线为,x z 轴，以与,CD CS 垂直的棱为y 轴，建立如图所示空间直角坐标系，则11(0,0,0),(1,1,)(01,)(001)(00),,,,,,1,2,2C A B SD ,设四棱锥S ABCD -的外接球球心为(,,)x y z ，半径为R ，则()()()()()22222222222222222211111221112x y z x y z x y z x y z x y z x y z ⎧⎛⎫⎛⎫-+-+-=+-+-⎪ ⎪ ⎝⎭⎝⎭⎪⎪++-=++⎨⎪⎛⎫⎪+-+-=++ ⎪⎪⎝⎭⎩，解得123812x y z ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩，即外接球球心为131(,,282，8R ==，验证8OD ==，符合题意，即四棱锥S ABCD -的外接球8R =，其表面积为24141π4π4π6416R =⨯=，故选：C二、多选题（共4个小题，每题不只有一个选项，每题5分，满分20分）9.已知向量()1,1a =-，()2,b n =- ，则下列说法正确的是（）A.若1n =，则a b -=B.若//a b，则2n =C.“2n >-”是“a 与b的夹角为钝角”的充要条件D.若()a b a +⊥，则0n =【答案】ABD 【解析】【分析】由向量的坐标表示可求得a b -=，A 正确；由向量平行的坐标表示可得B 正确；利用向量数量积的坐标运算可知“2n >-”是“a 与b的夹角为钝角”的必要不充分条件，C 错误；由向量垂直的坐标表示可求得0n =，D 正确.【详解】对于A ，由1n =可得()3,2a b -=- ，所以可得a b -== ，即A 正确；对于B ，由向量平行的坐标表示可得120n ⨯-=，解得2n =，可知B 正确；对于C ，若2n >-可得20a b n ⋅=--<r r，即a 与b的夹角为90180θ<≤ ，当2n =时，2b a =- 可得a 与b反向，充分性不成立；若a 与b的夹角为钝角可得20a b n ⋅=--<r r且2n ≠，解得2n >-且2n ≠，即必要性成立，所以“2n >-”是“a 与b的夹角为钝角”的必要不充分条件，C 不正确；对于D ，由()a b a +⊥ 可得()0a b a +⋅=，即()1110n -⨯--=，解得0n =，故D 正确；故选：ABD10.已知n S 是等差数列{}n a 的前n 项和，且70a >，5100a a +<，则下列选项正确的是（）A.数列{}n a 为递减数列B.80a <C.n S 的最大值为7SD.140S >【答案】ABC 【解析】【分析】由已知条件结合等差数列性质可判断B ；判断出数列的公差小于0，可判断A ；根据数列各项的正负情况以及单调性可判断C ；利用前n 项和公式结合等差数列性质判断D.【详解】设等差数列{}n a 的公差为d ，由于70a >，5100a a +<，故571080a a a a +=+<，则80a <，B 正确；870d a a =-<，则数列{}n a 为递减数列，A 正确，由以上分析可知127,,,0a a a > ，8n ≥时，0n a <，故n S 的最大值为7S ，C 正确；5101141414()14()202S a a a a ++==<，D 错误，故选：ABC11.南宋数学家秦九韶在《数书九章》中提出“三斜求积术”，即以小斜幂，并大斜幕，减中斜幂，余半之，自乘于上：以小斜幂乘大斜幂，减上，余四约之，为实：一为从隅，开平方得积可用公式S =（其中a 、b 、c 、S 为三角形的三边和面积）表示．在ABC 中，a 、b 、c 分别为角A 、B 、C 所对的边，若3b =cossin CC =，则下列命题正确的是（）A.ABCB.c =C.b =D.ABC【答案】AB 【解析】【分析】cossin CC=，利用两角和的正弦公式可得sin C A =，结合正弦定理角化边可判断B ；利用S =B 的结论化简并结合二次函数性质可得ABC 面积的最大值，判断A ，D ；假设b =正确，结合面积公式推出矛盾，判断C.cossin CC=，得sin sin cos C B C B C =，即sin cos cos sin ))C B C B C B C =+=+,即sin C A =，结合正弦定理得c =，B 正确；由S =S ==，当29a =，即3a =时，ABC 面积取到最大值是4=，A 正确，D 错误，对于C ，假设b =，由于3b =，c =，故1c a ==，则22222223191331()2024c a b c a =⎛⨯⎫+-⎭+--=--⎪⎝< ，这与三角形面积S =有意义不相符，C 错误，故选：AB12.在棱长为2的正方体1111ABCD A B C D -中，M 为BC 边的中点，下列结论正确的有（）A.AM 与11D B所成角的余弦值为10B.过三点A 、M 、1D 的截面面积为112C.四面体11A C BD 的内切球的表面积为π3D.E 是1CC 边的中点，F 是AB 边的中点，过E 、M 、F 三点的截面是六边形．【答案】AD 【解析】【分析】对于A ，建立空间直角坐标系，利用空间向量的夹角公式求解；对于B ，作出过三点A 、M 、1D 的截面，即可求其面积；对于C ，利用等体积法求出内切球的半径，即可求解；对于D ，利用几何作图，作出过E 、M 、F 三点的截面，即可判断.【详解】对于A ，以1A 为坐标原点，以11111,,A D A B A A 所在直线为,,x y z轴，建立空间直角坐标系，11(0,0,2),(1,2,2),(0,2,0),(2,0,0)A M B D ，则()()11120220,,,,,B A D M ==-,则111111cos ,10||||D B D B AM D B AM AM ⋅〈〉==，AM 与11D B 所成角的范围为π(0,]2，故AM 与11D B 所成角的余弦值为1010，A 正确；对于B ，设N 为1CC 的中点，连接MN ，则11MN BC AD ∥∥，且111122MN BC AD ==，则梯形1AMND 即为过三点A 、M 、1D 的截面，11MN AD AM D N ====322=，故梯形面积为为19222S =⨯=，B 错误；对于C ，如图，四面体11A C BD 的体积等于正方体体积减去四个角上的直三棱锥的体积，即33118242323V =-⨯⨯⨯=，该四面体的棱长为，其表面积为1π4sin 23S =⨯⨯=设四面体内球球半径为r ，则18,333r r ⨯=∴=，故四面体11A C BD 的内切球的表面积为24π4π3r =，C 错误；对于D ，如图，延长ME 和11B C 的延长线交于J ，则MCE △≌1JC E ，则1JC MC =，设H 为11A D 的中点，则11JC D H =，连接HJ ，则1JC G ≌1HD G ，则11C G D G =，故G 为11D C 的中点，故11HG A C AC FM ∥∥∥，同理延长,MF DA 交于L ，连接LH ，交1AA 于K ，K 即为1AA 的中点，则K ，E 在,FM HG 确定的平面内，则六边形FMEGHK 即过E 、M 、F 三点的截面，是六边形，D 正确，故选：AD【点睛】难点点睛：本题综合考查了空间几何中的线线角、截面、以及内切球问题，难度较大，解答时要发挥空间想象能力，明确空间的位置关系，结合空间向量以及等体积法和几何作图解决问题.三、填空题（共4个小题，每题5分，满分20分）13.函数()tan(6f x x π=-的定义域为___________.【答案】}2{|+3x x k k Z ππ≠∈，【解析】【分析】根据函数有意义列不等式，求函数()tan(6f x x π=-的定义域.【详解】∵()tan()6f x x π=-有意义，∴62x k πππ-≠+，Z k ∈，∴23x k ππ≠+,Z k ∈，∴函数()tan()6f x x π=-的定义域为}2{|+3x x k k Z ππ≠∈，，故答案为：}2{|+3x x k k Z ππ≠∈，，14.(2,1)a =- ，b = ，且()10a b a +⋅= ，则a ，b 的夹角为______．【答案】0##0︒【解析】【分析】求出向量(2,1)a =- 的模长，根据()10a b a +⋅= 求出a b ⋅ 的值，根据向量的夹角公式即可求得答案.【详解】由题意知(2,1)a =- ，b = ，且()10a b a +⋅= ，故a == ，则()210a b a a a b +⋅=+⋅= ，则5a b ⋅=，故cos ,1||||a b a b a b ⋅〈〉== ，由于,[0,π]a b 〈〉∈ ，故,0a b 〈〉= ，故答案为：015.在三棱锥O ABC -中，60AOB BOC AOC ︒∠=∠=∠=，则直线OA 与平面BOC 所成角的正弦值为_______.【答案】63【解析】【分析】构建正四面体模型，从而可求直线OA 与平面BOC 所成角的正弦值.【详解】如图，在射线OB 上截取OB OA '=，在射线OC 截取OC OA '=，得到如下图所示的几何体.因为OA OB '=，π3B OA '∠=，故B OA ' 为等比三角形，故OA OB AB ''==，同理OA OC AC ''==，而π3B OC '∠=，故OB C ''△为等比三角形，故OB OC B C ''''==，故几何体A B OC ''-为正四面体.过A 作平面B OC ''的垂线，垂足为S ，则S 为OB C ''△的中心，连接OS ，则AOS ∠为OA 与平面B OC ''（即平面BOC ）所成的角，设2OA a =，则23232323OS a =⨯⨯=，故3AS ==，故6sin 3AOS ∠=.所以线OA 与平面BOC 所成角的正弦值为63.故答案为：3.16.若{}n a 是公差不为0的等差数列，2a ，4a ，8a 成等比数列，11a =，n S 为{}n a 的前n （N n *∈）项和，则12101113412S S S ++⋅⋅⋅+的值为______．【答案】65132【解析】【分析】设数列{}n a 的公差为()d d ≠0，根据题意，求得1d =，得到(1)2n n n S +=，进而化简得到1211(2)(1)(2)(1)(1)(2)n n S n n n n n n n ==-++++++，结合裂项法求和，即可求解.【详解】设数列{}n a 的公差为()d d ≠0，因为248,,a a a 成等比数列，11a =，可得2111(3)()(7)a d a d a d +=++，即2(13)(1)(17)d d d +=++，解得1d =，所以1(1)1n a n n =+-⨯=，则(1)2n n n S +=，所以12(1)n S n n =+，则1211(2)(1)(2)(1)(1)(2)n n S n n n n n n n ==-++++++，所以1210111()111111122323341011111((2)3412S S S ---⨯⨯⨯⨯++⋅⨯⋅⋅=++⨯++ 1165121112132-=⨯⨯=.故答案为：65132.四、解答题（共6题，第17题10分，第18至第22题每题12分，共70分）17.在ABC 中a ，b ，c 分别为内角A ，B ，C 的对边，()()2sin 2sin 2sin a A b c B c b C =-+-．（1）求A 的大小；（2）若ABC 是锐角三角形，求cos cos B C +的取值范围．【答案】（1）π3A =（2）(2【解析】【分析】（1）应用正弦定理的边角互化结合余弦定理即可求解;（2）设ππ,B C αα=+=-33，ππ(,)α∈-66，代入结合两角和与差的余弦即可求解.【小问1详解】由()()2sin 2sin 2sin a A b c B c b C =-+-，由正弦定理得()()2222a b c b c b c =-+-，即222bc b c a =+-，则2221cos 22b c a A bc +-==，因为(0,π)A ∈，则π3A =【小问2详解】由（1）得2π3B C +=，设ππ,B C αα=+=-33，因为π,(0,)2B C ∈，则ππ(,)α∈-66，则ππcos cos cos()cos()33B C αα+=++-πcos cos cos (]αα==∈2132，则cos cos B C +的取值范围是(,1]2.18.已知数列{}n a 中，13a =，()12N 12,n n a n n a *-≥∈=-（1）求证：数列11n a ⎧⎫⎨⎬-⎩⎭是等差数列，并求出{}n a 的通项公式；（2）设()213n n n b n a =-⋅，求数列{}n b 的前n 项和nT【答案】（1）证明见解析；*21,N 21n n a n n +=∈-（2）13n n T n +=⋅【解析】【分析】（1）由递推公式112n n a a -=-可得111111n n a a --=--，即可证明数列11n a ⎧⎫⎨⎬-⎩⎭是等差数列，由等差数列定义即可求得*21,N 21n n a n n +=∈-；（2）由（1）可得()213n n b n =+⋅，利用错位相减法即可求得数列{}n b 的前n 项和13n n T n +=⋅.【小问1详解】当2n ≥时，由112n n a a -=-可得1111111n n n n a a a a -----=-=，易知10n a -≠；两边同时取倒数可得11111111111111n n n n n n a a a a a a ------==-+-=-+-，即111111n n a a --=--，由等差数列定义可得11n a ⎧⎫⎨⎬-⎩⎭是以11112a =-为首项，公差1d =的等差数列，所以()211111212n n n a -=+⨯=--，即2121n a n -=-，可得2121n n a n +=-，显然1n =时，13a =符合上式，即{}n a 的通项公式为*21,N 21n n a n n +=∈-；【小问2详解】由（1）可得()()213213n n n n b n a n =-⋅=+⋅，所以()()1213353213213n n n T n n -⋅+⋅+⋅⋅⋅+-⋅=++⋅，()()23133353213213n n n n T n +⋅+⋅+⋅⋅⋅++⋅=⋅+-，两式相减可得()1231332323232132n n n n T +-⋅+⋅+⋅⋅⋅⋅+⋅-+⋅=()()11313322132313n n n n n ++-=+⨯-+⋅=-⋅-，所以13n n T n +=⋅19.{}n a ，{}n b 是正项等比数列．且3n n n b a =-，且221210a a +=，（1）求{}n a 的通项公式；（2）设100n n c a =-，求数列{}n c 的前n 项和nT 【答案】（1）13n n a -=；（2）31100,6231100758,62n n n n n T n n ⎧--+<⎪⎪=⎨-⎪-+≥⎪⎩.【解析】【分析】（1）利用3212b b b b =，和221210a a +=建立方程组，求出113a q =⎧⎨=⎩，写出通项公式即可；（2）表示出数列100n n c a =-，在求数列{}n c 的前n 项和n T 时，进行分类讨论即可.【小问1详解】因为{}n a ，{}n b 是正项等比数列．且3nn n b a =-，所以3212b b b b =，即32322123333a a a a --=--，所以2111192739a q a q a a q--=--，又因为221210a a +=，所以21111222119273910a q a q a a q a a q ⎧--=⎪--⎨⎪+=⎩，解得113a q =⎧⎨=⎩，所以{}n a 的通项公式为：1113n n n a a q--==.【小问2详解】结合题意:13100n n a -=<,得到6n <，所以100,6100100,6n n n n a n c a a n -<⎧=-=⎨-≥⎩，当6n <时，()()()12312100100100n n n T c c c c a a a =++++=-+-++- ，()()()121331100100100100100132n n n n T a a a n n --=-+-++-=-=-+- ;当6n ≥时，()()()()()()12312567100100100100100100n n n T c c c c a a a a a a =++++=-+-++-+-+-++- ，()()()()()()121251001001002100100100n n T a a a a a a ⎡⎤=-+-++-+-+-++-⎣⎦ ，13311002379100758132n n n T n n --=-+⨯=-+-，综上所述：31100,6231100758,62n n n n n T n n ⎧--+<⎪⎪=⎨-⎪-+≥⎪⎩.20.如图，四棱锥P ABCD -的底面是矩形，AM PB ⊥，PD BD ⊥，M 为BC的中点，AD =，1DC =.（1）证明：PD ⊥底面ABCD（2）若1PD =，求二面角A MP B --的正弦值．【答案】（1）证明见解析（2）7014【解析】【分析】（1）先证明AM BD ⊥，即可证明AM ⊥平面PBD ，从而证明AM PD ⊥，根据线面垂直的判定定理即可证明结论；（2）建立空间直角坐标系，求得相关点坐标，求出平面AMP 和平面PBM 的法向量，根据空间角的向量求法，结合同角的三角函数关系，即可求得答案.【小问1详解】设,AM BD 交于E ，四棱锥P ABCD -的底面是矩形，AD =，1DC =,M 为BC的中点，则AD AB AB BM==故Rt DAB ∽Rt ABM ，则ADB BAM ∠=∠,而π2ADB ABD ∠+∠=，则π2BAM ABD ∠+∠=，故π2AEB ∠=，故AM BD ⊥，又AM PB ⊥，且,,BD PB B BD PB ⋂=⊂平面PBD ，故AM ⊥平面PBD ，PD ⊂平面PBD ，故AM PD ⊥，又PD BD ⊥，,,AM BD E AM BD =⊂ 平面ABCD ，所以PD ⊥底面ABCD ；【小问2详解】以点D 为坐标原点，以,,DA DC DP 所在直线为,,x y z轴，建立空间直角坐标系，则((0,0,1)2A B M P ，则(,1,0),(1),(222AM PM BM =-=-=- ，设平面PAM 的一个法向量为(,,)n x y z = ，则00n AM n PM ⎧⋅=⎪⎨⋅=⎪⎩ ，即0202x y x y z ⎧-+=⎪⎪+-=⎩，令1y =，则2)n = ，设平面PBM 的一个法向量为(,,)m a b c = ，则00m BM m PM ⎧⋅=⎪⎨⋅=⎪⎩ ，即0202a abc ⎧-=⎪⎪+-=⎩，令1b =，则(0,1,1)m = ，则314cos ,14||||n m n m n m ⋅〈〉=== ，由于二面角A MP B --的取值范围为[0,π]14=.21.已知双曲线C ：22221x y a b -=(),0a b >过点()，右焦点F为()，左顶点为A （1）求双曲线C 的方程（2）动直线12y x t =+交双曲线C 于M ，N 两点，求证：AMN 的垂心在双曲线C 上．【答案】（1）22144x y -=（2）联立直线（2）证明见解析【解析】【分析】（1）根据双曲线过的点以及双曲线的焦点坐标，列方程求出a 2，即可求得答案；12y x t =+与双曲线C 的方程，可得根与系数关系式，过点A 作MN 的垂线，设该垂线与双曲线的另一个交点为H ，结合根与系数的关系式化简AN MH k k ，从而证明H 为AMN 的高线,AH MH 的交点，即可证明结论.【小问1详解】由题意知双曲线C ：22221x y a b -=(),0a b >过点()，右焦点F为()，故228c a b =∴+=，即228b a =-，则222148a a -=-，解得24a =，故双曲线C 的方程为22144x y -=；【小问2详解】联立2212144y x t x y ⎧=+⎪⎪⎨⎪-=⎪⎩，得22344(4)0x tx t --+=，满足264(3)0t ∆=+>，设()()1122,,,M x y N x y ,则2121244(4)3,3t x x t x x ++==-，又(2,0)A -，过点A 作MN 的垂线，设该垂线与双曲线的另一个交点为H，则直线AH 的方程为y x =--24，由22424x y y x ⎧-=⎨=--⎩，可得2316200x x ++=，解得2x =-（舍）或103x =-，则108(,)33H -，则()11222122121811813223210201022333AN MHy y x t x t x t k k x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫++-+ ⎪ ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭==⎛⎫+ ⎪⎝⎭-++++()2121221122233344084236()2x x t x x t x t x x x x x ++--+++++=2222222222(4)2348448414(4)84204844t t t x t t x t t t x t t x -+++-----===--++++-+++，故MH AN ⊥，即H 为AMN 的高线,AH MH 的交点，即H 为AMN 的垂心，故AMN 的垂心在双曲线C 上.【点睛】难点点睛：本题考查双曲线方程的求解以及直线和双曲线位置关系中的证明问题，综合性强，难点在于证明AMN 的垂心在双曲线C 上，解答时要通过证明H 为AMN 的高线,AH MH 的交点来证明，计算过程较为复杂，需要计算十分细心.22.已知0a >，函数()2ln 12f x x x x ax =+-．（1）当0a =时，求曲线()y f x =在点()()1,1f 处的切线方程：（2）证明()f x 存在唯一的极值点（3）若存在a ，使得()f x a b ≥-+对任意,()0x ∈+∞成立，求实数b 的取值范围．【答案】（1）4230--=x y （2）证明见解析；（3）1,2⎛⎤-∞ ⎥⎝⎦【解析】【分析】（1）利用导数的几何意义求出其在()()1,1f 处的斜率，利用直线的点斜式方程即可求出结果；（2）令导函数()0ln 1f x x x a '=++-=，构造函数()1ln g x x x =++，求得其单调性可知当0a >时，导函数()f x '有唯一变号零点，即可得出证明；（3）将不等式恒成立问题转化成求()f x a +的最小值问题，构造函数()()21ln 1,0,2h x x x x -+∈=++∞，依题意可得()max 12b h x =≤，即可得出实数b 的取值范围．【小问1详解】当0a =时,可得()2ln 12f x x x x =+，即()1ln f x x x '=++，所以切线斜率为()12k f '==，又()112f =，所以切线方程为()1212y x -=-，即4230--=x y ；【小问2详解】易知()l 1n f x x x a '=++-，令()0f x '=可得1ln a x x =++，令()()1,0,ln g x x x x =++∈+∞，则()1110x g x x x+'=+=>在()0,∞+上恒成立，即可得()g x 在()0,∞+单调递增，当x 趋近于0时，()g x 趋近于-∞，当x 趋近于+∞时，()g x 趋近于+∞；其图象如下图所示：所以当0a >时，y a =与()g x 的图像仅有一个交点，令()0g x a =，则当()00,x x ∈时，()a g x >，即()0ln 1f x x x a '=++-<，()f x 在()00,x 单调递减，当()0,x x ∈+∞时，()a g x <，即()0ln 1f x x x a '=++->，()f x 在()0,x +∞单调递增，所以可知0x x =为()f x 的极小值点，即()f x 存在唯一的极值点；【小问3详解】由（2）可知()()0min f x f x =，此时001ln a x x =++，所以()f x a +的最小值为()()22000000000001111ln 1n 2ln l 2ln f x x x x x x x x x x x a =+-++++++=-++，令()()21ln 1,0,2h x x x x -+∈=++∞，则()211x h x x x x--+=='，当()0,1x ∈时，()0h x '>，即()h x 在()0,1上单调递增，()1,x ∈+∞时，()0h x '<，即()h x 在()0,1上单调递减；所以()h x 在1x =处取得极大值，也是最大值()()max 121h x h ==若存在a ，使得()f x a b ≥-+对任意,()0x ∈+∞成立，即存在a 使得()f x b a +≥在(0,)+∞成立，即()max 12b h x =≤，所以实数b 的取值范围为1,2⎛⎤-∞ ⎥⎝⎦.【点睛】方法点睛：在求解函数不等式恒（能）成立问题时，往往根据题意通过构造函数并利用导数求出函数单调性得出函数的最值，即可得出结论.。

2019-2020学年黑龙江省哈师大附中高一(上)期中数学试卷 (含答案解析)

2019-2020学年黑龙江省哈师大附中高一（上）期中数学试卷一、选择题（本大题共12小题，共60.0分）1.已知集合M={y|y≥0}，N={y|y=−x2+1}，即M∩N=()A. (0,1)B. [0,1]C. [0,+∞)D. [1,+∞)2.下列式子正确的是()A. 3a√a=√a(a>0)B. lg6lg2=lg6−lg2C. a−2=√a(a>0) D. lg[(−3)⋅(−5)]=lg(−3)+lg(−5)3.下列函数中，在区间(0,+∞)上为增函数的是()A. y=√x+1B. y=(x−1)2C. y=2−xD. y=log0.5(x+1)4.函数的图象恒过的定点是()A. (0,−3)B. (0,−2)C. (1,0)D. (0,0)5.已知a=log32，b=(log32)2，c=log423，则()A. a<c<bB. c<b<aC. a<b<cD. b<a<c6.函数f(x)=ln(x2−2x−8)的单调递增区间是()A. (−∞,−2)B. (−∞,−1)C. (1,+∞)D. (4,+∞)7.若函数f(x)=1−2x，g[f(x)]=x2−1x2(x≠0)，则g(3)=()A. 1B. 0C. 89D. 24258.若函数f(x)是奇函数，当x<0时，f(x)的解析式是f(x)=x(1−x)，则当x>0时，f(x)的解析式是f(x)=()A. −x(1−x)B. x(1−x)C. x(1+x)D. −x(1+x)9.设f(x)是定义在R上的偶函数，且在(−∞,0)上是增函数，则f(−2)与f(a2−2a+3)(a∈R)的大小关系为()A. f(−2)<f(a2−2a+3)B. f(−2)≥f(a2−2a+3)C. f(−2)>f(a2−2a+3)D. f(−2)=f(a2−2a+3)10.函数y=log3|x−1|的图象是()A. B. C. D.11. 已知函数y =√ax 2−ax +1的定义域R ，则实数a 的取值范围为( )A. a ≤0或a ≥4B. 0<a <4C. 0≤a ≤4D. a ≥412. 设函数f(x)={x 2+bx +2,x ≤0|2−x|,x >0，若f(−4)=f(0)，则函数y =f(x)−ln(x +2)的零点个数有( )A. 6B. 4C. 5D. 7 二、填空题（本大题共4小题，共20.0分） 13. 不等式3x−42x+5>0的解集为______ ．14. 若3a =2，b =log 23，则ab =________，2b +2−b =________．15. 若幂函数y =(m 2−2m −2)x −4m−2在x ∈(0,+∞)上为减函数，则实数m 的值是______．16. 已知函数f(x)=ax 2−12x −34(a >0)，若在任意长度为2的闭区间上总存在两点x 1、x 2，使得|f(x 1)−f(x 2)|≥14成立，则a 的最小值为______ ．三、解答题（本大题共6小题，共70.0分）17. 设集合A ={x|x 2−3x +2=0}，B ={x|ax +1=0}．(1)若A ∩B ={2}，求实数a 的值；(2)若B ⊆A ，求实数a 的值．18. 求值：(1)(√23×√3)6−4×(1649)−12−(−2008)0(2)2log32−log3329+log38−52log5319.已知函数f(x)=√2−x+lg(3x−13)的定义域为M．(Ⅰ)求M；(Ⅱ)当x∈M时，求g(x)=4x−2x+1+2的值域．20.已知a∈R，函数f(x)=log2(1x+a)．(1)当a=4时，求f(x)的定义域；(2)若关于x的方程f(x)−log2[(a−3)x+2a−4]=0的解集中恰有一个元素，求a的取值集合；(3)设a>0，若对任意t∈[1,2]，函数f(x)在区间[t,3t−1]上的最大值和最小值的差不超过1，求a的取值范围．21.设定义在(0,+∞)上的函数f(x)，对于任意正实数a、b，都有f(a⋅b)=f(a)+f(b)−1，f(2)=0，且当x>1时，f(x)<1．)的值；(1)求f(1)及f(12(2)求证：f(x)在(0,+∞)上是减函数．22.已知函数f(x)=−2x+b(x∈R)是奇函数．2x+1+a(1)求实数a，b的值;(2)若对任意的t∈R，不等式f(t2−2t)+f(2t2−k)<0恒成立，求实数k的取值范围．-------- 答案与解析 --------1.答案：B解析：【分析】本题考查交集运算，考查计算能力，属于基础题．可求出集合N ={y|y ≤1}，然后进行交集的运算即可．【解答】解：N ={y|y ≤1}，且M ={y|y ≥0}；∴M ∩N =[0,1]．故选B ．2.答案：A解析：解：∵a >0，∴3a √a =(a ⋅a 12)13=(a 32)13=a (32×13)=a 12=√a ，故A 正确；对于B ，lg6lg2≠lg6−lg2，故B 错误；对于C ，a −2=1a 2≠√a ，故C 错误；而D ，lg(−3)与lg(−5)无意义，故D 错误；故选A ．利用指数幂的运算性质与对数的性质即可得到答案．本题考查不等关系与不等式，考查有理数指数幂的化简求值与对数的运算性质，属于基础题． 3.答案：A解析：利用函数的单调性或函数的图像逐项验证.A.函数y =√x +1在[−1,+∞)上为增函数，所以函数在(0,+∞)上为增函数，故正确；B.函数y =(x −1)2在(−∞,1)上为减函数，在[1,+∞)上为增函数，故错误；C.函数y =2−x =(12)x 在R 上为减函数，故错误；D.函数y =log 0.5(x +1)在(−1,+∞)上为减函数，故错误． 4.答案：A解析：【分析】本题主要考查了对数函数及其性质，属于基础题．根据对数函数图象恒过定点(1,0)求出对应x ，y 的值，点(x,y)即为函数所过定点．解析：解：令x+1=1，得x=0，此时，故函数的图象恒过定点(0,−3)，故选A．5.答案：B解析：解：∵0=log31<a=log32<log33=1，∴0<b=(log32)2<a=log32，<log41=0，∵c=log423∴c<b<a．故选：B．本题考查对数函数比较大小，利用对数函数性质求解即可，属于中档题．6.答案：D解析：【分析】本题考查复合函数的单调区间以及对数函数的性质，属于基础题．令t=x2−2x−8>0，则y=lnt，在定义域内单调递增，根据复合函数的单调性，就是求t=x2−2x−8>0的单调增区间，由此即可得到答案．【解答】解：由x2−2x−8>0得：x∈(−∞,−2)∪(4,+∞)，令t=x2−2x−8，则y=lnt，在定义域内单调递增，而x∈(−∞,−2)时，t=x2−2x−8为减函数；x∈(4,+∞)时，t=x2−2x−8为增函数；故函数f(x)=ln(x2−2x−8)的单调递增区间是(4,+∞)，故选D．7.答案：B解析：本题考查函数的表示法，利用函数的解析式求值.要求g(3)，只要令f(x)=1−2x=3，求出x，再代入g[f(x)]的解析式即可．【解答】解：令f(x)=1−2x=3，得：x=−1，∴g(3)=g[f(−1)]=(−1)2−1=0．(−1)2故选B．8.答案：C解析：【分析】本题考查利用奇函数的性质求解析式，属于基础题．利用奇函数的性质即可求出f(x)的解析式是解题的关键．【解答】解：当x>0时，−x<0，则f(−x)=−x[1−(−x)]=−x(1+x)，由函数f(x)为奇函数可得f(x)=−f(−x)=x(1+x)，故选C．9.答案：B解析：【分析】本题考查函数的奇偶性与单调性的综合应用，涉及不等式的大小比较，属于基础题．根据题意，由函数的奇偶性与单调性分析可得f(x)在(0,+∞)上为减函数，进而分析可得f(2)≥f(a2−2a+3)，可得f(−2)=f(2)≥f(a2−2a+3)，即可得出答案．【解答】解：根据题意，f(x)是定义在R上的偶函数，且在(−∞,0)上是增函数，则f(x)在(0,+∞)上为减函数，因为a2−2a+3=(a−1)2+2≥2，所以f(2)≥f(a2−2a+3)，又由f(x)是定义在R上的偶函数，则f(−2)=f(2)≥f(a2−2a+3)，故选：B．10.答案：B解析：解：当x−1≥0时，即x≥1时，函数y=log3(x−1)，此时为增函数，当x−1<0时，即x>1时，函数y=log3(1−x)，此时为减函数，故选：B．根据函数的单调性即可判断．本题考查了复合函数的单调性和函数图象的识别，属于基础题．11.答案：C解析：【分析】根据根式函数的性质将定义域转化为ax 2−ax +1≥0恒成立即可．本题主要考查不等式恒成立问题，注意要对a 进行讨论．【解答】解：要使函数y =√ax 2−ax +1的定义域R ，则ax 2−ax +1≥0恒成立，若a =0，则不等式ax 2−ax +1≥0等价为1≥0恒成立，此时满足条件．若a ≠0，要使ax 2−ax +1≥0恒成立，则{a >0△=a 2−4a ≤0, 即{a >00≤a ≤4，解得0<a ≤4，综上0≤a ≤4．故选C ．12.答案：B解析：【分析】本题考查函数零点的个数判断，函数图象的应用，考查学生分析解决问题的能力，比较基础．先求出b ，再画出f(x)与y =ln(x +2)的图象，即可得出结论．【解答】解：∵函数f(x)={x 2+bx +2,x ≤0|2−x|,x >0，f(−4)=f(0)， ∴b =4，∴f(x)={x 2+4x +2,x ≤0|2−x|,x >0， f(x)={x 2+4x +2,x ≤0|2−x|,x >0与y =ln(x +2)的图象如图所示，∴函数y =f(x)−ln(x +2)的零点个数有4个，故选：B ．13.答案：{x|x >43或x <−52}解析：解：不等式3x−42x+5>0化为(3x −4)(2x +5)>0，所以不等式的解集为{x|x >43或x <−52}；故答案为：{x|x >43或x <−52}.将分式不等式化为整式不等式，解一元二次不等式即可．本题考查了分式不等式的解法，关键是转为整式不等式，然后解之． 14.答案：1;103解析：【分析】本题考查了对数的运算和指数幂的运算，属于基础题．根据对数的运算和指数幂的运算法则表示出a ，b ，即可求出ab 的值和2b +2−b 的值．【解答】解：3a =2，则a =log 32∵b =log 23，∴ab =log 32·log 23=1，，故答案为1;103． 15.答案：m =3解析：解：因为函数y =(m 2−2m −2)x −4m−2既是幂函数又是(0,+∞)的减函数，所以{m 2−2m −2=1−4m −2<0，⇒{m =3或m =−1m >−12，解得：m =3．故答案为：m =3．根据给出的函数为幂函数，由幂函数概念知m 2−m −1=1，再根据函数在(0,+∞)上为减函数，得到幂指数应该小于0，求得的m 值应满足以上两条．本题考查了幂函数的概念及性质，解答此题的关键是掌握幂函数的定义，此题极易把系数理解为不等于0而出错，属基础题．16.答案：14解析：【分析】要使函数f(x)在任意长度为2的闭区间上总存在两点x 1，x 2，使|f(x 1)−f(x 2)|≥14成立，只需要|f(14a −1)−f(14a )|≥14恒成立，从而可求实数a 的最小值．本题以新定义为素材，考查对新定义的理解，考查学生分析解决问题的能力，解题的关键是将问题转化为恒成立．【解答】解：要使函数f(x)=ax 2−12x −34(a >0)在任意长度为2的闭区间上总存在两点x 1，x 2，使|f(x 1)−f(x 2)|≥14成立，只需要|f(14a −1)−f(14a )|≥14恒成立，∵f(x)=ax 2−12x −34=a(x −14a )2−116a −34，∴|f(14a −1)−f(14a )|=|a|≥14，∵a >0，∴a ≥14，∴实数a 的最小值为14，故答案为：14． 17.答案：解：(1)因为A ∩B ={2}，所以2∈B ，则2a +1=0，解得a =−12，(2)由x 2−3x +2=0得，x =1或x =2，则A ={1,2}，因为B ⊆A ，所以B =⌀或{1}或{2}，当B =⌀时，则a =0，当B ={1}时，则a +1=0，得a =−1，当B ={2}时，则2a +1=0，得a =−12，综上得，实数a 的值是0或−1或−12．解析：(1)由A ∩B ={2}得2∈B ，把2代入ax +1=0代入求出a 的值；(2)由x 2−3x +2=0求出集合A ，由子集的定义和B ⊆A 求出B 所有的情况，再依次代入求出a 的值．本题考查交集及其运算，子集的定义，以及一元二次方程的解法，属于基础题．18.答案：解：(1)(213×312)6−4×[(47)2]−12−1=22×33−4×74−1=100 (2)2log 32−log 3329+log 38−52log 53=log 34−log 3329+log 38−5log 59=log 3(4×932×8)−9=log 39−9=−7解析：本题考查了对数与指数幂的运算性质，考查了推理能力与计算能力，属于基础题．(1)利用指数的运算性质即可得出；(2)利用对数的运算性质即可得出．19.答案：解：(Ⅰ)要使f(x)有意义，则{2−x ≥03x −13>0，∴−1<x ≤2，∴M =(−1,2]，(Ⅱ)g(x)=4x −2x+1+2=(2x )2−2⋅2x +2=(2x −1)2+1；∵x ∈(−1,2]；∴2x ∈(12,4]； ∴2x =1，即x =0时，g(x)min =1；2x =4，即x =2时，g(x)max =10；∴g(x)的值域为[1,10]．解析：本题考查函数的定义域、值域的概念及求法，指数函数的单调性，是基础题．(Ⅰ)要使得函数f(x)有意义，则需满足{2−x ≥03x −13>0，从而得出定义域M =(−1,2]；(Ⅱ)变形g(x)=(2x −1)2+1，根据x ∈M 即可得出2x ∈(12,4]，从而可求g(x)的最大和最小值，从而得出g(x)的值域．20.答案：解：(1)函数f(x)=log 2(1x +4)，由4+1x >0，即x(1+4x)>0，解得x >0或x <−14，可得f(x)的定义域为{x|x >0或x <−14}；(2)由f(x)−log 2[(a −3)x +2a −4]=0得log 2(1x +a)−log 2[(a −3)x +2a −4]=0．即log 2(1x +a)=log 2[(a −3)x +2a −4]，即1x +a =(a −3)x +2a −4>0，①则(a −3)x 2+(a −4)x −1=0，即(x +1)[(a −3)x −1]=0，②，当a =3时，方程②的解为x =−1，代入①，成立；当a =2时，方程②的解为x =−1，代入①，成立当a ≠3且a ≠2时，方程②的解为x =−1或x =1a−3，若x =−1是方程①的解，则1x +a =a −1>0，即a >1，若x =1a−3是方程①的解，则1x +a =2a −3>0，即a >32，则要使方程①有且仅有一个解，则1<a ≤32．综上，若方程f(x)−log 2[(a −3)x +2a −4]=0的解集中恰好有一个元素，则a 的取值范围是(1,32]∪{2，3}；(3)函数f(x)在区间[t,3t −1]上单调递减，由题意得f(t)−f(3t −1)≤1，即log 2(1t +a)−log 2(13t−1+a)≤1，即1t +a ≤2(13t−1+a)，即a ≥1t −23t−1=t−1t(3t−1)，设r =t −1，则0≤r ≤1，可得t−1t(3t−1)=r (r+1)(3r+2)=r 3r 2+5r+2，当r =0时，r 3r 2+5r+2=0；当0<r ≤1时，r 3r +5r+2=13r+2r +5在(0,√63)递增，在(√63,1)递减，可得r =√63处r3r 2+5r+2取得最大值5−2√6，可得a 的取值范围是a ≥5−2√6．解析：本题主要考查函数最值的求解，以及对数不等式的应用，利用换元法结合对勾函数的单调性是解决本题的关键．综合性较强，难度较大(1)由对数的真数大于0，结合分式不等式的解法，可得所求定义域；(2)根据对数的运算法则进行化简，转化为一元二次方程，讨论a 的取值范围进行求解即可；(3)根据f(x)的单调性得到f(t)−f(3t −1)≤1恒成立，利用换元法进行转化，结合对勾函数的单调性进行求解即可．21.答案：解：(1)令a =b =1得f(1)=f(1)+f(1)−1，得f(1)=1，∵f(2)=0，∴f(2×12)=f(2)+f(12)−1=f(1)，则0+f(12)−1=1，得f(12)=2(2)证明：设0<x 1<x 2，可得x 2x 1>1，可得f(x2x 1)<1，由f(x 2)=f(x 1⋅x 2x 1)=f(x 1)+f(x 2x 1)−1<f(x 1)，可得函数f(x)在(0,+∞)上是减函数．解析：(1)令a =b =1，a =2，b =12，即可求得f(1)及f(12)的值；(2)当x >1时，f(x)<1，根据函数单调性的定义讨论函数的单调性；本题主要考查抽象函数的应用，利用赋值法以及结合函数单调性的定义进行转化是解决本题的关键． 22.答案：解：(1)因为函数f(x)=−2x +b 2x+1+a (x ∈R)是奇函数，所以f(0)=0，得b =1，所以f(x)=−2x +12x+1+a ，又函数的定义域为R ，所以f(−1)=−f(1)，可得：−12+11+a =−−2+14+a ，解得a =2，所以a =2，b =1;(2)由(1)可得f(x)=−2x +12x+1+2=−12+12x +1，易得f(x)在(−∞,+∞)是减函数，又f(x)是奇函数，所以f(t 2−2t)+f(2t 2−k)<0可化为f(t 2−2t)<−f(2t 2−k)=f(k −2t 2)，所以t 2−2t >k −2t 2，即3t 2−2t −k >0恒成立，所以Δ=4+12k <0，解得k <−13．解析：本题考查函数的奇偶性和函数的单调性，属于中档题．(1)根据函数是奇函数，可得f(0)=0，f(−1)=−f(1)，即可解得；(2)先判断函数的单调性，结合函数的奇偶性，转换为3t 2−2t −k >0恒成立，从而解答即可．。

黑龙江省哈师大附中2020-2021学年高一英语上学期期中试题

黑龙江省哈师大附中2020-2021学年高一英语上学期期中试题本试卷分为第I卷（选择题）和第II卷（非选择题）两部分。

满分150分。

考试时间为120分钟。

第I卷第一部分听力（共两节，满分20分）第一节（共5小题；每小题1分，满分5分）听下面5段对话。

每段对话后有一个小题, 从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1.Wh en is the girl’s birthday?A.May 5th.B. May 15th.C. May 16th.2.W hat is the man’s hobby?A.Taking photos.B. Listening to music.C. Collecting stamps.3.What did the man buy yesterday?A. A shirt.B. A jacket.C. A sweater.4.Where does the conversation most probably take place?A.At school.B. At a hospital.C. At a stadium.5.What does the man mean?A.They should ask about the fee first.B.Their neighbor will help them paint the house.C.They haven’t got enough money to paint the house.第二节（共15小题；每小题1分，满分15分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题, 每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

长春市东北师大附中2020-2021学年上学期期中试卷高一数学试题(解析版)

东北师大附中2020-2021学年高一年级数学学科试卷上学期期中试卷一､单项选择题(本大题共8个小题，每小题4分，共32分，再每小题给出的四个选项中，只有一项符合题目要求)1. 已知集合{15}A x x =-<<，{}0B x x =≥，则A B =（）A. {5}x x <B. {05}x x <<C. {05}x x ≤<D. {1}x x >-【答案】C 【解析】【分析】直接由交集的定义求解即可【详解】解：因为{15}A x x =-<<，{}0B x x =≥，所以{05}A B x x ⋂=≤<，故选：C2. 已知集合{1,2,3,4}P =，则满足{1,2}Q P ⊆⊆的集合Q 的个数是（） A. 1 B. 2C. 3D. 4【答案】D 【解析】【分析】列举出满足题意的集合Q 后可得结论．【详解】解：由题题意可知，满足条件的集合Q 有{1,2}，{1,2,3}，{1,2,4}，{1,2,3,4}共4个. 故选：D ．3. 设x ∈R ，则“03x <<”是|1|1x -<的（） A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 既不充分也不必要条件【答案】B 【解析】由绝对值不等式的求解结合充分条件、必要条件的定义即可得解. 【详解】因为|1|1x -<，所以111x -<-<即02x <<，所以“03x <<”是“|1|1x -<”的必要不充分条仵. 故选：B.4. 下列各组函数表示同一函数的是（）A. ()f x x =，()2g x =B. ()21f x x =+，()21g t t =+C. ()1f x =，()x g x x= D. ()f x x =，()g x =【答案】B 【解析】【分析】求出各选项中两个函数的定义域，并化简函数解析式，利用函数相等的概念可得出合适的选项.【详解】对于A 选项，函数()f x x =的定义域为R ，函数()2g x =的定义域为[)0,+∞，两个函数的定义域不相同，A 选项中的两个函数不相等；对于B 选项，函数()21f x x =+与()21g t t =+的定义域均为R ，两个函数的对应法则也相同，B 选项中的两个函数相等；对于C 选项，函数()1f x =的定义域为R ，函数()xg x x=的定义域为{}0x x ≠，两个函数的定义域不相同，C 选项中的两个函数不相等；对于D 选项，函数()f x x =与()g x =R ，且()g x x ==，两个函数的对应法则不相同，D 选项中的两个函数不相等. 故选：B.5. 命题“10,13xx ⎛⎫∀≥≤ ⎪⎝⎭”的否定是（） A. 10,13xx ⎛⎫∃≥> ⎪⎝⎭ B. 10,13xx ⎛⎫∃<> ⎪⎝⎭ C. 10,13x x ⎛⎫∀<≤ ⎪⎝⎭D. 10,13xx ⎛⎫∀≥> ⎪⎝⎭【答案】A【分析】由全称命题否定为特称命题求解即可【详解】解：因为命题“10,13xx ⎛⎫∀≥≤ ⎪⎝⎭”，所以此命题的否定为10,13xx ⎛⎫∃≥> ⎪⎝⎭，故选：A6. 设0.70.7a =， 1.60.7b =，0.71.6c =，则的大小关系是（） A. a b c << B. a c b << C. b c a << D. b a c <<【答案】D 【解析】【分析】利用指数函数的单调性比较a 、b 的大小，利用幂函数的单调性比较a 、c 的大小，进而可得出这三个实数的大小.【详解】指数函数0.7xy =为R 上的减函数，则0.7 1.60.70.7>，即a b >；幂函数0.7y x=为()0,∞+上的增函数，则0.70.70.7 1.6<，即a c <.因此，b a c <<. 故选：D.7. 若0x ∃>，使得40x m x+-≤，则实数m 取值范围是（） A. 4m > B. 4m ≥C. 4m <D. 4m ≤【答案】B 【解析】【分析】不等式变形为4x m x+≤，然后求出4x x +在0x >时的最小值，即可得．【详解】解：∵40x m x+-≤，∴4x m x +≤，其中44x x +≥=，当且仅当4x x=，即2x =时等号成立， ∴4m ≥．故选：B8. 若函数2()2f x x ax =-+与()(1)x g x a -=+在区间[1,2]上都是减函数，则a 的取值范围是（） A. (1,0)- B. (0,1) C. (0,1] D. (1,0)(0,1)-【答案】C 【解析】【分析】先求出2()2f x x ax =-+的对称轴x a =，则由题意可得1a ≤，而()(1)xg x a -=+=11xa ⎛⎫ ⎪+⎝⎭在[1,2]上为减函数，则有1011a <<+，从而可求出a 的取值范围【详解】解：因为2()2f x x ax =-+的对称轴为x a =，抛物线开口向下，且在[1,2]上为减函数，所以1a ≤，因为()(1)xg x a -=+=11xa ⎛⎫ ⎪+⎝⎭，且在[1,2]上为减函数，所以1011a <<+，可得0a > 综上(0,1]a ∈，故选：C二､多项选择题(本大题共4个小题，每小题4分，共16分，再每小题给出的四个选项中，有多项符合题目要求，全部选对的得4分，部分选对的得2分，有选错的得0分)9. 下列命题中为真命题的是（） A. 若a b >，则1a b> B. 若22a b c c>，则a b > C. 若0c a b >>>，则a bc a c b>-- D. 若a b >，则33a b >【答案】BCD 【解析】【分析】根据不等式的性质判断．D 可用函数单调性判断．【详解】解析：A 项，若0b <时，1ab>显然不成立 B 项，22a b c c>，则a b >正确 C 项，若0c a b >>>，a bc a c b>--可变形为ac ab bc ab ->-，a b >正确D 项，3()f x x =为单调增函数，若a b >，则33a b >正确．故答案为：BCD ．10. 下列函数中，在各自定义域内既为增函数又为奇函数的是（） A. y x = B. 1y x=-C. ||y x x =D. x xxxa a y a a---=+ 【答案】ACD 【解析】【分析】根据基本初等函数的性质直接判断AB ，去掉绝对值号变为分段函数判断C ，化简D 可得2211xxa y a -=+，利用奇函数定义判断，利用单调性定义判断为增函数.【详解】A 项，y x =是奇函数，满足()()f x f x =--，且为增函数 B 项，1y x=-图像关于原点对称，是奇函数，单子啊定义域内不是单调增函数 C 项，22,0,0x x y x x x x ⎧≥==⎨-<⎩，在定义域内为增函数，且关于原点对称D 项，221()1x x x x xx a a a f x a a a ----==++，221()1x x xx x x a a a f x a a a -----==++ ()()f x f x =--成立，为奇函数.设12x x >()()()()()()()1212121212222222122222111111()1111x x x x x x x x x x a a a a a a f x f x a a a a -+-+----=-=++++ 分子()()()1212212122222211x x x x x x x x aa a a a a ++=-+--+--()12222x x a a =-，当1a >时，分子大于0分母明显大于0，故()()120f x f x ->得证，()f x 为增函数. 故选：ACD【点睛】基本初等函数的奇偶性，单调性根据函数解析式可直接得出结论，复杂的函数一般先化简解析式，然后利用奇偶性、单调性定义判断即可.11. 设函数()21,,,xf x a b c R =-∈，且a b c <<，下列说法正确的是（） A. 函数()y f x =有最小值0，无最大值B. 函数()y f x =与直线1y =的图像有两个不同的公共点C. 若()()()f a f c f b >>，则222a c +<D. 若()()f a f b =，则222a b +的取值范围是7,24⎡⎫⎪⎢⎣⎭【答案】ACD 【解析】【分析】由题意画出()f x 图像，由图像可知()f x 的最小值为0，无最大值，且图像与1y =只有一个公共点，从而可对选项A,B 进行判断，a b c <<，且()()()f a f c f b >>可知,,a b c 在图像中如图，()1f a <，且0a <，()1f c <，且0c >，由此可对C 选项进行判断，由图可知()1f a <，()1f b <，且0a <，0b >，从而由()()f a f b =得222a b +=，则2221722222(2)24a b a a a =-+=-++，再由021a <<，可求得其范围【详解】解：由题意画出()f x 图像.A 项，当0x =时，()0f x =，无最大值，所以A 正确B 项，与1y =只有一个公共点，所以B 错误C 项， a b c <<，且()()()f a f c f b >>可知，,,a b c 在图像中如图，()1f a <，且0a <，()1f c <，且0c >，则01c <<，则0()()1f c f a <<<，所以2112c a -<-，所以222a c +<，所以C 正确对于D ，由图可知()1f a <，()1f b <，且0a <，0b >，则()()f a f b =可写为2121ab-=-，1221a b -=-， 222a b +=，所以222b a =-，所以2221722222(2)24ab a a a =-+=-++，因为0a <，所以021a <<，所以22217722(2),2244222a a ab a ⎡⎫=-+=-+∈⎢⎣+⎪⎭所以D 正确，故选：ACD【点睛】关键点点睛：此题考查指数函数的图像和性质的应用，解题的关键是准确的画出函数的图像，利用数形结合的思想解题，属于中档题12. 已知函数2,1 ()2,1xxfxx xx⎧+<⎪=⎨+≥⎪⎩，下列说法正确的是（）A.((0))3f f=B. 函数()y f x=的值域为[2,)+∞C. 函数()y f x=的单调递增区间为[0,)+∞D. 设a R∈，若关于x的不等式()2x f x a≥+在R上恒成立，则a的取值范围是[2,2]-【答案】ABD 【解析】【分析】作出函数()f x的图象，先计算(0)f，然后计算((0))f f，判断A，根据图象判断BC，再作出2x y a=+的图象，它应在()y f x=图象的下方，对()f x的两段分别观察得出a的范围，综合后可得a的范围，从而判断D．【详解】解析：画出函数()f x图像.如图，A项，(0)2f=，((0))(2)3f f f==B项，由图像易知，值域为[2,)+∞C项，有图像易知，[0,)+∞区间内函数不单调D项，2x a +的斜率为12k =则增长速度小于||2x +，即||2a ≤时与左支无交点成立，右支最低点为x =，a +≤2a ≤≤ 综上||2a ≤，即[2,2]a ∈-．故选：ABD ．【点睛】关键点点睛：本题考查分段函数的性质，解题方法是数形结合思想，作出函数的图象，由图象观察得出函数的性质，用图象解不等式，使得结论的得出形象直观，易于理解．三､填空题(本大题共4个小题，每小题4分，共16分)13. 不等式121x <-的解集是__________. 【答案】3(,1),2⎛⎫-∞⋃+∞ ⎪⎝⎭【解析】【分析】根据分母的正负分类解不等式．【详解】解：当10x ->即1x >时，121x <-⇒122x <-⇒32x > 当10x -<即1x <时，121x <-⇒122x >-⇒32x < 综上3(,1),2⎛⎫-∞⋃+∞⎪⎝⎭．故答案为：3(,1),2⎛⎫-∞⋃+∞⎪⎝⎭． 14. 如图，一个长为5，宽为3的矩形被平行于边的两条直线所割，其中矩形的左上角是一个边长为x 的正方形，则阴影部分面积的最小值为______________.【答案】7 【解析】【分析】由题可得()2227S x =-+，利用二次函数性质即可求解. 【详解】解析：设阴影部分的面积为S ，其中03x << 则()222(5)(3)2815227S x x x x x x =+--=-+=-+当2x =时，S 有最小值为7. 故答案为：7.15. 已知关于x 的不等式为()()()110ax x a R -+≤∈，若1a =，则该不等式的解集是___________，若该不等式对任意的[]1,1x ∈-均成立，则a 的取值范围是___________. 【答案】 (1). {}11x x -≤≤ (2). []1,1- 【解析】【分析】当1a =时，结合一元二次不等式的解法即可求解；若不等式对任意的[]1,1x ∈-均成立，则需分类讨论参数a 的大小，进一步确定图像两零点与定区间[]1,1-的关系，进而求解. 【详解】当1a =时，()()110x x -+≤，解得：11x -≤≤. 故解集为{}11x x -≤≤. 令()()11y ax x =-+，[]1,1x ∈-. 当0a =时，1y x =--，为减函数，所以当1x =-时，y 取得最大值0，即0y ≤恒成立.当0a >时，()()11y ax x =-+，如图所示：要满足[]1,1x ∈-，()()110ax x -+≤恒成立，只需满足：00111a a a>⎧⎪⇒<≤⎨≥⎪⎩. 当0a <时，()()11y ax x =-+，如图所示：要满足[]1,1x ∈-，()()110ax x -+≤恒成立，只需满足：1011a a a<⎧⎪⇒-≤<⎨≤-⎪⎩. 综上：11a -≤≤.故答案为：{}11xx -≤≤∣，[]1,1- 【点睛】本题考查一元二次不等式的解法，含参二次不等式在定区间恒成立问题，属于中档题.16. 古希腊数学家希波克拉底曾研究过下面的几何图形.此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC 的斜边BC ，直角边AB ，AC .若以AB ，AC 为直径的两个半圆的弧长总长度为2π，则以斜边BC 为直径的半圆面积的最小值为___________.【答案】π 【解析】【分析】先设2,2AB x AC y ==，则BC =再根据题意得2x y +=，故结合不等式22222x y x y ++⎛⎫≥ ⎪⎝⎭得以斜边BC 为直径的半圆面积()222S x y ππ=+≥.【详解】解：设2,2AB x AC y ==，则BC =故根据以AB ，AC 为直径的两个半圆的弧长总长度为2π得()2x y ππ+=，故2x y +=，以斜边BC 为直径的半圆面积()222S xy π=+，由于222122x y x y ++⎛⎫≥= ⎪⎝⎭，所以()22222S x y πππ=+≥⨯=，当且仅当1x y ==时等号成立，故答案为：π【点睛】本题考查利用重要不等式22222x y x y ++⎛⎫≥ ⎪⎝⎭求最值，考查运算能力，是中档题.四､解答题(本大题共6个小题，共56分.解答应写出必要的文字说明，证明过程及演算步骤)17. 设集合{}2230A x x x =+-<，集合{}1B x x a =+<. （1）若3a =，求AB ；（2）设命题p ：x A ∈，命题q ：x B ∈，若p 是q 成立的必要不充分条件，求实数a 的取值范围. 【答案】（1）{}41x x -<<；（2）02a ≤≤. 【解析】分析】（1）化简集合,A B ，即得解；（2）化简集合,A B ，得到集合B 是集合A 的真子集，解不等式组1311a a --≥-⎧⎨-≤⎩即得解.【详解】（1）{}{}223031A x x x x x =+-<=-<<. 因为3a =，所以{}{}3142B x x x x =+<=-<<-，因此{}41A B x x ⋃=-<<；（2）{}31A x x =-<<，{}{}111B x x a x a x a =+<=--<<-，因为p 是q 成立的必要不充分条件，所以集合B 是集合A 的真子集，因此有1311a a --≥-⎧⎨-≤⎩，解得02a ≤≤.【点睛】本题主要考查集合的关系和运算，考查一元二次不等式和绝对值不等式的解法，考查必要不充分条件的应用，意在考查学生对这些知识的理解掌握水平. 18. （1）已知2x <，求()92f x x x =+-的最大值；（2）已知x 、y 是正实数，且9x y +=，求13x y+的最小值. 【答案】（1）4-；（2【解析】【分析】（1）根据x 的范围，可得20x ->，原式转化为()()()99222222f x x x x x ⎡⎤=+-+=-+-⎢⎥--⎣⎦，结合基本不等式，即可得结果；（2）根据基本不等式，“1”的妙用，即可求解. 【详解】（1）因为2x <，20x ∴->，()()()9922222422f x x x x x ⎡⎤∴=+-+=-+-≤-=-⎢⎥--⎣⎦，当且仅当922x x-=-时，即当1x =-时，等号成立，因此，函数()92f x x x =+-（2x <）的最大值为4-；（2）x 、y 是正实数，且9x y +=，19x y+∴=，则()131131314449999y x x y x y x y x y ⎛⎫⎛⎫⎛⎫++=++=++≥⋅= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，当且仅当3y x x y =且9x y +=时取等号，此时13x y +取得最小值49+. 【点睛】本题考查基本不等式的应用，考查“1”的妙用，考查逻辑思维能力和运算求解能力，属于常考题. 19. 已知函数2()4ax bf x x -=-是定义在(2,2)-上的单调函数，且是奇函数，满足1(1)3f =. （1）求()f x 的解析式并判断()f x 在(2,2)-上的单调性(不需证明)；（2）解关于t 的不等式(1)()0f t f t -+<. 【答案】（1）2()4x f x x =-，()f x 为增函数；（2）112t -<< 【解析】【分析】（1）由()f x 是(2,2)-上的奇函数，可得(0)0f =，即可求出b ，再结合1(1)3f =，可求出a ，即可得到()f x 的解析式，由(1)(0)f f >，可判断出()f x 为增函数.（2）由()f x 是(2,2)-上的奇函数，可将原不等式转化为(1)()f t f t -<-，结合()f x 在(2,2)-上为增函数，可得到12122222t t t t t -<--<-<-<<-<-<⎧⎪⎪⎨⎪⎪⎩，解不等式即可.【详解】（1）由()f x 是(2,2)-上的奇函数，则有(0)0f =，即04b-=，得0b =，将1x =代入，得()114133a b a f -===-，即1a =，所以2()4xf x x =-，由(1)(0)f f >，且()f x 是(2,2)-上的单调函数，可判断出()f x 为增函数. （2）由()f x 是(2,2)-上的奇函数，可将原不等式转化为(1)()f t f t -<-，因为()f x 在(2,2)-上为增函数，所以12122222t t t t t -<--<-<-<<-<-<⎧⎪⎪⎨⎪⎪⎩，解得112t -<<.20. 心理学研究表明，学生在课堂上个时间段的接受能力不同.上课开始时，学生的兴趣高昂，接受能力渐强，随后有一段不太长的时间，学生的接受能力保持较理想的状态；渐渐地学生的注意力开始分散，接受能力渐弱并趋于稳定.设课上开始x 分钟时，学生的接受能力为()f x (()f x 值越大，表示接受能力越强)，()f x与x 的函数关系为：20.1 2.644,(010)60,(1015)()3105,(1525)30.(2540)x x x x f x x x x ⎧-++<≤⎪<≤⎪=⎨-+<≤⎪⎪<≤⎩ （1）开讲后多少分钟，学生的接受能力最强？能维持多少时间？（2）试比较开讲后5分钟､20分钟､35分钟，学生的接受能力的大小；（3）若一个数学难题，需要至少56的接受能力(即()56f x ≥)以及12分钟时间，请问：老师能否及时在学生一直打达到所需接受能力的状态下讲述完这个难题？说明你的理由.【答案】（1）开讲后10分钟接受能力最强，且能维持5分钟；（2）接受能力在开讲后5分钟大于20分钟大于35分钟；（3）不能，理由见解析. 【解析】【分析】（1）求学生的接受能力最强其实就是要求分段函数的最大值，方法是分别求出各段的最大值取其最大即可；（2）比较5分钟、20分钟、35分钟学生的接受能力大小，方法是把5x =代入第一段函数，把20x 代入第二段函数中，把35x =代入第四段函数，比较大小即可；（3）在每段上解不等式()56f x ≥，求出满足条件的x ，从而得到接受能力56及以上的时间，然后与12进行比较即可【详解】解：（1）由题意可知，当010x <≤时，2()0.1(13)60.9f x x =--+ 所以当10x =时，()f x 的最大值为60，因为当1015x <≤时，()60f x =所以开讲后10分钟接受能力最强，且能维持5分钟. （2）(5)54.5f =，(20)45f =，(35)30f = 则接受能力在开讲后5分钟大于20分钟大于35分钟（3）当010x <≤，()56f x ≥ 解得610x ≤≤，当1015x <≤时，()6056f x =>，满足要求当1525x <≤时，310556x -+≥ 解得115163x <≤故111661033-=分钟<12分钟老师不能再所需接受能力和状态下讲完这个难题.21. 已知二次函数()f x 满足(1)()2f x f x x +-=，且(0)1f =. （1）求()f x 的解析式；（2）设函数()(2)(R)g x f x a a =-∈，[1,1]x ∈-，求()g x 的最大值()h a ，并求()h a 的最小值.【答案】（1）2()1f x x x =-+；（2）221372()133,2a a a h a a a a ⎧++≥-⎪⎪=⎨⎪-+<-⎪⎩，最小值为194. 【解析】【分析】（1）设二次函数为2()f x mx bx c =++，由(0)1f =，得1c =，再由(1)()2f x f x x +-=得，2()2mx m b x ++=，从而可求出,m b 的值，进而可求得二次函数的解析式；（2）由（1）可得22()4(42)1g x x a x a a =-++++，求得对称轴为214a x +=，由于抛物线开口向上，所以分2104a +≥和2104a +<求函数的最大值即可，【详解】解：（1）设二次函数为2()f x mx bx c =++，因为(0)1f =，所以1c =，所以2()1f x mx bx =++ 由题意：22(1)(1)112m x b x mx bx x ⎡⎤++++---=⎣⎦2()2mx m b x ++=所以022m b m +=⎧⎨=⎩，解得1,1m b ==-，所以2()1f x x x =-+（2）()2()(2)21g x x a x a =---+22()4(42)1g x x a x a a =-++++对称轴为214a x +=，抛物线开口向上当2104a +≥时，1x =-时，()g x 有最大值2()57h a a a =++ 即12a ≥-时，()h a 最小值为min 119()()24h a h =-= 当2104a +<时，1x =时，()g x 有最大值，2()33h a a a =-+ 即12a <-时，()119()24h a h >-= 综上2max2157,2()()1332a a a g x h a a a a ⎧++≥-⎪⎪==⎨⎪-+<-⎪⎩，min 19()4h a =【点睛】关键点点睛：此题考查待定系数法求函数解析式，考查二次函数的图像与性质的应用，求二次函数最值时，最关键的是讨论抛物线的对称轴与区间中点的位置关系，由于抛物线的开口向上，所以距离对称轴越远函数值越大22. 若定义在R 上的函数()f x 满足：1x ∀，2x ∈R ，都有()()()12121f x x f x f x +=++成立，且当0x >时，()1f x >-.（1）求证：()1f x +为奇函数；（2）求证：()f x 为R 上的增函数；（3）若(1)1f =，且0x ∀≥，0y ∀≥，()22222447f x m xy y m y ⎡⎤-+++≥⎣⎦恒成立，求实数m 的取值范围.【答案】（1）证明见解析；（2）证明见解析；（3）13m ≥或0m ≤. 【解析】【分析】（1）首先令121,0x x ==求得(0)1f =-，然后令12,x x x x ==-可得奇函数的结论；（2）设12x x >，由121212()(())()()1f x x f x x f x f x -=+-=+-+，再根据奇函数得，然后根据已知不等关系可得证；（3）由函数定义求得(4)7f =，由单调性化简不等式为关于x 的一元二次不等式，由一元二次不等式恒成立，判别式0∆≤可求得m 的范围．【详解】解：（1）(10)(1)(0)1f f f +=++(0)1f =-(()]()()1f x x f x f x +-=+-+ 1()()1f x f x -=+-+()1(()1)f x f x +=--+可得()1f x +为奇函数（2）设12x x >()()()()12121f x x f x f x +-=+-+ ()()()()12121f x x f x f x -=-+ ()()()12121f x x f x f x -=--()()()12121f x x f x f x -+=+∵12x x > ∴120x x ->当0x >时，()1f x >-，则等式左边大于0 故()()120f x f x ->，增函数得证. （3）(2)(11)(1)(1)13f f f f =+=++=(4)(2)(2)17f f f =++=.故()2222244(4)f x m xy ym yf ⎡⎤-+++≥⎣⎦()f x 为增函数，可得()22222444x m xy y m y -+++≥2222240x ymx my m y --+≥∵0x ≥恒成立 ∴0∆≤()222224440m y my m y --+≤整理得22230m y my -+≤230m m -≤13m ≥或0m ≤．【点睛】关键点点睛：本题考查抽象函数的奇偶性与单调性的证明，考查不等式恒成立问题，奇偶性与单调性定义的掌握是解题关键，利用赋值法与奇偶性、单调性结合完成证明，有了单调性，不等式可通过单调性进行化简转化为通常的二次不等式问题完成求解．。

黑龙江省哈尔滨师范大学附属中学2020-2021学年高一上学期期中考试数学试题(含答案)

哈师大附中2020级高一上期中考试数学试卷第Ⅰ卷（60分）一、选择题:本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合2{|0}1x A x x -=≥+，集合{|20}B x x =-<<，则A B =（） A ．{|21}x x -<<-B ．{|21}x x -≤<-C ．{|21}x x -<≤-D ．{|10}x x -≤≤2.函数0()f x =的定义域为（）A ．{|3}x x ≤B ．{|3}x x <C ．{|3,1}x x x ≤≠且D ．{|3,1}x x x <≠且 3.若a b >，则下列不等式成立的是（） A ．11a b <B ．22a b >C ．||||a c b c >D ．2211a bc c >++ 4.设a ∈R ，则“38a <”是“11a -<”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件 5.已知,a b R ∈，且0ab >，则下列结论恒成立的是（）A ．a b +≥B ．222a b ab +>C ．2a bb a +≥D ．11a b +>6.函数()f x 的单调增区间为（）A ．(,2]-∞B ．[2,)+∞C ．[1,2]D ．[2,3]7.已知函数()||2f x x x x =-，则下列结论正确的是（） A ．()f x 是偶函数，单调递增区间是[0,)+∞B ．()f x 是偶函数，单调递减区间是(,1]-∞C ．()f x 是奇函数，单调递减区间是[1,1]-D ．()f x 是奇函数，单调递增区间是(,0]-∞8.已知31()f x x x=+，则函数()f x 的图象的是( )9.如图所示的锐角三角形空地中，欲建一个面积不小于2300m 的内接矩形花园，则其边长x (单位：m )的取值范围是( )A ．[15,20]B ．[12,25]C ．[10,30]D ．[20,30]10.已知定义域(1,1)-的奇函数()y f x =，当[0,1)x ∈时，函数()f x 为增函数，若(3)f a -+2(9)0f a -<，则实数a 的取值范围为（）A.（22,3） B ．（3,10） C ．（22,4） D ．(2,3)-11.已知关于x 的方程2(3)10ax a x +-+=在区间1(,)2+∞上存在两个实数根，则实数a 的取值范围是（） A.2332a << B.213a <≤ C.9a ≥ D.293a <≤12.若函数()f x 同时满足：（1）对于定义域上的任意x ，恒有()()0f x f x +-=；（2）对于定义域上的任意12,x x ，当12x x ≠时，恒有11122122()()()()x f x x f x x f x x f x ->-，则称函数()f x 为“理想函数”.给出下列四个函数：①2()f x x =；②3()f x x =；③21()21x f x x -=+；④224,0()4,0x x x f x x x x ⎧+≥⎪=⎨-+<⎪⎩，其中被称为“理想函数”的有（） A ．1个 B ．2个C ．3个D ．4个第Ⅱ卷（90分）二、填空题：本大题共4小题，每小题5分，共20分．把答案填在答题卡上的相应位置.13.幂函数)(x f y =的图像过点(8,22)，则(9)f =________________．14.函数2()(21)5f x x a x =+-+在区间,1]-∞（单调递减，则实数a 的取值范围为____________ ． 15. 函数()21f x x x =-+的值域为______________________．16．设函数211()231x x f x x x x +≤⎧=⎨-+>⎩，，,①若()2f x =，则x =____________；②若()(1)2f x f x +->，则x 取值范围是_____________ .三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17.（本小题满分10分）已知集合2{|}A x a x a =<<，2{|540}B x x x =-+->．（Ⅰ）若1A ∉，求实数a 的取值范围；（Ⅱ）若:,:p x A q x B ∈∈，且p 是q 的充分不必要条件，求实数a 的取值范围．18.（本小题满分12分）已知()f x 是定义在R 上的奇函数，当0x >时，1()1f x x=+．（Ⅰ）求当0x ≤时，()f x 的解析式；（Ⅱ）用定义法证明：函数()f x 在区间()0+∞，上单调递增．19.（本小题满分12分）已知函数2()6f x x ax =-+(0)a >.（Ⅰ）关于x 的不等式()0f x <的解集为}32|{<<x x ，求()f x y x=在区间[2,4]的最小值；（Ⅱ）关于x 的不等式1()5f x x a<+. 20.（本小题满分12分）若二函数2()(0)f x ax bx c a =++≠满足(1)()2f x f x x +-=，且(0)1f =.（Ⅰ）求()f x 的解析式；（Ⅱ）当[1,3]x ∈时，不等式()(2)f x m x <+恒成立，求实数m 的取值范围．21.（本小题满分12分）已知函数2()1mx nf x x+=+是定义在[1,1]-上的奇函数，且(1)1f =. （Ⅰ）求()f x 的解析式；（Ⅱ）已知0,0a b >>，且128a b +=，若存在,a b 使()2bf t a >+成立，求实数t 的取值范围.22．（本小题满分12分）在函数()f x 定义域内的某个区间D 上，任取两个自变量12x x 、，若都有（Ⅰ）当1a =时，判断函数()f x 在区间(0,)+∞上的凹凸性，并证明你的结论；（Ⅱ）若对任意的(0,1)x ∈，都有()(1)1f x f x ⋅-≥恒成立，求实数a 的取值范围．。

黑龙江省哈尔滨师范大学附属中学学年高一上学期期中考试数学试卷Word版含解析

黑龙江省哈尔滨师范大学附属中学2021-2021 学年高一上学期期中考试数学一、选择题：共12 题1．全集,集合,那么A. B. C. D.【答案】 A【解析】此题考查了交、并、补集的混合运算；∵全集 ,集合∴∴.2．以下函数是偶函数并且在区间上是增函数的是A. B.C. D.【答案】 D【解析】此题考查命题真假的判断；在 A 中，是偶函数，在区间上是减函数，故 A 错误；在 B 中，是非奇非偶函数，在区间上是增函数，故 B 错误；在 C 中，是非奇非偶函数，在区间上是增函数，故 C 错误；在 D 中，是偶函数并且在区间上是增函数，故 D 正确 .3．不等式的解集为A. 或B. 或C.或D. 或【答案】 B【解析】此题考查了高次不等式的解法；不等式等价于∴将这三个根按从小到大顺序在数轴上标出来，如图：由图可看出不等式的解集为或.4．函数且恒过定点A. B. C. D.【答案】 D【解析】此题考查指数函数的图象和性质，考查恒过定点问题的求解方法;由得此时∴函数且恒过定点5．以下各组函数中不表示同一函数的是A.B.C.D.【答案】 C【解析】此题考查了判断两个函数是否为同一函数的问题；A.的定义域是 ,的定义域为定义域相同，对应关系也相同，∴是同一函数B.的定义域都是R ，定义域相同，对应关系也相同，∴是同一函数；C.的定义域为的定义域为，定义域不同，∴不是同一函数D. 的定义域都是R ，定义域相同，对应关系也相同，∴是同一函数.6．函数,那么函数的解析式为A. B. C. D.【答案】 A【解析】此题考查了函数解析式的求法；令,那么∴∴.7．,那么A. B. C. D.【答案】 B【解析】此题主要是考查对数值、指数值比拟大小；∵，，．.8．函数的定义域为,那么函数的定义域为A. B. C. D.【答案】 C【解析】此题考查了求函数的定义域问题，考查不等式问题;∵函数的定义域为∴解得 .9．为定义在实数集R 上的奇函数,且在区间(0,＋∞)上是增函数,又,那么不等式的解集是A. B.C. D.【答案】 D【解析】此题主要考查了函数的奇偶性的性质，以及函数单调性的应用等有关知识;∵为定义在实数集R 上的奇函数,且在区间(0,＋∞)上是增函数又∴在内是增函数∵∴或∴10．函数的单调递增区间为A. B. C. D.【答案】 C【解析】此题考查的知识点是复合函数的单调性;函数的定义域为令，那么，∵为增函数，在上为减函数，在上为增函数，故函数的单调递增区间为.11．函数的图象是【答案】 B【解析】此题考查函数的图象的综合应用，对数函数的单调性的应用;由得或∴函数的定义域为所以选项 A 、 D 不正确 ;当时 ,是增函数∴是增函数，排除 C.12．定义函数,假设存在常数,对于任意的,存在唯一的,使,那么称函数在上的“均值〞为,,那么函数在上的“均值〞为A. B. C. D.【答案】 B【解析】这种题型可称为创新题型或叫即时定义题型；由题意，令当时，选定∴.二、填空题：共 4 题13．函数,那么= ________.【答案】 10【解析】分段函数分段处理，这是研究分段函数图象和性质最核心的理念，具体做法是：分段函数的定义域、值域是各段上x、 y 取值范围的并集，分段函数的奇偶性、单调性要在各段上分别论证；分段函数的最大值，是各段上最大值中的最大者；令，那么，由，得所以，所以14．函数的值域为________.【答案】【解析】此题主要考查函数值域的求解，根据根式的性质是解决此题的关键;∵∴则,∴∴∴函数的值域是15．关于的方程有两个不相等的实数解,那么实数的取值范围是 ________.【答案】【解析】此题主要考查方程根的存在性以及个数判断;∵关于的方程有两个不相等的实数解，∴的图象和直线有 2 个交点，当时，，在R 上单调递增，不满足条件，故a＞ 0．当趋于时，的值趋于；当趋于时，的值趋于，故有，那么实数的取值范围为.16．函数在区间上的最大值为,最小值为 ,那么________.【答案】 4【解析】此题考查了函数的奇偶性和函数的单调性问题;∵ 是奇函数，∴而在时取最大值，时取最小值，∴，∴三、解答题：共 6 题17．计算：.【答案】===0【解析】此题考查对数的运算性质; 直接利用对数的运算性质化简得答案.18．集合.(Ⅰ )求集合及；(Ⅱ )假设 ,求实数的取值范围.【答案】 (Ⅰ ),(Ⅱ ),且由 .【解析】此题主要考查了不等式的计算能力和集合的根本运算;(Ⅰ )根据题意化简求出集合，集合．根据集合的根本运算即可求，(Ⅱ )先求出，在根据，建立条件关系即可求实数 a 的取值范围 .19．函数是定义在上的奇函数,当时 ,.(Ⅰ )求；(Ⅱ )求在上的解析式；(Ⅲ )求不等式的解集.【答案】 (Ⅰ )(Ⅱ )当时 ,,.(Ⅲ )①当时 ,,且 .②当时 ,且 .综上：解集为 .【解析】此题考查函数的奇偶性的应用，函数的解析式的求法，不等式的解法; (Ⅰ )利用函数的奇偶性即可求；(Ⅱ )利用函数的奇偶性的性质即可求的解析式；(Ⅲ )利用函数的解析式，列出不等式求解即可.20．函数是奇函数.(Ⅰ )求实数的值；(Ⅱ )用定义证明函数在上的单调性；(Ⅲ )假设对任意的 ,不等式恒成立 ,求实数的取值范围.【答案】 (Ⅰ )∵函数的定义域为R,且是奇函数,∴,解得,此时 ,满足 ,即是奇函数 ,∴.(Ⅱ ) 任取 ,且 ,那么 ,于是 =,即,故函数在上是增函数.(Ⅲ )由及是奇函数 ,知又由在上是增函数,得 ,即对任意的恒成立∵当时 ,取最小值 ,∴ .【解析】此题考查的知识点是函数恒成立问题，函数的奇偶性，函数的单调性; (Ⅰ )函数的定义域为，且是奇函数，故，解得值；(Ⅱ ) 任取，作差判断与的大小，根据函数单调性的定义，可得函数在上的单调性；(Ⅲ )根据函数的单调性和奇偶性得,即对任意的恒成立，求出的最小值即可.21．二次函数,且.(Ⅰ )求函数的解析式；(Ⅱ )假设函数 ,求函数的最值.【答案】 (Ⅰ )∴∴∴ ,∴ .(Ⅱ )①当时 ,即时 ,当时 ,当时；②当时 ,即时 ,当时 ,当时；③当时 ,即时 ,当时 ,当或 2 时；④当时 ,即时 ,当时 ,当时；⑤当时 ,即时 ,当时 ,当时 .【解析】此题考查的知识点是二次函数的图象和性质；(Ⅰ ) 由中，求出的值，可得函数f〔 x〕的解析式 .(Ⅱ )的图象开口朝上，且以直线为对称轴，由，对对称轴的位置进行分类讨论，可得函数的最值 .22．f ( x)当点在的图象上运动时,点在函数的图象上运动 (). log 2 x ,(Ⅰ )求和的表达式；(Ⅱ )关于的方程有实根,求实数的取值范围；(Ⅲ )设 ,函数的值域为 ,求实数的值 .【答案】 (Ⅰ )由得 ,.由得 ,.(Ⅱ )方程有实根 ,,别离得 .设.(Ⅲ )下面证明在上是减函数任取 ,那么即在上递减 ,故在在上递减,即解得 ,故.【解析】此题主要考查了求函数的解析式以及求利用函数的单调性求函数的值域；(Ⅰ )当点在的图象上运动可得，点在函数的图象上运动可得故再用代即可求出的表达式. (Ⅱ )由 (Ⅰ )可得要使关于的方程有实根，，可得：在有实根, 设，求出的取值范围即可. (Ⅲ )在上是减函数，即可求出的值.。

2020-2021学年黑龙江省哈师大附中高一上学期期中数学试题(解析版)

2020-2021学年黑龙江省哈师大附中高一上学期期中数学试题一、单选题1．设集合2|01x A x x -⎧⎫=≥⎨⎬+⎩⎭，集合{}|20B x x =-<<，则A B =（） A ．{}|21x x -<<- B ．{}|21x x --<≤ C ．{}|21x x -<≤-D ．{}|10x x -≤≤ 【答案】A【分析】由201x x -≥+求出集合A (注意分母不能为零)，然后根据集合的交运算求交集即可．【详解】由201x x -≥+得：2x ≥或1x <-，所以{|1A x x =<-或}2x ≥，又{}|20B x x =-<<，所以{}|21A B x x =-<<-．故选：A ．2．函数0()f x = ） A ．{|3}x x B ．{|3}x x < C ．{|3x x ，且1}x ≠ D ．{|3x x <，且1}x ≠【答案】D【分析】可看出，要使得()f x 有意义，需满足1030x x -≠⎧⎨->⎩，然后解出x 的范围即可．【详解】解：要使()f x 有意义，则1030x x -≠⎧⎨->⎩，解得3x <且1x ≠， ()f x ∴的定义域为{|3x x <，且1}x ≠．故选：D ．3．如果a b >，那么下列不等式中正确的是( ) ．A ．11a b <B ．22a b >C ．a c b c >D ．2211a b c c >++【答案】D【分析】通过反例1a =，1b =-，0c可排除,,A B C ；利用不等式的性质可证得D 正确.【详解】若1a =，1b =-，则1111a b =>=-，221a b ==，则A ，B 错误；若a b >，0c ，则0a c b c ==，则C 错误； 211c +≥ 21011c ∴<≤+，又a b > 2211a b c c ∴>++，则D 正确. 故选D 【点睛】本题考查根据不等式的性质比较大小的问题，对于此类问题通常采用排除法来进行排除，属于基础题.4．设a R ∈，则“38a <”是“|1|1a -<”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件【答案】B【分析】先化简解出不等式，由充分必要条件的定义判断出即可．【详解】解：由“38a <”得2a <，由“|1|1a -<”解得02a <<， 2a <推不出02a <<，02a <<可推出2a <，故“38a <”是“|1|1a -<”的必要不充分条件，故选：B ．5．函数y =的单调增区间是（）A ．(-∞，2]B ．[1，2]C ．[1，3]D ．[2，3] 【答案】B【分析】求出函数的定义域，利用复合函数单调性求出增区间即可．【详解】解：由2430x x -+-得2430x x -+，得13x ，设243t x x =-+-，则对称轴为2x =，则y =为增函数，要求函数y =的单调增区间，根据复合函数单调性可知，只需要求243t x x =-+-的递增区间，243t x x =-+-的递增区间为[1，2]，∴函数243y x x =-+-的单调增区间是[1，2]，故选：B ．6．已知函数()||2f x x x x =-，则有（）A ．()f x 是偶函数，递增区间为[0，)+∞B ．()f x 是偶函数，递增区间为(-∞，1]C ．()f x 是奇函数，递减区间为[1-，1]D ．()f x 是奇函数，递增区间为(-∞，0]【答案】C【分析】由已知结合函数奇偶性的定义可判断函数奇偶性，作出函数的图象，结合图象可求单调区间．【详解】解：因为()||2f x x x x =-，所以()22()f x x x x x x x f x -=--+=-+=-，故()f x 为奇函数，因为222,0()2,0x x x f x x x x ⎧-=⎨--<⎩，结合二次函数性质可知，()f x 的单调递减区间为[1-，1]．故选：C ．7．已知31()f x x x=+，则函数()f x 的图象的是（） A ． B ．C ．D ．【答案】A【分析】先判断函数的奇偶性，再根据基本不等式即可判断．【详解】解：31()()f x xf x x-=--=-，()f x 的定义域为(-∞，0)(0⋃，)+∞， ∴函数()f x 为奇函数，其图象关于原点对称，故排除CD ，当0x >时，333441111111()4?··33333327f x x x x x x x x x x x =+=+++=，当且仅当313x x=，即413x =<时取等号，故排除B ，故选：A ．【点睛】思路点睛：函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势；(3)从函数的奇偶性，判断图象的对称性；(4)从函数的特征点，排除不合要求的图象.8．在如图所示的锐角三角形空地中, 欲建一个面积不小于300m 2的内接矩形花园(阴影部分), 则其边长x(单位m)的取值范围是（）A ．[15,20]B ．[12,25]C ．[10,30]D ．[20,30]【答案】C 【详解】如图△ADE ∽△ABC ，设矩形的另一边长为y ，则22404040ADE ABC x S y S ∆∆-⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭=，所以40y x =-，又300xy ，所以(40)300x x -，即2403000x x -+，解得1030x .【考点定位】本题考查平面几何知识和一元二次不等式的解法，对考生的阅读理解能力、分析问题和解决问题的能力以及探究创新能力都有一定的要求.属于中档题.9．已知定义域()1,1-的奇函数()y f x =，当[)0,1x ∈时，函数()f x 为增函数，若()()2390f a f a -+-<，则实数a 的取值范围为（）A．()B．( C．()4 D ．()2,3-【答案】B【分析】推导出函数()f x 是定义在()1,1-上的增函数，且为奇函数，由()()2390f a f a -+-<可得()()233f a f a -<-，根据题中条件可得出关于实数a 的不等式组，由此可解得实数a 的取值范围.【详解】()f x 是定义在()1,1-上的奇函数，∴由()()2390f a f a -+-<，得()()()22399f a f a f a -<--=-．当[)0,1x ∈时，函数()f x 为增函数，所以，函数()f x 在(]1,0-上为增函数，所以，函数()f x 在()1,1-上是增函数，∴2213119139a a a a -<-<⎧⎪-<-<⎨⎪-<-⎩，解得3a <<所以，实数a的取值范围是(．故选：B ．【点睛】方法点睛：利用函数的奇偶性与单调性求解抽象函数不等式，要设法将隐性划归为显性的不等式来求解，方法是：（1）把不等式转化为()()f g x f h x >⎡⎤⎡⎤⎣⎦⎣⎦；（2）判断函数()f x 的单调性，再根据函数的单调性把不等式的函数符号“f ”脱掉，得到具体的不等式（组），但要注意函数奇偶性的区别.10．已知关于x 的方程2(3)10ax a x +-+=在区间1(,)2+∞上存在两个实数根，则实数a 的取值范围是（）A ．2332a <<B ．213a <C ．9aD ．293a < 【答案】B【分析】可设2()(3)1f x ax a x =+-+，0a ≠，讨论0a >，0a <，结合对称轴与区间的关系和1()2f 的符号、判别式的符号，解不等式可得所求范围．【详解】解：方程有两个实数根，显然0a ≠，可设2()(3)1f x ax a x =+-+，对称轴是32a x a -=，当0a >时，要使二次方程在区间1(,)2+∞上有两个实数根，如图所示，则需3122a a ->，且113()10242a f a -=++>，且2(3)40a a ∆=--，即为302a <<且23a >，且9a 或1a ，则213a <；当0a <时，要使二次方程在区间1(,)2+∞上有两个实数根，如图所示，则需3122a a ->，且113()10242a f a -=++<，且2(3)40a a ∆=--，即为302a <<且23<a ，且9a 或1a ，则a ∈∅．综上可得，a 的取值范围是213a <．故选：B ．【点睛】本题解题关键是结合二次函数的图象特征研究二次方程根的分布，分类讨论借助图象准确列出不等关系，突破难点.11．若函数()f x 同时满足：（1）对于定义域上的任意x ，恒有()()0f x f x +-=；（2）对于定义域上的任意1x ，2x ，当12x x ≠时，恒有()()()()11122122x f x x f x x f x x f x ->-，则称函数()f x 为“理想函数”．给出下列四个函数：①()2f x x =；②()3f x x =；③()2121x x f x -=+；④()224,04,0x x x f x x x x ⎧+≥=⎨-+<⎩，其中被称为“理想函数”的有（） A ．1个B ．2个C ．3个D ．4个【答案】B【分析】首先确定“理想函数”满足的条件为①奇函数；②函数在定义域内为单调递增函数；进一步对①②③④这四个函数进行判断即可．【详解】由（1）知：()f x 为定义域上的奇函数；由（2）知：()()()11120x x f x f x -->⎡⎤⎣⎦，可知()f x 单调递增.即“理想函数”满足①奇函数；②函数在定义域内为单调递增函数；对于①，()2f x x =是偶函数，在定义域内不单调递增，①不是“理想函数”；对于②，()3f x x =；满足函数是奇函数，在定义域内单调递增，②为“理想函数”；对于③，()()21212121x x f x f x x x --+-==≠--+-，函数不是奇函数，③不是“理想函数”；对于④，()224,04,0x x x f x x x x ⎧+≥=⎨-+<⎩，当0x <时，0x ->，则()()()2244f x x x x x f x -=--=-=-，又()00f =，可知()f x 为定义域上的奇函数；又当0x ≥时，()f x 单调递增，由奇函数性质知：()f x 在(],0-∞上单调递增，则()f x 在定义域内单调递增，④为“理想函数”.故选：B ．【点睛】关键点点睛：本题的解题关键是能够明确新定义函数的具体要求，即函数需为奇函数且在定义域内单调递增，进而利用函数奇偶性和单调性的判断方法依次判断各个选项.二、多选题12．若a ，b ∈R ，且ab >0，则下列不等式中，恒成立的是（）A ．a b +≥B ．222a b ab +≥C ．2b aa b +≥ D ．11a b +> 【答案】BC【分析】AD 可举例排除，BC 利用基本不等式来判断..【详解】解：A.当1a b ==-时，112--≥，不成立；B.由基本不等式得222a b ab +≥，当且仅当a b =时，等号成立，成立；C.由基本不等式得2b a a b +≥=，当且仅当a b =时，等号成立，成立；D.当1a b ==-时，112-->，不成立；故选：BC.【点睛】本题考查基本不等式的应用，是基础题.三、填空题13．幂函数()y f x =的图象过点(8,，则()9f =______.【答案】3【分析】设()af x x =，由已知得出()88a f ==a 的值，进而可求得()9f 的值.【详解】设幂函数()af x x =（a 为常数），幂函数()y f x =的图象过点(8,，8a ∴=，解得12a =， ()f x ∴=，因此，()93f =.故答案为：3.14．函数2()(21)5f x x a x =+-+在区间(-∞，1]单调递减，则实数a 的取值范围为__．【答案】(-∞，1]2-．【分析】由已知结合二次函数的单调性与对称轴的位置关系，求出实数a 的取值范围．【详解】解：因为2()(21)5f x x a x =+-+在区间(-∞，1]单调递减，所以1212a -，解得，12-a ．故答案为：(-∞，1]2-．15．函数g(x)＝2x ________．【答案】17,8⎡⎫-+∞⎪⎢⎣⎭【解析】＝t ，(t≥0)，则x ＋1＝t 2，即x ＝t 2－1，∴y＝2t 2－t －2＝2117248t ⎛⎫-- ⎪⎝⎭，t≥0， ∴当t ＝14时，y min ＝－178，∴函数g(x)的值域为17,8⎡⎫-+∞⎪⎢⎣⎭,故填17,8⎡⎫-+∞⎪⎢⎣⎭.四、双空题16．设函数21,1()23,1x x f x x x x +⎧=⎨-+>⎩． ①若()2f x =，则x =__；②若()(1)2f x f x +->，则x 取值范围是__．【答案】1 1(2，)+∞．【分析】①对x 分情况讨论，分段求出x 的值即可．②对x 分1x 和12x <和2x >三种情况讨论，分别求出()f x 和(1)f x -的解析式，化简整理解出x 的取值范围，最后再求并集即可．【详解】解：①当1x 时，()1f x x =+，12x ∴+=，1x ∴=，当1x >时，2()23=-+f x x x ， 2232x x ∴-+=，解得：1x =（舍去），综上所述，若()2f x =，则1x =．②()i 当1x 时，10x -，∴不等式()(1)2f x f x +->可化为：1(1)12x x ++-+>，即212x +>，解得：12x >， ∴112x <， ()ii 当12x <时，11x -，∴不等式()(1)2f x f x +->可化为：223(1)12x x x -++-+>，即232x x -+>， △140=-<，12∴<x ，()iii 当2x >时，11x ->，∴不等式()(1)2f x f x +->可化为：2223(1)2(1)32x x x x -++---+>，即22670x x -+>，△36427200=-⨯⨯=-<，2x ∴>，综上所述，x 取值范围是：1(2，)+∞．故答案为：1，1(2，)+∞．【点睛】本题主要考查了分段函数的应用，主要运用分类讨论的数学思想，考查了解一元二次不等式．五、解答题17．已知集合{}2A x a x a =<<，{}2540B x x x =-+->．（1）若1A ∉，求实数a 的取值范围；（2）若:p x A ∈，:q x B ∈，且p 是q 的充分不必要条件，求实数a 的取值范围．【答案】（1）[)1,-+∞；（2）[]0,2．【分析】（1）由1A ∈可得出实数a 的不等式组，求得对应的实数a 的取值范围，利用补集思想可求得当1A ∉时，实数a 的取值范围；（2）利用p 是q 的充分不必要条件，建立不等式关系，即可求实数a 的取值范围．【详解】（1）若1A ∈，则211a a <⎧⎨>⎩，解得1a <-. 因此，当1A ∉时，1a ≥-，则实数a 的取值范围是[)1,-+∞；（2）由2540x x -+->，得2540x x -+<，解得14x <<，即()1,4B =， :p x A ∈，:q x B ∈，且p 是q 的充分不必要条件，A ∴ B ，当A =∅时，即2a a ≤，解得01a ≤≤，满足题意；当A ≠∅时，由A B ，可得2214a a a a ⎧>⎪≥⎨⎪≤⎩，解得12a <≤.当2a =时，()2,4A =，()1,4B =，则A B 成立.综上所述，实数a 的取值范围为[]0,2.【点睛】结论点睛：本题考查利用充分不必要条件求参数，一般可根据如下规则求解：（1）若p 是q 的必要不充分条件，则q 对应集合是p 对应集合的真子集；（2）p 是q 的充分不必要条件，则p 对应集合是q 对应集合的真子集；（3）p 是q 的充分必要条件，则p 对应集合与q 对应集合相等；（4）p 是q 的既不充分又不必要条件，则q 对的集合与p 对应集合互不包含． 18．已知()f x 是定义在R 上的奇函数，当0x >时，1()1f x x=+．（Ⅰ）求当0x 时，()f x 的解析式；（Ⅱ）用定义法证明：函数()f x 在区间(0,)+∞上单调递增．【答案】（Ⅰ）0,0()11,0x f x x x =⎧⎪=⎨-<⎪⎩；（Ⅱ）证明见解析. 【分析】（Ⅰ）根据题意，由奇函数的定义可得(0)0f =，当0x <时，0x ->，求出()f x -的表达式，结合函数的奇偶性分析可得()f x 的表达式，综合可得答案；（Ⅱ）根据题意，利用函数的单调性定义可得结论．【详解】解：（Ⅰ）根据题意，()f x 是定义在R 上的奇函数，则(0)0f =，当0x <时，0x ->，则11()11f x x x-=+=+-，又由()f x为奇函数，则1()()1f x f x x=--=-，则当0x时，0,0()11,0x f x x x =⎧⎪=⎨-<⎪⎩，（Ⅱ）证明：设120x x <<，则1212121111()()11)()f x f x x x x x -=+-+=--121212121()x x x x x x x x -==-，又由120x x <<，则12()0x x -<0>，1210x x >，则12())0(f x f x -<，则函数()f x 在区间(0,)+∞上单调递增．【点睛】方法点睛：定义法判定函数()f x 在区间D 上的单调性的一般步骤： 1.取值：任取1x ，2x D ∈，规定12x x <， 2.作差：计算()()12f x f x -； 3.定号：确定()()12f x f x -的正负； 4.得出结论：根据同增异减得出结论. 19．已知函数2()6(0)f x x ax a =-+>．（Ⅰ）关于x 的不等式()0f x <的解集为{|23}x x <<，求()f x y x=在区间[2，4]的最小值；（Ⅱ）解关于x 的不等式1()5f x x a<+．【答案】（Ⅰ）5；（Ⅱ）答案见解析.【分析】（Ⅰ）根据不等式和方程的关系求出a 的值，从而求出()f x y x=的解析式，求出函数的最小值即可；（Ⅱ）问题转化为()10a x x a a ⎛⎫--< ⎪⎝⎭，通过讨论a 的范围，求出不等式的解集即可．【详解】解：（Ⅰ）不等式()0f x <的解集为{|23}x x <<2∴和3是方程260x ax -+=的根23a +=，解得：5a =故2()56f x x x =-+()665255f x y x x x x x∴==+-⋅-=当且仅当x =“=”成立故()f x y x=在区间[2，4]的最小值是5；（Ⅱ）1()5f x x a <+即2165x ax x a-+<+，(0)a >故22(1)0ax a x a -++<，故1()0a x x a a ⎛⎫--< ⎪⎝⎭1()0x x a a ⎛⎫∴--< ⎪⎝⎭①1a a <即1a >时，1x a a << ②1a a =即1a =时，不等式无解 ③1a a >即01a <<时，1a x a<< 综上：1a >时，不等式的解集是1{|}x x a a<< 1a =时，不等式无解01a <<时，不等式的解集是1}|{x a x a<<．20．若二次函数2()(0)f x ax bx c a =++≠满足(1)()2f x f x x +-=，且(0)1f =．（Ⅰ）求()f x 的解析式；（Ⅱ）当[1x ∈，3]时，不等式()(2)f x m x <+恒成立，求实数m 的取值范围．【答案】（Ⅰ）2()1f x x x =-+；（Ⅱ）7(5，)+∞.【分析】（Ⅰ）由(0)1f =，可得c ，再由恒等式的性质可得a ，b 的方程，求得a ，b ，即可得到()f x 的解析式；（Ⅱ）由题意可得2(1)120x m x m -++-<在[1x ∈，3]恒成立，考虑二次函数的图象，可得g （1）0<，且g （3）0<，解不等式可得所求范围．【详解】解：（Ⅰ）由(0)1f =，可得1c =，由22(1)()(1)(1)()22f x f x a x b x c ax bx c ax a b x +-=++++-++=++=，即为22a =，0a b +=，解得1a =，1b =-，则2()1f x x x =-+；（Ⅱ）当[1x ∈，3]时，不等式()(2)f x m x <+恒成立，即为21(2)x x m x -+<+恒成立，则2(1)120x m x m -++-<在[1x ∈，3]恒成立，设2()(1)12g x x m x m =-++-，可得g （1）1(1)120m m =-++-<，且g （3）93(1)120m m =-++-<，即为13m >且75m >，则75m >，即m 的取值范围是7(5，)+∞．【点睛】关键点点睛：本题考查二次函数的解析式的求法，以及不等式恒成立问题解法，考查待定系数法和转化思想、运算能力和推理能力，一元二次不等式恒成立，可转化为求出对应二次函数的最值．由最值满足的关系求得参数范围． 21．已知函数2()1mx nf x x+=+是定义在[]1,1-上的奇函数，且()11f =．（1）求()f x 的解析式；（2）已知0a >，0b >，且128a b+=，若存在a ，b 使()2b f t a >+成立，求实数t的取值范围．【答案】（Ⅰ）22()1xf x x=+；（Ⅱ）(2⎤-⎦．【分析】（1）根据题意分析可得()()0011f f ⎧=⎪⎨=⎪⎩，解可得m 、n 的值，则可得出函数()f x 的解析式；（2）因为128a b+=，所以112282b b a a a b ⎛⎫⎛⎫+=++ ⎪⎪⎝⎭⎝⎭，展开利用基本不等式可得122b a +≥，则只需使1()2f t >，然后求解不等式即可解得实数t 的取值范围．【详解】解：（1）根据题意，函数2()1mx nf x x +=+是定义在[]1,1-上的奇函数，则(0)0f =，可得0n =，则2()1mxf x x =+，又由()11f =得，则12m=，可得2m =，则22()1xf x x=+．（2）因为0a >，0b >，且128a b+=，所以1121211222828282b b b a a a a b a b ⎛⎛⎫⎛⎫⎛⎫+=++=++≥+= ⎪⎪ ⎪ ⎝⎭⎝⎭⎝⎭⎝，当且仅当22b a a b =，即14a =，12b =时，等号成立，若存在a ，b 使()2b f t a >+成立，则1()2f t >，即22112t t >+，解得：22t -<<[]1,1t ∈-，所以实数t的取值范围是(2⎤⎦．【点睛】本题主要考查根据函数奇偶性求解函数的解析式，考查基本不等式的运用，解答本题时注意以下几点：（1）当奇函数()f x 在0x =处有意义时，则有()00f =；（2）若存在a ，b 使()2b f t a >+成立，只需使min ()2b f t a ⎛⎫>+ ⎪⎝⎭，然后根据128a b +=，利用基本不等式求解2ba +的最小值． 22．在函数()f x 定义域内的某个区间D 上，任取两个自变量1x 、2x ，若都有1212()()()22++≤x x f x f x f ，则称()f x 为D 上的凹函数；若都有1212()()()22x x f x f x f ++≥，则称()f x 为D 上的凸函数．已知函数()()af x x a R x =-∈．（1）当1a =时，判断函数()f x 在区间(0,)+∞上的凹凸性，并证明你的结论；（2）若对任意的(0,1)x ∈，都有()()11f x f x ⋅-≥恒成立，求实数a 的取值范围．【答案】（1）()f x 在区间(0,)+∞上为凹函数．证明见解析；（2）1a ≥或14a -≤．【分析】（1）函数1()f x x x=-在区间(0,)+∞上为凹函数．由函数的凹凸性的定义，运用作差法和因式分解，可得结论；（2）将原不等式化为222(1)[(1)](1)a a ax x x x x x -+-≥+--，可令(1)t x x =-，运用二次函数求得t 的范围，解关于t 的不等式，结合恒成立思想可得a 的范围．【详解】解：（1）函数1()f x x x=-在区间(0,)+∞上为凹函数．理由：设1x 、2(0,)x ∈+∞，121212121212()()2111()()2222x x f x f x x x f x x x x x x +++-=---+-+ 22221212121212121212121212121212124()14()()()1·()()2()22()2()x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x -+--++-+=++=++++22121212121212124()()02()2()x x x x x x x x x x x x x x -+-==-++，即有1212()()()22++≤x x f x f x f ，即()f x 在区间(0,)+∞上为凹函数．（2）()()11f x f x ⋅-≥即为()(1)11a ax x x x--+≥-在(0,1)x ∈上恒成立，由01x <<，可得011x <-<，上式化为22()[(1)](1)a x a x x x ---≥-，即为2222[(1))][(1)](1)a a x x x x x x -+-+-≥-，即有222(1)[(1)](1)a a ax x x x x x -+-≥+--，可令(1)t x x =-，2111(1)0,244t x x x ⎛⎫⎛⎤=-=--+∈ ⎪ ⎥⎝⎭⎝⎦，则上式化为22(21)()0t a t a a +-+-≥，可得()(1)0t a t a ++-≥，解得1t a ≥-，或t a ≤-在104t <≤上恒成立，故10a -≤或14a -≥，解得1a ≥或14a -≤．【点睛】本题解题关键是紧扣新定义，利用作差法证明1212()()()22++≤x x f x f x f ，即判断()f x 是凹函数；恒成立问题的常见方法是分离参数法、构造函数法和数形结合法，本题采用分离参数法，巧妙换元(1)t x x =-，再进行因式分解，即转化成1t a ≥-，或t a ≤-在104t <≤上恒成立，即突破难点.。

2023-2024学年黑龙江省哈尔滨师大附中高三上学期第二次调研考试数学试题及答案

哈师大附中2021级高三第二次调研考试数学试题（满分150分，考试时间120分钟）一、选择题（前8个小题为单选题，每题只有一个选项，每题5分，满分40分；后4小题为多选题，每题不只有一个选项，每题5分，满分20分）1.已知集合{}25,A y y x x ==-∈R，(){}3log 22,B x x x =+<∈R ，则A B = （）．A.{}27x x -<<B.{}5x x ≤C.{}57x x ≤< D.{}25x x -<≤2.已知:02p x <<，那么p 的一个充分不必要条件是（）．A 01x << B.11x -<< C.02x <≤ D.03x <<3.()sin 1230-︒=（）．A.12B. 12-C.D.4.已知2727a ⎛⎫= ⎪⎝⎭，2737b ⎛⎫= ⎪⎝⎭，27log 2c =，则（）．A.a b c<< B.b a c<< C.c b a<< D.c a b<<5.若正数,x y 满足63x y +=，则31y x y+最小值为（）．A 4B.98C. D.26.已知函数()f x 的定义域为R ，其导函数为()f x '，且()()50x f x '-<，则下列关系一定正确的是（）．A.()()()3524f f f +<B.()()()4625f f f +<C.()()050f f ⋅=D.()()()3725f f f +=7.将函数()()πsin 206g x x ωω⎛⎫=-> ⎪⎝⎭图像上所有点的横坐标变为原来的2倍，纵坐标不变，得到函数()f x ，函数()f x 在区间()0,π上有且只有两个零点，则ω的取值范围为（）．.的.A. 611,56⎛⎤ ⎥⎝⎦B. 611,56⎛⎫⎪⎝⎭C. 713,66⎛⎤⎥⎝⎦D. 713,66⎛⎫⎪⎝⎭8. 我国古代数学家赵爽在《周髀算经》一书中利用“赵爽弦图”巧妙的证明了勾股定理，该图形是以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成．类比“赵爽弦图”，可构造如图所示的图形，它是由3个全等的三角形与中间一个小等边三角形拼成的一个较大的等边三角形，若3AF EF = ，3AF =，则AF AB AC λμ=+ ，则λμ+=（）．A.1519B.619C.919D.多选题（共4个小题，每题不只有一个选项，每题5分，满分20分）9. 如图所示是()y f x =的导数()y f x '=的图象，下列结论中正确的有（）．A. ()f x 的单调递增区间是()()1,24,-+∞B. =1x -是()f x 极小值点C. ()f x 在区间()2,4上单调递减，在区间()1,2-上单调递增D. 2x =是()f x 极小值点10. 若0a >，0b >，4a b +=，则下列结论正确的是（）．A.2≤ B. 228a b +≥C. ()()221332a b +++≤ D. 2243a b +≥11. 函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>><⎪⎝⎭的部分图象如图所示，下列说法正确的是（）．的的A. 函数()21y f x =+的周期是π2B. 点5π,03⎛⎫⎪⎝⎭是函数()y f x =的图象的对称中心C. 函数()y f x =在5ππ,6⎡⎤--⎢⎥⎣⎦上单调递减D. ()1f x >对于5π2π,3x ⎡⎤∀∈--⎢⎥⎣⎦恒成立12. 已知定义在R 上的奇函数()f x 满足()()2=f x f x -，当[]0,1x ∈时，()f x x =，定义符号函数1,0sgn 0,01,0x x x x >⎧⎪==⎨⎪-<⎩，则下列结论正确的是（）．A. ()sgn f x ⎡⎤⎣⎦是奇函数B. ()()2023sgn 2023f f =⎡⎤⎣⎦C. ()()sgn 211k f k +=⎡⎤⎣⎦∈Z D. ()sgn f x ⎡⎤⎣⎦关于直线3x =对称二、填空题（共4个小题，每题5分，满分20分）13. 已知幂函数()()2277mf x m m x =-+为非奇非偶函数，则实数m =__________．14. 函数()()12log 4f x ax =-在区间()2,3上是单调递增，则实数a 的取值范围是___________．15. 已知向量a ，b ，2= a ，3b = ，a 与b的夹角为2π3，则a xb + 的值最小时，实数x 的值为__________．16. 在ABC中，AB =，π3C =，当3BC AC +取最大值时，AC =__________．三、解答题（共6题，第17题10分，第18至第22题每题12分，共70分）17. 已知角α的顶点与坐标原点重合，始边与x 轴的非负半轴重合，角α的终边过点()5,12A --．（1）求3πsin 22α⎛⎫+ ⎪⎝⎭的值；（2）若()0,2πα∈，π0,2β⎛⎫∈ ⎪⎝⎭，()4sin 5αβ-=-，求cos β的值．18. 已知正四棱柱1111ABCD A B C D -中，1AB =，12AA =，E 为线段11A B 的中点，F 为线段AB 的中点．（1）求直线1BB 与平面1AEC 所成角的正弦值；（2）证明：直线//FC 平面1AEC 并且求出直线FC 到平面1AEC 的距离．19. 已知数列{}n a 为等差数列，且2410a a +=，416S =．（1）求{}n a 的通项公式；（2）数列{}n b满足)n b n *=∈N ，数列{}n b 的前n 项和为n S ，求证：112nS <．20. 在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若()()()sin sin sin sin a b A B c B C +-=+．（1）求角A 的大小；（2）若D 为BC 上一点，12BAD BAC ∠=∠，3AD =，求4b c +的最小值．21. 已知双曲线()2222:10,0x y C a b a b -=>>的渐近线为y x =，点P 在C 上，直线:l y kx t =+与双曲线C 相交于两点M ，N ，线段MN 的垂直平分线分别与x ，y 轴相交于A ，B两点．（1）若直线l 过点()0,1，且点M ，N 都在双曲线的左支上，求k 的取值范围；（2）若AOB （O 为坐标原点）的面积为812，且0k ≠，求k 的取值范围．22. 已知函数()1eln -=-x f x a x ．（1）当1a =-时，求曲线()y f x =在()()1,1f 处的切线方程；（2）当0a >，若不等式()ln f x a a a ≥+恒成立，求a 的取值范围．哈师大附中2021级高三第二次调研考试数学试题（满分150分，考试时间120分钟）一、选择题（前8个小题为单选题，每题只有一个选项，每题5分，满分40分；后4小题为多选题，每题不只有一个选项，每题5分，满分20分）1. 已知集合{}25,A y y x x ==-∈R，(){}3log 22,B x x x =+<∈R ，则A B = （）．A. {}27x x -<< B. {}5x x ≤C. {}57x x ≤< D. {}25x x -<≤【答案】D 【解析】【分析】根据二次函数的值域与对数不等式的运算求解即可.【详解】{}5A y y =≤，(){}{}{}33log 2log 902927B x x x x x x =+<=<+<=-<<.故}5A B x ⋂=<≤.故选：D2. 已知:02p x <<，那么p 的一个充分不必要条件是（）．A. 01x << B. 11x -<< C. 02x <≤ D. 03x <<【答案】A 【解析】【分析】根据充分不必要条件定义，结合推出关系依次判断各个选项即可.【详解】对于A ，0102x x <<⇒<< ，0201x x <<<<¿，01x ∴<<是p 的一个充分不必要条件，A 正确；对于B ，1102x x -<<<< ¿，0211x x <<-<<¿，11x ∴-<<是p 的一个既不充分也不必要条件，B 错误；对于C ，0202x x <≤<< ¿，0202x x <<⇒<≤，20x ∴<≤是p 的一个必要不充分条件，C 错误；对于D ，0302x x <<<< ¿，0203x x <<⇒<<，03x ∴<<是p 的一个必要不充分条件，D 错误.故选：A.3. ()sin 1230-︒=（）．A12B. 12-C.D. 【答案】B 【解析】【分析】利用诱导公式及特殊角的三角函数值计算即可.【详解】()()sin 1230sin 3604210sin 210-︒=-︒⨯+︒=︒()1sin 18030sin 302=︒+︒=-︒=-．故选：B 4. 已知2727a ⎛⎫= ⎪⎝⎭，2737b ⎛⎫= ⎪⎝⎭，27log 2c =，则（）．A. a b c << B. b a c<< C. c b a<< D. c a b<<【答案】D 【解析】【分析】由幂函数、指数函数的单调性即可比较大小.【详解】一方面因为幂函数27y x =在[)0,∞+上单调递增，所以227723077a b ⎛⎫⎛⎫<=<=⎪ ⎪⎝⎭⎝⎭，另一方面因为对数函数27log y x =在()0,∞+上单调递减，所以2277log 2log 20c =<=，结合以上两方面有：0c a b <<<.故选：D.5. 若正数,x y 满足63x y +=，则31y x y+的最小值为（）．A. 4 B.98C. D. 2【答案】A 【解析】【分析】由已知等式可得31323y y x x y x y+=++，利用基本不等式可求得结果.【详解】,x y 为正数，63x y +=，.3136322433y y x y y x x y x y x y +∴+=+=++≥+=（当且仅当33y x x y =，即1x =，13y =时取等号），即31y x y+的最小值为4.故选：A.6. 已知函数()f x 的定义域为R ，其导函数为()f x '，且()()50x f x '-<，则下列关系一定正确的是（）．A. ()()()3524f f f +<B. ()()()4625f f f +<C. ()()050f f ⋅=D. ()()()3725f f f +=【答案】B 【解析】【分析】根据()()50x f x '-<可确定()f x 单调性，并得到()()max 5f x f =；由反例可说明ACD 错误；根据单调性可说明B 正确.【详解】()()50x f x '-< ，∴当5x <时，()0f x ¢>；当5x >时，()0f x '<；()f x \在(),5-∞上单调递增，在()5,+∞上单调递减；又()f x 在R 上可导，()f x \连续，()()max 5f x f ∴=；对于A ，若()()25e x f x --=，满足()f x 在(),5-∞上单调递增，在()5,+∞上单调递减，()4413e e f -∴==，()05e 1f -==，()114e e f -==，()()()412351124e ef f f ∴+=+>>=，A 错误；对于B ，()()45f f < ，()()65f f <，()()()4625f f f ∴+<，B 正确；对于C ，若()()251f x x =--+，满足()f x 在(),5-∞上单调递增，在()5,+∞上单调递减，()024f ∴=-，()51f =，()()05240f f ∴⋅=-≠，C 错误；对于D ，若()5e e xf x x =-，满足()f x 在(),5-∞上单调递增，在()5,+∞上单调递减，()5333e e f ∴=-，()5777e e f =-，()5555e e f =-，()()()5373710e e e f f ∴+=-+，()552510e 2e f =-，又375e e 2e +≠，()()()3725f f f ∴+≠，D 错误.故选：B.7. 将函数()()πsin 206g x x ωω⎛⎫=-> ⎪⎝⎭图像上所有点的横坐标变为原来的2倍，纵坐标不变，得到函数()f x ，函数()f x 在区间()0,π上有且只有两个零点，则ω的取值范围为（）．A. 611,56⎛⎤ ⎥⎝⎦B. 611,56⎛⎫⎪⎝⎭C. 713,66⎛⎤⎥⎝⎦ D. 713,66⎛⎫⎪⎝⎭【答案】C 【解析】【分析】利用函数的伸缩变换及三角函数的性质即可求解.【详解】由题意可知，()()πsin 06f x x ωω⎛⎫=-> ⎪⎝⎭，因为0πx <<，所以ππππ666x ωω-<-<-，又因为函数()f x 在区间()0,π上有且只有两个零点，所以πππ2π6ω<-≤，解得71366ω<≤，所以ω的取值范围为713,66⎛⎤⎥⎝⎦.故选：C.8. 我国古代数学家赵爽在《周髀算经》一书中利用“赵爽弦图”巧妙的证明了勾股定理，该图形是以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成．类比“赵爽弦图”，可构造如图所示的图形，它是由3个全等的三角形与中间一个小等边三角形拼成的一个较大的等边三角形，若3AF EF= ，3AF =，则AF AB AC λμ=+ ，则λμ+=（）．A.1519B.619C.919D.【答案】A 【解析】【分析】利用向量的数乘、加减法运算可整理得到21039AF AB AC AF =+-，化简整理可得,λμ的值，从而求得结果.【详解】由3AF EF = 知：3CE DE = ，3BD FD =；()5333AF EF DF DE DB CE CB CD CE CB CE==-=-=--=-()()5252210333339AB AC AE AC AB AC AF AB AC AF =---=+-⨯=+- ，19293AF AB AC ∴=+ ，961919AF AB AC ∴=+ ，则919λ=，619μ=，9615191919λμ∴+=+=.故选：A.【点睛】思路点睛；本题考查平面向量基本定理的应用，解题的基本思路是能够利用向量的加减法和数乘运算，利用基底表示出所求向量或构造出关于所求向量的方程，从而求得参数的值.多选题（共4个小题，每题不只有一个选项，每题5分，满分20分）9. 如图所示是()y f x =的导数()y f x '=的图象，下列结论中正确的有（）．A. ()f x 的单调递增区间是()()1,24,-+∞B. =1x -是()f x 的极小值点C. ()f x 在区间()2,4上单调递减，在区间()1,2-上单调递增D. 2x =是()f x 的极小值点【答案】BC 【解析】【分析】利用导数正负与函数的单调性的关系，结合函数的极值与极值点的定义即可求解.的【详解】由导函数的图象可知，当1x <-或24x <<时，()0f x '<；当12x -<<或>4x 时，()0f x ¢>；所以()f x 的单调递增区间为()1,2-和()4,+∞，单调递减区间为(),1-∞-和()2,4.故A 错误，C 正确；所以1x =-或4x =是()f x 取得极小值点；故B 正确；所以2x =是()f x 取得极大值点；故D 错误.故选：BC.10. 若0a >，0b >，4a b +=，则下列结论正确的是（）．A. 2≤ B. 228a b +≥C. ()()221332a b +++≤ D. 2243a b +≥【答案】BD【解析】【分析】通过反例可说明A 错误；由基本不等式可得B 正确；将4b a =-代入CD 选项中，将不等式左侧化为关于a 的二次函数，结合a 的范围和二次函数单调性可求得CD 正误.【详解】对于A ，若2a b ==2=>，A 错误；对于B ，228a b +≥==（当且仅当2a b ==时取等号），B 正确；对于C ，4a b += ，40b ∴=->，04a ∴<<，()()()()22222131721250a b a a a a ∴+++=++-=-+，221250y x x =-+ 在()0,3上单调递减，在()3,4上单调递增，221250291235032a a ∴-+≥⨯-⨯+=（当且仅当3a =时取等号），C 错误；对于D ，由C 知：()2222244816333a a ab a a +=+-=-+，248163y x x =-+ 在()0,3上单调递减，在()3,4上单调递增，24481698316433a a ∴-+≥⨯-⨯+=，即2243a b +≥，D 正确.故选：BD.11. 函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，下列说法正确的是（）．A. 函数()21y f x =+的周期是π2B. 点5π,03⎛⎫ ⎪⎝⎭是函数()y f x =的图象的对称中心C. 函数()y f x =在5ππ,6⎡⎤--⎢⎥⎣⎦上单调递减D. ()1f x >对于5π2π,3x ⎡⎤∀∈--⎢⎥⎣⎦恒成立【答案】BCD【解析】【分析】根据图象可确定()f x 最小正周期和最小值，由此可得,A ω，利用7π26f ⎛⎫=- ⎪⎝⎭可求得ϕ，由此可得()f x ；验证()π2g x g x ⎛⎫+≠ ⎪⎝⎭可知A 错误；利用代入检验法可知BC 正确；根据正弦型函数值域求法可知D 正确.【详解】由图象可知：若()f x 的最小正周期为T ，则37ππ3π4632T ⎛⎫=--= ⎪⎝⎭，3π42π23T ∴=⨯=，2π1Tω∴==；又()min 2f x =-，0A >，2A ∴=，7π7π2sin 266f ϕ⎛⎫⎛⎫∴=+=- ⎪ ⎪⎝⎭⎝⎭，()7π3π2π62k k ϕ∴+=+∈Z ，解得：()π2π3k k ϕ=+∈Z ，π2ϕ< ，π3ϕ∴=，()π2sin 3f x x ⎛⎫∴=+ ⎪⎝⎭；对于A ，设()()π212sin 213g x f x x ⎛⎫=+=++ ⎪⎝⎭，则πππππ2sin 212sin π2112sin 222333g x x x x ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=+++=+++=-+ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，()π2g x g x ⎛⎫∴≠+ ⎪⎝⎭，π2∴不是()g x 的周期，A 错误；对于B ，当5π3x =时，π2π3x +=，此时()2sin 2π0f x ==，5π,03⎛⎫∴ ⎪⎝⎭是()f x 图象对称中心，B 正确；对于C ，当5ππ,6x ⎡⎤∈--⎢⎥⎣⎦时，π2ππ,332x ⎡⎤+∈--⎢⎥⎣⎦，sin y x = 在2ππ,32⎡⎤--⎢⎥⎣⎦上单调递减，()f x \在5ππ,6⎡⎤--⎢⎥⎣⎦上单调递减，C 正确；对于D ，当5π2π,3x ⎡⎤∈--⎢⎥⎣⎦时，π5π4π,333x ⎡⎤+∈--⎢⎥⎣⎦，()()min 5π2π213f x f f ⎛⎫∴=-=-==> ⎪⎝⎭，D 正确.故选：BCD.12. 已知定义在R 上的奇函数()f x 满足()()2=f x f x -，当[]0,1x ∈时，()f x x =，定义符号函数1,0sgn 0,01,0x x x x >⎧⎪==⎨⎪-<⎩，则下列结论正确的是（）．A. ()sgn f x ⎡⎤⎣⎦是奇函数B. ()()2023sgn 2023f f =⎡⎤⎣⎦C. ()()sgn 211k f k +=⎡⎤⎣⎦∈Z D. ()sgn f x ⎡⎤⎣⎦关于直线3x =对称【答案】ABD【解析】【分析】利用奇偶性和对称性可推导得到()f x 是以4为周期的周期函数，并确定()f x 的图象，结合图象可确定x 位于不同范围时，()f x 的正负；由奇偶性定义依次验证()sgn f x ⎡⎤⎣⎦与()sgn f x -⎡⎤⎣⎦的关系即可得到A 正确；由周期性和符号函数的定义可求得B 正确；通过反例可说明C 错误；推导可得()()33f x f x +=-，由此可知D 正确.【详解】()f x 为奇函数，()()f x f x ∴-=-，图象关于原点对称；()()2f x f x -= ，()f x \关于1x =对称；的()()()22f x f x f x =-=--Q ，()()()()42f x f x f x f x ∴+=-+=--=⎡⎤⎣⎦，()f x \是以4为周期的周期函数，结合当[]0,1x ∈时，()f x x =可得()f x 图象如下图所示，∴当()()4,42x k k k ∈+∈Z 时，()0f x >；当()()42,4x k k k ∈-∈Z 时，()0f x <；当()2x k k =∈Z 时，()0f x =；对于A ，若()()4,420,x n n n n ∈+≥∈Z ，()0f x >，()sgn 1⎡⎤=⎣⎦f x ；()()42,40,x n n n n -∈---≥∈Z ，()0f x -<，()sgn 1f x -=-⎡⎤⎣⎦，则()()sgn sgn f x f x -=-⎡⎤⎡⎤⎣⎦⎣⎦；若()()42,40,x n n n n ∈-<∈Z ，()0f x <，()sgn 1f x =-⎡⎤⎣⎦；()()4,420,x n n n n -∈--+<∈Z ，()0f x ->，()sgn 1f x -=⎡⎤⎣⎦，则()()sgn sgn f x f x -=-⎡⎤⎡⎤⎣⎦⎣⎦；当()2x k k =∈Z 时，()()0f x f x =-=，()()sgn sgn 0f x f x ∴-=-=⎡⎤⎡⎤⎣⎦⎣⎦；综上所述：()sgn f x ⎡⎤⎣⎦为定义在R 上奇函数，A 正确；对于B ，()()()()202345061111f f f f =⨯-=-=-=- ，()[]sgn 2023sgn 11f =-=-⎡⎤⎣⎦，()()2023sgn 2023f f ∴=⎡⎤⎣⎦，B 正确；对于C ，当()21k n n =+∈Z 时，()()()214331f k f n f +=+==-，此时()[]sgn 21sgn 11f k +=-=-⎡⎤⎣⎦，C 错误；对于D ，()f x 的周期为4，()()31f x f x ∴+=-，()()()3341f x f x f x -=-+=--⎡⎤⎣⎦，又()f x 为奇函数，()()11f x f x ∴--=-+，()()11f x f x -=--，()f x 关于1x =对称，()()11f x f x ∴+=-，()()11f x f x ∴--=-，的即()()33f x f x +=-，()()sgn 3sgn 3f x f x ∴+=-⎡⎤⎡⎤⎣⎦⎣⎦，()sgn f x ∴⎡⎤⎣⎦关于直线3x =对称，D 正确.故选：ABD.【点睛】关键点点睛：本题考查函数中的新定义问题的求解，解题关键是能够利用抽象函数关系式，确定()f x 的对称性和周期性，从而结合函数图象来分析新定义函数的相关性质.二、填空题（共4个小题，每题5分，满分20分）13. 已知幂函数()()2277m f x m m x =-+为非奇非偶函数，则实数m =__________．【答案】32【解析】【分析】先由函数是幂函数求出m 的值，再对m 进行讨论即可.【详解】由题意函数()()2277m f x m m x =-+是幂函数，所以22771m m -+=，即22760-+=m m ，解得2m =或32m =，当2m =时，()2f x x =是偶函数，不满足题意，当32m =时，()32f x x ==()0,∞+，不关于原点对称，即()f x =是非奇非偶函数，满足题意.故答案为：32.14. 函数()()12log 4f x ax =-在区间()2,3上是单调递增，则实数a 的取值范围是___________．【答案】40,3⎛⎤ ⎥⎝⎦【解析】【分析】结合复合函数单调性的判断方法和对数真数大于零可构造不等式组求得结果.【详解】12log y u = 在()0,∞+上单调递减，∴若()()12log 4f x ax =-在()2,3上单调递增，则4u ax =-在()2,3上单调递减且0u >在()2,3上恒成立，0430a a >⎧∴⎨-≥⎩，解得403a <≤，即实数a 的取值范围为40,3⎛⎤ ⎥⎝⎦.故答案为：40,3⎛⎤ ⎥⎝⎦.15. 已知向量a ，b ，2= a ，3b = ，a 与b 的夹角为2π3，则a xb + 的值最小时，实数x 的值为__________．【答案】13【解析】【分析】利用向量的数量积的定义及向量的模公式，结合二次函数的性质即可求解.【详解】因为2= a ，3b = ，a 与b 的夹角为2π3，所以2π1cos 23332a b a b ⎛⎫⋅==⨯⨯-=- ⎪⎝⎭.所以a xb +=== ,当13x =时，a xb + 的值最小.故答案为：13.16. 在ABC 中，AB =，π3C =，当3BC AC +取最大值时，AC =__________．【解析】【分析】用正弦定理将3BC AC +转化求得最大值，根据3C π=用余弦定理联立方程组即可求解.【详解】设BC a =，AC b =，AB c =，c = ，3C π=，2sin sin sin a b c A B C∴===，32sin 6sin a b A B ∴+=+，32sin 6sin()a b A A C ∴+=++，32sin 6sin()3a b A A π∴+=++，35sin a b A A ∴+=+，3)a b A ϕ∴+=+，其中cos ϕ=，sin 0ϕ> ，cos 0ϕ>，2(0,)3A π∈，∴当)22(Z A k k ϕππ++∈=时3a b +取最大值3C π= ，2221cos 22a b c C ab +-∴==，2233122a b a b ab⎧+=⎪∴⎨+-=⎪⎩，12b b ==∴，即AC.三、解答题（共6题，第17题10分，第18至第22题每题12分，共70分）17. 已知角α的顶点与坐标原点重合，始边与x 轴的非负半轴重合，角α的终边过点()5,12A --．（1）求3πsin 22α⎛⎫+ ⎪⎝⎭的值；（2）若()0,2πα∈，π0,2β⎛⎫∈ ⎪⎝⎭，()4sin 5αβ-=-，求cos β的值．【答案】（1）119169 （2）6365【解析】【分析】（1）根据终边所过点可得sin ,cos αα，利用诱导公式和二倍角余弦公式可求得结果；（2）根据角的范围和同角三角函数平方关系可求得()cos αβ-，由()cos cos βααβ=--⎡⎤⎣⎦，利用两角和差余弦公式可求得结果.【小问1详解】角α的终边过点()5,12A--，12 sin13α∴==-，5cos13α==-，23π25119sin2cos212cos122169169ααα⎛⎫∴+=-=-=-⨯=⎪⎝⎭.【小问2详解】()0,2πα∈，sin0α<，cos0α<，3ππ,2α⎛⎫∴∈ ⎪⎝⎭；π0,2β⎛⎫∈ ⎪⎝⎭，π,02β⎛⎫∴-∈- ⎪⎝⎭，π3π,22αβ⎛⎫∴-∈ ⎪⎝⎭，()3cos5αβ∴-==-，()()()cos cos cos cos sin sinβααβααβααβ⎡⎤∴=--=-+-⎣⎦531246313513565⎛⎫⎛⎫⎛⎫⎛⎫=-⨯-+-⨯-=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.18. 已知正四棱柱1111ABCD A B C D-中，1AB=，12AA=，E为线段11A B的中点，F为线段AB的中点．（1）求直线1BB与平面1AEC所成角的正弦值；（2）证明：直线//FC平面1AEC并且求出直线FC到平面1AEC的距离．【答案】（1（2）证明见解析，直线FC到平面1AEC【解析】【分析】（1）以1D 为坐标原点建立空间直角坐标系，利用线面角的向量求法可求得结果；（2）根据0FC n ⋅= ，由线面平行向量证明可得结论；将所求距离转化为点F 到平面1AEC 的距离，由点面距离的向量求法可求得结果.【小问1详解】以1D 为坐标原点，11111,,D A D C D D 正方向为,,x y z 轴正方向，可建立如图所示空间直角坐标系，则()1,0,2A ，11,,02E ⎛⎫ ⎪⎝⎭，()10,1,0C ，()11,1,0B ，()1,1,2B ，10,,22AE ⎛⎫∴=- ⎪⎝⎭，()11,1,2AC =-- ，()10,0,2B B = ，设平面1AEC 的法向量(),,n x y z = 则1120220AE n y z AC n x y z ⎧⋅=-=⎪⎨⎪⋅=-+-=⎩ ，令4y =，解得：2x =，1z =，()2,4,1n ∴=，111cos ,B B n B B n B B n ⋅∴===⋅ 即直线1BB 与平面1AEC【小问2详解】由（1）知：11,,22F ⎛⎫ ⎪⎝⎭，()0,1,2C ，11,,02FC ⎛⎫∴=- ⎪⎝⎭ ，10,,02FA ⎛⎫=- ⎪⎝⎭ ，11240102FC n ⋅=-⨯+⨯+⨯= ，FC n ∴⊥ ，又⊄FC 平面1AEC ，//FC ∴平面1AEC ，∴直线FC 到平面1AEC 的距离即为点F 到平面1AEC 的距离，设该距离为d ，的则FA ndn⋅===，即直线FC到平面1AEC.19.已知数列{}n a为等差数列，且2410a a+=，416S=．（1）求{}n a的通项公式；（2）数列{}n b满足()1113n nn nnb na a*+++=∈⋅N，数列{}nb的前n项和为nS，求证：112nS<．【答案】（1）21na n=-（2）证明见解析【解析】【分析】（1）利用等差数列通项和求和公式可构造方程组求得a1,d，由此可得通项公式；（2）由（1）可得b n，采用裂项相消法可求得S n，进而分析得到结论.【小问1详解】设等差数列{}n a的公差为d，则24314112241043446162a a a a dS a d a d+==+=⎧⎪⎨⨯=+=+=⎪⎩，解得：112ad=⎧⎨=⎩，()12121na n n∴=+-=-.【小问2详解】由（1）得：()()()()111111321214213213n n n nnbn n n n++⎡⎤+==-⎢⎥-+-+⎣⎦，()()1223341 1111111114133333535373213213 n n nSn n+⎡⎤∴=-+-+-+⋅⋅⋅+-⎢⨯⨯⨯⨯⨯⨯-+⎣⎦()()11111114321312843n nn n++⎡⎤=-=-⎢⎥++⎣⎦，()11843nn+>+，112nS∴<.20.在ABC中，角A，B，C的对边分别为a，b，c，若()()()sin sin sin sina b A B c B C+-=+．（1）求角A的大小；（2）若D 为BC 上一点，12BAD BAC ∠=∠，3AD =，求4b c +的最小值．【答案】（1）2π3A =（2）27【解析】【分析】（1）利用正弦定理化角为边，再根据余弦定理即可得解；（2）根据ABC ABD ACD S S S =+ 求出,b c 的关系，再利用基本不等式即可得解.【小问1详解】因为()()()sin sin sin sin a b A B c B C +-=+，由正弦定理得()()()a b a b c b c +-=+，即222a b bc c -=+，222c b a bc +-=-，所以2221cos 22b c a A bc +-==-，又()0,πA ∈，所以2π3A =；【小问2详解】由12BAD BAC ∠=∠，得1π23BAD CAD BAC ∠=∠=∠=，因为ABC ABD ACD S S S =+ ，所以12π1π1πsin 3sin 3sin 232323bc c b =⋅⋅+⋅⋅，即()3bc c b =+，331b c bc c b +=+=，所以()3312344151527b c b c b c c b c b ⎛⎫+=++=++≥+=⎪⎝⎭，当且仅当123b c c b=，即29c b ==时等号成立，所以4b c +的最小值为27．21. 已知双曲线()2222:10,0x y C a b a b -=>>的渐近线为y x =，点P 在C 上，直线:l y kx t =+与双曲线C 相交于两点M ，N ，线段MN 的垂直平分线分别与x ，y 轴相交于A ，B 两点．（1）若直线l 过点()0,1，且点M ，N 都在双曲线的左支上，求k 的取值范围；（2）若AOB （O 为坐标原点）的面积为812，且0k ≠，求k 的取值范围．【答案】（1）（2）5,,4⎛⎫⎛⎛⎛⎫-∞+∞ ⎪ ⎪ ⎪ ⎝⎝⎭⎝⎭⎝ 【解析】【分析】（1）利用双曲线的渐近线及点在双曲线上，将直线与双曲线联立方程组，利用直线与双曲线相交（2）将直线与双曲线联立方程组，利用直线与双曲线相交的条件及韦达定理，再利用中点坐标公式及直线的点斜式方程，结合三角形的面积公式及一元二次不等式的解法可得答案.【小问1详解】∵b a =，且225514a b -=，∴2a =，b =，故双曲线22:145x y C -=，设()11,M x y ，()22,N x y ，当直线l 过点()0,1时，1t =，直线l 的方程为1y kx =+，如图所示由221145y kx x y =+⎧⎪⎨-=⎪⎩，得()22548240k x kx ---=，由2540k -≠，()226496540k k ∆=+->，解得k <<k ≠，122854k x x k +=-，1222454x x k -=-．因为点M ，N 都在左支上，∴10x <，20x <，∴1228054k x x k +=<-，12224054x x k -=>-k <<．所以k的取值范围为．【小问2详解】将y kx t =+代入22145x y -=并整理得()2225484200k x ktx t ----=，由2540k -≠，()()()22284544200kt k t ∆=-+-+>，得22540t k +->，122854kt x x k +=-，212242054t x x k--=-，设线段MN 的中点为()00,x y ，则12024254x x kt x k +==-，002554t y kx t k =+=-，所以线段MN 的垂直平分线的方程为225145454t kt y x k k k ⎛⎫-=-- ⎪--⎝⎭，所以A 点的坐标为29,054kt k ⎛⎫ ⎪-⎝⎭，B 点的坐标为290,54t k ⎛⎫ ⎪-⎝⎭，因为AOB 的面积为812，所以2219981254542kt t k k ⋅=--，整理得()22254k tk -=，所以()22254540k k k -+->，所以()()2245450k k k --->，解得0k <<或54k >，所以k的取值范围为55,,44⎛⎫⎛⎛⎫⎛⎫-∞-+∞ ⎪ ⎪ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭⎝ ．22. 已知函数()1e ln -=-x f x a x ．（1）当1a =-时，求曲线()y f x =在()()1,1f 处的切线方程；（2）当0a >，若不等式()ln f x a a a ≥+恒成立，求a 的取值范围．【答案】（1）210x y --=（2）(]0,1【解析】【分析】（1）利用导数几何意义可求得切线斜率()1f '，结合()11f =可得切线方程；（2）方法一：构造()()ln g x f x a a a =--，将问题转化为()0g x ≥恒成立；利用导数和零点存在定理可说明()g x 的单调性，得到00012ln 0x x x --≥；令()12ln u x x x x=--，利用导数可得()u x 单调性，从而确定0x 的范围，再次构造函数()()1e01x t x x x -=<≤，利用导数可求得()0t x 的范围，即为所求的a的取值范围；方法二：采用同构法，将恒成立的不等式化为()()ln 111e ln 1e ax x x ax +-⎡⎤-⎣⎦≥+⎡⎤⎣⎦，构造函数()()1e 0x h x x x -=>，利用导数求得()h x 单调性，从而得到()ln 1x ax ≥+，采用分离变量法可得()1e 0x a x x-≤>，令()()1e 0x u x x x-=>，利用导数可求得()min u x ，由此可得a 的取值范围；方法三：由恒成立不等式可确定()11ln f a a a =≥+，构造函数()ln S a a a a =+，利用导数可求得()S a 的单调性，结合()11S =可求得a 的范围为(]0,1；通过证明当(]0,1a ∈时，()ln f x a a ≥+恒成立和1a >时，不等式不恒成立可得到最终范围.【小问1详解】当1a =-时，()1e ln x f x x -=+，则()11e x f x x-'=+，()01e 12f '∴=+=，又()01e ln11f =+=，()y f x ∴=在()()1,1f 处的切线方程为：()121y x -=-，即210x y --=.【小问2详解】方法一：令()()1ln e ln ln x g x f x a a a a x a a a -=--=---，则()0g x ≥恒成立，()g x 的定义域为()0,∞+，()1e x a g x x -'=-且0a >；令()()h x g x '=，则()12e 0x a h x x-'=+>，()h x ∴在()0,∞+上单调递增，即()g x '在()0,∞+上单调递增，又()11e e 1011aa a g a a a '+=-=-+>++，11e 101a a g a a -+⎛⎫'=--< ⎪+⎝⎭，0,11a x a a ⎛⎫∴∃∈+ ⎪+⎝⎭，使得()00g x '=，且当()00,x x ∈时，()0g x '<；当()0,x x ∈+∞时，()0g x '>；()g x ∴在()00,x 上单调递减，在()0,x +∞上单调递增，()()0100min e ln ln x g x g x a x a a a -∴==--，由()00g x '=得：010e x a x -=，00ln 1ln x x a ∴+-=，010e x a x -=，()()000011110000000e e ln e e ln 1x x x x g x x x x x x x ----∴=---+-()012000e 12ln x x x x -=--，()012000e 12ln 0x x x x -∴--≥，即00012ln 0x x x --≥，令()12ln u x x x x=--，则()u x 在()0,∞+上单调递减，又()000012ln 0u x x x x =--≥，()10u =，001x ∴<≤，设()()1e 01x t x x x -=<≤，则()()11e 0x t x x -'=+>，()t x ∴在(]0,1上单调递增，()01t x ∴<≤，0100e 1x x -∴<≤，又010e x a x -=，a ∴的取值范围为(]0,1.方法二：由()ln f x a a a ≥+得：1e ln ln x a a a a x -≥++，()()()()ln 111e 1ln ln ln 1ln 1e ax x x ax a x ax ax ax +-⎡⎤-⎣⎦∴≥++=+=+⎡⎤⎡⎤⎣⎦⎣⎦，当()ln 10ax +≤时，()1e 0ln 1x x ax ->≥+在0a >，0x >时恒成立，0a ∴>；当()ln 10ax +>时，设()()1e 0x h x x x -=>，则()()()ln 1h x h ax ≥+，()()11e 0x h x x -'=+> ，()h x ∴在()0,∞+上单调递增，()ln 1x ax ∴≥+，即()1e 0x ax x -≤>，()1e 0x a x x-∴≤>，令()()1e 0x u x x x -=>，则()()121e x x u x x--'=，∴当()0,1x ∈时，()0u x '<；当()1,x ∈+∞时，()0u x '>；()u x ∴在()0,1上单调递减，在()1,+∞上单调递增，()()min 11u x u ∴==，1a ∴≤，又0a >，01a ∴<≤；综上所述：实数a 的取值范围为(]0,1.方法三：()f x 定义域为()0,∞+，()ln f x a a a ≥+恒成立，()11ln f a a a ∴=≥+必然成立；令()ln S a a a a =+，则()2ln S a a '=，∴当()20,e a -∈时，()0S a '<；当()2e ,a -∈+∞时，()0S a '>；()S a ∴在()20,e -上单调递减，在()2e ,-+∞上单调递增，又()11S =，当10e a -<<时，()()1ln 0S a a a =+<，∴当01a <≤时，ln 1a a a +≤；下面证明：当01a <≤时，()ln f x a a a ≥+恒成立.ln 0a a ≤ ，()ln ln ln ln 1a x a a a a x a a x ∴++≤+=+，()11e ln ln e ln 1x x a x a a a a x --∴---≥-+，令()()1e ln 1x F x a x -=-+，则()1e x a F x x-'=-，令()()G x F x '=，则()12e 0x a G x x-'=+>，()F x '∴在()0,∞+上单调递增，当1a =时，()11e x F x x-'=-，()10F '=，∴当()0,1x ∈时，()0F x '<；当()1,x ∈+∞时，()0F x '>；()F x ∴在()0,1上单调递减，在()1,+∞上单调递增，()()10F x F ∴≥=，1e ln ln 0x a x a a a -∴---≥恒成立，即()ln f x a a a ≥+恒成立；当01a <<时，()110F a '=->，()1e 10a F a -'=-<，()0,1x a ∴∃∈，使得()00F x '=，且当()00,x x ∈时，()0F x '<；当()0,x x ∈+∞时，()0F x '>；()F x ∴在()00,x 上单调递减，在()0,x +∞上单调递增，()()()0100e ln 1x F x F x a x -∴≥=-+，由()00F x '=得：010e x a x -=，00ln ln 1x a x =+-，()()000001ln 1ln a F x a a x a x a a a x x ⎛⎫∴=-+-=+-- ⎪⎝⎭，()0,1x a ∈ ，0012x x ∴+>，()()0001ln ln 1ln 0F x a x a a a a a a a a x ⎛⎫∴=+-->-=-> ⎪⎝⎭，()()00F x F x ∴≥>，∴e x −1 −a ln x −a ln a −a ≥0恒成立，即 f (x ≥ )a ln a +a 恒成立；当a >1时， f (1= )1 <a (1 +ln a = )a +a ln a ，显然不满足 f (x ≥ )a +a ln a 恒成立；综上所述：实数a 的取值范围为(0,1 ].【点睛】方法点睛：本题重点考查了导数中的恒成立问题的求解；本题求解恒成立的基本方法有：1.通过直接构造函数的方式，将问题转化为含参数函数的单调性的讨论和最值的求解问题，利用最值求得参数的取值范围；2.采用同构法，将问题转化为同一函数的不同函数值的大小关系的问题，从而通过求解函数的单调性得到自变量的大小关系；3.采用由特殊到一般的思路，通过特殊位置必然成立的思路得到a 的一个取值范围，再证明在此范围时不等式恒成立，并通过反例说明不在此范围时不等式不恒成立来得到最终范围.。

黑龙江省哈尔滨师范大学附属中学2021-2022学年高三上学期第一次月考数学(理)试题

得，
当，；，；
所以在上单调递减，上单调递增，而要使有两个零点，要满足，
即；
因为，，令，由，
所以，即，因此，
而要证，
只需证，即证，即证，
由，只需证，
令，则，
令，则，
故在上递增，，
故在上递增，，
所以．
关键点点睛：（1）第（Ⅱ）问中隐零点的问题，解题关键在于的化简要用到，即；
由两边平方可求，再由平方关系求 .
由题得，，所以，
又，所以，
所以，
所以 .
故答案为： .
15.递增的等比数列的每一项都是正数，设其前项的和为，若则 _______.
364
由等比数列的性质将化为，再由可求出，然后列出关于的方程组，求出，进而可以求出结果
设等比数列的公比为，
A. B. C. D.
A
通过函数的奇偶性，，，可分别排除D，C，B，即得解
因为，所以是奇函数，排除D；
当时，，．
由，可排除C；，排除B故选：A
11.已知数列的前n项和，若，恒成立，则实数的最大值是（）
A.3B.4C.5D.6
C
先由求出，根据得到，求出的最小值，即可得出结果.
C. D.
C
根据等比数列与等差数列的求和公式，用分组求和的方法，即可求出结果.
因为，
所以数列的前n项和
.故选C
本题主要考查数列的求和，根据分组求和的方法，结合等差数列与等比数列的求和公式即可求解，属于常考题型.
6.已知菱形ABCD的边长为4，点M是线段CD的中点，，则 =（）

2020-2021学年黑龙江省哈师大附中高二第一学期期中数学(理)试题【解析版】

2020-2021学年黑龙江省哈师大附中高二第一学期期中数学（理）试题【解析版】一、单选题1350x y +-=的倾斜角为（） A ．300 B ．600C ．1200D ．1500【答案】C【解析】∵350x y +-=的斜率为：3-直线的倾斜角为α，所以tan 3α=-120α=︒，故选C.2．已知直线l 过点(1,2)-且与直线2340x y -+=垂直，则l 的方程是（） A ．3210x y +-= B ．3270x y ++= C ．2350x y -+= D ．2380x y -+=【答案】A【详解】直线2x –3y +1=0的斜率为2,3则直线l 的斜率为3,2-所以直线l 的方程为32(1).3210.2y x x y -=-++-=即故选A3．抛物线22y x =的焦点坐标为（） A ．(1,0) B ．1(4，0)C ．1(0,)4D ．1(0,)8【答案】D【分析】将抛物线方程化为标准方程，即可得出开口方向和p ，进而求出焦点坐标. 【详解】解：整理抛物线方程得212x y =∴焦点在y 轴，14p =∴焦点坐标为1(0,)8故选D4．设F 1，F 2分别是椭圆2212516x y +=的左，右焦点，P 为椭圆上一点，M 是F 1P 的中点，|OM |＝3，则P 点到椭圆左焦点的距离为( ) A ．4 B ．3 C ．2 D ．5【答案】A【解析】由题意知OM 是12PF F △的中位线，∵3OM =，∴26PF =，又12210PF PF a +==，∴14PF =，故选A.5．点(4,2)P -与圆224x y +=上任一点连线的中点的轨迹方程是（） A ．22(2)(1)1x y -++= B ．22(2)(1)4x y -++= C ．22(4)(2)4x y ++-= D ．22(2)(1)1x y ++-= 【答案】A【解析】试题分析：设圆上任一点为()00,Q x y ，PQ 中点为(),M x y ，根据中点坐标公式得，0024{22x x y y =-=+，因为()00,Q x y 在圆224x y +=上，所以22004x y +=，即()()2224224x y -++=，化为22(2)(1)1x y -++=，故选A.【解析】1、圆的标准方程；2、“逆代法”求轨迹方程.【方法点晴】本题主要考查圆的标准方程、“逆代法”求轨迹方程，属于难题.求轨迹方程的常见方法有:①直接法，设出动点的坐标(),x y ，根据题意列出关于,x y 的等式即可；②定义法，根据题意动点符合已知曲线的定义，直接求出方程；③参数法，把,x y 分别用第三个变量表示，消去参数即可；④逆代法，将()()00x g x y h x =⎧⎪⎨=⎪⎩代入()00,0=f x y .本题就是利用方法④求M 的轨迹方程的.6．过原点的直线l 与双曲线226x y -=交于A ,B 两点，点P 为双曲线上一点，若直线PA 的斜率为2，则直线PB 的斜率为（）A ．4B ．1C ．12D ．14【答案】C【分析】设(,)A m n ，(,)B m n --，(,)P x y ，代入双曲线的方程，作差，可得22221y nx m-=-，再由直线的斜率公式，结合平方差公式，计算可得所求值. 【详解】由题意可设(,)A m n ，(,)B m n --，(,)P x y ，则226m n -=，226x y -=，即有2222y n x m -=-，即22221y n x m -=-，由PA y n k x m -=-，PB y nk x m+=+，可得2222·1PA PBy n k k x m -==-，因为2PA k =，所以12PB k =. 故选：C .7．如果椭圆221369x y +=的弦被点()4,2平分，则这条弦所在的直线方程是（）A ．20x y -=B ．240x y +-=C ．23120x y +-=D ．280x y +-=【答案】D【分析】设这条弦的两端点1122(,),(,)A x y B x y ,则：2222112211369369x y x y +=+=，,用点差法得到：12120369x x y y k +++=，代入中点坐标，即得解斜率k . 【详解】设这条弦的两端点1122(,),(,)A x y B x y ，斜率为1212y y k x x -=-，则：2222112211369369x y x y +=+=，两式相减得：2222121212121212()()()()00369369x x y y x x x x y y y y ---+-++=∴+=变形得：12120369x x y y k +++=，又弦中点为：()4,2，故12k =-故这条弦所在得直线方程为：1242()y x -=--，即280x y +-= 故选：D【点睛】本题考查了点差法在弦中点问题中的应用，考查了学生转化与划归，数学运算的能力，属于中档题.8．设12,F F 是双曲线22124y x -=的两个焦点,P 是双曲线上的一点,且1234PF PF =,则12PF F △的面积等于（） A ．2 B ．83C ．24 D ．48【答案】C【详解】双曲线的实轴长为2,焦距为1210F F =.根据题意和双曲线的定义知1222241233PF PF PF PF PF =-=-=,所以26PF =,18PF =, 所以2221212PF PF F F +=,所以12PF PF ⊥.所以121211682422PF F SPF PF =⋅=⨯⨯=. 故选：C【点睛】本题主要考查了焦点三角形以及椭圆的定义运用,属于基础题型.9．已知抛物线22y px =（0p >）的焦点F 与双曲线22145x y -=的右焦点重合，抛物线的准线与x 轴的交点为K ，点A 在抛物线上且2AK =，则A 点的横坐标为（） A ．2 B ．3C ．23D ．4【答案】B【详解】因为已知条件中，抛物线22(0)y px p =>的焦点F 与双曲22145x y -=的右焦点重合，而双曲线中，a=2，5b =可知右焦点（3,0），抛物线的准线x=-2p,故点K （-2p ，0），设点A （x,y ）,且22(0)y px p =>，则2AK AF =，可知222()2()()2222p p px y x x px ++=+∴+=，且由于3,62p p ==，解得点A 的横坐标为3，故选：B.点评：解决该试题的关键是利用双曲线的性质以及抛物线的定义，运用坐标表示处关系式2AK AF =，然后借助于等式来求解点A 的坐标，属于基础题．10．已知抛物线2:8y x τ=，过抛物线τ的焦点且斜率为k 的直线l 交τ于M ，N 两点，已知(2,3)P -，0PM PN =，则k =（） A ．34B ．43C ．12D ．2【答案】B【分析】本题先根据题意写出直线l 的直线方程，然后联立直线l 与抛物线τ的方程，消去y ，化简整理可得关于x 的一元二次方程，根据韦达定理可得12284x x k+=+，124x x =，接着计算出12y y +，12y y 关于k 的表达式，写出向量PM ，PN 的坐标式，代入并化简计算PM PN ，根据0PM PN =可进一步计算出k 的值，得到正确选项. 【详解】解：由题意，画图如下：由抛物线方程28y x =，可知抛物线τ的焦点坐标为(2,0)，则直线l 的直线方程为：(2)y k x =-，显然0k ≠. 设1(M x ，1)y ，2(N x ，2)y ，则联立2(2)8y k x y x =-⎧⎨=⎩，消去y ，整理得22224(2)40k x k x k -++=，故12284x x k+=+，124x x =， 121212288(2)(2)(4)(44)y y k x k x k x x k k k∴+=-+-=+-=+-=， 2221212121228(2)(2)[2()4][42(4)4]16y y k x x k x x x x k k=--=-++=-++=-，1(2PM x =+，13)y -，2(2PN x =+，23)y -，∴1212·(2)(2)(3)(3)PM PN x x y y =+++--121212122()43()9x x x x y y y y =++++-++28842(4)41639k k =+++--⋅+22(34)k k -=，0PM PN =，∴22(34)0k k-=，解得43k =. 故选：B .【点睛】关键点睛：本题主要考查向量与解析几何的综合问题.考查了方程思想，韦达定理的应用，向量的运算能力，解答本题的关键是由题意1212·(2)(2)(3)(3)PM PN x x y y =+++--，然设出直线方程，与抛物线方程联立，写出韦达定理，在代入得到关于k 的方程.本题属中档题.11．点(),0F c 为双曲线()222210,0x y a b a b-=>>的右焦点，点P 为双曲线左支上一点，线段PF 与圆22239c b x y ⎛⎫-+= ⎪⎝⎭相切于点Q ，且2PQ QF =，则双曲线的离心率是（） A 2 B 3C 5D ．2【答案】C【解析】试题分析：设1(,0)F c -是双曲线的左焦点，圆222()39c b x y -+=的圆心为(,0)3c M ，半径为3b ，由于14233c cF M c MF =+==，又2PQ QF =，因此1//PF QM ，所以1F P PF ⊥，13PF MQ b ==，222243PF c b c a =-=+，由双曲线定义得12PF PF a -=，2232c a b a +=，解得5ce a==．故选C ．【解析】双曲线的几何性质，双曲线的定义，直线与圆的位置关系．【名师点睛】本题考查直线与双曲线相交问题，解题时，借助几何方法得出1PFF ∆中线段与,,a b c 的关系及1PFF ∆的性质，大大减少了计算量，而且明确得出了,,a b c 的等式，方便求出双曲线的离心率．这是我们在解解析几何问题要注意地方法． 12．如图，椭圆的中心在坐标原点，焦点在x 轴上，A 1，A 2，B 1，B 2为椭圆的顶点，F 2为右焦点，延长B 1F 2与A 2B 2交于点P ，若∠B 1PB 2为钝角，则该椭圆离心率的取值范围是（）A ．52⎫-⎪⎪⎝⎭B ．52⎛- ⎝⎭C ．510,2⎛⎫⎪ ⎪⎝⎭ D ．51,12⎛⎫- ⎪⎪⎝⎭【答案】C【分析】过1B 作直线22A B 的垂线l ，题意说明射线1B P 在直线l 上方，由此可得,,a b c 的不等关系（利用直线与x 轴交点得出不等式），从而可得离心率的范围．【详解】设直线l 为过1B 且与22A B 垂直的直线，易知22,B A bk a=-则直线l 的斜率为a k b=，而()10,B b -，则该直线l 的方程为ay x b b=-，所以该直线与x 轴的交点坐标为2,0b a ⎛⎫ ⎪⎝⎭，要使得12B PB ∠为钝角，则说明直线1B P 在直线l 上方，故满足2b c a <，结合222b a c =-，得到22,,cac a c e a<-=结合得210e e +-<，结合01,e <<解得51e ⎛-∈ ⎝⎭. 故选：C.【点睛】本题考查求椭圆离心率的范围，解题关键是利用过1B 与直线22A B 垂直的直线l 与射线1B P 关系得出不等式．二、填空题13．若,x y 满足约束条件1020220x y x y x y -+≥-≤+-≤⎧⎪⎨⎪⎩，则z x y =+的最大值为_____________．【答案】32【解析】试题分析：由下图可得在1(1,)2A 处取得最大值，即max 13122z =+=.【解析】线性规划.【方法点晴】本题考查线性规划问题，灵活性较强，属于较难题型.考生应注总结解决线性规划问题的一般步骤（1）在直角坐标系中画出对应的平面区域，即可行域；（2）将目标函数变形为a zy x b b=-+；（3）作平行线：将直线0ax by +=平移，使直线与可行域有交点，且观察在可行域中使zb最大（或最小）时所经过的点，求出该点的坐标；（4）求出最优解：将（3）中求出的坐标代入目标函数，从而求出z 的最大（小）值.14．若双曲线C 经过点(2，2)，且与双曲线2214y x -=具有相同渐近线，则双曲线C的标准方程为．【答案】221312x y -=【解析】试题分析：由题意设双曲线C 的标准方程为224y x λ-=，又过点(2，2)，所以3,λ=-221312x y -=．【解析】双曲线渐近线15．倾斜角为45的直线l 经过抛物线24y x =的焦点F ，且与抛物线交于A ，B 两点，则AB 的长为__________________. 【答案】8【分析】直线l 的方程为1y x =-，与抛物线方程联立可得2610x x -+=，从而可得6A B x x +=，再根据抛物线的定义即可求出AB 的长.【详解】抛物线24y x =的焦点F 的坐标为(1,0)，所以直线l 的方程为0tan 45(1)y x -=-，即1y x =-，由214y x y x=-⎧⎨=⎩，得2610x x -+=，所以6A B x x +=，由抛物线的定义可知628A B AB x x p =++=+=，所以AB 的长为8. 故答案为：8【点睛】本题主要考查直线与抛物线的位置关系，考查抛物线焦点弦长的求法，属于中档题.16．已知过抛物线2:4C y x =焦点F 的直线交抛物线C 于P ，Q 两点，交圆2220x y x +-=于M ，N 两点，其中P ，M 位于第一象限，则11PM QN+的最小值为_____．【答案】2【分析】设11(,)P x y ，22(,)Q x y ，根据题意可设直线PQ 的方程为1x my =+，将其与抛物线C 方程联立可求出121=x x ，结合图形及抛物线的焦半径公式可得12||||1PM QN x x ⋅==，再利用基本不等式，即可求出11PM QN+的最小值. 【详解】圆2220x y x +-=可化为22(1)1x y -+=，圆心坐标为(1,0)，半径为1，抛物线C 的焦点(1,0)F ，可设直线PQ 的方程为1x my =+，设11(,)P x y ，22(,)Q x y ，由214x my y x=+⎧⎨=⎩，得2440y my --=，所以124y y =-，又2114y x =，2224y x =，所以222121212()14416y y y y x x =⋅==，因为1212||||(||||)(||||)(11)(11)1PM QN PF MF QF NF x x x x ⋅=--=+-+-==，所以111122PM QN PM QN+≥⋅=，当且仅当||||1PM QN ==时，等号成立. 所以11PM QN+的最小值为2. 故答案为：2【点睛】本题主要考查抛物线的几何性质，基本不等式求最值，考查基本运算能力，属于中档题.三、解答题17．已知动圆M 过点(2,0)F ，且与直线2x =-相切．（Ⅰ）求圆心M 的轨迹E 的方程；（Ⅱ）斜率为1的直线l 经过点F ，且直线l 与轨迹E 交于点,A B ，求线段AB 的垂直平分线方程．【答案】（Ⅰ）28y x =；（Ⅱ）100x y +-=.【分析】（Ⅰ）由题意得圆心M 到点(2,0)F 等于圆心到直线2x =-的距离，利用两点间距离公式，列出方程，即可求得答案.（Ⅱ）求得直线l 的方程，与椭圆联立，利用韦达定理，可得1212,x x x x +的值，即可求得AB 中点00(,)P x y 的坐标，根据直线l 与直线AB 垂直平分线垂直，可求得直线AB 垂直平分线的斜率，利用点斜式即可求得方程.【详解】（Ⅰ）设动点(,)M x y 22(2)|2|x y x -+=+，化简得轨迹E 的方程：28y x =；（Ⅱ）由题意得：直线l 的方程为：2y x =-，由228y x y x=-⎧⎨=⎩，得21240x x -+=，2124140∆=-⨯⨯>，设1122(,),(,)A x y B x y ，AB 中点00(,)P x y 则121212,4x x x x +==，所以12062x x x +==，0024y x =-=，又AB 垂直平分线的斜率为-1，所以AB 垂直平分线方程为100x y +-=.【点睛】本题考查抛物线方程的求法，抛物线的几何性质，解题的关键是直线与曲线联立，利用韦达定理得到1212,x x x x +的表达式或值，再根据题意进行化简和整理，考查计算求值的能力，属基础题.18．已知圆22 :(3)(4)4C x y -+-=，（1）若直线1l 过定点1,0A ，且与圆C 相切，求1l 的方程.（2）若圆D 的半径为3，圆心在直线2:20l x y +-=上，且与圆C 外切，求圆D 的方程.【答案】（1）1x =或()314y x =-；（2）()()22319x y -++=或()()22249x y ++-=.【分析】（1）将1l 的斜率分成存在和不存在两种情况，结合圆心到直线的距离等于半径，求得1l 的方程.（2）设出圆D 的圆心，利用两圆外切的条件列方程，由此求得圆心D 的坐标，进而求得圆D 的方程.【详解】（1）圆C 的圆心为()3,4C ，半径为12r =.当直线1l 斜率不存在时，即直线1x =，此时直线与圆相切.当直线1l 斜率存在时，设直线1l 的方程为()1y k x =-，即kx y k 0--=，由于1l 与圆C 相切，圆心到直线的距离等于半径，即23421k k k --=+，即221k k -=+34k =，直线1l 的方程为()314y x =-. 综上所述，直线1l 的方程为1x =或()314y x =-. （2）由于圆D 圆心在直线2l 上，设圆心(),2D a a -+，圆D 的半径23r =，由于圆D 与圆C 外切，所以12CD r r =+()()22324235a a -+-+-=+=，即()()223225a a -++=，解得3a =或2a =-.所以圆心()3,1D -或()2,4D -.所以圆D 的方程为()()22319x y -++=或()()22249x y ++-=.【点睛】本小题主要考查直线和圆的位置关系，考查圆与圆的位置关系，考查直线方程和圆的方程的求法，属于基础题.19．如图，在四棱锥P ABCD -中，四边形ABCD 为菱形，60BAD ∠=︒，PAD ∆为正三角形，平面PAD ⊥平面ABCD ，且E ，F 分别为AD ，PC 的中点.（1）求证：//DF 平面PEB ；（2）求直线EF 与平面PDC 所成角的正弦值. 【答案】（1）证明见解析；（2）65. 【分析】（1）取PB 中点G ，推出//FG BC ，证明四边形DEGF 是平行四边形，得到//DF EG ，然后证明//DF 平面PEB .（2）以E 为原点，EA ，EB ，EP 分别为x ，y ，z 轴建立空间直角坐标系，求出平面PDC 的法向量，求出EF ，利用空间向量的数量积求解EF 与平面PDC 所成角的正弦值.【详解】（1）证明：取PB 中点G ，因为F 是PC 中点，//FG BC ∴，且12FG BC =，E 是AD 的中点，则//DE BC ，且12DE BC =， //FG DE ∴，且FG DE =，∴四边形DEGF 是平行四边形，//DF EG ∴，又DF ⊂/平面PEB ，EG ⊂平面PEB ，//DF ∴平面PEB .（2）因为E 是正三角形PAD 边为AD 的中点，则PE AD ⊥.因为平面PAD ⊥平面ABCD ，平面PAD 平面ABCD AD =，PE ⊂平面PAD ，PE ∴⊥平面ABCD ，四边形ABCD 为菱形，60BAD ∠=︒，∴正三角形BAD 中，BE AD ⊥，以E 为原点，EA ，EB ，EP 分别为x ，y ，z 轴建立空间直角坐标系，不妨设菱形ABCD 的边长为2，则1AE ED ==，2PA =，3PE =223BE AB AE =-=则点33(0,0,0),(1,0,0),(3,0),3),(1,)22E D C PF ---， ∴(1DC =-30)，(1DP =，03)，设平面PDC 的法向量为(n x =，y ，)z ，则·0·0n DC n DP ⎧=⎨=⎩，即3030x z x y ⎧=⎪⎨-+=⎪⎩，解得33x x z⎧=⎪⎨=⎪⎩，不妨令1z =，得(3n =-，1-，1)；又33(22EF =-，设EF 与平面PDC 所成角为θ，∴36sin |cos |55?2EF n θ=<>=⋅=，.所以EF 与平面PDC 6. 【点睛】对于线面角可以转化为直线的方向向量与平面的法向量的夹角运算，对于证明线线关系，线面关系，面面关系等方面的问题，必须在熟练掌握有关的定理和性质的前提下，再利用已知来进行证明.20．如图，正三棱柱111ABC A B C -中，12AB AA ==，点D ，E 分别为AC ，1AA 的中点.（1）求点1B 到平面BDE 的距离；（2）求二面角1D BE C --的余弦值. 【答案】（12；（2）14. 【分析】（1）建立空间坐标系，求出平面BDE 的法向量n ，则1B 到平面BDE 的距离为1·nB n B ；（2）求出平面1BEC 的法向量m ，计算m ，n 的夹角得出二面角的大小. 【详解】解：（1）取11A C 的中点1D ，连结1DD ，则1DD ⊥平面ABC ，ABC ∆是等边三角形，BD AC ∴⊥，以D 为原点，分别以DA ，DB ，1DD 所在直线为坐标轴建立空间直角坐标系D xyz -，则(0D ，0，0)，(0B 30)，(1E ，0，1)，1(0B 32)，1(1C -，0，2)，∴(0DB =30)，(1DE =，0，1)，1(0BB =，0，2)，设平面BDE 的法向量为1(n x =，1y ，1)z ，则·0·0n DB n DE ⎧=⎨=⎩，即111300x z ⎧=⎪⎨+=⎪⎩，令11z =可得(1n =-，0，1)，∴点1B 到平面BDE 的距离为1·22B n nB ==（2）(1BE =，3-1)，1(2EC =-，0，1)，设平面1BEC 的法向量为2(m x =，2y ，2)z ，则1·0·0m BE m EC ⎧=⎪⎨=⎪⎩，即222223020xy z x z ⎧-+=⎪⎨-+=⎪⎩，令21x =可得(1m =，3，2)，cos m ∴<，·14222m n n m n >===⨯， ∴二面角1D BE C --的余弦值为14.【点睛】关键点睛：（1）解题关键是建立空间坐标系，求出平面BDE 的法向量n ，进而用公式求解；（2）解题关键是设平面1BEC 的法向量为2(m x =，2y ，2)z ，则1·0·0m BE m EC ⎧=⎪⎨=⎪⎩，求出m 后，利用公式求解二面角1D BE C --的余弦值，难度属于中档题21．已知椭圆()2222:10x y C a b a b+=>>的左顶点和下顶点分别为A ，B ，25AB =过椭圆焦点且与长轴垂直的弦的长为2. （1）求椭圆C 的方程；（2）已知M 为椭圆C 上一动点（M 不与A ，B 重合），直线AM 与y 轴交于点P ，直线BM 与x 轴交于点Q ，证明：AQ BP ⋅为定值.【答案】（1）221164x y +=；（2）证明见解析. 【分析】（1）根据25AB =2225a b +=，再由过椭圆焦点且与长轴垂直的弦的长为2，得到2a b =，列出方程组，求得22,a b 的值，即可求解；（2）由（1）得到点,A B 的坐标，设出,,M P Q 的坐标，由点M 在椭圆上，结合,,A P M 三点共线，求得AQ BP ⋅表示，即可求解.【详解】（1）由题意，椭圆C 的左顶点和下顶点分别为,A B ，可得(,0),(0,)A a B b -- 因为25AB =2225AB a b =+=又由过椭圆焦点且与长轴垂直的弦的长为2，可得222b a=，即2a b =，联立方程组，解得2216,4a b ==，所以椭圆的方程为221164x y +=.（2）由（1）可得(4,0),(0,2)A B --，设00(,),(0,),(,0)P Q M x y P y Q x ，因为点M 在椭圆上，所以2200416x y +=，由,,A P M 三点共线，可得0044P y y x =+，同理可得0022Q x x y =+，所以0000002482484242Q P x y x y x y x y AQ BP ++++⋅=+⋅+=⋅++2200000000000000004(4164816)4(16164816)(8)(2)248x y x y x y x y x y x y x y x y +++++++++==+++++000000002481616248x y x y x y x y +++==+++，即16AQ BP ⋅=，所以AQ BP ⋅为定值.【点睛】本题主要考查了椭圆的标准方程的求解，以及椭圆的性质的综合应用，其中解答中根据椭圆的方程，结合三点共线求得P y 和Q x 是解答得关键，着重考查推理与运算能力，属于难题.22．已知椭圆2222:1(0)x y C a b a b+=>>经过点3()-，且短轴长为2. （1）求椭圆C 的标准方程；（2）若直线l 与椭圆C 交于P ，Q 两点，且OP OQ ⊥，求OPQ △面积的取值范围.【答案】（1）2214x y +=；（2）4[,1]5. 【分析】（1）利用已知条件求出a ，b ，然后求解椭圆方程；（2）()i 当OP ，OQ 斜率一个为0，一个不存在时，1OPQ S ∆=；()ii 当OP ，OQ 斜率都存在且不为0时，设:OP l y kx =，1(P x ，1)y ，2(Q x ，2)y ，由2214y kx x y =⎧⎪⎨+=⎪⎩求出P 的坐标，然后推出Q 坐标，求解||OP ，||OQ ，求出三角形的面积的表达式，利用基本不等式求解最值. 【详解】（1）由题意知，221314a b+=，22b =，解得2a =，1b =，故椭圆方程为：2214x y +=.（2）()i 当OP ，OQ 斜率一个为0，一个不存在时，1OPQ S ∆=，()ii 当OP ，OQ 斜率都存在且不为0时，设:OP l y kx =，1(P x ，1)y ，2(Q x ，2)y ，由2214y kx x y =⎧⎪⎨+=⎪⎩消y 得212414x k =+，2222112414k y k x k ==+， 22114y x k x y ⎧⎪⎪⎨=-+=⎪⎪⎩，得222244k x k =+，222222144y x k k ==+， ∴2222221122224444,144k k OP x y OQ x y k k ++=+==+=++ ∴22222421144441··2922144421OPQk k S OP OQ k k k k k ∆++===+++++ 又24222999012142k k k k k <=≤++++，所以415OPQ S ∆<，综上，OPQ △面积的取值范围为4[,1]5.【点睛】方法点睛：与圆锥曲线有关的最值和范围问题的讨论常用以下方法解决：（1）几何法：结合定义利用图形中几何量之间的大小关系或曲线之间位置关系列不等式，再解不等式.（2）函数值域求解法：把所讨论的参数作为一个函数、一个适当的参数作为自变量来表示这个函数，通过讨论函数的值域来求参数的变化范围.（3）利用代数基本不等式.代数基本不等式的应用，往往需要创造条件，并进行巧妙的构思.（4）结合参数方程，利用三角函数的有界性.直线、圆或椭圆的参数方程，它们的一个共同特点是均含有三角式.（5）利用数形结合分析解答.。

2019-2020学年黑龙江省哈师大附中高一(上)期中数学试卷(PDF版含答案)

又 f (x) g(x) 3x ， ①
f (x) g(x) 3x ，
f (x) g(x) 3x ， ②
由①②得 f (x) 3x 3x ； 2
故选： D ．
9．若函数 f (x) 是定义在 R 上的偶函数，在 ( ， 0] 上是减函数，且 f （2） 0 ，则
a ， b ， c 的大小关系为 a c b ．
故选： D ．
) D． a c b
6．函数 f (x) lg(x2 x 2) 的单调递增区间是 ( )
A． (1, )
B． ( 1 , ) 2
C． (, 1) 2
D． (, 2)
【解答】解：函数 f (x) lg(x2 x 2) ， x2 x 2 0 ，求得 x 2 ，或 x 1 ，
故函数的定义域为{x | x 2 ，或 x 1 }．
函数 f (x) 的增区间，即 y 0 时， y x2 x 2 的增区间，
利用二次函数的性质可得， y 0 时， y x2 x 2 的增区间为 (1, ) ，
故选： A ．
7．已知
g(x)
1
2x
，
f
B．若 2M 2N ，则 M N
C．若 loga M 2 loga N 2 ，则 M N
1
1
D．若 M N ，则 M 2 N 2
【解答】解： a 0 ， a 1．
A ．若 M N 0 ，则 loga M loga N 不成立；
B ．若 2M 2N ，则 M N ，正确；
-3-
22．已知定义在
R
上的奇函数
f
(x)

黑龙江省哈师大附中2020-2021学年高一上学期期中考试物理试题含答案

1黑龙江省哈师大附中2020-2021学年高一上学期期中考试物理试题一、选择题（本题共15小题，共45分。

其中第1-10小题为单选题，第11-15小题为多选题。

每小题3分，多选题选对但不全得2分，只要选错就得零分） 1．下列说法正确的是（）A ．导弹将目标锁定敌舰的要害，如弹药舱，可将敌舰视为质点B ．速率即瞬时速度的大小，平均速率即平均速度的大小C ．速度变化量很大，加速度可能很小D ．跳伞运动过程中，运动员身上掉下的钮扣做自由落体运动 2．下列各组物理量中，全部属于矢量的是（） A ．位移、时间、速度、加速度 B ．速度、平均速度、位移、加速度 C ．质量、力、速度、平均速度 D ．位移、力、路程、加速度3．汽车原以大小为v 的速度匀速行驶，刹车时做加速度大小为a 的匀减速直线运动，则t 秒后其位移为（以汽车前进方向为正方向）（）A ．212vt at -B ．22v aC ．212vt at -+D ．无法确定4．关于摩擦力，下列说法正确的是（） A ．受静摩擦力的物体一定是静止的B ．两个相互接触的粗糙物体间发生相对滑动时，就会产生滑动摩擦力C．两个相对静止的物体间的正压力增大，两者之间的摩擦力一定增大D．摩擦力的方向与物体的运动方向可以不同，摩擦力可以充当动力，也可以充当阻力5．对于一对相互作用力的理解，以下说法正确的有（）A．它们可以平衡B．一定等大，反向C．可以是不同性质的力D．大小可以不等6.一质点沿直线Ox方向做变速运动，它离开O点的距离随时间变化的关系为x=5+2t3（m），它的速度随时间t变化的关系为v=6t2（m/s）。

该质点在t=2s时刻的速度和t=1s到t=3s间的平均速度分别为（）A．12m/s，12m/s B．6m/s，6m/s C．13m/s，26m/s D．24m/s，26m/s7．如图所示，A、B、C三个物体叠放在水平地面上，有F＝1N的两个水平力分别作用于A、B两个物体上，A、B、C都静止，则地面对A物体、A物体对B物体、B物体对C物体的摩擦力大小分别为（）A．1N、2N、1NB．1N、0、1NC．0、1N、0D．1N、1N、0N8．P、Q、R三点在同一条直线上，一物体从P点由静止开始做匀加速直线运动，经过Q点时的速度为v，经过R点时的速度为3v，则PQ与QR之间的距离之比PQ∶QR等于（）A．l∶8 B．l∶6 C．l∶5 D．1∶39．如图甲所示，两位同学根据课本提示的方法，利用自由落体运动做反应时间的测量。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。