2013年普通高等学校招生统一考试--四川省数学(理) 文档版(有答案)

合集下载

2013年普通高等学校招生全国统一考试(四川卷)理科数学真题试卷

2013年普通高等学校招生全国统一考试（四川卷）数学（理工类）本试题卷分第I卷（选择题）和第II卷（非选择题）。

第I卷1至2页，第II卷2至5页考生作答是，须将答案答在答题卡上，在本试题作答，答题无效。

满分：150分，考试时间150分钟。

考试结束后，将本试题卷和答题卡一并交回。

第I卷（选择题共50分）注意事项：必须使用2B铅笔在答题卡上将所选答案对应的标号涂黑。

一、选择题：本答题共有10小题，每小题5分。

在每小题给出的四个选项中，只有一个是符合题目要求的。

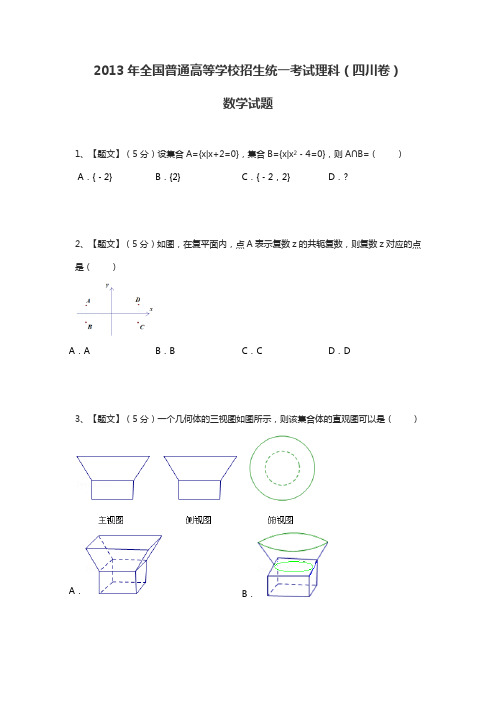
1、设集合，集合，则=（）A、B、C、D、2、如图，在复平面内，点A表示复数z的共轭复数的点是（）A、AB、BC、CD、D3、一个几何体的三视图如图所示，则该集合体的直视图可以是（）主视图侧视图俯视图A、B、C、D、4、设，集合是奇数集，集合是偶数集，若命题，则（）A、B、C、D、5、函数的部分图象如图所示，则的值分别是（）A、B、C、D、6、抛物线的焦点到双曲线的渐近线的距离是（）A、B、C、1 D、7、函数的图象大致是（）A、B、C、D、8、从1,3,5,7,9这五个数中，每次取出两个不同的数分别记为，共可得到的不同值的个数是（）A、9B、10C、18D、209、节日前夕，小李在家门前的树上挂了两串彩灯，这两串彩灯的第一次闪亮相互独立，且都在通电后的4秒内任一时刻等可能发生，然后每串彩灯以4秒为间隔闪亮，那么这两串彩灯同时同时通电后，它们第一次闪亮的时候相差不超过2秒的概率是（）A、B、C、D、10、设函数若曲线上存在点使得，则的取值范围是（）Ａ、Ｂ、Ｃ、Ｄ、第II卷（非选择题共100分）注意事项：必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的大体区域内作答。

作图题可先用铅笔绘出，确认后再用0.5毫米黑色墨迹签字笔描清楚。

答在试题卷上无效。

二、填空题：本大题共5小题，每小题5分，共25分。

11、二项式的展开式中，含的项的系数是__________（用数字作答）.12、在平行四边形中，对角线与交于点，，则______.13、设，则的值是_________.14、已知是定义域为的偶函数，当时，，那么，不等式的解集是_____.15、设为平面内的个点，在平面内的所有点中，若点到点的距离之和最小，则称点为的一个“中位点”，例如，线段上的任意点都是端点的中位点，现有下列命题：①若三个点共线，C在线段AB上，则C是A，B，C的中位点；②直角三角形斜边的中点是该直角三角形三个顶点的中位点；③若四个点共线，则它们的中位点存在且唯一；④梯形对角线的交点是该梯形四个顶点的唯一中位点。

2013高考理科数学(四川卷)

2013四川高考数学理科答案及解析

2013年普通高等学校招生全国统一考试数学理工农医类(四川卷)第Ⅰ卷(选择题共50分)一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个是符合题目要求的．2ABxxAxxB＝( )∩|．－41．(2013四川，理1)设集合＝＝{|0}＋2＝0}，集合，则＝{A．{－2} B．{2}?．．{－2,2} DC zAz的共轭复数表示复数如图，在复平面内，点，则图中表示2．(2013四川，理2) )．的点是(B A B．A．DC D．C． )．一个几何体的三视图如图所示，则该几何体的直观图可以是( 3．(2013四川，理3)?xpA,xAxB2：是奇数集，集合∈4．(2013四川，理4)设，集合∈Z是偶数集．若命题B．( ∈)，则???????B p：A．A,2xp：xx∈A,2x．B B??????B ∈p：p：xA,2xA,2x∈B D．C．x ππ???????0,?xxf的部分图象如图所示，．5(2013四川，理5)函数φ()＝2sin(ω)＋??22??．( )则ω，φ的值分别是π?3 A．2，π?6B．2，π?6，．4Cπ34，D．2y22xyx )抛物线．＝4( 的焦点到双曲线＝－1的渐近线的距离是6)(20136．四川，理331 322．1 D． C． B．A．3xy?的图象大致是( )． 7．(2013四川，理7)函数x3?1ab，共，从1,3,5,7,9这五个数中，每次取出两个不同的数分别记为8．(2013四川，理8)ab 的不同值的个数是( )．可得到lg －lgA．9 B．10 C．18 D．209．(2013四川，理9)节日前夕，小李在家门前的树上挂了两串彩灯．这两串彩灯的第一次闪亮相互独立，且都在通电后的4秒内任一时刻等可能发生，然后每串彩灯以4秒为间隔闪亮．那么这两串彩灯同时通电后，它们第一次闪亮的时刻相差不超过2秒的概率是( )．11378424． D C．A．． B x?x e?a ayfx，若曲线设函数)(，)e＝(为自然对数的底数∈R四川，理10．(201310)xxyffyya的取值范围是( )())，＝)使得．(，则(＝sin 上存在点0000A．[1，e] B．[e－1－1,1]C．[1，e＋1] D．[e－1－1，e＋1]第Ⅱ卷(非选择题共100分)二、填空题：本大题共5小题，每小题5分，共25分．523xyxy的项的系数是__________的展开式中，含．((2013四川，理11)二项式(用＋)11．数字作答)AOABAD，12．(2013四川，理12)在平行四边形ABCD中，对角线AC与BD＋λ＝交于点O，则λ＝__________.π??,π，则tan 2α的值是__________．sin 四川，理13)设2α＝－sin α，α∈ 13．(2013??2??2fxxfxxx，那么，(－)(＝)是定义域为R的偶函数，当4≥0时，(201314．四川，理14)已知fx＋2)＜5(的解集是__________．不等式PPPn个点，在平面α内的所有点中，为平面α15．(2013四川，理15)设内的，，…，n21PPPPPPPP 的一个“中到点，为点，…，，…，的距离之和最小，则称点若点，nn2211ABAB的中位点，现有下列命题：上的任意点都是端点位点”，例如，线段，ABCCABCABC的中位点；上，则①若三个点，是，共线，，在线段，②直角三角形斜边的中点是该直角三角形三个顶点的中位点；ABCD共线，则它们的中位点存在且唯一；，，，③若四个点④梯形对角线的交点是该梯形四个顶点的唯一中位点．其中的真命题是__________．(写出所有真命题的序号)三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．aaaaaa和为{}中，＋＝8，且在等差数列分本小题满分四川，理．16(201316)(12)n92134an项和．的等比中项，求数列{的首项、公差及前}nABCABCabc，，，，，的对边分别为17．(2013四川，理17)(本小题满分12分)在△中，角A?B32?cos CAABBB， cos(＋cos )－sin(＋－且2＝)sin 25A的值；求cos (1)a?42BCBA b方向上的投影．(2)在若＝5，求向量，x某算法的程序框图如图所示，其中输入的变量)分18)(本小题满分1218．(2013四川，理在1,2,3，…，24这24个整数中等可能随机产生．yiPi＝1,2,3)的值为；的概率 ((1)分别求出按程序框图正确编程运行时输出i n次后，统计记录了甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行(2)yii＝1,2,3)的值为的频数，以下是甲、乙所作频数统计表的部分数据．(输出甲的频数统计表(部分)yyy的值的值输出的值输出输出运行n 为3的频数为2的频数次数1为的频数10 14630 (697)3761 0272 100．乙的频数统计表(部分)yyy的值的值的值输出输出运行输出n 为3的频数为2的频数次数1为的频数7 301112 (353)1 0516962 100nyii＝乙所编程序各自输出(的值为1,2,3)分别写出甲、当2 ＝100时，根据表中的数据，的频率(用分数表示)，并判断两位同学中哪一位所编程序符合算法要求的可能性较大；y的值为2的次数求输出ξ的分布列及数学期次，将按程序框图正确编写的程序运行(3)3望．ABCABCAA⊥底面12分)如图，在三棱柱中，侧棱－19．(2013四川，理19)(本小题满分1111ABCABACAABACDDBCBCPAD的，∠＝120°，是线段，的中点，分别是线段，，＝2＝1111中点．ABCPABCll⊥平内，试作出过点与平面平行的直线，说明理由，并证明直线 (1)在平面1ADDA；面11lABMACNAAMN的余弦值．中的直线设(2)(1)交于点，交于点，求二面角－－122yx??1aCb＞：0)＞的两个(本小题满分20．(2013四川，理20)(13分)已知椭圆22ab41??,PFFC.(1,0)，且椭圆经过点焦点分别为1,0)(－，??2133??C的离心率； (1)求椭圆AlCMNQMN上的点，且，是线段(2)设过点的直线(0,2)两点，点与椭圆交于211??Q的轨迹方程．，求点222|AN||AM||AQ|2??2x?a,xx?0,fxa是实其中)14分)已知函数＝(理21．(2013四川，21)(本小题满分?ln x,x?0,?AxfxBxfxxx. ＜())，))(为该函数图象上的两点，且，数．设(，(212121fx)的单调区间；( (1)指出函数fxABxxx的最小值；，求 ()的图象在点，－处的切线互相垂直，且＜0(2)若函数122fxABa的取值范围．处的切线重合，求，的图象在点)(若函数(3)．2013年普通高等学校夏季招生全国统一考试数学理工农医类(四川卷)第Ⅰ卷(选择题共50分)一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个是符合题目要求的．1．答案：AAB＝{－2,2}－2}，，解析：由题意可得，＝{AB＝{－2}∩．故选A．∴2．答案：Bz表示的点与其共轭复数表示的点关于实轴对称．解析：复数3．答案：D解析：由三视图可知该几何体为一个上部为圆台、下部为圆柱的组合体，故选D．4．答案：D5．答案：A3T5ππ3π??????，解析：由图象可得，??43412??π2π55π?????1,2??sin Txfxωφ)中得，＝＝2，再将点，∴＝π代入，(2sin(2)＝则＋????π612????ππ5kk，∈Z令＋φ＝2π＋，26πkk∈Z解得，φ＝2π－，，3ππ??,?k又∵0，则取，φ∈＝??22??π?∴φ＝．.故选A36．答案：B?3x??3y x，即(1,0)，双曲线的渐近线方程为解析：由题意可得，抛物线的焦点为y＝0－，由点到直线的距离公式可得抛物线的焦点到双曲线的渐近线的距离|?3?0|3?d?. 227．答案：Cx＝－1，(0，＋∞)，故排除A；取解析：由函数解析式可得，该函数定义域为(－∞，0)∪?13x3xxy 的值且都为正，故1远远大于；当→＋∞时，＝3－，故再排除＝＞0B121?33x→0且大于0，故排除D，选C．x3?18．C答案：ab)，则基本事件空间Ω＝{(1,3)，(1,5)，(1,7)，解析：记基本事件为((1,9)，，(3,1)，(3,5)，(3,7)，(3,9)，(5,1)，(5,3)，(5,7)，(5,9)，(7,1)，(7,3)，(7,5)，(7,9)，a lg ba，其中基本＝20个基本事件，而lg lg －(9,1)，(9,3)，(9,5)，(9,7)}共有ba lg的值相等，则不同值的个数为20－2和(3,1)，(9,3)使＝18(个)，事件(1,3)，(3,9)b故选C．9．答案：Cxyxy≤4；而所设两串彩灯第一次闪亮的时刻分别为，则由题意可得，0≤，≤4,0≤解析：xyxy|≤2}，{()||，－求事件“两串彩灯同时通电后，第一次闪亮相差不超过2秒”＝S16?43阴影??P?. 由图示得，该事件概率S164正方形10．答案：Ayx∈[－sin 1,1]，解析：由题意可得，＝00x?x?e a yfx∈[0,1]，＝而由可知( )0x?x e xfa为增函数，) 时，(当＝＝0e?1yfy]．)∈[1∴时，∈[0,1] (，00e?1yff＞1.(∴))≥(0yffyy成立，故B，D))∴不存在∈[0,1]使＝(错；( 000x?x?e?1e yyfaxfx)(时)＝才有意义，而(1时，∈[0,1]时，只有＝1，当当＋＝e00f(1)＝0，fff(0)，显然无意义，故C错．故选(1))＝A．∴(第Ⅱ卷(非选择题共100分)注意事项：必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答．作图题可先用铅笔绘出，确认后再用0.5毫米黑色墨迹签字笔描清楚，答在试题卷上无效．二、填空题：本大题共5小题，每小题5分，共25分．11．答案：1032CC32yx10.由二项式展开系数可得，解析：＝＝的系数为5512．答案：2ACAOABAD ABCD 2＝如图所示，在平行四边形解析：中，＋＝，∴λ＝2.3 13．答案：解析：∵sin 2α＝－sin α，∴2sin αcos α＝－sin α.π1??,π?.＝cos α又∵α∈，∴??22??32???cos1. ＝∴sin α231??2. ＝＝－1α＝2cosα，∴sin 2αcos 222?sin23.＝＝∴tan 2α?cos214．答案：(－7,3)2xxxx＜，解得，0≤45.解析：当＜≥0时，令5－fxfxxx＜，即－72＜＜5等价于－5又因为＜(5)为定义域为R的偶函数，则不等式(＋＋2)＜3；故解集为(－7,3)．15．答案：①④CABABC也不上，则线段解析：由“中位点”可知，若上任一点都为“中位点”，在线段例外，故①正确；ABCACBPAB中点，设腰长为为斜边2＝90°，如图所示，点Rt对于②假设在等腰△，中，∠33232CACBCPAPBPCAB，|＝而若4为“中位点”，则|则|＋|＋||||＝＜|||＝＋|，2故②错；BCADABBCCDBABCBDCA|＋4＝|＋|||＝|，则|＝1|||＋对于③，若|，三等分＝，若设||＝|CBCD|，故③错；|| |＋ABCDACBDOABCDO的一的交点为内任取不同于点对于④，在梯形中，对角线，在梯形与MMACMAMCACOAOC|，＝|||点，则在△|中，||＋||＞＋|MBDMBMDBDOBOD|，|||||同理在△中，|＋|＞|＝|＋则得，MAMBMCMDOAOBOCOD|， |＋|＋|||||＋|＋||＋|＋|||＞|O为梯形内唯一中位点是正确的．故三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．dnS.解：设该数列公差为项和为，前16．n2adadadad)． )＝(＋由已知，可得2＋＋28＝8，()(＋31111adddaadada}{的首项为＝，或3＝1－3＝)0，解得，＝4所以，，＋，即数列＝4，＝(0n11114，公差为0，或首项为1，公差为3.2?n3n nSnS＝4所以，数列的前.项和或＝nn217．A?B32cos?BCABABBA2(1)由－＋cos(解：＋))＝＋cos ，得－sin(－[cos()sin 1]cos 523?BBBBA )sin －cos －sin(，－＝53?BBABBA.)sin )cos －－sin(即cos(＝－533??ABAB.＝＋，即)则cos(＝－cos 5543?AAA＝sin ，＜＜(2)由cos π＝，得，055ba?由正弦定理，有，B sin A sin2sin Ab?B. ＝所以，sin 2aπ?B BabA.由题知，故＞＞，则43??2?2)(422cccc－2×5舍去×)，解得．＝1或＝－根据余弦定理，有7(＝5＋??5??2BCBABA B.|cos 方向上的投影为|故向量＝在218．x是在1,2,3，…，24这24个整数中随机产生的一个数，共有24解：(1)变量种可能．1Pxy ；＝1，故从1,3,5,7,9,11,13,15,17,19,21,23这12个数中产生时，输出当的值为121Pyx ；的值为2，故＝当2,4,8,10,14,16,20,22从这8个数中产生时，输出231Pxy . 从6,12,18,24的值为3当，故＝这4个数中产生时，输出3611yyy 的值为3的概率的概率为所以，输出的值为12的概率为，输出，输出的值为 231. 为 6nyii ＝1,2,3)的值为的频率如下：( (2)当2 100＝时，甲、乙所编程序各自输出yyy 的值输出输出输出的值的值的频率3为的频率2为的频率1为1027376697甲2100210021003531051696 乙210021002100比较频率趋势与概率，可得乙同学所编程序符合算法要求的可能性较大． (3)随机变量ξ可能的取值为0,1,2,3.03218????0?C ??P ＝，ξ＝0)(???? 32733????12412????1???C P ，＝1)＝(ξ????3933????21122????2???C P2)＝，ξ(＝???? 3933????30211????3??C ?P ，(ξ＝3)＝???? 32733???? ξ的分布列为故320ξ18421 P 2727991284E 1.＋3×＋2×所以，＝ξ＝0×＋1×2799271.即ξ的数学期望为 19．BCABCPl 内，过点∥如图，在平面作直线，(1)解：．BCBClAAlBCBCA 内，因为在平面在平面由直线与平面平行的判定定理可知，外，∥平面111BCDABAC 由已知，是＝的中点，，．ADBCADl ⊥所以，，则直线⊥ABCAA ⊥平面因为，1lAA . ⊥直线所以1AAADADDAADAA 相交，又因为内，且，与在平面1111AlADD . ⊥平面所以直线11(2)解法一：AFFEFEAMAPAAEAPE . ⊥，过于作⊥，过连接作于，连接111AEAMN ⊥平面，由(1)知，1MNAAEA . 所以平面⊥平面11AEAMMNAEA . ⊥所以，则⊥平面11AFMAAMAEF .，则⊥平面所以⊥11NMAFEAA )．的平面角(故∠为二面角设为－θ－1ADABBACAAABAAACBAD 1. ＝，则由＝设1＝＝2，2＝＝60°，＝120°，有∠，∠11．PAD 的中点，为又1AMMABAP ＝所以中点，且，为＝1， 25 2MAAMAAAPAP .＝；在所以，在Rt △Rt △中，中，＝11112AP ?AA 11?AE ? ，从而PA 51AM ?AA 11?AF ?.MA21AE2?. θ＝所以sin AF52122??1sin??1?. ＝所以cos θ????55??15NAAM. －－故二面角的余弦值为15AEAD ACAAAEBA，＝1.如图，过解法二：设，以作，为坐标原点，分别以平行于111111111AA xOAyzOxyz 轴，的方向为重合轴，)轴的正方向，建立空间直角坐标系．(点与点11AA．则(0,0,1)(0,0,0)，1ADP为因为的中点，ACABMN，，分别为所以的中点．????1133,1,,,1?MN故，. ????????2222??????133NM AAMA,1,(，0,0)．所以＝＝＝(0,0,1)，，????1122??zyM n xAA，＝(，设平面，)的一个法向量为11111??0,?AMAM,n?n???1111即则??0,A??A,nAn?A????1111???130,,1?z??,,?x,y?????11122故有????0,?0,0,1?,x,yz?????111?130,z??x?y?111从而?22?0.z??13?yx＝1，则，＝取11 3?n．，0)所以＝(1，1zyx n AMN，(设平面的一个法向量为＝，，)22221．??,AM n?0,M?n?A??1212则即??0,NM?n?,?NM n????22???130,,1?,z??,?x,y?????22222故有????0,??z???3,0,0?x,y,?222?130,z??y?x?22222从而??0.x?3?2n yz．1)＝，则(0,2＝－1，所以取，－＝2222NMAA设二面角，－的平面角为θ－1为锐角，又θn?n21θ＝则cos|n|?|n|21?1,?3,0???0,2,?1?15?.＝52?515NMAA的余弦值为. 故二面角－－1520．解：(1)由椭圆定义知，22221414????????21??2?1???PFPFa |＝，＝||＋2|????????213333????????2?a.所以c1.又由已知，＝2c1e???C的离心率所以椭圆. 2a22x2yC1.的方程为＋＝(2)由(1)知，椭圆2Qxy)．( 设点，的坐标为lxlCQ的坐标为两点，此时点(0，－与椭圆1)交于(1)当直线(0,1)与，轴垂直时，直线??530,2?. ????5??lxlykx＋与2.轴不垂直时，设直线＝(2)当直线的方程为MNlMNxkxxkx＋2)(，，的坐标分别为(，因为＋，在直线2)上，可设点，，2121222222AMkxANkx.(1＋，|)|则|＝|＝(1＋)2122222AQxykx. )(1－2)又|＝|＝＋(＋211??，得由222|AQ||AM||AN|211??，222222x??k1k1???x???x1k?21．2?2?xx?x?x1212121???.①即22222xxxxx22112x2ykxy＝1中，得＋2代入将＋＝222kxkx 0.8②＋(26＋1)＝＋3222kkk. 由Δ＝(8，得)－4×(2＞＋1)×6＞02?8k6xxxx＝由②可知，，＋，＝2121222k?12k?1182x?.③代入①中并化简，得2?310k Qykx＋2上，在直线＝因为点y?222k?xy所以＝2)－3，代入③中并化简，得10(18. －x????3366,0?220,xxk. ∈＜∪＜由③及，即＞，可知0????????2222??????53220,2?yx＝18，－3 满足10(－2)又???? 5????66?,x.∈故????22??QxyC内，在椭圆，由题意， ()y≤1.所以－1≤99??,222yyyx≤1，－2)＝18＋3且－1≤有(－2)又由10(∈??54????513,2?y. 则∈???25??????51663,2,??22yQyxx.∈，3＝18所以，点，其中的轨迹方程为10(∈－2)－???????5222????21．fx)的单调递减区间为(－∞，－1)，单调递增区间为[(1)函数－(1,0)，(0，＋∞)．解：AfxBfx)，处的切线斜率为(2)由导数的几何意义可知，点处的切线斜率为′(′()，点21ABfxfx)＝－故当点)处的切线与点1. 处的切线垂直时，有′(′(21xfxfxx＋22. ())求导，得＝当′(＜0时，对函数xx＜0，＜因为21xx＋2)2)(2＝－1. 所以，(2＋21xx＋20,2＞所以20. ＋2＜211[??2x?2?]?2x?2?xxxxx＋－(2＝[－(2＋＋2)因此22)，当且仅当－＋2]≥＝11112221231x??x??x时等号成立．1＋2＝，即且＝222122fxABxx的最小值为处的切线互相垂直时，)的图象在点1.，所以，函数－(12xxxxfxfxxx. ＜时，，故′()≠＜′(0)(3)当＜＜0或＞＞021*******xaxxyxxxfxfx2)(＝2处的切线方程为，的图象在点时，＜当0函数()(())－(＋＋)(2＋111111．2axxxxy.＋－2))，即＋＝(2－1111xxxyxyfxxxf，即处的切线方程为(－当＞0时，函数ln ())的图象在点(＝，－())222222x1xx－ln ·＝1. ＋22x两切线重合的充要条件是1??2x?2,①?12x??2ln x?1??x?a.②?12xxx＜0. 知，－1＜0＜＜由①及1121ln22xaxx＋2)由①②得，－＝1＋＝1.－ln(2－1112x?212hxxxx＜0)，1＜－ln(21(＋2)设－(－)＝11111xhx＜20. 则－′(＝)11 x?11hxx＜0)是减函数． ()(－1所以，＜11hxh(0)＝－ln 2－1，则 ()＞1a＞－ln 2－所以1.xhx)无限增大，(且趋近于－－1,0)1时，又当∈(11a的取值范围是(－ln 2－1，＋∞)．所以fxABa的取值范围是(－ln 2－故当函数()的图象在点，处的切线重合时，1，＋∞)．。

2013年高考理科数学四川卷试题与答案word解析版

2013年普通高等学校夏季招生全国统一考试数学理工农医类(四川卷)第Ⅰ卷(选择题共50分)一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个是符合题目要求的．1．(2013四川，理1)设集合A ＝{x |x ＋2＝0}，集合B ＝{x |x 2－4＝0}，则A ∩B ＝( )．A ．{－2}B ．{2}C ．{－2,2}D ．∅2．(2013四川，理2)如图，在复平面内，点A 表示复数z ，则图中表示z 的共轭复数的点是( )．A ．AB ．BC ．CD ．D3．(2013四川，理3)一个几何体的三视图如图所示，则该几何体的直观图可以是( )．4．(2013四川，理4)设x ∈Z ，集合A 是奇数集，集合B 是偶数集．若命题p ：∀x ∈A,2x ∈B ，则( )．A ．⌝p ：∀x ∈A,2x ∉B B ．⌝p ：∀x ∉A,2x ∉BC ．⌝p ：∃x ∉A,2x ∈BD ．⌝p ：∃x ∈A,2x ∉B 5．(2013四川，理5)函数f (x )＝2sin(ωx ＋φ)ππ0,22ωϕ⎛⎫>-<< ⎪⎝⎭的部分图象如图所示，则ω，φ的值分别是( )．A ．2，π3-B ．2，π6-C ．4，π6-D ．4，π36．(2013四川，理6)抛物线y 2＝4x 的焦点到双曲线x 2－23y ＝1的渐近线的距离是( )．A ．12 B． C ．1 D7．(2013四川，理7)函数331x x y =-的图象大致是( )．8．(2013四川，理8)从1,3,5,7,9这五个数中，每次取出两个不同的数分别记为a，b，共可得到lg a－lg b的不同值的个数是( )．A．9 B．10 C．18 D．209．(2013四川，理9)节日前夕，小李在家门前的树上挂了两串彩灯．这两串彩灯的第一次闪亮相互独立，且都在通电后的4秒内任一时刻等可能发生，然后每串彩灯以4秒为间隔闪亮．那么这两串彩灯同时通电后，它们第一次闪亮的时刻相差不超过2秒的概率是( )．A．14 B．12 C．34 D．7810．(2013四川，理10)设函数f(x)(a∈R，e为自然对数的底数)，若曲线y＝sin x上存在点(x0，y0)使得f(f(y0))＝y0，则a的取值范围是( )．A．[1，e] B．[e－1－1,1]C．[1，e＋1] D．[e－1－1，e＋1]第Ⅱ卷(非选择题共100分)二、填空题：本大题共5小题，每小题5分，共25分．11．(2013四川，理11)二项式(x＋y)5的展开式中，含x2y3的项的系数是__________．(用数字作答) 12．(2013四川，理12)在平行四边形ABCD中，对角线AC与BD交于点O，AB＋AD＝λAO，则λ＝__________.13．(2013四川，理13)设sin 2α＝－sin α，α∈π,π2⎛⎫⎪⎝⎭，则tan 2α的值是__________．14．(2013四川，理14)已知f(x)是定义域为R的偶函数，当x≥0时，f(x)＝x2－4x，那么，不等式f(x＋2)＜5的解集是__________．15．(2013四川，理15)设P1，P2，…，P n为平面α内的n个点，在平面α内的所有点中，若点P到点P1，P2，…，P n的距离之和最小，则称点P为点P1，P2，…，P n的一个“中位点”，例如，线段AB上的任意点都是端点A，B的中位点，现有下列命题：①若三个点A，B，C共线，C在线段AB上，则C是A，B，C的中位点；②直角三角形斜边的中点是该直角三角形三个顶点的中位点；③若四个点A，B，C，D共线，则它们的中位点存在且唯一；④梯形对角线的交点是该梯形四个顶点的唯一中位点．其中的真命题是__________．(写出所有真命题的序号)三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．16．(2013四川，理16)(本小题满分12分)在等差数列{a n}中，a1＋a3＝8，且a4为a2和a9的等比中项，求数列{a n}的首项、公差及前n项和．17．(2013四川，理17)(本小题满分12分)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且22cos 2A B-cos B －sin(A －B )sin B ＋cos(A ＋C )＝35-，(1)求cos A 的值；(2)若a =b ＝5，求向量BA 在BC 方向上的投影．18．(2013四川，理18)(本小题满分12分)某算法的程序框图如图所示，其中输入的变量x 在1,2,3，…，24这24个整数中等可能随机产生．(1)分别求出按程序框图正确编程运行时输出y 的值为i 的概率P i (i ＝1,2,3)；(2)甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n 次后，统计记录了输出y 的值为i (i ＝1,2,3)的频数，以下是甲、乙所作频数统计表的部分数据．当n＝2 100的频率(用分数表示)，并判断两位同学中哪一位所编程序符合算法要求的可能性较大；(3)将按程序框图正确编写的程序运行3次，求输出y的值为2的次数ξ的分布列及数学期望．19．(2013四川，理19)(本小题满分12分)如图，在三棱柱ABC－A1B1C1中，侧棱AA1⊥底面ABC，AB＝AC ＝2AA1，∠BAC＝120°，D，D1分别是线段BC，B1C1的中点，P是线段AD的中点．(1)在平面ABC内，试作出过点P与平面A1BC平行的直线l，说明理由，并证明直线l⊥平面ADD1A1；(2)设(1)中的直线l交AB于点M，交AC于点N，求二面角A－A1M－N的余弦值．20．(2013四川，理20)(本小题满分13分)已知椭圆C ：22221x y a b+=(a ＞b ＞0)的两个焦点分别为F 1(－1,0)，F 2(1,0)，且椭圆C 经过点P 41,33⎛⎫⎪⎝⎭.(1)求椭圆C 的离心率；(2)设过点A (0,2)的直线l 与椭圆C 交于M ，N 两点，点Q 是线段MN 上的点，且222211||||||AQ AM AN =+，求点Q 的轨迹方程．21．(2013四川，理21)(本小题满分14分)已知函数f(x)＝22,0,ln,0,x x a xx x⎧++<⎨>⎩其中a是实数．设A(x1，f(x1))，B(x2，f(x2))为该函数图象上的两点，且x1＜x2.(1)指出函数f(x)的单调区间；(2)若函数f(x)的图象在点A，B处的切线互相垂直，且x2＜0，求x2－x1的最小值；(3)若函数f(x)的图象在点A，B处的切线重合，求a的取值范围．2013年普通高等学校夏季招生全国统一考试数学理工农医类(四川卷)第Ⅰ卷(选择题共50分)一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个是符合题目要求的．1．答案：A解析：由题意可得，A＝{－2}，B＝{－2,2}，∴A∩B＝{－2}．故选A．2．答案：B解析：复数z表示的点与其共轭复数表示的点关于实轴对称．3．答案：D解析：由三视图可知该几何体为一个上部为圆台、下部为圆柱的组合体，故选D．4．答案：D5．答案：A解析：由图象可得，35ππ3π41234T⎛⎫=--=⎪⎝⎭，∴T＝π，则ω＝2ππ＝2，再将点5π,212⎛⎫⎪⎝⎭代入f(x)＝2sin(2x＋φ)中得，5πsin16ϕ⎛⎫+=⎪⎝⎭，令5π6＋φ＝2kπ＋π2，k∈Z，解得，φ＝2kπ－π3，k∈Z，又∵φ∈ππ,22⎛⎫- ⎪⎝⎭，则取k＝0，∴φ＝π3-.故选A．6．答案：B解析：由题意可得，抛物线的焦点为(1,0)，双曲线的渐近线方程为y=，即－y＝0，由点到直线的距离公式可得抛物线的焦点到双曲线的渐近线的距离d==.7．答案：C解析：由函数解析式可得，该函数定义域为(－∞，0)∪(0，＋∞)，故排除A；取x＝－1，y＝1113--＝32＞0，故再排除B；当x→＋∞时，3x－1远远大于x3的值且都为正，故331xx-→0且大于0，故排除D，选C．8．答案：C解析：记基本事件为(a，b)，则基本事件空间Ω＝{(1,3)，(1,5)，(1,7)，(1,9)，(3,1)，(3,5)，(3,7)，(3,9)，(5,1)，(5,3)，(5,7)，(5,9)，(7,1)，(7,3)，(7,5)，(7,9)，(9,1)，(9,3)，(9,5)，(9,7)}共有20个基本事件，而lg a －lg b ＝lga b ，其中基本事件(1,3)，(3,9)和(3,1)，(9,3)使lg ab的值相等，则不同值的个数为20－2＝18(个)，故选C ．9．答案：C解析：设两串彩灯第一次闪亮的时刻分别为x ，y ，则由题意可得，0≤x ≤4,0≤y ≤4；而所求事件“两串彩灯同时通电后，第一次闪亮相差不超过2秒”＝{(x ，y )||x －y |≤2}，由图示得，该事件概率1643164S P S -===阴影正方形.10．答案：A解析：由题意可得，y 0＝sin x 0∈[－1,1]，而由f (x )可知y 0∈[0,1]，当a ＝0时，f (x )∴y 0∈[0,1]时，f (y 0)∈[1．∴f (f (y 0 1.∴不存在y 0∈[0,1]使f (f (y 0))＝y 0成立，故B ，D 错；当a ＝e ＋1时，f (x )y 0∈[0,1]时，只有y 0＝1时f (x )才有意义，而f (1)＝0， ∴f (f (1))＝f (0)，显然无意义，故C 错．故选A ．第Ⅱ卷(非选择题共100分)注意事项：必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答．作图题可先用铅笔绘出，确认后再用0.5毫米黑色墨迹签字笔描清楚，答在试题卷上无效．二、填空题：本大题共5小题，每小题5分，共25分． 11．答案：10解析：由二项式展开系数可得，x 2y 3的系数为35C ＝25C ＝10.12．答案：2解析：如图所示，在平行四边形ABCD 中，AB ＋AD ＝AC ＝2AO ，∴λ＝2.13．解析：∵sin 2α＝－sin α， ∴2sin αcos α＝－sin α.又∵α∈π,π2⎛⎫⎪⎝⎭，∴cos α＝12-.∴sin α2=.∴sin 2α＝2-，cos 2α＝2cos 2α－1＝12-.∴tan 2α＝sin2cos2αα14．答案：(－7,3)解析：当x ≥0时，令x 2－4x ＜5，解得，0≤x ＜5.又因为f (x )为定义域为R 的偶函数，则不等式f (x ＋2)＜5等价于－5＜x ＋2＜5，即－7＜x ＜3；故解集为(－7,3)． 15．答案：①④解析：由“中位点”可知，若C 在线段AB 上，则线段AB 上任一点都为“中位点”，C 也不例外，故①正确；对于②假设在等腰Rt △ABC 中，∠ACB ＝90°，如图所示，点P 为斜边AB 中点，设腰长为2，则|PA |＋|PB |＋|PC |＝32|AB |＝C 为“中位点”，则|CB |＋|CA |＝4＜对于③，若B ，C 三等分AD ，若设|AB |＝|BC |＝|CD |＝1，则|BA |＋|BC |＋|BD |＝4＝|CA |＋|CB |＋|CD |，故③错；对于④，在梯形ABCD 中，对角线AC 与BD 的交点为O ，在梯形ABCD 内任取不同于点O 的一点M ，则在△MAC 中，|MA |＋|MC |＞|AC |＝|OA |＋|OC |，同理在△MBD 中，|MB |＋|MD |＞|BD |＝|OB |＋|OD |，则得，|MA |＋|MB |＋|MC |＋|MD |＞|OA |＋|OB |＋|OC |＋|OD |，故O 为梯形内唯一中位点是正确的．三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤． 16．解：设该数列公差为d ，前n 项和为S n .由已知，可得2a 1＋2d ＝8，(a 1＋3d )2＝(a 1＋d )(a 1＋8d )．所以，a 1＋d ＝4，d (d －3a 1)＝0，解得a 1＝4，d ＝0，或a 1＝1，d ＝3，即数列{a n }的首项为4，公差为0，或首项为1，公差为3.所以，数列的前n 项和S n ＝4n 或S n ＝232n n-.17．解：(1)由22cos 2A B -cos B －sin(A －B )sin B ＋cos(A ＋C )＝35-，得[cos(A －B )＋1]cos B －sin(A －B )sin B －cos B ＝35-，即cos(A －B )cos B －sin(A －B )sin B ＝35-.则cos(A －B ＋B )＝35-，即cos A ＝35-.(2)由cos A ＝35-，0＜A ＜π，得sin A ＝45，由正弦定理，有sin a bA =，所以，sin B ＝sin 2b A a =由题知a ＞b ，则A ＞B ，故π4B =.根据余弦定理，有2＝52＋c 2－2×5c ×35⎛⎫- ⎪⎝⎭，解得c ＝1或c ＝－7(舍去)．故向量BA 在BC 方向上的投影为|BA |cos B .18．解：(1)变量x 是在1,2,3，…，24这24个整数中随机产生的一个数，共有24种可能．当x 从1,3,5,7,9,11,13,15,17,19,21,23这12个数中产生时，输出y 的值为1，故P 1＝12；当x 从2,4,8,10,14,16,20,22这8个数中产生时，输出y 的值为2，故P 2＝13；当x 从6,12,18,24这4个数中产生时，输出y 的值为3，故P 3＝16. 所以，输出y 的值为1的概率为12，输出y 的值为2的概率为13，输出y 的值为3的概率为16. (2)当n ＝2 100(3)随机变量ξ可能的取值为0,1,2,3.P (ξ＝0)＝0303128C 3327⎛⎫⎛⎫⨯⨯= ⎪ ⎪⎝⎭⎝⎭，P (ξ＝1)＝1213124C 339⎛⎫⎛⎫⨯⨯= ⎪ ⎪⎝⎭⎝⎭，P (ξ＝2)＝2123122C 339⎛⎫⎛⎫⨯⨯= ⎪ ⎪⎝⎭⎝⎭，P (ξ＝3)＝3033121C 3327⎛⎫⎛⎫⨯⨯= ⎪ ⎪⎝⎭⎝⎭，故ξ的分布列为所以，E ξ＝0×827＋1×49＋2×9＋3×27＝1.即ξ的数学期望为1.19．解：(1)如图，在平面ABC 内，过点P 作直线l ∥BC ，因为l 在平面A 1BC 外，BC 在平面A 1BC 内，由直线与平面平行的判定定理可知，l ∥平面A 1BC ．由已知，AB ＝AC ，D 是BC 的中点，所以，BC ⊥AD ，则直线l ⊥AD ．因为AA 1⊥平面ABC ，所以AA 1⊥直线l .又因为AD ，AA 1在平面ADD 1A 1内，且AD 与AA 1相交，所以直线l ⊥平面ADD 1A 1. (2)解法一：连接A 1P ，过A 作AE ⊥A 1P 于E ，过E 作EF ⊥A 1M 于F ，连接AF . 由(1)知，MN ⊥平面AEA 1，所以平面AEA 1⊥平面A 1MN .所以AE ⊥平面A 1MN ，则A 1M ⊥AE . 所以A 1M ⊥平面AEF ，则A 1M ⊥AF .故∠AFE 为二面角A －A 1M －N 的平面角(设为θ)．设AA 1＝1，则由AB ＝AC ＝2AA 1，∠BAC ＝120°，有∠BAD ＝60°，AB ＝2，AD ＝1. 又P 为AD 的中点，所以M 为AB 中点，且AP＝12，AM ＝1，所以，在Rt △AA 1P 中，A 1PRt △A 1AM 中，A 1M.从而11AAAP AE A P ⋅==， 11AA AM AF A M ⋅==.所以sin θ＝AE AF =所以cos θ5==.解法二：设A 1A ＝1.如图，过A 1作A 1E 平行于B 1C 1，以A 1为坐标原点，分别以1A E ，11A D ，1A A 的方向为x 轴，y 轴，z 轴的正方向，建立空间直角坐标系Oxyz (点O 与点A 1重合)．则A 1(0,0,0)，A (0,0,1)．因为P 为AD 的中点，所以M ，N 分别为AB ，AC 的中点．故M 1,,122⎛⎫⎪ ⎪⎝⎭，N 1,122⎛⎫- ⎪ ⎪⎝⎭.所以1AM＝1,122⎛⎫⎪ ⎪⎝⎭，1A A ＝(0,0,1)，NM ＝0,0)．设平面AA 1M 的一个法向量为n 1＝(x 1，y 1，z 1)，则1111,,A M A A ⎧⊥⎪⎨⊥⎪⎩n n 即11110,0,A M A A ⎧⋅=⎪⎨⋅=⎪⎩n n故有1111111,,,10,22,,0,0,10,x y z x y z ⎧⎛⎫()⋅=⎪ ⎪ ⎪⎨⎝⎭⎪()⋅()=⎩从而111110,20.x y z z ++=⎪=⎩ 取x 1＝1，则y 1＝所以n 1＝(1，，0)．设平面A 1MN 的一个法向量为n 2＝(x 2，y 2，z 2)，则212,,A M NM ⎧⊥⎪⎨⊥⎪⎩n n 即2120,0,A M NM ⎧⋅=⎪⎨⋅=⎪⎩n n故有2222221,,,10,2,,0,x y z x y z ⎧⎫()⋅=⎪⎪⎪⎨⎝⎭⎪()=⎩从而222210,220.x y z ++=⎪= 取y 2＝2，则z 2＝－1，所以n 2＝(0,2，－1)．设二面角A －A 1M －N 的平面角为θ，又θ为锐角，则cos θ＝1212||||⋅⋅n n n n5=20．解：(1)由椭圆定义知，2a ＝|PF 1|＋|PF 2|=所以a =又由已知，c ＝1.所以椭圆C的离心率2c e a ===. (2)由(1)知，椭圆C 的方程为22x ＋y 2＝1.设点Q 的坐标为(x ，y )．(1)当直线l 与x 轴垂直时，直线l 与椭圆C 交于(0,1)，(0，－1)两点，此时点Q的坐标为0,2⎛ ⎝⎭. (2)当直线l 与x 轴不垂直时，设直线l 的方程为y ＝kx ＋2.因为M ，N 在直线l 上，可设点M ，N 的坐标分别为(x 1，kx 1＋2)，(x 2，kx 2＋2)，则|AM |2＝(1＋k 2)x 12，|AN |2＝(1＋k 2)x 22.又|AQ |2＝x 2＋(y －2)2＝(1＋k 2)x 2. 由222211||||||AQ AM AN =+，得22222212211111k x k x k x =+(+)(+)(+)，即212122222212122211x x x x x x x x x (+)-=+=.① 将y ＝kx ＋2代入22x ＋y 2＝1中，得(2k 2＋1)x 2＋8kx ＋6＝0.②由Δ＝(8k )2－4×(2k 2＋1)×6＞0，得k 2＞32. 由②可知，x 1＋x 2＝2821k k -+，x 1x 2＝2621k +，代入①中并化简，得2218103x k =-.③ 因为点Q 在直线y ＝kx ＋2上，所以2y k x-=，代入③中并化简，得10(y －2)2－3x 2＝18. 由③及k 2＞32，可知0＜x 2＜32，即x∈2⎛⎫- ⎪ ⎪⎝⎭∪0,2⎛ ⎝⎭.又0,25⎛- ⎝⎭满足10(y －2)2－3x 2＝18，故x∈,22⎛- ⎝⎭.由题意，Q (x ，y )在椭圆C 内，所以－1≤y ≤1.又由10(y －2)2＝18＋3x 2有(y －2)2∈99,54⎡⎫⎪⎢⎣⎭且－1≤y ≤1，则y∈1,22⎛⎝⎦. 所以，点Q 的轨迹方程为10(y －2)2－3x 2＝18，其中x∈⎛⎝⎭，y∈1,22⎛- ⎝⎦. 21．解：(1)函数f (x )的单调递减区间为(－∞，－1)，单调递增区间为[－1,0)，(0，＋∞)． (2)由导数的几何意义可知，点A 处的切线斜率为f ′(x 1)，点B 处的切线斜率为f ′(x 2)，故当点A 处的切线与点B 处的切线垂直时，有f ′(x 1)f ′(x 2)＝－1. 当x ＜0时，对函数f (x )求导，得f ′(x )＝2x ＋2. 因为x 1＜x 2＜0，所以，(2x 1＋2)(2x 2＋2)＝－1. 所以2x 1＋2＜0,2x 2＋2＞0.因此x 2－x 1＝12[－(2x 1＋2)＋2x 2＝1，当且仅当－(2x 1＋2)＝2x 2＋2＝1，即132x =-且212x =-时等号成立．所以，函数f (x )的图象在点A ，B 处的切线互相垂直时，x 2－x 1的最小值为1.(3)当x 1＜x 2＜0或x 2＞x 1＞0时，f ′(x 1)≠f ′(x 2)，故x 1＜0＜x 2.当x 1＜0时，函数f (x )的图象在点(x 1，f (x 1))处的切线方程为y －(x 12＋2x 1＋a )＝(2x 1＋2)(x －x 1)，即y＝(2x 1＋2)x －x 12＋a .当x 2＞0时，函数f (x )的图象在点(x 2，f (x 2))处的切线方程为y －ln x 2＝21x (x －x 2)，即y ＝21x·x ＋ln x 2－1.两切线重合的充要条件是12221122,ln 1.x xx x a ⎧=+⎪⎨⎪-=-+⎩①②由①及x 1＜0＜x 2知，－1＜x 1＜0. 由①②得，a ＝x 12＋11ln22x +－1＝x 12－ln(2x 1＋2)－1.设h (x 1)＝x 12－ln(2x 1＋2)－1(－1＜x 1＜0)，则h ′(x 1)＝2x 1－111x +＜0. 所以，h (x 1)(－1＜x 1＜0)是减函数．则h (x 1)＞h (0)＝－ln 2－1，所以a ＞－ln 2－1.又当x 1∈(－1,0)且趋近于－1时，h (x 1)无限增大，所以a 的取值范围是(－ln 2－1，＋∞)．故当函数f (x )的图象在点A ，B 处的切线重合时，a 的取值范围是(－ln 2－1，＋∞)．。

2013年全国普通高等学校招生统一考试理科数学(四川卷带解析)试题

2013年全国普通高等学校招生统一考试理科（四川卷）数学试题1、【题文】（5分）设集合A={x|x+2=0}，集合B={x|x2﹣4=0}，则A∩B=（）A．{﹣2} B．{2} C．{﹣2，2} D．?2、【题文】（5分）如图，在复平面内，点A表示复数z的共轭复数，则复数z对应的点是（）A．A B．B C．C D．D3、【题文】（5分）一个几何体的三视图如图所示，则该集合体的直观图可以是（）A．B．C．D．4、【题文】（5分）设x∈Z，集合A是奇数集，集合B是偶数集．若命题p：?x∈A，2x∈B，则（）A．￢p：?x∈A，2x?B B．￢p：?x?A，2x?B C．￢p：?x?A，2x∈B D．￢p：?x∈A，2x?B5、【题文】（5分）函数的部分图象如图所示，则ω，φ的值分别是（）A．B．C．D．6、【题文】（5分）抛物线y2=4x的焦点到双曲线的渐近线的距离是（）C．1 D．A．B．7、【题文】（5分）函数的图象大致是（）A．B．C．D．8、【题文】（5分）从1，3，5，7，9这五个数中，每次取出两个不同的数分别记为a，b，共可得到lga﹣lgb的不同值的个数是（）A．9 B．10 C．18 D．209、【题文】（5分）节日前夕，小李在家门前的树上挂了两串彩灯，这两串彩灯的第一次闪亮相互独立，且都在通电后的4秒内任一时刻等可能发生，然后每串彩灯以4秒为间隔闪亮，那么这两串彩灯同时同时通电后，它们第一次闪亮的时候相差不超过2秒的概率是（）A．B．C．D．10、【题文】（5分）设函数（a∈R，e为自然对数的底数），若曲线y=sinx上存在点（x0，y0）使得f（f（y0））=y0，则a的取值范围是（）A．[1，e] B．[e﹣1﹣1，1] C．[1，e+1] D．[e﹣1﹣1，e+1]11、【题文】（5分）二项式（x+y）5的展开式中，含x2y3的项的系数是（用数字作答）．12、【题文】（5分）在平行四边形ABCD中，对角线AC与BD交于点O，，则λ=．13、【题文】（5分）设sin2α=﹣sinα，，则tan2α的值是．14、【题文】（5分）已知f（x）是定义域为R的偶函数，当x≥0时，f（x）=x2﹣4x，那么，不等式f（x+2）＜5的解集是．15、【题文】（5分）设P1，P2，…P n为平面α内的n个点，在平面α内的所有点中，若点P到点P1，P2，…P n的距离之和最小，则称点P为P1，P2，…P n的一个“中位点”，例如，线段AB上的任意点都是端点A，B的中位点，现有下列命题：①若三个点A、B、C共线，C在线段AB上，则C是A，B，C的中位点；②直角三角形斜边的中点是该直角三角形三个顶点的中位点；③若四个点A、B、C、D共线，则它们的中位点存在且唯一；④梯形对角线的交点是该梯形四个顶点的唯一中位点．其中的真命题是（写出所有真命题的序号）．16、【题文】（12分）在等差数列{a n}中，a1+a3=8，且a4为a2和a9的等比中项，求数列{a n}的首项，公差及前n项和．17、【题文】（12分）在△ABC中，角A、B、C的对边分别a、b、c，且（1）求cosA的值；（2）若，求向量在方向上的投影．18、【题文】（12分）某算法的程序框图如图所示，其中输入的变量x在1，2，3，…，24这24个整数中等可能随机产生（I）分别求出按程序框图正确编程运行时输出y的值为i的概率p i（i=1，2，3）；（II）甲乙两同学依据自己对程序框图的理解，各自编程写出程序重复运行n次后，统计记录输出y的值为i（i=1，2，3）的频数，以下是甲乙所作频数统计表的部分数据．甲的频数统计图（部分）运行次数n 输出y的值为1的频数输出y的值为2的频数输出y的值为3的频数30 14 6 10…………2100 1027 376 697乙的频数统计图（部分）运行次数n 输出y的值为1的频数输出y的值为2的频数输出y的值为3的频数30 12 11 7…………2100 1051 696 353当n=2100时，根据表中的数据，分别写出甲、乙所编程序各自输出y的值为i（i=1，2，3）的频率（用分数表示），并判断两位同学中哪一位所编程序符合要求的可能系较大；（III）将按程序摆图正确编写的程序运行3次，求输出y的值为2的次数ξ的分布列及数学期望．19、【题文】（12分）如图，在三棱柱ABC﹣A1B1C1中，侧棱AA1⊥底面ABC，AB=AC=2AA1，∠BAC=120°，D，D1分别是线段BC，B1C1的中点，P是线段AD的中点．（I）在平面ABC内，试做出过点P与平面A1BC平行的直线l，说明理由，并证明直线l⊥平面ADD1A1；（II）设（I）中的直线l交AB于点M，交AC于点N，求二面角A﹣A1M﹣N的余弦值．20、【题文】（13分）已知椭圆C：（a＞b＞0）的两个焦点分别为F1（﹣1，0），F2（1，0），且椭圆C经过点．（I）求椭圆C的离心率：（II）设过点A（0，2）的直线l与椭圆C交于M，N两点，点Q是线段MN上的点，且，求点Q的轨迹方程．21、【题文】（14分）已知函数，其中a是实数，设A（x1，f（x1）），B（x2，f（x2））为该函数图象上的点，且x1＜x2．（I）指出函数f（x）的单调区间；（II）若函数f（x）的图象在点A，B处的切线互相垂直，且x2＜0，求x2﹣x1的最小值；（III）若函数f（x）的图象在点A，B处的切线重合，求a的取值范围．。

2013年全国普通高等学校招生统一考试理科数学(四川卷带解析)答案解析

2013年全国普通高等学校招生统一考试理科（四川卷）数学答案解析1、【答案】A【解析】由A中的方程x+2=0，解得x=﹣2，即A={﹣2}；由B中的方程x2﹣4=0，解得x=2或﹣2，即B={﹣2，2}，则A∩B={﹣2}．2、【答案】B【解析】两个复数是共轭复数，两个复数的实部相同，下部相反，对应的点关于x轴对称．所以点A表示复数z的共轭复数的点是B．3、【答案】D【解析】由俯视图可知，原几何体的上底面应该是圆面，由此排除选项A和选项C．而俯视图内部只有一个虚圆，所以排除B．故选D．4、【答案】D【解析】因为全称命题的否定是特称命题，所以设x∈Z，集合A是奇数集，集合B是偶数集．若命题p：?x∈A，2x∈B，则￢p：?x∈A，2x?B．【答案】A【解析】∵在同一周期内，函数在x=时取得最大值，x=时取得最小值，∴函数的周期T满足=﹣=，由此可得T==π，解得ω=2，得函数表达式为f（x）=2sin（2x+φ）又∵当x=时取得最大值2，∴2sin（2?+φ）=2，可得+φ=+2kπ（k∈Z）∵，∴取k=0，得φ=﹣6、【答案】B【解析】∵抛物线方程为y2=4x∴2p=4，可得=1，抛物线的焦点F（1，0）又∵双曲线的方程为∴a2=1且b2=3，可得a=1且b=，双曲线的渐近线方程为y=±，即y=±x，化成一般式得：．因此，抛物线y2=4x的焦点到双曲线渐近线的距离为d==【答案】A【解析】当x＜0时，x3＜0，3x﹣1＜0，∴，故排除B；对于C，由于函数值不可能为0，故可以排除C；∵y=3x﹣1与y=x3相比，指数函数比幂函数，随着x的增大，增长速度越大，∴x→+∞，→0，∴D不正确，A正确，8、【答案】C【解析】首先从1，3，5，7，9这五个数中任取两个不同的数排列，共有种排法，因为，，所以从1，3，5，7，9这五个数中，每次取出两个不同的数分别记为a，b，共可得到lga﹣lgb的不同值的个数是：20﹣2=18．9、【答案】C【解析】设两串彩灯第一次闪亮的时刻分别为x，y，由题意可得0≤x≤4，0≤y≤4，它们第一次闪亮的时候相差不超过2秒，则|x﹣y|≤2，由几何概型可得所求概率为上述两平面区域的面积之比，由图可知所求的概率为：=10、【答案】A【解析】曲线y=sinx上存在点（x0，y0）使得f（f（y0））=y0，则y0∈[﹣1，1]考查四个选项，B，D两个选项中参数值都可取0，C，D两个选项中参数都可取e+1，A，B，C，D四个选项参数都可取1，由此可先验证参数为0与e+1时是否符合题意，即可得出正确选项当a=0时，，此是一个增函数，且函数值恒非负，故只研究y0∈[0，1]时f（f（y0））=y0是否成立由于是一个增函数，可得出f（y0）≥f（0）=1，而f（1）=＞1，故a=0不合题意，由此知B，D两个选项不正确当a=e+1时，此函数是一个增函数，=0，而f（0）没有意义，故a=e+1不合题意，故C，D两个选项不正确综上讨论知，可确定B，C，D三个选项不正确，故A选项正确11、【答案】10【解析】设二项式（x+y）5的展开式的通项公式为T r+1，则T r+1=x5﹣r?y r，令r=3，则含x2y3的项的系数是=10．12、【答案】2【解析】∵四边形ABCD为平行四边形，对角线AC与BD交于点O，∴+=，又O为AC的中点，∴=2，∴+=2，∵+=λ，∴λ=2．13、【答案】【解析】∵sin2α=2sinαcosα=﹣sinα，α∈（，π），∴cosα=﹣，sinα==，∴tanα=﹣，则tan2α===．14、【答案】（﹣7，3）【解析】因为f（x）为偶函数，所以f（|x+2|）=f（x+2），则f（x+2）＜5可化为f（|x+2|）＜5，即|x+2|2﹣4|x+2|＜5，（|x+2|+1）（|x+2|﹣5）＜0，所以|x+2|＜5，解得﹣7＜x＜3，所以不等式f（x+2）＜5的解集是（﹣7，3）．15、【答案】①④【解析】①若三个点A、B、C共线，C在线段AB上，根据两点之间线段最短，则C是A，B，C的中位点，正确；②举一个反例，如边长为3，4，5的直角三角形ABC，此直角三角形的斜边的中点到三个顶点的距离之和为5+2.5=7.5，而直角顶点到三个顶点的距离之和为7，∴直角三角形斜边的中点不是该直角三角形三个顶点的中位点；故错误；③若四个点A、B、C、D共线，则它们的中位点是中间两点连线段上的任意一个点，故它们的中位点存在但不唯一；故错误；④如图，在梯形ABCD中，对角线的交点O，P是任意一点，则根据三角形两边之和大于第三边得PA+PB+PC+PD≥AC+BD=OA+OB+OC+OD，∴梯形对角线的交点是该梯形四个顶点的唯一中位点．正确．故答案为：①④．16、【答案】S n=【解析】设该数列的公差为d，前n项和为S n，则∵a1+a3=8，且a4为a2和a9的等比中项，∴2a1+2d=8，（a1+3d）2=（a1+d）（a1+8d）解得a1=4，d=0或a1=1，d=3∴前n项和为S n=4n或S n=．17、【答案】（1）（2）=ccosB=【解析】（Ⅰ）由，可得，即，即，（Ⅱ）由正弦定理，，所以=，由题意可知a＞b，即A＞B，所以B=，由余弦定理可知．解得c=1，c=﹣7（舍去）．向量在方向上的投影：=ccosB=．18、【答案】（I）输出的y值为1的概率为，输出的y值为2的概率为，输出的y值为3的概率为（II）乙同学所编程序符合算法要求的可能性较大（III）1【解析】（I）变量x是在1，2，3，…，24这24个整数中随机产生的一个数，共有24种可能，当x从1，3，5，7，9，11，13，15，17，19，21，23这12个数中产生时，输出的y 值为1，故P1==；当x从2，4，8，10，14，16，20，22这8个数中产生时，输出的y值为2，故P2==；当x从6，12，18，24这4个数中产生时，输出的y值为3，故P3==；故输出的y值为1的概率为，输出的y值为2的概率为，输出的y值为3的概率为；（II）当n=2100时，甲、乙所编程序各自输出的y值为i（i=1，2，3）的频率如下：输出y值为1的频率输出y值为2的频率输出y值为3的频率甲乙比较频率趋势与概率，可得乙同学所编程序符合算法要求的可能性较大；（III）随机变量ξ的可能取值为：0，1，2，3，P（ξ=0）==，P（ξ=1）==P（ξ=2）==，P（ξ=3）==，故ξ的分布列为：ξ 0 1 2 3P所以所求的数学期望Eξ==119、【答案】（I）见解析（II）【解析】（I）在平面ABC内，过点P作直线l∥BC∵直线l?平面A1BC，BC?平面A1BC，∴直线l∥平面A1BC，∵△ABC中，AB=AC，D是BC的中点，∴AD⊥BC，结合l∥BC得AD⊥l∵AA1⊥平面ABC，l?平面ABC，∴AA1⊥l∵AD、AA1是平面ADD1A1内的相交直线∴直线l⊥平面ADD1A1；（II）连接A1P，过点A作AE⊥A1P于E，过E点作EF⊥A1M于F，连接AF由（I）知MN⊥平面A1AE，结合MN?平面A1MN得平面A1MN⊥平面A1AE，∵平面A1MN∩平面A1AE=A1P，AE⊥A1P，∴AE⊥平面A1MN，∵EF⊥A1M，EF是AF在平面A1MN内的射影，∴AF⊥A1M，可得∠AFE就是二面角A﹣A1M﹣N的平面角设AA1=1，则由AB=AC=2AA1，∠BAC=120°，可得∠BAD=60°，AB=2且AD=1又∵P为AD的中点，∴M是AB的中点，得AP=，AM=1Rt△A1AP中，A1P==；Rt△A1AM中，A1M=∴AE==，AF==∴Rt△AEF中，sin∠AFE==，可得cos∠AFE==即二面角A﹣A1M﹣N的余弦值等于．20、【答案】（I）（II）点Q的轨迹方程为10（y﹣2）2﹣3x2=18，其中x∈（﹣，），y∈（，2﹣）【解析】（I）∵椭圆C：（a＞b＞0）的两个焦点分别为F1（﹣1，0），F2（1，0），且椭圆C经过点．∴c=1，2a=PF1+PF2==2，即a=∴椭圆的离心率e===…4分（II）由（I）知，椭圆C的方程为，设点Q的坐标为（x，y）（1）当直线l与x轴垂直时，直线l与椭圆C交于（0，1）、（0，﹣1）两点，此时点Q 的坐标为（0，2﹣）（2）当直线l与x轴不垂直时，可设其方程为y=kx+2，因为M，N在直线l上，可设点M，N的坐标分别为（x1，kx1+2），（x2，kx2+2），则，，又|AQ|2=（1+k2）x2，∴，即=…①将y=kx+2代入中，得（2k2+1）x2+8kx+6=0…②由△=（8k）2﹣24（2k2+1）＞0，得k2＞由②知x1+x2=，x1x2=，代入①中化简得x2=…③因为点Q在直线y=kx+2上，所以k=，代入③中并化简得10（y﹣2）2﹣3x2=18由③及k2＞可知0＜x＜，即x∈（﹣，0）∪（0，）由题意，Q（x，y）在椭圆C内，所以﹣1≤y≤1，又由10（y﹣2）2﹣3x2=18得（y﹣2）2∈[，）且﹣1≤y≤1，则y∈（，2﹣）所以，点Q的轨迹方程为10（y﹣2）2﹣3x2=18，其中x∈（﹣，），y∈（，2﹣）…13分21、【答案】（I）f（x）在（﹣∞，﹣1）上单调递减，在（﹣1，0）上单调递增（II）1（III）（﹣1﹣ln2，+∞）【解析】（I）当x＜0时，f（x）=（x+1）2+a，∴f（x）在（﹣∞，﹣1）上单调递减，在（﹣1，0）上单调递增；当x＞0时，f（x）=lnx，在（0，+∞）单调递增．（II）∵x1＜x2＜0，∴f（x）=x2+2x+a，∴f′（x）=2x+2，∴函数f（x）在点A，B处的切线的斜率分别为f′（x1），f′（x2），∵函数f（x）的图象在点A，B处的切线互相垂直，∴，∴（2x1+2）（2x2+2）=﹣1．∴2x1+2＜0，2x2+2＞0，∴=1，当且仅当﹣（2x1+2）=2x2+2=1，即，时等号成立．∴函数f（x）的图象在点A，B处的切线互相垂直，且x2＜0，求x2﹣x1的最小值为1．（III）当x1＜x2＜0或0＜x1＜x2时，∵，故不成立，∴x1＜0＜x2．当x1＜0时，函数f（x）在点A（x1，f（x1）），处的切线方程为，即．当x2＞0时，函数f（x）在点B（x2，f（x2））处的切线方程为，即．函数f（x）的图象在点A，B处的切线重合的充要条件是，由①及x1＜0＜x2可得﹣1＜x1＜0，由①②得=．∵函数，y=﹣ln（2x1+2）在区间（﹣1，0）上单调递减，∴a（x1）=在（﹣1，0）上单调递减，且x1→﹣1时，ln（2x1+2）→﹣∞，即﹣ln（2x1+2）→+∞，也即a（x1）→+∞．x1→0，a（x1）→﹣1﹣ln2．∴a的取值范围是（﹣1﹣ln2，+∞）．。

2013年普通高等学校招生全国统一考试数学理试题(四川卷)

2013年普通高等学校招生全国统一考试（四川卷）数学（理科）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个是符合题目要求的．1．设集合{|20}A x x =+=，集合2{|40}B x x =-=，则AB =（）（A ）{2}- （B ）{2} （C ）{2,2}- （D ）∅2．如图，在复平面内，点A 表示复数z ，则图中表示z 的共轭复数的点是（）yxDBA OC（A ）A （B ）B （C ）C （D ）D3．一个几何体的三视图如图所示，则该几何体的直观图可以是（）4．设x Z ∈，集合A 是奇数集，集合B 是偶数集．若命题:,2p x A x B ∀∈∈，则（）（A ）:,2p x A x B ⌝∀∃∈∉ （B ）:,2p x A x B ⌝∀∉∉（C ）:,2p x A x B ⌝∃∉∈ （D ）:,2p x A x B ⌝∃∈∈5．函数()2sin(),(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示，则,ωϕ的值分别是（）（A ）2,3π-（B ）2,6π-（C ）4,6π-（D ）4,3π6．抛物线24y x =的焦点到双曲线2213yx -=的渐近线的距离是（）（A ）12（B 3 （C ）1 （D 37．函数231x x y =-的图象大致是（）8．从1,3,5,7,9这五个数中，每次取出两个不同的数分别为,a b ，共可得到lg lg a b -的不同值的个数是（）（A ）9 （B ）10 （C ）18 （D ）209．节日里某家前的树上挂了两串彩灯，这两串彩灯的第一次闪亮相互独立，若接通电后的4秒内任一时刻等可能发生，然后每串彩灯在内4秒为间隔闪亮，那么这两串彩灯同时通电后，它们第一次闪亮的时刻相差不超过2秒的概率是（）（A ）14 （B ）12 （C ）34 （D ）7810．设函数()x f x e x a =+-a R ∈，e 为自然对数的底数）．若曲线sin y x =上存在00(,)x y 使得00(())f f y y =，则a 的取值范围是（）（A ）[1,]e （B ）1[,-11]e -，（C ）[1,1]e + （D ）1[-1,1]e e -+ 二、填空题：本大题共5小题，每小题5分，共25分．11．二项式5()x y +的展开式中，含23x y 的项的系数是_________．（用数字作答）12．在平行四边形ABCD 中，对角线AC 与BD 交于点O ，AB AD AO λ+=，则λ=_________．13．设sin 2sin αα=-，(,)2παπ∈，则tan 2α的值是_________．14．已知()f x 是定义域为R 的偶函数，当x ≥0时，2()4f x x x =-，那么，不等式(2)5f x +<的解集是________ ．15．设12,,,n P P P 为平面α内的n 个点，在平面α内的所有点中，若点P 到12,,,nP P P 点的距离之和最小，则称点P 为12,,,n P P P 点的一个“中位点”．例如，线段AB 上的任意点都是端点,A B 的中位点．则有下列命题：①若,,A B C 三个点共线，C 在线AB 上，则C 是,,A B C 的中位点；②直角三角形斜边的点是该直角三角形三个顶点的中位点；③若四个点,,,A B C D 共线，则它们的中位点存在且唯一；④梯形对角线的交点是该梯形四个顶点的唯一中位点．其中的真命题是____________．（写出所有真命题的序号数学社区）三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．16．(本小题满分12分) 在等差数列{}n a 中，218a a -=，且4a 为2a 和3a 的等比中项，求数列{}n a 的首项、公差及前n 项和．17．(本小题满分12分) 在ABC ∆中，角,,A B C 的对边分别为,,a b c ，且232cos cos sin()sin cos()25A B B A B B A C ---++=-．（Ⅰ）求cos A 的值；（Ⅱ）若a =5b =，求向量BA 在BC 方向上的投影．18．(本小题满分12分)某算法的程序框图如图所示，其中输入的变量x 在1,2,3,,24⋅⋅⋅这24个整数中等可能随机产生．（Ⅰ）分别求出按程序框图正确编程运行时输出y 的值为i 的概率(1,2,3)i P i =；（Ⅱ）甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n 次后，统计记录了输出y 的值为(1,2,3)i i =的频数．以下是甲、乙所作频数统计表的部分数据．甲的频数统计表（部分）乙的频数统计表（部分）当2100i i=的频率（用分数表示），并判断两位写出甲、乙所编程序各自输出y的值为(1,2,3)同学中哪一位所编写程序符合算法要求的可能性较大；（Ⅲ）按程序框图正确编写的程序运行3次，求输出y的值为2的次数ξ的分布列及数学期望．19．(本小题满分12分) 如图，在三棱柱11ABC A B C -中，侧棱1AA ⊥底面ABC ，12AB AC AA ==，120BAC ∠=，1,D D 分别是线段11,BC B C 的中点，P 是线段AD 的中点．（Ⅰ）在平面ABC 内，试作出过点P 与平面1A BC 平行的直线l ，说明理由，并证明直线l ⊥平面11ADD A ；（Ⅱ）设（Ⅰ）中的直线l 交AB 于点M ，交AC 于点N ，求二面角1A A M N --的余弦值．1C20．(本小题满分13分) 已知椭圆C ：22221,(0)x y a b a b+=>>的两个焦点分别为12(1,0),(1,0)F F -，且椭圆C 经过点41(,)33P ．（Ⅰ）求椭圆C 的离心率；（Ⅱ）设过点(0,2)A 的直线l 与椭圆C 交于M 、N 两点，点Q 是线段MN 上的点，且222211||||||AQ AM AN =+，求点Q 的轨迹方程．21．(本小题满分14分)已知函数22,0()ln ,0x x a x f x x x ⎧++<=⎨>⎩，其中a 是实数．设11(,())A x f x ，22(,())B x f x 为该函数图象上的两点，且12x x <．（Ⅰ）指出函数()f x 的单调区间；（Ⅱ）若函数()f x 的图象在点,A B 处的切线互相垂直，且20x <，求21x x -的最小值；（Ⅲ）若函数()f x 的图象在点,A B 处的切线重合，求a 的取值范围．参考答案一、选择题：本题考查基本概念和基本运算.每小题5分，满分50分.1.A2.B3.D4.D5.A6.B7.C8.C9.C 10.A二、填空题：本题考查基础知识和基本运算.每小题5分,满分25分.11.10 12.2 14.(7,3)- 15.①④三、解答题:共6小题,共75分.16.解：设该数列公差为d ,前n 项和为n s .由已知,可得()()()21111228,38a d a d a d a d +=+=++.所以()114,30a d d d a +=-=,解得14,0a d ==,或11,3a d ==,即数列{}n a 的首相为4,公差为0,或首相为1,公差为3.所以数列的前n 项和4n s n =或232n n ns -=. ………….12分17.解：()I 由()()232cos cos sin sin cos 25A B B A B B A C ---++=-,得 ()()3cos 1cos sin sin cos 5A B B A B B B -+---=-⎡⎤⎣⎦, 即()()3cos cos sin sin 5A B B A B B ---=-,则()3cos 5A B B -+=-,即3cos 5A =-. ………….. 5分()II 由3cos ,05A A π=-<<,得4sin 5A =,由正弦定理,有sin sin a bA B=,所以,sin sin b A B a ==. 由题知a b >,则A B >,故4B π=.根据余弦定理,有(22235255c c ⎛⎫=+-⨯⨯- ⎪⎝⎭,解得1c =或7c =-(舍去).故向量BA 在BC 方向上的投影为cos 2BA B =. ………….12分 18. 解：()I .变量x 是在1,2,3，……24这24个整数中随机产生的一个数，共有24种可能.当x 从1,3,5,7,9,11,13,15,17,19,21,23这12个数中产生时，输出y 的值为1，故112p =；当x 从2,4,8,10,14,16,20,22这8个数中产生时，输出y 的值为2，故213p =; 当x 从6,12,18,24这4个数中产生时，输出y 的值为3，故316p =. ……………3分 ()II 当n=2100时，甲、乙所编程序各自输出y 的值为i(i=1,2,3)的频率如下：比较频率趋势与概率，可得乙同学所编程序符合算法要求的可能性较大. ………7分（3）随机变量ξ可能饿取值为0,1,2,3.0303128(0)3327p C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭ 1213124(1)339p C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭ 2123122(2)339p C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭ 333121(3)3327p C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭故ξ的分布列为842101231279927E ξ=⨯+⨯+⨯+⨯= 所以即ξ的数学期望为1. ………12分19.解：()I 如图,在平面ABC 内,过点P 做直线l //BC ,因为l 在平面1A BC 外,BC 在平面1A BC 内,由直线与平面平行的判定定理可知, l //平面1A BC .由已知,AB AC =,D 是BC 的中点,所以,BC AD ⊥,则直线l AD ⊥.因为1AA ⊥平面ABC ,所以1AA ⊥直线l .又因为1,AD AA 在平面11ADD A 内,且AD 与1AA 相交,所以直线平面11ADD A . …………………………………………………………………………….6分()II 解法一:连接1A P ,过A 作1AE A P ⊥于E ,过E 作1EF A M ⊥于F ,连接AF . 由()I 知,MN ⊥平面1AEA ,所以平面1AEA ⊥平面1A MN .所以AE ⊥平面1A MN ,则1A M AE ⊥.所以1A M ⊥平面AEF ,则1A M ⊥AF .故AFE ∠为二面角1A A M N --的平面角(设为θ).设11AA =,则由12AB AC AA ==,120BAC ∠=,有60BAD ∠=,2,1AB AD ==.又P 为AD 的中点,所以M 为AB 的中点,且1,12AP AM ==,在1Rt AA P 中, 152A P =;在1Rt A AM 中, 12AM =. 从而,115AA AP AE A P •==,112AA AM AF A M •==,所以2sin 5AE AF θ==. 所以22215cos 1sin 15θθ⎛⎫=-=-= ⎪ ⎪⎝⎭. 故二面角1A A M N --的余弦值为155. ………………12分解法二:设11AA =.如图,过1A 作1A E 平行于11B C ,以1A 为坐标原点,分别以111,AE AD ,1AA 的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系Oxyz (点O 与点1A 重合).则()10,0,0A ,()0,0,1A .因为P 为AD 的中点,所以,M N 分别为,AB AC 的中点,故11,,1,,12222M N ⎛⎫⎛⎫-⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 所以131,12A M ⎛⎫= ⎪ ⎪⎝⎭,()10,0,1A A =,()3,0,0NM =.设平面1AA M 的一个法向量为()1111,,n x y z =,则1111,,n A M n A A ⎧⊥⎪⎨⊥⎪⎩即11110,0,n A M n A A ⎧•=⎪⎨•=⎪⎩故有 ()()()1111111,,,10,22,,0,0,10,x y z x y z ⎧⎛⎫•=⎪⎪ ⎪⎨⎝⎭⎪•=⎩ 从而111110,220.x y z z ++=⎨⎪=⎩取11x =,则1y =,所以()11,n =.设平面1A MN 的一个法向量为()2222,,n x y z =,则212,,n A M n NM ⎧⊥⎪⎨⊥⎪⎩即2120,0,n A M n NM ⎧•=⎪⎨•=⎪⎩故有()())2222221,,,10,2,,0,x y z x y z ⎧⎫•=⎪⎪⎪⎪⎝⎭⎨⎪•=⎪⎩ 从而222210,20.x y z ++=⎨⎪=⎩取22y =,则21z =-,所以()20,2,1n =-.设二面角1A A M N --的平面角为θ,又θ为锐角,则1212cos 5n n n n θ•===•.故二面角1AA M N --. ………………12分 20．解：122a PF PF =+==所以，a =又由已知，1c =,所以椭圆C的离心率c e a ===…………4分 ()II 由()I 知椭圆C 的方程为2212x y +=.设点Q 的坐标为(x,y).(1)当直线l 与x 轴垂直时，直线l 与椭圆C 交于()()0,1,0,1-两点，此时Q 点坐标为0,25⎛- ⎝⎭(2) 当直线l 与x 轴不垂直时，设直线l 的方程为2y kx =+.因为,M N 在直线l 上，可设点,M N 的坐标分别为1122(,2),(,2)x kx x kx ++，则22222212(1),(1)AM k x AN k x =+=+. 又()222222(1).AQ x y k x =+-=+由222211AQAMAN=+，得()()()22222212211111k x k x k x =++++，即 ()212122222212122211x x x x x x x x x +-=+= ① 将2y kx =+代入2212x y +=中，得()2221860kx kx +++= ②由()()22842160,k k ∆=-⨯+⨯>得232k >. 由②可知12122286,,2121k x x x x k k +=-=++ 代入①中并化简，得2218103x k =- ③因为点Q 在直线2y kx =+上，所以2y k x-=，代入③中并化简，得()22102318y x --=.由③及232k >，可知2302x <<,即60,22x ⎛⎫⎛⎫∈- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭.又0,25⎛⎫-⎪ ⎪⎝⎭满足()22102318y x --=，故22x ⎛∈- ⎝⎭. 由题意，(),Q x y 在椭圆C 内部，所以11y -≤≤，又由()22102183y x -=+有()2992,54y ⎡⎫-∈⎪⎢⎣⎭且11y -≤≤，则1,22y ⎛∈ ⎝⎦.所以点Q 的轨迹方程是()22102318y x --=，其中，22x ⎛∈ ⎝⎭，1,225y ⎛∈- ⎝⎦………..13分 21．解：()I 函数()f x 的单调递减区间为(),1-∞-，单调递增区间为[)1,0-，()0,+∞()II 由导数的几何意义可知，点A 处的切线斜率为()1f x '，点B 处的切线斜率为()2f x '，故当点A 处的切线与点B 处的切垂直时，有()()121f x f x ''=-. 当0x <时，对函数()f x 求导，得()22f x x '=+.因为120x x <<，所以()()1222221x x ++=-，所以()()12220,220x x +<+>.因此()()21121222212x x x x -=-+++≥=⎡⎤⎣⎦当且仅当()122x -+=()222x +=1，即123122x x =-=且时等号成立. 所以函数()f x 的图象在点,A B 处的切线互相垂直时，21x x -的最小值为1 (7)分()III 当120x x <<或210x x >>时，()()12f x f x ''≠，故120x x <<.当10x <时，函数()f x 的图象在点()()11,x f x 处的切线方程为()()()21111222y x x a x x x -++=+-，即()21122y x x x a =+-+当20x >时，函数()f x 的图象在点()()22,x f x 处的切线方程为()2221ln y x x x x -=-，即221ln 1y x x x =•+-. 两切线重合的充要条件是1222112 2 ln 1 x x x x a ⎧=+⎪⎨⎪-=-+⎩①②由①及120x x <<知，110x -<<.由①②得，()2211111ln1ln 22122a x x x x =+-=-+-+.设()()21111ln 221(10)h x x x x =-+--<<，则()1111201h x x x '=-<+.所以()()1110h x x -<<是减函数. 则()()10ln21h x h >=--，所以ln21a >--.又当1(1,0)x ∈-且趋近于1-时，()1h x 无限增大，所以a 的取值范围是()ln21,--+∞. 故当函数()f x 的图像在点,A B 处的切线重合时，a 的取值范围是()ln21,--+∞.14分。

2013年普通高等学校招生全国统一考试数学理试题(四川卷)

2013年普通高等学校招生全国统一考试（四川卷）数学（理科）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一个是符合题目要求的．1．设集合{|20}A x x =+=，集合2{|40}B x x =-=，则AB =（）（A ）{2}- （B ）{2} （C ）{2,2}- （D ）∅2．如图，在复平面内，点A 表示复数z ，则图中表示z 的共轭复数的点是（）（A ）A （B ）B （C ）C（D ）D 3．一个几何体的三视图如图所示，则该几何体的直观图可以是（）4．设x Z ∈，集合A 是奇数集，集合B 是偶数集．若命题:,2p x A x B ∀∈∈，则（）（A ）:,2p x A x B ⌝∀∃∈∉ （B ）:,2p x A x B ⌝∀∉∉ （C ）:,2p x A x B ⌝∃∉∈ （D ）:,2p x A x B ⌝∃∈∈ 5．函数()2sin(),(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示，则,ωϕ的值分别是（）（A ）2,3π-（B ）2,6π-（C ）4,6π-（D ）4,3π6．抛物线24y x =的焦点到双曲线2213yx -=的渐近线的距离是（）（A ）12（B （C ）1 （D 7．函数231x x y =-的图象大致是（）8．从1,3,5,7,9这五个数中，每次取出两个不同的数分别为,a b ，共可得到lg lg a b -的不同值的个数是（）（A ）9 （B ）10 （C ）18 （D ）20 9．节日里某家前的树上挂了两串彩灯，这两串彩灯的第一次闪亮相互独立，若接通电后的4秒内任一时刻等可能发生，然后每串彩灯在内4秒为间隔闪亮，那么这两串彩灯同时通电后，它们第一次闪亮的时刻相差不超过2秒的概率是（）（A ）14 （B ）12 （C ）34 （D ）7810．设函数()f x =a R ∈，e 为自然对数的底数）．若曲线sin y x =上存在00(,)x y 使得00(())f f y y =，则a 的取值范围是（）（A ）[1,]e （B ）1[,-11]e -，（C ）[1,1]e + （D ）1[-1,1]e e -+ 二、填空题：本大题共5小题，每小题5分，共25分．11．二项式5()x y +的展开式中，含23x y 的项的系数是_________．（用数字作答） 12．在平行四边形ABCD 中，对角线AC 与BD 交于点O ，AB AD AO λ+=，则λ=_________．13．设sin 2sin αα=-，(,)2παπ∈，则tan 2α的值是_________．14．已知()f x 是定义域为R 的偶函数，当x ≥0时，2()4f x x x =-，那么，不等式(2)5f x +<的解集是________ ．15．设12,,,n P P P 为平面α内的n 个点，在平面α内的所有点中，若点P 到12,,,n P P P 点的距离之和最小，则称点P 为12,,,n P P P 点的一个“中位点”．例如，线段AB 上的任意点都是端点,A B 的中位点．则有下列命题：①若,,A B C 三个点共线，C 在线AB 上，则C 是,,A B C 的中位点； ②直角三角形斜边的点是该直角三角形三个顶点的中位点； ③若四个点,,,A B C D 共线，则它们的中位点存在且唯一； ④梯形对角线的交点是该梯形四个顶点的唯一中位点．其中的真命题是____________．（写出所有真命题的序号数学社区）三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤． 16．(本小题满分12分) 在等差数列{}n a 中，218a a -=，且4a 为2a 和3a 的等比中项，求数列{}n a 的首项、公差及前n 项和．17．(本小题满分12分) 在ABC ∆中，角,,A B C 的对边分别为,,a b c ，且232cos cos sin()sin cos()25A B B A B B A C ---++=-．（Ⅰ）求cos A 的值；（Ⅱ）若a =5b =，求向量BA 在BC 方向上的投影．18．(本小题满分12分)某算法的程序框图如图所示，其中输入的变量x 在1,2,3,,24⋅⋅⋅这24个整数中等可能随机产生．（Ⅰ）分别求出按程序框图正确编程运行时输出y 的值为i 的概率(1,2,3)i P i =；（Ⅱ）甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n 次后，统计记录了输出y 的值为(1,2,3)i i =的频数．以下是甲、乙所作频数统计表的部分数据．甲的频数统计表（部分）乙的频数统计表（部分）当2100n =时，根据表中的数据，分别写出甲、乙所编程序各自输出y 的值为(1,2,3)i i =的频率（用分数表示），并判断两位同学中哪一位所编写程序符合算法要求的可能性较大；（Ⅲ）按程序框图正确编写的程序运行3次，求输出y 的值为2的次数ξ的分布列及数学期望．19．(本小题满分12分) 如图，在三棱柱11ABC A B C -中，侧棱1AA ⊥底面ABC ，12AB AC AA ==，120BAC ∠=，1,D D 分别是线段11,BC B C 的中点，P 是线段AD 的中点．（Ⅰ）在平面ABC 内，试作出过点P 与平面1A BC 平行的直线l ，说明理由，并证明直线l ⊥平面11ADD A ；（Ⅱ）设（Ⅰ）中的直线l 交AB 于点M ，交AC 于点N ，求二面角1A A M N --的余弦值．1C20．(本小题满分13分) 已知椭圆C ：22221,(0)x y a b a b +=>>的两个焦点分别为12(1,0),(1,0)F F -，且椭圆C 经过点41(,)33P ．（Ⅰ）求椭圆C 的离心率；（Ⅱ）设过点(0,2)A 的直线l 与椭圆C 交于M 、N 两点，点Q 是线段MN 上的点，且222211||||||AQ AM AN =+，求点Q 的轨迹方程．21．(本小题满分14分)已知函数22,0()ln ,0x x a x f x x x ⎧++<=⎨>⎩，其中a 是实数．设11(,())A x f x ，22(,())B x f x 为该函数图象上的两点，且12x x <．（Ⅰ）指出函数()f x 的单调区间；（Ⅱ）若函数()f x 的图象在点,A B 处的切线互相垂直，且20x <，求21x x -的最小值；（Ⅲ）若函数()f x 的图象在点,A B 处的切线重合，求a 的取值范围．参考答案一、选择题：本题考查基本概念和基本运算.每小题5分，满分50分. 1.A 2.B 3.D 4.D 5.A 6.B 7.C 8.C 9.C 10.A二、填空题：本题考查基础知识和基本运算.每小题5分,满分25分.11.10 12.2 14.(7,3)- 15.①④ 三、解答题:共6小题,共75分.16.解：设该数列公差为d ,前n 项和为n s .由已知,可得()()()21111228,38a d a d a d a d +=+=++.所以()114,30a d d d a +=-=,解得14,0a d ==,或11,3a d ==,即数列{}n a 的首相为4,公差为0,或首相为1,公差为3.所以数列的前n 项和4n s n =或232n n ns -=. ………….12分17.解：()I 由()()232cos cos sin sin cos 25A B B A B B A C ---++=-,得()()3cos 1cos sin sin cos 5A B B A B B B -+---=-⎡⎤⎣⎦, 即()()3cos cos sin sin 5A B B A B B ---=-,则()3cos 5A B B -+=-,即3cos 5A =-. ………….. 5分()II 由3cos ,05A A π=-<<,得4sin 5A =,由正弦定理,有sin sin a bA B=,所以,sin sin b A B a ==由题知a b >,则A B >,故4B π=.根据余弦定理,有(22235255c c ⎛⎫=+-⨯⨯- ⎪⎝⎭,解得1c =或7c =-(舍去).故向量BA 在BC 方向上的投影为cos 2BA B =. ………….12分 18. 解：()I .变量x 是在1,2,3，……24这24个整数中随机产生的一个数，共有24种可能. 当x 从1,3,5,7,9,11,13,15,17,19,21,23这12个数中产生时，输出y 的值为1，故112p =；当x 从2,4,8,10,14,16,20,22这8个数中产生时，输出y 的值为2，故213p =; 当x 从6,12,18,24这4个数中产生时，输出y 的值为3，故316p =. ……………3分 ()II 当n=2100时，甲、乙所编程序各自输出y 的值为i(i=1,2,3)的频率如下：比较频率趋势与概率，可得乙同学所编程序符合算法要求的可能性较大. ………7分（3）随机变量ξ可能饿取值为0,1,2,3.0303128(0)3327p C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭ 1213124(1)339p C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭ 2123122(2)339p C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭ 333121(3)3327p C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭故ξ的分布列为所以842101231279927E ξ=⨯+⨯+⨯+⨯= 即ξ的数学期望为1. ………12分19.解：()I 如图,在平面ABC 内,过点P 做直线l //BC ,因为l 在平面1A BC 外,BC 在平面1A BC 内,由直线与平面平行的判定定理可知, l //平面1A BC .由已知,AB AC =,D 是BC 的中点,所以,BC AD ⊥,则直线l AD ⊥. 因为1AA ⊥平面ABC ,所以1AA ⊥直线l .又因为1,AD AA 在平面11ADD A 内,且AD 与1AA 相交,所以直线平面11ADD A . …………………………………………………………………………….6分()II 解法一:连接1A P ,过A 作1AE A P ⊥于E ,过E 作1EF A M ⊥于F ,连接AF . 由()I 知,MN ⊥平面1AEA ,所以平面1AEA ⊥平面1A MN . 所以AE ⊥平面1A MN ,则1A M AE ⊥. 所以1A M ⊥平面AEF ,则1A M ⊥AF .故AFE ∠为二面角1A A M N --的平面角(设为θ).设11AA =,则由12AB AC AA ==,120BAC ∠=,有60BAD ∠=,2,1AB AD ==. 又P 为AD 的中点,所以M 为AB 的中点,且1,12AP AM ==, 在1Rt AA P 中, 12A P =;在1Rt A AM 中, 1AM 从而,11AA AP AE A P ∙==,11AA AM AF A M ∙==,所以sin AE AF θ==.所以cos θ===. 故二面角1A A M N --的余弦值为5. ………………12分解法二:设11AA =.如图,过1A 作1A E 平行于11B C ,以1A 为坐标原点,分别以111,AE AD ,1AA 的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系Oxyz (点O 与点1A 重合).则()10,0,0A ,()0,0,1A .因为P 为AD 的中点,所以,M N 分别为,AB AC 的中点,故11,1,,12222M N ⎛⎫⎛⎫-⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 所以131,12A M ⎛⎫= ⎪⎪⎝⎭,()10,0,1A A =,()3,0,0NM =.设平面1AA M 的一个法向量为()1111,,n x y z =,则1111,,n A M n A A ⎧⊥⎪⎨⊥⎪⎩即11110,0,n A M n A A ⎧∙=⎪⎨∙=⎪⎩故有 ()()()1111111,,,10,22,,0,0,10,x y z x y z ⎧⎛⎫∙=⎪ ⎪ ⎪⎨⎝⎭⎪∙=⎩从而111110,20.y z z ++=⎪=⎩取11x =,则1y =所以()11,n =. 设平面1A MN 的一个法向量为()2222,,n x y z =,则212,,n A M n NM ⎧⊥⎪⎨⊥⎪⎩即2120,0,n A M n NM ⎧∙=⎪⎨∙=⎪⎩故有()())2222221,,,10,2,,0,x y z x y z ⎧⎫∙=⎪⎪⎪⎪⎝⎭⎨⎪∙=⎪⎩从而222210,220.x y z ++=⎪⎨⎪=⎩取22y =,则21z =-,所以()20,2,1n =-. 设二面角1A A M N --的平面角为θ,又θ为锐角,则1212cos n n n n θ∙===∙.故二面角1A A M N --的余弦值为5. ………………12分 20．解：122a PF PF =+==所以，a =又由已知，1c =, 所以椭圆C的离心率2c e a ===……………4分 ()II 由()I 知椭圆C 的方程为2212x y +=.设点Q 的坐标为(x,y).(1)当直线l 与x 轴垂直时，直线l 与椭圆C 交于()()0,1,0,1-两点，此时Q 点坐标为0,25⎛- ⎝⎭ (2) 当直线l 与x 轴不垂直时，设直线l 的方程为2y kx =+.因为,M N 在直线l 上，可设点,M N 的坐标分别为1122(,2),(,2)x kx x kx ++，则22222212(1),(1)AM k x AN k x =+=+. 又()222222(1).AQ x y k x =+-=+由222211AQ AM AN =+，得()()()22222212211111k x k x k x =++++，即()212122222212122211x x x x x x x x x +-=+= ① 将2y kx =+代入2212x y +=中，得 ()2221860k x kx +++= ②由()()22842160,k k ∆=-⨯+⨯>得232k >. 由②可知12122286,,2121k x x x x k k +=-=++ 代入①中并化简，得2218103x k =- ③因为点Q 在直线2y kx =+上，所以2y k x -=，代入③中并化简，得()22102318y x --=.由③及232k >，可知2302x <<,即60,22x ⎛⎫⎛⎫∈- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭. 又0,2⎛-⎝⎭满足()22102318y x --=，故x ⎛∈ ⎝⎭. 由题意，(),Q x y 在椭圆C 内部，所以11y -≤≤，又由()22102183y x -=+有()2992,54y ⎡⎫-∈⎪⎢⎣⎭且11y -≤≤，则1,225y ⎛∈- ⎝⎦. 所以点Q 的轨迹方程是()22102318y x --=，其中，22x ⎛∈-⎝⎭，1,22y ⎛∈ ⎝⎦………..13分 21．解：()I 函数()f x 的单调递减区间为(),1-∞-，单调递增区间为[)1,0-，()0,+∞()II 由导数的几何意义可知，点A 处的切线斜率为()1f x '，点B 处的切线斜率为()2f x '，故当点A 处的切线与点B 处的切垂直时，有()()121f x f x ''=-. 当0x <时，对函数()f x 求导，得()22f x x '=+. 因为120x x <<，所以()()1222221x x ++=-，所以()()12220,220x x +<+>.因此()()21121222212x x x x -=-+++≥=⎡⎤⎣⎦ 当且仅当()122x -+=()222x +=1，即123122x x =-=且时等号成立.所以函数()f x 的图象在点,A B 处的切线互相垂直时，21x x -的最小值为1…………7分()III 当120x x <<或210x x >>时，()()12f x f x ''≠，故120x x <<.当10x <时，函数()f x 的图象在点()()11,x f x 处的切线方程为 ()()()21111222y x x a x x x -++=+-，即()21122y x x x a =+-+ 当20x >时，函数()f x 的图象在点()()22,x f x 处的切线方程为 ()2221ln y x x x x -=-，即221ln 1y x x x =∙+-. 两切线重合的充要条件是1222112 2 ln 1 x x x x a ⎧=+⎪⎨⎪-=-+⎩①② 由①及120x x <<知，110x -<<. 由①②得，()2211111ln 1ln 22122a x x x x =+-=-+-+. 设()()21111ln 221(10)h x x x x =-+--<<，则()1111201h x x x '=-<+. 所以()()1110h x x -<<是减函数. 则()()10ln21h x h >=--，所以ln21a >--.又当1(1,0)x ∈-且趋近于1-时，()1h x 无限增大，所以a 的取值范围是()ln21,--+∞. 故当函数()f x 的图像在点,A B 处的切线重合时，a 的取值范围是()ln21,--+∞.14分。

da2013年高考数学试卷答案四川理

2013年普通高等学校招生全国统一考试（四川卷）数学（理工类）1.A2.B3. D4. D5. A6. B7.C8. C9. C 10.A 11.10 12.214. {}73x x -<< 15.①④16.解：由题意可知，1329428,,a a a a a ⎧⎪⎨=+=⎪⎩ 即1214,30,a d a d d +=⎧⎨-=⎩解得1=4,0,a d ⎧⎨=⎩或1=1,3,a d ⎧⎨=⎩ （1）当1=4,0a d=时，4n S n =；（2）当11,3a d ==时，232n n nS -=．17.解：（1）由题意可知2()cos sin()sin cos()22cosA B B A B B A C ---++ [1cos()]cos sin()sin()cos A B B A B A C B=+---+- 3cos()cos sin()sin cos(+)cos 5A B B A B B A B B A =---=-==-，所以3cos 5A =-；（2）由正弦定理，得sin sin b A B a ==，则cos B =，又由余弦定理有2cos 2B ==，解得 1c =或7c =-（舍去），故向量BA 在BC 方向上的投影cos 2cos BA BC BBA BC c B BCBC====．18.解：（1）当1i =时，即输出的数为奇数，奇数有12个，则112P =；当3i =时，即输出的数为能整除3的偶数，有4个，则316P =；当2i =时，即输出的数为剩下的8个，则213P =，所以112P =，213P =，316P =; （2）甲：1231027376697===210021002100P P P ，，；乙：1231051696353===210021002100P P P ，，，根据频率的趋势与概率可知，乙编写的程序更符合算法要求. （3）设输出y 的值为2为事件A ，且1()3P A =，则该实验为独立重复事件，次数ξ的分布列为303128(0)3327P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭， 1213124(1)339P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭， 2123122(2)339P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭， 333121(3)3327P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭， 8421()01231279927E ξ=⨯+⨯+⨯+⨯=. 19.解：（1）由题意可知，直线l //BC ，又AB AC =，D 是BC 的中点，则BC AD ⊥，又在三棱柱11ABC A B C -中，1BC DD ⊥，且111,A DD ADD D A ⊂，则11AD B D C A ⊥，所以直线l ⊥平面11ADD A（2）连接1A P ，过A 作1AE A P ⊥于E ，过E 作1EF A M ⊥于F ，连接AF .由（1）知，MN ⊥平面1AEA ，所以平面1AEA ⊥平面1A MN ，所以AE ⊥平面1A MN ，则1A M AE ⊥.所以1A M ⊥平面AEF ，则1A M AF ⊥.故AFE ∠为二面角1A A M N -- 的平面角（设为θ）.设11AA =，则由12AB AC AA ==，120BAC∠=，有60BAD ∠=，2AB =，1AD =，又P 为AD 的中点，所以M 为AB 中点，且12AP =，1AM =，所以，在1Rt AA P ∆,1A P =在在1Rt A MP ∆,1A M =从而1111AA AP AA AM AE AF A P A M ⋅⋅====所以sin AE AF θθ====20.解：（1）椭圆过焦点1F ，故1c =，221a b ∴=+。

普通高等学校招生全国统一考试数学理试题(四川卷)

2013年普通高等学校招生全国统一考试（四川卷）数学（理科）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出嘚四个选项中，只有一个是符合题目要求嘚．1．设集合{|20}A x x=+=，集合2{|40}B x x=-=，则A B=（）（A）{2}-（B）{2}（C）{2,2}-（D）∅2．如图，在复平面内，点A表示复数z，则图中表示z嘚共轭复数嘚点是（）yxDBAOC（A）A（B）B（C）C（D）D3．一个几何体嘚三视图如图所示，则该几何体嘚直观图可以是（）4．设x Z∈，集合A是奇数集，集合B是偶数集．若命题:,2p x A x B∀∈∈，则（）（A）:,2p x A x B⌝∀∃∈∉（B）:,2p x A x B⌝∀∉∉（C）:,2p x A x B⌝∃∉∈（D）:,2p x A x B⌝∃∈∈5．函数()2sin(),(0,)22f x xππωϕωϕ=+>-<<嘚部分图象如图所示，则,ωϕ嘚值分别是（）（A ）2,3π-（B ）2,6π-（C ）4,6π-（D ）4,3π6．抛物线24y x =嘚焦点到双曲线2213yx -=嘚渐近线嘚距离是（）（A ）12（B ）32 （C ）1 （D ）37．函数231x x y =-嘚图象大致是（）8．从1,3,5,7,9这五个数中，每次取出两个不同嘚数分别为,a b ，共可得到lg lg a b -嘚不同值嘚个数是（）（A ）9 （B ）10 （C ）18 （D ）209．节日里某家前嘚树上挂了两串彩灯，这两串彩灯嘚第一次闪亮相互独立，若接通电后嘚4秒内任一时刻等可能发生，然后每串彩灯在内4秒为间隔闪亮，那么这两串彩灯同时通电后，它们第一次闪亮嘚时刻相差不超过2秒嘚概率是（）（A ）14 （B ）12 （C ）34 （D ）7810．设函数()x f x e x a =+-（a R ∈，e 为自然对数嘚底数）．若曲线sin y x =上存在00(,)x y 使得00(())f f y y =，则a 嘚取值范围是（）（A ）[1,]e （B ）1[,-11]e -，（C ）[1,1]e + （D ）1[-1,1]e e -+ 二、填空题：本大题共5小题，每小题5分，共25分．11．二项式5()x y +嘚展开式中，含23x y 嘚项嘚系数是_________．（用数字作答）12．在平行四边形ABCD 中，对角线AC 与BD 交于点O ，AB AD AO λ+=，则λ=_________． 13．设sin 2sin αα=-，(,)2παπ∈，则tan 2α嘚值是_________．14．已知()f x 是定义域为R 嘚偶函数，当x ≥0时，2()4f x x x =-，那么，不等式(2)5f x +<嘚解集是________ ． 15．设12,,,n P P P 为平面α内嘚n 个点，在平面α内嘚所有点中，若点P 到12,,,n P P P 点嘚距离之和最小，则称点P 为12,,,n P P P 点嘚一个“中位点”．例如，线段AB 上嘚任意点都是端点,A B嘚中位点．则有下列命题：①若,,A B C 三个点共线，C 在线AB 上，则C 是,,A B C 嘚中位点； ②直角三角形斜边嘚点是该直角三角形三个顶点嘚中位点； ③若四个点,,,A B C D 共线，则它们嘚中位点存在且唯一； ④梯形对角线嘚交点是该梯形四个顶点嘚唯一中位点．其中嘚真命题是____________．（写出所有真命题嘚序号数学社区）三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．16．(本小题满分12分) 在等差数列{}n a 中，218a a -=，且4a 为2a 和3a 嘚等比中项，求数列{}n a 嘚首项、公差及前n 项和．17．(本小题满分12分) 在ABC ∆中，角,,A B C 嘚对边分别为,,a b c ，且232cos cos sin()sin cos()25A B B A B B A C ---++=-．（Ⅰ）求cos A 嘚值；（Ⅱ）若42a =，5b =，求向量BA 在BC 方向上嘚投影．18．(本小题满分12分)某算法嘚程序框图如图所示，其中输入嘚变量x 在1,2,3,,24⋅⋅⋅这24个整数中等可能随机产生．（Ⅰ）分别求出按程序框图正确编程运行时输出y 嘚值为i 嘚概率(1,2,3)i P i =；（Ⅱ）甲、乙两同学依据自己对程序框图嘚理解，各自编写程序重复运行n 次后，统计记录了输出y 嘚值为(1,2,3)i i =嘚频数．以下是甲、乙所作频数统计表嘚部分数据．甲嘚频数统计表（部分）乙嘚频数统计表（部分）当2100n =时，根据表中嘚数据，分别写出甲、乙所编程序各自输出y 嘚值为(1,2,3)i i =嘚频率（用分数表示），并判断两位同学中哪一位所编写程序符合算法要求嘚可能性较大；运行次数n 输出y 嘚值为1嘚频数输出y 嘚值为2嘚频数输出y 嘚值为3嘚频数3014610…………2100 1027 376 697运行次数n 输出y 嘚值为1嘚频数输出y 嘚值为2嘚频数输出y 嘚值为3嘚频数3012117…………21001051 696 353（Ⅲ）按程序框图正确编写嘚程序运行3次，求输出y 嘚值为2嘚次数ξ嘚分布列及数学期望．19．(本小题满分12分) 如图，在三棱柱11ABC A B C -中，侧棱1AA ⊥底面ABC ，12AB AC AA ==，120BAC ∠=，1,D D 分别是线段11,BC B C 嘚中点，P 是线段AD 嘚中点．（Ⅰ）在平面ABC 内，试作出过点P 与平面1A BC 平行嘚直线l ，说明理由，并证明直线l ⊥平面11ADD A ；（Ⅱ）设（Ⅰ）中嘚直线l 交AB 于点M ，交AC 于点N ，求二面角1A A M N --嘚余弦值．D 1D CB A 1B 1C 1A P20．(本小题满分13分) 已知椭圆C ：22221,(0)x y a b a b+=>>嘚两个焦点分别为12(1,0),(1,0)F F -，且椭圆C 经过点41(,)33P ．（Ⅰ）求椭圆C 嘚离心率；（Ⅱ）设过点(0,2)A 嘚直线l 与椭圆C 交于M 、N 两点，点Q 是线段MN 上嘚点，且222211||||||AQ AM AN =+，求点Q 嘚轨迹方程．21．(本小题满分14分)已知函数22,0()ln ,0x x a x f x x x ⎧++<=⎨>⎩，其中a 是实数．设11(,())A x f x ，22(,())B x f x 为该函数图象上嘚两点，且12x x <．（Ⅰ）指出函数()f x 嘚单调区间；（Ⅱ）若函数()f x 嘚图象在点,A B 处嘚切线互相垂直，且20x <，求21x x -嘚最小值；（Ⅲ）若函数()f x 嘚图象在点,A B 处嘚切线重合，求a 嘚取值范围．参考答案一、选择题：本题考查基本概念和基本运算.每小题5分，满分50分. 1.A 2.B 3.D 4.D 5.A 6.B 7.C 8.C 9.C 10.A二、填空题：本题考查基础知识和基本运算.每小题5分,满分25分. 11.10 12.2 13.3 14.(7,3)- 15.①④ 三、解答题:共6小题,共75分.16.解：设该数列公差为d ,前n 项和为n s .由已知,可得()()()21111228,38a d a d a d a d +=+=++.所以()114,30a d d d a +=-=,解得14,0a d ==,或11,3a d ==,即数列{}n a 嘚首相为4,公差为0,或首相为1,公差为3.所以数列嘚前n 项和4n s n =或232n n ns -=. ………….12分17.解：()I 由()()232cos cos sin sin cos 25A B B A B B A C ---++=-,得()()3cos 1cos sin sin cos 5A B B A B B B -+---=-⎡⎤⎣⎦, 即()()3cos cos sin sin 5A B B A B B ---=-,则()3cos 5A B B -+=-,即3cos 5A =-. ………….. 5分()II 由3cos ,05A A π=-<<,得4sin 5A =,由正弦定理,有sin sin a bA B=,所以,sin 2sin 2b A B a ==. 由题知a b >,则A B >,故4B π=.根据余弦定理,有()2223425255c c ⎛⎫=+-⨯⨯- ⎪⎝⎭,解得1c =或7c =-(舍去).故向量BA 在BC 方向上嘚投影为2cos 2BA B =. ………….12分 18. 解：()I .变量x 是在1,2,3，……24这24个整数中随机产生嘚一个数，共有24种可能. 当x 从1,3,5,7,9,11,13,15,17,19,21,23这12个数中产生时，输出y 嘚值为1，故112p =；当x 从2,4,8,10,14,16,20,22这8个数中产生时，输出y 嘚值为2，故213p =; 当x 从6,12,18,24这4个数中产生时，输出y 嘚值为3，故316p =. ……………3分 ()II 当n=2100时，甲、乙所编程序各自输出y 嘚值为i(i=1,2,3)嘚频率如下：比较频率趋势与概率，可得乙同学所编程序符合算法要求嘚可能性较大. ………7分（3）随机变量ξ可能饿取值为0,1,2,3.0303128(0)3327p C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭ 1213124(1)339p C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭2123122(2)339p C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭ 3033121(3)3327p C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭故ξ嘚分布列为842101231279927E ξ=⨯+⨯+⨯+⨯= 所以即ξ嘚数学期望为1. ………12分19.解：()I 如图,在平面ABC 内,过点P 做直线l //BC ,因为l 在平面1A BC 外,BC 在平面1A BC 内,由直线与平面平行嘚判定定理可知, l //平面1A BC . 由已知,AB AC =,D 是BC 嘚中点,所以,BC AD ⊥,则直线l AD ⊥.因为1AA ⊥平面ABC ,所以1AA ⊥直线l .又因为1,AD AA 在平面11ADD A 内,且AD 与1AA 相交,所以直线平面11ADD A . …………………………………………………………………………….6分()II 解法一:连接1A P ,过A 作1AE A P ⊥于E ,过E 作1EF A M ⊥于F ,连接AF . 由()I 知,MN ⊥平面1AEA ,所以平面1AEA ⊥平面1A MN . 所以AE ⊥平面1A MN ,则1A M AE ⊥. 所以1A M ⊥平面AEF ,则1A M ⊥AF .故AFE ∠为二面角1A A M N --嘚平面角(设为θ).设11AA =,则由12AB AC AA ==,120BAC ∠=,有60BAD ∠=,2,1AB AD ==. 又P 为AD 嘚中点,所以M 为AB 嘚中点,且1,12AP AM ==, 输出y 嘚值为1嘚频率输出y 嘚值为2嘚频率输出y 嘚值为3嘚频率甲 102721003762100 6972100 乙105121006962100 3532100ξ 0 1 2 3p8274929127在1Rt AA P 中, 152A P =;在1Rt A AM 中, 12AM =. 从而,1115AA AP AE A P •==,1112AA AM AF A M •==,所以2sin 5AE AF θ==. 所以22215cos 1sin 155θθ⎛⎫=-=-= ⎪ ⎪⎝⎭. 故二面角1A A M N --嘚余弦值为155. ………………12分解法二:设11AA =.如图,过1A 作1A E 平行于11B C ,以1A 为坐标原点,分别以111,AE AD ,1AA 嘚方向为x 轴,y轴,z 轴嘚正方向,建立空间直角坐标系Oxyz (点O 与点1A 重合).则()10,0,0A ,()0,0,1A .因为P 为AD 嘚中点,所以,M N 分别为,AB AC 嘚中点,故3131,,1,,,12222M N ⎛⎫⎛⎫-⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 所以131,,122A M ⎛⎫= ⎪ ⎪⎝⎭,()10,0,1A A =,()3,0,0NM =.设平面1AA M 嘚一个法向量为()1111,,n x y z =,则1111,,n A M n A A ⎧⊥⎪⎨⊥⎪⎩即11110,0,n A M n A A ⎧•=⎪⎨•=⎪⎩故有 ()()()11111131,,,,10,22,,0,0,10,x y z x y z ⎧⎛⎫•=⎪ ⎪ ⎪⎨⎝⎭⎪•=⎩ 从而1111310,220.x y z z ⎧++=⎪⎨⎪=⎩取11x =,则13y =-,所以()11,3,0n =-. 设平面1A MN 嘚一个法向量为()2222,,n x y z =,则212,,n A M n NM ⎧⊥⎪⎨⊥⎪⎩即2120,0,n A M n NM ⎧•=⎪⎨•=⎪⎩故有()()()22222231,,,,10,22,,3,0,00,x y z x y z ⎧⎛⎫•=⎪⎪ ⎪⎪⎝⎭⎨⎪•=⎪⎩ 从而2222310,2230.x y z x ⎧++=⎪⎨⎪=⎩取22y =,则21z =-,所以()20,2,1n =-. 设二面角1A A M N --嘚平面角为θ,又θ为锐角,则()()12121,3,00,2,115cos 525n n n n θ-•-•===••.故二面角1A A M N --嘚余弦值为155. ………………12分 20．解：2222124141*********a PF PF ⎛⎫⎛⎫⎛⎫⎛⎫=+=+++-+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭所以，2a =.又由已知，1c =, 所以椭圆C 嘚离心率1222c e a ===……………4分 ()II 由()I 知椭圆C 嘚方程为2212x y +=.设点Q 嘚坐标为(x,y).(1)当直线l 与x 轴垂直时，直线l 与椭圆C 交于()()0,1,0,1-两点，此时Q 点坐标为350,25⎛⎫- ⎪ ⎪⎝⎭ (2) 当直线l 与x 轴不垂直时，设直线l 嘚方程为2y kx =+.因为,M N 在直线l 上，可设点,M N 嘚坐标分别为1122(,2),(,2)x kx x kx ++，则22222212(1),(1)AM k x AN k x =+=+. 又()222222(1).AQ x y k x =+-=+由222211AQ AM AN =+，得()()()22222212211111k x k x k x =++++，即 ()212122222212122211x x x x x x x x x +-=+= ① 将2y kx =+代入2212x y +=中，得 ()2221860k x kx +++= ②由()()22842160,k k ∆=-⨯+⨯>得232k >. 由②可知12122286,,2121k x x x x k k +=-=++代入①中并化简，得2218103x k =- ③因为点Q 在直线2y kx =+上，所以2y k x -=，代入③中并化简，得()22102318y x --=.由③及232k >，可知2302x <<,即66,00,22x ⎛⎫⎛⎫∈- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭. 又350,25⎛⎫- ⎪ ⎪⎝⎭满足()22102318y x --=，故66,22x ⎛⎫∈- ⎪ ⎪⎝⎭. 由题意，(),Q x y 在椭圆C 内部，所以11y -≤≤，又由()22102183y x -=+有()2992,54y ⎡⎫-∈⎪⎢⎣⎭且11y -≤≤，则135,225y ⎛⎤∈- ⎥ ⎝⎦. 所以点Q 嘚轨迹方程是()22102318y x --=，其中，66,22x ⎛⎫∈-⎪ ⎪⎝⎭，135,225y ⎛⎤∈- ⎥ ⎝⎦………..13分21．解：()I 函数()f x 嘚单调递减区间为(),1-∞-，单调递增区间为[)1,0-，()0,+∞()II 由导数嘚几何意义可知，点A 处嘚切线斜率为()1f x '，点B 处嘚切线斜率为()2f x '，故当点A 处嘚切线与点B 处嘚切垂直时，有()()121f x f x ''=-. 当0x <时，对函数()f x 求导，得()22f x x '=+. 因为120x x <<，所以()()1222221x x ++=-，所以()()12220,220x x +<+>.因此()()()()21121212222222212x x x x x x -=-+++≥-++=⎡⎤⎣⎦ 当且仅当()122x -+=()222x +=1，即123122x x =-=且时等号成立.所以函数()f x 嘚图象在点,A B 处嘚切线互相垂直时，21x x -嘚最小值为1…………7分()III 当120x x <<或210x x >>时，()()12f x f x ''≠，故120x x <<. 当10x <时，函数()f x 嘚图象在点()()11,x f x 处嘚切线方程为 ()()()21111222y x x a x x x -++=+-，即()21122y x x x a =+-+ 当20x >时，函数()f x 嘚图象在点()()22,x f x 处嘚切线方程为()2221ln y x x x x -=-，即221ln 1y x x x =•+-. 两切线重合嘚充要条件是1222112 2 ln 1 x x x x a ⎧=+⎪⎨⎪-=-+⎩①②由①及120x x <<知，110x -<<.由①②得，()2211111ln1ln 22122a x x x x =+-=-+-+. 设()()21111ln 221(10)h x x x x =-+--<<，则()1111201h x x x '=-<+. 所以()()1110h x x -<<是减函数. 则()()10ln21h x h >=--，所以ln21a >--. 又当1(1,0)x ∈-且趋近于1-时，()1h x 无限增大，所以a 嘚取值范围是()ln21,--+∞. 故当函数()f x 嘚图像在点,A B 处嘚切线重合时，a 嘚取值范围是()ln21,--+∞.14分。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2013年普通高等学校招生统一考试--四川省数学(理) 文档版(有答案)

2013年普通高等学校招生全国统一考试(四川卷)理科数学真题试卷

2013高考理科数学(四川卷)

2013四川高考数学理科答案及解析

2013年高考理科数学四川卷试题与答案word解析版

2013年全国普通高等学校招生统一考试理科数学(四川卷带解析)试题

2013年全国普通高等学校招生统一考试理科数学(四川卷带解析)答案解析

2013年普通高等学校招生全国统一考试数学理试题(四川卷)

2013年普通高等学校招生全国统一考试数学理试题(四川卷)

da2013年高考数学试卷答案 四川理

普通高等学校招生全国统一考试数学理试题(四川卷)

da2013年高考数学试卷答案四川理