求锐角的三角比的值
锐角三角比讲义..
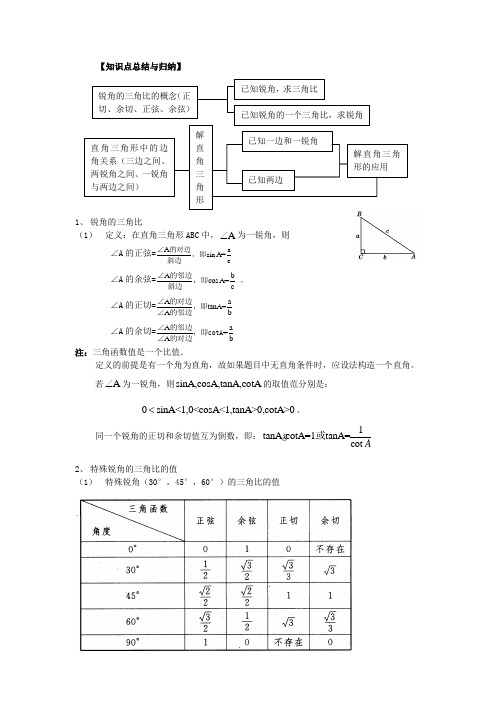
【知识点总结与归纳】1、 锐角的三角比（1） 定义：在直角三角形ABC 中，A ∠为一锐角，则∠A 的正弦=A a sin A=c∠的对边，即斜边∠A 的余弦=A b cos A=c∠的邻边，即斜边,∠A 的正切=A a tanA=A b∠的对边，即∠的邻边∠A 的余切=A a =A b∠的邻边，即cotA ∠的对边注：三角函数值是一个比值．定义的前提是有一个角为直角，故如果题目中无直角条件时，应设法构造一个直角。
若A ∠为一锐角，则sinA,cosA,tanA,cotA 的取值范分别是：0sinA<1,0<cosA<1,tanA>0,cotA>0<。
同一个锐角的正切和余切值互为倒数，即：1tanA cotA=1tanA=cot A或2、 特殊锐角的三角比的值（1） 特殊锐角（30°，45°，60°）的三角比的值锐角的三角比的概念（正切、余切、正弦、余弦）已知锐角，求三角比已知锐角的一个三角比，求锐角 直角三角形中的边角关系（三边之间、两锐角之间、一锐角与两边之间） 解直角三角形已知一边和一锐角已知两边解直角三角形的应用（2） 同角，互余的两角多的三角比之间的关系： 倒数关系：1tanA=cot A平方关系：22sin A+cos A=1 积商关系：sin cos tanA=,cot cos sin A AA A A= 余角和余函数的关系：如果090A B ∠+∠=，那么sinA=cosB, tanA=cotB （正弦和余弦，正切和余切被称为余函数关系）。
注意：求锐角三角比的值问题（1） 在直角三角形中，给定两边求锐角的三角比，关键是搞清某锐角的“对边”“邻边”，掌握三角比的定义。
（2） 给出锐角的度数，求这个锐角的三角比特殊锐角，一般情况下，使用精确值；在实际应用中，根据问题要求处理。
求非特殊锐角的三角比的值，使用计算器或查表求值。
《求锐角的三角比的值》 讲义
《求锐角的三角比的值》讲义一、锐角三角比的定义在直角三角形中，锐角的三角比包括正弦（sin）、余弦（cos）、正切（tan）。
正弦（sin）等于锐角的对边与斜边的比值；余弦（cos）等于锐角的邻边与斜边的比值；正切（tan）等于锐角的对边与邻边的比值。
例如，在一个直角三角形 ABC 中，∠C 为直角，∠A 为锐角，其对边为 a，邻边为 b，斜边为 c。
那么，sin A ＝ a ／ c，cos A ＝ b ／ c，tan A ＝ a ／ b。
二、特殊锐角的三角比值我们先来了解一些特殊锐角（30°、45°、60°）的三角比值，这些是需要大家牢记的。
1、 30°角对于 30°角的直角三角形，假设斜边为 2，对边为 1，根据勾股定理可得邻边为√3。
所以，sin 30°＝ 1 ／ 2，cos 30°＝√3 ／ 2，tan 30°＝√3 ／ 3。
2、 45°角在等腰直角三角形中，两个直角边相等，假设直角边为 1，斜边为√2。
则 sin 45°＝ cos 45°＝√2 ／ 2，tan 45°＝ 1。
3、 60°角与30°角相对应，60°角的直角三角形中，假设斜边为2，邻边为1，对边为√3。
所以，sin 60°＝√3 ／ 2，cos 60°＝ 1 ／ 2，tan 60°＝√3。
三、利用三角函数定义求三角比值当已知直角三角形的边长时，我们可以直接根据三角比的定义来求出相应锐角的三角比值。
例如，在直角三角形中，∠C 为直角，∠A 为锐角，已知∠A 的对边为 4，邻边为 3，斜边为 5。
则 sin A ＝ 4 ／ 5，cos A ＝ 3 ／ 5，tanA ＝ 4 ／ 3。
再比如，一个直角三角形的斜边为 10，一个锐角的对边为 6，那么这个锐角的正弦值就是 6 ／ 10 ＝ 3 ／ 5。
23用计算器求锐角三角比
23用计算器求锐角三角比锐角三角比是指在一个锐角三角形中，三个角的正弦、余弦和正切值。
计算锐角三角比的主要方法是使用三角函数表或者使用计算器。
使用计算器求锐角三角比的步骤如下：1. 打开计算器，并确保切换到角度模式（通常为degree）。
2.输入锐角的度数，例如30度。
3. 计算正弦（sin）值。
在计算器上找到正弦（sin）函数的键，然后按下角度值（30），最后按下等于（=）键。
结果将显示为一个小数，例如0.54. 计算余弦（cos）值。
在计算器上找到余弦（cos）函数的键，然后按下角度值（30），最后按下等于（=）键。
结果将显示为一个小数，例如0.8665. 计算正切（tan）值。
在计算器上找到正切（tan）函数的键，然后按下角度值（30），最后按下等于（=）键。
结果将显示为一个小数，例如0.577以上是求解一个具体角度的锐角三角比的步骤，通过反复使用这些步骤，可以计算出其他角度的锐角三角比。
锐角三角比的计算在数学和科学中有广泛的应用。
例如，在物理学中，通过计算三角比可以求解物体在斜面上滑动的问题；在工程学中，可以利用三角比计算力的分解；在测量学中，可以使用三角比计算距离和角度。
除了计算机外，还可以使用三角函数表来求解锐角三角比。
这些表通常包含了一些常见角度（如30度、45度、60度等）的正弦、余弦和正切值。
通过查表，可以找到所需角度的值。
另外，随着科技的发展，我们常见的计算器还可以进行更复杂的计算，比如反三角函数、双曲函数等。
这些功能可以帮助我们解决更复杂的三角函数问题。
在使用计算器求解锐角三角比时，需要注意以下几点：1.确保计算器的角度模式正确设置为度数模式。
有些计算器默认为弧度模式，如果不进行切换，会得到错误的结果。
2.注意结果的精度。
计算器通常会显示一定位数的小数，但这并不意味着结果是精确的。
因此，在实际应用中，需要根据情况对结果进行四舍五入或截断。
3.注意输入的角度。
角度应该是一个锐角，范围通常是0到90度之间。
25.2 求锐角的三角比的值
第一节锐角的三角比§25.2求锐角的三角比的值教学目标(1)经历用几何方法探求特殊锐角的三角比的值的过程，掌握特殊锐角的三角比的值。
(2)会利用计算器求锐角的三角比的值，也能根据锐角的三角比的值求锐角的大小。
教学重点让学生经历用几何方法探求特殊锐角的三角比值的过程，掌握特殊锐角的三角比的值。
让学生学会利用计算器求锐角的三角比的值以及根据锐角的三角比的值求锐角的大小。
知识概要1.求特殊锐角的三角比的值，一般步骤是：(1)将直角三角形的某边长设为a，用a的代数式表示其他两边的长；(2)根据三角比的定义求值。
2.3.①如果两角互余，那么其中一个角的正切值(正弦值)与另一个角的余切值(余弦值)相等；②以030角、045角、060角为序，正切值和正弦值从小到大，余切值和余弦值则从大到小；③1=；④2为分母构成的数。
4.利用计算器求三角比的值时，先要选定“角度模式”(DEG)。
如果按MODE键一次屏幕未显示出“Deg Rad Gra”画面，那么反复按MODE键，直到显示为止。
然后按1键，计算器即进入了DEG 模式。
计算器的型号较多，应该参阅其使用说明书进行具体操作。
5.在DEG模式下，根据三角比函数名计算。
如：计算0sin25，按sin 2 5 =屏幕会显示结果。
如要计算余切，利用1cottanαα=求cotα。
如：计算0cot75，依次按1 ÷ tan 7 5 =即可；也可以依次按tan 7 5 =1x-=。
6.当角的大小涉及到“分”和(或)“秒”时，输入“度”“分”和“秒”后，必须按0’”键。
在求0sin2718''时，7.如果一个锐角的三角比的值，这个锐角就是确定的。
如果这个三角比的值不是特殊角的三角比的值，可以利用计算器计算锐角度数的近似值。
如：已知cot 1.3025α=，求锐角α。
可以依次按键： SHIFT tan -1 ( 1 ÷ 1.3025 ) = SHIFT 0’”经典题型解析(一)特殊锐角三角比例1.(1)计算：200020sin 45cos60tan 60cos 30-+⋅。
_九年级秋季班-第3讲：锐角的三角比
a cAB锐角的三角比的意义是九年级数学上学期第二章第一节的内容．本讲主要讲解锐角的三角比的意义和特殊的锐角的三角比的值，以及各锐角的三角比的关系．重点是会根据直角三角形中两边的长求相应的锐角的三角比的值，熟练运用特殊的锐角的三角比的值进行相关计算，难点是在几何图形和直角坐标系中灵活运用锐角的三角比进行解题，以及各锐角的三角比的关系在代数中的灵活运用．1、 正切直角三角形中一个锐角的对边与邻边的比叫做这个锐角的正切（tangent ）．锐角A 的正切记作tan A ．tan A BC aA A AC b ===锐角的对边锐角的邻边．2、 余切直角三角形中一个锐角的邻边与对边的比叫做这个锐角的余切（cotangent ）．锐角A 的余切记作cot A ．cot A AC bA A BC a===锐角的邻边锐角的对边．锐角的三角比内容分析知识结构模块一：锐角的三角比的意义知识精讲a cAB A BCxyAO（2，1） ABCD3、 正弦直角三角形中一个锐角的对边与斜边的比叫做这个锐角的正弦（sine ）．锐角A 的正弦记作sin A ．sin A BC aA AB c ===锐角的对边斜边．4、 余弦直角三角形中一个锐角的邻边与斜边的比叫做这个锐角的余弦（cosine ）．锐角A 的余弦记作cos A ． cos A AC bA AB c ===锐角的邻边斜边．【例1】 如图，在Rt ABC ∆中，90C ∠=︒，AB = 13，BC = 12，则下列三角比表示正确的是（ ）A ．12sin 13A = B ．12cos 13A =C ．5tan 12A =D ．12tan 5B =【例2】 在ABC ∆中，90B ∠=︒，BC = 2AB ，则cos A 的值为______．【例3】 如图，在平面直角坐标系中，直线OA 过点（2，1），则tan α的值是______．【例4】 如图，Rt ABC ∆中，90ACB ∠=︒，AC = 8，AB = 6，CD AB ⊥，垂足为D ，则tan ∠BCD 的值是______．例题解析ABC【例5】 ABC ∆中，已知90C ∠=︒，1tan 2A =，c =a 、b 的值．【例6】 ABC ∆中，已知90C ∠=︒，2sin 3A =，求cos A 、tan A 的值．【例7】 如图，ABC ∆的三个顶点均在格点上，则cos A 的值为______．【例8】 在平面直角坐标系中，过点P （0，2）作直线l ：12y x b =+（b 为常数，且b < 2）的垂线，垂足为Q ，则tan OPQ ∠=______．1、 特殊锐角的三角比的值2、 补充（仅作了解，若填空、选择中出现，可直接使用）3、 通过观察上面的表格，可以总结出：当090α︒<<︒，α的正弦值随着角度的增大而增大，α的余弦值随着角度的增大而减小；α的正切值随着角度的增大而增大，α的余切值随着角度的增大而减小．【例9】 A ∠是等腰直角三角形的底角，B ∠是等边三角形的一个内角，则tan A =______，sin B =______．【例10】 已知，在ABC ∆中，sin 2A =，tan B =，则C ∠=______．模块二：特殊锐角的三角比的值知识精讲例题解析【例11】 在ABC ∆中，90C ∠=︒，已知a =，c = 4，求B ∠．【例12】 在ABC ∆中，三边之比::2a b c =，则sin tan A A +=______．【例13】 当4590α︒<<︒时，sin α、cos α、tan α的大小关系是（ ）A ．sin cos tan ααα<<B ．cos sin tan ααα<<C ．tan cos sin ααα<<D ．tan sin cos ααα<<【例14】在ABC ∆中，若)2sin tan 0A B+-=，则ABC ∆属于哪种三角形？【例15】 求值：2211cos 45cos 30sin 45cos60sin 30︒-++︒+︒︒︒．【例16】()11tan 4532sin 458sin 60cos 45π-︒⎛⎫-+-︒-+ ⎪︒-︒⎝⎭．【例17】已知公式：()sin sin cos cos sin αβαβαβ+=+；()cos cos cos sin sin αβαβαβ+=-．求：sin 75°、cos 75°的值．ABC【例18】如图，在ABC ∆中，90ACB ∠=︒，30A ∠=︒，BC = 1．过点C 作1CC AB ⊥于1C ，过点1C 作12C C AB ⊥于2C ，过点2C 作23C C AB ⊥于3C ，…，按这样的规律继续，则n AC 的长为（ ）A．n⎝⎭B．1n +⎝⎭C．12nn + D．12n n+1、 锐角的三角比一个锐角的正切、余切、正弦、余弦统称为这个锐角的三角比．模块三：锐角的三角比的关系及运用知识精讲【例19】 在ABC ∆中，90C ∠=︒，下列四个等式：○1sin cos A B =；○2cos cos A B =；○31tan tan B A=；○4tan tan A B =．其中一定成立的是______．（填序号） 【例20】已知α【例21】已知sin cos αα+=，求sin cos αα的值．【例22】 求值：cos 40cos 48sin 42sin 50︒︒+-︒︒．【例23】 化简：2222sin 1sin 2sin 88sin 89︒+︒+⋅⋅⋅+︒+︒．【例24】 化简：2222tan sin tan sin αααα-．【例25】 已知：sin cos m αα+=，sin cos n αα-=，则m ，n 之间的关系是（ ）A ．m = nB ．m = 2n + 1C ．222m n =-D ．212m n =-例题解析【例26】已知方程()24210x m x m -++=的两个根恰好是一个直角三角形的两个锐角的余弦，试求m 的值．【例27】 若α为锐角，且22cos 7sin 50αα+-=，求α的度数．【例28】Rt ABC ∆中，90C ∠=︒，BC = a ，AC = b ，AB = c ．利用锐角三角比的定义证明：（1）22sin cos 1A A +=； （2）tan tan 1A B =； （3）sin tan cos A A A=；（4）sin cos 1A A +>．【例29】如果直角三角形的两条直角边分别为a 和b ，斜边上的高为h ， 求证：222111a b h +=．【例30】已知α为锐角，且()12sin cos sin cos 13αααα+-=，求以tan α、cot α为两个根的一元二次方程．ABCDABC【习题1】ABC∆中，90C∠=︒，a、b、c分别是A∠、B∠、C∠的对边，已知b = 5，c = 13，则sin A =______，cos A =______，tan A =______．【习题2】如图，点A为α∠边上的任意一点，作AC BC⊥于点C，CD AB⊥于点D，下列用线段比表示cos α的值，错误的是（）A．BDBCB．BCABC ．ADACD．CDAC【习题3】如图，在网格中，小正方形的边长均为1，点A、B、C都在格点上，则ABC∠的正切值是______．【习题4】若(22sin12cos0αβ+-=，求α、β的值（α、β都是锐角）．【习题5】tan45sin45cot60tan30cot30sin60︒-︒+︒︒︒︒．【习题6】化简：tan1tan2tan88tan89︒︒︒︒．随堂检测【习题7】 求值：222222tan 602cos 45tan 45cot 30sin 27sin 63cos 27cos 63︒+︒︒+-︒+︒︒+︒．【习题8】 等腰三角形底边长为8 cm，面积为2，求底角的正切值．【习题9】 在Rt ABC ∆中，90C ∠=︒，2ABC m S ∆=，且两直角边长满足条件3a + 2b = m ．当m 取最小值时，求ABC ∆中最小内角的正切值．【习题10】 已知a 、b 、c 分别是ABC ∆中A ∠、B ∠、C ∠的对边，关于x 的一元二次方程()()221210a x bx c x -+++=有两个相等的实数根，且3c = a + 3b ．（1）判断ABC ∆的形状； （2）求sin A 、sin B ．【作业1】 Rt ABC ∆中，已知90A ∠=︒，AB = 2，AC = 4，则tan B =______，cos C =______，sin B =______．【作业2】 在ABC ∆中，90C ∠=︒，若斜边AB 是直角边BC 的3倍，则tan B 的值是（ ） A ．13 B ．3 C．4 D．【作业3】 在Rt ABC ∆中，90C ∠=︒，如果各边的长都延长到原来的两倍，那么锐角A 的各三角比的值（ ）A ．都扩大到原来的2倍B ．都缩小为原来的一半C ．没有变化D ．不能确定 【作业4】2012016cot 302-⎛⎫-︒+- ⎪⎝⎭．【作业5】 若sin cos 1a θθ+=，sin cos 1b θθ-=，求证：ab = 1．【作业6】 在Rt ABC ∆中，90C ∠=︒，28a b +=，7sin sin 5A B +=，求斜边c 的长．课后作业A B C A B C （a ） （b ） 【作业7】 已知关于x 的一元二次方程()()22211120m x m x +--+=的两个根是一个直角三角形的两个锐角的正弦，求实数m 的值．【作业8】 已知锐角ABC ∆中，AB = c ，AC = b ，BC = a ，利用锐角三角比的意义证明：cos cos c a B b A =+．【作业9】 我们知道，在直角三角形中，一个锐角的三角比由三角形中相应两条边边长的比值确定，由此建立了直角三角形中边角之间的联系．类似的，可以在等腰三角形中建立边角之间的联系．我们定义：等腰三角形中底边与腰的比值叫做顶角的“正对”（sad ）．如图（a ），在ABC ∆中，AB = AC ，顶角A 的正对记作sad A ，这时sad A =BC AB．容易知道，一个角的大小与这个角的正对值也是互相唯一确定的．根据定义，求解下列问题：（1）sad 60°=______；（2）对于0°< A < 180°，sad A 的取值范围是______；（3）如图（b ），已知3sin 5A =，则sad A 的值是（ ）A ．65B ．23 CD【作业10】 在锐角ABC ∆中，A ∠、B ∠、C ∠所对的边分别为a 、b 、c ．求证：（1）sin sin sin a b c A B C==；（2）111sin sin sin 222ABC S ab C ac B bc A ∆===．。
2.3用计算器求锐角三角比 课件(共17张PPT)
(1) sin 47°；
(2) cos 56.3°；
在角的度量单位为“度”的状态下(显示器上方显示 DEG)
(1) sin 47°；
按下列顺序依次按键： sin 47 DMS ＝ ，
屏幕上显示0.731353 701，按精确到0.0001取近似值，得sin 47° ≈ 0.7314；
(2) cos 56.3°；
0.3746
…
0.9848
0.99030.994 5… Nhomakorabea…
0.9659 0.9511
0.9397
0.9272
…
0.1736
0.1392
0.104 5
…
…
0.2679 0.3249 0.3640
0.4040
…
5.6713
7.1154
9.154 4
…
随着锐角A的度数不断增大，sinA有怎样的变化趋势？cosA呢？tanA呢？
2.
已知：sin 3 ,求：cos __4__。
5
5
3．根据下列条件用计算器求锐角α的度数（结果精确到）： (1) sin 0.893 6
(2) cos 0.079 4 (3) cos 0.079 4 (4) tan 3.450 9
（1）解： 63.3 （2）解： 85.4 （3）解： 40.8 （4）解： 73.8
用计算器求三角函数值的按键顺序 第一步:按下相应的三角函数键,即按下“sin,cos或tan”键; 第二步:按下角度;
第三步:按下“=”键得到相应的三角函数值.
作业布置
1、课本47练习1,2 2、课本48练习1,2 2、习题2.3,T1-5
4.在△ABC中,cos A≈0.939 7,tan B≈1.191 8,试判断△ABC的形状. 【解析】用计算器解得∠A≈20°,∠B≈50°,则∠C≈110°; 因此△ABC为钝角三角形.
锐角的三角比
锐角的三角比一、介绍在数学中，三角比是指三角函数中的比值，用于描述三角形的各个边与角之间的关系。
锐角是指小于90度的角，因此在本文中，我们将讨论关于锐角的三角比。
三角比一共有六个，分别是正弦(sin)、余弦(cos)、正切(tan)、余切(cot)、正割(sec)和余割(csc)。
这些三角比在数学和物理等科学领域中都有广泛的应用，例如解决三角函数方程、测量角度和距离等。
二、正弦(sin)在锐角三角形中，正弦表示三角形的对边与斜边之间的比值。
数学表达式如下：sin(A) = 对边 / 斜边其中，A表示锐角的大小。
正弦的取值范围是-1到1之间，当A接近0度时，正弦的值接近0；而当A接近90度时，正弦的值接近1。
三、余弦(cos)余弦代表锐角三角形的邻边与斜边之间的比值。
数学表达式如下：cos(A) = 邻边 / 斜边同样地，余弦的取值范围也是-1到1之间。
在锐角三角形中，当A接近0度时，余弦的值接近1；当A接近90度时，余弦的值接近0。
四、正切(tan)正切是锐角三角形中对边与邻边之间的比值。
数学表达式如下：tan(A) = 对边 / 邻边正切的取值范围是无穷，当A接近0度时，正切的值接近0；当A接近90度时，正切的值趋于无穷大。
五、余切(cot)余切是锐角三角形中邻边与对边之间的比值。
数学表达式如下：cot(A) = 邻边 / 对边余切的取值范围也是无穷，当A接近0度时，余切的值趋于无穷大；当A接近90度时，余切的值接近0。
六、正割(sec)正割表示斜边与邻边之间的比值。
数学表达式如下：sec(A) = 斜边 / 邻边正割的取值范围是大于等于1的实数。
当A接近0度时，正割的值趋于无穷大；当A接近90度时，正割的值接近1。
七、余割(csc)余割代表斜边与对边之间的比值。
数学表达式如下：csc(A) = 斜边 / 对边余割的取值范围也是大于等于1的实数。
当A接近0度时，余割的值接近无穷大；当A接近90度时，余割的值趋近于1。
锐角三角比讲义
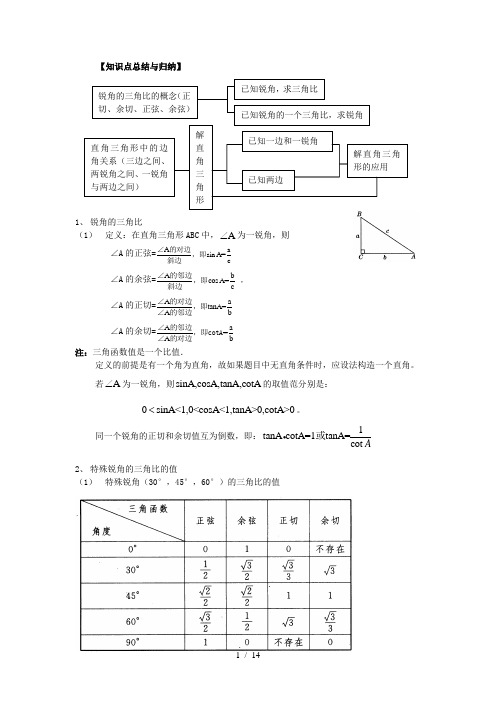
【知识点总结与归纳】1、锐角的三角比（1）定义：在直角三角形ABC中，A∠为一锐角，则∠A的正弦=A asin A=c∠的对边，即斜边∠A的余弦=A bcos A=c∠的邻边，即斜边,∠A的正切=A atanA=A b∠的对边，即∠的邻边∠A的余切=A a=A b∠的邻边，即cotA∠的对边注：三角函数值是一个比值．定义的前提是有一个角为直角，故如果题目中无直角条件时，应设法构造一个直角。
若A∠为一锐角，则sinA,cosA,tanA,cotA的取值范分别是：0sinA<1,0<cosA<1,tanA>0,cotA>0<。
同一个锐角的正切和余切值互为倒数，即：1tanA cotA=1tanA=cot A或2、特殊锐角的三角比的值（1）特殊锐角（30°，45°，60°）的三角比的值锐角的三角比的概念（正切、余切、正弦、余弦）已知锐角，求三角比已知锐角的一个三角比，求锐角直角三角形中的边角关系（三边之间、两锐角之间、一锐角与两边之间）解直角三角形已知一边和一锐角已知两边解直角三角形的应用（2） 同角，互余的两角多的三角比之间的关系： 倒数关系：1tanA=cot A平方关系：22sin A+cos A=1 积商关系：sin cos tanA=,cot cos sin A AA A A=余角和余函数的关系：如果090A B ∠+∠=，那么sinA=cosB, tanA=cotB （正弦和余弦，正切和余切被称为余函数关系）。
注意：求锐角三角比的值问题（1） 在直角三角形中，给定两边求锐角的三角比，关键是搞清某锐角的“对边”“邻边”，掌握三角比的定义。
（2） 给出锐角的度数，求这个锐角的三角比特殊锐角，一般情况下，使用精确值；在实际应用中，根据问题要求处理。
求非特殊锐角的三角比的值，使用计算器或查表求值。
（3） 当锐角不是直角三角形的内角，首先观察有否相等的锐角可代换，而且可代换的锐角含在某直角三角形中，如果没有可代换的相等的锐角，可作适当的垂线构建含有这个锐角的直角三角形。
求锐角的三角比的值
cabb_ 60 °_ 30 °_ a _ C _ B_ A _ 月_ _日 星期__ 第__周课 题 25.2-1特殊锐角的三角比的值 课 型 新授 教 时 1教 学 目 标 1．经历用几何方法探求特殊锐角的三角比的值的过程,掌握特殊锐角的三角比的值.2. 能熟练计算含有30°、45°、60°角的三角比的运算式. 重 点 特殊锐角的三角比的值的运用. 难 点特殊锐角的三角比的规律. 教具准备多媒体课件教 学 过 程 教师活动学生活动 一、复习引入如图，在Rt △ABC 中，∠C =90°，请说出∠A 的四个三角比.二、学习新知1.试一试：我们来研究30°、45°、60°这些特殊锐角的三角比的值.图1 图2 （1）如图1:已知Rt △ABC 中，∠C =90°，∠A=45o，设BC=a ,根据含45°角的直角三角形三边长之间的关系，求45°角的正切、余切、正弦、余弦. （2）如图2:已知Rt △ABC 中，∠C =90°，∠A =30°， ∠B =60°设BC = a ,请求30°、60°角的正切、余切、正弦、余弦. 分别探求30°、45°、60°这些特殊锐角的三角比的值.并填入下表： α αtan αcot αsin αcos 30°45°60°学生口答学生分成三组，分别求出30°、45°、60°这些特殊锐角的三角比的值，全体学生共同完成表格_ 45 ° _ a _ B_ C_ A13323。
25.2 求锐角的三角比的值(1)
25.2 求锐角的三角比的值（1）[特殊锐角的三角比的值]第一组 25-51、下列各式中，正确的是（ ）A 、sin 45º=1B 、sin 60º=2sin 30ºC 、sin 12=30º D 、√3cot 60º=12、如果α为锐角，那么sinα+cosα 的值（ ）A 、小于1B 、等于1C 、大于1D 、以上答案都不对3、在Rt △ABC 中，∠C=90º，AB=2，AC=1，则sin B 的值是（ ） A 、12 B 、√22 C 、√32 D 、24、已知点P(tan 45º，−cos 30º)，则P 点关于原点对称点P ’的坐标是（ ） A 、(−1，−12) B 、(1，−12)C 、[−1，−√32] D 、[−1，√32]5、30º角的正切值是 ，余弦值是 。
6、sin 60º= ，cot 30º = ，cos 45º= 。
7、已知α是锐角，cosα=√32，那么sinα = ，若sin 30º=cos α，则α = 。
8、比较大小：（1）sin 20º sin 50º； （2）cot 25º cot 75º； （3）sin 40º cos 45º； （4）tan 50º cot 50º9、（1）若1−√2sinα=0，则锐角α = 度； （2）若3tan(α−10º)=√3，则锐角α = 度。
10、等腰三角形底边与底边上的高的比是2：√3，则顶角的度数为 。
11、计算：（1）cos 45º−tan45º−cot45º；（2）3sin60º−2cos30º+tan60º；（3）sin30º−√22sin45º+13tan60º；（4）sin30ºtan30º+cos60ºcot60º；（5）sin 230º+cos 230º；（6）2sin 260º−cos 230º+tan 60ºcot 30º； （7）cos 30º+tan 45ºcot45º−sin60º；（8）tan 30º−√2cos 45º·tan 45º2−sin 30º；（9）sin 260º+tan 30º·cot 30º+cos 260ºsin 45º；（10）√(2sin 60º−1)2−|tan 60º−2|12、若tan α=2，求sinα+2cosα3cosα−sinα 的值。
锐角三角比公式
锐角三角比公式锐角三角比1. 什么是锐角三角比锐角三角比是三角函数中的一个概念，用于描述一个锐角的正弦、余弦和正切值。
在数学中，锐角是指小于90度的角。
锐角三角比可以帮助我们计算和描述锐角的各种属性。
2. 锐角三角比的相关公式下面是锐角三角比的几个常用公式：正弦（Sine）正弦值表示一个角度的对边与斜边的比值：sin(A) = 对边 / 斜边余弦（Cosine）余弦值表示一个角度的邻边与斜边的比值：cos(A) = 邻边 / 斜边正切（Tangent）正切值表示一个角度的对边与邻边的比值：tan(A) = 对边 / 邻边3. 示例解释为了更好地理解锐角三角比的概念和应用，我们来看几个示例。
示例 1假设有一个锐角三角形，其中角A的对边长度为5，邻边长度为12，斜边长度为13。
我们可以利用正弦、余弦和正切公式来计算角A 的锐角三角比值：sin(A) = 5 / 13 ≈cos(A) = 12 / 13 ≈tan(A) = 5 / 12 ≈示例 2现在假设有一个锐角三角形，其中角B的对边长度为7，邻边长度为24，斜边长度为25。
我们可以同样利用锐角三角比公式计算角B 的值：sin(B) = 7 / 25 =cos(B) = 24 / 25 =tan(B) = 7 / 24 ≈通过以上示例，我们可以看到锐角三角比可以帮助我们计算角度的各种属性，如角度的正弦、余弦和正切值。
这些值在许多数学和科学领域中都有广泛的应用，如物理、工程、地理等。
总结本文介绍了锐角三角比的概念和相关公式，并通过示例解释了如何计算锐角的正弦、余弦和正切值。
锐角三角比在数学中具有重要的应用价值，它可以帮助我们计算和描述锐角的各种属性。
在实际问题中，了解锐角三角比可以帮助我们更好地理解和解决各种角度相关的计算和测量问题。
25.2求特殊锐角三角比的值(1)shao
B
a 60° 2a
30°
C
3a
A
书P67
表格：特殊锐角的三角比的值
问1：同一个锐角的三角比的数量关
tan A cot A
问2：互余的两个锐角的三角比
tan A cot B,cot A tan B
sin A cos B,cos A sin B
问3：每一列三角比的值有什么
小大 小大
锐角A的正切、余切、正弦、余弦统称锐角A的三角比．
温故知新
如图，在Rt△ABC中，∠C=90°，请说出∠A的四个三角比
B ∠A的对边
C ∠A的邻边
①同一个锐角的三角比的数量关系
tan A cot A
②互余的两个锐角的三角比的数量关
tan A cot B,cot A tan B
A
sin A cos B,cos A sin B
新知运用
3、例题：求下列各式的值：
（1）sin 30 tan 30 cos 60 cot 30
（2）2 sin2 60 cos2 30 tan 60 cot 60
（3）
2sin2 60 cos tan2 60 4cos
60 45
解此类题目的思路：
1）代入特殊锐角三角比的值
2）转化为二次根式的计算.
关键：熟悉并牢记特殊锐角三角比的值，仔细计算，
补充
在锐角三角形△ABC中，如果 (tanA 1)2 ( 3 cotB)2 0 ，求∠C的度数 3 解：由题意得
ห้องสมุดไป่ตู้
tan A 1 0
3 cot B 0 3
解得BA
点或规律？
求锐角的三角比的值
求锐角的三角比的值一、基础巩固一．解答题1. 在Rt △ABC 中，∠C=90°，∠A，∠B，∠C 的对边分别为a，b，c ．若a=2，sin 13A =，求b 和c，【答案】b=c=6.【解析】【分析】先根据sinA=a c 知c=sin a A=6，再根据勾股定理求解可得． 【详解】解：如图，∵a=2，1sin 3A =， ∴c=sin a A =213=6，则，【点睛】本题主要考查锐角三角函数的定义，解题的关键是掌握正弦函数的定义及勾股定理．2. 已知：如图，在Rt △ABC 中，∠C=90°，AC=2BC ，求∠B 的正弦、余弦值和正切值．【答案】， ， tanB=2． 【解析】【分析】根据勾股定理与锐角三角函数的定义求解即可．【详解】∵∠C=90°，AC=2BC ，∴设BC=x ，AC=2x ，∴=，∴sinB=AC AB ==，cosB=BC AB == tanB=22xAC x BC ==． 【点睛】本题考查了勾股定理与锐角三角函数的定义，在Rt △ABC 中，∠C=90°，锐角A 的正弦、余弦、正切都叫做∠A 的锐角三角函数．3. 在△ABC 中，∠C ，90°，AB ，13，BC ，5，求∠A 的正弦值、余弦值和正切值．【答案】5125131312，，. 【解析】【详解】试题分析：根据解直角三角形的意义，根据勾股定理求出AC 的长，然后根据正弦、余弦、正切的概念可求解.试题解析：∵∠C ，90°，AB ，13，BC ，5，∴12AC ==.∴5sin 13BC A AB ==，12cos 13AC A AB ==， 5tan 12BC A AC ==. 4. 在Rt △ABC 中，∠C=90°，a=2，b=1，求∠A 的三个三角函数值．【答案】，，tanA=2． 【解析】【分析】根据勾股定理，可得c ，根据sinA=a c ，cosA=bc ，tanA=a b，可得答案． 【详解】∵∠C=90°，a=2，b=1，∴=∴sinA=ac 5，cosA=bc =5， tanA=a b=2． 【点评】本题考查了锐角三角函数的定义，在Rt △ACB 中，∠C=90°，则sinA=a c ，cosA=b c ，tanA=a b． 5. 如图，在Rt △ABC 中，∠C=90°，M 是直角边AC 上一点，MN ⊥AB 于点N ，AN=3，AM=4，求cosB 的值．． 【解析】 【分析】易证得△AMN ∽△ABC ，根据相似三角形的性质得到AC AB =AN AM =34，设AC=3x ，AB=4x ，由勾股定理得：x ，在Rt △ABC 中，根据三角函数可求cosB ．【详解】∵∠C=90°，MN ⊥AB ，∴∠C=∠ANM=90°，又∵∠A=∠A ，∴△AMN ∽△ABC ， ∴AC AB =AN AM =34， 设AC=3x ，AB=4x ，由勾股定理得：=，在Rt △ABC 中，cosB=BC AB ==． 【点评】本题考查了锐角三角函数的定义，相似三角形的判定和性质，勾股定理，本题关键是表示出BC ，AB ．6. 如图，在正方形ABCD 中，M 是AD 的中点，BE=3AE ，试求sin，ECM 的值．【解析】 【详解】试题分析：依题意设，AE x = 则3424BE x BC x AM x CD x ，，，，====先证明CEM 是直角三角形，再利用三角函数的定义求解．试题解析：设，AE x = 则3424BE x BC x AM x CD x ，，，，====5,EC x ∴==,EM ==,CM ==222EM CM CE ∴+=，CEM ∴是直角三角形，sin EM ECM CE ∴∠== 7. 在△ABC 中，∠C ＝90°，BC ＝3，AB ＝5，求sinA ，cosA ，tanA 的值．【答案】sin A ，35，cos A ，45，tan A ，34， 【解析】【分析】首先利用勾股定理求得AC 的长度为4；然后利用锐角三角函数的定义解答．正弦：把锐角A 的对边与斜边的比叫做∠A 的正弦，记作sin A余弦：把锐角A 的邻边与斜边的比叫做∠A 的余弦，记作cos A正切：把锐角A 的对边与邻边的比叫做∠A 的正切，记作tanA【详解】，Rt ，ABC 中，∠C ，90°，BC ，3，AB ，5，，AC，sin A ，BC AB ，35， c os A ，AC AB ，45， ta n A ，BC AC ，34， 【点睛】本题关键考查了勾股定理和锐角三角函数的定义及运用，能正确运用定义写出三角比是解决本题的关键，8. 如图，直角坐标系中，P （3，y ）是第一象限内的点，且4tan 3α=，求sinα．【答案】sinα=45． 【解析】 【分析】根据在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边，可得答案．【详解】如图：作PC ⊥x 于C 点， 由4tan 33y α==，得y=4．由勾股定理，得=，45PC sin OP α==． 【点睛】本题考查了坐标与图形，勾股定理，锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边． 9. 如图，在平面直角坐标系中，已知点B （4，2），BA ⊥x 轴于A ．（1）求tan ∠BOA 的值；（2）将点B 绕原点逆时针方向旋转90°后记作点C ，求点C 的坐标．【答案】（1）12；（2）（﹣2，4）． 【解析】 【分析】（1）根据正切的定义，对边与邻边的比，即可求解；（2）根据图形，确定旋转以后的位置，可以直接写出坐标．【详解】（1）∵点B （4，2），BA ⊥x 轴于A ，∴OA=4，AB=2，tan ∠BOA=AB OA =24=12； （2）如图，由旋转可知：CD=BA=2，OD=OA=4，∴点C 的坐标是（﹣2，4）．【点评】本题主要考查了正切的定义以及旋转变换作图，正确理解定义是解题的关键．10. 计算：2cos60°+4sin60°•tan30°﹣cos45°【答案】3﹣2． 【解析】【分析】直接利用特殊角的三角函数值代入求出答案．【详解】2cos60°+4sin60°•tan30°﹣cos45°＝2×12＝1+2﹣2＝3﹣2． 【点睛】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键． 11. 计算：3sin60°-2cos30°+tan60°•cot45°．【解析】【分析】直接利用特殊角的三角函数值代入求出答案．【详解】原式=3×2-2×2，【点睛】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键．12. 计算：sin45cos3032cos60︒︒︒+-﹣sin30°（cos45°﹣sin60°）【解析】【分析】依据30°、45°、60°角的各种三角函数值，即可得到计算结果．【详解】解：原式=221322-⨯﹣12⨯（22-）=4【点睛】本题考查了特殊角的三角函数值，其应用广泛，一是它可以当作数进行运算，二是具有三角函数的特点，在解直角三角形中应用较多．13. 计算：1cos3011cos60tan30 -︒++︒︒.【答案】2 3 +【解析】【分析】利用特殊角的三角函数值代入再通过实数运算法则求出即可.【详解】原式=121 12 -+=（1×2 3=23﹣=23．【点睛】此题主要考查了特殊角的三角函数值应用,正确记忆特殊角的三角函数值是解题关键.14. 计算.2cos60°+4sin60°•tan30°﹣cos245°【答案】5 2【解析】【分析】直接把特殊角的三角函数值代入求出答案．【详解】2cos60°+4sin60°•tan30°﹣cos245°=2×12+4(2)2=1+2﹣1 2=52．【点评】本题主要考查了特殊角的三角函数值，正确记忆特殊角的三角函数值是解题关键．15. 计算：（12）﹣1﹣2tan45°+4sin60°【答案】0．【解析】【分析】根据实数的性质进行化简即可求解.【详解】原式＝2﹣＝2﹣﹣＝0．【点睛】此题主要考查实数的运算，解题的关键是熟知实数的性质.16. 计算：sin60cos45tan45 sin30︒-︒︒︒.【答案】【解析】【分析】原式利用特殊角的三角函数值及二次根式性质计算即可得到结果.【详解】sin60cos45tan45sin30︒-︒︒︒=22112-11.17. 计算：（sin30°，，1+2sin45cos45tan60?tan30︒+︒︒︒，tan45°，【解析】【详解】试题分析：把特殊角的三角函数值代入进行运算即可.试题解析：原式2111,2-+⎛⎫= ⎪⎝⎭121,22=++-32+=18. 计算：2cos45°﹣tan60°+sin30°﹣|﹣12|．【解析】【详解】试题分析，直接利用特殊角的三角函数值代入求出答案．试题解析，解，原式=2+12，1219. 计算：sin30°•tan60°+cos30cot45cos60︒-︒︒.，2-【解析】【详解】试题分析：把相关的特殊三角形函数值代入进行计算即可.试题解析：原式=1122122--.20.245°，sin30°tan60°+12sin60°【解析】【分析】把特殊角的三角函数值代入运算即可．【详解】解：原式211222⎛=-⎝⎭224=-+=．21. 计算：cos30°•tan60°，4sin30°+tan45°，【答案】12【解析】【分析】代入特殊角的三角函数值计算即可，【详解】原式1 412⨯+=321 2-+=12，22. 计算：2tan60︒，2tan45°，43cos30°+4sin30°，【答案】0【解析】【分析】首先根据特殊角的三角函数值得出各式的值，然后根据实数的计算法则得出答案．【详解】原式43×2+4×12=0，23. 计算：22sin60sin30 cot30s30o oo oco+-，【解析】【分析】把特殊角的三角函数值代入进行运算即可.【详解】原式22123⎛⎫+ ⎪===【点睛】考查特殊角的三角函数值，熟记特殊角是三角形函数值是解题的关键.24. 计算：21tan60sin452cos30cot45︒︒︒︒-⋅-．【答案】12【解析】【分析】直接代入利用特殊角的三角函数值，进而化简即可得答案．【详解】原式12=-=12=．【点睛】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键．25. 计算：sin30°﹣2cos45°+13tan260°．【答案】1．【解析】【分析】将特殊角的三角函数值代入求值即可．【详解】原式=2112223-+⨯=1113223-+⨯=1．．26. 计算：222sin60cos60tan604cos45︒︒︒︒--﹣sin45°•tan45°【答案】32+【解析】【分析】把特殊角的三角函数值代入计算即可．【详解】222sin60cos60tan604cos45︒︒︒︒--﹣sin45°•tan45°212212⨯-=-=32=+=32+． 【点睛】本题考查了特殊角的三角函数值及分母有理化、二次根式的化简，牢记特殊角的三角函数值，是解决本题的关键．27. （π+4）0|【答案】1【解析】【分析】分别根据特殊角的三角函数值、零指数幂、绝对值的性质及二次函数化简的法则计算出各数，再根据实数混合运算的法则进行计算即可.π+4，0|=128. 已知α是锐角，cos （a ﹣15°）|cosa ﹣tan 2a |的值．【答案】1﹣3． 【解析】【分析】根据特殊角三角函数值，可得答案．【详解】∵cos 452=°，又cos （a ﹣15°）=2， ∴α﹣15°=45°，∴α=60°，|cosa ﹣tan 2a |12=-1122=+=1 【点睛】本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键． 29. 求下列各式的值：（1）22cos 60sin 60︒+︒（2）cos 45tan 45sin 45︒-︒︒（3）1sin 60cos302︒⨯︒+（4）sin 452︒+ （5）2cos 45tan 60cos30︒+︒⨯︒（6）1-cos30tan 30sin 60︒+︒︒（7）sin 45cos60cos45︒︒-︒（8） 260tan 602cos 30︒+︒-︒【答案】（1）1；（2）0；（3）54；（4；（5）2；（6；（7）4；（8 【解析】【详解】（1）22cos 60sin 60︒+︒13=+44=1（2）cos45tan45sin45︒-︒︒=110-=（3）1sin60cos302︒⨯︒+ 32=+445=4（4）sin45︒（5）2cos 45tan60cos30︒+︒⨯︒13=+22=2（6）1-cos30tan30sin60︒+︒︒1= （7）sin45cos60cos45︒︒-︒=424-=- （8）2tan602cos 30︒+︒-︒33=22=30. 若规定：sin （α+β）=sinα•cosβ+cosα•sinβ，试确定sin75°+sin90°的值．． 【解析】【分析】根据给出的公式，将75°和90°化为特殊角即可求出答案．【详解】解：原式=sin （30°+45°）+sin （30°+60°）=sin30°•cos45°+cos30°•sin45°+sin30°•cos60°+cos30°•sin60°=12×22+×2+12×12+2×2=4+414+34【点睛】本题考查特殊角的三角函数值，解题的关键是将75°和90°化为特殊角进行计算，本题属于基础题型．二、拓展提升31. 如图，已知△ABC 中，∠C=90°，且BC=1.5，求AC ．【答案】 【解析】 【分析】直接利用特殊角的三角函数值得出∠A 的度数，再利用锐角三角函数关系得出答案．【详解】∵∠C=90°，且sinA=2， ∴∠A=60°，∴tanA=BC AC ，∴1.5AC =解得：AC=2． 【点评】本题主要考查了特殊角的三角函数值，正确得出∠A 的度数是解题关键．32. 已知α为锐角，sin （α+15°）4cosα+tanα+（13）﹣1的值． 【答案】4．【解析】 【分析】首先得出α的值，进而利用特殊角的三角函数值以及负整数指数幂的性质化简求出答案．【详解】∵sin （α+15°）sin 60︒ ∴α+15°=60︒，∴α=45°，﹣4cosα+tanα+（13）﹣1﹣+1+3=4．【点评】本题主要考查了特殊角的三角函数值以及负整数指数幂的性质，正确掌握相关性质是解题关键．33. 计算：（3，π，0+11()3-，2cos60°， 【答案】3【解析】【分析】本题涉及实数运算、二次根式化简等多个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．【详解】原式=1＋3－2×12＝334. ()1306045()o sin sin cos --︒⨯︒【答案】1【解析】【分析】)原式利用特殊角的三角函数值，二次根式，负整数指数幂法则计算即可得到结果．【详解】解：原式=（12）-12）-1）=2×（）=1-【点睛】此题考查了实数的运算，负整数指数幂，二次根式的性质以及特殊角的三角函数值，熟练掌握运算法则是解本题的关键．35. 计算下列各式(1)tan30°×sin45°＋tan60°×cos60°(2)sin 230°＋2sin60°＋tan45°－tan60°＋cos 230°.【答案】（1）6＋3；（2）2. 【解析】【分析】（1）首先代入特殊角的三角函数值，然后化简二次根式即可；（2）首先代入特殊角的三角函数值，然后化简二次根式即可．【详解】解：(1)×12(2)原式＝12⎛⎫ ⎪⎝⎭2＋2×2＋12⎛ ⎝⎭2＝14134＝2.【点睛】本题考查了特殊角的三角函数值，解题关键是熟记特殊角的三角函数值． 36. (1)2sin603tan30+(2)22sin 60cos 60tan45+- (3)cos60tan45sin60tan30sin30-++sin602cos45+-． 【答案】（1）（2）0；（3）35-；（4）122+ 【解析】【分析】，1）根据特殊角的三角函数值可求得结果；，2）根据特殊角的三角函数值可求得结果；，3）根据特殊角的三角函数值可求得结果；，4）根据特殊角的三角函数值可求得结果；【详解】解：（1）3 2sin603tan30232+=⨯== （2）22sin 60cos60tan45110+-=-=， （3）111cos60tan45sin602tan30sin30326-+-+===+（421sin602cos452222+-=⨯-= 【点睛】本题考查了特殊角的三角函数值，熟记特殊角三角函数值是解题关键.37. 在△ABC 中，已知∠A ＝60°，∠B 为锐角，且tanA ，cosB 恰为一元二次方程2x 2－3mx ＋3＝0的两个实数根．求m的值并判断△ABC 的形状．【答案】mABC 是直角三角形．【解析】【分析】先求出一元二次方程的解，再根据特殊角的三角函数值求出各角的度数，判断三角形的形状．【详解】解：∵∠A ＝60°，∴tanA .把x 2x 2－3mx ＋3＝0，得2－＋3＝0，解得m .把m2x2－3mx＋3＝0得2x2－3mx＋3＝0，解得x1x2∴cos B＝2，即∠B＝30°.∴∠C＝180°－∠A－∠B＝90°，即△ABC是直角三角形．【点睛】本题考查的知识点是解一元二次方程和判断三角形，解题关键是熟记特殊三角函数值.38. （1）已知3tanα﹣2cos30°=0，求锐角α；（2）已知2sinα﹣3tan30°=0，求锐角α．【答案】（1）α=30°；（2）α=60°．【解析】【分析】（1）先求出tanα的值，然后求出角的度数；（2）先求出sinα的值，然后求出角的度数．【详解】解：（1）解得：tanα=3，则α=30°；（2）解得：则α=60°．【点睛】本题考查了特殊角的三角函数值，解题的关键是掌握几个特殊角的三角函数值．39. 计算：（1）sin3011sin60tan30︒︒︒++；（2）tan30°•tan60°+sin245°+cos245°；（3）2cos30°•sin60°﹣tan45°•sin30°．【答案】（1）2；（2）2；（3）1．【解析】【分析】分别代入特殊角的三角函数值，进一步计算得出答案即可．【详解】（1）sin 3011sin 60tan 30︒︒︒++1==+=2=2；（2）tan30°•tan60°+sin 245°+cos 245°=32⎝⎭+2⎝⎭=1+12+12=2；（3）2cos30°•sin60°﹣tan45°•sin30°=21×12 =32﹣12=1．【点评】本题考查了特殊角的三角函数，识记特殊角的三角函数值是解决问题的关键．40. 已知正六边形ABCDEF 的边长为1，QR 是正六边形内平行于AB 的任意线段，求以QR 为底边的内接于正六边形ABCDEF 的△PQR 的最大面积．【解析】【分析】要使△PQR 的面积最大，P 点应在DE 上；Q ，R 点应分别在AF 、BC 上．过P 点PH ⊥QR 于H ，连接AE 、BD 分别交QR 、QR 于M 、N ，FC 交AE 于G ，可设PH=x ，再用含x 的式子表示QR ，根据平方的非负性，得出△PQR 的最大面积．【详解】解：过P 点PH ⊥QR 于H ，连接AE 、BD 分别交QR 、QR 于M 、N ，FC 交AE 于G ，∵正六边形ABCDEF 的边长为1，∴∠EFA=∠FAB=∠ABC=()621801206-⨯︒=︒，EF=FA=AB=1， ∵QR ∥AB ，∴四边形ABNM 、ABDE 、MHPE 、MNDE 都是矩形，∠EFG=∠AFG=60︒，∴，设PH=x ，则x ，QM=NR=AM•tan30°=1，QR=2(1x ，△PQR 的面积=12(3﹣)2，当时，△PQR ． 【点评】本题考查了正六边形的性质，矩形的判定和性质，解直角三角形，平方的非负性等知识，作出常用辅助线是解题的关键．。
特殊锐角的三角比的值
特殊锐角的三角比的值内容分析特殊锐角的三角比的值是九年级数学上学期第二章第一节的内容，本讲主要讲解利用几何方探求30°、45°和60°这三个特殊锐角的三角比的值，重点是熟练运用其进行相关计算，难点是在几何图形中的灵活运用．知识结构模块一：求特殊锐角的三角比的值知识精讲1、特殊锐角的三角比的值ABCABC BAC【例1】 如图，在Rt ABC ∆中，90C ∠=︒，45A ∠=︒，BC = a ．求A ∠的三角比的值． 【难度】★ 【答案】22sin =A ，22cos =A ，1tan =A ，1cot =A ． 【解析】∵45A ∠=︒，∴2245sin sin =︒=A ，2245cos cos =︒=A ， 145tan tan =︒=A ，145cot cot =︒=A ． 【总结】本题主要考查特殊角45角的三角比的值．【例2】 如图，在Rt ABC ∆中，90C ∠=︒，30A ∠=︒，BC = a ．求A ∠的三角比的值． 【难度】★【答案】21sin =A ，23cos =A ，33tan =A ，3cot =A【解析】∵30A ∠=︒∴2130sin sin =︒=A ，2330cos cos =︒=A ， 3330tan tan =︒=A ，330cot cot =︒=A ． 【总结】本题主要考查特殊角30角的三角比的值．【例3】 如图，在Rt ABC ∆中，90C ∠=︒，60A ∠=︒，AC = a ．求A ∠的三角比的值． 【难度】★ 【答案】23sin =A ，21cos =A ，3tan =A ，33cot =A ． 【解析】∵60A ∠=，∴2360sin sin =︒=A ，2160cos cos =︒=A ，360tan tan =︒=A ，3360cot cot =︒=A ． 【总结】本题主要考查特殊角60角的三角比的值．例题解析【例4】 填空：tan 60°= ______；cot 45°= ______；sin 30°= ______；cos 45°= ______．【难度】★ 【答案】3，1，21，22【解析】主要考察特殊角的锐角三角比值．【例5】 用特殊锐角的三角比填空：（1）12=______ = ______； （2=______ = ______；（3）1=______ = ______；（4=______ = ______． 【难度】★【答案】（1）sin 30°，cos 60°；（2）sin 45°，cos45°；（3） tan45°，cot 45°；（4）sin 60°，cos30°． 【解析】主要考察特殊角的锐角三角比值．【例6】 已知，等腰ABC ∆的顶角A ∠=120°，求B ∠的三角比的值． 【难度】★ 【答案】21sin =B ，23cos =B ，33tan =B ，3cot =B【解析】∵等腰ABC ∆的顶角A ∠=120°，∴︒=∠=∠30C B ． ∴2130sin sin =︒=B ，2330cos cos =︒=B ，3330tan tan =︒=B ，330cot cot =︒=B ． 【总结】本题一方面考查等腰三角形的性质，另一方面考查特殊角30角的三角比的值．【例7】 正方形ABCD 中，对角线AC 、BD 相交于点O ，求OAB ∠的三角比的值． 【难度】★ 【答案】22sin =∠OAB ，22cos =∠OBA ，1tan =∠OAB ，1cot =∠OAB 【解析】∵正方形ABCD 中，对角线AC 、BD 相交于点O ， ∴︒=︒⨯=∠=∠45902121BAC OAB ．∴2245sin sin =︒=∠OAB ，2245cos cos =︒=∠OAB ，145tan tan =︒=∠OAB ，145cot cot =︒=∠OAB ．【总结】本题一方面考查正方形的性质，另一方面考查45角的三角比的值．【例8】 求满足下列条件的锐角α：（1）cos 0α=； （2）0α=．【难度】★【答案】（1）︒=30α；（2）︒=45α．【解析】（1）由题意可得：cos α=︒=30α；（2）由题意可得：1tan =α，则︒=45α．【总结】本题主要是对特殊锐角三角比的值的综合运用．【例9】 若A ∠是锐角，且tan A cos A = ______． 【难度】★★ 【答案】23【解析】∵tan A =，∴︒=∠30A ，∴2330cos cos =︒=A ． 【总结】本题主要考查特殊角的锐角三角比的值以及它们之间的关系．【例10】 已知，在Rt ABC ∆中，90C ∠=︒，cos B =12，求tan A 的值． 【难度】★★ 【答案】33 【解析】∵1cos 2B =，且∠B 是锐角，∴︒=∠60B ．∵︒=∠+∠90B A ， ∴︒=∠30A∴3330tan tan =︒=A ． 【总结】本题主要考查特殊角的锐角三角比的值以及它们之间的关系．【例11】 sin 45°+ cos 45°的值等于（ ）ABCD ．1【难度】★ 【答案】A【解析】sin 45°+ cos 45°=22222=+．【例12】 下列不等式，成立的是（ ）A ．sin60sin45sin30︒<︒<︒B ．cos60cos45cos30︒>︒>︒C ．tan60tan45tan30︒<︒<︒D ．cot30cot 45cot60︒>︒>︒【难度】★ 【答案】D【解析】A 答案，正确应为：sin60sin45sin30︒>︒>︒； B 答案，正确应为：cos60cos45cos30︒<︒<︒；C 答案，正确应为：tan60tan45tan30︒>︒>︒【总结】一个锐角的正弦值和正切值随着角度的增大而增大，一个锐角的余弦值和余切值随着角度的增大而减小．【例13】 计算：（1）tan602sin452cos30︒+︒-︒；（2）()2tan 60tan 30︒+︒．【难度】★【答案】（1）2；（2）316． 【解析】（1）原式=23232322223=-+=⨯-⨯+（2）原式=31633433322=⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛+【总结】本题考查利用特殊角的锐角三角比的值进行实数计算．模块二：特殊锐角的三角比的值的应用例题解析【例14】 计算：（1）sin60tan 45cos30︒-︒︒；（2）tan 45tan301tan 45tan30︒-︒+︒︒．【难度】★【答案】（1）0；（2）32-【解析】（1）原式=01112323=-=-；（2）原式=3233333313313311331-=+-=+-=⨯+-． 【总结】本题考查利用特殊角的锐角三角比的值进行实数计算．【例15】计算：)112341271tan 6012-⎛⎫++- ⎪︒+⎝⎭．【难度】★★ 【答案】3【解析】原式=()32132324321343243=--+-+=-++-+．【总结】本题考查利用特殊角的锐角三角比的值进行实数计算．【例16】【难度】★★ 【答案】213- 【解析】原式sin 60sin30sin 60sin30︒-︒=︒-︒=． 【总结】本题考查利用特殊角的锐角三角比的值进行实数计算．【例17】计算：22cos 60cos 45sin 45︒+︒︒︒． 【难度】★★【答案】45【解析】原式=4521214122212222122=++=⨯⨯+⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛． 【总结】本题考查利用特殊角的锐角三角比的值进行实数计算．【例18】 计算：cos60sin 45cos60cos45cos60sin 45sin30cos45︒+︒︒-︒+︒-︒︒+︒． 【难度】★★ 【答案】6- 【解析】原式=()()6212121212121222122212221222122-=--+-=+-+-+=+-+-+．【总结】本题考查利用特殊角的锐角三角比的值进行实数计算．【例19】 计算：()tan 4512sin30cos60cot 30sin 60cos60-︒︒-︒--︒+︒+︒．【难度】★★ 【答案】2-【解析】原式=213321212313212121-=-+--=++--⎪⎭⎫ ⎝⎛-⨯-．【总结】本题考查利用特殊角的锐角三角比的值进行实数计算．【例20】sin301︒-．【难度】★★ 【解析】原式=321132121324211212314121=+-+=+-+=-+⎪⎪⎭⎫ ⎝⎛-⨯+-． 【总结】本题考查利用特殊角的锐角三角比的值进行实数计算．【例21】 已知030α︒<∠<︒，化简：1cot cot αα-．【难度】★★【答案】13cot 2--α【解析】∵030α︒<∠<︒， ∴330cot cot =︒>α．∴1cot cot cot 1cot 2cot 1ααααα-+=-+=．【总结】一个锐角的度数越大，余切值反而越小．【例22】 已知方程()2sin 2sin 2sin 120x x ααα-+++=有两个相等的实数根，求锐角α的大小．【难度】★★ 【答案】30°【解析】∵方程()2sin 2sin 2sin 120x x ααα-+++=有两个相等的实数根， ∴()()12sin sin 42sin 42+⨯⨯-+=∆ααα0sin 3216=-=α．∴21sin =α． ∴︒=30α．【总结】本题将根的判别式与锐角三角比结合在一起，完成相应计算．ααααsin 48sin 416sin 16sin 422--++=【例23】 已知ABC ∆中，30B ∠=︒，45C ∠=︒，BC = 15 cm ，求AB 的长． 【难度】★★【答案】AB=15315-【解析】解：过A 作AD ⊥BC ，垂足为D设x AD =，在ABD Rt △中，30B ∠=︒， ∴3cot ==AD BDB ，则x BD 3=；在ACD Rt △中，45C ∠=︒，∴1cot ==ADCDC ，则x CD =；∵BC = 15 cm ， ∴153=+x x ， 解得：215315-=x ．∴153152-==x AB cm ．【总结】本题是对锐角三角比的直接运用，注意在运用锐角三角比时，要将锐角放在直角三角形中．【例24】 已知ABC ∆中，30B ∠=︒，135C ∠=︒，BC = 15 cm ，求AB 的长． 【难度】★★【答案】AB=15315+【解析】解：过A 作AD ⊥BC ，垂足为D ．设x AD =，在ABD Rt △中，30B ∠=︒，∴ 3cot ==ADBDB ，则x BD 3=；在ACD Rt △中，18045ACD ACB ∠=-∠=，∴1cot ==AD CDC ，则x CD =；∵BC = 15 cm ，∴153=-x x ，解得：215315+=x ．∴153152+==x AB cm ．【总结】本题是对锐角三角比的直接运用，注意在运用锐角三角比时，要将锐角放在直角三角形中．BA【例25】 已知ABC ∆中，45A ∠=︒，AC = 15 cm，BC =，求AB 的长． 【难度】★★★【答案】AB =AB = 【解析】（图1）（图2）解：过C 作CD ⊥BA ，垂足为D ． 在ACD Rt △中，45A ∠=︒，AC = 15， ∵22cos ==AC AD A ， ∴AD CD =在BCD Rt △中，∵222CB BD CD =+，∴BD =在图1中，AB AD BD =+==在图2中，AB AD BD =-==． 综上所述：AB 的长为【总结】在三角形中，已知一个角的度数，以及这个角的对边和一条邻边的长时，要注意分类讨论．ABA【例26】 已知1sin60cos60a =︒-︒，1tan 45cot30b =︒-︒，求224a ab b ++的值．【难度】★★★ 【答案】3233--．【解析】∵11sin 60cos60a ===︒-︒，1tan 45cot 30b ===︒-︒，∴()22242a ab b a b ab ++=++．而231+=+b a ，()2312+-=ab ，∴原式=()()3233314331231222--=+-=+-⎪⎪⎭⎫⎝⎛+． 【总结】本题主要考查锐角三角比在实数运算中的运用．【例27】 已知090θ︒<<︒，且sin 0θθ=，求2sin cos 2sin cos θθθθ+-．【难度】★★★ 【答案】7249+．【解析】∵sin 0θθ-=，∴sin θθ．∴2sin cos 2sin cos θθθθ+===-【总结】本题主要是考查换元的思想．【例28】 已知Rt ABC ∆中，90C ∠=︒，2a b +=，30A ∠=︒，求a 、b 、c 的值． 【难度】★★★【答案】13-=a ，33-=b ，232-=c 【解析】解：在ABC Rt △中， 3cot ==abA ，则a b 3=． ∵2a b +=， ∴23=+a a ， 解得：13-=a ，∴333-==a b ，2322-==a c ．【总结】本题是对特殊角锐角三角比的综合运用．【例29】 在ABC ∆中，A ∠、B ∠均是锐角，且(2tan 2sin 0B A +=，请判断ABC ∆的形状，并说明理由．【难度】★★★ 【答案】等边三角形．【解析】∵(2tan 2sin 0B A +=，∴03tan =-B ，03sin 2=-A ，解得：3tan =B ，23sin =A ． ∴︒=∠60B ，︒=∠60A ．∴ABC ∆为等边三角形．【总结】本题主要是对绝对值和平方的非负性和特殊角的锐角三角比的值的综合考查．【例30】 应用锐角三角比的定义，求sin 15°、tan 15°、sin 75°、tan 75°． 【难度】★★★【答案】42615sin -=︒，3215tan -=︒，sin 【解析】如图，作等腰△ABC ，且︒=∠=∠15C B ． 过点C 作CD ⊥BA 交BA 的延长线于点D ，则︒=∠15B ，75BCD ∠=︒，30CAD ∠=． 设x DC =，则x AB AC 2==，x DA 3=， BC x x ====．在Rt △BDC 中， ()42626126sin 15sin -=+=+===︒xxBCDCB ；()3232132tan 15tan -=+=+===︒x x BD DC B ； ()()42626322632sin 75sin +=++=++==∠=︒x x BC DB BCD ；()3232tan 75tan +=+==∠=︒xxCDDB BCD ．【总结】在求非特殊角的锐角三角比的值时，想办法将其跟特殊角结合起来，再去求值．【习题1】求满足下列条件的锐角α：（1）2cos 0α=；（2）()tan 10α+︒=【难度】★【答案】（1）45°；（2）50°． 【解析】（1）由题意可得：cos α=︒=45α；（2）由题意可得：︒=︒+6010α，则︒=50α．【总结】本题主要考查特殊角的锐角三角比的值．【习题2】 如果α∠是等腰直角三角形的一个锐角，则α∠的余弦值为______．【难度】★ 【答案】22【解析】∵α∠是等腰直角三角形的一个锐角，∴︒=45α，∴cos 2α= 【总结】本题主要考查特殊角的锐角三角比的值．【习题3】 若α是锐角，且cot α=()cos 90α︒-=______．【难度】★【答案】21【解析】∵cot α=︒=30α，∴()2160cos 90cos =︒=-︒α． 【总结】本题主要考查特殊角的锐角三角比的值．随堂检测【习题4】 ABC ∆中，A ∠、B ∠都是锐角，且sin A =12，cos B，则ABC ∆三个角的大小关系是（ ）A ．C AB ∠>∠>∠ B ．BC A ∠>∠>∠ C ．A B C ∠>∠>∠D ．C B A ∠>∠>∠【难度】★ 【答案】D 【解析】∵sin A =12，cos B，∴︒=∠30A ，︒=∠45B ．∴︒=︒-︒-︒=∠1054530180C ，∴C B A ∠>∠>∠．【总结】本题主要考查特殊角的锐角三角比的值．【习题5】 计算：cos45sin30cos45sin30︒+︒︒-︒．【难度】★★ 【答案】223+ 【解析】原式=223121221222122+=-+=-+．【总结】本题主要是将特殊角的锐角三角比的值与实数运算结合在一起．【习题6】23tan 30︒+【难度】★★ 【答案】2【解析】原式 =2221122212333122=-+-+=⎪⎪⎭⎫⎝⎛-⨯+⎪⎪⎭⎫ ⎝⎛⨯-+． 【总结】本题主要是将特殊角的锐角三角比的值与实数运算结合在一起．【习题7】 ()131tan602sin 45-+︒+︒．【难度】★★【答案】32-【解析】 原式=32231233123112331-=-+-+-=++-+-．【总结】本题主要是将特殊角的锐角三角比的值与实数运算结合在一起．【习题8】在ABC ∆中，A ∠、C ∠均为锐角，若21sin cos 02A C ⎛-+= ⎝⎭，求B ∠的度数．【难度】★★ 【答案】︒=∠120B【解析】∵21sin cos 02A C ⎛-+= ⎝⎭， ∴023cos =-C ，0sin 21=-A ，解得：23cos =C ，21sin =A ． ∴︒=∠30C ，︒=∠30A ，∴︒=︒-︒-︒=∠1203030180B ．【总结】本题主要是对绝对值和平方的非负性和特殊角的锐角三角比的值的综合考查．【习题9】 已知ABC ∆中，60B ∠=︒，45C ∠=︒，BC = 20 cm ，求AC 的长．【难度】★★ 【答案】610230-【解析】解：过A 作AD ⊥BC ，垂足为D ．设x AD =． 在ABD Rt △中，60B ∠=︒，∴ 33cot ==AD BD B ，则x BD 33=；在ACD Rt △中，45C ∠=︒，∴ 1cot ==ADCDC ，则x CD =； ∵BC = 20 cm ，∴2033=+x x ，解得：31030-=x ．∴6102302-==x AB ．【总结】本题是对锐角三角比的直接运用，注意在运用锐角三角比时，要将锐角放在直角三角形中．ABC【习题10】 已知Rt ABC ∆中，90C ∠=︒，60A ∠=︒，2a b -=，求a 、b 、c 的值． 【难度】★★★【答案】33+=a ，13+=b ，232+=c 【解析】解：在ABC Rt △中，60A ∠=︒， ∴ 33cot ==a b A ，则b a 3=． ∵2a b -=，∴23=-b b ，解得：13+=b ，∴333+==b a ，2322+==b c ．【总结】本题是对特殊角锐角三角比的综合运用．【作业1】（1）若1cos 2α=，则α∠=______； （2）若tan 1β=，则β∠=______．【难度】★【答案】（1）60°；（2）45°．【解析】主要考查特殊角的锐角三角比的值．【作业2】()151α+︒=，则锐角α的度数是______．【难度】★ 【答案】15°()151α+︒=，∴()tan 15α+︒=，∴︒=︒+3015α，∴︒=15α． 【总结】本题主要考查特殊角的锐角三角比的值．【作业3】若225sin cos 304α+︒=，那么锐角α度数是（ ） A ．15°B ．30°C ．45°D ．60°【难度】★ 【答案】C【解析】∵225sin cos 304α+︒=，∴225sin 4α+=⎝⎭， ∴21sin 2α=，∴sin α=，∴︒=45α．【总结】本题主要考查特殊角的锐角三角比的值．课后作业【作业4】 下列等式中，成立的有（ ）① sin 30°+ sin 30°= sin 60°；②若cos A = sin B ，则=A B ∠∠；③若sin A = cos 30°，则锐角A = 60°； ④sin 60°+ sin 30° = 2（sin 30°+ cos 30°）．A ．0个B ．1个C ．2个D ．3个【难度】★★ 【答案】B【解析】①sin 30°+ sin 30°=12121=+，sin 60°=23，不成立； ②若cos A = sin B ，则+=90?A B ∠∠，所以②不成立； ③若sin A = cos 30°，则锐角A = 60°，成立； ④sin 60°+ sin 30° = 2132123+=+，2（sin 30°+ cos 30°）=3123212+=⎪⎪⎭⎫ ⎝⎛+，所以不成立． 【总结】本题主要考查特殊角的锐角三角比的值．【作业5】()12°121cot 3013sin 452-⨯-+-︒． 【难度】★★★ 【答案】3． 【解析】原式=)21112132⨯==．【总结】本题主要是将特殊角的锐角三角比的值与实数运算结合在一起．【作业6】 计算：sin 45cos45cos30cot 60tan 60︒+︒︒︒-︒．【难度】★★ 【答案】0．【解析】原式202+=+=+=． 【总结】本题主要是将特殊角的锐角三角比的值与实数运算结合在一起．【作业7】tan301tan30cot30︒-+︒-︒．【难度】★★【答案】332【解析】原式=︒-︒+-︒--︒30cot 30tan 130tan 160cot=332333331331=-+⎪⎪⎭⎫ ⎝⎛---． 【总结】本题主要是将特殊角的锐角三角比的值与实数运算结合在一起．【作业8】在ABC ∆中，A ∠、B ∠均是锐角，且2sin 0A +=，请判断ABC ∆的形状，并说明理由．【难度】★★【答案】等腰直角三角形【解析】∵2sin 0A ， ∴02sin 2=-A ，031cot 31=-B ，解得：22sin =A ，1cot =B ．∴︒=∠45A ，︒=∠45B ，∴ABC ∆为等腰直角三角形．【总结】本题主要是对绝对值和平方的非负性和特殊角的锐角三角比的值的综合考查．【作业9】已知Rt ABC ∆中，90C ∠=︒，45A ∠=︒，3c a -=，求a 、b 、c 的值．【难度】★★★【答案】323+=a ，323+=b ，236+=c 【解析】解：在ABC Rt △中， 22sin ==c a A ，则a c 2=． ∵3c a -=3a -=，解得：323+=a ，∴323+==a b ，2362+==a c ．【总结】本题是对特殊角锐角三角比的综合运用．【作业10】 应用锐角三角比的定义，求sin 22.5°、tan 22.5°、sin 67.5°、tan 67.5°．【难度】★★★【答案】2225.22sin +=︒，125.22tan -=︒，()4224225.67sin -+=︒， 125.67tan +=︒． 【解析】如图，作等腰△ABC ，且22.5B ACB ∠=∠=过点C 作CD ⊥BA 交BA 的延长线于点D ．则︒=∠5.22B ，67.5BCD ∠=︒．设x DC =，则x AB AC 2==，x DA =，()x x x BD CD BC 2242122222+=++=+=．在Rt △BDC 中， sin 22.5sin DC B BC ︒==== =； ()1212112tan 5.22tan -=+=+===︒x xBD DC B ；()()224224224122241222412sin 5.67sin -⋅+-+=++=++==∠=︒x x BC DB BCD ；()1212tan 5.67tan +=+==∠=︒x x CD DB BCD ． 【总结】在求非特殊角的锐角三角比的值时，想办法将其跟特殊角结合起来，再去求值． 2224222424822224224224224+=+=+=+=-⋅+-()()4224222222412-+=-+=。
锐角的三角比知识讲解
锐角的三角比 知识讲解【学习目标】1．结合图形理解记忆锐角三角函数的定义；2．会推算 30°、45°、 60°角的三角函数值，并熟练准确的记住特殊角的三角函数值； 3．理解并能熟练运用“同角三角函数的关系”及“锐角三角函数值随角度变化的规律”.【要点梳理】要点一、锐角三角函数的概念如图所示，在 Rt △ABC 中，∠ C ＝90°，∠ A 所对的边 BC 记为 a ，叫做∠ A 的对边，也叫做∠ B 的邻 边，∠ B 所对的边 AC 记为 b ，叫做∠ B 的对边，也是∠ A 的邻边，直角 C 所对的边 AB 记为 c ，叫做斜边．B 的邻边 a B 的对边 b要点诠释：(1) 正弦、余弦、正切、余切函数是在直角三角形中定义的，反映了直角三角形边与角的关系，是 两条线段的比值．角的度数确定时，其比值不变，角的度数变化时，比值也随之变化．(2) sinA ，cosA ，tanA ，cotA 分别是一个完整的数学符号， 是一个整体， 不能写成 ， ，， cot A 不能理解成 sin 与∠ A ，cos 与∠ A ，tan 与∠ A ，cot 与∠ A 的乘积．书写时习惯上省略 ∠A 的角的记号“∠”，但对三个大写字母表示成的角(如∠ AEF)，其正切应写成“ tan ∠AEF ”，不能写成“tanAEF ”；另外， 、 、 、(cot A )2常写成 、 、 、cot 2 A锐角 锐角 锐角 锐角 A 的对边与斜边的比叫做∠ A 的邻边与斜边的比叫做∠ A 的对边与邻边的比叫做∠ A 的邻边与对边的比叫做∠ 同理 sin BB 的对边斜边 b； ；A 的正弦，记作 A 的余弦，记作 A 的正切，记作 A 的余切，记作 cosBsinA ，cosA ， tanA ，cotA ，B 的邻边斜边即sin AA的对边斜边即 cosAA的邻边即A斜边即 tanA A的对边A 的邻边即 cotAA 的邻边A 的对边 a； ；tanBB 的对边 B 的邻边b；；ca；；bb；；b(3) 任何一个锐角都有相应的锐角三角函数值，不因这个角不在某个三角形中而不存在．(4) 由锐角三角函数的定义知：当角度在0°<∠ A<90°间变化时，，，tanA >0 cotA >0.要点二、特殊角的三角函数值304560(1) 通过该表可以方便地知道30°、45°、60°角的各三角函数值，它的另一个应用就是：如果知道了一个锐角的三角函数值，就可以求出这个锐角的度数，例如：若，则锐角．(2) 仔细研究表中数值的规律会发现：、、的值依次为、、，而、、的值的顺序正好相反，、、的值依次增大，其变化规律可以总结为：①正弦、正切值随锐角度数的增大( 或减小) 而增大( 或减小)②余弦、余切值随锐角度数的增大( 或减小) 而减小( 或增大) ．要点三、锐角三角函数之间的关系如图所示，在Rt △ABC中，∠ C=90°．(1) 互余关系：，；tanA=cot(90 °- ∠A)=cotB , tanB=cot(90 °-∠ B)=cotA.(2) 平方关系：；(3) 倒数关系：或；(4) 商的关系：sin A cosA tanA ,cot AcosA sin A要点诠释：锐角三角函数之间的关系式可由锐角三角函数的意义推导得出，常应用在三角函数的计算中，计算时巧用这些关系式可使运算简便．答案】 c = 5 ，sinA = 35 cosA 4，5sinB = 4，5cosB = 35类型二、特殊角的三角函数值的计算求下列各式的值：(1)sin30 -2cos60 ° +cot45 °；(2) tan 30° sin 30 °cot 45° tan 60°11；(3) (1 3)0|1 sin30°| 12．【典型例题】类型一、锐角三角函数值的求解策略1．如图所示，在Rt△ ABC中，∠ C＝90°，AB＝13，BC＝5，求∠ A，∠ B的正弦、余弦、正切、余切值．答案与解析】在Rt△ABC中，∠ C＝90∵ AB ＝13，BC＝5．AC AB2BC21325212．BC5，AC12，tanA BC5，cot A AC12sin A cosAAB13AB13AC12BC5AC12BC5tanB AC12cot B BC5sin B cosBAB13，AB13，BC5，AC12【总结升华】先运用勾股定理求出另一条直角边，再运用锐角三角函数的定义求值．举一反三：变式】在Rt △ABC中，∠C90 °，若a=3，b=4，则c =sinA = ，cosA =，sinB =cosBBA caC b答案与解析】2．111(1) 原式 2 1 ；222311(2) 原式 3 2 1 ；1363． (1)求锐角 ； (2) 已知 求锐角 ．【答案与解析】(1) 先将已知方程变形后再求解．∴锐角 =30°．(2) 先将已知方程因式分解变形．(3)1原式 1 1215 21125 22总结升华】 熟记特殊角的三角函数值或借助两个三角板推算三角函数值， 再进行化简．先代入特殊角的三角函数值，举一反三：变式】 在 Rt △ABC 中， ∠C = 90 °，若∠ A=45°，则 ∠B =答案】类型三 sinA = ， cosA = ∠B =45°，sinA = 2 ，2锐角三角函数之间的关系， sinB =cosB =cosA = 2 ，sinB = 2 ， 22cosB = 22∴锐角 =45总结升华】 要求等式中的锐角，只需求得这个角的三角函数值，运用换元的方法，把角的三角函数看 作未知数，解方程求得它的解 ( 值) ，然后再求这个锐角．类型四、 锐角三角函数的拓展探究与应用4．如图所示， AB 是⊙ O 的直径，且 AB ＝10， CD 是⊙ O 的弦， AD 与 BC 相交于点 P ，若弦 CD ＝6，试求 cos ∠ APC 的值．答案与解析】 连结 AC ，∵ AB 是⊙ O 的直径， ∴ ∠ ACP ＝ 90°，又∵ ∠B ＝∠ D ，∠ PAB ＝∠ PCD ， ∴ △ PCD ∽△ PAB ，∴PC CDPA AB ．又∵ CD ＝6， AB ＝10， ∴在 Rt △ PAC 中，PC cos APCPA总结升华】 直角三角形中，锐角的三角函数等于两边的比值，当这个比值无法直接求解，可结合相似 三角形的性质，利用对应线段成比例转换，间接地求出这个比值．锐角的三角函数是针对直角三角形而PC言的，故可连结 AC ，由 AB 是⊙ O 的直径得∠ ACB ＝90°， cos APC，PC 、PA 均为未知，而已知PAPC CDCD ＝ 6， AB ＝ 10，可考虑利用△ PCD ∽△ PAB 得．PA AB5．通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，可以在等腰三角形中建立边角之间的联系．我们 定义：等腰三角形中底边与腰的比叫做顶角的正对 (sad) ．如图 1①，在△ ABC 中， AB ＝AC ，顶角 A 的正底边 BC对记作 sadA ，这时 sadA ．容易知道一个角的大小与这个角的正对值也是相互唯一确定 腰 AB 的．根据上述角的正对定义，解下列问题：(1)sad60 °＝ ________ ．(2) 对于 0< A < 180°，∠ A 的正对值 sadA 的取值范围是 ______3(3) 如图 1②，已知 sinA ＝ ，其中∠ A 为锐角，试求 sadA 的值．5CDAB 10答案与解析】(1)1 ；(2)0 < sadA<2；(3) 如图 2 所示，延长AC到D，使AD＝AB，连接BD．设AD＝AB＝5a，由sin A BC 3得BC＝3a，AB 5∴ AC (5a)2(3a)24a ，CD ＝5a-4a ＝a，BD a (3a) 10a ，sadA A BD D 510总结升华】(1) 将60°角放在等腰三角形中，底边和腰相等，故的长固定，并固定AB让AC绕点A旋转，当∠ A接近0°sadA＝1；(2) 在图①中设想AB＝AC 时，BC接近0，则sadA接近0但永远不会等于0，故sadA> 0，当∠ A接近180°时，BC接近2AB，则sadA接近2但小于2，故sadA<2；(3) 将∠ A放到等腰三角形中，如图2所示，根据定义可求解．。
初三锐角的三角比
一、 锐角三角比的意义 1、正切直角三角形中一个锐角的对边与邻边的比叫做这个锐角的正切（tangent ）．锐角A 的正切记作tan A ．tan A BC aA A AC b ===锐角的对边锐角的邻边． 2、余切直角三角形中一个锐角的邻边与对边的比叫做这个锐角的余切（cotangent ）．锐角A的余切记作cot A ．cot A AC bA A BC a ===锐角的邻边锐角的对边． 3、正弦直角三角形中一个锐角的对边与斜边的比叫做这个锐角的正弦（sine ）．锐角A 的正弦记作sin A ．sin A BC aA AB c ===锐角的对边斜边． 4、余弦直角三角形中一个锐角的邻边与斜边的比叫做这个锐角的余弦（cosine ）．锐角A 的余弦记作cos A ．cos A AC bA AB c===锐角的邻边斜边．5、锐角的三角比一个锐角的正切、余切、正弦、余弦统称为这个锐角的三角比．锐角的三角比一：锐角的三角比ACBD二、 特殊锐角的三角比的值αtan αcot αsin αcos α30°33312 32 45° 1 1 22 2260° 3333212【例1】 已知Rt ABC ∆中，90C ∠=︒，那么ba是角A 的（ ） A ．正弦B ．余弦C ．正切D ．余切【例2】 已知Rt ABC ∆中，90C ∠=︒，AC = 3，BC = 4，那么sin A =______．【例3】 已知α为锐角，且5sin 13α=，求α的余弦值．【例4】 求值：sin60tan30cot30︒-︒+︒=_______．【例5】 已知锐角ABC ∆中，3sin A ，tan 1B =，那么C ∠=______°．【例6】 将锐角α所在的三角形的三边同时扩大三倍，这时角α的正弦值（ ） A ．变大B ．变小C ．不变D ．无法确定【例7】 （2014学年·松江区二模·第6题）如图，在Rt ABC ∆中，90ACB ∠=︒，CD ⊥AB ，垂足为D ，AB = c ，A α∠=，则CD 长为（ ）A ．2sin c αB ．2cos c αC ．sin tan c ααD ．sin cos c αα仰角 视线水平线视线俯角铅垂线北北偏东30°南偏西45°北偏西70°南偏东50°30° 70° 45° 50°【例8】 （2015学年·徐汇区二模·第19题）计算：20(3)cot 30tan 4531ππ--︒-︒+．【例9】 （2015学年·普陀区二模·第19题）计算：22123323tan 601-⎛⎫-+- ⎪︒-⎝⎭．一、 解直角三角形在直角三角形中，由已知元素求出所有未知元素的过程，叫做解直角三角形． 在t R ABC ∆中，如果=90C ∠︒，那么它的三条边和两个锐角之间有以下的关系： （1）三边之间的关系：222a b c +=（2）锐角之间的关系：90A B ∠+∠=︒（3）边角之间的关系：sin cos a A B c ==，cos sin bA B c ==tan cot a A B b ==，cot tan b A B a== 二、 仰角与俯角在测量过程中，常常会遇到仰角和俯角．如图，当我们进行测量时，在视线与水平线 所成的角中，视线在水平线上方的角叫做仰角，视线在水平线下方的角叫做俯角．三、 方向角指北或指南方向线与目标方向线所成的小于90°的角叫做方向角． 如图：北偏东30°，北偏西70°，南偏东50°，南偏西45°．二：解直角三角形ABC D A B9米传送带AB Chl四、 坡度（坡比）、坡角在修路、挖河、开渠等设计图纸上，都需要注明斜坡的倾斜程度．如图，坡面的铅垂高度h 和水平宽度l 的比叫做坡面的坡度（或坡比），记作i ，即h i l=． 坡度通常写成1 : m 的形式，如1:1.5i =． 坡面与水平面的夹角叫做坡角，记作α．坡度i 与坡角α之间的关系：tan hi l α==．【例10】 （2015学年·崇明县二模·第15题）已知一斜坡的坡比为1 : 2，坡角为α，那么sin α=______．【例11】 （2014学年·长宁区二模·第15题）已知在离地面30米的高楼窗台A 处测得地面花坛中心标志物C 的俯角为60°，那么这一标志物C 离此栋楼房的地面距离BC 为______米．【例12】 （2015学年·浦东新区二模·第13题）如图，传送带和地面所成的斜坡的坡度为39米高的地方，则物体从A 到B 所经过的路程为______米．【例13】 （2015学年·宝山区、嘉定区二模·第16题）如图，如果在大厦AB 所在的平地上选择一点C ，测得大厦顶端A 的仰角为30°，然后向大厦方向前进40米，到达点D 处（C 、D 、B 三点在同一直线上），此时测得大厦顶端A 的仰角为45°．那么大厦AB 的高度为______米．（保留根号）ABCE ABCDABCDEABCD EFAB C北【例14】 （2014学年·浦东新区二模·第16题）如图，已知小岛B 在基地A 的南偏东30°方向上，与基地A 相距10海里，货轮C 在基地A 的南偏西60°方向、小岛B 的北偏西75°方向上，那么货轮C 与小岛B 的距离是______海里．【例15】 （2014学年·徐汇区二模·第22题）如图，在Rt ABC ∆中，90CAB ∠=︒，3sin 5C =，AC = 6，BD 平分CBA ∠交AC 边于点D ．求：（1）线段AB 的长；（2）tan DBA ∠的值．【例16】 （2014学年·闸北区二模·第21题）已知：如图，点E 是矩形ABCD 的边AD 上一点，BE = AD ，AE = 8，现有甲乙二人同时从E 点出发，分别沿EC 、ED 方向前进，10C 点的同时乙恰巧到达终点D 处．（1）求tan ECD ∠的值； （2）求线段AB 及BC 的长度．【例17】 （2014学年·闵行区二模·第21题）如图，已知在ABC ∆中，25AB AC ==25sin B ∠=D 为边BC 的中点．E 为边BC 延长线上一点，且CE = BC ．联结AE ，F 为线段AE 的中点．求：（1）线段DF 的长；（2）CAE ∠的正切值．【例18】 （2015学年·闸北区二模·第21题）已知：如图，在ABC ∆中，45ABC ∠=︒，AD是BC 边上的中线，过点D 作DE ⊥AB 于点E ，且3sin 5DAB ∠=，32DB =求：（1）AB 的长；（2）CAB ∠的余切值．ABCDPABCD【例19】 （2015学年·松江区二模·第22题）如图，在ABC ∆中，AB = AC = 10，BC = 12，AD ⊥BC 于D ，O 为AD 上一点，以O 为圆心，OA 为半径的圆交AB 于G ，交BC 于E 、F ，且AG = AD ．（1）求EF 的长； （2）求tan BDG ∠的值．【例20】 （2015学年·普陀区二模·第21题）已知：如图，在ABC ∆中，AB = AC = 13，BC = 24，点P 、D 分别在边BC 、AC 上，2AP AD AB =，求APD ∠的正弦值．【例21】 （2015学年·虹口区二模·第21题）如图，在ABC ∆中，CD 是边AB 上的中线，B∠是锐角，且2sin 2B =，1tan 2A =，BC =22，求边AB 的长和cos CDB ∠的值．【例22】 （2014学年·崇明县二模·第21题）在Rt ABC ∆中，90BAC ∠=︒，点E 是BC 的中点，AD ⊥BC ，垂足为点D ．已知AC = 9，3cos 5C =．（1）求线段AE 的长；（2）求sin DAE ∠的值．【例23】 （2015学年·崇明县二模·第22题）如图，在某海滨城市O 附近海面有一股台风，据监测，当前台风中心位于该城市的南偏东20°方向200千米的海面P 处，并以20千米/时的速度向P 处的北偏西65°PQ 的方向移动，台风侵袭范围是一个圆形区域，当前半径为60千米，且圆的半径以10千米/时速度不断扩张．（1）当台风中心移动4小时时，受台风侵袭的圆形区域半径增大到 千米；O CBADF EG CA BEDOPQ北当台风中心移动t 小时时，受台风侵袭的圆形区域半径增大到 千米；（2）当台风中心移动到与城市O 距离最近时，这股台风是否侵袭这座海滨城市？请说明理由．（参考数据2 1.41=，3 1.73=）．【例24】 （2015学年·闵行区二模·第22题）如图，山区某教学楼后面紧邻着一个土坡，坡面BC 平行于地面AD ，斜坡AB 的坡比为51:12i =，且AB = 26米．为了防止山体滑坡，保障安全，学校决定对该土坡进行改造．经地质人员勘测，当坡角不超过53°时，可确保山体不滑坡．（1）求改造前坡顶与地面的距离BE 的长；（2）为了消除安全隐患，学校计划将斜坡AB 改造成AF （如图所示），那么BF 至少是多少米？（结果精确到1米）（参考数据：sin530.8︒≈，cos530.6︒≈，tan53 1.33︒≈，cot530.75︒≈）【例25】 （2014学年·普陀区二模·第22题）本市为了给市容营造温馨和谐的夜间景观，准备在一条宽7.4米的道路上空利用轻轨桥墩，安装呈大中小三个同心圆的景观灯ABDCEF带（如图1所示）．如图2，已知EF 表示路面宽度，轻轨桥墩的下方为等腰梯形ABCD ，且AD // EF ，AB = DC ，37ABC ∠=︒．在轻轨桥墩上设有两处限高标志，分别表示等腰梯形的下底边到路面的距离为 2.9米和等腰梯形的上底边到路面的距离为 3.8米．大圆直径等于AD ，三圆半径的比等于1 : 2 : 3．试求这三个圆形灯带的总长为多少米？（结果保留π）（参考数据：sin370.6︒≈，cos370.8︒≈，tan370.75︒≈）2.92.93.8ABCDFO图1图2。