高三数学周周练(5)
高三数学下学期第5周周练试题理(2021学年)

江西省横峰县2017届高三数学下学期第5周周练试题理编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(江西省横峰县2017届高三数学下学期第5周周练试题理)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为江西省横峰县2017届高三数学下学期第5周周练试题理的全部内容。
江西省横峰县2017届高三数学下学期第5周周练试题 理一、选择题: 1、设方程1|ln |2=x x 有两个不等的实根和,则( )A.B .C.D.2、已知双曲线C 的中心在原点,焦点在y 轴上,若双曲线C 的一条渐近线与直线340x y +-=平行,则双曲线C 的离心率为( ) A.233B.2 C。
3 D.2 3、设()[)[]221,1,11,1,2x x f x x x ⎧-∈-⎪=⎨-∈⎪⎩,则()21f x dx -=⎰的值为( )A 。
423π+ B. 32π+ C 。
443π+ D 。
34π+ 4、已知椭圆)0(1:2222>>=+b a b y a x C 的离心率为23,过右焦点F且斜率为)0(>k k 的直线与C 相交于A、B 两点,若FB AF 3=,则k =( ) A、1 B 2 C、3 D 、2 5、方程22200720071sin(19)cos(19)x y +=所表示的曲线是( )A .双曲线B .焦点在x 轴上的椭圆 C.焦点在y 轴上的椭圆 D .以上都不对6、抛物线)0(2:21>=p py x C 的焦点与双曲线13:222=-y x C 的右焦点的连线交1C 于第一象限的 点.若1C 在点M 处的切线平行于2C 的一条渐近线,则=p ( )A 。
2021年高三周练(5)数学理试题 含答案

2021年高三周练(5)数学理试题含答案参考公式:圆锥的侧面积公式,其中是圆锥的底面半径,是圆锥的母线长.一、选择题1.设集合,,则().A. B. C. D.2.已知,则().A. B. C. D.3.设,则“”是“直线与直线平行”的().A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.一个几何体的三视图如图所示,其中正视图与侧视图都是底边长为6、腰长为5的等腰三角形,则这个几何体的全面积为().A. B.C. D.5.在△ABC中,,,则△ABC的面积为().A.3B.4C.6D.6.函数的零点所在的一个区间是().A. B. C. D.7.若双曲线的渐近线与圆相切,则双曲线的离心率为().A. B. C.2 D.8.若过点的直线与曲线和都相切,则的值为( ). A.2或 B.3或 C.2 D.二、填空题(一)必做题(9~13题)9.若复数满足,则复数的实部是 . 10.的展开式中的常数项是 .(用数字作答) 11.执行如图所示的程序框图,则输出的S 的值是 . 12.已知实数满足,则的最大值是 .13.在区间上随机取一个数,在区间上随机取一个数, 则关于的方程有实根的概率是 .(二)选做题(14~15题,考生只能从中选做一题) 14.(几何证明选讲选做题)如图,AB 为⊙O 的直径,弦AC 、BD 相交于点P ,若, ,则的值为 .15.(坐标系与参数方程选做题)已知曲线C 的参数方程是(为参数),以直角坐标系的原点O 为极点,轴的正半轴为极轴,并取相同的长度单位建立极坐标系,则曲线C 的极坐标方程是 . 三、解答题16.已知函数()sin()(0,0,0)f x A x A ωϕωϕπ=+>><<,的最大值是1,最小正周期是,其图像经过点.(1)求的解析式; (2)设、、为△ABC 的三个内角,且,,求的值.17.某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的50位顾客的相关数据,如下表所示:一次购物量(件) 1≤n ≤34≤n ≤6 7≤n ≤9 10≤n ≤12n ≥13 顾客数(人)20105结算时间(分钟/人)0.5 1 1.5 2 2.5 已知这50位顾客中一次购物量少于10件的顾客占80%.(1)确定与的值;(2)若将频率视为概率,求顾客一次购物的结算时间的分布列与数学期望;(3)在(2)的条件下,若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过...2分钟的概率.18.如图,菱形的边长为4,,.将菱形沿对角线折起,得到三棱锥,点是棱的中点,.(1)求证:平面;(2)求证:平面平面;(3)求二面角的余弦值.19.(本小题满分14分)已知函数.(1)是否存在点,使得函数的图像上任意一点P关于点M对称的点Q也在函数的图像上?若存在,求出点M的坐标;若不存在,请说明理由;(2)定义2111221()()()()n n i i n S f f f f n n n n-=-==++⋅⋅⋅+∑,其中,求; (3)在(2)的条件下,令,若不等式对且恒成立,求实数的取值范围.高三理科数学周练卷(5)答案 2013-09-14二、填空题9.1 10. 11. 12. 13. 14. 15. 三、解答题16.(1)依题意得.由,解得.所以.因为函数的图像经过点,所以,即. 因为,所以.所以. (2)由(1)得,所以,.因为,所以,.因为为△ABC 的三个内角,所以()cos cos[()]cos()f C C A B A B π==-+=-+ .17.(1)依题意得,,,解得,.(2)该超市所有顾客一次购物的结算时间组成一个总体,所以收集的50位顾客一次购物的结算时间可视为总体的一个容量为50的随机样本,将频率视为概率得, ,,, ,.所以的分布列为的数学期望为.(3)记“该顾客结算前的等候时间不超过2分钟”为事件A ,该顾客前面第位顾客的结算时间为,由于各顾客的结算相互独立,且的分布列都与的分布列相同,所以121212()(0.5(0.5)(0.5(1)(0.5( 1.5)P A P X P X P X P X P X P X ==⋅=+=⋅=+=⋅=)))121212(1(0.5)(1(1)( 1.5(0.5)P X P X P X P X P X P X +=⋅=+=⋅=+=⋅=)))0.20.20.20.40.20.20.40.20.40.40.20.20.44=⨯+⨯+⨯+⨯+⨯+⨯= 为所求.18.(1)因为O 为AC 的中点,M 为BC 的中点,所以.因为平面ABD ,平面ABD ,所以平面.(2)因为在菱形ABCD 中,,所以在三棱锥中,.在菱形ABCD 中,AB =AD =4,,所以BD =4.因为O 为BD 的中点, 所以.因为O 为AC 的中点,M 为BC 的中点,所以.因为,所以,即.因为平面ABC ,平面ABC ,,所以平面ABC . 因为平面DOM ,所以平面平面.(3)作于,连结DE .由(2)知,平面ABC ,所以AB .因为,所以平面ODE .因为平面ODE ,所以. 所以是二面角的平面角.在Rt △DOE 中,,,,所以.所以二面角的余弦值为.19.(1)假设存在点,使得函数的图像上任意一点P 关于点M 对称的点Q 也在函数的图像上,则函数图像的对称中心为. 由,得,即对恒成立,所以解得所以存在点,使得函数的图像上任意一点关于点M 对称的点也在函数的图像上. (2)由(1)得.令,则.因为1221()()(2)(2)n S f f f f n n nn=++⋅⋅⋅+-+-①, 所以1221(2)(2)()()n S f f f f n n n n=-+-+⋅⋅⋅++②,由①+②得,所以.所以.(3)由(2)得,所以.因为当且时,2()121ln ln 2n amnmn n ma n n ⋅>⇔⋅>⇔>-. 所以当且时,不等式恒成立. 设,则. 当时,,在上单调递减; 当时,,在上单调递增. 因为,所以, 所以当且时,. 由,得,解得.所以实数的取值范围是.深圳市高级中学xx 届第一次月考数学(理)试题注:请将答案填在答题卷...........相应的位置.....上.一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合要求的.1. 已知全集,集合,则A. B. C. D.2. 如果函数上单调递减,则实数满足的条件是 A . B . C . D .3. 下列函数中,满足的是 A . B . C . D .4. 已知函数,下面结论错误..的是A .函数的最小正周期为B .函数是偶函数C .函数的图象关于直线对称D .函数在区间上是增函数 5. 给出如下四个命题:①若“且”为假命题,则、均为假命题; ②命题“若且,则”的否命题为“若且,则”; ③在中,“”是“”的充要条件。
2021-2022年高三上学期第五次周练数学试题 含答案

2021年高三上学期第五次周练数学试题 含答案一、选择题1.已知人订合}0|{},1|{>=<=x x N x x M ,则M ∩N=A .B .C .D .2.复数,则复数在复平面内对应的点位于:A .第一象限B .第二象限C .第三象限D .第四象限3.公差不为零的等差数列的第二、三、六项依次成等比数列,则公比是:A .2B .3C .4D .54.过抛物线的焦点作直线交抛物线于A 、B 两点,若线段AB 中点的横坐标为3则|AB|等于:A .2B .4C .8D .165.如图1,一个空间几何体的主视图、左视图都是边长为1且一个内角为60°的菱形,俯视图是圆,那么这个几何体的表面积为:A .B .C .D .6.P 是所在平面内一点,若⋅=⋅=⋅,则P 是的:A .外心B .垂心C .重心D .内心7.函数)1,0(23≠>-=+a a a y x 且的图象恒过定点A ,且点A 在直线上,则的最小值为:A .12B .10C .8D .148.函数),2||.0,0()sin(R x A B x A y ∈<>>++=πϕωϕω的部分图象如图2所示,则函数表达式为: ( )A .B .C .D .9.四名男生三名女生排成一排照相,则三名女生有且仅有两名相邻的排法数有:A . 3600B .3200C .3080D .288010.函数时,下列式子大小关系正确的是:A .C .D .11.数列中,,且)()!1(1++∈++=N n n na a n n ,则为:A .B .C .D .12.已知是R 上的偶函数,若的图象向右平移一个单位后,则得到一个奇函数的图象,则的值为:A .1B .0C .-1D .二、填空题13.若对任意实数都有33323241505)2(y x a y x a y x a x a y x +++=-,则=+++++543210a a a a a a 。
【高三】高三数学第5周周训练题

【关键字】高三宜宾市一中高三上期周训练(五)姓名:_______ 班级:_________ 成绩:________一:选择题(共48分,每小题6分)1.在中,,则的面积为()A.B.或C.或D.2.在△ABC中,角A,B,C的对边分别是a,b,c.已知a=5,c=10,A=30°,则B等于()A.105° B.60° C.15° D.105°或15°3.制作一个面积为,形状为直角三角形的铁架框,有下列四种长度的铁管供选择,较经济的(够用,又耗材最少)是()A.B.C.D.4.在中,若,则的形状是()A.直角三角形B.等边三角形C.等腰三角形D.不能确定5.已知在中,角所对的边分别为,若,则()6.已知的内角所对应的边分别为,且面积为6,周长为12,,则边为()A.B.C.D.7.已知为的三个角所对的边,若,则()A.2:3 B.4:.3:1 D.3:28.若为所在平面内一点,且满足,则的形状为()A.等边三角形B.直角三角形C.等腰三角形D.等腰直角三角形2、填空题(24分,每小题6分)9.在△ABC中,已知sinA∶sinB∶sinC=3∶5∶7,则此三角形的最大内角的度数等于________.10.如图,为测量出山高,选择和另一座山的山顶为测量观测点,从点测得点的仰角点的仰角以及,从点测得,已知山高,则山高.11.在△中,,,分别是,,的对边长,已知,且,则实数.12.给出四个命题:(1)若,则为等腰三角形;(2)若,则为直角三角形;(3)若,则为钝角三角形;(4)若,则为正三角形,以上正确命题的是.三、解答题(本大题共2小题,每小题14分,共28分)13.在中,角的对边分别为,已知向量与向量互相垂直.(1)求角;(2)求的取值范围.参考答案一:选择题(共48分,每小题6分)1.B 2.D 3 .C 4.C 5.A 6.C 7.C 8.C2、填空题(24分,每小题6分)9..10.11.12.(3)(4)三、解答题(本大题共2小题,每小题14分,共28分)13.【答案】(1);(2).试题解析:(1)由已知可得,,所以;所以的取值范围是.14.【答案】(1)(2)试题解析:(1)由余弦定理,得,∴(2)∵∴,由正弦定理,,考点:正余弦定理解三角形此文档是由网络收集并进行重新排版整理.word可编辑版本!。
高三数学周周练(含答案)

高三数学周周练2018.9一、填空题(本大题共14小题,每小题5分,共计70分.不需要写出解答过程,请将答案填写在答题卡相应得位置上..........) 1.设集合A ={﹣1,0,1},B ={0,1,2,3},则A B = .2.若复数12miz i-=+(i 为虚数单位)得模等于1,则正数m 得值为 . 3.命题“(0x ∀∈,)2π,sin x <1”得否定就是 命题(填“真”或“假”).4.已知1sin 4α=,(2πα∈,)π,则tan α= . 5.函数()sin(2)sin(2)33f x x x ππ=-++得最小正周期为 .6.函数2()log f x x =在点A(2,1)处切线得斜率为 .7.将函数sin(2)6y x π=+得图像向右平移ϕ(02πϕ<<)个单位后,得到函数()f x 得图像,若函数()f x 就是偶函数,则ϕ得值等于 .8.设函数240()30x x f x x x ⎧->=⎨--<⎩,,,若()(1)f a f >,则实数a 得取值范围就是 .9.已知函数2()f x x =,()lg g x x =,若有()()f a g b =,则b 得取值范围就是 .10.已知函数322()7f x x ax bx a a =++--在1x =处取得极小值10,则ba得值为 .11.已知函数()sin ([0f x x x =∈,])π与函数1()tan 2g x x =得图像交于A,B,C 三点,则△ABC 得面积为 .12.已知210()ln 0x x f x x x +≤⎧⎪=⎨>⎪⎩,,,则方程[()]3f f x =得根得个数就是 .13.在△ABC 中,若tanA =2tanB,2213a b c -=,则c = .14.设函数2()x af x e e=-,若()f x 在区间(﹣1,3﹣a )内得图像上存在两点,在这两点处得切线相互垂直,则实数a 得取值范围就是 .二、解答题(本大题共6小题,共计90分.请在答题纸指定区域.......内作答,解答应写出文字说明,证明过程或演算步骤.) 15.(本题满分14分)已知函数2()cos cos f x x x x =-.(1)求()f x 得最小正周期; (2)若()1f x =-,求2cos(2)3x π-得值. 16.(本题满分14分)已知a ,b ,c 分别为△ABC 三个内角A,B,C 得对边,且满足cos B sin C b =+.(1)求∠C 得值;(2)若c =求2a +b 得最大值. 17.(本题满分14分)已知函数()33()xxf x R λλ-=+⋅∈.(1)当1λ=时,试判断函数()33xxf x λ-=+⋅得奇偶性,并证明您得结论; (2)若不等式()6f x ≤在[0x ∈,2]上恒成立,求实数λ得取值范围. 18.(本题满分16分)如图,在C 城周边已有两条公路l 1,l 2在点O 处交汇,现规划在公路l 1,l 2上分别选择A,B两处为交汇点(异于点O)直接修建一条公路通过C 城,已知OC =)km ,∠AOB =75°,∠AOC =45°,设OA =x km,OB =y km.(1)求y 关于x 得函数关系式并指出它得定义域; (2)试确定点A 、B 得位置,使△ABO 得面积最小.19.(本题满分16分)已知函数2()2ln ()f x x x a x a R =-+∈.(1)当a =2时,求函数()f x 在(1,(1)f )处得切线方程 ; (2)求函数()f x 得单调区间;(3)若函数()f x 有两个极值点1x ,2x (1x <2x ),不等式12()f x mx ≥恒成立,求实数m 得取值范围. 20.(本题满分16分)给出定义在(0,+∞)上得两个函数2()ln f x x a x =-,()g x x a x =-(1)若()f x 在1x =处取最值,求a 得值;(2)若函数2()()()h x f x g x =+在区间(0,1]上单调递减,求实数a 得取值范围; (3)试确定函数()()()6m x f x g x =--得零点个数,并说明理由.附加题21.(本题满分10分)已知矩阵2A=4⎡⎢-⎣ 13-⎤⎥⎦,4B=3⎡⎢-⎣ 11-⎤⎥⎦,求满足AX =B 得二阶矩阵X.22.(本题满分10分)在如图所示得四棱锥S —ABCD 中,SA ⊥底面ABCD,∠DAB =∠ABC =90°,SA =AB =BC =a ,AD =3a (a >0),E 为线段BS 上得一个动点.(1)证明:DE 与SC 不可能垂直;(2)当点E 为线段BS 得三等分点(靠近B)时,求二面角S —CD —E 得余弦值.23.(本题满分10分)某公司对新招聘得员工张某进行综合能力测试,共设置了A,B,C 三个测试项目.假定张某通过项目A 得概率为12,通过项目B 、C 得概率均为a (0<a <1),且这三个测试项目能否通过相互独立.用随机变量X 表示张某在测试中通过得项目个数,求X 得概率分布与数学期望E(X)(用a 表示). 24.(本题满分10分)在集合A ={1,2,3,4,…,2n}中,任取m(m ≤n,m,n N *∈)个元素构成集合A m .若A m 得所有元素之与为偶数,则称A m 为A 得偶子集,其个数记为()f m ;A m 得所有元素之与为奇数,则称A m 为A 得奇子集,其个数记为()g m .令()()()F m f m g m =-.(1)当n =2时,求(1)F ,(2)F ,(3)F 得值; (2)求()F m .参考答案1.{0,1}2.23.假4.15155.π6.12ln 27.3π8.(-∞,1)(1-,)+∞9.[1,)+∞10.12-11.34π 12.5 13.1 14.1(2-,1)215.(1)π,(2)12-. 16.(1)3π,(2)47. 17.(1)偶函数,(2)27λ≤-. 18.19.20.21.22.23.24.。
2013届高三数学周周练五(学生版)2012.11.10

高三数学周周练五2012.9.16
考试范围:集合与简易逻辑、函数与导数、三角与向量、立体几何
考试时间:120分钟;命题人:缪建中
一、填空题
1.已知集合 , ,则 ( ) ______.
2.设 为两个不重合的平面, 为两条不重合的直线,给出下列四个命题:
①若 则 ∥ ;②若 则 ;
(1)写出体积V关于 的函数关系式;
(2)当 为何值时,才能使做出的圆柱形罐子体积V最大?
19.(本小题满分16分)设二次函数 满足条件:①当 时, ,且 ;② 在 上的最小值为 .
(1)求 的值及 的解析式;
(2)若 在 上是单调函数,求 的取值范围;
(3)求最大值 ,使得存在 ,只要 ,就有 .
10.若关于x的方程 上有解,则实数a的取值范围为
.
11.在 中,过中线 中点 任作一直线分别交 于 两点,设 ,则 的最小值是.
12.已知扇形的圆心角为 (定值),半径为 (定值),分别按图一、二作扇形的内接矩形,若按图一作出的矩形面积的最大值为 ,则按图二作出的矩形面积的最大值为.
13.如右图,在直角梯形 中, , , , ,点 是梯形 内(包括边界)的一个动点,点 是 边的中点,则 的最大值是.
(1)若 ,求向量 的夹角的余弦值;
(2)若 ,在AC上确定一点D的位置,使得 达到最小,并求出最小值.
17.(本小题满分14分)在三棱柱 中,侧棱 ,点 是 的中点, .
(1)求证: ∥平面 ;
(2) 为棱 的中点,试证明: .
18.(本小题满分16矩形材料OABC,其中点B在圆弧上,点A、C在两半径上,现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长 ,圆柱的体积为 .
2022-2023学年高三下学期周考数学试题
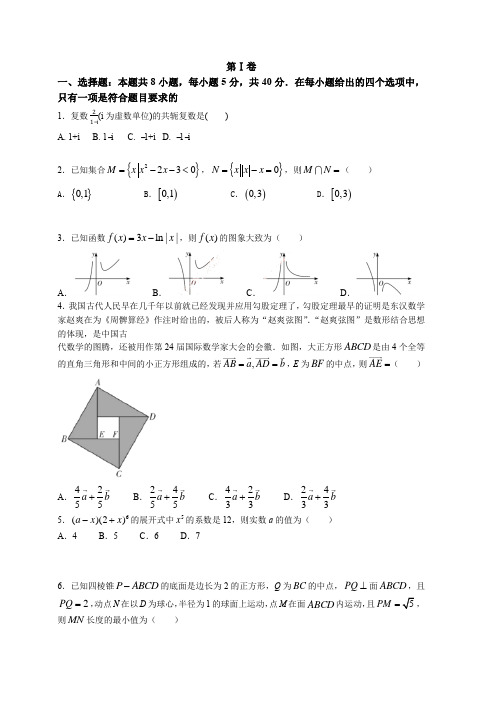
第Ⅰ卷一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.复数 21−i(i 为虚数单位)的共轭复数是( )A. 1+iB. 1−iC. −1+iD. −1−i2.已知集合{}2230M x x x =--<,{}0N x x x =-=,则M N =( )A .{}0,1B .[)0,1C .()0,3D .[)0,33.已知函数()3ln ||f x x x =-,则()f x 的图象大致为( )A .B .C .D .4.我国古代人民早在几千年以前就已经发现并应用勾股定理了,勾股定理最早的证明是东汉数学家赵爽在为《周髀算经》作注时给出的,被后人称为“赵爽弦图”.“赵爽弦图”是数形结合思想的体现,是中国古代数学的图腾,还被用作第24届国际数学家大会的会徽.如图,大正方形ABCD 是由4个全等的直角三角形和中间的小正方形组成的,若,AB a AD b ==,E 为BF 的中点,则AE =( )A .4255a b + B .2455a b + C .4233a b + D .2433a b + 5.6()(2)a x x -+的展开式中5x 的系数是12,则实数a 的值为( ) A .4 B .5 C .6 D .76.已知四棱锥P ABCD -的底面是边长为2的正方形,Q 为BC 的中点,PQ ⊥面ABCD ,且2PQ =,动点N 在以D 为球心,半径为1的球面上运动,点M 在面ABCD 内运动,且5PM =,则MN 长度的最小值为( )A 352B .23-C 52D 332- 7.设1sin 819,e 1,ln 47a b c ==-=,e 为自然对数的底数,则( )A .a b c >>B .a c b >>C .c a b >>D .b c a >>8.已知函数213()3sin sin 0)222xf x x ωωω=+->,若()f x 在3,22ππ⎛⎫⎪⎝⎭上无零点,则ω的取值范围是( ) A .280,,99⎛⎤⎡⎫+∞ ⎪⎥⎢⎝⎦⎣⎭ B .2280,,939⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦ C .280,,199⎛⎤⎡⎤⎥⎢⎥⎝⎦⎣⎦D .28,[1,)99⎛⎤+∞ ⎥⎝⎦二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.9.已知正方体1111ABCD A B C D -的棱长为1,点P 是棱1CC 上的一个动点(包含端点),则下列说法不正确的是( )A .存在点P ,使DP ∥面11AB D B .二面角1P BB D --的平面角为60︒C .1PB PD +5 D .P 到平面11AB D 310.定义:如果函数()f x 在[,]a b 上存在()1212,x x a x x b <<<,满足()()12()()f a f b f x f x a b''-==-,则称12,x x 为[,]a b 上的“对望数”,函数()f x 为[,]a b 上的“对望函数”.下列结论正确的是( )A .若函数()f x 为[,]a b 上的“对望函数”,则()f x 在[,]a b 上单调B .函数2()f x x mx n =++在任意区间[,]a b 上都不可能是“对望函数”C .函数321()23f x x x =-+是[0,2]上的“对望函数” D .函数()sin f x x x =+是11,66ππ⎡⎤⎢⎥⎣⎦上的“对望函数” 11.已知双曲线2222:1(0)x y C a b a b-=>>的左,右顶点分别为12,A A ,点P ,Q 是双曲线C 上关于原点对称的两点(异于顶点),直线121,,PA PA QA 的斜率分别为121,,PA PA QA k k k ,若1234PA PA k k ⋅=,则下列说法正确的是( ) A .双曲线C 的渐近线方程为34y x =±B .双面线C 的离心率为72C .11PA QA k k ⋅为定值D .12tan A PA ∠的取值范围为(0,)+∞12.定义在R 上的函数()f x 与()g x 的导函数分别为()f x '和()g x ',若(1)(2)2,()(1)g x f x f x g x +-'='-=-,且(2)g x +为奇函数,则下列说法一定正确的是( )A .(2)0g =B .函数()f x '关于2x =对称C .函数()f x 是周期函数D .20231()0k g k ==∑第Ⅱ卷三、填空题共4小题,每小题5分,共20分.13.4(1)(21)x x +-展开式中含有3x 项的系数为_____________.14.()62112x x x x ⎛⎫--+ ⎪⎝⎭的展开式中4x 项的系数为_______.15.已知12,F F 分别为椭圆2222:1(0)x yC a b a b+=>>的左,右焦点,,P Q 是椭圆上两点,线段PQ 经过点1F ,且223,4PQ PF PQ PF ⊥=,则椭圆C 的离心率为__________. 16.如图,椭圆Γ:()222210x y a b a b+=>>离心率为e ,F 是Γ的右焦点,点P 是Γ上第一角限内任意一点,,,若e λ<,则e 的取值范围是_______.四、解答题共70分,解答应写出文字说明,演算步骤或证明过程.17.在ABC 中,设角A B C 、、所对的边分别为a b c 、、,且()cos 4cos 0a B b c A +-=. (1)求cos A ;(2)若2,1BD DC AD ==,求2c b +的最大值.18.已知数列满足,,设. ⑴求; ⑵判断数列是否为等比数列,并说明理由; ⑶求的通项公式.19.如图,在多面体ABCDMN 中,四边形ABCD 为直角梯形,ABCD ,22AB =BC DC ⊥,2BC DC AM DM ===BDMN 为矩形.(1)求证:平面ADM ⊥平面ABCD ;(2)线段MN 上是否存在点H ,使得二面角H AD M --25若不存在,请说明理由.若存在,确定点H 的位置.20.某棉纺厂为了解一批棉花的质量,在该批棉花中随机抽取了容量为120的样本,测量每个样本棉花的纤维长度(单位:mm ,纤维长度是棉花质量的重要指标),所得数据均在区间[]20,32内,将其按组距为2分组,制作成如图所示的频率分布直方图,其中纤维长度不小于28mm 的棉花为优质棉.(1)求频率分布直方图中a 的值;(2)已知抽取的容量为120的样本棉花产自于A ,B 两个试验区,部分数据如下2×2列联表:A 试验区B 试验区合计{}n a 11a =()121n n na n a +=+nn a b n=123b b b ,,{}n b {}n a优质棉 10 非优质棉 30 合计120(3)若从这批120个样本棉花中随机抽取3个,其中有X 个优质棉,求X 的分布列和数学期望()E X . 注:①独立性检验的临界值表:()20P x χ≥0.15 0.10 0.05 0.025 0.010 0.005 0.001 0x2.0722.7063.8415.0246.6357.87910.828②()()()()()22n ad bc a b c d a c b d χ-=++++,其中n a b c d =+++.21.(12分)椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ,上顶点为A ,且12122,60F F AF F =∠=︒.(1)求C 的方程;(2)若椭圆2222:(01)x y E a bλλλ+=>≠且,则称E 为C 的λ倍相似椭圆,如图,已知E 是C 的3倍相似椭圆,直线:l y kx m =+与两椭圆C ,E 交于4点(依次为M ,N ,P ,Q ,如图),且||||MN NP =,证明:点(,)T k m 在定曲线上.22.设函数()e kx f x x a =+,()'f x 为()f x 的导函数.(1)当1k =-时,①若函数()f x 的最大值为0,求实数a 的值;②若存在实数0x >,使得不等式()ln f x x x ≥-成立,求实数a 的取值范围.(2)当1k =时,设()()'g x f x =,若()()12g x g x =,其中12x x ≠,证明:124x x >.。
高三第五次周练数学

2015级驻马店高中高三第五次周练数学(理)试题命题教师 刘大高一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.5. 设a=30.3,b=log 3,c=log 0.3 e 则a ,b ,c 的大小关系是A .a<b<cB .c<b<aC .b<a<cD .c<a<b6.如图所示,使用模拟方法估计圆周率值的程序框图,P 表示估计的结果,则图中空白框内应填入P =A .2017MB .2017MC .42017MD .20174M8.已知实数x ,y 满足2,6,1,y x x y x ⎧⎪⎨⎪⎩≥++≤≥则z =2|x -2|+|y |的最小值是A .6B .5C .4D .39.北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积.设隙积共n 层,上底由a×b 个物体组成,以下各层的长、宽依次各增加一个物体,最下层(即下底)由c×d 个物体组成,沈括给出求隙积中物体总数的公式为S =6n [(2b +d )a +(b +2d )c]+6n (c -a ).已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为A .83B .84C .85D .8610.已知函数()()221x f x x x e =--,则方程()()()290ef x tf x e t R +-=∈⎡⎤⎣⎦的根的个数为A. 5B. 4C. 3D.2二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若⎝⎛⎭⎫3x -1x n 展开式中各项系数之和为32,则该展开式中含x 3的项的系数为 14.已知三棱锥P ABC -中,平面PAC ⊥平面ABC ,321,90,1202BC PA PAC BAC ==∠=∠=,则三棱锥P ABC -的外接球的表面积为 .三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)18.如图,在四棱锥P—ABCD中,侧面P AD⊥底面ABCD,侧棱P A=PD=2,P A⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD的中点.(1)求B点到平面PCD的距离;(2)线段PD上是否存在一点Q,使得二面角Q—AC—D的余弦值为63?若存在,求出PQQD的值;若不存在,请说明理由.(20)2013河南省全国新课标1卷理科高考题(本小题满分12分)已知圆M:(x+1)2+y2=1,圆N:(x-1)2+y2=9,动圆P与圆M外切并与圆N内切,圆心P的轨迹为曲线 C(Ⅰ)求C的方程;(Ⅱ)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学周周练五
一、填空题(每小题4分,满分48分)
1 已知全集{}5,4,3,2,1=U ,集合{}{}4,3,2,3,2,1==B A ,则=)(B A C U ________________.
2已知集合{}1≤=x x A ,{}a x x B ≥=,且R B A = ,则实数a 的取值范围是________________.
3 设b a ,都是实数,则命题“若b a ,都是奇数,则b a +是偶数”的否命题是________________________________.
4已知集合{}062=--=x x x A ,{}
012=-=kx x B ,若B B A = ,则实数k 的值为_________.
5 不等式13
4≤+x 的解集为______________. 6函数)4lg()(x x f -=和43)(2--=x x x g 的定义域分别为A 和B ,则=B A _________________.
7若22=+b a ,则b a 42+的最小值为_________.
8若关于x 的不等式0622≥+-ax ax 对任意实数都成立,则实数a 的取值范围是________________.
9若03
:<+-x m x p 成立的一个充分不必要条件是312:<+x q ,则实数m 的取值范围是____________.
10 在R 上定义运算b a ab b a ++=⊕⊕2:,则满足0)2(<-⊕x x 的实数x 的取值范围是___________________.
11 若1-<x ,则函数1
432+++=x x x y 的值域为______________. 12设0a >b >,则()
211a ab a a b ++-的最小值是是_____.
二、选择题(每小题4分,满分8分)
13 下面四个条件中,使b a >成立的充分而不必要条件是( )
(A) 1+>b a (B) 1->b a (C) 22b a > (D) 33b a >
(本题满分8分)解不等式6121≥-++x x .
14。
