《计量经济学》建模案例
计量经济学模型案例

计量经济学模型案例计量经济学是经济学的一个重要分支,它运用数理统计和经济理论来研究经济现象。
在实际应用中,计量经济学模型可以帮助我们分析经济数据,预测经济变化,评估政策效果等。
下面我们将通过几个实际案例来展示计量经济学模型的应用。
首先,我们来看一个关于劳动力市场的案例。
假设我们想要研究教育水平对个体工资收入的影响。
我们可以建立一个计量经济学模型,以教育水平作为自变量,工资收入作为因变量,控制其他可能影响工资收入的因素,如工作经验、性别、地区等。
通过对大量的劳动力市场数据进行回归分析,我们可以得出教育水平对工资收入的影响程度,进而评估教育政策对经济的影响。
其次,我们来考虑一个关于消费行为的案例。
假设我们想要研究收入水平对消费支出的影响。
我们可以建立一个消费函数模型,以收入水平作为自变量,消费支出作为因变量,控制其他可能影响消费支出的因素,如家庭规模、价格水平、偏好等。
通过对消费者调查数据进行计量经济学分析,我们可以得出收入水平对消费支出的弹性,从而预测未来的消费趋势,指导政府制定经济政策。
最后,我们来看一个关于市场竞争的案例。
假设我们想要研究市场结构对企业利润的影响。
我们可以建立一个产业组织模型,以市场结构(如垄断、寡头、完全竞争)作为自变量,企业利润作为因变量,控制其他可能影响企业利润的因素,如生产成本、市场需求、技术创新等。
通过对不同产业的数据进行计量经济学分析,我们可以得出不同市场结构下的企业利润水平,为政府监管和产业政策提供依据。
通过以上案例的介绍,我们可以看到计量经济学模型在实际经济分析中的重要作用。
它不仅可以帮助我们理解经济现象的规律,还可以指导政策制定和企业决策。
当然,计量经济学模型的建立和分析也需要注意数据的质量、模型的假设条件等问题,只有在严谨的理论基础和丰富的实证分析基础上,我们才能得出可靠的经济结论。
综上所述,计量经济学模型在经济学研究中具有重要的地位和作用,它为我们提供了一种强大的工具来分析经济现象,预测经济变化,评估政策效果。
计量经济学建模案例

计量经济学建模案例在计量经济学中,建模是一项非常重要的工作。
通过建立合适的模型,我们可以对经济现象进行定量分析,揭示经济规律,为政策制定和预测提供有力的支持。
下面,我们将通过一个实际的案例来介绍计量经济学建模的过程。
首先,我们需要确定研究的问题。
在这个案例中,我们关注的是劳动力市场对经济增长的影响。
我们希望通过建立一个模型,来分析劳动力市场的变化对经济增长的影响程度。
接下来,我们需要收集相关数据。
在这个案例中,我们需要收集劳动力市场的就业率、失业率、劳动生产率等数据,以及经济增长率、投资率、消费率等数据。
这些数据可以通过国家统计局、国际组织的数据库等渠道获取。
然后,我们需要选择合适的模型。
在这个案例中,我们可以选择使用计量经济学中的时间序列模型,如VAR模型、ARIMA模型等,来分析劳动力市场和经济增长之间的关系。
我们还可以考虑使用面板数据模型,来控制个体和时间的固定效应。
接着,我们需要进行模型估计和检验。
在这个案例中,我们可以利用计量经济学中的OLS回归、固定效应模型、随机效应模型等方法,对模型进行估计,并进行参数显著性检验、模型拟合优度检验等。
最后,我们需要进行模型的解释和政策建议。
通过对模型的估计结果进行分析,我们可以得出劳动力市场对经济增长的影响程度,进而提出相应的政策建议,如促进就业、提高劳动生产率等。
通过以上案例,我们可以看到计量经济学建模的基本流程,确定研究问题、收集数据、选择模型、估计检验、解释政策建议。
在实际应用中,我们还需要根据具体问题灵活运用各种模型和方法,以期得出准确可靠的分析结论。
总之,计量经济学建模是一项复杂而又重要的工作。
通过建立合适的模型,我们可以更好地理解经济现象,为政策制定和预测提供有力的支持。
希望本文的案例分析能够对读者有所启发,进一步深入学习和应用计量经济学建模方法。
《计量经济学》建模案例

《计量经济学》建模案例案例1:用回归模型预测木材剩余物伊春林区位于黑龙江省东北部。
全区有森林面积2189732公顷,木材蓄积量为23246.02万m 3。
森林覆盖率为62.5%,是我国主要的木材工业基地之一。
1999年伊春林区木材采伐量为532万m 3。
按此速度44年之后,1999年的蓄积量将被采伐一空。
所以目前亟待调整木材采伐规划与方式,保护森林生态环境。
为缓解森林资源危机,并解决部分职工就业问题,除了做好木材的深加工外,还要充分利用木材剩余物生产林业产品,如纸浆、纸袋、纸板等。
因此预测林区的年木材剩余物是安排木材剩余物加工生产的一个关键环节。
下面,利用简单线性回归模型预测林区每年的木材剩余物。
显然引起木材剩余物变化的关键因素是年木材采伐量。
伊春林区16个林业局1999年木材剩余物和年木材采伐量数据见附表。
散点图见图2.14。
观测点近似服从线性关系。
建立一元线性回归模型如下:y t = β0 + β1 x t + u t5101520253010203040506070XY图 年剩余物y t 和年木材采伐量x t 散点图图1 Eviews 输出结果Eviews 估计结果见图1。
下面分析Eviews 输出结果。
先看图1的最上部分。
LS 表示本次回归是最小二乘回归。
被解释变量是y t 。
本次估计用了16对样本观测值。
输出格式的中间部分给出5列。
第1列给出截距项(C )和解释变量x t 。
第2列给出相应项的回归参数估计值(0ˆβ和1ˆβ)。
第根据Eviews 输出结果(图2.15),写出OLS 估计式如下:t yˆ= -0.7629 + 0.4043 x t (-0.6) (12.1) R 2= 0.91, s. e . = 2.04其中括号内数字是相应t 统计量的值。
s.e .是回归函数的标准误差,即σˆ=)216(ˆ2−∑t u 。
R 2是可决系数。
R 2 = 0.91说明上式的拟合情况较好。
y t 变差的91%由变量x t 解释。
计量经济学建模案例

计量经济学建模案例计量经济学是一种运用数学和统计方法对经济现象进行定量分析的方法,可以帮助经济学家解释和预测经济现象,并制定相应的政策。
下面是一种计量经济学建模案例:假设我们要研究某个城市的房价与房屋面积之间的关系。
我们可以使用多元线性回归模型来建模,其中自变量是房屋面积,因变量是房价。
为了使模型更加准确,我们还可以引入其他可能影响房价的变量,如地理位置、房屋年龄、房屋类型等。
首先,我们需要收集相关的数据。
我们可以通过调查和市场价格来获得房屋面积、房价以及其他相关变量的数据。
假设我们收集了100个样本数据来建立模型。
接下来,我们需要进行数据的预处理。
这包括数据清洗、缺失值处理、异常值处理等。
我们可以使用统计软件进行数据处理和分析。
然后,我们可以使用多元线性回归模型来建立房价与房屋面积以及其他相关变量之间的关系。
模型的形式可以表示为:房价= β0 + β1 × 房屋面积+ β2 × 地理位置+ β3 × 房屋年龄 +β4 × 房屋类型+ ε其中,β0、β1、β2、β3、β4是模型的回归系数,表示不同变量对房价的影响程度。
ε是误差项,表示模型无法解释的部分。
接着,我们可以使用最小二乘法估计回归系数,并进行统计显著性检验和模型拟合度检验。
这可以帮助我们判断模型的准确性和可解释性。
最后,我们可以使用估计的回归模型来进行预测和分析。
通过对模型的解释和系数的分析,我们可以得出不同变量对房价的影响程度,并制定相应的政策措施。
总之,计量经济学建模能够帮助我们理解和预测经济现象,对于研究者和政策制定者具有重要意义。
以上是一个简单的计量经济学建模案例,实际的建模过程可能更加复杂,需要根据具体问题进行相应的分析和处理。
计量经济学建模案例

计量经济学建模案例计量经济学是经济学的一个重要分支,它运用数理统计、数学经济学和经济计量学的方法,对经济现象进行定量分析和研究。
计量经济学建模是计量经济学的一个重要环节,通过建立合适的模型来对经济现象进行描述、预测和政策分析。
本文将通过一个实际的案例,介绍计量经济学建模的基本步骤和方法。
首先,我们需要确定研究的目的和问题。
在实际研究中,我们通常会针对某一经济现象或政策进行研究,比如通货膨胀对经济增长的影响。
在确定研究问题后,我们需要收集相关的数据,这些数据通常包括宏观经济指标、产业数据、企业调查数据等。
在收集数据时,我们需要注意数据的质量和可靠性,确保数据的准确性和完整性。
接下来,我们需要对收集的数据进行描述性统计分析。
描述性统计分析可以帮助我们了解数据的分布特征、相关性和变化趋势,为后续的建模分析提供基础。
在描述性统计分析的基础上,我们可以利用计量经济学的方法,建立相应的经济模型。
比如,我们可以运用回归分析的方法,来探讨通货膨胀率对经济增长的影响,建立相应的经济增长模型。
建立模型后,我们需要进行模型的估计和检验。
模型的估计可以通过最小二乘法等方法来进行,通过估计得到的参数,我们可以对模型的拟合效果进行评估。
同时,我们还需要对模型的假设进行检验,确保模型的有效性和可靠性。
在估计和检验的基础上,我们可以对模型进行修正和改进,以提高模型的解释能力和预测精度。
最后,我们需要对建立的模型进行政策分析和预测。
通过建立的模型,我们可以对不同政策措施的影响进行评估和预测,为政策制定提供决策支持。
比如,我们可以利用建立的经济增长模型,来评估不同通货膨胀率下的经济增长效果,为货币政策的制定提供参考。
综上所述,计量经济学建模是一个系统的过程,需要从确定研究问题、数据收集、描述性统计分析、模型建立、模型估计和检验、政策分析和预测等多个环节进行。
通过本文的案例介绍,希望读者能够对计量经济学建模有一个清晰的认识,为实际研究和应用提供参考。
案例分析 计量经济学

案例分析1一、研究的目的要求居民消费在社会经济的持续发展中有着重要的作用。
居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长,而且这也是人民生活水平的具体体现。
改革开放以来随着中国经济的快速发展,人民生活水平不断提高,居民的消费水平也不断增长。
但是在看到这个整体趋势的同时,还应看到全国各地区经济发展速度不同,居民消费水平也有明显差异。
例如,2002年全国城市居民家庭平均每人每年消费支出为6029.88元, 最低的黑龙江省仅为人均4462.08元,最高的上海市达人均10464元,上海是黑龙江的2.35倍。
为了研究全国居民消费水平及其变动的原因,需要作具体的分析。
影响各地区居民消费支出有明显差异的因素可能很多,例如,居民的收入水平、就业状况、零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。
为了分析什么是影响各地区居民消费支出有明显差异的最主要因素,并分析影响因素与消费水平的数量关系,可以建立相应的计量经济模型去研究。
二、模型设定我们研究的对象是各地区居民消费的差异。
居民消费可分为城市居民消费和农村居民消费,由于各地区的城市与农村人口比例及经济结构有较大差异,最具有直接对比可比性的是城市居民消费。
而且,由于各地区人口和经济总量不同,只能用“城市居民每人每年的平均消费支出”来比较,而这正是可从统计年鉴中获得数据的变量。
所以模型的被解释变量Y 选定为“城市居民每人每年的平均消费支出”。
因为研究的目的是各地区城市居民消费的差异,并不是城市居民消费在不同时间的变动,所以应选择同一时期各地区城市居民的消费支出来建立模型。
因此建立的是2002年截面数据模型。
影响各地区城市居民人均消费支出有明显差异的因素有多种,但从理论和经验分析,最主要的影响因素应是居民收入,其他因素虽然对居民消费也有影响,但有的不易取得数据,如“居民财产”和“购物环境”;有的与居民收入可能高度相关,如“就业状况”、“居民财产”;还有的因素在运用截面数据时在地区间的差异并不大,如“零售物价指数”、“利率”。
计量经济学建模与分析
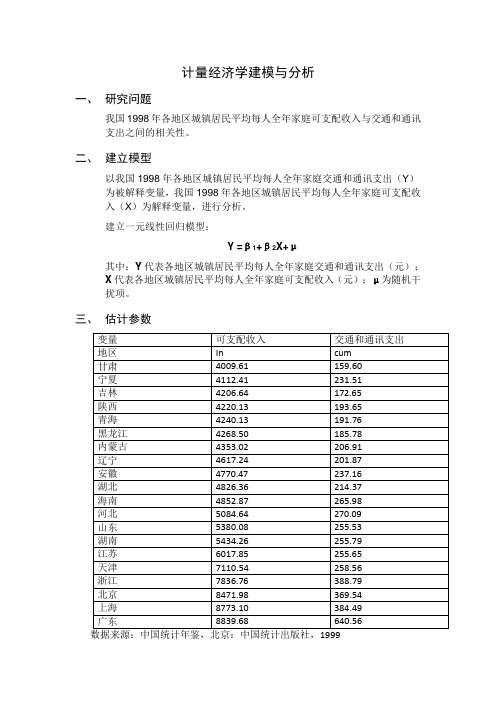
计量经济学建模与分析一、研究问题我国1998年各地区城镇居民平均每人全年家庭可支配收入与交通和通讯支出之间的相关性。
二、建立模型以我国1998年各地区城镇居民平均每人全年家庭交通和通讯支出(Y)为被解释变量,我国1998年各地区城镇居民平均每人全年家庭可支配收入(X)为解释变量,进行分析。
建立一元线性回归模型:Y =β1+β2X+μ其中:Y代表各地区城镇居民平均每人全年家庭交通和通讯支出(元);X代表各地区城镇居民平均每人全年家庭可支配收入(元);μ为随机干扰项。
三、估计参数利用普通最小二乘法,根据上表数据,可估计出该回归方程为:2. .6(45.9411)(0.0079)( 1.0464)(7.1461)0.739451.0672i ieY t F XSR∧=-+==-==4807220056四、 检验模型由于地区之间存在不同的人均可支配收入,因此各个地区家庭交通和通讯支出也会有所不同,这种差异使得模型很容易产生异方差。
故作出残差图如下:通过分析残差图可大致判断该模型很可能存在异方差。
但是否确实存在异方差还应通过更进一步的检验:22120122222220.050.05=+++14.788,=0.05=14.788=,i in n e v X X R R ααααχχχχ==>运用怀特检验,因为本例为一元回归,故无交叉乘积项,则相应的辅助回归为 由怀特检验知,在的情况下,查分布表,得临界值(2)5.9915。
比较计算的统计量与临界值,因为(2)5.9915所以拒绝原假设,表明模型存在异方差。
现运用加权最小二乘法来1/1/1/i i i ie w w X ===消除异方差,分别取权数,,得到估计结果分别如式(1)(2)(3)233.9985.40(1)(37.7364)(0.0075)(0.9009)(7.2209)0.0431=1.744152.1411i i eY t DW F X SR∧=-+==-==005229.0684 .29(2)(38.7023)(0.0083)(0.7511)(6.3688)0.7350=2.133140.5617i i eY t DW F X SR∧=-+==-==005235.0684 .40(3)(3.7056)(0.0074)(9.4639)(73.0966)0.9998=2.50755343.106i i eY t DW F X SR∧=-+==-==00532220.053.1047,= 3.1047(2) 5.9915,t F n n w R R αχ==<= 比较上面三种回归结果,发现用权数的效果最好。
计量经济模型案例

计量经济模型案例
计量经济学是经济学的一个重要分支,它旨在利用数理统计和经济理论工具来分析经济现象。
计量经济模型是计量经济学研究的核心内容之一,它通过建立数学模型来描述经济现象,并对其进行定量分析。
接下来,我们将通过一个实际的案例来介绍计量经济模型的应用。
假设我们想要研究教育水平对个体收入的影响。
我们可以建立一个计量经济模型来分析这一问题。
首先,我们需要收集个体的教育水平、工作经验、行业、地区等信息作为自变量,收入作为因变量。
然后,我们可以运用多元线性回归模型来估计教育水平对收入的影响。
在模型估计之后,我们可以进行假设检验来验证教育水平对收入是否显著影响,同时还可以计算教育水平对收入的弹性系数,以衡量其影响程度。
通过上述案例,我们可以看到计量经济模型的应用过程。
首先,我们需要明确研究的问题,然后选择合适的模型来进行分析。
在模型估计之后,我们需要进行统计推断来验证模型的有效性,最后对结果进行解释和政策建议。
除了多元线性回归模型,计量经济学还有许多其他重要的模型,如时间序列模型、面板数据模型等,它们都在不同的经济领域有着重要的应用。
例如,时间序列模型可以用来分析经济增长、通货膨胀等宏观经济问题,面板数据模型可以用来分析企业的生产效率、市场竞争等微观经济问题。
总之,计量经济模型是计量经济学研究的重要工具,它通过建立数学模型来描述经济现象,并进行定量分析。
通过上述案例,我们可以看到计量经济模型在实际问题中的应用,它为我们提供了一种有效的分析经济现象的方法,对于经济政策制定和实践具有重要的意义。
希望本文对您有所帮助,谢谢阅读!。
