浙教版数学八年级下册课时训练： 5.1 .docx

合集下载

浙教版数学八年级下册八下第五章特殊平行四边形拔尖训练(含答案)

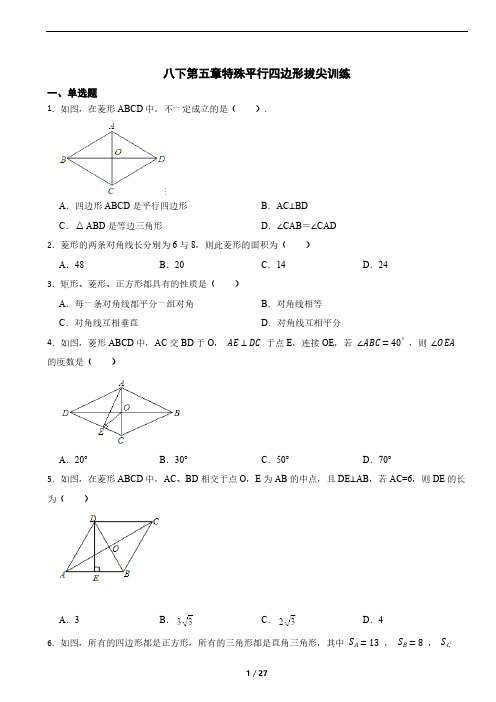
八下第五章特殊平行四边形拔尖训练一、单选题1．如图，在菱形ABCD中，不一定成立的是（）.A．四边形ABCD是平行四边形B．AC⊥BDC．△ABD是等边三角形D．∠CAB＝∠CAD2．菱形的两条对角线长分别为6与8，则此菱形的面积为（）A．48B．20C．14D．243．矩形、菱形、正方形都具有的性质是（）A．每一条对角线都平分一组对角B．对角线相等C．对角线互相垂直D．对角线互相平分4．如图，菱形ABCD中，AC交BD于O，AE⊥DC于点E，连接OE，若∠ABC=40°，则∠OEA 的度数是（）A．20°B．30°C．50°D．70°5．如图，在菱形ABCD中，AC、BD相交于点O，E为AB的中点，且DE⊥AB，若AC=6，则DE的长为（）A．3B．C．D．46．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中S A=13，S B=8，S C=10，S D=5，则S=（）A．25B．36C．32D．407．如图，在矩形ABCD中，E、F分别是边AB、CD上的点，AE=CF，连接EF、BF，EF与对角线AC交于点O，且BE=BF，∠BEF=2∠BAC，FC=2，则AB的长为（）A．23B．43C．4D．68．如图，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（）．A．8B．3C．4D．329．如图，P是正方形ABCD的对角线BD上任意一点，PE⊥AB于点E，PF⊥AD于点F，连接EF.有下列结论：①CP=EF；②CP⊥EF；③△CPD一定是等腰三角形；④∠PFE=∠BCP；⑤PD=2AE．其中，正确结论的序号是（）A．①②③④B．②③④⑤C．①②④⑤D．①③④⑤10．如图，正方形ABCD的边长为2cm，正方形CEFG的边长为1cm，若正方形CEFG绕点C旋转，则点F 到点A的距离最小值为（）A．3B．22C．32D．2二、填空题11．菱形定义：一组相等的平行四边形叫菱形．12．如图，矩形ABCD中，AB=4，AD=6．在边AD上取一点E，使BE=BC，过点C作CF⊥BE，垂足为点F，则BF的长为．13．如图是一幅赵爽弦图，利用此图可以证明勾股定理.现连接BE，发现AB＝BE，若DE＝1，则正方形ABCD的面积为 .14．如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=6cm，BC=8cm，则△AEF的周长= cm．15．如图，大正方形ABCD中，AB=3，小正方形AEFG中，AE=3，在小正方形绕A点旋转的过程中，当C，F，G三点共线时，线段CF的长为．16．如图，在边长为2的正方形ABCD中，点E，F分别为AD，CD边上的动点（不与端点重合），连接BE，BF，分别交对角线AC于点P，Q.点E，F在运动过程中，始终保持∠EBF=45°，连接EF，PF，PD.下列结论：①PB=PD；②∠EFD=2∠FBC；③PQ=PA+CQ；④△BPF为等腰直角三角形；⑤若过点B作BH⊥EF，垂足为H，连接DH，则DH的最小值为22−2，其中所有正确结论的序号是 .三、作图题17．图1，图2，图3，图4是四张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，A，C两点都在格点上，连结AC，请完成下列作图：（1）以AC为对角线在图1中作一个正方形，且正方形各顶点均在格点上．（2）以AC为对角线在图2中作一个矩形，使得矩形面积为6，且矩形各顶点均在格点上．（3）以AC为对角线在图3和图4中分别作出一个面积为8的平行四边形（不含矩形），且平行四边形顶点在格点上.四、综合题18．如图，把长方形纸片ABCD沿EF折叠后．点D与点B重合，点C落在点C′的位置上．若∠1=60°，AE=1．（1）求∠2、∠3的度数；（2）求长方形纸片ABCD的面积S．19．如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于F．（1）求证：AE=DF；（2）若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．20．如图，矩形ABCD中，对角线AC的垂直平分线EF分别交BC，AD于点E、F.（1）求证：四边形AECF是菱形；（2）当BE=3，AF=5时，求AC的长.21．如图，AC是平行四边形ABCD的对角线，∠BAC=∠DAC．（1）求证：AB=BC；（2）若AB=4，AC=4 3，求平行四边形ABCD的面积．22．如图，在菱形ABCD中，AB＝10，S菱形ABCD＝60，点E从点B出发在边BC上向终点C运动．过点E作边BC的垂线，交菱形其它的边于点F，在EF的右侧作矩形EFGH．（1）如图1，点G在AC上．①求证：FA＝FG；②若点G是AC的中点，求证：BF＝FG；（2）若EF＝FG，当EF过AC中点时，求AG的长．23．已知：在边长为4的正方形ABCD中，点P为对角线BD上一点，且BP=32．将三角板的直角顶点与点P重合，一条直角边与直线BC交于点E，另一条直角边与射线BA交于点F（点F 不与点B重合），将三角板绕点P旋转．（1）如图，当点E、F在线段BC、AB上时，求证：PE=PF；（2）当∠FPB=30°时，求△BEP的面积；（3）当△BEP为等腰三角形时，求线段BF的长．五、实践探究题24．如图，点E为正方形ABCD内一动点，∠AEB=90°．过点B作BG⊥BE，且BG=BE，连接CG，DE．（1）求证：∠EAB=∠GCB；（2）延长AE交CG于点F，求证：EF=BE；（3）在（2）的条件下，若点E在运动过程中，存在四边形CFBE为平行四边形，试探究此时DE、CD满足的数量关系．答案解析部分1．【答案】C【解析】【解答】菱形是特殊的平行四边形，故A正确，根据菱形的性质：对角线互相平分且平分对角得B、D正确，所以选C．【分析】此题主要考查菱形的基本性质：菱形的对角线互相垂直平分，且每一条对角线平分一组对角；以及和平行四边形的联系．2．【答案】D【解析】【解答】6×8÷2=24故答案为：D.【分析】根据S菱形等于两对角线乘积的一半可求解.3．【答案】D【解析】【解答】解：矩形、菱形、正方形都具有的性质是：对角线互相平分，故答案为：D.【分析】根据矩形、菱形、正方形的性质判断求解即可。

期末复习五特殊平行四边形-2020春浙教版八年级数学下册课时训练

期末复习五特殊平行四边形复习目标必备知识与防范点一、必备知识：1．矩形的性质及判定：（1）矩形的________ 个角都是直角；矩形的对角线________ ；矩形既是________对称图形，又是________ 对称图形，它至少有________ 条对称轴．（2）有一个角是________ 的________ 是矩形；有________个角是直角的四边形是矩形；对角线相等的________是矩形．2．菱形的性质及判定：（1）菱形的________ 条边都相等；菱形的对角线________ ，并且每条对角线平分________ ．（2）一组________ 相等的________ 是菱形；四条边相等的四边形是________ ；对角线的平行四边形是菱形．3．正方形的性质及判定：（1）正方形的________个角都是直角，四条边都________ ；正方形的对角线________ ，并且________，每条对角线平分一组________ ．（2）有一组________相等，并且有一个角是________ 的平行四边形是正方形；有一组邻边相等的________ 是正方形；有一个角是直角的________ 是正方形．二、防范点：1．矩形、菱形、正方形的判定书写要规范；2．矩形、菱形、正方形的性质可从边、角、对角线、整体四个角度去考虑.例题精析考点一矩形的性质与判定例1 （1）如图，在矩形ABCD中，AB=6，AD=8，P是AD上不与A和D重合的一个动点，过点P分别作AC和BD的垂线，垂足为E、F，则PE+PF的值为（）A．10B．4.8C．6D．5（2）如图，在矩形ABCD中，有以下结论：①△AOB是等腰三角形；②S△ABO=S△ADO；③AC=BD；④AC⊥BD. 正确的结论是________ .（3）如图，在矩形ABCD中，AC、BD相交于点O. ①若矩形的一组邻边为3和4，则对角线长是________；②若矩形的对角线所成的角之一是65°，则对角线与各边所成的角度是________ ；③若∠AOB=60°，AB=4，则矩形的对角线AC= ________ .（4）如图，矩形ABCD中，点R沿CD边从点C向点D运动，点M在BC边上运动，E、F分别是AM、MR的中点，则EF的长度随着点M、点R的运动________（填①变短；②变长；③不变）.（5）如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点E处，且CE与AB交于F，则S△ACF=________ .反思：（1）解题的根据是熟记各种特殊几何图形的特征．（2）熟练掌握矩形的性质，并能进行推理计算是解决问题的关键．（3）正确把握三角形中位线等于第三边的一半的性质是解题关键．（4）熟练掌握矩形的性质、折叠的性质、勾股定理、全等三角形的性质，并能进行推理计算是解决问题的关键．（5）熟记性质并利用三角形的面积列出方程是解题的关键．例2 （1）下列判断不正确的是（）A．有一个角是直角的平行四边形是矩形B．有三个角是直角的四边形是矩形C．对角线相等的四边形是矩形D．对角线互相平分且相等的四边形是矩形（2）如果平行四边形的四个内角的平分线能够围成一个四边形，那么这个四边形一定是（）A．平行四边形B．矩形C．菱形D．正方形（3）如图，在△ABC中，AB=AC，将△ABC绕点C旋转180°得到△FEC，连结AE、BF．当∠ACB为________ 度时，四边形ABFE为矩形．（4）在平面直角坐标系上，有点A（-2，-2），B（2，2），C（0，4），当点D的坐标为________ 时，四边形ABCD是矩形．反思：熟练掌握矩形的判定，并能进行推理论证与计算是解决问题的关键．考点二菱形的性质与判定例3 （1）如图，四边形ABCD是菱形，过点A作BD的平行线交CD的延长线于点E. 有以下结论：①BD=CE；②DA=DE；③∠EAC=90°；④∠ABC=2∠E. 则成立的结论是________ .（2）一个菱形的两条对角线的长分别为5和8，那么这个菱形的面积是.（3）如图，菱形ABCD的周长为24cm，对角线AC、BD相交于O点，E是AD的中点，连结OE，则线段OE的长等于________ cm．（4）如图，在菱形ABCD中，∠A=60°，AB=2，E，F两点分别从A，B两点同时出发，以相同的速度分别向终点B，C移动，连结EF，在移动的过程中，EF的最小值为________ .反思：熟记菱形性质是解题的关键，解题时注意数形结合思想的应用．例4 （1）平面直角坐标系中，四边形ABCD的顶点坐标分别是A（-3，0），B（0，2），C（3，0），D（0，-2），则四边形ABCD是（）A．矩形B．菱形C．正方形D．平行四边形（2）如图，在△ABC中，点D是BC的中点，点E、F分别在线段AD及其延长线上，且DE=DF，给出下列条件：①BE⊥EC；②AB=AC；③BF∥EC. 从中选择一个条件使四边形BECF是菱形，你认为这个条件是________（只填写序号）．（3）如图，在△ABC中，∠ABC=90°，D，E分别为AB，AC的中点，延长DE到点F，使EF=2DE．①求证：四边形BCFE是平行四边形；②当∠ACB=60°时，求证：四边形BCFE是菱形．反思：掌握平行四边形、菱形的判定方法，利用数形结合是解题的关键．考点三正方形的性质与判定例5 （1）如图，ABCD中，E为BC边上一点，以AE为边作正方形AEFG，若∠BAE=40°，∠CEF=15°，则∠D的度数是________ .（2）（菏泽中考）如图，E，F是正方形ABCD的对角线AC上的两点，AC＝8，AE＝CF ＝2，则四边形BEDF的周长是________ ．反思：（1）解题的关键是灵活运用所学知识解决问题，学会用转化的思想思考问题.（2）从对称角度看图形结构，寻求两个图形的公共线段DB，从而求解.例6 （1）如图，在△ABC中，点D、E、F分别在边BC，AB，CA上，且DE∥CA，DF ∥BA．下列结论：①四边形AEDF是平行四边形；②如果∠BAC=90°，那么四边形AEDF 是矩形；③如果AD平分∠BAC，那么四边形AEDF是菱形；④如果∠BAC=90°，AD平分∠BAC，那么四边形AEDF是正方形，你认为正确的是________ .（2）如图，在矩形ABCD中，M、N分别是边AD、BC的中点，E、F分别是边BM、CM 的中点，当AB∶AD= ________ 时，四边形MENF是正方形．反思：熟练应用平行四边形、菱形、矩形及正方形的判定方法是解题关键．考点四特殊平行四边形的开放探究例7 如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM.【探究展示】（1）证明：AM＝AD＋MC；（2）AM＝DE＋BM是否成立？若成立，请给出证明；若不成立，请说明理由；【拓展延伸】（3）若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）（2）中的结论是否成立？请分别作出判断，不需要证明.反思：（1）常规辅助线：“中点＋平行”构造全等，角平分线构造全等；（2）证“一条线段＝两线段和”类型常用截长补短法；（3）第（1）小题也可过E作EH⊥AM于H，再证HM ＝CM得证.考点五特殊平行四边形的变换例8 已知：线段AB，BC，∠ABC=90°．求作：矩形ABCD．以下是甲、乙两同学的作业：甲：①以点C为圆心，AB长为半径画弧；②以点A为圆心，BC长为半径画弧；③两弧在BC上方交于点D，连结AD，CD，四边形ABCD即为所求（如图1）．乙：①连结AC，作线段AC的垂直平分线，交AC于点M；②连结BM并延长，在延长线上取一点D，使MD=MB，连结AD，CD，四边形ABCD即为所求（如图2）．对于两人的作业，下列说法正确的是（）A．甲正确，乙错误B．乙正确，甲错误C．甲、乙均正确D．甲、乙均错误反思：利用作图的方法，再运用矩形的判定，并进行推理论证是解决问题的关键．例9 已知，一张矩形纸片ABCD的边长分别为9cm和3cm，把顶点A和C叠合在一起，得折痕EF（如图）：（1）求证：四边形AECF是菱形；（2）求折痕EF的长.反思：利用特殊平行四边形的变换，再运用矩形、菱形的性质及判定，求解一些简单的计算及推理问题.考点六特殊平行四边形的综合运用例10 如图，在矩形ABCD中，AD＝6，DC＝10，菱形EFGH的三个顶点E，G，H分别在矩形ABCD的边AB，CD，DA上，AH＝2，连结CF，BF.（1）若DG＝2，求证：四边形EFGH为正方形；（2）若AE＝x，求△EBF的面积S关于x的函数表达式，并判断是否存在x，使△EBF的面积是△CGF面积的2倍. 若存在，求出x的值；若不存在，请说明理由；（3）求△GCF面积的最小值.反思：（1）证第（1）小题图形不准，要抓住△GDH≌△HAE（HL），证明∠GHE＝90°；（2）解第（2）小题的关键是构造△FNG≌△HAE，△FEM≌△HGD；（3）求△GCF面积的最小值要抓住GC边上的高不变，GC最小只要DG最大，DH＝4，∴GH＝HE最大，∴点E与点B重合时，△GCF的面积取最小.校内练习1．如图，在菱形ABCD中，E，F分别是边AB和BC的中点，EP⊥CD于点P，设∠A＝x°，则∠FPC的度数为（）2．如图所示，点B，C分别在两条直线y=2x和y=kx上，点A，D是x轴上两点，已知四边形ABCD是正方形，则k的值为.3．（南充中考）如图，正方形ABCD和正方形CEFG边长分别为a和b，正方形CEFG 绕点C旋转，给出下列结论：①BE=DG；②BE⊥DG；③DE2+BG2=2a2+b2，其中正确结论是________.（填序号）4. 定义：若点P为四边形ABCD内一点，且满足∠APB+∠CPD=180°，则称点P为四边形ABCD的一个“互补点”．（1）如图1，点P为四边形ABCD的一个“互补点”，∠APD=63°，求∠BPC的度数；（2）如图2，点P是菱形ABCD对角线上的任意一点，求证：点P为菱形ABCD的一个“互补点”．5．已知：如图，△ABC中，AB＝AC，AD⊥BC，且AD＝BC＝4，若将此三角形沿AD 剪开成为两个三角形，在平面上把这两个三角形拼成一个四边形，你能拼出所有不同形状的四边形吗？写出所拼四边形对角线的长（不要求写计算过程，只需写出结果）.6．如图1，在正方形ABCD中，P是对角线AC上的一点，点E在BC的延长线上，且PE=PB．（1）求证：△BCP≌△DCP；（2）求证：∠DPE=∠ABC；（3）把正方形ABCD改为菱形，其他条件不变（如图2），若∠ABC=58°，则∠DPE= 度．7．如图，在正方形ABCD中，DE与HG相交于点O.（1）如图1所示，若∠GOD＝90°，①求证：DE＝GH；②连结EH，求证：GD＋EH≥DE；（2）如图2所示，若∠GOD＝45°，AB＝4，HG＝2，求DE的长.参考答案【必备知识与防范点】1. （1）四相等中心轴两（2）直角平行四边形三平行四边形2. （1）四互相垂直平分一组对角（2）邻边平行四边形菱形互相垂直3. （1）四相等相等互相垂直平分对角（2）邻边直角矩形菱形【例题精析】例1 （1）如图，连结OP，∵AB=6，AD=8，∴BD===10，∵四边形ABCD是矩形，∴OA=OD=×10=5，∵S△AOD=S△AOP+S△DOP，∴××6×8=×5·PE+×5·PF，解得PE+PF=4.8．故选：B．（2）①②③（3）①5 ②57.5°和32.5°③8 （4）①（5）10例2 （1）C （2）B （3）60 （4）（-4，0）例3 （1）②③④（2）20 （3）3（4）连结DB，作DH⊥AB于H，如图，∵四边形ABCD为菱形，∴AD=AB=BC=CD，而∠A=60°，∴△ABD和△BCD都是等边三角形，∴∠ADB=∠DBC=60°，AD=BD，在Rt△ADH中，AH=1，AD=2，∴DH=，在△ADE和△BDF中，∴△ADE≌△BDF，∴∠2=∠1，DE=DF，∴∠1+∠BDE=∠2+∠BDE=∠ADB=60°，∴△DEF为等边三角形，∴EF=DE，而当E点运动到H点时，DE的值最小，其最小值为，∴EF的最小值为．例4 （1）B （2）②（3）①∵D，E为AB，AC中点，∴DE为△ABC的中位线，DE=BC，∴DE∥BC，即EF∥BC，∵EF=2DE，∴EF=BC，∴四边形BCFE为平行四边形．②∵四边形BCFE为平行四边形，∠ABC=90°，∠ACB=60°，E为AC的中点，∴BC=CE=BE，∴四边形BCFE是菱形．例5 （1）65°（2）8例6 （1）①②③④（2）1∶2例7 （1）证明：延长AE、BC交于点N，如图1所示，∵四边形ABCD是正方形，∴AD ∥BC. ∴∠DAE=∠ENC.∵AE平分∠DAM，∴∠DAE=∠MAE. ∴∠ENC=∠MAE. ∴MA=MN. 在△ADE和△NCE中，∴△ADE≌△NCE（AAS）. ∴AD=NC. ∴MA=MN=NC+MC=AD+MC.（2）AM=DE+BM成立.证明：过点A作AF⊥AE，交CB的延长线于点F，如图2所示. ∵四边形ABCD是正方形，∴∠BAD=∠D=∠ABC=90°，AB=AD，AB∥DC. ∵AF⊥AE，∴∠FAE=90°. ∴∠FAB=90°-∠BAE=∠DAE. 在△ABF和△ADE中，∴△ABF≌△ADE（ASA）. ∴BF=DE，∠F=∠AED. ∵AB∥DC，∴∠AED=∠BAE. ∵∠FAB=∠EAD=∠EAM，∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠FAB=∠FAM. ∴∠F=∠FAM. ∴AM=FM. ∴AM=FB+BM=DE+BM.（3）探究展示（1）AM＝AD＋MC仍成立；（2）AM＝DE＋BM不成立.例8 C例9 （1）∵四边形ABCD为矩形，∴AB∥CD，∠AFE=∠CEF. ∵矩形ABCD沿EF折叠，点A和C重合，∴∠CEF=∠AEF，AE=CE，∴∠AFE=∠AEF，∴AE=AF. ∴AF=CE，又∵AF∥CE，∴四边形AECF为平行四边形，∵AE=EC，∴四边形AECF为菱形.（2）连结AC，∵AB=9cm，BC=3cm，∴AC=3cm，AF=CF，∴在Rt△BCF中，设BF=xcm，则CF=（9-x）cm，由勾股定理可得（9-x）2=x2+32，即18x=72，解得x=4，则CF=5cm，BF=4cm，由面积可得：·AC·EF=AF·BC，即·3·EF=5×3，∴EF=cm.例10 （1）在△HDG和△AEH中，∵四边形ABCD是矩形，∴∠D=∠A=90°，∵四边形EFGH是菱形，∴HG=HE，在Rt△HDG和Rt△EAH中，∴Rt△HDG≌Rt△EAH，∴∠DHG=∠AEH，∴∠DHG+∠AHE=90°，∴∠GHE=90°，∴菱形EFGH为正方形；（2）过F作FM⊥AB，垂足为M，交DC延长线于点N，连结GE，∴FN⊥CD，∵CD∥AB，∴∠DGE=∠MEG，∵GH∥EF，∴∠HGE=∠FEG，∴∠DGH=∠MEF，在Rt△HDG和Rt△FME中，∴Rt△HDG≌Rt△FME，∴DH=MF，∵AH=2，∴DH=MF=4，∵AE=x，∴BE=10-x. ∴S△EBF=BE·FM=2（10-x）=20-2x. 同理可证Rt △AHE≌Rt△NFG，∴FN=AH=2，∵AH=2，AE=x，∴HE=HG==，∴DG==，∴CG=10-，∴S△GCF=CG·FN=10-，若△EBF的面积是△CGF面积的2倍，则20-2x=2（10-），整理得：x2=x2-12，此方程无解，所以不存在x，使△EBF的面积是△CGF 面积的2倍.（3）当点E与点B重合时，△GCF的面积取最小，最小值为10-2.【校内练习】1. D2.3. ①②4. （1）∵点P为四边形ABCD的一个“互补点”，∠APD=63°，∴∠BPC=180°-∠APD=180°-63°=117°.（2）如图，连结AP、CP，∵四边形ABCD是菱形，∴AD=CD，∠ADP=∠CDP．而DP=DP，∴△ADP≌△CDP，∴∠APD=∠CPD．又∠APB+∠APD=180°，∴∠APB+∠CPD=180°，即点P为菱形ABCD的一个“互补点”．5. （1）图1是矩形，两条对角线长相等，均为2；图2是平行四边形，两条对角线长为4和4；图3是平行四边形，两条对角线长为2和2；图4是一般的四边形，两条对角线长为2和.6. （1）在正方形ABCD中，BC=DC，∠BCP=∠DCP=45°，∵在△BCP和△DCP中，∴△BCP≌△DCP（SAS）；（2）证明：由（1）知，△BCP≌△DCP，∴∠CBP=∠CDP，∵PE=PB，∴∠CBP=∠E，∵∠1=∠2（对顶角相等），∴180°-∠1-∠CDP=180°-∠2-∠E，即∠DPE=∠DCE，∵AB ∥CD，∴∠DCE=∠ABC，∴∠DPE=∠ABC；（3）与（2）同理可得：∠DPE=∠ABC，∵∠ABC=58°，∴∠DPE=58°．故答案为58.7. （1）①作DM∥GH交BC延长线于点M，如图1，∵正方形ABCD中，GD∥BC，∴四边形GHMD为平行四边形，则GH=DM，GD=MH，∴∠GOD=∠MDE=90°，∴∠MDC+∠EDC=90°，∵∠ADE+∠EDC=90°，∴∠MDC=∠ADE，在△ADE和△CDM中，∴△ADE≌△CDM，∴DE=DM，∴DE=GH；②连结EM，∵DM=DE，∠EDM=90°，∴△EDM是等腰直角三角形，∴EM=DM=DE，∵MH+EH≥EM，GD=MH，∴EH+GD≥EM，∴GD+EH≥DE；（2）过点D作DN∥GH交BC于点N，如图2，则四边形GHND是平行四边形，∴DN=HG，GD=HN，∵∠C=90°，CD=AB=4，HG=DN=2，∴CN==2，∴BN=BC-CN=4-2=2，作∠ADM=∠CDN，DM交BA延长线于M，在△ADM和△CDN中，∴△ADM≌△CDN（ASA），∴AM=NC，DM=DN，∵∠GOD=45°，∴∠EDN=45°，∴∠ADE+∠CDN=45°，∴∠ADE+∠ADM=45°=∠MDE，在△MDE和△NDE中，∴△MDE≌△NDE（SAS），∴EM=EN，即AE+CN=EN，设AE=x，则BE=4-x，在Rt△BEN中，22+（4-x）2=（x+2）2，解得x=，∴DE=。

浙教版数学八年级下册课时训练： 5.1 .doc

浙江省嵊州市谷来镇中学2014-2015学年度课时训练： 5.1 矩形考试范围： 5.1 矩形；考试时间：100分钟；命题人：蒋小铭评卷人得分一、选择题（每小题6分，共30分）1．矩形具有而菱形不具有的性质是( )A ．对角线相等B ．两组对边分别平行C ．对角线互相平分D ．两组对角分别相等2．在Rt △ABC 中，∠C=90°，AC=3，BC=4，D 是AB上一动点（不与A 、B 重合），DE ⊥AC 于点E ，DF⊥BC 于点F ，点D 由A 向B 移动时，矩形DECF 的周长变化情况是（）A ．逐渐减小B ．逐渐增大C ．先增大后减小D ．先减小后增大3．用矩形纸片折出直角的平分线，下列折法正确的是4．下列说法中的错误的是( )．D C BAA 、一组邻边相等的矩形是正方形B 、一组邻边相等的平行四边形是菱形C 、一组对边相等且有一个角是直角的四边形是矩形D 、一组对边平行且相等的四边形是平行四边形5．下列命题是真命题的是（）A ．对角线相等且互相垂直的四边形是菱形B ．有一边与两角相等的两三角形全等C ．对角线相等的四边形是矩形D ．有一组邻边相等且垂直的平行四边形是正方形评卷人得分二、填空题（每小题6分，共30分）6．如图，矩形ABCD 中，AB ＝2，BC ＝3，对角线AC 的垂直平分线分别交AD ，BC 于点E 、F ，连接CE ，则CE 的长________.7．如图，将矩形纸片ABCD 沿EF 折叠，使点B 与CD 的中点重合，若AB=2，BC=3，则△FCB ′与△B ′DG 的面积之比为．8．矩形的两条对角线的一个交角为600，两条对角线的长度的和为8cm ，则这个矩形的一条较短边为cm.9．我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形．．．．．．则矩形的中点四边形的是．10．如图，在矩形ABCD 中，AB=1，AD=2，将AD 绕点A 顺时针．．．旋转，当点D 落在BC 上点D ′时，则∠DAD ′=__________度评卷人得分三、解答题（每小题20分，共40分）11．（8分）如图，要在长32m ，宽20m 的长方形绿地上修建宽度相同的道路，六块绿地面积共570m ，问道路宽应为多宽？12．如图所示，折叠长方形一边AD ，点D 落在BC 边的点F 处，已知BC=10厘米，AB=8厘米，求FC 的长。

浙教版数学八年级下册【课时训练】5.1矩形(1).doc

5.1矩形（1）1．我们把__________叫做矩形．2．矩形是特殊的____________，所以它不但具有一般________的性质，而且还具有特殊的性质：（1）_________；（2）___________．3．矩形既是______图形，又是________图形，它有_______条对称轴．4．如图1所示，矩形ABCD的两条对角线相交于点O，图中有_______个直角三角形，•有____个等腰三角形．5．矩形的两条邻边分别是5、2，则它的一条对角线的长是______．6．如图所示，矩形ABCD的两条对角线相交于点O，若∠AOD=60°，OB=•4，•则DC=________．7．矩形具有而一般平行四边形不具有的性质是（）A．对角线相等 B．对角相等 C．对边相等 D．对角线互相平分8．若矩形的对角线长为4cm，一条边长为2cm，则此矩形的面积为（）A．83cm2 B．43cm2 C．23cm2 D．8cm29．如图2所示，在矩形ABCD中，∠DBC=29°，将矩形沿直线BD折叠，顶点C落在点E处，则∠ABE的度数是（）A．29° B．32° C．22° D．61°10．矩形ABCD的周长为56，对角线AC，BD交于点O，△ABO与△BCO的周长差为4，•则AB的长是（） A．12 B．22 C．16 D．2611．如图3所示，在矩形ABCD中，E是BC的中点， AE=AD=2，则AC的长是（）A．5 B．4 C． 23 D．712．如图所示，在矩形ABCD中，点E在DC上，AE=2BC，且AE=AB，求∠CBE的度数．13．如图所示，在矩形ABCD中，对角线AC，BD交于点O，过顶点C作CE∥BD，交A•孤延长线于点E，求证：AC=CE．14．如图所示，在矩形ABCD中，AB=8，AD=10，将矩形沿直线AE折叠，顶点D恰好落在BC边上的点F处，求CE的长．15．如图所示，在矩形ABCD中，AB=5cm，BC=4cm，动点P以1cm/s的速度从A点出发，•经点D，C到点B，设△ABP的面积为s（cm2），点P运动的时间为t（s）．（1）求当点P在线段AD上时，s与t之间的函数关系式；（2）求当点P在线段BC上时，s与t之间的函数关系式；（3）在同一坐标系中画出点P在整个运动过程中s与t之间函数关系的图像．答案:1．有一个角是直角的平行四边形2．平行四边形，平行四边形（1）矩形的四个角都是直角（2）矩形的对角线相等3．中心对称，轴对称，2 4．4，4 5．3 6．37．A 8．B 9．B 10．C 11．D 12． 15°13．证四边形BDCE是平行四边形，得CE=•BD=AC14． 3 15．（1）s=52t （2）s=-52t+35 （3）略初中数学试卷。

浙教版数学八年级下册【课时训练】5.1矩形(2).doc

& 鑫达捷致力于精品文档精心制作仅供参考 &
鑫达捷 5.1矩形（2）
【基础练习】
一、填空题：
1.四边形ABCD 中，∠A =∠B =∠C =∠D , 则四边形ABCD 是；
2.若矩形两对角线相交所成的角等于120°，较长边为6cm ，则该矩形的对角线长为 cm ；
3.直角三角形两直角边长分别为6cm 和8cm, 则斜边上的中线长为 cm ，斜边上的高为 cm.
二、选择题：
1.下列命题是真命题的是（）；
A.有一个角是直角的四边形是矩形
B.两条对角线相等的四边形是矩形
C.有三个角是直角的四边形是矩形
D.对角线互相垂直的四边形是矩形
2.若矩形两邻边的长度之比为2︰3，面积为54cm 2, 则其周长为（）.
A. 15cm
B. 30cm
C. 45cm
D. 90cm
三、解答题：
1.如图3-12， ABCD 中，∠DAC =∠ADB , 求证：四边形ABCD 是矩形.
2.如图3-13，P 是 ABCD 的边的中点，且PB = PC . 求证：四边形ABCD
是矩形.
【综合练习】如图3-14， ABCD 的四个内角的平分线相交于点E 、F 、G 、H. 求证：EG = FH .
参考答案【基础练习】一、1. 矩形； 2. 43； 3. 5，4.8. 二、1. C ； 2. B.
三、1.提示：证明AC = BD ；
2. 提示：证∠A =∠D =∠ABC = 90°. 【综合练习】提示：证四边形EFGH 是矩形.
初中数学试卷
图3-12B A C D O P D C
A B 图3-13
图3-14H G F E B
A C D。

浙教版八年级数学下册第五章特殊平行四边形课堂同步练习习题合集(含答案解析)

5.1 矩形（第1课时）课堂笔记有一个角是的叫做矩形；矩形的个角都是直角；矩形的对角线；矩形既是对称图形，又是对称图形，它至少有条对称轴. 课时训练A 组基础训练1. 下面图形中，既是中心对称图形，又是轴对称图形的是（） A. 等腰三角形 B. 平行四边形 C. 等边三角形D. 矩形2. 已知一矩形的周长是24cm ，相邻两边之比是1∶2，那么这个矩形的面积是（） A. 24cm 2B. 32cm 2C. 48cm 2D. 128cm 23. 矩形具有而一般的平行四边形不具有的特征是（） A. 对角线相等B. 对边相等C. 对角相等D. 对角线互相平分 4. 如图，E 为矩形ABCD 的边BC 的中点，且BE=21AE ，AE=2，则AC 等于（） A. 3 B. 22 C. 6D. 75. 如图，在矩形ABCD 中，AB ＝2AD ，E 是CD 上一点，且AE ＝AB ，则∠CBE 等于（） A. 15° B. 22.5° C. 30°D. 45°6. 如图，在矩形ABCD 中，∠DBC=29°，将矩形沿直线BD 折叠，顶点C 落在点E 处，则∠ABE 的度数是（）A. 29°B. 32°C. 22°D. 61°7. 如图，矩形ABCD中，AB=3，两条对角线AC、BD所夹的钝角为120°，则对角线BD的长为 .8. 如图，一个平行四边形的活动框架，对角线是两根橡皮筋．若改变框架的形状，则∠α也随之变化，两条对角线长度也在发生改变．当∠α为度时，两条对角线长度相等.9. 如图，矩形ABCD中，点E、F分别是AB、CD的中点，连结DE和BF，分别取DE、BF的中点M、N，连结AM，CN，MN，若AB=22，BC=23，则图中阴影部分的面积为 .10. 如图，在Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4，P为边BC上一动点，PE⊥AB于点E，PF⊥AC于点F，连结EF，则EF的最小值为 .11. 如图，矩形ABCD，P是矩形外一点，且PA=PD，求证：PB=PC.12. 如图，在矩形ABCD中，对角线AC，BD交于点O，DE平分∠ADC，交BC于点E，∠BDE 的度数为15°. 则请求出∠COD的度数.13. 如图，四边形ABCD是矩形，对角线AC，BD相交于点O，BE∥AC交DC的延长线于点E.（1）求证：BD=BE；（2）若∠DBC=30°，BO=4，求四边形ABED的面积.B组自主提高14.如图，在矩形ABCD中，AB=3，AD=4，P是AD上一动点，PE⊥AC于E，PF⊥BD于F，则PE+PF= .15. 如图所示，将矩形ABCD沿BD对折，使点C落在C＇处，BC＇交AD于点E，AD＝8，AB ＝4.（1）求证：BE＝ED；（2）求△BED的面积.参考答案5.1 矩形（第1课时）【课堂笔记】直角平行四边形四相等中心轴两【课时训练】 1—3. DBA4. D 由于AE=2，BE=21AE ，∠B=90°，可知AB=3. 又E 为BC 中点，BE=1，∴BC=2. 在Rt △ABC 中运用勾股定理可知AC=7. 故选D. 5. A6. B 【点拨】∠ABE=90°-2∠DBC=32°. 故选B.7. 68. 909. 26 10. 2.411. ∵PA=PD ，∴∠PAD=∠PDA. ∵矩形ABCD ，∴AB=CD ，∠BAD=∠CDA=90°，∴∠PAB=∠PDC ，∴△PAB ≌△PDC （SAS ），∴PB=PC. 12. ∠COD=60°13. （1）∵四边形ABCD 是矩形，∴AC=BD ，AB ∥CD. ∵BE ∥AC ，∴四边形ABEC 是平行四边形. ∴AC=BE ，∴BD=BE ；（2）∵在矩形ABCD 中，BO=4，∴BD=2BO=2×4=8. ∵∠DBC=30°，∴CD=21BD=21×8=4，∴AB=CD=4，DE=CD+CE=CD+AB=4+4=8. 在Rt △BCD 中，BC=22CD BD -=2248-=43，∴S 四边形ABED=21（AB+DE ）·BC=21（4+8）×43=243. 14. 2.415. （1）根据折叠得：∠EBD ＝∠DBC ，又矩形ABCD ，∴AD ∥BC ，∴∠EDB ＝∠DBC ，∴∠EBD ＝∠EDB ，∴EB ＝ED.（2）设BE ＝DE ＝x ，在△ABE 中，（8－x ）2+42=x2，解得：x=5，∴S △BED ＝21×5×4＝10.5.1 矩形（第2课时）课堂笔记有个角是直角的四边形是矩形；对角线相等的是矩形.课时训练A组基础训练1. 下列命题中假命题是（）A. 有三个角都是直角的四边形是矩形B. 对角线相等的平行四边形是矩形C. 对角线互相平分且相等的四边形是矩形D. 对角线相等的四边形是矩形2. 如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连结EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（）A. AB=BEB. DE⊥DCC. ∠ADB=90°D. CE⊥DE3. 四边形ABCD的对角线AC，BD，下面给出的三个条件中，选取两个，能使四边形ABCD是矩形，①AC，BD互相平分；②AC⊥BD；③AC=BD，则正确的选法是（）A. ①②B. ①③C. ②③D. 以上都可以4. 矩形的三个顶点坐标分别是（-2，-3），（1，-3），（-2，-4），那么第四个顶点坐标是（）A. （1，-4）B. （-8，-4）C. （1，-3）D. （3，-4）5．如图，已知四边形ABCD的两条对角线AC，BD互相垂直，E，F，G，H分别是四边形ABCD 各边中点. 若AC＝8，BD＝6，则四边形EFGH的面积为（）A． 48 B． 24C． 12 D．无法计算6. 如图，将平行四边形ABCD的边DC延长到E，使CE=CD，连结AE交BC于F，∠AFC=n∠D，当n= 时，四边形ABEC是矩形.7. 在四边形ABCD中，AD=BC，AB=CD，请再添加一个条件，使四边形ABCD是矩形. 你添加的条件是（写出一种即可）.8. 如图，ABCD的对角线AC，BD相交于点O，△AOD是正三角形，AD=4，则ABCD的面积为 .9. 如图，矩形ABCD中，E，F分别是AD，AB上的点，若EF=EC，EF⊥EC，DE=2，矩形的周长为16，则AE的长为 .10. 工人师傅做铝合金窗框分下面三个步骤进行：（1）先截出两对符合规格的铝合金窗料（如图1），使AB=CD，EF=GH；（2）摆放成如图2的四边形，则这时窗框的形状是形，根据的数学道理是：；（3）将直角尺靠紧窗框的一个角（如图3），调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时（如图4），说明窗框合格，这时窗框是形，根据的数学道理是： .11．如图，AB∥CD，EF交AB于E，交CD于F，且EF截AB、CD所得的两对同旁内角的平分线分别相交于G，H. 求证：四边形EGFH是矩形.12．如图，在ABCD中，E为BC的中点，连结AE并延长交DC的延长线于点F.（1）求证：AB＝CF；（2）当BC与AF满足什么数量关系时，四边形ABFC是矩形，并说明理由.B组自主提高13．四边形四边长分别是a，b，c，d，其中a，c为对边，且满足a2+b2+c2+d2=2ab+2cd，则顺次连结四边形各边中点所组成的四边形必是 .14. 如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE 的延长线于点F，且AF=DC，连结CF.（1）求证：D是BC的中点；（2）如果AB=AC，试猜测四边形ADCF的形状，并证明你的结论.参考答案5.1 矩形（第2课时）【课堂笔记】三平行四边形【课时训练】 1—5. DBBAC 6. 27. 答案不唯一. 如：∠A=90°，AC=BD 等 8. 163 9. 310. （2）平行四边两组对边分别相等的四边形是平行四边形（3）矩有一个角是90°的平行四边形是矩形11. ∵AB ∥CD ，∴∠AEF+∠CFE=180°，∵FG ，EG 分别平分∠CFE 和∠AEF ，∴∠GEF=21∠AEF ，∠GFE=21∠CFE ，∴∠GEF+∠GFE=90°，∴∠G=90°，同理可得∠H=90°，∵FH 平分∠EFD ，∴∠EFH=21∠EFD ，∴∠GFE+∠EFH=21∠CFE+21∠EFD=90°，∴四边形EGFH 是矩形.12. （1）∵四边形ABCD 是平行四边形，∴AB ∥CD ，∵点F 为DC 的延长线上的一点，∴AB ∥DF ，∴∠BAE=∠CFE ，∠ECF=∠EBA ，∵E 为BC 中点，∴BE=CE ，则在△BAE 和△CFE 中，∠BAE=∠CFE ，∠EBA=∠ECF ，BE=CE ，∴△BAE ≌△CFE ，∴AB=CF.（2）满足BC ＝AF 时，四边形ABFC 是矩形. 理由：由（1）得AB=CF ，又∵AB ∥CF ，∴四边形ABFC 是平行四边形，又∵BC=AF ，∴?荀ABFC 是矩形（对角线相等的平行四边形为矩形） 13. 矩形14. （1）∵AF ∥BC ，∴∠AFE=∠DBE. ∵E 是AD 的中点，∴AE=DE. 又∵∠AEF=∠DEB ，∴△AEF ≌△DEB ，∴AF=DB. ∵AF=DC ，∴DB=DC ，即D 是BC 的中点. （2）四边形ADCF 是矩形.证明：∵AF ∥DC ，AF=DC ，∴四边形ADCF 是平行四边形. ∵AB=AC ，D 是BC 的中点，∴AD ⊥BC. ∴四边形ADCF 是矩形.【点拨】（1）利用平行得角相等，从而证明△AEF≌△DEB，由此可得BD=DC；（2）只要利用等腰三角形“三线合一”的性质说明AD⊥BC即可.5.2 菱形（第1课时）课堂笔记一组相等的平行四边形叫菱形. 菱形的四条边；菱形的对角线，并且每条对角线平分；菱形既是对称图形，又是对称图形，它至少有条对称轴.课时训练A组基础训练1. 下列特征中，菱形具有而矩形不一定具有的是（）A. 对边平行且相等B. 对角线互相平分C. 内角和等于外角和D. 每一条对角线所在直线都是它的对称轴2. 如图，四边形ABCD是菱形，过点A作BD的平行线交CD的延长线于点E，则下列式子不成立的是（）A. DA=DEB. BD=CEC. ∠EAC=90°D. ∠ABC=2∠E3.如图，在菱形ABCD中，∠BAD=80°，AB的垂直平分线交对角线AC于点F，交AB于点E，连结DF，则∠CDF等于（）A. 80°B. 70°C. 65°D. 60°4. 菱形的周长为16cm，一个内角为60°，则菱形的面积为（）A. 163cm2B. 83cm2C. 43cm2D. 16cm25. 如图，菱形ABCD 中，对角线AC 、BD 相交于点O ，H 为AD 边中点，菱形ABCD 的周长为28，则OH 的长等于（） A. 3.5 B. 4C. 7D. 146. 如图，菱形ABCD 的对角线AC 、BD 的长分别是6cm 、8cm ，AE ⊥BC 于点E ，则AE 的长是（）A.548cm B.524cm C. 512cmD. 53cm7. 在菱形ABCD 中，AB=5，∠BCD=120°，则对角线AC 等于 .8. 如图，在菱形ABCD 中，对角线AC ，BD 交于点O ，则∠AOD= 度，若AC=AB=6，则BD= .9. 如图，是利用四边形的不稳定性制作的菱形晾衣架，已知每个菱形的边长为20cm ，∠1=60°，则在墙上悬挂晾衣架的两个铁钉A ，B 间的距离是 cm.10. 如图，菱形ABCD 中，CE ⊥AB 交AB 的延长线于点E ，CF ⊥AD 交AD 的延长线于点F ，请你猜想CE 与CF 的大小关系，并说明理由.11. （黄冈中考）如图，四边形ABCD 是菱形，对角线AC ，BD 相交于点O ，DH ⊥AB 于点H ，连结OH，求证：∠DHO=∠DCO.12. 已知：如图，在菱形ABCD中，对角线AC、BD相交于点O，DE∥AC，AE∥BD.（1）求证：四边形AODE是矩形；（2）若AB=6，∠BCD=120°，求四边形AODE的面积.B组自主提高13. 如图，已知菱形ABCD的对角线AC＝10，BD＝24，则周长是多少？面积呢？若AE⊥CD 于点E，求AE的长.14. 已知△ABC为等边三角形，点D为直线BC上一动点（点D不与B，C重合）. 以AD为边作菱形ADEF，使∠DAF=60°，连结CF.（1）如图1，当点D在边BC上时：①求证：∠ADB=∠AFC；②请直接判断结论∠AFC=∠ACB+∠DAC是否成立；（2）如图2，当点D在边BC的延长线上时，其他条件不变，结论∠AFC=∠ACB+∠DAC是否成立？若不成立，请写出∠AFC，∠ACB，∠DAC之间存在的等量关系，并写出证明过程；（3）如图3，当点D在边CB的延长线上，且点A，F分别在直线BC的异侧时，其他条件不变，请补全图形，并直接写出∠AFC，∠ACB，∠DAC之间存在的等量关系.参考答案5.2 菱形（第1课时）【课堂笔记】邻边都相等互相垂直一组对角中心轴两【课时训练】 1—5. DBDBA 6. B 7. 5 8. 90 63 9. 20310. CE=CF. ∵四边形ABCD 是菱形，∴AD ∥BC ，AB ∥CD ，CD=BC. ∴∠A=∠CBE ，∠A=∠FDC. ∴∠CBE=∠FDC. ∵CF ⊥AD ，CE ⊥AB ，∴∠CEB=∠CFD=90°，在△CDF 和△CBE 中，∠CDF=∠CBE ，∠CFD=∠CEB ，CD=CB ，∴△CDF ≌△CBE （AAS ）. ∴CE=CF.【点拨】本题方法多样，连结AC ，利用AC 平分∠DAB 得解；也可由垂直联想面积，由S 菱形ABCD ＝AB ×CE ＝AD ×CF 得解.11. 证明：∵四边形ABCD 是菱形，∴OD=OB ，∠COD=90°. 又∵DH ⊥AB ，∴OH=OB ，∴∠OHB=∠OBH. ∵AB ∥CD ，∴∠OBH=∠ODC ，∴∠OHB=∠ODC. 在Rt △COD 中，∠ODC+∠OCD=90°，又DH ⊥AB ，∴∠DHO+∠OHB=90°，∴∠DHO=∠DCO. 12. （1）略（2）93 13. 周长52，面积120，AE ＝13120. 14. （1）提示：①证△ABD ≌△ACF （SAS ），得∠ADB=∠AFC ；②结论成立.（2）不成立，关系为∠AFC=∠ACB-∠DAC ，证△ABD ≌△ACF ，得∠ADC=∠AFC. ∵∠ACB=∠ADC+∠DAC. ∴∠AFC=∠ACB- ∠DAC.（3）补全图形略，等量关系是：∠AFC=2∠ACB -∠DAC 或∠AFC+∠DAC+∠ACB =180°，这两个等式的变式都行.5.2 菱形（第2课时）课堂笔记四条边相等的四边形是；对角线的平行四边形是菱形.课时训练A组基础训练1. 下列命题是假命题的是（）A．四个角相等的四边形是矩形B．对角线相等的平行四边形是矩形C．对角线垂直的四边形是菱形D．对角线垂直的平行四边形是菱形2. 用直尺和圆规作一个以线段AB为边的菱形，作图痕迹如图所示，能得到四边形ABCD是菱形的依据是（）A．一组邻边相等的四边形是菱形B．四边相等的四边形是菱形C．对角线互相垂直的平行四边形是菱形D．每条对角线平分一组对角的平行四边形是菱形3. 如图，顺次连结四边形ABCD各边的中点得到四边形EFGH，要使EFGH是菱形，应添加的条件是（）A. AD∥BCB. AC=BDC. AC⊥BDD. AD=AB4. 将一张矩形纸对折再对折，如图，然后沿着图中的虚线剪下，得到①，②两部分，将①展开后得到的平面图形是（）A. 矩形B. 三角形C. 梯形 D . 菱形5. 如图，已知DE∥AC，D F∥AB，添加下列条件后，不能判断四边形DEAF为菱形的是（）A. AD平分∠BACB. AB=AC且BD=CDC. AD为中线D. EF⊥AD6. 如图，在Rt△ABC中，∠C=90°，AC=BC=6cm，点P从点A出发，沿AB方向以每秒2cm 的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，将△PQC沿BC翻折，点P的对应点为点P′．设点Q运动的时间为t秒，若四边形QPCP′为菱形，则t的值为（）A. 2B. 2C. 22D. 37.如图，四边形ABCD的对角线互相平分，要使它变为菱形，需要添加的条件是（只需填一个）.8. 命题“菱形的对角线互相垂直”的逆命题是，它是命题. （填“真”或“假”）9. 如图，P是菱形ABCD对角线AC上一点，PE⊥AB，且PE=3，则点P到AD的距离为 .10.如图，在△ABC中，点D，E，F分别在边BC，AB，CA上，且DE∥CA，DF∥BA.下列四种说法：①四边形AEDF是平行四边形；②如果∠BAC=90°，那么四边形AEDF是矩形；③如果AD平分∠BAC，那么四边形AEDF是菱形；④如果AD⊥BC且AB=AC，那么四边形AEDF 是菱形. 其中正确的有（只填写序号）.11．如图，将宽度为2cm的两张纸条交叉重叠在一起，得到的重叠部分为四边形ABCD. （1）四边形ABCD是菱形吗？请说明理由.（2）若∠ABC＝45°，求四边形ABCD的面积.12. 如图在ABCD中，O为AC的中点，过O作EF⊥AC交AD，BC于点E，F，求证：四边形AFCE是菱形.B组自主提高13. 如图，在平面直角坐标系中，A点与B点关于x轴对称并且点A的坐标为（3，1），平面内是否存在点N，使以O，A，B，N为顶点的四边形是菱形，请写出所有满足条件N点的坐标为 .14. 在ABCD中，E、F分别是AB、CD的中点，AF与DE相交于点G，CE与BF相交于点H．（1）求证：四边形EHFG是平行四边形；（2）若四边形EHFG是矩形，则ABCD应满足什么条件？（不需要证明）；（3）若四边形EHFG是菱形，则ABCD应满足什么条件？（不需要证明）.参考答案5.2 菱形（第2课时）【课堂笔记】菱形互相垂直【课时训练】1—5. CBBDC 6. B7. 答案不唯一. 如：AB=BC等8. 对角线互相垂直的四边形是菱形假 9. 310. ①②③④【点拨】由两组对边互相平行得到说法①正确；根据矩形的定义得说法②正确；根据菱形的判定定理得说法③④正确.11. （1）四边形ABCD是菱形，用面积法说明邻边相等；（2）四边形ABCD的面积＝42cm2.12. 先证△AOE≌△COF，得OE=OF，又∵AO=CO，∴四边形AFCE是平行四边形. ∵AC⊥EF，∴AFCE是菱形.13. （0，2）、（0，-2）、（23，0）14. （1）∵四边形ABCD是平行四边形，∴AE∥CF，AB=CD，∵E是AB的中点，F是CD的中点，∴AE=CF，∴四边形AECF是平行四边形，∴AF∥CE．同理可得DE∥BF，∴四边形FGEH 是平行四边形；（2）当平行四边形ABCD满足AB=2AD时，平行四边形EHFG是矩形；（3）当平行四边形ABCD是矩形时，平行四边形EHFG是菱形.5.3 正方形（第1课时）课堂笔记有一组相等，并且有一个角是的平行四边形叫做正方形；有一组邻边相等的是正方形. 有一个角是直角的是正方形.课时训练A组基础训练1. 下列命题错误的是（）A．有一组邻边相等的平行四边形叫做正方形B．有一组邻边相等的矩形是正方形C．有一组邻边相等并且有一个角是直角的平行四边形叫做正方形D．有一个角是直角的菱形是正方形2. 如图，四边形EFGH是菱形，要使四边形EFGH是正方形. 则（）A. BD=ACB. BD⊥ACC. ∠HEF=90°D. AB=CD3. （威海中考）如图，在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB 于点E，且BE=BF，添加一个条件，仍不能证明四边形BECF为正方形的是（）A. BC=ACB. CF⊥BFC. BD=DFD. AC=BF4. 顺次连结四边形ABCD各边中点所组成的四边形是正方形，则四边形ABCD的对角线（） A．互相垂直但不相等 B．相等且互相垂直C．相等但不互相垂直 D．互相平分5. 如图，将一张长方形纸片对折两次，然后剪下一个角，打开．如果要剪出一个正方形，那么剪口线与折痕成（）A． 22.5°角 B． 30°角C． 45°角 D． 60°角6. 如图是甲，乙两张不同的矩形纸片，将它们分别沿着虚线剪开后，各自要拼一个与原来面积相等的正方形，则（）A．甲、乙都可以 B．甲、乙都不可以C．甲不可以，乙可以 D．甲可以，乙不可以7．黑板上画有一个图形，学生甲说它是多边形，学生乙说它是平行四边形，学生丙说它是菱形，学生丁说它是矩形，老师说这四名同学的答案都正确，则黑板上画的图形是 .8. 如图所示，一张矩形纸片，要折叠出一个最大的正方形，小明把矩形上的一个角沿折痕AE翻折上去，AB与AD边上的AF重合，则四边形ABEF就是一个大的正方形，他判定的方法是 .9. 已知四边形ABCD中，∠A=∠B=∠C=90°，若添加一个条件即可判定该四边形是正方形，那么这个条件可以是 .10. 菱形ABCD中，对角线AC，BD相交于点O，若再补充一个条件能使菱形ABCD成为正方形，则这个条件是（只填一个条件即可）.11. 如图所示，在Rt△ABC中，CF为∠ACB的平分线，FD⊥AC于D，FE⊥BC于点E，试说明四边形CDFE是正方形.12. 如图，△ABC中，AB=AC，AD是△ABC的角平分线，点O为AB的中点，连结DO并延长到点E，使OE=OD，连结AE，BE.（1）求证：四边形AEBD是矩形；（2）当△ABC满足什么条件时，矩形AEBD是正方形.B组自主提高13. 如图，在等腰Rt△ABC中，∠C=90°，AC=8，F是AB边上的中点，点D，E分别在AC，BC边上运动，且保持AD=CE. 连结DE，DF，EF. 在此运动变化的过程中，下列结论：①△DFE是等腰直角三角形；②四边形CDFE不可能为正方形；③DE长度的最小值为4；④四边形CDFE的面积保持不变；⑤△CDE面积的最大值为8. 其中正确的结论是（）A. ①②③B. ①④⑤C. ①③④D. ③④⑤14. 如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB上一动点，过点D 作DE⊥BC，交直线MN于点E，垂足为点F，连结CD、BE.（1）求证：CE＝AD；（2）当D运动到AB中点时，四边形BECD是什么特殊四边形？说明你的理由；（3）若D运动到AB中点，则∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由.参考答案5.3 正方形（第1课时）【课堂笔记】邻边直角矩形菱形【课时训练】1—5. ACDBC 6. A7. 正方形8. 有一组邻边相等的矩形是正方形9. 答案不唯一. 如AB=BC等10. 答案不唯一. 如AC=BD等11. ∵∠FEC=∠ECD=∠CDF=90°，∴四边形ECDF是矩形. ∵CF平分∠ACB，FD⊥AC，FE⊥BC，∴EF=DF，∴四边形ECDF是正方形.12. （1）∵AO=BO，DO=EO，∴四边形ADBE是平行四边形. ∵AB=AC，AD平分∠BAC，∴AD ⊥BC，即∠ADB=90°，∴ADBE是矩形.（2）当∠BAC=90°时，矩形AEBD是正方形.13. B 【点拨】此题的关键在于判断△DEF是否为等腰直角三角形，作常规辅助线连结CF，由SAS定理可证△CFE和△AFD全等，从而可证∠DFE=90°，DF=EF．所以△DEF是等腰直角三角形．可证①正确，②错误，再由割补法可知④是正确的；判断③，⑤比较麻烦，因为△DEF是等腰直角三角形，DE=2DF，当DF与AC垂直，即DF最小时，DE取最小值42，故③错误，△CDE的最大面积等于四边形CDFE的面积减去△DEF的最小面积，由③可知⑤是正确的．故只有①④⑤正确．14. （1）∵DE⊥BC，∴∠DFB=90°，∵∠ACB=90°，∴∠ACB=∠DFB，∴AC∥DE，∵MN∥AB，即CE∥AD，∴四边形ADEC是平行四边形，∴CE=AD；（2）四边形BECD是菱形，理由是：∵D为AB中点，∴AD=BD，∵CE=AD，∴BD=CE，∵BD ∥CE，∴四边形BECD是平行四边形，∵∠ACB=90°，D为AB中点，∴CD=BD，∴四边形BECD 是菱形；（3）当∠A=45°时，四边形BECD是正方形，理由是：∵∠ACB=90°，∠A=45°，∴∠ABC=∠A=45°，∴AC=BC，∵D为BA中点，∴CD⊥AB，∴∠CDB=90°，∵四边形BECD是菱形，∴菱形BECD是正方形，即当∠A=45°时，四边形BECD是正方形.5.3 正方形（第2课时）课堂笔记正方形的个角都是直角，四条边；正方形的对角线，并且，每条对角线平分一组；正方形既是对称图形，又是对称图形，有条对称轴.课时训练A组基础训练1. 如图，已知正方形ABCD，AC和BD交于点O，下列说法错误的是（）A. AC=BDB. OA≠OBC. OA=OB，OC=ODD. ∠BAO=45°2. 如图，正方形ABCD中，∠DAF=25°，AF交对角线BD于点E，那么∠BEC等于（A． 45° B． 60° C． 70° D． 75°3. 如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连结EF．给出下列五个结论：①AP=EF；②AP⊥EF；③△APD一定是等腰三角形；④∠PFE=∠BAP；⑤PD=2EC．其中正确结论的序号是（）A．①②③④ B．①②④⑤C．②③④⑤ D．①③④⑤4. 如图所示，正方形ABCD的对角线相交于点O，点E是DC上任意一点，EG⊥BD于G，EF ⊥AC于F，若AC=10，则EG+EF的值为（）A. 10B. 4C. 8D. 55. 如图，正方形ABCD的边长为8，点M在DC上且DM=2，N是AC上一动点，则DN+MN的最小值为（）A. 8B. 82C. 217D. 106. 边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′C′D′，两图叠成一个“蝶形风筝”（如图中阴影部分），则这个风筝的面积是（）A. 2-33B. 332 C. 2-43 D. 2 7. 已知：如图所示，点E 是正方形ABCD 内一点，且AE=EB ，∠ABE=60°，则∠AEC= .8. 如图，直线a 经过正方形ABCD 的顶点A ，分别过此正方形的顶点B 、D 作BF ⊥a 于点F 、DE ⊥a 于点E ，若DE=8，BF=5，则EF 的长为 .9. 如图，由4个相同的小正方形组成的格点图中，∠1+∠2+∠3= 度.10．如图，E ，F 分别是正方形ABCD 的边CD ，AD 上的点，且CE ＝DF ，AE ，BF 相交于点O ，下列结论：①AE ＝BF ；②AE ⊥BF ；③AO ＝OE ；④S △AOB ＝S 四边形DEOF 中正确的有 . （填序号）11. 如图，正方形ABCD 的边CD 在正方形ECGF 的边CE 上，连结BE ，DG ，观察猜想BE 与DG 之间的大小关系与位置关系，并证明你的猜想.12．如图，在正方形ABCD 中，点E ，F 分别在边AB ，BC 上，∠ADE ＝∠CDF.（1）求证：AE ＝CF ；（2）连结DB 交EF 于点O ，延长OB 至点G ，使OG ＝OD ，连结EG ，GF ，判断四边形DEGF 是否是菱形，并说明理由.B组自主提高13. 如图，将正方形对折后展开（图4是连续两次对折后再展开），再按图示方法折叠，能够得到一个直角三角形（阴影部分），且它的一条直角边等于斜边的一半．这样的图形有（）A. 4个B. 3个C. 2个D. 1个14．如图，在正方形ABCD中，E是CD边的中点，AC与BE相交于点F，连结DF.（1）在不增加点和线的前提下，直接写出图中所有的全等三角形；（2）连结AE，试判断AE与DF的位置关系，并证明你的结论；（3）延长DF交BC于点M，试判断BM与MC的数量关系（直接写出结论）.参考答案5.3 正方形（第2课时）【课堂笔记】四相等相等互相垂直平分对角中心轴 4【课时训练】1—5. BCBDD6. A 阴影部分的面积=两个正方形的面积和-两个正方形的重叠部分的四边形的面积，观察重叠的四边形，是由两个全等的直角三角形组成，通过计算这两个直角三角形的面积为63，因此蝶形风筝的面积为1+1-2×63=2-33. 故选A. 7. 135°8. 139. 13510. ①②④11. BE=GD ，BE ⊥DG ，延长GD 交BE 于点H ，先证△BCE ≌△DCG ，得BE=DG ，∠CDG=∠EBC. ∵∠CDG+∠CGD=90°，∴∠CGD+∠EBC=90°，∴∠GHB=90°，∴BE ⊥GD.12. （1）在正方形ABCD 中，AD=CD ，∠A=∠C=90°，在△ADE 和△CDF 中，∠ADE=∠CDF ，AD=CD ，∠A=∠C=90°，∴△ADE ≌△CDF （ASA ），∴AE=CF ；（2）四边形DEGF 是菱形. 理由如下：在正方形ABCD 中，AB=BC ，∵AE=CF ，∴AB-AE=BC-CF ，即BE=BF ，∵△ADE ≌△CDF ，∴DE=DF ，∴BD 垂直平分EF ，又∵OG=OD ，∴四边形DEGF 是菱形.13. C14. （1）△ADF ≌△ABF ，△ADC ≌△ABC ，△CDF ≌△CBF.（2）AE ⊥DF. 设AE 与DF 相交于点H. ∵四边形ABCD 是正方形，∴AD=AB ，∠DAF=∠BAF. 又∵AF=AF ，∴△ADF ≌△ABF. ∴∠1=∠2. 又∵AD=BC ，∠ADE=∠BCE=90°，DE=CE ，∴△ADE ≌△BCE. ∴∠3=∠4. ∵∠2+∠4=90°，∴∠1+∠3=90°，∴∠AHD=90°. ∴AE ⊥DF.（3）∵∠ADE=90°，AE ⊥DF. ∴∠1+∠5=90°，∠3+∠1=90°. ∴∠3=∠5，∵∠3=∠4，∴∠4=∠5. ∵DC=BC ，∠DCM=∠BCE=90°，∴△DCM ≌△BCE. ∴CE=CM ，又∵E 为CD 中点，且CD=CB ，∴CE=21CD=21BC ，∴CM=21CB ，即M 为BC 中点，∴BM=MC.。

【高效课时通】八年级数学下册课时达标训练期末专项复习(共38课时,pdf) 浙教版

章末专题训练 …………………………… (37)
第 4 章平行四边形
4 . 1 多边形 ……………………………… (39)
课时 1 多边形的相关概念及四边形课时 2 多边形的内角和定理及推论的内角和 …………………… (39) ……………………………… (40)
2 . 2 一元二次方程的解法 …………… (15)
要点 1 四边形的内角和定理的验证及应用( P39) 4. 1 多边要点 2 多边形的对角线的应用( P40) 形要点 3 多边形的内角和定理及推论的应用( P40) 要点 1 平行四边形的边㊁角的性质( P43) 要点 2 两条平行线之间的距离( P43) 要点 3 平行四边形对角线的性质( P44) 要点 1 识别中心对称图形的方法( P48) 要点 2 确定对称中心的方法( P48) 要点 1 应用边判定平行四边形( P50) 要点 2 平行四边形的判定方法( P51) 要点 1 三角形的中位线( P54) 要点 1 反证法的一般证明步骤( P56) 专题 1 多边形的内角和定理及推论的应用( P58) 专题 2 平行四边形的性质与判定( P58) 专题 3 中心对称( P59) 专题 4 三角形的中位线( P59) 要点 1 矩形的性质( P60) 要点 2 矩形的判定方法( P61) 要点 1 菱形的性质( P64) 要点 2 菱形的判定( P65)
1 . 2 二次根式的性质 ………………… ( 3 )
3 . 2 中位数和众数 ……………………… (30)
1 . 3 二次根式的运算 ………………… ( 6 )
章末专题训练 …………………………… (11)
综合提升训练( 1 . 3 ) ………………… ( 9 )
3 . 3 方差和标准差 ……………………… (35)

浙教版数学八年级下册课时训练： 5.1 .docx

浙教版数学八年级下册八下第五章 特殊平行四边形 拔尖训练(含答案)

期末复习五 特殊平行四边形-2020春浙教版八年级数学下册课时训练