全等三角形经典例题整理
全等三角形经典题型50题(含答案)
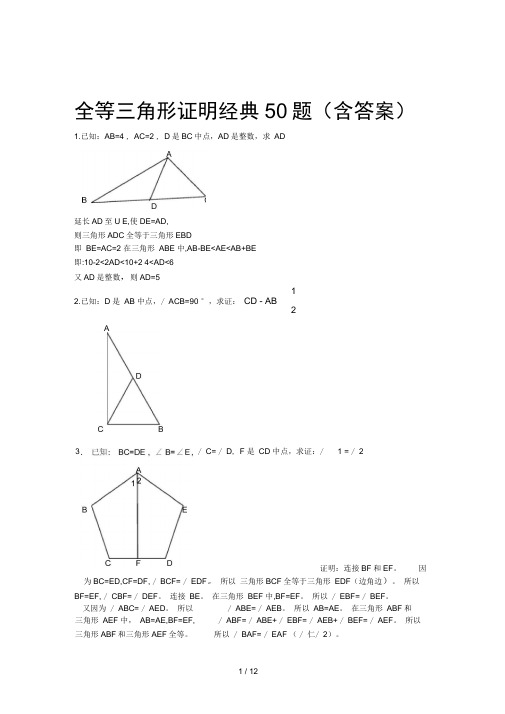
全等三角形证明经典50题(含答案)1.已知:AB=4 , AC=2 , D 是BC 中点,AD 是整数,求 AD延长AD 至U E,使DE=AD, 则三角形ADC 全等于三角形EBD即 BE=AC=2 在三角形 ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=512.已知:D 是 AB 中点,/ ACB=90 °,求证: CD - AB2为BC=ED,CF=DF, / BCF= / EDF 。
所以 三角形BCF 全等于三角形 EDF (边角边)。
所以BF=EF, / CBF= / DEF 。
连接 BE 。
在三角形 BEF 中,BF=EF 。
所以 / EBF= / BEF 。
/ ABE= / AEB 。
所以 AB=AE 。
在三角形 ABF 和 / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF 。
所以/ C= / D , F 是 CD 中点,求证:/ 1 = / 2证明:连接BF 和EF 。
因又因为 / ABC= / AED 。
所以 三角形 AEF 中, AB=AE,BF=EF, 三角形ABF 和三角形AEF 全等。
所以 / BAF= / EAF ( / 仁/ 2)。
A3因为 EB = EF ,CE = CE , 所以△ CEBCEF 所以/ B = / CFE 因为/ B +/ D = 180° / CFE + / CFA = 180° 所以/ D = / CFA 因为 AC 平分/ BAD 所以/ DAC = / FAC 又因为 AC = AC 所以△ ADC 也厶AFC ( SAS ) 所以AD = AF 所以AE = AF + FE = AD + BE12.如图,四边形 ABCD 中,AB // DC ,BE 、CE 分别平分/ ABC 、/ BCD ,且点 E 在AD 上。
全等三角形经典例题整理

CB全等三角形的典型习题一、全等在特殊图形中的运用1、如图,等边△ABC 中,D 、E 分别是AB 、CA 上的动点,AD =CE ,试求∠DFB 的度数.2、如下图所示,等边△ABC 中,D 、E 、F 是AB 、BC 、CA 上动点,AD =BE =CF ,试判断△DEF 的形状.3、如图,△ABC 和△ADE 都是等边三角形,线段BE 、CD 相交于点H ,线段BE 、AC 相交于点G ,线段BE 、CD 相交于点H .请你解决以下问题:(1) 试说明BE =CD 的理由;(2) 试求BE 和CD 的夹角∠FHE 的度数Ex1、如下图所示,△ABC 和△ADE 都是等边三角形,且点B 、A 、D 在同一直线上,AC 、BE 相交于点G ,AE 、CD 相交于点F ,试说明AG =AF 的理由.Ex2、如图,四边形ABCD 与BEFG 都是正方形,AG 、CE 相交于点O ,AG 、BC 相交于点M ,BG 、CE 相交于点N ,请你猜测AG 与CE 的关系(数量关系和位置关系)并说明理由.4、△ABC 是等腰直角三角形,AB =AC ,∠BAC =90°,∠B =∠C =45°,D 是底边BC 的中点,DE ⊥DF ,试用两种不同的方法说明BE 、CF 、EF 为边长的三角形是直角三角形。
ADD ACm二.证明全等常用方法(截长发或补短法)5、如图所示,在△ABC 中,∠ABC =2∠C ,∠BAC 的平分线交BC 于点D .请你试说明AB +BD =AC 的理由.Ex1,∠C +∠D =180°,∠1=∠2,∠3=∠4.试用截长法说明AD +BC =AB .Ex2、五边形ABCDE 中,AB =AE,∠BAC +∠DAE =∠CAD,∠ABC +∠AED =180°,连结AC ,AD .请你用补短法说明BC +DE =CD .(也可用截长法,自己考虑)6、如图,正方形ABCD 中,E 是AB 上的点,F 是BC 上的点,且∠EDF=45°.请你试用补短法说明AE +CF =EF .Ex1.、如图所示,在△ABC 中,边BC 在直线m 上,△ABC 外的四边形ACDE 和四边形ABFG 均为正方形,DN ⊥m 于N ,FM ⊥m 于M .请你说明BC =FM +DN 的理由.(分别用截长法和补短法) (连结GE ,你能说明S △ABC =S △AGE 吗?)三.全等在探究题中的运用7、数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=,且EF 交正方形外角DCG ∠的平行线CF 于点F ,求证:AE =EF .经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =. (1) 请你写出说明△ABC ≌△ECF 的理由; 在此基础上,同学们作了进一步的研究: (2)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由; (3)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.BB FC ABA D F C G EB 图1 A D FC G E B 图2 AD F C GE B 图3(第2题图)Ex1、如图1,一等腰直角三角尺GEF (∠EGF=90°,∠GEF=∠GFE=45°,GE=GF )的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转. (1)如图2,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想FN ,BM 相等吗?并说明理由;(2)若三角尺GEF 旋转到如图3所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与GF 的延长线相交于点N ,此时,(1)中的猜想还成立吗?请说明理由.Ex2.在平面内,旋转变换是指某一图形绕一个定点按顺时针或逆时针旋转一定的角度而得到新位置图形的一种变换. 活动一:如图1,在Rt △ABC 中,D 为斜边 AB 上的一点,AD =2,BD =1,且四边形DECF 是正方形,求阴影部分的面积.小明运用图形旋转的方法,将△DBF 绕点D 逆时针旋转90°,得到△DGE (如图2所示),一眼就看出这题的答案,请你写出阴影部分的面积: .活动二:如图3,在四边形ABCD 中,AB =AD ,∠BAD =∠C =90°,BC =5,CD =3,过点A 作AE ⊥BC ,垂足为点E ,求AE 的长.小明仍运用图形旋转的方法,将△ABE 绕点A 逆时针旋转90°,得到△ADG (如图4所示),则①四边形AECG 是怎样的特殊四边形?答: .②AE 的长是 .活动三:如图5,在四边形ABCD 中,AB ⊥AD ,CD ⊥AD ,将BC 按逆时针方向绕点B 旋转90°得到线段BE ,连接AE .若AB =2,DC =4,求△ABE 的面积.图2图3图1A ( G )B ( E)图1 B 图2图5BCDA ED G 图4A BD 图E四.动点问题中的全等、8如图,已知ABC △中,20AB AC ==厘米,BC=16厘米,点D 为AB 的中点. (1)如果点P 在线段BC 上以6厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动 速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多 长时间点P 与点Q 第一次在ABC △的哪条边上相遇?。
三角形全等例题+练习(常用方法)
B
DE C
7
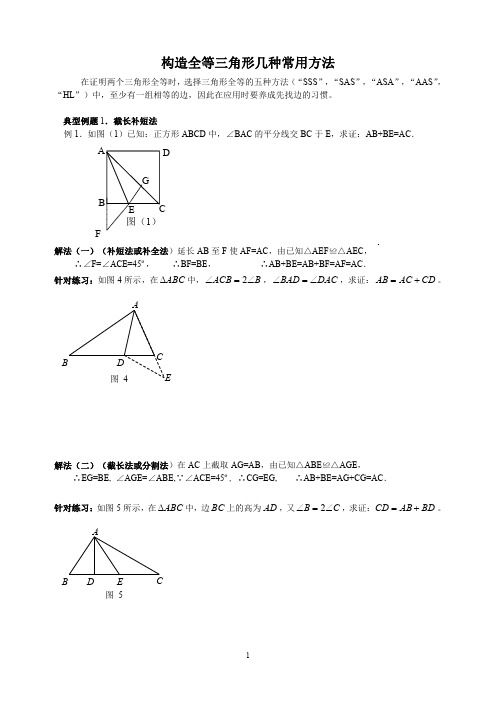
典型例题 5.翻折法 若题设中含有垂线、角的平分线等条件的,可以试用轴对称性质,沿轴翻转图形来构造全等三角形.
例 5.如图(8)已知:在△ABC 中,∠A=45º, AD⊥BC,若 BD=3,DC=2, 求:△ABC 的面积.
A
E
F
B DC
G
针对练习 1:如图2所示,已知 ABC 中, AC BC , ACB 90 , BD 平分 ABC , 求证: AB BC CD 。
0
60
,
C
400
,P,Q
分别在
BC,CA
上,并且
AP
、BQ 分别是 BAC , ABC 的角平分线。求证:BQ+AQ=AB+BP
A
B Q
P
C
截长补短 4、如图,在四边形 ABCD 中,BC>BA,AD=CD,BD 平分 ABC , 求证: A C 1800
A D
B
C
截长补短 5、如图在△ABC 中,AB>AC,∠1=∠2,P 为 AD 上任意一点,求证;AB-AC>PB-PC
∠MBN 60 ,∠MBN 绕 B 点旋转,它的两边分别交 AD,DC (或它们的延长线)于
E,F . 当∠MBN 绕 B 点旋转到 AE CF 时(如图 1),易证 AE CF EF . 当∠MBN 绕 B 点旋转到 AE CF 时,在图 2 和图 3 这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,线段 AE,CF , EF 又有怎样的数量关系?请写出你的 猜想,不需证明.
A
B
EM
A
B
EM
A B
CF
全等三角形经典题型50题(含答案)

全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF。
又因为 ∠ABC=∠AED。
所以 ∠ABE=∠AEB。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
BADBCC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA,∠DGE=∠2又∵CD=DE∴⊿ADC≌⊿GDE (AAS )∴EG=AC∵EF//AB∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE∴EF=E G ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE 证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE⊥AB 所以∠CEB=∠CEF=90° 因为EB =EF ,CE =CE , 所以△CEB≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE+∠CFA=180° 所以∠D=∠CFA 因为AC 平分∠BAD 所以∠DAC=∠FAC 又因为AC =AC 所以△ADC≌△AFC(SAS ) 所以AD =AF所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形经典题型整理

1. 如图,Rt △ABC 中,∠BAC=90°,AB=AC ,分别过点B 、C 作过点A 的垂线BC 、CE ,垂足分别为D 、E ,若BD=3,CE=2,则DE= 2. 如图所示,在△ABC 中,AD 为∠BAC 的角平分线,D E ⊥AB 于E ,DF ⊥AC 于F ,△ABC 的面积是28cm 2,AB=20cm ,AC=8cm ,求DE 的长。
3. 如图,AD=BD ,A D ⊥BC 于D ,BE ⊥AC 于E ,AD 与BE 相交于点H ,则BH 与AC 相等吗?为什么?4. 如图所示,已知,AD 为△ABC 的高,E 为AC 上一点,BE 交AD 于F ,且有BF=AC ,FD=CD ,求证:B E ⊥AC5. △DAC 、△EBC 均是等边三角形,AF 、BD 分别与CD 、CE 交于点M 、N ,求证:(1)AE=BD (2)CM=CN(3)△CMN 为等边三角形 (4)MN ∥BC6. 已知:如图1,点C 为线段AB 上一点,△ACM 、△CBN 都是等边三角形,AN 交MC 于点E ,BM 交CN于点F(1) 求证:AN=BM(2) 求证:△CEF 为等边三角形(3) 将△ACM 绕点C 按逆时针方向旋转90°,其他条件不变,在图2中补出符合要求的图形,并判断第(1)、(2)两小题的结论是否仍然成立(不要求证明)。
7. 如图所示,已知△ABC 和△BDE 都是等边三角形,下列结论:①AE=CD ;②BF=BG ;③BH 平分∠AHD ;④∠AHC=60°;⑤△BFG 是等边三角形;⑥FG ∥AD ,其中正确的有( ) A .3个 B. 4个 C. 5个 D. 6个 8. 已知:BD 、CE 是△ABC 的高,点F 在BD 上,BF=AC ,点G 在CEB B A B C图1A 图2MA G ⊥AF9. 如图:在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD=AC ,在CF 的延长线上截取CG=AB ,连结AD 、AG 求证:(1)AD=AG(2) AD 与AG 的位置关系如何10. 如图所示,已知在△AEC 中,∠E=90°,AD 平分∠EAC ,DF ⊥AC ,垂足为F ,DB=DC ,求证:BE=CF11. 已知:如图,BF ⊥AC 于点F ,CE ⊥AB 于点E ,且BD=CD求证:(1)△BDE ≌△CDF(2) 点D 在∠A 的平分线上12. 在△ABC 中,∠ACB=90°,AC=BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E (1)当直线MN 绕点C 旋转到图①的位置时,求证:DE=AD+BE (2)当直线MN 绕点C 旋转到图②的位置时,求证:DE=AD-BE(3)当直线MN 绕点C 旋转到图③的位置时,试问DE 、AD 、BE 具有怎样的等量关系?请直接写出这个等量关系。
全等三角形经典题型50题(含问题详解)

全等三角形经典题型50题(含问题详解)全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<ae<ad<2ad2. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为BC=ED,CF=DF,∠BCF=∠EDF 。
所以三角形BCF 全等于三角形EDF(边角边)。
所以BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以∠EBF=∠BEF 。
又因为∠ABC=∠AED 。
所以∠ABE=∠AEB 。
所以AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以三角形ABF 和三角形AEF 全等。
所以∠BAF=∠EAF (∠1=∠2)。
ADC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB=∠CEF =90° 因为EB =EF ,CE =CE ,所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS )所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
全等三角形证明经典30题

全等三角形证明经典30题1. 两角和相等定理证明:设△ABC 和△DEF 是两个三角形,如果∠A = ∠D 且∠B = ∠E,则可以通过以下步骤证明△ABC ≌△DEF:步骤一:通过顶角顶点 C 、 F、和共边 CF 作直线段 CF,延长直线段 CF 至点 X,使得 CX = CE。
步骤二:连接线段 AX。
步骤三:证明∠AXB = ∠EXF:由于∠A = ∠D,所以∠AXB = ∠DXE(共同的角度)。
又由于∠B = ∠E,所以∠DXE = ∠EXF。
因此,∠AXB = ∠EXF。
步骤四:证明∠ABX = ∠EFX:由于∠B = ∠E,所以∠ABX = ∠EXF(共同的角度)。
因此,∠ABX = ∠EFX。
步骤五:证明 AB = EF:由于 CX = CE,且∠ABX = ∠EFX,根据 SSS(边-边-边)全等三角形定理,则可得∆ABX ≌ ∆EFX。
因此,AB = EF。
综上所述,根据两角和相等定理,已经证明了△ABC ≌△DEF。
2. SAS全等三角形定理证明:设△ABC 和△DEF 是两个三角形,如果 AB = DE,∠A = ∠D,且 AC = DF,则可以通过以下步骤证明△ABC ≌△DEF:步骤一:连接线段 BC 和 EF。
步骤二:证明∠ABC = ∠DEF:由于 AB = DE,且∠A = ∠D,根据线段角度定理,可得∠ABC = ∠DEF。
步骤三:证明 BC = EF:由于 AC = DF,且∠ABC = ∠DEF,根据 SAS(边-角-边)全等三角形定理,可得△ABC ≌△DEF。
综上所述,根据SAS全等三角形定理,已经证明了△ABC ≌△DEF。
3. SSS全等三角形定理证明:设△ABC 和△DEF 是两个三角形,如果 AB = DE,BC = EF,且AC = DF,则可以通过以下步骤证明△ABC ≌△DEF:步骤一:连接线段 AC 和 DF。
步骤二:连接线段 BC 和 EF。
全等三角形经典题型50题[含答案]
![全等三角形经典题型50题[含答案]](https://img.taocdn.com/s3/m/6ec7153dbed5b9f3f80f1c1f.png)
全等三角形证明经典50题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
因为 BC=ED,CF=DF,∠BCF=∠EDF 。
所以 三角形BCF 全等于三角形EDF(边角边)。
所以 BF=EF,∠CBF=∠DEF 。
连接BE 。
在三角形BEF 中,BF=EF 。
所以 ∠EBF=∠BEF 。
又因为 ∠ABC=∠AED 。
所以 ∠ABE=∠AEB 。
所以 AB=AE 。
在三角形ABF 和三角形AEF 中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。
所以 三角形ABF 和三角形AEF 全等。
所以 ∠BAF=∠EAF (∠1=∠2)。
ADBC4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE (AAS )∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS )∴∠AED=∠B ,DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE证明: 在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥AB 所以∠CEB=∠CEF =90° 因为EB =EF ,CE =CE , 所以△CEB ≌△CEF 所以∠B =∠CFE 因为∠B +∠D =180°,∠CFE +∠CFA =180° 所以∠D =∠CFA 因为AC 平分∠BAD 所以∠DAC =∠FAC 又因为AC =AC 所以△ADC ≌△AFC (SAS ) 所以AD =AF 所以AE =AF +FE =AD +BE12. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形的典型习题、全等在特殊图形中的运用
1如图,等边△ ABC中,D、E分别是AB、CA上的动点,AD = CE,试求
/ DFB的度数.
BC、CA 上动点,AD =BE 2、如下图所示,等边△ ABC中,D、E、F是AB、
=CF,试判断△ DEF的形状.
3、如图,△ ABC和厶ADE都是等边三角形,线段BE、CD相交于点H,线段BE、AC相交于点G,线段BE、CD相交于点H .请你解决以下问题:
(1)试说明BE = CD的理由;
(2)试求BE和CD的夹角/ FHE 的度数
Ex1、如下图所示,△ ABC和厶ADE都是等边三角形,且点B、A、D在同一
直线上,AC、BE相交于点G,AE、CD相交于点F,试说明AG = AF的理由.
Ex2、如图,四边形ABCD与BEFG都是正方形,
BC相交于点M , BG、CE相交于点N,请你猜测
和位置关系)并说明理由.
F
4、A ABC是等腰直角三角形,AB = AC,/ BAC = 90° / B
=Z C= 45° D是底边BC 的中点,DE丄DF,试用两种不同的方法说明BE、CF、EF为边长的三角形
是直角三角
精选文档
•证明全等常用方法(截长发或补短法)
5、如图所示,在厶
ABC 中,/ ABC = 2/ C , 你
试说明AB + BD = AC 的理由.
Ex1,Z C+Z D = 180°,/ 1 = AB.
形。
Z 2,Z 3=Z 4.试用截长法说明 AD + BC = C
A
Ex2、五边形ABCDE 中,AB = AE, / BAC+Z DAE = / CAD, / ABC + Z AED =
180°,连结AC, AD •请你用补短法说明
自己考虑)
6、如图,正方形ABCD中,E是AB上的点,F 是BC上的点,且Z EDF = 45° •请
你试用补短法说明AE + CF= EF .
Ex1.、如图所示,在厶ABC中,边BC在直线m上,△ ABC外的四边形ACDE 和四边形ABFG均为正方形,DN丄m于N , FM丄m于M .请你说明BC= FM + DN的理由.
三.全等在探究题中的运用
7、数学课上,张老师出示了问题:如图1四边形ABCD是正方形,点E是边
BC的中点. AEF 90°,且EF交正方形外角DCG的平行线CF于点F,求证:
AE = EF•经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则
AM=EC,易证△ AME ◎△ ECF,所以AE EF •
(1)请你写出说明△ ABC^A ECF的理由;
在此基础上,同学们作了进一步的研究:
(2)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B, C夕卜)的任意一点”,其它条件不变,那么结论“ AE = EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(3)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“ AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;
图1 图2 图3
(第2题图)
Ex1、如图1, 一等腰直角三角尺GEF (/ EGF=90。
,/ GEF= / GFE=45 ° ,GE=GF )的两条直角边与正方形ABCD的两条边分别重合在一起•现正方形ABCD保持不动,将三角尺GEF绕斜边EF 的中点0 (点0也是BD中点)按顺时针方向旋转.
(1)如图2,当EF与AB相交于点M, GF与BD相交于点N时,通过观察或测量BM, FN的长度,猜想FN, BM相等吗?并说明理由;
(2)若三角尺GEF旋转到如图3所示的位置时,线段FE的延长线与AB的延长线相交
请说明理由.
图1
C
B
图2
G
图3
于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?
Ex2 .在平面内,旋转变换是指某一图形绕一个定点按顺时针或逆时针旋转一定的角度而
得到新位置图形的一种变换. 活动一:如图1,在Rt A ABC 中,D 为斜边
AB 上的一点,AD =2, BD =1,且四边形DECF 是
正方形,求阴影部分的面积.
A
小明运用图形旋转的方法, 将厶DBF 绕点D 逆时
针旋转90。
,得到厶DGE (如图2所示), 一眼就看出这题的答案,请你写出阴影部分的面积: 活动二:如图 3,在四边形 ABCD 中,AB =AD ,/ BAD = / C =90 ° , BC =5 , CD =3,过
点A 作AE 丄BC ,垂足为点E ,求AE 的长.
小明仍运用图形旋转的方法,将△ ABE 绕点A 逆时针旋转90。
,得到厶
ADG (如图4 所示),则①四边形 AECG 是怎样的特殊四边形?答:
__________________________________________________________________ •②AE 的长 是 _________ .
AB 丄AD , CD 丄AD ,将BC 按逆时针
方向绕点
活动三:如图5,在四边形 ABCD 中, 图1 D
B
旋转90。
得到线段BE,连接AE .若AB=2 , DC=4,求△ ABE 的面积.
四.动点问题中的全等、
8如图,已知△ ABC中,AB AC 20厘米,BC=16厘米,点D为AB的中点.
(1)如果点P在线段BC上以6厘米/秒的速度由B点向C点运动,同时,点Q在线段
CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△ BPD与厶CQP是否全等,
请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使
△ BPD与厶CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动
速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多
长时间点P与点Q第一次在△ ABC的哪条边上相遇?。
