差分方法实验报告
实验报告_差分式放大电路
实验报告_差分式放大电路一、实验目的：1.了解差分式放大电路的工作原理；2.熟悉差分放大电路的实际应用场景；3.掌握实验中的测量方法和仪器的使用。
二、实验仪器与设备：1.示波器；2.信号发生器；3.双踪电压表。
三、实验原理和内容：差分放大电路是一种常用的放大电路，它是以运放为核心组成的，通过对输入信号进行差分放大，从而实现信号放大和滤波等功能。
差分放大电路的输入端是由两个输入信号和一个共模信号组成的，一般情况下，差分输入电路的两个输入端的信号具有相同的幅值和频率，相位差为180°。
本实验使用两个预先设定的输入电压，分别作为差分放大电路的输入信号，并利用示波器测量输出信号的放大后的幅值和相位。
四、实验步骤：1.将差分放大电路的输入端分别与信号发生器的正负端子相连，并将信号发生器的输出设置为正弦信号；2.调节信号发生器的幅值和频率，观察并记录信号发生器的输出波形；3.分别将差分放大电路的输出端和电压表的两个测量端相连，调节电压表的量程，记录输出电压的幅值和相位差；4.调节信号发生器的频率，观察并记录输出信号的变化情况；5.分别改变其中一个输入信号的幅值和频率，观察并记录输出信号的变化；6.对实验数据进行处理和分析，总结实验结果和心得体会。
五、实验数据处理：1.绘制输入电压和输出电压随频率变化的曲线图；2.对输入电压和输出电压的幅值和相位差进行统计和比较；3.分析数据的相关性和实验结果的可靠性；4.从实验结果中得出结论，总结实验心得和体会。
六、实验结论：通过本实验，我们对差分式放大电路有了更深入的理解，了解了差分放大电路的基本工作原理和应用场景。
实验结果显示，差分放大电路能够有效放大输入信号，并且输出信号的幅值和相位差与输入信号有一定的关系。
实验数据的分析和处理结果也验证了差分放大电路的性能和可靠性。
七、实验改进：在实验过程中，可以尝试调整不同的输入信号和改变差分放大电路的其他参数，进一步研究其对输出信号的影响。
差分方程模型
实验八： 差分方程模型
实验目的：
1. 掌握一阶和二阶常系数线性差分方程的求解方法；
2. 利用差分方程建模。
实验练习：
1. 求下列一阶常系数线性差分方程的通解： (1) 134n n y y ++=； (2)
12cos()n n n y y n p +-=.
注：若12()cos sin f n b n b n w w =+，则特解可设为
*cos sin n y n n a w b w =+其中,a b 为待定系数，求解关于,a b 的
方程组，若系数矩阵为0，则特解可设为
*(cos sin )n y n n n a w b w =+
2. 教材P173，习题4.
3. 求下列二阶常系数线性差分方程的通解：
()()2222cos sin .
n n n n y y p p ++=-安徽师
范大学
数计 学院实验报告
专业名称数学与应用数学实验室2号实验楼#201 实验课程Matlab
实验名称差分方程模型
姓名张顺强
学号100701185
同组人员无
实验日期2013.。
仿真实验--差分电路仿真实验
仿真实验三差分电路仿真实验一、实验目的（1）通过Multisim来仿真电路，测试差分放大电路的静态工作点、差模电压放大倍数、输入电阻和输出电阻；（2）加深对差分放大电路原理的理解；（3）通过仿真，体会差分放大电路对温漂的抑制作用；二、实验平台Multisim 10.0三、实验原理差放的外信号输入分差模和共模两种基本输入状态。
当外信号加到两输入端子之间，使两个输入信号V i1、V i2的大小相等、极性相反时，称为差模输入状态。
此时，外输入信号称为差模输入信号，以V id表示，且有:当外信号加到两输入端子与地之间，使V i1、V i2大小相等、极性相同时，称为共模输入状态，此时的外输入信号称为共模输入信号，以V ic表示，且:当输入信号使V i1、V i2的大小不对称时，输入信号可以看成是由差模信号Vid和共模信号V ic两部分组成，其中动态时分差模输入和共模输入两种状态。
(1)对差模输入信号的放大作用当差模信号V id输入(共模信号V ic=0)时，差放两输入端信号大小相等、极性相反，即V i1=－V i2=V id/2,因此差动对管电流增量的大小相等、极性相反，导致两输出端对地的电压增量，即差模输出电压V od1、V od2大小相等、极性相反，此时双端输出电压V o=V od1－V od2=2V od1=V od,可见，差放能有效地放大差模输入信号。
要注意的是：差放公共射极的动态电阻R e对差模信号不起(负反馈)作用。
(2)对共模输入信号的抑制作用当共模信号V ic输入(差模信号V id=0)时，差放两输入端信号大小相等、极性相同，即V i1=V i2=V ic,因此差动对管电流增量的大小相等、极性相同，导致两输出端对地的电压增量，即差模输出电压V oc1、V oc2大小相等、极性相同，此时双端输出电压V o=V oc1－V oc2=0,可见，差放对共模输入信号具有很强的抑制能力。
此外，在电路对称的条件下，差放具有很强的抑制零点漂移及抑制噪声与干扰的能力。
差分法求解偏微分方程MAAB
南京理工大学课程考核论文课程名称：高等数值分析论文题目：有限差分法求解偏微分方程姓名：罗晨学号：成绩：有限差分法求解偏微分方程一、主要内容1.有限差分法求解偏微分方程，偏微分方程如一般形式的一维抛物线型方程：具体求解的偏微分方程如下：2.推导五种差分格式、截断误差并分析其稳定性；3.编写MATLAB程序实现五种差分格式对偏微分方程的求解及误差分析；4.结论及完成本次实验报告的感想。
二、推导几种差分格式的过程：有限差分法（finite-differencemethods ）是一种数值方法通过有限个微分方程近似求导从而寻求微分方程的近似解。
有限差分法的基本思想是把连续的定解区域用有限个离散点构成的网格来代替；把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似；把原方程和定解条件中的微商用差商来近似，积分用积分和来近似，于是原微分方程和定解条件就近似地代之以代数方程组，即有限差分方程组，解此方程组就可以得到原问题在离散点上的近似解。
推导差分方程的过程中需要用到的泰勒展开公式如下：()2100000000()()()()()()()......()(())1!2!!n n n f x f x f x f x f x x x x x x x o x x n +'''=+-+-++-+-(2-1)求解区域的网格划分步长参数如下：11k k k kt t x x h τ++-=⎧⎨-=⎩(2-2) 2.1古典显格式2.1.1古典显格式的推导由泰勒展开公式将(,)u x t 对时间展开得2,(,)(,)()()(())i i k i k k k uu x t u x t t t o t t t∂=+-+-∂(2-3) 当1k t t +=时有21,112,(,)(,)()()(())(,)()()i k i k i k k k k k i k i k uu x t u x t t t o t t tuu x t o tττ+++∂=+-+-∂∂=+⋅+∂(2-4)得到对时间的一阶偏导数1,(,)(,)()=()i k i k i k u x t u x t uo t ττ+-∂+∂(2-5) 由泰勒展开公式将(,)u x t 对位置展开得223,,21(,)(,)()()()()(())2!k i k i k i i k i i u uu x t u x t x x x x o x x x x∂∂=+-+-+-∂∂(2-6)当11i i x x x x +-==和时，代入式(2-6)得2231,1,1122231,1,1121(,)(,)()()()()(())2!1(,)(,)()()()()(())2!i k i k i k i i i k i i i i i k i k i k i i i k i i i iu u u x t u x t x x x x o x x x xu u u x t u x t x x x x o x x x x ++++----⎧∂∂=+-+-+-⎪⎪∂∂⎨∂∂⎪=+-+-+-⎪∂∂⎩(2-7) 因为1k k x x h +-=，代入上式得2231,,22231,,21(,)(,)()()()2!1(,)(,)()()()2!i k i k i k i k i k i k i k i ku u u x t u x t h h o h x xu u u x t u x t h h o h x x +-⎧∂∂=+⋅+⋅+⎪⎪∂∂⎨∂∂⎪=-⋅+⋅+⎪∂∂⎩(2-8) 得到对位置的二阶偏导数2211,22(,)2(,)(,)()()i k i k i k i k u x t u x t u x t uo h x h+--+∂=+∂(2-9) 将式(2-5)、(2-9)代入一般形式的抛物线型偏微分方程得(2-10)为了方便我们可以将式(2-10)写成11122k kk k k k i i i i i i u u u u u f h ατ++-⎡⎤--+-=⎢⎥⎣⎦(2-11) ()11122k k k k k k i i i i i i u u uu u f hτατ++----+=(2-12)最后得到古典显格式的差分格式为()111(12)k k k k k i i i i i u ra u r u u f ατ++-=-+++(2-13)2r hτ=其中，古典显格式的差分格式的截断误差是2()o h τ+。
三轮DES差分分析实验报告-刘杰
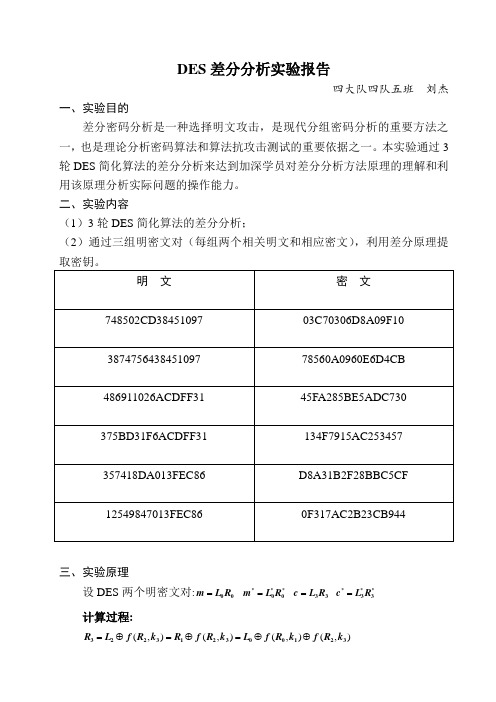
DES 差分分析实验报告四大队四队五班 刘杰一、实验目的差分密码分析是一种选择明文攻击，是现代分组密码分析的重要方法之一，也是理论分析密码算法和算法抗攻击测试的重要依据之一。
本实验通过3轮DES 简化算法的差分分析来达到加深学员对差分分析方法原理的理解和利用该原理分析实际问题的操作能力。
二、实验内容（1）3轮DES 简化算法的差分分析；（2）通过三组明密文对（每组两个相关明文和相应密文），利用差分原理提三、实验原理设DES 两个明密文对:=00m L R ***=00m L R =33c L R ***=33c L R计算过程:(,)(,)(,)(,)=⊕=⊕=⊕⊕322312300123R L f R k R f R k L f R k f R k(,)(,)****=⊕⊕300123R L f R k f R k令：*'=⊕000L L L (,)(,)(,)(,)***''=⊕=⊕⊕⊕⊕333001012323R R R L f R k f R k f R k f R k 观察得：在本次实验原始数据中，明文对*=00R R ，即*'=⊕=00000000000R R R 则(,)(,)**''=⊕=⊕⊕33302323R R R L f R k f R k 同时有：=00m L R ***=00m L R =23R L **=23R L则可计算出：*'=⊕000L L L *'=⊕333R R R (,)(,)*''⊕=⊕232330f R k f R k R L则可得出：S 盒输入差：(())(())()()**⊕⊕⊕=⊕232333E R k E R k E L E LS 盒输出差：()*-''⊕=⊕130D D P R L分析过程：令：()()*⊕=3312345678E L E L B B B B B B B B()-''⊕=13012345678P R L C C C C C C C C ()=312345678E L A A A A A A A A =312345678k J J J J J J J J()⊕=3312345678E L k X X X X X X X X *()⊕=3312345678E L k Y Y Y Y Y Y Y Y基本思路：（分别计算12345678J J J J J J J J ）{|,()()}∈=⊕⊕=⊕=i i i i i i i J Test x A x y B S x S y C ,,,,,,,=12345678i对于本次实验的3个具有明文差（*,0）的明密文对，则可构造上面的3个Test 集合，显然 ()()()∈12i i i i J Test Test Test t ,,,,,,,=12345678i一种确定Ji 的直接方法：1.建立26=64长度的数组J[64]={0};2.对Testi(r)，r = 1,2,…,t ，若a ∈Testi(r)，则 J[a] = J[a] + 1。
实验报告书9-差分方程数值解
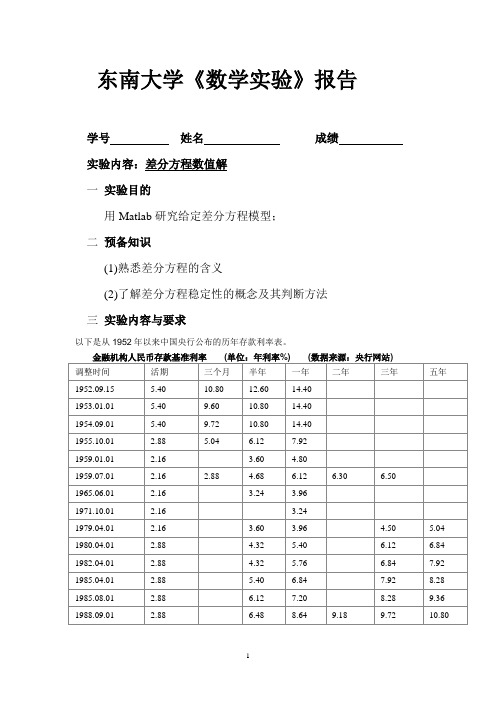
东南大学《数学实验》报告学号姓名成绩实验内容：差分方程数值解一实验目的用Matlab研究给定差分方程模型；二预备知识(1)熟悉差分方程的含义(2)了解差分方程稳定性的概念及其判断方法三实验内容与要求以下是从1952年以来中国央行公布的历年存款利率表。
以下是从1991年以来中国央行公布的历年贷存款利率表。
银行利息税变化时间表利息税始于1950年，当年颁布的《利息所得税条例》规定，对存款利息征收10％（后降为5％）的所得税，1959年利息税停征，1999年11月1日再次恢复征收。
储蓄存款在1999年11月1日前孳生的利息所得，不征收个人所得税；储蓄存款在1999年11月1日至2007年8月14日孳生的利息所得，按照20％的比例税率征收个人所得税；储蓄存款在2007年8月15日至2008年10月8日孳生的利息所得，按照5％的比例税率征收个人所得税。
储蓄存款在2008年10月9日(含)后孳生的利息所得，暂停征收个人所得税。
个人活期存款在每个季度的最后一个月20日结息一次，涉及到的2008年10月9日之前孳生的利息所得，还要按照5％的比例税率征收个人所得税。
问题1.如果张三1952年9月15日以长期定额存款（5年以上）形式存入银行100万元，请问到2010年12月31日，张三的账户余额是多少？（假设其间未发生存取款行为）问题2.如果李四、王五、赵六分别于1991年4月24日、2002年2月1日贷款100万，期限为10年，则他们贷款到期分别需要一共支付多少利息？问题3.请根据上面两张表，建立模型，预测一下下一次存贷款利率调整的结果？问题4某人于2011年元旦从银行公积金贷款40万元，还款期限为15年，已知贷款时年利率为4.05%，若采用等额本息法还贷（即每月所还本金加上利息为固定数额）。
假设15年内利率不变，试问他每月应当还银行多少钱？15年的总利息有多少？他想缩短总还款期限到10年，则正常还款1年后需要一次性提前还贷多少钱？每月还款多少？他想缩短总还款期限到5年，则正常还款1年后需要一次性提前还贷多少钱？每月还款多少？若年利率每年上浮0.5%，在同一年度之内利率不变，则15年的总利息有多少？若年利率每年上下随机浮动，浮动范围不超过0.5%，在同一年度之内利率不变，若贷款期限为5年，则总利息有多少？试建立差分模型为主的数学模型，描述上述各种情形。
差分放大电路实验报告
差分放大电路实验报告差分放大电路实验报告引言：差分放大电路是电子工程中常见的一种电路，它具有放大信号、抑制噪声等优点，因此在信号处理、通信系统等领域得到了广泛的应用。
本实验旨在通过搭建差分放大电路并进行实际测量，验证其性能和特点。
一、实验器材和原理本实验所需器材包括函数发生器、示波器、电阻、电容、运放等。
差分放大电路由两个输入端和一个输出端组成，输入端通过电阻与电源相连，输出端与负反馈电阻相连。
差分放大电路的原理是：当两个输入端的电压不同时，输出端会产生一个差分电压，其放大倍数由负反馈电阻决定。
二、实验步骤1. 按照电路图连接实验电路，注意正确接线和电阻、电容的数值。
2. 将函数发生器的输出接入电路的输入端，设置合适的频率和幅度。
3. 使用示波器测量电路的输入电压和输出电压，并记录数据。
4. 逐渐改变函数发生器的频率和幅度，观察电路的响应情况，并记录数据。
三、实验结果及分析在实验中，我们分别测量了电路的输入电压和输出电压，并记录了数据。
通过数据的分析，我们可以得出以下结论：1. 输入电压与输出电压之间存在一定的线性关系，即差分放大电路具有线性放大的特性。
2. 随着输入电压的增加，输出电压也相应增加，但增长的速率逐渐减小，说明差分放大电路具有饱和特性。
3. 在一定频率范围内，输入电压和输出电压之间的相位差保持不变，说明差分放大电路具有相位不变性。
四、实验总结通过本次实验，我们对差分放大电路的原理和性能有了更深入的了解。
差分放大电路在实际应用中具有很高的实用性，可以用于信号放大、噪声抑制等方面。
在今后的学习和工作中，我们将进一步探索差分放大电路的应用，并不断提高自己的实验技能和理论水平。
结语：差分放大电路是一种重要的电子电路，在信号处理和通信系统中具有广泛的应用。
通过本次实验，我们不仅加深了对差分放大电路的理解，还提高了实验操作和数据分析的能力。
希望今后能够将所学知识应用于实际工程中，为科学技术的发展做出自己的贡献。
差分放大电路实验报告
差分放大电路实验报告一、实验目的1.了解差分放大电路的基本原理和特点；2.掌握差分放大电路的设计和调试方法；3.熟悉差分放大电路的频率特性；4.学习使用示波器进行电路信号的观测和测量。
二、实验器材1.差分放大电路实验箱；2.示波器；3.信号源；4.直流电压源。
三、实验原理差分放大电路是众多电子设备中常见的一类电路，采用了差分输入方式可以有效降低共模干扰，提高了电路的抗干扰能力。
它由两个共模输入信号为零的晶体管组成，通过二极管连接的虚地点对共模信号进行抑制，只放大差模信号。
差模信号指的是两个输入信号的差值，共模信号指的是两个输入信号的平均值。
在差分放大电路中，晶体管的放大倍数由输入电流决定，输入电流越大，放大倍数越大。
同时，将两个输入信号松耦合，可以大幅度减小共模信号的放大倍数，从而达到抑制共模干扰的目的。
四、实验步骤1.搭建差分放大电路，接入示波器和信号源；2.分别接入正向输入信号和负向输入信号，将其调节至理想值；3.调节直流电压源和输入电阻，使差分放大电路的工作点稳定；4.调节输入信号频率，记录输出信号幅度和相位的变化情况；5.结束实验，关闭相关设备。
五、实验结果与分析通过实验，我们可以得到差分放大电路的输入输出特性曲线。
根据实验数据，我们可以计算出差分传输增益、共模抑制比和输出相位等。
实验结果显示，差分放大电路能够很好地放大差模信号，同时将共模信号压制得很低。
由于输入阻抗大，输入信号能够有效地传入差分放大电路中，而输出阻抗小，可以将信号有效地传递到下一个级联电路中。
此外，差分放大电路的相位可以随输入信号的频率变化而变化，相位差可达到180度。
六、实验总结通过本次实验，我们了解了差分放大电路的基本原理和特点，掌握了差分放大电路的设计和调试方法。
实验结果表明，差分放大电路能够有效地抑制共模干扰，提高电路的抗干扰能力。
在实际应用中，差分放大电路被广泛应用于增加电路增益、提高系统灵敏度、减小噪声等方面。
差分分析实验报告
差分分析实验报告
差分分析是一种统计方法，用于比较多组数据之间的差异性。
它可以帮助我们确定多个组别之间是否存在显著差异，并进一步分析这些差异的原因。
差分分析实验报告通常包括以下几个部分：引言、实验设计、数据收集和处理、结果分析和讨论。
在引言部分，我们需要介绍差分分析的背景和目的。
我们要解释为什么选择差分分析方法，以及对于我们的研究问题有何重要性。
接下来是实验设计部分。
我们需要明确实验的目标和假设，并描述实验的参与者、材料和方法。
我们要确保实验设计具有合理性和可靠性，以便得到可信的结果。
数据收集和处理是实验中重要的一步。
我们需要准备好数据收集表格，并告知参与者如何进行实验和记录数据。
收集到的数据需要进行清理和整理，以确保其准确性和可靠性。
然后是结果分析部分。
我们需要运用合适的统计方法，比如方差分析（ANOVA），来分析数据，并确定多组数据之间的差异性是否显著。
如果结果显著，我们可以进一步进行事后比较（post-hoc comparison）来确定哪些组别之间存在显著差异。
最后是结果讨论部分。
我们需要解释和解读结果，并将其与已有的研究结果进行比较。
我们也可以探讨结果的实际意义和可能的原因。
同时，我们还要指出研究可能存在的局限性，并提出改进的建议。
总之，差分分析实验报告需要包括引言、实验设计、数据收集和处理、结果分析和讨论几个主要部分。
在写作时要注意逻辑性和严谨性，确保报告的准确性和可靠性。
实验二差分方程的求解和离散系统频率响应的描述
实验二 差分方程的求解和离散系统频率响应的描述一、 实验目的1、掌握用MATLAB 求解差分方程的方法。
2、掌握绘制系统的零极点分布图和系统的频率响应特性曲线的方法。
3、 观察给定系统的冲激响应、阶跃相应以及系统的幅频特性和相频特性二、 实验内容1、已知描述离散新天地差分方程为：y(n+2)-0,25y(n+1)+0.5y(n)=x(n)+x(n-1)，且知该系统输入序列为)()2/1()(n u n x n =，试用MATLAB 实现下列分析过程：画出输入序列的时序波形；求出系统零状态响应在0～20区间的样值；画出系统的零状态响应波形图。
2、一离散时间系统的系统函数：5731053)(2323-+-+-=z z z zz z z H ，试用MA TLAB 求出系统的零极点；绘出系统的零极点分布图；绘出响应的单位阶跃响应波形。
三、 实验报告要求1、求出各部分的理论计算值， 并与实验结果相比较。
2、绘出实验结果波形（或曲线），并进行分析。
3、写出实验心得。
附录：本实验中所要用到的MATLAB 命令1、系统函数H(z)在MATLAB 中可调用函数zplane （），画出零极点分布图。
调用格式为： zplane （b,a ） 其中a 为H （z ）分母的系数矩阵，b 为H(z)分子的系数矩阵。
例2－1：一个因果系统：y （n ）－0.8y(n －1)＝x(n)由差分方程可求系统函数 8.0,8.011)(1>-=-z z z H零极点分布图程序：b=[1,0];a=[1,-0.8];zplane(b,a)2、求解差分方程在MA TLAB中，已知差分方程的系数、输入、初始条件，调用filter（）函数解差分方程。
调用filter（）函数的格式为：y=filtier(b,a,x,xic)，参数x为输入向量（序列），b,a分别为（1-30）式中的差分方程系数，xic是等效初始状态输入数组（序列）。
确定等效初始状态输入数组xic（n），可使用Signal Processing toolbox中的filtic（）函数，调用格式为：y=filtic(b,a,y,x) 。
建模实验报告差分方程模型上机实验
20 12 ——20 13 学年第二学期合肥学院数理系实验报告课程名称：数学模型实验项目：差分方程模型上机实验实验类别：综合性□设计性□验证性□专业班级：10级数学（1）班姓名：汪勤学号：1007021004 实验地点：35#611实验时间：2013-05-09指导教师：闫老师成绩：一.实验目的：掌握用Matlab软件进行差分方程的数值求解。
二.实验内容：用差分方法建立如下问题的离散模型，并用Matlab计算其数值据统计，某种山猫在较好、中等及较差的自然环境下，年平均增长率分别为1.68%，0.55%和-4.50%，假定开始时有100只山猫，按以下情况讨论山猫数量逐年变化过程及趋势：（1）建立差分方程模型；（2）求解3种自然环境下25年的变化过程（作图）；（3）如果每年捕获3只，会发生什么情况？山猫会灭绝吗？如果每年捕获一只呢？（计算相应数据并作图，然后结合图像和数据给出相应结论）。
三. 实验方案（程序设计说明）四. 实验步骤或程序（经调试后正确的源程序）五．程序运行结果六．实验总结学生签名：年月日七．教师评语及成绩教师签名：年月日实验报告说明1．实验项目：即实验题目，要求与实验指导书中一致。
2．实验目的：目的要明确，抓住重点，符合实验指导书中的要求。
3．实验方法：是实验报告极其重要的内容，包括算法设计思路，必要的流程图，界面设计说明，使用模块和变量说明等。
4．实验步骤或程序：实验完成的主要步骤与程序代码等。
5．出现的问题及解决方法：记录实验过程中遇到的问题，解决问题的方法。
6. 注：实验报告成绩将记入实验成绩，要按照实验教师要求及时上交。
7．模版中蓝色字部分在完成实验报告后删除。
8．签名、日期必须手写。
范例（部分，有些部分略）一. 实验目的：掌握用Access创建查询的方法能够使用SQL语言进行简单查询二. 实验内容：(1) 学习掌握创建表的方法。
(2) 学习向表中添加记录的方法。
(3) 学习设定表之间的关系。
差分电路实验报告
差分电路实验报告差分电路实验报告引言：差分电路是电子工程中常见的一种电路结构，它具有抵抗共模干扰、增强信号传输质量等优点，因此在许多应用场景中被广泛使用。
本实验旨在通过搭建差分电路并进行实际测试，探究其原理和性能。
实验材料：- 电源- 电阻- 电容- 信号发生器- 示波器- 多用电表- 连接线等实验步骤：1. 搭建基本差分电路将两个电阻相等的电阻连接到一个电源的正负极上，形成一个基本的差分电路。
确保电阻之间没有短路，并将信号发生器连接到差分电路的输入端。
2. 测量输入电压使用示波器测量信号发生器输出的电压，并记录下来。
同时，使用多用电表测量差分电路两个输入端的电压，记录下来。
3. 测量输出电压将示波器连接到差分电路的输出端，测量输出电压的幅值，并记录下来。
4. 改变输入信号频率在信号发生器上改变输入信号的频率，从低频到高频逐步改变，并记录下不同频率下的输入电压和输出电压。
5. 分析实验结果根据实验数据，绘制输入电压和输出电压的幅频特性曲线。
分析曲线的变化趋势，探究差分电路在不同频率下的响应特性。
实验结果与分析：通过实验测量得到的数据，我们可以绘制出差分电路的幅频特性曲线。
从曲线上可以观察到以下几个现象和结论：1. 差分电路的增益特性通过测量输出电压和输入电压的比值，可以得到差分电路的增益特性。
在低频区域，差分电路的增益较高，能够有效放大输入信号。
随着频率的增加，增益逐渐下降，直至趋近于1。
这是因为差分电路的频率响应受到电容和电阻的影响，在高频下出现衰减。
2. 共模抑制比差分电路的一个重要指标是共模抑制比（CMRR），它表示差分电路对共模信号的抑制能力。
在实验中，我们可以通过测量共模电压和差分电压的比值，得到CMRR的数值。
较高的CMRR值表示差分电路对共模干扰的抑制能力较强。
3. 差分电路的相位特性除了幅频特性，差分电路还具有相位特性。
通过测量输入信号和输出信号的相位差，可以得到差分电路的相位特性曲线。
差分放大电路实验报告
一、实验目的1. 加深对差分放大电路性能及特点的理解。
2. 学习差分放大电路主要性能指标的测试方法。
3. 掌握差分放大电路的组装与调试技巧。
4. 分析差分放大电路在实际应用中的优势。
二、实验原理差分放大电路由两个结构相同、参数对称的共射放大电路组成，其核心原理是利用两个输入信号之间的差分来抑制共模信号，提高电路的共模抑制比（CMRR）。
差分放大电路具有以下特点：1. 差模放大：对差模信号有放大作用，对共模信号有抑制作用。
2. 共模抑制：提高CMRR，降低共模干扰。
3. 零点漂移抑制：通过调整电路参数，减小零点漂移。
4. 输出阻抗高：提高电路的驱动能力。
差分放大电路的原理图如下：```+---------+| Q1 | Q2+---------+ +---------+| || |+-------+ +-------+| | | || R1 | | R2 || | | |+-------+ +-------+| || |+---------+||V+-------+| || Vout || |+-------+```三、实验设备及器材1. 模拟电路实验箱2. 实验线路板3. 万用电表4. 信号发生器5. 示波器6. 线路连接线四、实验过程及数据记录1. 按照原理图搭建差分放大电路。
2. 调整电路参数，使电路工作在最佳状态。
3. 使用信号发生器输入差模信号和共模信号，观察输出波形。
4. 测量差模电压放大倍数、共模电压放大倍数、共模抑制比等性能指标。
5. 记录实验数据。
五、数据处理与分析1. 分析差模电压放大倍数、共模电压放大倍数、共模抑制比等性能指标与理论值的差异。
2. 分析电路参数对性能指标的影响。
3. 总结差分放大电路在实际应用中的优势。
六、实验结论1. 通过本次实验，加深了对差分放大电路性能及特点的理解。
2. 掌握了差分放大电路主要性能指标的测试方法。
3. 熟悉了差分放大电路的组装与调试技巧。
差分发大电路实验报告
差分发大电路实验报告实验课程：差分发大电路实验实验目的：1.了解差分发大电路的工作原理；2.学习差分放大电路的特点及应用；3.掌握差分放大电路的设计和调试方法。
实验仪器：1.函数发生器；2.示波器；3.电压表；4.实验电路板；5.其他常用仪器。
实验材料：1.电阻、电容、二极管等无源元件；2.集成电路及其外围元件；3.其他辅助材料。
实验原理：差分放大电路是一种常用的信号放大电路，由两个互补的晶体管或运放组成。
其输入信号通过一个耦合电容耦合到两个晶体管的基极，晶体管的发射极与负电源相连，集电极通过负载电阻与正电源相连。
差分放大电路的优点是具有较好的抗共模干扰能力，可以实现较大的信号增益。
实验步骤：1.按照电路图搭建差分发大电路，并连接所需的外围元件；2.将函数发生器连接到输入端，调整函数发生器的输出频率、幅值和波形，并将示波器连接到输出端来观察输出信号；3.逐渐调整输入信号的幅度，并记录输入和输出电压的数值；4.通过改变负载电阻的数值来观察输出信号的改变，并记录相应的数据；5.分析实验结果，绘制输入输出电压的关系曲线，并计算出差分放大电路的增益；6.根据实验结果，总结出差分放大电路的特点和应用。
实验结果和数据：1.通过调整函数发生器的输出频率、幅值和波形，观察到输出信号随输入信号的变化；2.记录了不同输入信号幅度下的输入输出电压数据，并绘制了相关曲线；3.通过改变负载电阻的数值，观察到输出信号的变化，并记录了相应的数据。
实验分析和讨论：1.根据实验数据，计算出差分放大电路的增益，并与理论值进行比较；2.通过观察实验数据，分析差分放大电路的特点和应用，如抗共模干扰能力和信号增益等；3.对比不同输入信号幅度、频率和负载电阻下的输出结果，探讨差分放大电路的适用范围和工作条件。
实验总结：通过本次实验，我对差分放大电路的工作原理、特点和应用有了更深入的理解。
通过搭建实验电路、调试和观察实验结果，我学会了差分放大电路的设计和调试方法，并能够根据实验数据进行相应的分析和计算。
差分放大电路实验报告
差分放大电路实验报告一、实验目的。
本实验旨在通过搭建差分放大电路并进行实验验证，加深对差分放大电路原理的理解，掌握差分放大电路的基本特性和参数测量方法。
二、实验仪器和设备。
1. 示波器。
2. 函数信号发生器。
3. 直流稳压电源。
4. 电阻、电容等元件。
5. 多用表。
三、实验原理。
差分放大电路是一种特殊的放大电路，它能够对输入信号进行差分放大，即对两个输入信号进行放大，并输出它们的差值。
差分放大电路通常由差分放大器和后级放大器组成，其中差分放大器起到差分放大的作用，后级放大器起到整体放大的作用。
四、实验步骤。
1. 按照电路图搭建差分放大电路，注意连接正确，电阻、电容等元件的参数选择要符合实验要求。
2. 将示波器和函数信号发生器连接到差分放大电路的输入端，设置合适的信号频率和幅度。
3. 调节直流稳压电源，给差分放大电路提供适当的工作电压。
4. 使用多用表测量差分放大电路的输入电压、输出电压等参数，并记录实验数据。
5. 调节输入信号的频率和幅度，观察差分放大电路的输出变化，并记录实验现象。
五、实验数据记录与分析。
1. 记录不同输入信号频率和幅度下的差分放大电路的输入电压、输出电压等参数，并绘制相应的波形图。
2. 根据实验数据和波形图，分析差分放大电路的放大倍数、频率响应等特性，验证差分放大电路的工作原理。
六、实验结果与讨论。
通过实验数据分析和波形图观察，我们得出差分放大电路在不同输入信号条件下的放大倍数、频率响应等特性。
实验结果与理论预期基本吻合，证明了差分放大电路的工作原理和特性。
七、实验总结。
本实验通过搭建差分放大电路并进行实验验证，加深了对差分放大电路原理的理解，掌握了差分放大电路的基本特性和参数测量方法。
同时，实验中我们也发现了一些问题，例如在实际搭建电路中要注意连接的稳定性，以及测量参数时要准确使用仪器等。
总之，本实验取得了良好的实验效果，对于差分放大电路的原理和特性有了更深入的了解，为今后的学习和科研打下了良好的基础。
差分放大电路实验报告
差分放大电路实验报告一、引言在现代电子科技发展中，放大电路是一项非常重要的技术。
差分放大电路是其中一种广泛应用于通信系统、测量仪器和音频设备中的放大电路。
本实验旨在通过搭建差分放大电路并进行相关参数测量，探究差分放大电路的原理和应用。
二、实验原理1. 差分放大电路介绍差分放大电路是由两个输入信号源、一个放大器和一个输出负载组成的系统。
两个输入信号源维持在不同的电位上，输入信号的差异将被放大器放大后传递给输出负载。
差分放大电路可以消除共模噪声并增强差模信号。
2. 放大器原理放大器是差分放大电路中最重要的组成部分。
常见的放大器类型包括共源共栅放大器、共集放大器等。
放大器可以实现信号的放大功能，通过选择合适的放大器类型和电路参数，可以获得所需的放大倍数和频率响应。
三、实验步骤1. 搭建差分放大电路根据实验指导书上的电路图，使用电路板等元器件搭建差分放大电路。
确保电路连接正确可靠，各器件之间没有接触不良或短路现象。
2. 连接信号源和输出负载将信号源与放大电路的输入端相连，一般使用函数信号发生器作为信号源。
将输出负载与放大电路的输出端相连，可以使用示波器或电阻等作为输出负载。
3. 测量电路参数使用示波器和万用表等测试仪器，测量差分放大电路的各项参数。
包括输入电阻、输出电阻、共模抑制比等。
通过测量数据分析，优化电路参数，以达到预期的放大效果。
四、实验结果与分析根据实验测量数据，可以获得差分放大电路的各项参数。
以差模电压增益为例，可以通过测量输入信号和输出信号的电压，计算出差模电压增益的数值大小。
进一步分析数据，可以研究不同的电路参数对于差分放大电路性能的影响。
五、实验应用差分放大电路在现实生活中应用广泛。
例如，在通信领域中，差分放大电路被用于传输线路和信号处理中，可以提高通信系统的抗干扰能力和信号质量。
此外，在音频设备中，差分放大电路也常用于扬声器驱动和音频放大等方面。
六、实验总结通过本次差分放大电路实验，我们深入了解了差分放大电路的原理和应用。
☆差分方程的求解和离散系统频率响应的描述
实验二 差分方程的求解和离散系统频率响应的描述一、 实验目的1、掌握用MATLAB 求解差分方程的方法。
2、掌握绘制系统的零极点分布图和系统的频率响应特性曲线的方法。
3、 观察给定系统的冲激响应、阶跃相应以及系统的幅频特性和相频特性二、 实验内容1、已知描述离散新天地差分方程为：y(n+2)-0,25y(n+1)+0.5y(n)=x(n)+x(n-1)，且知该系统输入序列为)()2/1()(n u n x n =，试用MATLAB 实现下列分析过程：画出输入序列的时序波形；求出系统零状态响应在0～20区间的样值；画出系统的零状态响应波形图。
2、一离散时间系统的系统函数：5731053)(2323-+-+-=z z z z z z z H ，试用MA TLAB 求出系统的零极点；绘出系统的零极点分布图；绘出响应的单位阶跃响应波形。
三、 实验报告要求1、求出各部分的理论计算值， 并与实验结果相比较。
2、绘出实验结果波形（或曲线），并进行分析。
3、写出实验心得。
附录：本实验中所要用到的MATLAB 命令1、系统函数H(z)在MATLAB 中可调用函数zplane （），画出零极点分布图。
调用格式为： zplane （b,a ） 其中a 为H （z ）分母的系数矩阵，b 为H(z)分子的系数矩阵。
例2－1：一个因果系统：y （n ）－0.8y(n －1)＝x(n)由差分方程可求系统函数 8.0,8.011)(1>-=-z zz H 零极点分布图程序：b=[1,0];a=[1,-0.8];zplane(b,a)2、求解差分方程在MA TLAB中，已知差分方程的系数、输入、初始条件，调用filter（）函数解差分方程。
调用filter（）函数的格式为：y=filtier(b,a,x,xic)，参数x为输入向量（序列），b,a分别为（1-30）式中的差分方程系数，xic是等效初始状态输入数组（序列）。
实验课7 全差分运放的仿真方法
CMOS模拟集成电路实验报告实验课7 全差分运放的仿真方法目标：1、了解全差分运放的各项指标2、掌握全差分运放各项指标的仿真方法,对全差分运放的各指标进行仿真，给出各指标的仿真结果。
本次实验课使用的全差分运放首先分析此电路图，全差分运算放大器是一种具有差分输入，差分输出结构的运算放大器。
其相对于单端输出的放大器具有一些优势：因为当前的工艺尺寸在减少，所以供电的电源电压越来越小，所以在供电电压很小的情况下，单端输出很难理想工作，为了电路有很大的信号摆幅，采用类似上图的全差分运算放大器，其主要由主放大器和共模反馈环路组成。
1、开环增益的仿真得到的仿真图为1.开环增益：首先开环增益计算方法是低频工作时(<200Hz) ，运放开环放大倍数；通过仿真图截点可知增益为73.3db。
2.增益带宽积：随着频率的增大，A0会开始下降，A0下降至0dB 时的频率即为GBW，所以截取其对应增益为0的点即可得到其增益带宽积为1.03GB。
3.相位裕度：其计算方法为增益为0的时候对应的VP的纵坐标，如图即为-118，则其相位裕度为-118+180=62，而为保证运放工作的稳定性，当增益下降到0dB 时，相位的移动应小于180 度，一般取余量应大于60度，即相位的移动应小于120 度；所以得到的符合要求。
在做以上仿真的时候，关键步骤在于设定VCMFB，为了得到大的增益，并且使相位裕度符合要求，一直在不停地改变VCMFB，最初只是0.93,0.94,0.95的变化，后来发现增益还是远远不能满足要求，只有精确到小数点后4为到5位才能得到大增益。
2.CMRR 的仿真分析此题可得共模抑制比定义为差分增益和共模增益的比值，它反映了一个放大器对于共模信号和共模噪声的抑制能力。
因此需要仿真共模增益和差分增益。
可以利用两个放大器，一个连成共模放大，一个连成差模放大，用图1仿真差分增益图1用图2仿真共模增益图2将两个仿真写在一个sp文件中可以得到如下结果：相角仿真因为CMRR 的相角为=Vp(V op,Von)-Vp(V o p)黄色的为Vp(Vo p)，红色的为Vp(V op,Von)，两者相减，得到CMRR 的相角的仿真图为，其中蓝线为CMRR的相角仿真图，其它两条为上面的线，将它们放在一起对比：CMRR的幅度仿真其CMRR 的幅值为=Vdb(V op,V on)-Vdb(V op)，蓝线为Vdb(V op,V on)，粉线为Vdb(V op)，两者相减得到绿线，即为CMRR的幅值特性曲线截取其在100HZ之前的增益值可得低频时增益为49.1db。
差分计算多项式
差分计算多项式
华中科技大学
计算机科学与技术学院
计算机组成原理
实验报告
报告人：
指导教师：
实验基本信息
实验名称：
差分计算多项式
实验目的：
了解多项式的运算，学会如何使用差分计算多项式。
实验内容：
1.读取多项式，并将其输出。
2.求出多项式的差分结果并输出。
实验运行结果：
原多项式：
3x4+2x3-4x2+x+6
差分结果：
12x3+6x2-8x+1
实验总结：
本实验中，我们学习了如何使用差分计算多项式。
计算过程中，
我们先把多项式拆分成一个个项，然后将每一项的指数减一，系数乘以原来的指数，最后将拆分出来的项重新组合成新的多项式，这就是差分的定义。
本实验掌握了如何使用差分计算多项式，为以后学习更多的复杂多项式运算奠定了基础。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验报告
课程名称：计算方法
院系：数学科学系
专业班级：数应1001
学号：1031110139
学生姓名：姚海保
指导教师：沈林
开课时间：2012至2013学年第一学期
一、学生撰写要求
按照实验课程培养方案的要求，每门实验课程中的每一个实验项目完成后，每位参加实验的学生均须在实验教师规定的时间内独立完成一份实验报告，不得抄袭，不得缺交。
学生撰写实验报告时应严格按照本实验报告规定的内容和要求填写。
字迹工整，文字简练，数据齐全，图表规范，计算正确，分析充分、具体、定量。
二、教师评阅与装订要求
1.实验报告批改要深入细致，批改过程中要发现和纠正学生实验报告中的问题，给出评语和实验报告成绩，签名并注明批改日期。
实验报告批改完成后，应采用适当的形式将学生实验报告中存在的问题及时反馈给学生。
2.实验报告成绩用百分制评定，并给出成绩评定的依据或评分标准（附于实验报告成绩登记表后）。
对迟交实验报告的学生要酌情扣分，对缺交和抄袭实验报告的学生应及时批评教育，并对该次实验报告的分数以零分处理。
对单独设课的实验课程，如学生抄袭或缺交实验报告达该课程全学期实验报告总次数三分之一以上，不得同意其参加本课程的考核。
3.各实验项目的实验报告成绩登记在实验报告成绩登记表中。
本学期实验项目全部完成后，给定实验报告综合成绩。
4.实验报告综合成绩应按课程教学大纲规定比例（一般为10-15%）计入实验课总评成绩；实验总评成绩原则上应包括考勤、实验报告、考核（操作、理论）等多方面成绩；
5.实验教师每学期负责对拟存档的学生实验报告按课程、学生收齐并装订，按如下顺序装订成册：实验报告封面、实验报告成绩登记表、实验报告成绩评定依据、实验报告（按教学进度表规定的实验项目顺序排序）。
装订时统一靠左侧按“两钉三等分”原则装订。
024********
-1
-0.8
-0.6
-0.4
-0.2
0.2
0.4
0.6
0.8
1
3、画出
2
2
2
2)
sin(
y
x
y
x
z
+
+
=所表示的三维曲面。
y
x,的取值范围是]8,8
[-。
clear;x=-8:0.5:8;
y=x';
X=ones(size(y))*x;
Y=y*ones(size(x));
R=sqrt(X.^2+Y.^2)+eps; %<5>
Z=sin(R)./R; %<6>
surf(X,Y,Z); %
colormap(cool) %
xlabel('x'),ylabel('y'),zlabel('z')
4、复数矩阵的生成及运算
A=[1,3;2,4]-[5,8;6,9]*i
B=[1+5i,2+6i;3+8*i,4+9*i]
C=A*B
A = 1.0000 - 5.0000i 3.0000 - 8.0000i
2.0000 - 6.0000i 4.0000 - 9.0000i
B =1.0000 + 5.0000i 2.0000 + 6.0000i
3.0000 + 8.0000i
4.0000 + 9.0000i
C =1.0e+002 *
0.9900 1.1600 - 0.0900i
1.1600 + 0.0900i 1.3700。