数据结构与算法习题讲解(全)
数据结构与算法分析习题与参考答案
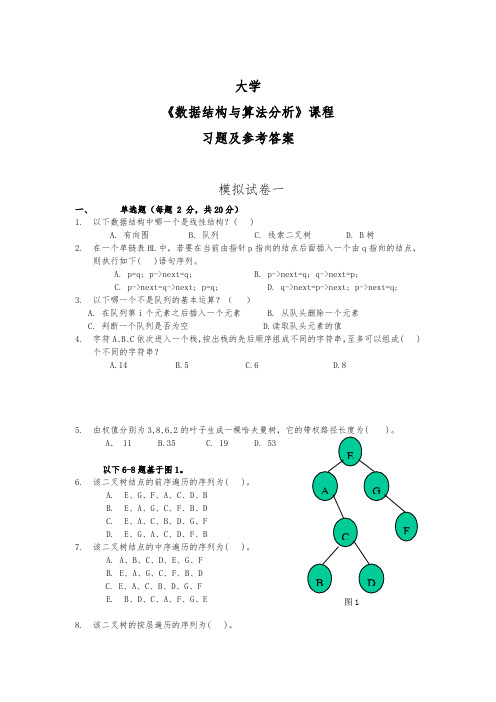
大学《数据结构与算法分析》课程习题及参考答案模拟试卷一一、单选题（每题 2 分，共20分）1.以下数据结构中哪一个是线性结构？( )A. 有向图B. 队列C. 线索二叉树D. B树2.在一个单链表HL中，若要在当前由指针p指向的结点后面插入一个由q指向的结点，则执行如下( )语句序列。
A. p=q; p->next=q;B. p->next=q; q->next=p;C. p->next=q->next; p=q;D. q->next=p->next; p->next=q;3.以下哪一个不是队列的基本运算？（）A. 在队列第i个元素之后插入一个元素B. 从队头删除一个元素C. 判断一个队列是否为空D.读取队头元素的值4.字符A、B、C依次进入一个栈，按出栈的先后顺序组成不同的字符串，至多可以组成( )个不同的字符串？A.14B.5C.6D.85.由权值分别为3,8,6,2的叶子生成一棵哈夫曼树，它的带权路径长度为( )。
以下6-8题基于图1。
6.该二叉树结点的前序遍历的序列为( )。
A.E、G、F、A、C、D、BB.E、A、G、C、F、B、DC.E、A、C、B、D、G、FD.E、G、A、C、D、F、B7.该二叉树结点的中序遍历的序列为( )。
A. A、B、C、D、E、G、FB. E、A、G、C、F、B、DC. E、A、C、B、D、G、FE.B、D、C、A、F、G、E8.该二叉树的按层遍历的序列为( )。
A．E、G、F、A、C、D、B B. E、A、C、B、D、G、FC. E、A、G、C、F、B、DD. E、G、A、C、D、F、B9.下面关于图的存储的叙述中正确的是( )。
A．用邻接表法存储图，占用的存储空间大小只与图中边数有关，而与结点个数无关B．用邻接表法存储图，占用的存储空间大小与图中边数和结点个数都有关C. 用邻接矩阵法存储图，占用的存储空间大小与图中结点个数和边数都有关D．用邻接矩阵法存储图，占用的存储空间大小只与图中边数有关，而与结点个数无关10.设有关键码序列(q，g，m，z，a，n，p，x，h)，下面哪一个序列是从上述序列出发建堆的结果?( )A. a，g，h，m，n，p，q，x，zB. a，g，m，h，q，n，p，x，zC. g，m，q，a，n，p，x，h，zD. h，g，m，p，a，n，q，x，z二、填空题（每空1分，共26分）1.数据的物理结构被分为_________、________、__________和___________四种。
数据结构与算法课后习题解答
数据结构与算法课后习题解答数据结构与算法课后习题解答第一章绪论（参考答案）1.3 (1) O(n)(2) (2) O(n)(3) (3) O(n)(4) (4) O(n1/2)(5) (5) 执行程序段的过程中，x,y值变化如下：循环次数x y0（初始）91 1001 92 1002 93 100。
9 100 10010 101 10011 9112。
20 9921 91 98。
30 101 9831 91 97到y=0时，要执行10*100次，可记为O（10*y）=O（n）数据结构与算法课后习题解答1.5 2100 , (2/3)n , log2n , n1/2 , n3/2 , (3/2)n , nlog2n , 2 n , n! , n n第二章线性表(参考答案)在以下习题解答中，假定使用如下类型定义：（1）顺序存储结构：#define ***** 1024typedef int ElemType;// 实际上，ElemTypetypedef struct{ ElemType data[*****];int last; // last}sequenlist;（2*next；}linklist;（3）链式存储结构（双链表）typedef struct node{ElemType data;struct node *prior,*next；数据结构与算法课后习题解答}dlinklist;（4）静态链表typedef struct{ElemType data;int next;}node;node sa[*****];2.1 la，往往简称为“链表la”。
是副产品）2.2 23voidelenum个元素，且递增有序，本算法将x插入到向量A中，并保持向量的{ int i=0,j;while (ielenum A[i]=x) i++; // 查找插入位置for (j= elenum-1;jj--) A[j+1]=A[j];// 向后移动元素A[i]=x; // 插入元素数据结构与算法课后习题解答} // 算法结束24void rightrotate(ElemType A[],int n,k)// 以向量作存储结构，本算法将向量中的n个元素循环右移k位，且只用一个辅助空间。
数据结构与算法设计课后习题及答案详解
数据结构与算法设计课后习题及答案详解1. 习题一：数组求和题目描述：给定一个整数数组，编写一个函数来计算它的所有元素之和。
解题思路：遍历数组，将每个元素累加到一个变量中，最后返回累加和。
代码实现：```pythondef sum_array(arr):result = 0for num in arr:result += numreturn result```2. 习题二：链表反转题目描述：给定一个单链表，反转它的节点顺序。
解题思路：采用三指针法，依次将当前节点的下一个节点指向上一个节点，然后更新三个指针的位置，直到链表反转完毕。
代码实现：```pythonclass ListNode:def __init__(self, val=0, next=None):self.val = valself.next = nextdef reverse_list(head):prev = Nonecurr = headwhile curr:next_node = curr.nextcurr.next = prevprev = currcurr = next_nodereturn prev```3. 习题三：二叉树的层序遍历题目描述：给定一个二叉树，返回其节点值的层序遍历结果。
解题思路：采用队列来实现层序遍历，先将根节点入队，然后循环出队并访问出队节点的值，同时将出队节点的左右子节点入队。
代码实现：```pythonclass TreeNode:def __init__(self, val=0, left=None, right=None): self.val = valself.left = leftself.right = rightdef level_order(root):if not root:return []result = []queue = [root]while queue:level = []for _ in range(len(queue)):node = queue.pop(0)level.append(node.val)if node.left:queue.append(node.left)queue.append(node.right)result.append(level)return result```4. 习题四：堆排序题目描述：给定一个无序数组，使用堆排序算法对其进行排序。
《数据结构与算法》习题与答案
《数据结构与算法》习题与答案（解答仅供参考）一、名词解释：1. 数据结构：数据结构是计算机存储、组织数据的方式，它不仅包括数据的逻辑结构（如线性结构、树形结构、图状结构等），还包括物理结构（如顺序存储、链式存储等）。
它是算法设计与分析的基础，对程序的效率和功能实现有直接影响。
2. 栈：栈是一种特殊的线性表，其操作遵循“后进先出”（Last In First Out, LIFO）原则。
在栈中，允许进行的操作主要有两种：压栈（Push），将元素添加到栈顶；弹栈（Pop），将栈顶元素移除。
3. 队列：队列是一种先进先出（First In First Out, FIFO）的数据结构，允许在其一端插入元素（称为入队），而在另一端删除元素（称为出队）。
常见的实现方式有顺序队列和循环队列。
4. 二叉排序树（又称二叉查找树）：二叉排序树是一种二叉树，其每个节点的左子树中的所有节点的值都小于该节点的值，而右子树中的所有节点的值都大于该节点的值。
这种特性使得能在O(log n)的时间复杂度内完成搜索、插入和删除操作。
5. 图：图是一种非线性数据结构，由顶点（Vertex）和边（Edge）组成，用于表示对象之间的多种关系。
根据边是否有方向，可分为有向图和无向图；根据是否存在环路，又可分为有环图和无环图。
二、填空题：1. 在一个长度为n的顺序表中，插入一个新元素平均需要移动______个元素。
答案：(n/2)2. 哈希表利用______函数来确定元素的存储位置，通过解决哈希冲突以达到快速查找的目的。
答案：哈希（Hash）3. ______是最小生成树的一种算法，采用贪心策略，每次都选择当前未加入生成树且连接两个未连通集合的最小权重边。
答案：Prim算法4. 在深度优先搜索（DFS）过程中，使用______数据结构来记录已经被访问过的顶点，防止重复访问。
答案：栈或标记数组5. 快速排序算法在最坏情况下的时间复杂度为______。
数据结构与算法设计课后习题及答案详解
第一章1.数据结构研究的主要内容包括逻辑结构、存储结构和算法。
2.数据元素是数据的基本单位，数据项是数据的最小标示单位。
3.根据数据元素之间关系的不同，数据的逻辑结构可以分为集合、树形、线性、图状。
4.常见的数据存储结构有四种类型：顺序、链式、索引、散列。
5.可以从正确性、可读性、健壮性、高效性四方面评价算法的质量。
6.在一般情况下，一个算法的时间复杂度是问题规模的函数。
7.常见时间复杂度有：常数阶O（1）、线性阶O（n）、对数阶O（log2 n）、平方阶O（n²）和指数阶O（2ⁿ）。
通常认为，具有常数阶量级的算法是好算法，而具有指数阶量级的算法是差算法。
8.时间复杂度排序由大到小（n+2）！>2ⁿ＋²>（n+2）4次方>nlog2 n>100000.问答题：1.什么叫数据元素？数据元素是数据的基本单位，是数据这个集合的个体，也称为元素、结点、顶点、记录。
2.什么叫数据逻辑结构？什么叫数据存储结构？数据逻辑结构：指数据元素之间存在的固有的逻辑结构。
数据存储结构：数据元素及其关系在计算机内的表示。
3.什么叫抽象数据类型？抽象数据类型是指数据元素集合以及定义在该集合上的一组操作。
4.数据元素之间的关系在计算机中有几种表示方法？顺序、链式、索引、散列。
5.数据的逻辑结构与数据的存储结构之间存在着怎样的关系？相辅相成，不可分割。
6.什么叫算法？算法的性质有哪些？算法：求解问题的一系列步骤的集合。
可行性、有容性、确定性、有输入、有输出。
7.评价一个算法的好坏应该从哪几方面入手？正确性、可读性、健壮性、高效性。
第二章1.线性表中，第一个元素没有直接前驱，最后一个元素没有直接后继。
2.线性表常用的两种存储结构分别是顺序存储结构和链式存储结构。
3.在长度为n的顺序表中，插入一个新元素平均需要移动表中的n/2个元素，删除一个元素平均需要移动（n-1）/2个元素。
4.在长度为n的顺序表的表头插入一个新元素的时间复杂度为O（n），在表尾插入一个新元素的时间复杂度为O（1）。
数据结构与算法习题讲解(全)分析99页PPT
25、学习是劳动，是充满思想的劳动。——乌申斯基
谢谢！
ห้องสมุดไป่ตู้
数据结构与算法习题讲解(全)分析
51、山气日夕佳，飞鸟相与还。 52、木欣欣以向荣，泉涓涓而始流。
53、富贵非吾愿，帝乡不可期。 54、雄发指危冠，猛气冲长缨。 55、土地平旷，屋舍俨然，有良田美 池桑竹 之属， 阡陌交 通，鸡 犬相闻 。
21、要知道对好事的称颂过于夸大，也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤，荒于嬉；行成于思，毁于随。——韩愈
数据结构复习与习题解析
1、访问指定的起始顶点；
2、若当前访问的顶点的邻接顶点有未被访问的，则任选一个访问 之；反之，退回到最近访问过的顶点；直到与起始顶点相通的 全部顶点都访问完毕；
3、若此时图中尚有顶点未被访问，则再选其中一个顶点作为起始 顶点并访问之，转 2； 反之，遍历结束。
4
8/5/2021
例题解析
j va5i
k
v9
v3
v8
(1) 从 ve(1) = 0 开始向前递推
v4 a6=2 v6
ve( j) Max{ve(i) dut( i, j )}, i, j T , 2 j n i
其 中T 是 所 有 以j 为 头 的 弧 的 集 合 。
(2) 从 vl(n) = ve(n) 开始向后递推
8/5/2021
例题解析
❖ 请分别用Prim算法和Kruskal算法构造以下网络的 最小生成树，并求出该树的代价。
9
8/5/2021
ቤተ መጻሕፍቲ ባይዱ
例题解析
【解析】Prim算法的操作步骤：首先从一个只 有一个顶点的集合开始，通过加入与其中顶点 相关联的最小代价的边来扩充顶点集，直到所 有顶点都在一个集合中。
10
22
8/5/2021
例题解析
例：设有一组关键字{32,75,63,48,94,25,36,18,70}，采用哈希函数： H(key)=key MOD 11并采用步长为1的线性探测法解决冲突，试在0--10的 散列地址空间中对该关键字序列构造哈希表。
0 1 2 3 4 5 6 7 8 9 10
70
25 48 36 94 18 63 75 32
H(36)=(4+1) MOD 11=5
数据结构与算法学习例题与解答
数据结构与算法学习例题与解答作为计算机科学领域的基础知识，数据结构与算法的学习对于提升编程能力和解决实际问题至关重要。
本文将介绍一些常见的数据结构与算法例题，并提供相应的解答。
一、线性表1.1 数组题目：给定一个整型数组，将所有的奇数放在偶数前面，并保持它们的相对顺序不变。
解答：```pythondef reorder(arr):if not arr or len(arr) < 2:return arrleft, right = 0, len(arr) - 1while left < right:while left < right and arr[left] % 2 == 1:left += 1while left < right and arr[right] % 2 == 0:right -= 1if left < right:arr[left], arr[right] = arr[right], arr[left]return arr```1.2 链表题目：给定一个链表，返回该链表的中间节点。
如果有两个中间节点，则返回第二个。
解答：```pythonclass ListNode:def __init__(self, val=0, next=None):self.val = valself.next = nextdef middleNode(head):slow = fast = headwhile fast and fast.next:slow = slow.nextfast = fast.next.nextreturn slow```二、栈与队列2.1 栈题目：设计一个支持 push，pop，top 操作，并且能在常数时间内检索到最小元素的栈。
解答：```pythonclass MinStack:def __init__(self):self.stack = []self.min_stack = []def push(self, x):self.stack.append(x)if not self.min_stack or x <= self.min_stack[-1]:self.min_stack.append(x)def pop(self):if self.stack.pop() == self.min_stack[-1]:self.min_stack.pop()def top(self):return self.stack[-1]def getMin(self):return self.min_stack[-1]```2.2 队列题目：使用栈实现队列的下列操作：push(x)，pop()，peek()，empty()。
数据结构与算法设计课后习题及答案详解
第一章1.数据结构研究的主要内容包括逻辑结构、存储结构和算法。
2.数据元素是数据的基本单位，数据项是数据的最小标示单位。
3.根据数据元素之间关系的不同，数据的逻辑结构可以分为集合、树形、线性、图状。
4.常见的数据存储结构有四种类型：顺序、链式、索引、散列。
5.可以从正确性、可读性、健壮性、高效性四方面评价算法的质量。
6.在一般情况下，一个算法的时间复杂度是问题规模的函数。
7.常见时间复杂度有：常数阶O（1）、线性阶O（n）、对数阶O（log2 n）、平方阶O（n²）和指数阶O（2ⁿ）。
通常认为，具有常数阶量级的算法是好算法，而具有指数阶量级的算法是差算法。
8.时间复杂度排序由大到小（n+2）！>2ⁿ＋²>（n+2）4次方>nlog2 n>100000.问答题：1.什么叫数据元素？数据元素是数据的基本单位，是数据这个集合的个体，也称为元素、结点、顶点、记录。
2.什么叫数据逻辑结构？什么叫数据存储结构？数据逻辑结构：指数据元素之间存在的固有的逻辑结构。
数据存储结构：数据元素及其关系在计算机内的表示。
3.什么叫抽象数据类型？抽象数据类型是指数据元素集合以及定义在该集合上的一组操作。
4.数据元素之间的关系在计算机中有几种表示方法？顺序、链式、索引、散列。
5.数据的逻辑结构与数据的存储结构之间存在着怎样的关系？相辅相成，不可分割。
6.什么叫算法？算法的性质有哪些？算法：求解问题的一系列步骤的集合。
可行性、有容性、确定性、有输入、有输出。
7.评价一个算法的好坏应该从哪几方面入手？正确性、可读性、健壮性、高效性。
第二章1.线性表中，第一个元素没有直接前驱，最后一个元素没有直接后继。
2.线性表常用的两种存储结构分别是顺序存储结构和链式存储结构。
3.在长度为n的顺序表中，插入一个新元素平均需要移动表中的n/2个元素，删除一个元素平均需要移动（n-1）/2个元素。
4.在长度为n的顺序表的表头插入一个新元素的时间复杂度为O（n），在表尾插入一个新元素的时间复杂度为O（1）。
《数据结构与算法》课后习题答案
2.3 课后习题解答2.3.2 判断题1．线性表的逻辑顺序与存储顺序总是一致的。
（×）2．顺序存储的线性表可以按序号随机存取。
（√）3．顺序表的插入和删除操作不需要付出很大的时间代价，因为每次操作平均只有近一半的元素需要移动。
（×）4．线性表中的元素可以是各种各样的，但同一线性表中的数据元素具有相同的特性，因此属于同一数据对象。
（√）5．在线性表的顺序存储结构中，逻辑上相邻的两个元素在物理位置上并不一定相邻。
（×）6．在线性表的链式存储结构中，逻辑上相邻的元素在物理位置上不一定相邻。
（√）7．线性表的链式存储结构优于顺序存储结构。
（×）8．在线性表的顺序存储结构中，插入和删除时移动元素的个数与该元素的位置有关。
（√）9．线性表的链式存储结构是用一组任意的存储单元来存储线性表中数据元素的。
（√）10．在单链表中，要取得某个元素，只要知道该元素的指针即可，因此，单链表是随机存取的存储结构。
（×）11．静态链表既有顺序存储的优点，又有动态链表的优点。
所以它存取表中第i个元素的时间与i无关。
（×）12．线性表的特点是每个元素都有一个前驱和一个后继。
（×）2.3.3 算法设计题1．设线性表存放在向量A[arrsize]的前elenum个分量中，且递增有序。
试写一算法，将x 插入到线性表的适当位置上，以保持线性表的有序性，并且分析算法的时间复杂度。
【提示】直接用题目中所给定的数据结构（顺序存储的思想是用物理上的相邻表示逻辑上的相邻，不一定将向量和表示线性表长度的变量封装成一个结构体），因为是顺序存储，分配的存储空间是固定大小的，所以首先确定是否还有存储空间，若有，则根据原线性表中元素的有序性，来确定插入元素的插入位置，后面的元素为它让出位置，（也可以从高下标端开始一边比较，一边移位）然后插入x ，最后修改表示表长的变量。
int insert (datatype A[],int *elenum,datatype x) /*设elenum为表的最大下标*/ {if (*elenum==arrsize-1) return 0; /*表已满，无法插入*/else {i=*elenum;while (i>=0 && A[i]>x) /*边找位置边移动*/{A[i+1]=A[i];i--;}A[i+1]=x; /*找到的位置是插入位的下一位*/(*elenum)++;return 1; /*插入成功*/}}时间复杂度为O(n)。
数据结构与算法学习例题与解答
数据结构与算法学习例题与解答在学习数据结构与算法的过程中，了解和实践一些例题并进行解答是非常重要的。
通过解答例题，我们可以更好地理解和掌握各种数据结构和算法的原理和应用。
本文将为大家介绍一些常见的数据结构与算法例题，并给出相应的解答。
一、数组反转问题描述：给定一个整数数组，将数组中的元素按照逆序重新排列。
解答：可以通过双指针的方法来解决这个问题，即将数组的首尾元素依次交换，直到首尾指针相遇为止。
```javapublic void reverseArray(int[] nums) {int start = 0;int end = nums.length - 1;while (start < end) {int temp = nums[start];nums[start] = nums[end];nums[end] = temp;start++;end--;}```二、链表反转问题描述：给定一个单链表，将链表中的元素按照逆序重新排列。
解答：可以采用迭代或者递归的方式来解决链表的反转问题。
迭代解法：```javapublic ListNode reverseList(ListNode head) {ListNode prev = null;ListNode current = head;ListNode next = null;while (current != null) {next = current.next;current.next = prev;prev = current;current = next;}return prev;```递归解法：```javapublic ListNode reverseList(ListNode head) {if (head == null || head.next == null) {return head;}ListNode newHead = reverseList(head.next);head.next.next = head;head.next = null;return newHead;}```三、二叉树的前序遍历问题描述：给定一个二叉树，按照前序遍历的顺序输出所有的节点值。
《数据结构与算法》课后习题答案
《数据结构与算法》课后习题答案一、算法分析和复杂度1.1 算法复杂度的定义算法的复杂度是指算法所需资源的度量，包括时间复杂度和空间复杂度。
时间复杂度描述了算法的执行时间随输入规模增长的增长速度，空间复杂度描述了算法执行期间所需的存储空间随输入规模增长的增长速度。
1.2 时间复杂度的计算方法时间复杂度可以通过估算算法的执行次数来计算。
对于循环结构，通常可以通过循环体内代码的执行次数来估算时间复杂度。
对于递归算法，则可以通过递归的深度和每次递归的复杂度来计算时间复杂度。
1.3 常见的时间复杂度在算法分析中，常见的时间复杂度有：O(1)、O(log n)、O(n)、O(n log n)、O(n^2)、O(n^3)等。
其中，O(1)表示算法的执行时间与输入规模无关，即常数时间复杂度；O(log n)表示算法的执行时间随输入规模呈对数增长；O(n)表示算法的执行时间随输入规模呈线性增长；O(nlog n)表示算法的执行时间随输入规模呈线性对数增长；O(n^2)表示算法的执行时间随输入规模呈平方增长；O(n^3)表示算法的执行时间随输入规模呈立方增长。
1.4 空间复杂度的计算方法空间复杂度可以通过估计算法执行过程中所需要的额外存储空间来计算。
对于递归算法，通常使用递归的深度来估算空间复杂度。
1.5 算法复杂度的应用算法的复杂度分析在实际应用中非常重要，可以帮助我们选择合适的算法来解决问题。
在时间复杂度相同的情况下，可以通过比较空间复杂度来选择更优的算法。
在实际开发中，我们也可以根据算法的复杂度来进行性能优化，减少资源的消耗。
二、搜索算法2.1 线性搜索算法线性搜索算法是一种简单直观的搜索算法，逐个比较待搜索元素和数组中的元素，直到找到匹配的元素或遍历完整个数组。
其时间复杂度为O(n)，空间复杂度为O(1)。
2.2 二分搜索算法二分搜索算法是一种高效的搜索算法，前提是数组必须是有序的。
算法首先取数组的中间元素进行比较，如果相等则返回找到的位置，如果大于中间元素则在右半部分继续搜索，如果小于中间元素则在左半部分继续搜索。
数据结构习题讲解
数据结构习题讲解第1章绪论一、判断题1. 数据的逻辑结构与数据元素本身的内容和形式无关。
（V ）2. 一个数据结构是由一个逻辑结构和这个逻辑结构上的一个基本运算集构成的整体。
（V ）3. 数据元素是数据的最小单位。
（X ） 4. 数据的逻辑结构和数据的存储结构是相同的。
（X ） 5. 程序和算法原则上没有区别，所以在讨论数据结构时可以通用。
（X ） 6. 从逻辑关系上讲，数据结构主要分为线性结构和非线性结构两类。
（V ） 7. 数据的存储结构是数据的逻辑结构的存储映象。
（V ） 8. 数据的物理结构是指数据在计算机内实际的存储形式。
（V ） 9. 数据的逻辑结构是依赖于计算机的。
（X ）10. 算法是对解题方法和步骤的描述。
（V ）二、填空题1. 数据有逻辑结构和存储结构两种结构。
-----------------2. 数据逻辑结构除了集合以外，还包括线性结构、树形结构和图形结构。
_________3. 数据结构按逻辑结构可分为两大类，它们是线性结构和非线性结构。
---------4. 树形结构和图形结构合称为非线性结构。
---------------------------------5. 在树形结构中，除了树根结点以外，其余每个结点只有1个前驱结点。
_6. 在图形结构中，每个结点的前驱结点数和后继结点数可以任意多个。
___________7. 数据的存储结构又叫物理结构。
________________8. 数据的存储结构形式包括顺序存储、链式存储、索引存储和散列存储 -------9. 线性结构中的元素之间存在一对一的关系。
------------- 10. 树形结构中的元素之间存在一对多的关系。
_____________ 11. 图形结构的元素之间存在多对多的关系。
--------------12. 数据结构主要研究数据的逻辑结构、存储结构和算法（或运算）3个方面的内容。
数据结构 复习与习题解析.ppt
基本概念和术语
【数据结构】相互之间存在一种或多种特定关系的数据 元素的集合
【数据】是对信息的一种符号表示。是可以输入计算机中， 能被计算机识别处理和输出的一切符号集合
。 【数据元素】是数据的基本单位，在计算机中通常作为一个
整体进行考虑和处理。也称为记录。 【数据项】一个数据元素可由若干个数据项组成。是数据不
（3）索引存储方式。除数据元素存储在一地址连续的内存空间外，尚需建立一个索引 表，索引表中索引指示存储结点的存储位置（下标）或存储区间端点（下标），兼 有静态和动态特性。
11
26/02/2021
算法效率的度量方法
❖ 事后统计方法
通过设计好的测试程序和数据，利用计算机测量其运行时间。 缺陷：需要先编写程序；和计算机软硬件相关；和测试数据相关。
❖ 事前分析估算方法（我们的选择）
依据统计方法对算法进行估算。m = f(n)，m是语句总的执行次数 ，n是输入的规模。
输出是指与输入有某种特定关系的量。
算法设计的要求
❖ 正确性（四个境界）
没有语法错误 对于合法的输入数据能够产生满足要求的输出 对于非法的输入数据能够得出满足规格说明的结果 对于任何测试数据都有满足要求的输出结果
❖ 可读性：便于阅读、理解和交流 ❖ 健壮性：不合法数据也能合理处理 ❖ 时间效率高和存储量低
数据的逻辑结构
（面向人类）
数据的存储结构
（面向计算机）
线性结构
非线性结构 顺序存储 链式存储 索引存储
线性表 栈 队列 串及数组
树形结构
图形结构
散列存储
数据的运算（操作）：检索、排序、插入、删除、修改等
6
26/02/2021
四种基本逻辑结构
数据结构与算法学习例题与解答
数据结构与算法学习例题与解答1. 介绍数据结构与算法是计算机科学中非常重要的基础知识，它们在解决实际问题和优化程序性能方面起着至关重要的作用。
本文将为读者介绍一些常见的数据结构与算法例题，并给出相应的解答。
通过对这些例题的学习与分析，读者将能更好地理解不同数据结构和算法的应用场景，提高编程能力和解决问题的能力。
2. 栈和队列2.1 栈栈是一种后进先出（LIFO）的数据结构，常用于表示函数调用、表达式求值以及实现撤销操作等。
下面是一个例题：例题：给定一个包含 n 个元素的数组 arr，要求使用栈实现对 arr 中元素的逆序输出。
解答：可以使用一个栈来辅助实现逆序输出。
首先将数组中的所有元素按顺序入栈，然后依次出栈并输出即可。
2.2 队列队列是一种先进先出（FIFO）的数据结构，常用于任务调度、消息传递等场景。
下面是一个例题：例题：设计一个简单的消息队列，支持消息的发布、订阅和取消订阅功能。
解答：可以使用两个队列来实现简单的消息队列。
一个队列用于存储已发布的消息，另一个队列用于存储订阅者。
当有新消息发布时，将其加入已发布消息的队列，同时遍历订阅者队列，将消息发送给每个订阅者。
3. 链表链表是一种动态数据结构，它通过指针将一组节点串联起来。
链表常用于表示链式存储的数据结构，如链表、树等。
下面是一个例题：例题：给定一个单向链表的头节点 head，要求设计一个算法找到链表的中间节点。
解答：可以使用快慢指针的方法来实现。
定义两个指针，分别称为 fast 和slow，初始时都指向链表的头节点。
fast 指针每次移动两个节点，slow 指针每次移动一个节点，直到 fast 指针到达链表末尾。
此时，slow 指针指向的节点即为链表的中间节点。
4. 树和图4.1 二叉树二叉树是一种每个节点最多有两个子节点的树结构。
二叉树常用于表示有层次关系的数据，如文件系统、算术表达式等。
下面是一个例题：例题：给定一棵二叉树的根节点 root，要求设计一个算法计算二叉树的节点个数。
数据结构和算法习题及答案解析
第1章绪论习题1．简述下列概念：数据、数据元素、数据项、数据对象、数据结构、逻辑结构、存储结构、抽象数据类型。
2．试举一个数据结构的例子，叙述其逻辑结构和存储结构两方面的含义和相互关系。
3．简述逻辑结构的四种基本关系并画出它们的关系图。
4．存储结构由哪两种基本的存储方法实现？5．选择题（1）在数据结构中，从逻辑上可以把数据结构分成（）。
A．动态结构和静态结构 B．紧凑结构和非紧凑结构C．线性结构和非线性结构 D．内部结构和外部结构（2）与数据元素本身的形式、内容、相对位置、个数无关的是数据的（）。
A．存储结构 B．存储实现C．逻辑结构 D．运算实现（3）通常要求同一逻辑结构中的所有数据元素具有相同的特性，这意味着（）。
A．数据具有同一特点B．不仅数据元素所包含的数据项的个数要相同，而且对应数据项的类型要一致C．每个数据元素都一样D．数据元素所包含的数据项的个数要相等（4）以下说法正确的是（）。
A．数据元素是数据的最小单位B．数据项是数据的基本单位C．数据结构是带有结构的各数据项的集合D．一些表面上很不相同的数据可以有相同的逻辑结构（5）以下与数据的存储结构无关的术语是（）。
A．顺序队列 B. 链表 C.有序表 D. 链栈（6）以下数据结构中，（）是非线性数据结构A．树 B．字符串 C．队 D．栈6．试分析下面各程序段的时间复杂度。
（1）x=90; y=100;while(y>0)if(x>100){x=x-10;y--;}else x++;（2）for (i=0; i<n; i++)for (j=0; j<m; j++)a[i][j]=0;（3）s=0;for i=0; i<n; i++)for(j=0; j<n; j++)s+=B[i][j];sum=s;（4）i=1;while(i<=n)i=i*3;（5）x=0;for(i=1; i<n; i++)for (j=1; j<=n-i; j++)x++;（6）x=n; //n>1y=0;while(x≥(y+1)* (y+1))y++;（1）O（1）（2）O（m*n）（3）O（n2）（4）O（log3n）（5）因为x++共执行了n-1+n-2+……＋1= n(n-1)/2，所以执行时间为O（n2）（6）O(n)第2章线性表1．选择题（1）一个向量第一个元素的存储地址是100，每个元素的长度为2，则第5个元素的地址是（）。
数据结构课后习题详解(超完整超经典)
数据结构课后习题详解（超完整超经典）第1章绪论1.1简述下列术语：数据，数据元素、数据对象、数据结构、存储结构、数据类型和抽象数据类型。
解：数据是对客观事物的符号表示。
在计算机科学中是指所有能输入到计算机中并被计算机程序处理的符号的总称。
数据元素是数据的基本单位，在计算机程序中通常作为一个整体进行考虑和处理。
数据对象是性质相同的数据元素的集合，是数据的一个子集。
数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
存储结构是数据结构在计算机中的表示。
数据类型是一个值的集合和定义在这个值集上的一组操作的总称。
抽象数据类型是指一个数学模型以及定义在该模型上的一组操作。
是对一般数据类型的扩展。
1.2试描述数据结构和抽象数据类型的概念与程序设计语言中数据类型概念的区别。
解：抽象数据类型包含一般数据类型的概念，但含义比一般数据类型更广、更抽象。
一般数据类型由具体语言系统内部定义，直接提供给编程者定义用户数据，因此称它们为预定义数据类型。
抽象数据类型通常由编程者定义，包括定义它所使用的数据和在这些数据上所进行的操作。
在定义抽象数据类型中的数据部分和操作部分时，要求只定义到数据的逻辑结构和操作说明，不考虑数据的存储结构和操作的具体实现，这样抽象层次更高，更能为其他用户提供良好的使用接口。
1.3设有数据结构(D,R)，其中Dd1,d2,d3,d4，Rr，rd1,d2,d2,d3,d3,d4试按图论中图的画法惯例画出其逻辑结构图。
解：1.4试仿照三元组的抽象数据类型分别写出抽象数据类型复数和有理数的定义（有理数是其分子、分母均为自然数且分母不为零的分数）。
解：数据对象：D={r,i|r,i为实数}数据关系：R={}基本操作：操作结果：构造一个复数C，其实部和虚部分别为re和imDetroyCmople某(&C)操作结果：销毁复数CGet(C,k,&e)操作结果：用e返回复数C的第k元的值操作结果：改变复数C的第k元的值为e操作结果：如果复数C的两个元素按升序排列，则返回1，否则返回0Put(&C,k,e)IAcending(C)ADTRationalNumber{数据对象：D={,m|,m为自然数，且m不为0}数据关系：R={}基本操作：InitRationalNumber(&R,,m)操作结果：构造一个有理数R，其分子和分母分别为和mDetroyRationalNumber(&R)操作结果：销毁有理数RGet(R,k,&e)操作结果：用e返回有理数R的第k元的值操作结果：改变有理数R 的第k元的值为e操作结果：若有理数R的两个元素按升序排列，则返回1，否则返回0操作结果：若有理数R的两个元素按降序排列，则返回1，否则返回0操作结果：用e返回有理数R的两个元素中值较大的一个操作结果：用e 返回有理数R的两个元素中值较小的一个Put(&R,k,e)IAcending(R)IDecending(R)Ma某(R,&e)Min(R,&e) IDecending(C)操作结果：如果复数C的两个元素按降序排列，则返回1，否则返回0操作结果：用e返回复数C的两个元素中值较大的一个操作结果：用e 返回复数C的两个元素中值较小的一个Ma某(C,&e)Min(C,&e) }ADTRationalNumber(1)product=1;i=1;while(i<=n){product某=i;i++;}(2)i=0;do{i++;}while((i!=n)&&(a[i]!=某));(3)witch{cae某1.5试画出与下列程序段等价的框图。
数据结构与算法习题讲解(全)
float find(float low, float high) { mid=(low+high)/2; if(fabs(f(mid))<=0.000001) return mid; else if(f(mid)*f(low)<0) find(low, mid); else find(mid,high); } 为使程序正常终止，必须设置基准情况。 （注意精度防止溢出）
答：a. 所有的算法都可以生成合法的置换。 很明显，前2个算法在测试中可以保证不生 成重复的数，并且它们是完全随机的，故 它们生成的置换是等可能。第3个算法轮换 数组中的元素，这个数组最初是没有重复 数的，也不会存在非法置换。 前2个算法很明显成立，第3个算法可以用 数学归纳法证明，详细证明如下：
b.第一个算法中，决定a[i]中一个之前没有 使用过的随机数是否被填入的时间是O(i)。 在那些需要测试的随机数中，需要产生期 望的随机数的次数为N/(N − i)次。得出结论 如下：n个数中有i个可能是重复的。因此， 置换成功的概率为(N − i)/N。因此，在独立 的测试中，期望数为N/(N − i)。时间复杂度 即为：
void find(float low, float high) { float mid=(low+high)/2; if(fabs(f(mid))<=0.0001) { c=mid; } else { if(f(mid)*f(low)<0) find(low, else find(mid,high); } }
②二项式法：令x=2x,有log2x<2x, 即x<2x 又2x =(1+1)x=C0x+C1x+…+Cxx =1+x+C2x+…+x+1>x 即2x>x, 得logx<x;命题得证 b. log(AB)=BlogA 证明：令2X=A, 则AB =(2X)B =2XB ; 则logAB =XB, X=logA;命题得证
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
②二项式法：令x=2x,有log2x<2x, 即x<2x 又2x =(1+1)x=C0x+C1x+…+Cxx =1+x+C2x+…+x+1>x 即2x>x, 得logx<x;命题得证 b. log(AB)=BlogA 证明：令2X=A, 则AB =(2X)B =2XB ; 则logAB =XB, X=logA;命题得证
注：证明时默认地利用了一个命题：当原序列为 互不相等的等可能序列时，新加入一个与原来序 列任何数值都不相等的数值，无论这个数值放在 原序列的哪个位置，都不可能使原不相等的序列 相等。 例：210, 021, 012, 201, 120, 102，这时加入一个新 的数值3，无论把3插入序列的哪个位置，因为原 来序列的排列不相等，所以，他们还是不会相等， 这样，才保证了最后k个序列的k+1种可能都不相 等，不会重复。
4) sum=0; for(i=0; i<n; i++) for(j=0; j<i; j++) sum++; O(N2)
5)sum=0; for(i=0; i<n; i++) for(j=0; j<i*i; j++) for(k=0; k<j; k++) sum++; O(N5)
j可等规模于i2, 同样也等 规模于N2. k等规模于j, 即N2. 则该程序段的运 行时间复杂度分析为 N*N2*N2, 即O(N5).
mid);
2.26 大小为N的数组A，其主元素是一个出 现超过N/2次的元素(从而这样的元素最多有 一个)。例如：数组：3,3,4,2,4,4,2,4,4有一个 主元素4；而数组3,3,4,2,4,4,2,4没有主元素。 如果没有主元素，那么你的程序应该指出 来。 a.递归如何终止？ b.当N是奇数时的情形如何处理？ c.该算法的运行时间是多少？ d.我们如何避免使用附加数组B？
第二章
2.1按增长率排列函数：N, N1/2, N1.5, N2, NlogN, Nlog(logN), Nlog2N, Nlog(N2), 2/N, 2N, 2N/2, 37, N2logN, N3。指出哪些函数以相同的增长率增长。 答：2/N, 37, N1/2, N, Nlog(logN), NlogN, Nlog(N2), Nlog2N, N1.5, N2, N2logN, N3, 2N/2, 2N. 其中，NlogN, Nlog(N2)有相同的增长率。 常见的几种计算时间的关系： O(1)<O(logN)<O(N)<O(NlogN)<O(N2)<O(N3) O(2N)<O(N!)<O(NN)
6) sum=0; for(i=1; i<n; i++) for(j=1; j<i×i; j++)* if(j%i==0) for(k=0; k<j; k++) sum++; O(N4)
注： *处的for语句的循环次数 为“12+22+32+…+n2”,
如上题所述if 语句至多要 执行N3次, 但是实际上只 有O(N2)次 (因为对每一个i， 实际上都严格执行了i次), 因此最内的循环只执行了 O(N2)次。 而每执行一次, 将花费 O(j2) = O(N2) 的时 间, 总数即为O(N4)。 个人理解： if(j%i==0) for(k=0; k<j; k++) sum++; 这段程序段的循环次数O(N)
一个例子： #include<stdio.h> #include<math.h> float f(float a) { return 5*a+1; } void find(float,float); float static c=0; void main() { find(-4,5.0); printf("%f\n",c); return 0; }
(a) 12000 times as large a problem, or input size 1,200,000. N=60*1000*100/0.5=12,000,000=1.2*107 (b) input size of approximately 425,000. 由NlogN=1.2*107 可得 (c) 120001/2 times as large a problem, or input size 10,954. 由N2=1.2*107 可得 (d) 120001/3 times as large a problem, or input size 2,289. 由N3=1.2*107 可得
第2个算法为每个随机数保留了因子i ，因 此，时间度平均减少到了O(NlogN) 。 第3个算法很明显是线性的，O(N)。
c. 算法1和算法2的最坏运行时间无法被界定， 在一直随机到重复数字的时候可以到达无 限大。算法3的运行时间是线性的——它的 运行时间并不依赖于随机数的次序。
2.12 一个算法对于大小为100的输入花费 0.5ms，如果运行时间如下：则用1min可以 解决多大的问题(设低阶项可以忽略)。 a.是线性的； b.为O(NlogN) c. 是二次的； d. 是三次的
2.18 数值分析中一个重要的问题是对某一 个任意的函数f找出方程f(x)=0的一个解。如 果该函数是连续的，并有两个点low和hign 使得f(low)和f(high)符号相反，那么在low与 high之间必然存在一个根。并且这个根可以 通过二分搜索求得。写一个函数，以f, low 和high为参数，并且解出一个零点。
b.第一个算法中，决定a[i]中一个之前没有 使用过的随机数是否被填入的时间是O(i)。 在那些需要测试的随机数中，需要产生期 望的随机数的次数为N/(N − i)次。得出结论 如下：n个数中有i个可能是重复的。因此， 置换成功的概率为(N − i)/N。因此，在独立 的测试中，期望数为N/(N − i)。时间复杂度 即为：
1.当n=1时，a[0]=1，都是100%，成立； 2.当n=2时，for(i = 1; i < n; ++i) swap (a[i],a[randInt(0,i)]); 第一次循环，当i=1时，即a[0]=1,a[i]=a[1]； 3.当 n=3时，第二次循环时，当i=2时，此时有两种可能， 原序列为0,1; 1,0的几率各为50%。randInt(0,2)可能为0,1,2 的几率各为1/3。此时,原序列为0,1时,randInt(0,2)为0,那么 此序列经过swap(a[2],a[0]),最后序列为2,1,0,此序列的可能 性为(1/2)*(1/3)=1/6; 同理易得,最后此序列为“210, 021, 012, 201, 120, 102”的几率各为1/6,而此序列的所有排列可 能为=3*2= 6,所以，此时成立。 4.假设此命题在n = k时成立，那么就是说，ｋ前面序列共 有序列k-1种，且所有序列的几率为1/((k-1)*k)。 5. 当n=k+1时,第k+1次循环时,前面序列正好为n=k时的情况, 此时i = k. randInt(0,k)共可能为0~k,k+1种可能。所以以前 的每个可能序列在置换后有k+1种可能，而以前共有k种等 可能序列，那么最后可能的序列为k*(k+1)种可能，并且， 因为原序列为等可能的，每个等可能序列产生的序列都是 k+1种，所以最后的序列也是等可能的。而当n=k+1时，应 该共有 =(k+1)*k种，所以，此命题得证。
void find(float low, float high) { float mid=(low+high)/2; if(fabs(f(mid))<=0.0001) { c=mid; } else { if(f(mid)*f(low)<0) find(low, else find(mid,high); } }
1.7证明下列公式 a. logx<x对所有的x>0成立 ①数学归纳法：当0<x≤1, 命题显然成立： x=1, 公式是成立的；当x<1时, logx 是负数。 同理可以很容易推出当1<x≤2时命题成立： x=2, 公式成立；当x<2, logx最大为1。假设 命题在p<x≤2p时成立(p为正整数), 这时考虑 有2p<Y≤4p (p ≥ 1)。则logy=1+log(y/2) <1+y/2<y/2+y/2≤y, 由此可推导出公式成立。
2.7对于下列六个程序片段中的每一个：给出运 行时间分析 1) sum=0; 2) sum=0; for(i=0; i<n; i++) for(i=0; i<n; i++) sum++; for(j=0; j<n; j++) O(N) sum++; O(N2)
3) sum=0; for(i=0; i<n; i++) for(j=0; j<n*n; j++) sum++; O(N3)
答：a. 所有的算法都可以生成合法的置换。 很明显，前2个算法在测试中可以保证不生 成重复的数，并且它们是完全随机的，故 它们生成的置换是等可能。第3个算法轮换 数组中的元素，这个数组最初是没有重复 数的，也不会存在非法置换。 前2个算法很明显成立，第3个算法可以用 数学归纳法证明，详细证明如下：第一章 Nhomakorabea