四川省2017级普通高中学业水平考试数学试卷
四川省成都市2017级高中毕业班第一次诊断性检测理数试题

成都市2017级高中毕业班第一次诊断性检测(数学理科)本试卷分选择题和非选择题两部分,第1卷(选择题)1至2页,第11卷(非选择题)3至4页,共4页,满分150分,考试时间120分钟. 注意事项:1,答题前,务必将自己的姓名、考籍号填写在答题卡规定的位置上。
2,答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
3,答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4,所有题目必须在答题卡上作答,在试题卷上答题无效。
5,考试结束后,只将答题卡交回。
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的1.若复数1z 与23z i =--(i 为虚数单位)在复平面内对应的点关于实轴对称,则1z = (A )i --3 (B )i +-3 (C )i +3 (D )i -32.已知集合{}m A ,0,1-=,{}2,1=B ,若{}2,1,0,1-=B A Y ,则实数m 的值为 (A )1-或0 (B )0或1 (C )1-或2 (D )1或23.若)2cos(5sin θπθ-=,则=θ2tan(A )35-(B )35 (C )25- (D )254.某校随机抽取100名同学进行“垃圾分类"的问卷测试,测试结果发现这100名同学的得分都在[50,100]内,按得分分成5组:[50,60),[60,70), [70,80),[80,90),[90,100],得到如图所示的频率分布直方 图,则这100名同学的得分的中位数为 (A )5.72 (B )75 (C )5.77(D )805.设等差数列{}n a 的前n 项和为n S ,且353a a =,则=59S S (A )59 (B )95 (C )35 (D )5276.已知βα,是空间中两个不同的平面,n m ,是空间中两条不同的直线,则下列说法正确的是 (A )若α//m ,β//n ,且βα//,则n m // (B )若α//m ,β//n ,且βα⊥,则n m // (C )若α⊥m ,β//n ,且βα//,则n m ⊥ (D )若α⊥m ,β//n ,且βα⊥,则n m ⊥ 7.62)1)(2(xx x -+的展开式的常数项为 (A )25(B )25- (C )5 (D )5- 8.将函数)64sin(π-=x y 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所得图象向左平移6π个单位长度,得到函数)(x f 的图象,则函数)(x f 的解析式为 (A ))62sin()(π+=x x f (B ))32sin()(π-=x x f(C ))68sin()(π+=x x f (D) )38sin()(π-=x x f9.已知抛物线x y 42=的焦点为F ,N M ,是抛物线上两个不同的点若5||||=+NF MF ,则线段MN 的中点到y 轴的距离为(A )3 (B )23 (C )5 (D )2510.已知212=a ,313=b ,23ln=c ,则 (A )c b a >> (B )b c a >> (C )c a b >>(D )a c b >>11.已知定义在R 上的数)(x f 满足)2()2(x f x f +=-,当2≤x 时()(1)1xf x x e =--.若关于x 的方程012)(=+-+-e k kx x f 有三个不相等的实数根,则实数k 的取值范围是(A )),2()0,2(+∞-Y (B )(2,0)(0,2)-U (C )),()0,(+∞-e e Y (D )),0()0,(e e Y -12.如图,在边长为2的正方形321P P AP 中,线段BC 的端点C B ,分别在边21P P 、32P P 上滑动,且x C P B P ==22,现将B AP 1∆,C AP 3∆分别沿AB ,AC 折起使点31,P P 重合,重合后记为点P ,得到三被锥ABC P -.现有以下结论: ①⊥AP 平面PBC ;②当C B ,分别为21P P 、32P P 的中点时,三棱锥ABC P -的外接球的表面积为π6; ③x 的取值范围为)224,0(-; ④三棱锥ABC P -体积的最大值为31. 则正确的结论的个数为(A )1 (B )2 (C )3 (D )4二、填空题(本大题共4小题,每小题5分,共20分)13.已知实数y x ,满足约束条件⎪⎩⎪⎨⎧≥≥+-≤-+002204y y x y x ,则y x z 2+=的最大值为_______.14.设正项等比数列{}n a 满足814=a ,3632=+a a ,则=n a _______.15.已知平面向量a ,b 满足2||=a ,3||=b ,且)(b a b -⊥,则向量a 与b 的夹角的大小为_______.16.已知直线kx y =与双曲线)0,0(1:2222>>=-b a by a x C 相交于不同的两点B A ,,F 为双曲线C 的左焦点,且满足||3||BF AF =,||OA b =(O 为坐标原点),则双曲线C 的离心率为_______.三、解答题(共70分。
2017年四川省高考数学试卷与解析word(理科)(全国新课标Ⅲ)
2017年四川省高考数学试卷(理科)(全国新课标Ⅲ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合A={(x,y)|x2+y2=1},B={(x,y)|y=x},则A∩B中元素的个数为()A.3 B.2 C.1 D.02.(5分)设复数z满足(1+i)z=2i,则|z|=()A.B.C.D.23.(5分)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是()A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.(5分)(x+y)(2x﹣y)5的展开式中的x3y3系数为()A.﹣80 B.﹣40 C.40 D.805.(5分)已知双曲线C:﹣=1 (a>0,b>0)的一条渐近线方程为y=x,且与椭圆+=1有公共焦点,则C的方程为()A.﹣=1 B.﹣=1 C.﹣=1 D.﹣=16.(5分)设函数f(x)=cos(x+),则下列结论错误的是()A.f(x)的一个周期为﹣2πB.y=f(x)的图象关于直线x=对称C.f(x+π)的一个零点为x=D.f(x)在(,π)单调递减7.(5分)执行如图的程序框图,为使输出S的值小于91,则输入的正整数N 的最小值为()A.5 B.4 C.3 D.28.(5分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A.πB. C.D.9.(5分)等差数列{a n}的首项为1,公差不为0.若a2,a3,a6成等比数列,则{a n}前6项的和为()A.﹣24 B.﹣3 C.3 D.810.(5分)已知椭圆C:=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,则C的离心率为()A.B.C.D.11.(5分)已知函数f(x)=x2﹣2x+a(e x﹣1+e﹣x+1)有唯一零点,则a=()A.﹣ B.C.D.112.(5分)在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若=λ+μ,则λ+μ的最大值为()A.3 B.2 C.D.2二、填空题:本题共4小题,每小题5分,共20分。
四川省2017年高考理科数学试题及答案
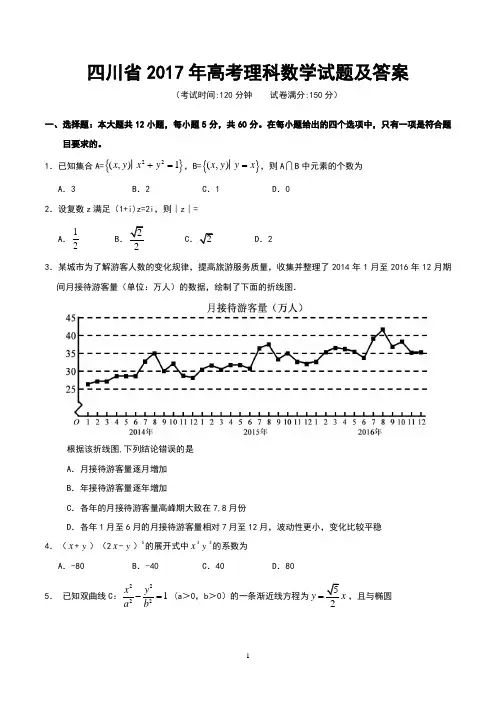
四川省2017年高考理科数学试题及答案(考试时间:120分钟 试卷满分:150分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={}22(,)1x y x y +=│,B={}(,)x y y x =│,则A B 中元素的个数为A .3B .2C .1D .02.设复数z 满足(1+i)z=2i ,则∣z ∣= A .12B .22C .2D .23.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客量逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月份D .各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳 4.(x +y )(2x -y )5的展开式中x 3y 3的系数为A .-80B .-40C .40D .805. 已知双曲线C :22221x y a b -= (a >0,b >0)的一条渐近线方程为52y x =,且与椭圆221123x y += 有公共焦点,则C 的方程为 A .221810x y -= B .22145x y -= C .22154x y -= D .22143x y -= 6.设函数f(x)=cos (x+3π),则下列结论错误的是 A .f (x )的一个周期为−2πB .y=f(x )的图像关于直线x=83π对称 C .f(x+π)的一个零点为x=6πD .f(x )在(2π,π)单调递减 7.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为 A .5 B .4C .3D .28.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A .πB .3π4C .π2D .π49.等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为 A .—24B .-3C .3D .810.已知椭圆C:22221x y a b+=,(a 〉b 〉0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A .63B .33C .23D .1311.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a=A .12-B .13C .12D .112.在矩形ABCD 中,AB=1,AD=2,动点P 在以点C 为圆心且与BD 相切的圆上.若AP =λ AB +μAD ,则λ+μ的最大值为A.3 B.CD.2二、填空题:本题共4小题,每小题5分,共20分.13.若x,y满足约束条件y020xx yy-≥⎧⎪+-≤⎨⎪≥⎩,则z34x y=-的最小值为__________.14.设等比数列{}n a满足a1 + a2 = –1, a1– a3 = –3,则a4 = ___________.15.设函数10()20xx xf xx+≤⎧=⎨>⎩,,,,则满足1()()12f x f x+->的x的取值范围是_________.16.a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:①当直线AB与a成60°角时,AB与b成30°角;②当直线AB与a成60°角时,AB与b成60°角;③直线AB与a所称角的最小值为45°;④直线AB与a所称角的最小值为60°;其中正确的是________。
四川省2017级高中毕业班诊断性测试理科数学答案

2k
2k
1
1
为定值,此题得证.
(11 分)
(12 分) (1 分) (2 分) (3 分) (4 分)
(5 分) (6 分) (7 分) (9 分)
(10 分) (12 分)
第2页,共5页
20.解:(1)由表格数据得,
x
5
3 15
25
9
,
y 0.13 0.23 0.31 0.41 0.52 0.32 . 5
又因为 a2=b2+c2,所以 a2 1 3a2 ,解得 a=2. 4
故椭圆 E 的方程为 x2 y2 1 . 4
(2)因为直线 BC 过点 P(2,1),且与轨迹 E 有两个不同交点,
所以直线 BC 的斜率一定存在且大于零.
于是可设直线 BC 的方程为 y=k(x-2)+1(k>0).
代入 x2+4y2=4 并整理得(3k2+1)x2-8k(2k-1)x+16k(k-1)=0(Δ>0).
因为 tan A tan B sin A sin B sin Acos B cos A sin B
பைடு நூலகம்
cos A cos B
cos Acos B
sinA B sin C .
cos Acos B cos Acos B
又 tan B sin B ,所以 b sin C 2c sin B ,即 b sin C 2c sin B .
设
B(x1,y1)、C(x2,y2),则
x1
x2
8k2k 1
3k 2 1
,
x1 x2
16kk 1
3k 2 1
.
设直线 AB 和 AC 的斜率分别为 k1 和 k2,则
四川省凉山州2017年中考数学真题试题(含扫描答案)

2017年凉山州高中阶段教育学校招生统一考试数学试题班级: 姓名: 学号:注意事项:1. 答题前,考生务必将自己的姓名、座位号、准考证号用0.5毫米的黑色签字笔填写在答题卡上,并在答题卡背面上方填涂座位号,同时检查条形码粘贴是否正确。
2. 选择题使用2B 铅笔涂在答题卡对应题目的位置上;非选择题用0.5毫米黑色签字笔书写在答题卡的对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
3. 考试结束后,教师将试题卷、答题卡、草稿纸一并收回。
本试卷共6页,分为A 卷(120分),B 卷(30分),全卷满分150分,考试时间120分钟。
A 卷又分为第I 卷和第II 卷。
A 卷(共120分)第Ⅰ卷(选择题 共48分)一、选择题:(共12个小题,每小题4分,共48分)在每小题给出的四个选项中只有一项是正确的,请把正确选项的字母填涂在答题卡上相应的位置。
1. 在2,3-,0,1-这四个数中,最小的数是( )A .2B .3-C .0D .1-2. 如右图,AB CD ∥,则下列式子一定成立的是( )A .13∠=∠B .23∠=∠C .123∠=∠+∠D .312∠=∠+∠ 3. 下列运算正确的是( ) A= B .32361126xy x y ⎛⎫-=- ⎪⎝⎭C .523()()x x x -÷-=D4=4. 指出下列事件中是随机事件的个数( )①投掷一枚硬币正面朝上;②明天太阳从东方升起;③五边形的内角和是560;④购买一张彩票中奖。
A .0B .1C .2D .35. 一列数4,5,6,4,4,7,x ,5的平均数是5,则中位数和众数分别是( )A .4,4B .5,4C .5,6D .6,76. 有一个数值转换器,原理如下:当输入的x 为64时,输出的y 是( )A.B. C. D .87. 小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1000米的书店。
小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家。
四川省眉山市2017年中考数学真题试题(含扫描答案)

眉山市2017年初中学业水平暨高中阶段学校招生考试数学试卷一、选择题(36分)1.下列四个数中,比-3小的数是( )A .0B .1C .-1D .-52.不等式-2x >12的解集是( ) A .x <-14 B . x <-1 C . x >-14D . x >-13.某微生物的直径为0.000 005 035m ,用科学记数法表示该数为( ) A .5.035×10-6 B . 50.35×10-5 C . 5.035×106 D . 5.035×10-54.如图所示的几何体的主视图是( )5.下列说法错误的是( )A .给定一组数据,那么这组数据的平均数一定只有一个B .给定一组数据,那么这组数据的中位数一定只有一个C .给定一组数据,那么这组数据的众数一定只有一个D .如果一组数据存在众数,那么该众数一定是这组数据中的某一个6.下列运算结果正确的是( )A .8-18=- 2B .(-0.1)-2=0.01C .(2a b )2÷b 2a =2a bD .(-m )3·m 2=-m 6 7.已知关于x ,y 的二元一次方程组⎩⎨⎧2ax +by =3ax -by =1的解为⎩⎨⎧x =1y =-1,则a -2b 的值是( ) A .-2 B .2 C .3 D .-38.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )A .1.25尺 B .57.5尺 C .6.25尺 D .56.5尺9.如图,在△ABC 中,∠A =66°,点I 是内心,则∠BIC 的大小为( )A .114°B .122°C .123°D .132°10.如图,EF 过□ABCD 对角线的交点O ,交AD 于E ,交BC 于F ,若□ABCD 的周长为18,OE =1.5,则四边形EFCD 的周长为( ).A .14B .13C .12D .1011.若一次函数y =(a +1)x +a 的图象过第一、三、四象限,则二次函数y =ax 2-ax ( ) A .有最大值a 4 B . 有最大值-a 4 C . 有最小值a 4 D . 有最小值-a 412.已知14m 2+14n 2=n -m -2,则1m -1n的值等于( ) A .1 B .0 C .-1 D .-14二、填空题(24分)13.分解因式:2ax 2-8a =__________.14.△ABC 是等边三角形,点O 是三条高的交点.若△ABC 以点O 为旋转中心旋转后能与原来的图形重合,则△ABC 旋转的最小角度是_______15.已知一元二次方程x 2-3x -2=0的两个实数根为x 1,x 2,则(x 1-1)(x 2-1)的值是________.16.设点(-1,m )和点(12,n )是直线y =(k 2-1)x +b (0<k <1)上的两个点,则m 、n 的大小关系为____________.17.如图,AB 是⊙O 的弦,半径OC ⊥AB 于点D ,且AB =8cm ,DC =2cm ,则OC =______cm .18.已知反比例函数y =2x,当x <-1时,y 的取值范围为___________. 三.解答题:(60分)19.(6分)先化简,再求值:(a +3)2-2(3a +4),其中a =-2.20.(6分)解方程:1x -2+2=1-x 2-x .21.(8分)在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC (顶点是网格线交点的三角形)的顶点A 、C 的坐标分别是(-4,6),(-1,4). ⑴请在图中的网格平面内建立平面直角坐标系;⑵请画出△ABC 关于x 轴对称的△A 1B 1C 1;⑶请在y 轴上求作一点P ,使△PB 1C 的周长最小,并写出点P 的坐标.22.(8分)如图,为了测得一棵树的高度AB ,小明在D 处用高为1m 的测角仪CD ,测得树顶A 的仰角为45°,再向树方向前进10m ,又测得树顶A 的仰角为60°,求这棵树的高度AB .23.(9分)一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是129.⑴求袋中红球的个数;⑵求从袋中任取一个球是黑球的概率.24.(9分)东坡某烘焙店生产的蛋糕礼盒分为六个档次,第一档次(即最低档次)的产品每天生产76件,每件利润10元.调查表明:生产提高一个档次的蛋糕产品,该产品每件利润增加2元.⑴若生产的某批次蛋糕每件利润为14元,此批次蛋糕属第几档次产品;⑵由于生产工序不同,蛋糕产品每提高一个档次,一天产量会减少4件.若生产的某档次产品一天的总利润为1080元,该烘焙店生产的是第几档次的产品?25.(9分)如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交BC于G.⑴求证:BG=DE;⑵若点G 为CD 的中点,求HG GF的值.26.(11分)如图,抛物线y =ax 2+bx -2与x 轴交于A 、B 两点,与y 轴交于C 点,已知A (3,0),且M (1,-83)是抛物线上另一点. ⑴求a 、b 的值;⑵连结AC ,设点P 是y 轴上任一点,若以P 、A 、C 三点为顶点的三角形是等腰三角形,求P 点的坐标;⑶若点N 是x 轴正半轴上且在抛物线内的一动点(不与O 、A 重合),过点N 作NH ∥AC 交抛物线的对称轴于H 点.设ON =t ,△ONH 的面积为S ,求S 与t 之间的函数关系式.。
2017年四川省成都市中考数学真题及答案 精品
成都市二O一四年高中阶段教育学校统一招生考试(含成都市初三毕业会考)数学注意事项:1. 全套试卷分为A卷和B卷,A卷满分100分,B卷满分50分;考试时间120分钟。
2. 在作答前,考生务必将自己的姓名,准考证号涂写在试卷和答题卡规定的地方。
考试结束,监考人员将试卷和答题卡一并收回。
3. 选择题部分必须使用2B铅笔填涂;非选择题部分也必须使用0.5毫米黑色签字笔书写,字体工整,笔迹清楚。
4. 请按照题号在答题卡上各题目对应的答题区域内作答,超出答题区域书写的答案无效;在草稿纸,试卷上答题均无效。
5. 保持答题卡清洁,不得折叠、污染、破损等。
A卷(共100分)第I卷(选择题,共30分)一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)1.在-2,-1、0、2这四个数中,最大的数是()(A)-2 (B)-1 (C)0 (D)22.下列几何体的主视图是三角形的是( )(A) (B) (C)(D)3.正在建设的成都第二绕城高速全长超过220公里,串起我市二、三圈层以及周边的广汉、简阳等地,总投资达290亿元,用科学计数法表示290亿元应为( )(A )290×810 (B )290×910 (C )2.90×1010 (D )2.90×1110 4.下列计算正确的是( )(A )32x x x =+ (B )x x x 532=+ (C )532)(x x = (D )236x x x =÷ 5.下列图形中,不是..轴对称图形的是( )(A) (B) (C) (D)6.函数5-=x y 中自变量x 的取值范围是( )(A )5-≥x (B )5-≤x (C )5≥x (D )5≤x 7.如图,把三角板的直角顶点放在直尺的一边上,若∠1=30°,则∠2的度数为( )(A )60° (B )50° (C )40° (D )30°8.近年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为进一步普及环保和健康知识,我市某校举行了“建设宜居成都,关注环境保护”的知识竞赛,某班的学生成绩统计如下:成绩(分)60708090100人 数4812115则该办学生成绩的众数和中位数分别是( )(A )70分,80分 (B )80分,80分 (C )90分,80分 (D )80分,90分9.将二次函数322+-=x x y 化为k h x y +-=2)(的形式,结果为( ) (A )4)1(2++=x y (B )2)1(2++=x y (C )4)1(2+-=x y (D )2)1(2+-=x y10.在圆心角为120°的扇形AOB 中,半径OA =6cm ,则扇形AOB 的面积是( )(A )π62cm (B )π82cm (C )π122cm (D )π242cm第Ⅱ卷(非选择题,共70分)二.填空题(本大题共4个小题,每小题4分,共16分,答案写在答题卡上)11.计算:=-2_______________.12.如图,为估计池塘两岸边A ,B 两点间的距离,在池塘的一侧选取点O ,分别去OA 、OB 的中点M ,N ,测的MN=32 m ,则A ,B 两点间的距离是_____________m.13.在平面直角坐标系中,已知一次函数12+=x y 的图像经过),(11y x P x ,),(222y x P 两点,若21x x <,则1y ________2y .(填”>”,”<”或”=”)14.如图,AB 是⊙O 的直径,点C 在AB 的延长线上,CD 切⊙O 于点D ,连接AD ,若∠A =25°,则∠C=__________度.三.解答题(本大题共6个小题,共54分,解答过程写在答题卡上) 15.(本小题满分12分,每题6分) (1)计算202)2014(30sin 49--+-π .(2)解不等式组⎩⎨⎧+<+>-②① . ,7)2(2513x x x16.(本小题满分6分)如图,在一次数学课外实践活动中,小文在点C 处测得树的顶端A 的仰角为37°,BC =20m ,求树的高度AB .(参考数据:60.037sin ≈ ,80.037cos ≈ ,75.037tan ≈ )17.(本小题满分8分) 先化简,再求值:221ba b b a a -÷⎪⎭⎫⎝⎛--,其中13+=a ,13-=b .18.(本小题满分8分)第十五届中国“西博会”将于2017年10月底在成都召开,现有20名志愿者准备参加某分会场的工作,其中男生8人,女生12人.(1)若从这20人中随机选取一人作为联络员,求选到女生的概率; (2)若该分会场的某项工作只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁参加,游戏规则如下:将四张牌面数字分别为2、3、4、5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲参加,否则乙参加.试问这个游戏公平吗?请用树状图或列表法说明理由.19.(本小题满分10分)如图,一次函数5+=kx y (k 为常数,且0≠k )的图像与反比例函数xy 8-=的图像交于()b A ,2-,B 两点. (1)求一次函数的表达式;(2)若将直线AB 向下平移)0(>m m 个单位长度后与反比例函数的图像有且只有一个公共点,求m 的值.20.(本小题满分10分)如图,矩形ABCD 中,AB AD 2=,E 是AD 边上一点,AD nDE 1= (n 为大于2的整数),连接BE ,作BE 的垂直平分线分别交AD 、BC 于点F ,G ,FG 与BE 的交点为O ,连接BF 和EG .(1)试判断四边形BFEG 的形状,并说明理由; (2)当a AB =(a 为常数),3=n 时,求FG 的长; (3)记四边形BFEG 的面积为1S ,矩形ABCD 的面积为2S ,当301721 S S 时,求n 的值.(直接写出结果,不必写出解答过程)B 卷(共50分)CDG一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)21. 在开展“国学诵读”活动中,某校为了解全校1300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据。
2017级成都市高三第一次诊断性检测数学试题(理科)
成都市2017级高中毕业班第一次诊断性检测数学(理科)本试卷分选择题和非选择题两部分。
第1卷(选择题)1至2页,第lI卷(非选择题)3至4页,共4页,满分150分,考试时间120分钟。
注意事项:1. 答题前,务必将自己的姓名考籍号填写在答题卡规定的位置上。
2. 答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦千净后,再选涂其它答案标号。
答非选择题时,必须使用05毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4. 所有题目必须在答题卡上作答,在试题卷上答题无效。
5. 考试结束后,只将答题卡交回。
第1卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1若复数Z 1与Zz =-— (i 为虚数单位)在复平面内对应的点关于实轴对称,则Z1=CA)-—i (B)-3+ (C)+i (D)—!2.已知集合A={—1,0,m},B={l ,2}. 若A U B = {-1,0,1,2}, 则实数m的值为(A)-1或0(B)O或1CC)—1或23.若si n e =乔cos(2穴-0),则tan20=石乔瓦CA)——CB) -CC)—一 2 4.某校随机抽取100名同学进行“垃圾分类”的问卷测试,测试结果发现这100名同学的得分都在[50,100]内,按得分分成5组:[50,60), [60, 70), [70, 80),[80,90),[90,100], 得到如图所示的频率分布直方图则这100名同学的得分的中位数为CA )72. 50.040 0.030 数学(理科)”一诊“考试题第1页(共4页)CD)l或2CD)-污2 彗0.015 (B )75 0.0100.005 (C)77. 5(D)80。
工丑扫已。
100得分5设等差数列{a ,}的前n项和为S,,,且a ,,-::/:-0.若as =a 3, 则—=s 9 S s 9 5 5 (A)了(B)了(C)了6已知a,/3是空间中两个不同的平面,m,n是空间中两条不同的直线,则下列说法正确的是(A)若m II a ,n II /3, 且a II /3,则m II n (B)若m II a ,n II /3, 且a_l/3,则m II n (C)若m_la ,n II /3, 且a II /3, 则m _l n (D)若m _la,n ll /3,且a_l/3,则m _l n7.(x 2+2)(x ——)6的展开式的常数项为(A)25(B)-25 (C)5(D )—5 8.将函数y =si n (4x -王)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所6 得图象向左平移王个单位长度,得到函数f(x)的图象,则函数f(x)的解析式为6 (A) f(x) =si n (2x +互)6 CA) C —2,0) LJ (2, 十=)穴CB) f(x) =si n (2x —一) 亢(C) f(x) =si n (8x +岊)(D) f(x) =si n (8x —一)9已知抛物线沪=4x 的焦点为F,M,N是抛物线上两个不同的点.若I M Fl+INFl =5,则线段MN的中点到y轴的距离为CA)3 3_2) B ( CC)5 10.巳知a =沪,b=3了,c =l n -2 ,则(A) a> b > c (B) a> c > b (C) b >a> c (D) b > c > a 11已知定义在R上的函数f(x)满足f(2-x)= f(Z +x), 当x冬2时,f(x)= (x —l)e< :--1 若关于x的方程f(x)-kx +zk —e +l=O 有三个不相等的实数根,则实数K的取值范围是(B)(—2,0) LJ (0,2)CC)C —e,O) U (e, 十oo)CD)C —e ,O) U (0, e ) 12.如图,在边长为2的正方形AP 1贮凡中,线段BC的端点B,C分别在边P1P 2,P 2P 3 _t 滑动,且P 2B =P心=x.现将丛AP 1B ,6AP 3C分别沿AB,A C折起使点P1,凡重合,重合后记为点P ,得到三棱锥P-ABC 现有以下结论:(DAP上平面PBC;@当B,C分别为P1P2,P 2凡的中点时,三棱锥P —ABC的外接球的表面积为67(;®x 的取值范圉为(0,4—2迈); 1 @三棱锥P —ABC体积的最大值为—.则正确的结论的个数为P 1 5_2、丿D ( A 27CD)一5 (A)l (B)2CC )3(D )4数学(理科)”一诊“考试题第2页(共4页)。
四川省成都市2017年中考数学真题试题(A卷,含答案)
成都市2017 年高中阶段教育学校统一招生考试数学A 卷(共100分)一、一、选择题(本大题共10 个小题,每小题3 分,共30 分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上).1. 《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别 叫做正数与负数.若气温为零上010C 记作010C +,则03C -表示气温为 ( ) A .零上03C B .零下03C C .零上07C D .零下07C 2. 如图所示的几何体是由4 个大小相同的小立方体搭成,其俯视图是( )A .B .C .D .3. 总投资647 亿元的西域高铁预计2017 年11月竣工,届时成都到西安只需3 小时,上午游武侯区,晚上看大雁塔将成为现实.用科学计数法表示647 亿元为( )A .864710⨯ B .96.4710⨯ C .106.4710⨯ D . 116.4710⨯ 4. 1x -x 的取值范围是( )A .1x ≥B . 1x > C. 1x ≤ D .1x < 5. 下列图标中,既是轴对称图形,又是中心对称图形的是( )A .B .C. D .6. 下列计算正确的是 ( )A .5510a a a += B . 76a a a ÷= C. 326a a a = D .()236aa -=-7. 学习全等三角形时,数学兴趣小组设计并组织了“生活中的全等”的比赛,全班同学的比赛结果统计如下表:则得分的众数和中位数分别为( )A .70 分,70 分B .80 分,80 分 C. 70 分,80 分 D .80 分,70 分 8. 如图,四边形ABCD 和A BCD '''' 是以点O 为位似中心的位似图形,若:2:3OA OA '= ,则四边形ABCD 与四边形A B C D ''''的面积比为( )A . 4:9B . 2:5 C. 2:3 D 239. 已知3x =是分式方程2121kx k x x--=-的解,那么实数k 的值为( ) A .-1 B . 0 C. 1 D .210. 在平面直角坐标系xOy 中,二次函数2y ax bx c =++的图像如图所示,下列说法正确的是 ( )A . 20,40abc b ac <-> B .20,40abc b ac >-> C. 20,40abc b ac <-< D .20,40abc b ac >-<二、填空题(本大题共4 个小题,每小题4 分,共16 分,答案写在答题卡上).11.)1=________________.12. 在ABC ∆中,::2:3:4A B C ∠∠∠=,则A ∠的度数为______________.13.如图,正比例函数11y k x =和一次函数22y k x b =+的图像相交于点()2,1A .当2x <时,1y2y .(填“>”或“<”)14.如图,在平行四边形ABCD 中,按以下步骤作图:①以A 为圆心,任意长为半径作弧,分别交,AB AD 于点,M N ;②分别以,M N 为圆心,以大于12MN 的长为半径作弧,两弧相交于点P ;③作AP 射线,交边CD 于点Q ,若2,3DQ QC BC ==,则平行四边形ABCD 周长为 .三、解答题(本大题共6 个小题,共54 分,解答过程写在答题卡上)15.(1212182sin 452-⎛⎫+ ⎪⎝⎭.(2)解不等式组:()2731423133x x x x ⎧-<-⎪⎨+≤-⎪⎩①② . 16.化简求值:2121211x x x x -⎛⎫÷- ⎪+++⎝⎭,其中31x = . 17. 随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识 的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类, 并将检查结果绘制成下面两个统计图.(1)本次调查的学生共有__________人,估计该校1200 名学生中“不了解”的人数是__________人. (2)“非常了解”的4 人有12,A A 两名男生,12,B B 两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.18. 科技改变生活,手机导航极大方便了人们的出行.如图,小明一家自驾到古镇C 游玩,到达A 地后, 导航显示车辆应沿北偏西60°方向行驶4 千米至B 地,再沿北偏东45°方向行驶一段距离到达古镇C ,小明发现古镇C 恰好在A 地的正北方向,求,B C 两地的距离.19. 如图,在平面直角坐标系xOy 中,已知正比例函数12y x =的图象与反比例函数ky x=的图象交于(),2,A a B -两点.(1)求反比例函数的表达式和点B 的坐标;(2)P 是第一象限内反比例函数图像上一点,过点P 作y 轴的平行线,交直线AB 于点C ,连接PO ,若POC ∆的面积为3,求点P 的坐标.20. 如图,在ABC ∆中,AB AC =,以AB 为直径作圆O ,分别交BC 于点D ,交CA 的延长线于点E ,过点D 作DH AC ⊥于点H ,连接DE 交线段OA 于点F . (1)求证:DH 是圆O 的切线; (2)若AE 为H 的中点,求EFFD的值;(3)若1EA EF ==,求圆O 的半径.B 卷(共50分)一、填空题(本大题共5 个小题,每小题4 分,共20 分,答案写在答题卡上) 21. 如图,数轴上点A 表示的实数是_____________.22.已知12,x x 是关于x 的一元二次方程250x x a -+=的两个实数根,且221210x x -=,则a =___________.23.已知O 的两条直径,AC BD 互相垂直,分别以,,,AB BC CD DA 为直径向外作半圆得到如图所示的图形.现随机地向该图形内掷一枚小针,记针尖落在阴影区域内的概率为1P ,针尖落在O 内的概率为2P ,则12P P =______________.24.在平面直角坐标系xOy 中,对于不在坐标轴上的任意一点(),P x y ,我们把点11,P x y ⎛⎫' ⎪⎝⎭称为点P 的 “倒影点”.直线1y x =-+上有两点,A B ,它们的倒影点,A B ''均在反比例函数ky x=的图像上.若AB =k =____________.25.如图1,把一张正方形纸片对折得到长方形ABCD ,再沿ADC ∠的平分线DE 折叠,如图2,点C 落在点C '处,最后按图3所示方式折叠,使点A 落在DE 的中点A '处,折痕是FG .若原正方形纸片的边长为6cm ,则FG =_____________cm .二、解答题(共3个小题 ,共30分)26. 随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的,,,,A B C D E 中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x ,(单位:千米),乘坐地铁的时间1y 单位:分钟)是关于x 的一次函数, 其关系如下表:(1)求1y 关于x 的函数表达式;(2)李华骑单车的时间(单位:分钟)也受x 的影响,其关系可以用22111782y x x =-+来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家里所需的时间最短?并求出最短时间.27.问题背景:如图1,等腰ABC ∆中,0,120AB AC BAC =∠=,作AD BC ⊥于点D ,则D 为BC 的中点,01602BAD BAC ∠=∠=,于是2BC BD AB AB==迁移应用:如图2,ABC ∆和ADE ∆都是等腰三角形,0120BAC ADE ∠=∠=,,,D E C 三点在同一条直线上,连接BD .① 求证:ADB AEC ∆≅∆;② 请直接写出线段,,AD BD CD 之间的等量关系式;拓展延伸:如图3,在菱形ABCD 中,0120BAC ∠=,在ABC ∠内作射线BM ,作点C 关于BM 的对称点E ,连接AE 并延长交BM 于点F ,连接,CE CF .① 证明:CEF ∆是等边三角形; ② 若5,2AE CE ==,求BF 的长.28.如图1,在平面直角坐标系xOy 中,抛物线2:C y ax bx c =++与x 轴相交于,A B 两点,顶点为()0,4D ,42AB =(),0F m 是x 轴的正半轴上一点,将抛物线C 绕点F 旋转180°,得到新的抛物线C '.(1)求抛物线C 的函数表达式;(2)若抛物线C '与抛物线C 在y 轴的右侧有两个不同的公共点,求m 的取值范围;(3)如图2,P 是第一象限内抛物线C 上一点,它到两坐标轴的距离相等,点P 在抛物线C '上的对应点为P',设M是C上的动点,N是C'上的动点,试探究四边形PMP N'能否成为正方形,若能,求出m的值;若不能,请说明理由.试卷答案一、选择题1-5:BCCAD 6-10: BCADB 二、填空题11. 1 12. 40° 13. < 14. 15 三、解答题 15.(1)【答案】3【解析】原式22122242122243-=-= (2)【答案】41x -<≤-【解析】①可化简为:2733x x -<-,4x -<,∴4x >-;②可化简为:213x ≤-,∴1x ≤- ∴ 不等式的解集为41x -<≤-. 16.【答案】33【解析】原式=()()2211211111111x x x x x x x x x -+--+÷==+-+++, 当31x =时,原式3311=-+17.【答案】(1)50,360;(2)23P =; 【解析】(1)由饼图可知“非常了解”为8%,由柱形图可知(条形图中可知)“非常了解”为4人,故本次调查的学生有4508%=(人) 由饼图可知:“不了解”的概率为18%22%40%30%---=,故1200名学生中“不了解”的人数为120030%360⨯=(人)(2)树状图:由树状图可知共有12种结果,抽到1男1女分别为1112212212112122A B A B A B A B B A B A B A B A 、、、、、、、 共8种. ∴82123P ==18.【答案】【解析】过点B 作BD AC ⊥,由题060,4BAD AB ∠==,∴0cos602AD AB ==,∵0145∠=, ∴045CBD ∠=,∴BD CD =,∵0sin 60BD AB ==∴CD =∴0cos 45BC BD ==19.【答案】(1)()8,4,2y B x =; (2)()2,4P 或P ⎛ ⎝⎭【解析】(1)把(),2A a -代入12y x =,4a ⇒=-,∴()4,2A --,把()4,2A --代入ky x =,8k ⇒=, ∴8y x =, 联立812y x y x⎧=⎪⎪⎨⎪=⎪⎩4x ⇒=-或4x =,∴()4,2B ;(2)如图,过点P 作//PE y 轴, 设8,P m m ⎛⎫⎪⎝⎭,AB y kx b =+,代入A B 、两点,12AB y x ⇒=, ∴1,2C m m ⎛⎫⎪⎝⎭, 118322POC S m m m ∆=-=,1862m m m -=,286272m m -=⇒=, 218622m m -=⇒=,∴7P ⎛⎫⎪ ⎪⎝⎭或()2,4P.20.【解析】(1)连接OD ,∵OB OD =,∴OBD ∆是等腰三角形,OBD ODB ∠=∠ ①,又在ABC ∆中, ∵AB AC =,∴ABC ACB ∠=∠ ②,则由①②得,ODB OBD ACB ∠=∠=∠,∴//OD AC ,∵DH AC ⊥,∴DH OD ⊥,∴DH 是O 的切线;(2)在O 中, ∵E B ∠=∠,∵由O 中可知,E B C ∠=∠=∠,EDC ∆是等腰三角形,又∵DH AC ⊥且点A 是EH 中点,∴设,4AE x EC x ==,则3AC x =,连接AD ,则在O 中,090ADB ∠=,即AD BD ⊥, 又∵ABC ∆是等腰三角形,∴D 是BC 中点,则在ABC ∆中,OD 是中位线, ∴13//,22OD AC OD x =,∵//OD AC , ∴E ODF ∠=∠,在AEF ∆和ODF ∆中,E ODF OFD AFE ∠=∠⎧⎨∠=∠⎩, ∴AEFODF ∆∆, ∴2,332EFAEAExFD OD OD x ===, ∴23EFFD =.(3)设O 半径为r ,即OD OB r ==,∵EF EA =, ∴EFA EAF ∠=∠,又∵//OD EC , ∴FOD EAF ∠=∠,则FOD EAF EFA OFD ∠=∠=∠=∠, ∴OF OD r ==, ∴1DE DF EF r =+=+,∴1BD CD DE r ===+,在O 中, ∵BDE EAB ∠=∠,∴BFD EFA EAB BDE ∠=∠=∠=∠,∵BF BD =,BDF ∆是等腰三角形,∴1BF BD r ==+,∴()2211AF AB BF OB BF r r r =-=-=-+=-, 在BFD ∆与EFA ∆中BFD EFAB E ∠=∠⎧⎨∠=∠⎩,∵BFD EFA ∆∆, ∴11,1EFBFr FA DF r r +==-, 解得121515r r +-==(舍)∴综上,O的半径为12.。
2017学年四川省成都七中高二上学期期末数学试卷及参考答案(理科)
2017学年四川省成都七中高二上学期期末数学试卷及参考答案(理科)2016-2017学年XXX(上)期末数学试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)命题p:“a=-2”是命题q:“直线ax+3y-1=0与直线6x+4y-3=0垂直”成立的()A。
充要条件 B。
充分非必要条件C。
必要非充分条件 D。
既不充分也不必要条件2.(5分)XXX为了全面落实素质教育,切实有效减轻学生课业负担,拟从林荫、高新两个校区的初高中学生中抽取部分学生进行调查,事先已了解到初中三个年级、高中三个年级学生的课业负担情况有较大差异,而男女生课业负担差异不大。
在下面的抽样方法中,最合理的抽样方法是()A。
简单随机抽样 B。
按性别分层抽样C。
按年级分层抽样 D。
系统抽样3.(5分)圆(x+2)²+y²=4与圆(x-2)²+(y-1)²=9的位置关系为()A。
内切 B。
相交 C。
外切 D。
相离4.(5分)已知双曲线的离心率为2,那么双曲线的渐近线方程为()A。
B。
x±y=0C。
2x±y=0 D。
5.(5分)函数f(x)=x²-x-2,x∈[-5,5],在定义域内任取一点x,使f(x)≤0的概率是()A。
B。
C。
D。
6.(5分)设实数x,y满足,则μ=的取值范围是()A。
[,2] B。
[,]C。
[,2] D。
[2,]7.(5分)有5名高中优秀毕业生回母校成都7中参加高2015级励志成才活动,到3个班去做研究经验交流,则每个班至少去一名的不同分派方法种数为()A。
200 B。
180C。
150 D。
2808.(5分)柜子里有3双不同的鞋,随机地取2只,下列叙述错误的是()A。
取出的鞋不成对的概率是0B。
取出的鞋都是左脚的概率是0C。
取出的鞋都是同一只脚的概率是0D。
取出的鞋一只是左脚的,一只是右脚的,但它们不成对的概率是1/39.(5分)执行如图所示的程序框图,若输出的结果为43,则判断框内应填入的条件是()A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
好记星书签
第1页 共4页 四川省2017级普通高中学业水平考试
数 学
(考试时间:90分钟;满分:100分)
本试卷分第Ⅰ卷和第Ⅱ卷两部分。
第Ⅰ卷为选择题,第Ⅱ卷为非选择题。
第Ⅰ卷 (选择题共40分)
注意事项:
1.答第Ⅰ卷前,考生务必用蓝,黑墨水钢笔成圆珠笔将自己的姓名,准考证号,考试科目等填写在答题卡上,考试结束时,由监考人员将试卷和答题卡一并收回。
2.每小选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再涂其它答案,不能答在试卷上。
一、选择题:本大题共10个小题,每小题4分,共40分,在每小题列出的四个选项中,只有一项是符合题目要求的。
1.已如集合A={x |x -1>0},B={x |x <2},则A ∩B=
A .(1,+∝)
B .(-∞,2)
C .(1,2)
D .[1,2]
2.已知i 为虚数单位,复数:=i (1+i )在复平面内对应的点在
A .第一象限
B .第二象限
C .第三象限
D .第四象限 3.双曲线x 216
-y 24=1的渐近线方程为 A .y =±14x
B .y =±13x
C .y =±12x
D .y =±x
4.已知向量a =(1,k ),b =(2,1).若a //b 则实数k 的值为
A .-12
B .12
C .-2
D .2 5.已知函数f (x )= 2x −1,x ≤1log 2 x −1 ,x >1
,则f (3)= A .2
B .log 26
C .1
D .6。
