混合动力汽车中锂离子动力电池参数辨识与状态估计
锂离子电池健康状态估计及寿命预测研究进展综述

锂离子电池健康状态估计及寿命预测研究进展综述一、本文概述随着可再生能源的快速发展和电动汽车市场的不断扩大,锂离子电池作为高效能量储存和转换的关键部件,其性能和使用寿命的评估受到了广泛关注。
锂离子电池健康状态(State of Health, SOH)估计和寿命预测对于电池管理系统(Battery Management System, BMS)的智能化和电池性能的优化至关重要。
本文旨在综述锂离子电池健康状态估计及寿命预测的最新研究进展,包括常见的评估方法、模型构建以及实际应用中的挑战与前景。
通过系统地梳理和分析现有文献,本文旨在为相关领域的研究人员提供全面而深入的参考,以推动锂离子电池健康管理技术的进一步发展。
二、锂离子电池基础知识锂离子电池(LIBs)是现代电子设备中广泛使用的能源存储技术。
它们以其高能量密度、无记忆效应和长循环寿命等优点,在便携式电子产品、电动汽车和储能系统中得到了广泛应用。
了解锂离子电池的基本原理和结构对于其健康状态估计和寿命预测的研究至关重要。
锂离子电池主要由正极、负极、隔膜、电解质以及外部封装结构组成。
其中,正极和负极是储存和释放锂离子的主要场所,常见的正极材料有钴酸锂、锰酸锂、磷酸铁锂等,而负极则主要采用石墨或硅基材料。
隔膜位于正负极之间,防止了电子的直接接触,只允许离子的通过。
电解质则起到传输离子的作用,通常采用液态或固态的有机电解质。
锂离子电池的充放电过程涉及到锂离子的嵌入和脱出。
充电时,锂离子从正极材料中脱出,通过电解质和隔膜,嵌入到负极材料中;放电过程则相反,锂离子从负极材料中脱出,再次嵌入到正极材料中。
这一过程中,正负极材料的化学结构会发生变化,进而影响到电池的性能。
锂离子电池的性能参数主要包括容量、能量密度、内阻、开路电压等。
容量指的是电池在特定条件下能够储存或释放的电量,通常以安时(Ah)或毫安时(mAh)表示。
能量密度则是指单位体积或单位质量的电池所能储存的能量,通常以瓦时/千克(Wh/kg)或瓦时/升(Wh/L)表示。
混合动力汽车用锂离子电池荷电状态的估计

第44 卷第5 期2014 年10 月电池BATTERY BIMONTHLYVol. 44,No. 5Oct. ,2014混合动力汽车用锂离子电池荷电状态的估计黄小玲,那伟,叶磊,刘永星( 上海航天电源技术有限责任公司,上海201615)摘要: 提出在行车过程中通过引入单体电池电压电流校正的修正手段,克服电池组系统现有的基础数据不足的问题。
通过整车试验数据对比发现,校正参数修正后荷电状态( SOC) 精度优于10% ,符合行业标准。
关键词: 混合动力汽车; 荷电状态( SOC) ; 参数校正; 电池组管理系统( BMS) ; 锂离子电池中图分类号: TM912. 9 文献标识码: A 文章编号: 1001 -1579( 2014) 05 -0290 -03Estimation of state of charge of Li-ion battery for hybrid vehicleHAUNG Xiao-ling,NA W ei,YE L ei,L IU Yong-xing( Shanghai Aerospace Power Technology C o.,Ltd.,Shanghai 201615,C hina)Abstract: A parameter correction method in driving process was illustrated,the problem of insufficient basic data could be overcame. By practical running data comparison,state of charge( SOC) difference could be controlled in 10% ,i n l ine with industry standards.Key words: hybrid v ehicle; state of charge( SOC) ; parameter calibra tion; battery manage syste m( BMS) ; Li-ion battery上海汽车集团在自主研发的上海牌燃料电池与锂离子电池混合动力汽车中,将动力电池作为辅助动力源。
电动汽车电池管理系统电池状态估算及均衡技术
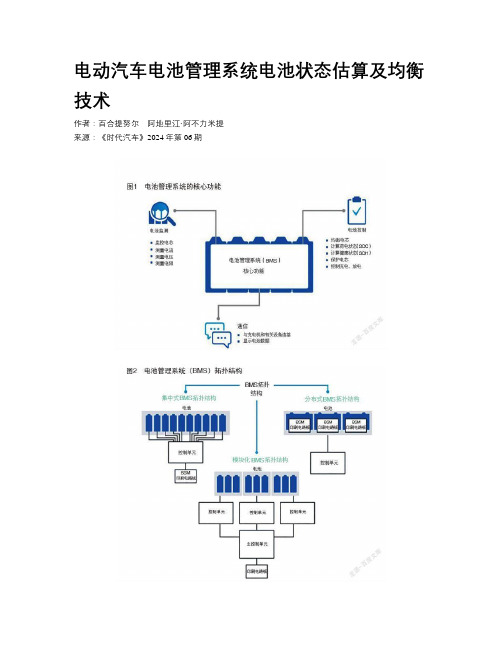
电动汽车电池管理系统电池状态估算及均衡技术作者:百合提努尔阿地里江·阿不力米提来源:《时代汽车》2024年第06期摘要:文章根據纯电动汽车和混合动力汽车的工作情况,归纳提出了电池管理系统(BMS)的核心功能和拓扑结构,对电池状态估算、电池监测系统和电池均衡系统等做了新的解析,简要的解释了电池常见故障原因以及预防措施等。
关键词:电池管理系统电池状态均衡1 电动汽车电池管理系统电池管理系统(Battery Management System,BMS)是电动汽车动力电池系统的重要组成部分,也是关键核心控制元件。
它一方面检测收集并初步计算电池实时状态参数,并根据检测值与允许值的比较关系来控制供电回路的通断;另一方面,将采集的关键数据上报给整车控制器,并接收控制器的指令,与车上的其他系统协同工作。
不同类型动力电池包的电芯(单体电池)对电池管理系统的要求是不尽相同的。
在任何一种电池管理系统(BMS)无论是简单还是复杂,均都有基本功能和实现这些功能的具体元器件。
如果需求越多,需要向系统中添加的元器件就越多。
如图1所示,电池管理系统(BMS)的核心功能。
2 电动汽车电池管理系统(BMS)拓扑结构电池管理系统的部件则是以几种不同的方式布置结构。
这些布置结构称为拓扑结构。
电池管理系统的拓扑结构主要分为集中式、分布式和模块化等类型,如图2所示。
在集中式BMS拓扑结构中有一个带有控制单元的BMS印刷电路板,其通过多个通信电路管理电池包中的所有电芯。
这种类型的结构体积大、不灵活,但成本低。
在分布式BMS拓扑结构中,每一个电芯都有BMS印刷电路板,控制单元通过单个通道连接到整个电池。
常用的环形连接(菊花链式连接)是分布式拓扑结构的一种类型,并用于容错需求较小的系统。
分布式BMS易于配置,但电子部件多、成本高。
在模块化BMS拓扑结构是集中式和分布式两种拓扑的组合。
这种布置也称为分散、星形或主从控拓扑。
有相互连接的几个控制单元(从控板),每个控制单元监测电池中的一组电芯。
锂离子动力电池参数辨识及其SOC估计

锂离子动力电池参数辨识及其SOC估计黄菊花;杨志平;曹铭;常江【摘要】基于三阶RC等效电路模型,提出断点分层的参数辨识方法,通过增加脉冲放电个数提高参数辨识准确度;同时模型参数受温度、电流等诸多因素的影响,且系统噪声的不确定性,可能导致估算算法不收敛,自适应扩展卡尔曼滤波在每次迭代更新的时候,测量数据对状态变量进行动态修正,不断估算并修改干扰噪声的统计特性因而得出的SOC估算值较为准确.最后把估算结果和安时积分法与开路电压法的结合算法得到的曲线作比较,结果表明:该算法估算误差维持在2%左右,表现出优良的估算效果.【期刊名称】《南昌大学学报(工科版)》【年(卷),期】2019(041)001【总页数】8页(P62-69)【关键词】参数辨识;断点分层技术;自适应扩展卡尔曼滤波;安时积分法;开路电压法【作者】黄菊花;杨志平;曹铭;常江【作者单位】南昌大学机电工程学院,江西南昌330031;南昌大学机电工程学院,江西南昌330031;南昌大学机电工程学院,江西南昌330031;南昌大学机电工程学院,江西南昌330031【正文语种】中文【中图分类】TM912;TP391.9锂离子动力电池凭借质量轻、能量密度高、功率密度高、自放电率低以及循环寿命长等特点,成为了电动汽车的最佳动力源,但相比于铅酸锰酸电池,锂电池表现出更为复杂的瞬态动力学特性,比如明显的迟滞现象和平衡电势的平台特性,这就对电池荷电状态(state of charge,SOC)的准确估算造成了很大的困难。
文献[1]基于多次实验,对磷酸铁锂电池的电动势特性和超电势特性做了大量的研究,针对迟滞现象提出在模型中增加阻容特性的算法。
锂电池的等效模型主要分为3类:电化学模型、等效电路模型和人工神经网络模型,其中等效电路模型是目前应用最为广泛的电池模型。
文献[2]对锂电池的电化学模型做了大量的研究,结果表明电化学模型能够很好的描述电池特性,但其结构复杂,方程中的各个参数都需要通过电化学方法测量获得,测试步骤繁琐;人工神经网络模型对电池的历史数据依赖性较大,对处理器的要求较高,并且需要大量的实验数据,均不适合应用在电动汽车上。
纯电动汽车锂电池组健康状态的估计研究

2、技术原理
充电均衡技术主要通过以下几种方式实现:
(1)被动均衡:利用并联电阻或电容等元件,将高电压或低电压的单体电 池能量转移至其他电池,以达到充电状态一致的目的。
(2)主动均衡:通过能量转移装置将能量从高电压单体电池转移到低电压 单体电池,或者从低电压单体电池转移到高电压单体电池。
(3)热能均衡:利用热能转换器将电池组中过热或过冷的单体电池进行热 能转移,使其温度趋于一致。
1、荷电状态(SOC)估计
SOC是指电池剩余电量与总电量的比值,它是电池管理系统中非常重要的参 数。SOC的估计主要通过电池的电压、电流和温度等参数进行计算。常用的 SOC 估计方法包括基于规则的方法、基于数学模型的方法和基于机器学习的方法等。
2、健康状态(SOH)估计
SOH是指电池的性能下降程度,它是电池管理系统中另一个重要的参数。SOH 的估计主要通过电池的容量、内阻和自放电率等参数进行计算。常用的 SOH估计 方法包括基于模型的方法和基于数据驱动的方法等。
2、考虑多种影响因素:电池的健康状态受到多种因素的影响,包括电池的 工作条件、充放电策略、环境温度、老化程度等。因此,需要研究如何综合考虑 这些因素对锂电池组健康状态的影响,以提高估计的准确性。
3、发展智能诊断技术:随着人工智能和机器学习技术的发展,可以考虑将 智能诊断技术应用于锂电池组健康状态的估计。通过深度学习和模式识别等方法, 可以实现对电池性能的实时监测和预警,提前发现潜在的问题并进行处理。
ห้องสมุดไป่ตู้
结论
纯电动汽车锂电池组充电均衡技术是保障车辆性能和延长电池寿命的关键。 本次演示通过对该技术的深入研究,总结出现状和发展趋势,并指出了存在的问 题和挑战。提出了加强新材料研发、优化电池管理系统、结合先进技术等建议和 展望,为进一步提高纯电动汽车的性能和普及程度提供理论支持。
动力电池的容量估算及健康状态判断

试讲人:
1
CONTENT
目录
1
基本概念
2SOC估算3 NhomakorabeaSOH估算
2
1 基本概念
SOC:State of Charge 动力电池的荷电状态,当前剩余容量与 最大可用容量的比。 SOH:State of Health 动力电池的健康状态,最大可用容量与 标称容量的比。
SOC估算方法分类
4
1.1 基于表征参数的方法
该方法分两步: ①建立动力电池表征参数与SOC的离线关系。 ②实时计算动力电池表征参数值,并以之标定动力电池SOC。 需满足两个前提: 所建立表征参数与SOC的离线关系应该相对稳定,所选表征参数
应该是易获取的。可选表征参数包括当前剩余容量、阻抗谱、开路电压(OCV) 等。 ① 当前剩余容量可通过放电实验法得到,该方法被认为是确定动力电池SOC最为直 接的方法。但是新能源汽车在运行中难以进行长时间的恒流放电来确定剩余容量, 使得该方法仅适用于实验室等特定环境。 ② 基于阻抗谱的方法则需要借助电化学工作站来测试动力电池不同SOC值的阻抗, 并制定SOC和参数的映射关系,进而采用查表的方式完成SOC的标定。 ③ OCV-SOC关系常被工业界用来标定动力电池SOC,大量的BMS产品也使用这一关 系来标定动力电池初始SOC,但OCV的准确直接测量要求动力电池静置足够长的 时间,因而在实际中往往需要与OCV在线辨识方法结合使用。
10
1.5 四类方法对比
11
2 SOH估算
动力电池的存储能力与快速充放电能力均会随着老化而不断下降,而SOH正 是用于评价动力电池老化程度的量化指标。动力电池SOC的准确估计依赖于精确 的SOH值,预知SOH开展的SOC估计不具有实用性,仅能为SOC估计方法提供初 步借鉴。
电动汽车用锂离子电池荷电状态估算方法综述
5 . 2展 望
综合上述三类 S O C 估计算法 的优缺 点以及 电动汽车 动力 性能的要求 ,未来 电动汽车用动力 电池 S O C估计算 法的研究 趋势主要包含 以下两个方面 : ①精确 的电池模型与非线性滤波算法 的结合 。在 电池建 模时考虑温度 、电池老化和充放 电效率等的影响 ,在测量手 段和 电池模 型参数辨识方法上进行深入研 究 另一方面 ,继 续研究非线性滤波算法 ,在 保证精确性的同时减小算法的复 杂性 ,以利于工程应用 。 ② 具有 在线学 习能 力的智能算法 。在 电池 使用过程 中 , 随时更新样本 ,训练智能算法 的模型参数 ,使得 S O C估算 能 够 自适应 ,同时也要在样本训练规则和样本选取上进行研究 , 减 少所花 费的资源 ,这是各类智能算法需要解决 的关键 问题 。
4 . 1神经网络算法及其 改进
神经 网络 算法 主要是以充放 电电流、电池端 电压 、环境 温度等作 为输入量 ,S O C作为输 出量 ,利用大量 的实验数据 对系 统进 行训练,进而得到 电池 的神经 网络模型 ,然后将 电 池 的实际输 入用于此模 型即可得到输 出量 S O C 。但算法的估 算效果受训练方法和训练样本的影响很大 ,而且样本训练过 程要消耗大量的资源 。 因此 , 需要将 神经网络算法进行改进 。 针对动力 电池在实际工况中参数变化较大的特 点,利用 全局搜索能力强 的遗传算法优化 网络初值 ,提 高了 S O C估算 精度 。基 于 P I D神经网络的车用锂 电池 S 0 C估算,以电池 电 压、 电流 、温度和 累计放 电电量为输入变量 ,S 0 C为输 出变 量 ,得到全局 的神经网络训练数据 ,对 电池 S O C的估算误差
基于多时间尺度锂电池在线参数辨识及SOC_和SOH_估计
第40卷第5期Vol.40㊀No.5重庆工商大学学报(自然科学版)J Chongqing Technol &Business Univ(Nat Sci Ed)2023年10月Oct.2023基于多时间尺度锂电池在线参数辨识及SOC 和SOH 估计姚昌兴,李㊀昕,邢丽坤安徽理工大学电气与信息工程学院,安徽淮南232001摘㊀要:电池的荷电状态和健康状态是衡量电池续航和寿命的重要指标,为解决电池参数的时变性问题,提高电池SOC (State of Charge )估算精度,减少硬件计算量,提出一种多时间尺度在线参数辨识双扩展卡尔曼滤波联合算法㊂以18650三元锂电池为研究对象,采用基于二阶RC 等效电路模型的多时间尺度DEKF 算法,针对电池参数的慢变特性和状态的快变特性进行双时间尺度在线参数辨识和SOC 估算;通过联邦城市驾驶计划(FUDS )测试验证,得出多时间尺度DEKF 算法和传统离线辨识EKF 算法对SOC 估计的平均绝对误差分别为0.97%和2.46%,均方根误差为1.19%和2.69%,容量估计值对参考值最大误差仅为0.00772Ah ;实验结果表明:所提出的多时间尺度DEKF 算法,具有更好的鲁棒性和SOC 估算精度并能实时反应SOH 变化趋势㊂关键词:多时间尺度;二阶等效电路;DEKF ;SOC ;SOH中图分类号:TM912㊀㊀文献标识码:A ㊀㊀doi:10.16055/j.issn.1672-058X.2023.0005.007㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀收稿日期:2022-03-05㊀修回日期:2022-05-18㊀文章编号:1672-058X(2023)05-0048-07基金项目:安徽省高校自然科学基金资助项目(KJ2019A0106).作者简介:姚昌兴(1998 ),男,安徽滁州人,硕士,从事电动汽车锂电池荷电状态与健康状态研究.引用格式:姚昌兴,李昕,邢丽坤.基于多时间尺度锂电池在线参数辨识及SOC 和SOH 估计[J].重庆工商大学学报(自然科学版),2023,40(5):48 54.YAO Changxing LI Xing XING Likun.On-line parameter identification and SOC and SOH estimation of lithium battery based onmulti-time scale J .Journal of Chongqing Technology and Business University Natural Science Edition 2023 40 5 48 54.On-line Parameter Identification and SOC and SOH Estimation of Lithium Battery Based on Multi-time Scale YAO Changxing LI Xing XING LikunSchool of Electrical and Information Engineering Anhui University of Science and Technology Anhui Huainan 232001 ChinaAbstract The state of charge SOC and state of health SOH of a battery are important indicators of battery endurance and lifetime.In order to solve the problem of time-varying battery parameters improve the accuracy of SOC estimation and reduce the hardware computation a joint multi-timescale online parameter identification algorithm with a double-extended Kalman filter was proposed.The multi-timescale DEKF algorithm based on the second-order RC equivalent circuit model was used for the online parameter identification and SOC estimation of the 18650ternary lithium battery with the slow-varying characteristics of the battery parameters and the fast-varying characteristics of the battery state.Through the test verification of the Federal Urban Driving Program FUDS the average absolute errors of the SOC estimation of the multi-time scale DEKF algorithm and the traditional offline identification EKF algorithm were 0.97%and 2.46% respectively the rms errors were 1.19%and 2.69% and the maximum error of the capacity estimation to the reference value was only 0.00772Ah.The experimental results show that the proposed time-scale DEKF algorithm has better robustness and SOC estimation accuracy and can respond to the SOH variation trend in real time.Keywords multi-time scales second-order equivalent circuit DEKF SOC SOH1㊀引㊀言在新能源电动汽车蓬勃发展的今天,新能源汽车正在逐渐取代传统燃油车㊂锂离子电池作为新能源汽车的动力电池,具有能量密度高㊁循环寿命长和环保等第5期姚昌兴,等:基于多时间尺度锂电池在线参数辨识及SOC和SOH估计特点,得到了广泛的应用㊂电池的荷电状态和健康状态SOH是衡量电池续航和寿命的重要指标;R SOC表示当前储存电量占可用容量的百分比;R SOH(State of Health)表征电池当前性能指标,表示与新电池对比,电池当前性能所能达到的水平,即电池当前性能与正常设计的偏离程度,一般用容量或者内阻的变化表示㊂对它们实时准确进行预测是优化锂电池充放电控制和电动汽车电池系统优化管理的重要环节㊂目前最为常见的SOC估算方法有开路电压法㊁安时积分法㊁神经网络法㊁卡尔曼滤波算法等㊂开路电压法[1]依赖于OCV-SOC曲线,需要将电池静置足够长时间以得到准确的开路电压值,不适用电池SOC在线估计㊂安时积分法[2]依赖于精确的初始值,但是并不能准确得到电流值,在积分过程中会累积难以消除的误差㊂神经网络法[3]具有较好的学习能力,能更准确地估算出电池SOC,但是神经网络法需要大量的数据集支撑,而且不同方法㊁不同变量㊁不同样本都容易导致最终结果出现比较大的偏差㊂卡尔曼滤波及其相关算法[4-6]解决了非线性和噪声处理问题,其中比较典型的就是扩展卡尔曼滤波(EKF)㊁无迹卡尔曼滤波(UKF)㊁自适应扩展卡尔曼滤波(AEKF)㊁自适应无迹卡尔曼滤波(AUKF)等算法,用其估计电池SOC,有着良好的预测结果㊂单个EKF算法[7]估计SOC方法的共同缺点是电池模型参数是用离线数据识别的,模型参数时变性被忽略㊂为了克服这一缺点,文献[8]提出了具有最优遗忘因子的递归最小二乘法进行在线电池参数辨识和SOC估计㊂然而,模型参数和SOC估计是在同一时间尺度下进行的,实际上在充放电过程中SOC是一个快速变化的量,电池参数是一个缓慢的变化量,同一时间尺度进行参数辨识和SOC估计会加大处理器的运算量㊂因此,很多文献开始提出不同时间尺度下电池参数和SOC估算的新方法:文献[9]提出一种基于多时间尺度的EKF-UKF参数辨识和SOC联合估算方法,实现了在宏观尺度下辨识电池参数,在微观尺度估算电池SOC,但该算法无法同时估计电池容量和模型参数㊂准确的容量估计对电池SOC估计来说是必不可少的,也是衡量电池健康状态(SOH)的重要指标;文献[10]提出了基于二阶RC等效电路模型的双卡尔曼滤波器联合估计电池SOC和SOH,虽然实现了电池SOC和容量的同时在线估计,但他们使用的仍然是离线辨识数据,没有考虑模型参数的时变性㊂上述方法均未能全面考虑电池模型参数的时变性和容量变化对电池状态估计造成的影响及处理器运算量等问题㊂为解决电池参数时变性问题,提高SOC估算精度,减少硬件计算量,针对上述方法对电池SOC估算的优缺点,以18650三元锂电池为研究对象,采用基于二阶RC等效电路模型的多时间尺度DEKF算法在线对电池的状态参数和SOC进行估算,对电池的容量状态进行跟踪㊂使用FUDS工况验证多时间尺度DEKF对电池状态参数和SOC的估算情况,验证了方法的可靠性㊂2㊀电池建模与参数辨识2.1㊀建立电池模型为准确估算电池的状态参数,一个合理准确的电池模型就显得极为重要㊂主流电池模型主要分为电化学模型㊁等效电路模型㊁神经网络模型等㊂其中电化学模型较为复杂,参数繁多,求解困难,难以在线直接应用;神经网络模型需要大量数据集用于模拟训练,耗时长㊂本文选取二阶RC等效电路模型,更加符合电池内部复杂的参数和化学变化,模型精度高,运算量小,适用于在线应用,如图1所示㊂R1R2R0U1U2UUo c vC1C2图1㊀二阶RC等效电路模型Fig.1㊀Second-order RC equivalent circuit model如图1所示:其中U ocv和U0分别是开路电压和端电压;R0是欧姆内阻;R1和C1表示电化学极化电阻和电容,具有较小的时间常数,模拟了电压急速变化的过程;R2和C2分别是浓度极化电阻和电容,具有较大的时间常数,模拟了电池使用过程中电压变化过程中逐渐稳定的过程;I为工作电流㊂根据等效电路模型建立模型表达式,如式(1)所示:U㊃1=-1R1C1U1+1C1IU㊃2=-1R2C2U2+1C2IU0=U ocv-IR0-U1-U2ìîíïïïïïï(1)2.2㊀实验确定OCV-SOC曲线和初始值本文以额定容量为2.2Ah的单体三元锂离子电池18650为研究对象,标称电压为3.7V,电压范围为2.5 V~4.2V㊂在恒温25ħ的保温箱内进行混合功率脉冲特性(HPPC)测试㊂开路电压可被认为是电池静置充分长时间以后的开路电压㊂根据HPPC测试实验可得94重庆工商大学学报(自然科学版)第40卷到OCV -SOC 对应的函数对应关系,如图2所示㊂拟合关系式如式(2)所示:U ocv =-20.7083R SOC 6+85.0152R SOC 5-133.5886R SOC 4+101.2818R SOC 3-37.8526R SOC 2+7.0109R SOC +3.0755(2)0.00.20.40.60.81.04.24.03.83.63.4开路电压U o c v/V R S O CO C V S O C拟合曲线图2㊀OCV -SOC 关系曲线Fig.2㊀OCV -SOC relationship curve根据混合功率脉冲特性(HPPC)测试,离线辨识参数作为在线参数辨识的初始值,后以实际工况为基础,利用算法实时在线辨识参数,参数初始值如表1所示:表1㊀模型参数初始值Table 1㊀Initial values of model parametersR 0/ΩR 1/ΩR 2/ΩC 1/FC 2/F0.03850.0080.049227.41027.82.3㊀联邦城市驾驶计划(FUDS )测试FUDS 是用于城市驾驶的汽车行业标准车辆时间速度曲线,多年来一直用于电动汽车性能测试㊂图3显示了FUDS 工况下电流和电压曲线㊂图4是在FUDS 工况下基于安时积分法100%到10%的SOC㊂24681012210-1-2-3-4电流/A t /s电流电压4.54.03.53.0电压/V103图3㊀FUDS 工况下电流和电压波形Fig.3㊀Current and voltage waveforms under FUDS conditions246810121.00.80.60.40.20.0R S O Ct /sS O C 变化曲线103图4㊀FUDS 工况下SOC 变化曲线Fig.4㊀SOC change curve under FUDS condition3㊀多时间尺度DEKF 算法3.1㊀电池模型状态方程电池SOC 表达式如式(3)所示:R SOC =R SOC,0-ηQ nʏt t 0I d τ(3)式(3)中,R SOC,0是初始值,Q n 是电池额定容量,η是电池库伦效率㊂将式(1)和式(3)联立离散化可得电池模型的状态方程和观测方程如式(4)㊁式(5)所示:R SOC,k +1U 1,k +1U 2,k +1éëêêêêùûúúúú=1000e -T τ1000e -T τ2éëêêêêêùûúúúúúR SOC,k U 1,k U 2,k éëêêêêùûúúúú+-ηT Q n R 11-e -kT τ1()R 21-e -kTτ2()éëêêêêêêêùûúúúúúúú㊃I k (4)U k =U ocv R SOC,k ()-U 1,k -U 2,k -R 0I k(5)式(4)中,T 表示系统采样时间,τ为时间常数,其中τ1=R 1C 1,τ2=R 2C 2,U 1,k 和U 2,k 代表极化电压㊂3.2㊀系统描述对于电池参数的慢变特性和电池状态的快变特性,采用多时间尺度方法构建离散状态空间表达式,对系统参数和状态进行宏观尺度和微观尺度预测,结合锂电池参数变化,得到系统的状态空间表达式如式(6)所示:x k ,l +1=f x k ,l ,θk ,u k ,l ()+ωk ,l ,θk +1=θk +ωθky k ,l =g x k ,l ,θk ,u k ,l ()+v k ,l ,y k =g x k ,θk ,u k ()+v θk{(6)其中,x k ,l +1是t k 时刻的系统状态矩阵,l =t k ,0+l ˑT (1ɤl ɤL ),其中T 是采样间隔,k 和l 分别是衡量宏观尺度和微观尺度的两个重要指标;参数状态变量θ=5第5期姚昌兴,等:基于多时间尺度锂电池在线参数辨识及SOC 和SOH 估计R 0,R p 1,C p 1,R p 2,C p 2,Q n []T ;ωk ,l 和ωθk 分别是状态和参数的过程噪声矩阵;v k ,l 和v θk 是状态和参数的测量噪声㊂Q k =E w k w T k []是状态过程噪声误差协方差,R k=E v k v T k []测量噪声误差协方差,Q θk =E ωθk ωθk ()T[]和R θk =E v θk v θk ()T[]是参数过程噪声误差协方差及其参数测量噪声协方差误差㊂3.3㊀多时间尺度DEKF 算法步骤步骤1㊀初始化状态变量x 0,0㊁参数状态变量θ0㊁状态变量误差协方差P x 0,0㊁参数变量误差协方差P θ0,表达式如式(7)所示:x 0,0=E x 0,0(),θ0=E θ0()P x 0,0=E x 0,0-x ^0,0()x 0,0-x ^0,0()T[]P θ0=E θ0-θ^0()θ0-θ^0()T []ìîíïïïï(7)步骤2㊀在宏观尺度上,参数估计的扩展卡尔曼滤波算法执行时间更新并计算先验参数估计θ-k 和误差协方差P -θk ,如式(8)所示:θ-k =θ^k -1P -θk =P -θk -1+Qθk{(8)步骤3㊀划分出宏观尺度L 和微观尺度l ,对于l ɪ{1, ,L },计算每个微尺度的先验状态变量估计值x -k ,l 及协方差误差P x-k -1,l,如式(9)所示:x -k -1,l =f x ^k -1,l -1,θ-k ,u k ,l -1()P x -k -1,l=A k -1,l -1P x ^k ,l -1A T k -1,l -1+Q k{(9)步骤4㊀在每个微观尺度上,状态估计卡尔曼滤波算法执行测量更新,随后是状态估计卡尔曼滤波算法的时间更新,其中状态扩展卡尔曼增益K SOC k -1,l ,后验状态估计值x ^k -1,l 及其误差协方差P x ^k -1,l,如式(10)所示:K SOC k -1,l =P x -k -1,l C T k -1,l C k -1,l P x -k -1,lC T k -1,l +R k ()-1x ^k -1,l =x -k -1,l +K SOC k -1,ly k -1,l -g x -k -1,l ,θk -1,u k -1,l ()[]P x ^k -1,l =I -K SOC k -1,l C k -1,l ()P x-k -1,lìîíïïïï(10)步骤5㊀在后验状态估计之后,比较微观尺度l 和宏观尺度L 的大小㊂如果l 没有达到水平L ,则状态估计x ^k -1,l 将传输到第三步作为时间的初始值,然后再次估计状态,对于时间序列计算l =1:L (l ңL ),则先验状态估计x -k -1,L 及其协方差误差P x -k -1,L,后验状态估计x ^k -1,L 及其误差协方差P x ^k -1,L,准备好进入宏观尺度更新,如式(11)所示:x -k -1,L =f x ^k -1,L -1,θ-k ,u k -1,L -1()P x -k -1,L =A k -1,L -1P x ^k -1,L -1A T k -1,L -1+Q k K SOC k -1,L =P x -k -1,l C k -1,L ()T C k -1,L P x -k -1,LC k -1,L ()T +R k []x ^k -1,L =x -k -1,L +K SOC k -1,L y k ,L -g x -k -1,L ,θ-k ,u k -1,L ()[]P x ^k -1,L=I -K SOC k -1,L C k -1,L ()P x-k -1,Lìîíïïïïïïïï(11)步骤6㊀时间尺度转换,更新所有微观尺度数据,时间t k -1,L 的估计值已准备好更新为t k ,0的值,用于参数估计和宏观状态估计,如式(12)所示:x ^k ,0=x ^k -1,L ,P x ^k ,0=P x ^k -1,Ly k .0=y k -1,L ,u k ,0=u k -1,L{(12)步骤7㊀宏观尺度的扩展卡尔曼滤波算法已经准备好执行测量更新,其中参数扩展卡尔曼增益K θk ㊁后验参数估计θ^k 和协方差P θ^k,如式(13)所示:K θk =P θ-k C θk ()T C θk P θ-kC θk ()T +R θk []-1θ^k =θ-k +K θky k ,0-g x ^k .0,θ-k ,u k ,0()[]P θ^k =I -K θk C θk ()P θ-kìîíïïïï(13)其中,θ0是初始系统参数,θ^0是它的猜测值;x 0,0是初始系统状态,并且x ^0,0是它的猜测值㊂两个扩展卡尔曼滤波在不同时间尺度运行,其中A k -1,l -1,C k -1,l ,C θk 如式(14)所示:A k -1,l -1=∂f x ,θ-k ,u k -1,l -1()∂x∣x =x ^k -1,l -1C k -1,l =∂g x ,θ-k ,u k -1,l ()∂x ∣x =x -k -1,l C θk=∂g x ^k .0,θ,u k ,0()d θ∣θ=θ-k ìîíïïïïïïïï(14)结合上述内容,为了同时实现电池参数和SOC 同时在线估计,设计了两个扩展卡尔曼滤波算法,其中一个EKF 用于电池参数在线辨识,另一个EKF 用于电池状态实时估计㊂首先,初始化参数变量和状态变量,状态估计EKF 在微观尺度下估计电池SOC,当时间进行到宏观尺度时,时间尺度变换,时间t k -1,L 的估计值已准备好更新为t k ,0的值,用于参数估计和宏观状态估计㊂更新后的参数用于微观尺度状态估计EKF 估计电池SOC,两个卡尔曼滤波算法在不同时间尺度运行,可得到不同时刻电池参数和SOC 估计值㊂多时间尺度DEKF 算法结构如图5所示:15重庆工商大学学报(自然科学版)第40卷参数辨识卡尔曼状态估计卡尔曼输入U 01,1初始化θ0,P θk 初始化x 0,0,P x 0,0时间尺度更新计算θk ,P θkk -1,l划分出宏观L 和微观尺度I ,计算微观尺度下x k ,l ,P x k +1k -1,l ,计算K S O C^x k -1,l ,^x k -1,lP l +1l +L ?否是K +1参数输入,更新电池模型和状态空间方程计算K θk,θk ^,P k θ^测量方程更新,计算I =L 条件下P x k -1,L-x k -1,L K S O C k -1,L x k -1,L ^P x k -1,L ^时间尺度变换用于参数和宏观状态估计x k ,0^,P x k ,0^,y u ,,,,k,0k ,0,图5㊀多时间尺度DEKF 算法结构图Fig.5㊀Structure diagram of multi -time scale DEKF algorithm4㊀实验验证与分析为验证多时间尺度DEKF 的估算精度,采用联邦城市驾驶计划(FUDS)测试数据,通过Matlab 编写多时间尺度DEKF 算法运行程序,对比在不同宏观和微观尺度下的SOC 估算误差,得出在宏观尺度为60s㊁微观尺度为1s 时有比较好的SOC 估算结果,实验误差在合理范围之内㊂4.1㊀在线参数辨识结果分析根据混合功率脉冲特性(HPPC)测试,离线辨识参数作为在线参数辨识的初始值,设置SOC 初始值为0.8,通过多时间尺度DEKF 算法,得到对R 0,R 1,R 2,C 1,C 2的辨识结果如图6㊁图7所示:0.0450.0440.0430.0420.0410.0400.0390.0380.0370.0360.03550100150200R 0/Ω次数(a )R 00.0240.0220.0180.0160.0140.0120.0100.00850100150200R 1/Ω次数(b )R 10.0500.0480.0460.0440.0420.0380.0360.0340.0320.03050100150200R 2/Ω次数(c )R 2图6㊀R 0,R 1,R 2参数辨识结果Fig.6㊀Identification results of parameters R 0,R 1and R 230025020015010050100150200C 1/F 次数(a )C 11800160014001200100050100150200C 2/F 次数(b )C 2图7㊀C 1,C 2参数辨识结果Fig.7㊀Identification results of parameters C 1and C 2由以上参数辨识结果可以得知:在参数辨识30次之前,各参数有比较剧烈的波动,这主要因为没有选取一个恰当的初值,之后模型各参数趋于稳定㊂模型参数本就不是一个定值,会随着温度㊁循环次数等条件的改变而发生变化㊂整个过程中,参数辨识结果R 0逐步缓慢上升,R 1先缓慢减小后缓慢增大,R 2先缓慢增大后缓慢减小,整个放电过程的阻值是增加的㊂C 1先趋于平稳后快速减小再趋于平稳,C 2先快速增加后趋于平稳,但模型时间常数τ1和τ2波动不大,且τ2始终大于τ1,符合锂电池实际放电特性㊂4.2㊀SOC 估计结果分析为验证电池SOC 在多时间尺度DEKF 算法下的精度,本文选取安时积分法作为真实SOC 参考值,FUDS25第5期姚昌兴,等:基于多时间尺度锂电池在线参数辨识及SOC 和SOH 估计工况电流电压值作为输入,采用离线参数辨识EKF 和多时间尺度在线参数辨识DEKF 滤波算法估算电池SOC,并与参考值作对比,得出估算结果及误差结果如图8㊁图9所示㊂1.00.80.60.40.20.02468101214R S O C安时积分法D E K F E K F1.00.90.8020*********t ?103/s图8㊀SOC 估算结果Fig.8㊀Estimation results of SOC0.200.150.100.050.00-0.052468101214误差D E K FE KF t ?103/s图9㊀SOC 估算误差Fig.9㊀Estimation errors of SOC由SOC 估算结果和SOC 估算误差可以得知:多时间尺度的DEKF 算法相对于EKF 算法对SOC 的估算结果更接近参考值,具有较好的鲁棒性,其平均绝对误差仅为0.97%,而EKF 算法则为2.46%㊂随着放电的不断进行,多时间尺度的DEKF 算法可以实时更新电池参数,其估算精度更高,具有极强的稳定性,其均方根误差为1.19%,而EKF 电池参数是定值,会随着放电时间的累积,误差不断增大,其均方根误差为2.69%㊂通过上述分析,可知多时间尺度的DEKF 算法具有比较好的估算精度和鲁棒性㊂4.3㊀SOH 估计结果分析本文假设容量的更新随着模型参数一起更新,但实际容量变化十分缓慢,正常情况下可以几天校准一次,容量辨识结果如图10所示㊂2.0502.0452.0402.0352.0302.0252.02050100150200R S O H/A h 参考值估计值次数图10㊀容量估算结果Fig.10㊀Capacity estimation results从图10可以看出:估计值对参考值有着良好的跟踪能力,最大误差仅为0.00772Ah㊂5㊀结㊀论本文以二阶RC 等效电路模型为基础,建立多时间尺度DEKF 滤波算法,该算法可以同时在线估计电池模型参数㊁容量和SOC,并在FUDS 工况下对该算法与传统离线参数辨识EKF 算法进行比较,体现了该算法在SOC 估计精度方面的优势㊂平均绝对误差和均方根误差都明显降低,解决了电池参数时变所造成的SOC 估算精度差的问题,减小了硬件计算量,提高了算法的精确度和鲁棒性,验证了该算法对电池容量的跟踪能力,该算法能够较好跟踪容量在该实验中的变化情况㊂本文虽然对电池SOC 和容量都进行了预测,但鉴于研究是基于恒温实验条件下进行,在电池使用过程中,温度对电池状态参数和SOC 影响较大,后续将对温度对电池参数和SOC 的影响做进一步研究㊂参考文献 References1 ㊀陈东 高文根 李鹏飞 等.磷酸铁锂电池SOC -OCV 曲线特性研究 J .黑龙江工业学院学报 综合版 2021 21 12 89 94.CHEN Dong GAO Wen-gen LI Peng-fei et al.Study onSOC-OCV curve characteristics of lithium iron phosphatebattery J .Journal of Heilongjiang Institute of TechnologyComprehensive Edition 2021 21 12 89 94.2 ㊀王文亮 何锋 郑永樑 等.基于RLS-EKF 联合算法的锂电池SOC 估算 J .电源技术 2020 44 10 1498 1501 1505.WANG Wen-liang HE Feng ZHENG Yong-liang et al.SOC estimation of lithium battery based on RLS-EKF joint algorithm J .Power Technology 2020 44 10 149835重庆工商大学学报(自然科学版)第40卷1501 1505.3 ㊀SHEN Y.Adaptive online state-of-charge determination basedon neuro-controller and neural network J .Energy Conversion &Management 2010 51 5 1093 1098.4 ㊀刘浩.基于EKF的电动汽车用锂离子电池SOC估算方法研究D .北京北京交通大学2010.LIU Hao.Research on SOC estimation method of lithium-ion battery for electric vehicle based on EKF D .Beijing Beijing Jiaotong University 2010.5 ㊀田茂飞安治国陈星等.基于在线参数辨识和AEKF的锂电池SOC估计J .储能科学与技术2019 84745 750.TIAN Mao-fei AN Zhi-guo CHEN Xing et al.Lithium battery SOC estimation based on online parameter identification and AEKF J .Energy Storage Science and Technology 2019 8 4 745 750.6 ㊀王震坡薛雪王亚超.基于自适应无迹卡尔曼滤波的分布式驱动电动汽车车辆状态参数估计J .北京理工大学学报2018 38 7 698 702.WANG Zhen-Po XUE Xue WANG Ya-chao.Estimation of state parameters of distributed drive electric vehicles based on adaptive unscented Kalman filtering J .Journal of Beijing Institute of Technology 2018 38 7 698 702.7 ㊀孙立珍赵乐乐刘广忱.基于近似二阶EKF的非线性滤波仿真J .计算机与数字工程2022 50 2 289 293.SUN Li-zhen ZHAO Le-le LIU Guang-chen.Simulation of nonlinear filtering based on approximate second-order EKF J .Computer and Digital Engineering 2022 502289 293.8 ㊀孙金磊邹鑫顾浩天等.基于FFRLS-EKF联合算法的锂离子电池荷电状态估计方法J .汽车工程2022 444505 513.SUN Jin-lei ZOU Xin GU Hao-tian et al.Estimation method of state of charge of lithium-ion battery based on FFRLS-EKF joint algorithm J .Automotive Engineering 2022 44 4 505 513.9 ㊀邢丽坤郭敏张梦龙等.多时间尺度下锂电池在线参数辨识及SOC估计J .安徽理工大学学报自然科学版2021 41 5 1 7.XING Li-kun GUO Min ZHANG Meng-long et al.On-line parameter identification and SOC estimation of lithium batteries under multiple time scales J .Journal of Anhui University of Science and Technology Natural Science Edition 2021 41 5 1 7.10 唐传雨韩华春史明明等.基于DEKF的储能电池系统SOC估计方法研究J .电力工程技术2021 4037 14.TANG Chuan-yu HAN Hua-chun SHI Ming-ming et al.Research on SOC estimation method of energy storage battery system based on DEKF J .Electric Power Engineering Technology 2021 40 3 7 14.11 杨世春华旸顾启蒙等.锂离子电池SOC及容量的多尺度联合估计J .北京航空航天大学学报2020 4681444 1452.YANG Shi-chun HUA Yang GU Qi-meng et al.Multi-scale joint estimation of SOC and capacity of lithium-ion batteries J .Journal of Beijing University of Aeronautics and Astronautics 2020 46 8 1444 1452.12 XIONG R SUN F CHEN Z et al.A data-driven multi-scaleextended Kalman filtering based parameter and state estimation approach of lithium-ion olymer battery in electric vehicles J .Applied Energy 2014 113 463 476.13 高晋艾田付徐新法等.基于UKF的磷酸铁锂电池电荷状态估算策略J .电子测量技术2018 41 3 12 16.GAO Jin AI Tianfu XU Xin-fa et al.State-of-charge estimation strategy for lithium-iron phosphate battery based on UKF J .Electronic Measurement Technology 2018 41312 16.14 袁翔周湘蒋鹏.电动汽车用锂电池模型参数辨识方法研究J .公路与汽运2015 4 13 16.YUAN Xiang ZHOU Xiang JIANG Peng.Research on parameter identification method of lithium battery model for electric vehicles J .Highway and Automobile Transportation 2015 4 13 16.15 印学浩宋宇晨刘旺等.基于多时间尺度的锂离子电池状态联合估计J .仪器仪表学报2018 39 8 118 126.YIN Xue-hao SONG Yu-chen LIU Wang et al.Joint estimation of lithium-ion battery state based on multiple time scales J .Chinese Journal of Instrumentation 2018 398118 126.16 CHAO H YOUN B D CHUNG J.A multiscale framework withextended Kalman filter for lithium-ion battery SOC and capacity estimation J .Applied Energy 2012 92 694 704.17 何锋王文亮蒋雪生等.双扩展卡尔曼滤波法估计锂电池组SOC与SOH J .农业装备与车辆工程2021 59737 40 61.HE Feng WANG Wen-liang JIANG Xue-sheng et al.Estimation of SOC and SOH of lithium battery pack by double extended Kalman filter method J .Agricultural Equipment and Vehicle Engineering 2021 59 7 37 40 61.责任编辑:李翠薇45。
电动汽车动力锂电池模型参数辨识
电动汽车动力锂电池模型参数辨识章群;严世榕【摘要】针对纯电动汽车上动力锂电池等效模型参数辨识的问题,以某纯电动汽车的由87个单体串联的84 Ah的镍钴锰三元锂电池组为研究对象,基于市区行驶的电池数据,选用了二阶RC电池等效模型,辨识了等效模型的参数.基于整体电池数据,选取出了8段在连续的12个(及12个以上)采样周期内相邻两个采样点的电流变化绝对值超过0.2C的电池数据段,分别对初始开路电压最大和最小的单体进行了参数辨识.以最小二乘法对电流连续变化最长的一段电池数据段作为参数辨识的结果,并结合整体电池数据对辨识得的结果进行了参数的验证.研究结果表明,初始开路电压最大单体的绝对误差平均值为3.62%,初始开路电压最小单体的绝对误差平均值为3.24%,满足工程要求,可运用于工程实践中.【期刊名称】《机电工程》【年(卷),期】2016(033)012【总页数】5页(P1506-1510)【关键词】二阶RC等效模型;电动汽车;三元锂电池;汽车行驶数据;最小二乘法;参数辨识【作者】章群;严世榕【作者单位】福州大学机械工程学院,福建福州350108;福州大学机械工程学院,福建福州350108【正文语种】中文【中图分类】TM912作为纯电动汽车的唯一动力来源,动力锂离子电池的性能对于整车的动力性、经济性、安全性以及平顺性至关重要[1-2]。
电池管理系统(battery management system,BMS)是电动汽车的关键部件。
BMS的基础功能之一就是准确地估算电池的SOC,电池等效模型的准确度对SOC估算精度影响极大。
根据建模的出发点不同,等效模型可以简单归类为化学模型与性能模型。
化学模型的建立需要对电池的电化学机理有很深的理解,复杂程度较高,考虑的因素繁多,因此,一般不适用于电动汽车的在线管理,多应用于电池的研发过程。
与化学模型相对应的是电池性能模型,目前常用的性能模型主要为等效电路电路模型,等效电路模型不考虑电池内部化学成分及其化学反应,仅通过电子元器件描述电池工作时的外特性,简单易用,结构可根据不同电池类型进行调整,普遍适用于电动汽车动力电池上。
基于电化学机理模型的锂离子电池参数辨识及SOC估计
基于电化学机理模型的锂离子电池参数辨识及SOC估计邓昊;杨林;邓忠伟;李冬冬;杨洋;蔡亦山;羌嘉曦【摘要】采用Fisher信息矩阵进行参数可辨识性分析,解决了参数的辨识问题,进而提出了基于简化电化学机理模型SP2D(simple pseudo-two-dimensional)的SOC(电池电量)在线估计方法.实验表明,该SOC估计方法较基于等效电路模型(一阶RC模型)的SOC估计方法,可将SOC估计的平均误差减小近30%,而在电池放电中后期更可减小达60%,有效解决了在电池全工作范围内的SOC高精度估计问题.【期刊名称】《上海理工大学学报》【年(卷),期】2018(040)006【总页数】9页(P557-565)【关键词】电化学模型;可辨识性分析;参数辨识;在线SOC估计【作者】邓昊;杨林;邓忠伟;李冬冬;杨洋;蔡亦山;羌嘉曦【作者单位】上海交通大学机械与动力工程学院,上海 200240;上海交通大学机械与动力工程学院,上海 200240;上海交通大学机械与动力工程学院,上海 200240;上海交通大学机械与动力工程学院,上海 200240;上海交通大学机械与动力工程学院,上海 200240;上海交通大学机械与动力工程学院,上海 200240;上海凌翼动力科技有限公司,上海 200240【正文语种】中文【中图分类】TM912电动汽车已成为国内外汽车科技发展的重点。
如何准确估计SOC(电池电量),是电动汽车发展中亟待解决的关键问题。
现有的SOC 估计方法,除基于完全依赖实验数据的数据模型外,主要基于等效电路模型(ECM),其具有模型简单、计算方便的优点[1-2]。
但数据模型的实验工作量大、难于全覆盖电池在电动汽车等应用的全部工况,等效电路模型亦属于经验模型,不能体现电池实际的物理参数,因而无法描述电池内部的电化学行为与物理特性。
相比而言,电化学机理模型(如P2D,pseudo-two-dimensional)[3]是根据电池内部机理建立电化学动力和传输方程组,因此,可以更准确地描述电池的运行状态、健康状态,提高了电池SOC 估计的准确性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
更多电动汽车相关资料论文可联系jijimaoioy@,与同行共同探讨混合动力汽车中锂离子动力电池参数辨识与状态估计魏学哲,孙泽昌,田佳卿(同济大学汽车学院,上海,200092)摘要:本文从锂离子动力电池的“电流激励-电压响应”出发,通过实验分析了FreedomCar电池模型存在的不足之处,对其提出了改进,并证明了改进模型在混合动力工况下的可行性。
根据该线性模型提出了基于最小二乘法的参数辨识的方法,并根据混合动力汽车的具体应用条件提出了并实现了基于“电流-时间窗口”的SOC校准方法。
关键词:锂离子动力电池蓄电池管理系统电池模型荷电状态参数辨识一、引言能源危机已经初露端倪,而全球范围内要求减少污染改善环保走可持续发展道路的呼声也日益高涨。
一方面,能源消耗与环境污染与汽车工业有着最直接的关系,而另一方面汽车工业由于涉及产业链很长,又常常是一个国家的支柱产业,面对这样的形势,整个汽车业又重新把目光投回到电动汽车上,并把开发电动汽车作为今后汽车工业发展的必然方向。
由于目前电池的能量密度与汽油相比还相差甚远,所以工程师们开发了混合动力汽车(HEV-Hybrid Electric V ehicle)。
无论对于“机电”混合动力汽车或者“电电”混合动力汽车,作为辅助动力源的蓄电池组都是整车动力系统中的一个重要部分,作用是辅助汽车主动力源,在汽车行驶中有大功率需求时及时响应提供动力,并吸收汽车制动回馈的能量。
由此,蓄电池组的工作特点是,在一定的荷电状态(SOC-State of Charge或DOD-Depth of Discharge)范围内工作(通常是30% ~ 70%),在瞬时提供或者吸收较大功率,承受较大的充放电电流,但由于充放电的持续时间不长,因而充放电深度都不大,消耗电池的能量和容量也不大。
锂离子电池以其能量密度和功率密度都较大、无记忆效应、自放电较小及循环寿命较长等特点逐渐受到人们的重视。
与之配备的蓄电池组管理系统则必须实时地告诉车辆管理器关于蓄电池组的信息,包括当前电池的荷电状态,电池的充放电能力(最大充放电功率)和电池的老化情况。
这些信息必须达到一定的精度要求,因为车辆管理系统将会根据获得的信息,结合整车动力控制策略进行功率和能量的配置,如果蓄电池管理系统提供的信息不能正确反应电池的实际情况,那将会影响整车的动力性能表现甚至引发严重的安全问题。
为获得这些信息,本文建立了锂离子电池的电路模型,在一定电流范围内比较准确地描述电池的电特性响应,并且利用该模型计算了一些能反映电池状态的参量。
而所有这些的基础,就是准确地确定了锂离子电池电路模型中的各个参数。
二、蓄电池的电路模型描述蓄电池电特性的模型有很多,通过对电池的试验及其结果的分析,我们认为由FreedomCAR【1】给出的电池电路模型比较好地描述了电池的电特性,模型如图1所示。
图1 FreedomCAR电池模型下面结合该模型,对电池试验结果作简要分析。
电池试验都是在室温下进行,使用的是Arbin电子负载设备。
图2是单体电池的恒流放电特征曲线,曲线的II部分,也就是混合动力汽车上蓄电池组主要工作的荷电状态范围,这一部分的曲线基本呈现直线的状态,类似一个电容,随着电容上电量的减少其两端的电压也相应下降,即对应模型中的电容C0。
图3是电池组经受恒流脉冲放电时的电压响应曲线,可以看到,在刚加载上电流以及刚撤除加载电流时,电压值都有一个跳变,类似电流加载到一个纯电阻上后的电压响应,即模型中的R0。
而图中两段电压缓慢变化的曲线,则用电流作用在RC并联环节上来描述。
使用Matlab/simulink对该模型仿真后的结果如图4所示,仿真曲线与试验数据在形状上相近,但可以看到两者的贴合程度并不理想,故我们对FreedomCAR给出的电路模型上进行适当修正,模型如图5所示,增加一个RC并联环节后的新模型相比原模型,能更准确地描述电池电特性的响应。
图2单体电池恒流充放电特征曲线3313323333343353363373383390.00010.00020.00030.00040.00050.00060.00070.00080.00090.000100.000时间(s )电压(V )331332333334335336337338339图3 实际电池组电流脉冲放电电压响应曲线图4 FreedomCAR 电池模型仿真结果与试验数据比较图5 基于试验修正的电池电路模型三、电池电路模型中的参数辨识锂离子电池充放电的电化学过程十分复杂,且锂离子电池又有非线性和时变性的特点,由理论分析来获得模型中的参数非常困难,所以我们通过对试验曲线的分析,即知道电流输入电压输出的情况下,来计算电池模型中的各个参数,也就是计算出C0、C1、C2、R0、R1和R2的值,再根据计算出的参数值估计电池当前所处的状态,从而做到对电池比较完善的管理,电池模型在整个电池管理系统中的作用如图6所示,其中电流、电压和温度是可以直接测得的一次量,电池管理系统就是要根据这些测得的一次量来估计电池的状态。
图6 电池模型在电池管理系统中的作用图3所示的电池组电流脉冲放电电压响应的试验曲线包含了丰富的信息。
利用该曲线可以计算出模型中的各参数,如下图所示:图7 电池模型中的参数辨识流程至此,即可把图1所示的电池电路模型中的C 0、C 1、C 2、R 0、R 1和R 2都计算出来了。
整个辨识参数流程可见图7。
把这些数值代入后,进行仿真,给电池模型同样加载上20s 的恒流负载,再与实际试验结果进行比较,得到了很好的模拟效果,如图8所示,其中黑色曲线为仿真结果。
图8 电池电路模型仿真结果与试验数据比较 四、基于模型的窗口法SOC 估计:在实车运行时,SOC 是电池管理系统向整车管理系统(VMS )传输的重要信息之一,对电池本身来说,电池的一些电特性也与其所处的荷电状态有关,因此做到正确地估算蓄电池的SOC 是十分必要的。
估算SOC 值比较简单的方法是电流积分法。
其计算公式如下,C idt SOC SOC initial ⎰+=,其中SOC initial 是每次行车开始前,根据电池的开路电压查SOC-OCV 关系表得到的SOC 初始值,C 是电池的容量,SOC-OCV 关系曲线可以事先在试验室内做好。
该算法存在的缺陷之一是由于采用积分方式,电流测量所引起的误差会逐渐累积起来,由于混合动力汽车电池的容量较小,而对于汽车来说连续行驶3-4小时是很平常的工况,因此较小的电流测量误差会随着时间的积累而变得与电池容量具有相当的可比性了,缺陷之二是电池的容量是随电池的电流变化的,而上述方法没有考虑这一点,因此该方法在行车时电池的SOC 值会变得很不准确,并且难以控制误差。
通过对电池的试验,即对电池作不同次数的来回充放电循环后再分别做出SOC-OCV 对应关系曲线,我们发现新老电池的SOC-OCV 对应关系曲线有很好的重合性,该现象说明开路电压对应的不是电池的绝对容量,而是电池的相对容量,用开路电压来查找对应的SOC 值可以获得比较好的准确度。
于是,为了消除电流积分带来的误差累积,在计算SOC 值时,仍旧使用C idt SOC SOC initial ⎰+=该公式,但可以每隔一定时间就用SOC-OCV 的对应关系来求一次SOC ,相当于每隔一定时间对SOC 作一次校正,即避免了误差的长期积累。
OCV 是电池静置足够长时间后电池的端电压(实验表明需大于15min ),但如何在电池有负载情况下,即行车过程中来获得某一时刻电池的OCV 值呢?借助电池的电路模型以及经辨识后的参数,可以找到适用在混合动力工况下的相应处理方法。
图9 UDDS 工况下电池电流分析“电-电混合”燃料电池轿车上蓄电池组的使用工况,如图9所示,该波形为电池在UDDS 工况下电流波形,由上图可知,电池上真正处于大电流的时段并不多,电池组大部分时间都处在较小电流的充放电状态,分析其他工况也能得出同样的结论,因此,可以比较容易在行车时得到一段在电池上只有较小电流加载的工况,此时电池近似满足线性化模型,可将某个时刻点之后的电压响应看成是在该时刻点的零输入响应与零状态响应的叠加,同时也记录下这段时间的电流输入。
将这段电流输入作用在电池模型上,即可以得到针对这段电流的零状态响应:⎪⎪⎭⎫ ⎝⎛+++++-=022110111)()()(SC S R S R R s I s U s Vc ττI(s)、U(s)可以通过测量得到,R 1、R 2、C 1、C 2可以通过参数辨识得到,进而RC 电路的时间常数τ=RC 也可以算出,V C(S)就可以算出确定的值。
而用记录下的总电压响应减去计算得到的零状态响应,即可获得了零输入响应,而零输入响应又等于:2211011)(ττs U s U OCV s Vc C C ++++= 其中OCV 、U C1、U C2是未知量。
因此,只要在设置的电流-时间窗口的任意三个时刻计算相应的零输入响应,即可列出一个三元三次方程组,从而计算出OCV 。
再根据SOC-OCV 关系也就得到了该时刻电池的SOC 值。
在离线环境下,按照上述方法对试验数据进行处理。
还是对整组蓄电池进行的试验,先用70A 大小的电流对电池组放电,持续10s ,之后即用六个三角波形状的电流对电池组放电,最大电流为10A ,之后即将电流卸除,整个电流加载过程可见图10。
相应地,试验结果电压响应与同样电流加载到电池模型上的仿真结果如图11所示。
从图中可以看到,在三角波形状电流加载时,由仿真得到的电压响应与实际的电压响应有很好的吻合,但三角波形状电流撤除后的电压响应与实际的电压响应已经出现一些偏移,原因是模型中的参数值是通过对小电流加载辨识得到的,即表明经小电流加载来确定的参数值已经不再适用于大电流加载的情况,也表明了电池具有的非线性性质,但误差仍在0.5V 之内。
如果把大电流70A 卸除时刻,即时间为第10s 的时刻之后的电压响应看成总响应,同时认为电池模型在小电流范围内可以足够精确地反映实际电池的电特性,把三角波形状的电流加载到电池模型后获得的电压响应看成是电池的零状态响应,那么将总响应减去零状态响应,即可得到此对应时刻之后的电池的零输入响应。
图10 试验流程中加载的电流波形图11 电压响应仿真与试验结果比较上面叙述了用该SOC算法对静态试验数据的处理。
同样,在MATLAB/Simulink环境下使用该算法进行仿真,以检验其在动态过程中的计算精度。
算法流程大致可以分成四步,如图12所示。
首先进行电流判断,辅助动力模式下对电池的小电流加载工况经常发生,因此设置一个电流-时间窗口,假设起始与终止时刻分别为t1和t2,记录下该时间段内的电流电压值,而该时间段内的电流大小的绝对值都小于20A,即认为在小电流情况下,电池模型参数不随电流输入的变化而改变;接着,将记录下的电流值作用到电池模型上,计算得电池的零状态响应,结合记录下的总电压响应,即可得电池在该时间窗口段的零输入响应;然后,用外推法计算电池在t1时刻的OCV,在前一步中虽然已求得电池的自t1时刻起到t2时刻止的零输入电压响应,但由于不可能把时间窗口设得无限长,因此实际上这段时间内的任何一个具体电压值都不能完全代表电池最终的OCV值,然而回到电池电路模型可知,这段时间是电容C1、C2分别在R1、R2上放电的过程,将这段电压扣除由欧姆电阻引起的压降再稍做变形处理后得出的电压响应是满足该放电过程的,故从中可反求得电容C1和C2上的初始电压,再补上先前扣除的欧姆压降,最终计算求得OCV;最后,利用OCV-SOC关系表查出电池在t时刻的SOC值。
