七年级下册数学直角坐标系压轴题
七年级下册数学培优训练 平面直角坐标系综合问题(压轴题)

(2)设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交与点P,求∠APD的度数?
(3)当D点在线段OB上运动时,作DM⊥AD交CB于M,∠BMD,∠DAO的平分线交于N,则D点在运动的过程中∠N的大小是否变化,若不变,求出其值;若变化,请说明理由。
【例7】在平面直角坐标系中,点B(0,4),C(-5,4),点A是x轴负半轴上一点,S四边形AOBC=24.
(1)线段BC的长为,点A的坐标为;
(2)如图1,EA平分∠CAO,DA平分∠CAH,CF⊥AE点F,试给出∠ECF与∠DAH之间满足的数量关系式,并说明理由;
(3)若点P是在直线CB与直线AO之间的一点,连接BP、OP,BN平分 ,ON平分 ,BN交ON于N,请依题意画出图形,给出 与 之间满足的数量关系式,并说明理由.
(4)在y轴上是否存在一点P,使线段AB平移至线段PQ时,由A、B、P、Q构成的四边形是平行四边形面积为10,若存在,求出P、Q的坐标,若不存在,说明理由;
【例3】如图,△ABC的三个顶点位置分别是A(1,0),B(-2,3),C(-3,0).
(1)求△ABC的面积;
(2)若把△ABC向下平移2个单位长度,再向右平移3个单位长度,得到△ ,请你在图中画出△ ;
(3)若点A、C的位置不变,当点P在y轴上什么位置时,使 ;
(4)若点B、 C的位置不变,当点Q在x轴上什么位置时,使 .
【例4】如图1,在平面直角坐标系中,于B.
(1)求三角形ABC的面积;
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等,若存在,求出P点坐标;若不存在,请说明理由.
部编数学七年级下册期末难点特训(三)和平面直角坐标系有关的压轴题(解析版)含答案

(1)已知点A的坐标为(﹣3,1),(1)请直接写出点A ,B ,C 的坐标;(2)如图(1),若点D 的坐标为()1,0-,点(),F m n 为线段DE 12,求m 的取值范围;(3)如图(2),若DE 与y 轴的交点G 在B 点上方,点P 为EBO Ð,BPD Ð,PDA Ð之间的数量关系.【答案】(1)()4,0A ,()0,2B ,()0,3C -14Q 将线段AB 平移到DE ,AB DE \=,AB DE ∥,AD =\四边形ABED 的面积25=´=152ABF ABEDS S D \==四边形,ABF ADF ABO ABFD S S S S D D D =+=+Q 四边形11155422(222n m \+´´=´´+´´-Q将线段AB平移到DE \∥,AD BE AB DE∥ADP BFD\Ð=Ð,\Ð=°-Ð=180180 PFB BFD Q,Ð=Ð+ÐEBO BPD BFPEBO BPD\Ð=Ð+°-Ð180Q将线段AB平移到DE \∥,AD BE\Ð+Ð=°,PDA BFD180\Ð=°-Ð,180BFP PDAÐ=Ð+ÐQ,EBO BFP BPF\Ð=°-Ð+180180 EBO PDA如图,当点P 在AD 的延长线与y 轴的交点T 上方时,EBO BEG EGB Ð=Ð+ÐQ ,又BE AD Q ∥,BEG GDT \Ð=Ð,由对顶角得EGB TGD Ð=Ð,PTD TGD TDG Ð=Ð+ÐQ ,PTD EBO \Ð=Ð,PDA PTD TPD Ð=Ð+ÐQ ,PDA EBO BPD\Ð=Ð+Ð综上所述:当点P 在点B 的下方时,180EBO BPD ADP Ð=Ð+°-Ð;当点P 在B 、与AD 的延长线与y 轴的交点之间时,360EBO PDA BPD Ð+Ð+Ð=°;当点P 在AD 的延长线与y 轴的交点T 上方时,PDA EBO BPD Ð=Ð+Ð.【点睛】本题是三角形综合题,考查了平移的性质,三角形面积公式,利用分类讨论思想解决问题是解题的关键.3.如图所示,在平面直角坐标系中,如图①,将线段AB 平移至线段CD ,点A 在x 轴的负半轴,点C 在y 轴的正半轴上,连接AC 、BD .(1)若(3,0)A -、(2,2)B --,(0,2)C ,直接写出点D 的坐标;(2)如图②,在平面直角坐标系中,已知一定点(2,0)M ,两个动点(,21)E a a +、(,23)F b b -+.请你探索是否存在以两个动点E 、F 为端点的线段EF 平行于线段OM 且等于线段OM ,若存在,求点E 、F 的坐标;若不存在,请说明理由;(3)如图③,在直线EF 上有两点A 、C ,分别引两条射线AB 、CD .110BAF Ð=°,//EF OM Q ,EF OM =,\点E 与F 的纵坐标相等,横坐标的差的绝对值为即2123a b +=-+,||a b -=如图①,AB 与CD 在EF 的两侧时,110BAF Ð=°Q ,60DCF Ð=°,18060312031203ACD t t t \Ð=°-°-°´=°-°´=°-°要使//AB CD ,则ACD BAF ÐÐ=,即120°-解得5t =,此时(18060)340°-°¸°=,040t \<<,∴a−6=0,c+8=0,∴a=6,c=−8,∴A(6,0),B(6,−8).当点P到AB的距离为2个单位长度时,运动路程s=6−2=4或s=6+8+2=16,∴4÷2=2s或16÷2=8s,故答案为:2s或8s;(2)①当0≤t≤3时,点P在OA上,此时,P(2t,0);②当3≤t≤7时,点P在AB上,此时PA=2t−6,由于点P在第四象限,纵坐标小于0,则P (6,6−2t);③当7≤t≤10时,点P在BC上,此时PB=2t−OA−AB=2t−14,PC=BC−PB=6−(2t−14)=20−2t,∴P(20−2t,−8);(3)当点P在线段AB上时,分两种情况:①如图3中,结论:∠PEA+∠PFC=160°,理由如下:连接OP,∵∠PFC=∠FPO+∠FOP,∠AEP=∠EOP+∠EPO,∴∠PEA+∠PFC=∠FPO+∠FOP+∠EOP+∠EPO=∠AOF+∠EPF=90°+70°=160°;②如图4中,结论:∠PFC−∠AEP=20°,理由如下:a______,b=______;(1)直接写出=轴上一点,且三角形ABP的面积为12,求点P=,设OC mAE BDQ∥,\ADQ=(1)求B 点的坐标时,小明是这样想的:先设B 点坐标为以()m n ,是方程2x y -=-的解;又因为B 点在直线BC 解,从而m ,n 满足228m n m n -=-ìí+=î,据此可求出B 点坐标为______;C 点坐标为______.(均直接写出结果)(2)若线段BC 上存在一点D ,使12OCD ABC S S =△△(O∵S△ABM+S梯形AMNF=S△FBN,∴1 2×4×4+12(4+FN)×3=12×FN×7,∴FN=7,∴F(-5,-3),过点∠MDQ=90°,△MDQ是等腰直角三角形,过点D作DG⊥x轴于E,过点M作MG⊥DG于G,同理得△BOA≌△AED,△MGD≌△DEQ,∴DE=MG=OA=2,OE=2+6=8,∴OE=8=m+2,∴m=6,∴OQ=OE+EQ=OE+DG=8+2+3m-6=3m+4=22,∴Q(22,0);③如图4,∠MDQ=90°,△MDQ 是等腰直角三角形,过点D作DE⊥x轴于E,过M作MG∥y轴,过点D作DG⊥MG于G,同理得:OA=DE=DG=2,∴m=2+6+2=10,∴OQ=EQ-OE=MG-OE=2+3m-6-8=18,∴Q(-18,0);综上,点Q的坐标为(-3,0)或(22,0)或(-18,0).【点睛】本题是三角形的综合题,考查了坐标与图形性质及非负数的性质,等腰直角三角形的性质和判定,三角形全等的性质和判定等知识,解决本题的关键是作辅助线构建三角形全等.过点过点过点(1)求点A ,B 的坐标;(2)如图1,将AB 平移到A B ¢¢,使点B 的对应点B ¢落在x 轴的正半轴上,在且20ABP Ð=°,试判断PB A ¢¢Ð与B PB ¢Ð之间的数量关系,并说明理由;(3)如图2,线段AB 与y 轴交于点M ,将AB 平移到A B ¢¢,连接MA ¢∵由平移得:AB A B ¢¢∥∴PQ A B ¢¢∥∴QPB PB A ¢¢¢Ð=Ð,20QPB PBA Ð=Ð=°∴PB A QPB B PB QPB B PB PBA ¢¢¢¢¢Ð=Ð=Ð+Ð=Ð+Ð∵ACDB ACOM OMDBS S S =+梯形梯形梯形∴()()(111826246222m ´´+=´++´´解得:4m =如图3,过点A ¢、B ¢构造矩形A GEF ¢∴A B M A GB MEB A GEF S S S S ¢¢¢¢¢¢=---矩形△△△(1118884488222n n =´-´´-´×-´×-64162324n n---+216n =+\Ð∵Q由平移可得:,MN PQ ∥180,MNQ PQN EQP MNE ENQ EQN \Ð+Ð=°=Ð+Ð+Ð+Ð 180,NEQ ENQ EQN Ð+Ð+Ð=°Q,NEQ EQP MNE \Ð=Ð+Ð如图,当E 在NQ 的右边,直线MN 的左边时,(包括E 在这两条直线上),同理可得:180,180,MNQ PQN QNE NEQ NQE Ð+Ð=°Ð+Ð+Ð=° 360,MNE NEQ EQP \Ð+Ð+Ð=°如图,当E 在直线MN 的右边时,记直线MN 与EQ 的交点为F ,同理,当C 点平移后的点不是“自大点时”, 1t …或3t …,\当平移后的正方形边界及其内部的所有点都不是“自大点”时,1t …或7t …,故答案为:1t …或7t ….【点睛】本题主要考查正方形的性质,坐标与图形的平移变化,根据题意,准确找出“自大点”的纵横坐标满足的关系是解答此题的关键.。
七(下)培优训练(三)平面直角坐标系综合问题(压轴题)

培优训练三:平面直角坐标系(压轴题)一、坐标与面积:【例1】如图,在平面直角坐标中,A (0,1),B (2,0),C (2,1.5). (1)求△AB C的面积;(2)如果在第二象限内有一点P(a ,0.5),试用a 的式子表示四边形ABOP 的面积;(3)在(2)的条件下,是否存在这样的点P ,使四边形ABOP 的面积与△AB C的面积相等?若存在,求出点P 的坐标,若不存在,请说明理由.yxPOCBA【例2】在平面直角坐标系中,已知A (-3,0),B (-2,-2),将线段AB 平移至线段CD .图1y xDO CB A图2y xDOCB AyxOBAyxOBA(1)如图1,直接写出图中相等的线段,平行的线段;(2)如图2,若线段AB 移动到CD ,C 、D 两点恰好都在坐标轴上,求C 、D 的坐标;(3)若点C 在y 轴的正半轴上,点D在第一象限内,且S△ACD =5,求C、D 的坐标;(4)在y 轴上是否存在一点P ,使线段AB 平移至线段PQ 时,由A 、B 、P、Q 构成的四边形是平行四边形面积为10,若存在,求出P 、Q的坐标,若不存在,说明理由;【例3】如图,△ABC 的三个顶点位置分别是A (1,0),B (-2,3),C (-3,0).(1)求△ABC 的面积;(2)若把△AB C向下平移2个单位长度,再向右平移3个单位长度,得到△A B C ''',请你在图中画出△A B C '''; (3)若点A、C的位置不变,当点P 在y 轴上什么位置时,使2ACPABCS S=;(4)若点B 、C的位置不变,当点Q在x 轴上什么位置时,使2BCQABCS S=.【例4】如图1,在平面直角坐标系中,A (a ,0),C (b,2),且满足2(2)20a b ++-=,过C 作CB ⊥x 轴于B.(1)求三角形ABC 的面积;(2)若过B作BD ∥AC 交y 轴于D,且AE ,D E分别平分∠CA B,∠ODB ,如图2,求∠AE D的度数;(3)在y 轴上是否存在点P ,使得三角形ABC 和三角形A CP 的面积相等,若存在,求出P 点坐标;若不存在,请说明理由.【例5】如图,在平面直角坐标系中,四边形AB CD 各顶点的坐标分别是A(0,0),B(7,0),C (9,5),D (2,7)(1)在坐标系中,画出此四边形; (2)求此四边形的面积;(3)在坐标轴上,你能否找一个点P ,使S △PBC =50, 若能,求出P 点坐标,若不能,说明理由.【例6】如图,A点坐标为(-2, 0), B 点坐标为(0, -3). (1)作图,将△ABO沿x轴正方向平移4个单位, 得到△DEF , 延长ED 交y 轴于C点, 过O点作O G⊥C E, 垂足为G ;(2) 在(1)的条件下, 求证: ∠C OG =∠E DF ; (3)求运动过程中线段A B扫过的图形的面积.【例7】在平面直角坐标系中,点B (0,4),C(-5,4),点A 是x轴负半轴上一点,S四边形A OBC =24.图1yxHOFEDAC B(1)线段B C的长为 ,点A的坐标为 ;(2)如图1,EA 平分∠CAO ,DA 平分∠CA H,CF ⊥A E点F,试给出∠ECF 与∠DAH 之间满足的数量关系式,并说明理由;(3)若点P 是在直线C B与直线AO 之间的一点,连接BP 、OP ,BN 平分CBP ∠,ON平分AOP ∠,BN 交ON 于N,请依题意画出图形,给出BPO ∠与BNO ∠之间满足的数量关系式,并说明理由. 【例8】在平面直角坐标系中,OA=4,O C=8,四边形ABC O是平行四边形.A(-2,0)B(0,-3)y x 0(1)求点B 的坐标及的面积ABCO S 四边形;(2)若点P 从点C以2单位长度/秒的速度沿CO 方向移动,同时点Q 从点O 以1单位长度/秒的速度沿OA 方向移动,设移动的时间为t 秒,△AQ B与△BPC 的面积分别记为AQB S ∆,BPC S ∆,是否存在某个时间,使AQB S ∆=3OQBPS 四边形,若存在,求出t 的值,若不存在,试说明理由;(3)在(2)的条件下,四边形Q BPO 的面积是否发生变化,若不变,求出并证明你的结论,若变化,求出变化的范围.【例9】如图,在平面直角坐标系中,点A ,B的坐标分别为(-1,0),(3,0),现同时将点A,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A,B 的对应点C,D 连结AC ,B D. (1)求点C ,D 的坐标及四边形ABD C的面积S 四边形ABDC ;(2)在y轴上是否存在一点P ,连结P A ,PB ,使S △PAB =S △明理由;(3)若点Q自O 点以0.5个单位/s 的速度在线段AB上移动,运动到B点就停止,设移动的时间为t 秒,(1)是否是否存在一个时刻,使得梯形CDQB 的面积是四边形ABCD 面积的三分之一?(4)是否是否存在一个时刻,使得梯形CDQB 的面积等于△ACO 面积的二分之一?【例10】在直角坐标系中,△AB C的顶点A (—2,0),B (2,4),C (5,0). (1)求△ABC 的面积(2)点D 为y负半轴上一动点,连BD 交x 轴于E ,是否存在点D 使得ADE BCE S S ∆∆=?若存在,请求出点D 的坐标;若不存在,请说明理由.(3)点F (5,n )是第一象限内一点,,连BF ,CF ,G 是x轴上一点,若△ABG 的面积等于四边形ABDC 的面积,则点G 的坐标为 (用含n 的式子表示)二、坐标与几何:【例1】如图,已知A (0,a),B (0,b),C (m ,b)且(a -4)2+|b+3|=0,S △ABC =14. (1)求C点坐标(2)作DE ⊥DC,交y 轴于E点,EF 为∠AED 的平分线,且∠DF E=900.求证:FD 平分∠ADO;(3)E 在y 轴负半轴上运动时,连E C,点P为A C延长线上一点,EM 平分∠AEC,且PM ⊥EM,PN ⊥x 轴于N点,PQ 平分∠APN,交x轴于Q点,则E 在运动过程中,错误!的大小是否发生变化,若不变,求出其值.【例2】如图,在平面直角坐标系中,已知点A(-5,0),B(5.0),D(2,7), (1)求C点的坐标;(2)动点P 从B 点出发以每秒1个单位的速度沿BA 方向运动,同时动点Q从C 点出发也以每秒1位的速度沿y轴正半轴方向运动(当P 点运动到A 点时,两点都停止运动)。
初一数学平面直角坐标系压轴题

初一数学平面直角坐标系压轴题一、在平面直角坐标系中,点A(3, -2)关于x轴对称的点的坐标是?A. (-3, -2)B. (3, 2)C. (-3, 2)D. (2, -3)(答案) B二、点B(-4, 5)关于y轴对称的点的坐标是什么?A. (-4, -5)B. (4, -5)C. (4, 5)D. (-4, 0)(答案) C三、若点C(a, b)在第二象限,则点C关于原点对称的点的坐标位于?A. 第一象限B. 第二象限C. 第三象限D. 第四象限(答案) D四、点D(6, -8)到x轴的距离是?A. 6B. 8C. -8D. -6(答案) B五、点E(-7, 9)到y轴的距离是?A. 7B. 9C. -7D. -9(答案) A六、在平面直角坐标系中,点F(0, -3)位于?A. x轴上B. y轴上C. 原点上D. 第一象限(答案) B七、点G(m, n)关于x轴对称的点与关于y轴对称的点重合,那么点G一定在?A. 第一象限B. 第二象限C. x轴上D. y轴上(答案) D八、若点H(p, q)关于原点对称的点的坐标是(2, -3),则p+q的值是?A. 5B. -5C. 1D. -1(答案) D九、在平面直角坐标系中,将点I(1, -2)向右平移3个单位,再向上平移4个单位,所得点的坐标是?A. (4, 2)B. (-2, -6)C. (-2, 2)D. (4, -6)(答案) A十、点J(x, y)满足x=y,且它到x轴的距离为5,则点J的坐标可能是?A. (5, -5)B. (-5, 5)C. (5, 5)D. (-5, -5)(答案) C。
七年级下学期压轴题(平面直角坐标系的综合题)含答案

七年级下学期压轴题(平面直角坐标系的综合题)1、如图,在长方形ABCD 中,边AB=8,BC=4,以点O 为原点,OA ,OC 所在的直线为y 轴和x 轴,建立直角坐标系.(1)点A 的坐标为(0,4),则B 点坐标为( ) ,C 点坐标为( ) ;(2)当点P 从C 出发,以2单位/秒速度向CO 方向移动(不过O 点),Q 从原点O 出发以1单位/秒速度向OA 方向移动(不过A 点),P ,Q 同时出发,在移动过程中,四边形OPBQ 的面积是否变化?若不变,求其值;若变化,求其变化范围.解:(1)∵长方形ABCD 中,AB=8,BC=4, ∴CD=AB=8,∴B (8,4),C (8,0);故答案为:(8,4),(8,0);(2)设运动时间为t ,则CP=2t ,AQ=4-t , S 四边形OPBQ=S 矩形ABCD-S △ABQ-S △BPC , =4×8-1/2×8(4-t )-1/2×4t , =32-16+4t-4t , =16,所以,四边形OPBQ 的面积不变,为16.2、如图,在平面直角坐标系中,已知A (0,a )、B (b ,0)、C (b ,c )三点,其中a 、b 、c 满足关系式|a-2|+(b-3)2+4-c =0, (1)求a 、b 、c 的值;(2)如果在第二象限内有一点⎪⎭⎫ ⎝⎛21,m P ,请用含m 的式子表示四边形ABOP 的面积;(3)在(2)的条件下,是否存在点P ,使四边形ABOP 的面积与△ABC 的面积相等?若存在,求出点P 的坐标;若不存在,请说明理由。
解:(1)a-2=0,a=2;b-3=0,b=3;c-4=0,c=4;(2)过点p 作PD ⊥y 轴于点D= ×2×3+ ×2×(-m)=3-m ;(3)存在点P 使四边形ABOP 的面积为△AOP 的面积的两倍 因为所以 ,即3-m=2×( ×2×3),解得m=-3所以P(-3, ).3、如图,△ABC 的三个顶点位置分别是A(1,0),B(-2,3),C(-3,0). (1)求△ABC 的面积;(2)若点P (0,m )在y 轴上,试用含m 的代数式表示三角形ACP 的面积; (3)若点A 、C 的位置不变,当点P 在y 轴上什么位置时,使S △ACP =2S △ABC ; (4)若点B 、C 的位置不变,当点Q 在x 轴上什么位置时,使S △BCQ =2S △ABC .4、如图1,在平面直角坐标系中,A (a ,0),C (b ,2),且满足(a+2)2+02-b,过C 作CB ⊥x 轴于B . (1)求△ABC 的面积.(2)若过B 作BD ∥AC 交y 轴于D ,且AE ,DE 分别平分∠CAB ,∠ODB ,如图2,求∠AED 的度数.(3)在y 轴上是否存在点P ,使得△ABC 和△ACP 的面积相等?若存在,求出P 点坐标;若不存在,请说明理由.解:(1)∵(a+2)2+√b-2=0, ∴a=2=0,b-2=0, ∴a=-2,b=2, ∵CB ⊥AB∴A (-2,0),B (2,2),C (2,0), ∴三角形ABC 的面积=1/2×2×4=4;(2)解:∵CB ∥y 轴,BD ∥AC ,∴∠CAB=∠5,∠ODB=∠6,∠CAB+∠ODB=∠5+∠6=90°, 过E 作EF ∥AC ,如图①, ∵BD ∥AC , ∴BD ∥AC ∥EF ,∵AE ,DE 分别平分∠CAB ,∠ODB ,∴∠3=1/2∠CAB=∠1,∠4=1/2∠ODB=∠2,∴∠AED=∠1+∠2=1/2(∠CAB+∠ODB )=45°;(3)解:①当P 在y 轴正半轴上时,如图②, 设P (0,t ),过P 作MN ∥x 轴,AN ∥y 轴,BM ∥y 轴, ∵S △APC=S 梯形MNAC-S △ANP-S △CMP=4, ∴4(t-2+t)/2-t-(t-2)=4,解得t=3, ②当P 在y 轴负半轴上时,如图③∵S △APC=S 梯形MNAC-S △ANP-S △CMP=4 ∴4(-t+2-t)/2+t-(2-t )=4,解得t=-1, ∴P (0,-1)或(0,3).5.如图,在平面直角坐标系中,点A ,B 的坐标分别为(-1,0),(3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD .(1)求点C ,D 的坐标及四边形ABDC 的面积(2)在y 轴上是否存在一点P ,连接PA ,PB ,使=,若存在这样一点,求出点P 的坐标,若不存在,试说明理由.(3)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在BD 上移动时(不与B ,D 重合)给出下列结论:①的值不变,②的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.(1)依题意知,将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,故C 、D 两点点y 值为2. 所以点C ,D 的坐标分别为C (0,2),D(4,2) , 四边形ABDC 的面积S 四边形ABDC =CO ×AB=2×4=8(2)(2)在y 轴上是否存在一点P ,使S △PAB=S 四边形ABDC .理由如下: 设点P 到AB 的距离为h ,S △PAB=×AB ×h=2h ,由S △PAB=S 四边形ABDC ,得2h=8, 解得h=4,∴P (0,4)或(0,-4).(3)①是正确的结论,过点P 作PQ ∥CD , 因为AB ∥CD ,所以PQ ∥AB ∥CD (平行公理的推论)∴∠DCP =∠CPQ ,∵∠BOP =∠OPQ(两直线平行,内错角相等), ∴∠DCP +∠BOP =∠CPQ +∠OPQ =∠CPO所以==1.6.如图,以直角三角形AOC 的直角顶点O 为原点,以OC ,OA 所在直线为x 轴和y 轴建立平面直角坐标系,点A (0,a ),C (b ,0)满足(a-2b )2+|b-2|=0.(1)则C 点的坐标为 ;A 点的坐标为 . (2)已知坐标轴上有两动点P 、Q 同时出发,P 点从C 点出发沿x 轴负方向以1个单位长度每秒的速度匀速移动,Q 点从O 点出发以2个单位长度每秒的速度沿y 轴正方向移动,点Q 到达A 点整个运动随之结束.AC 的中点D 的坐标是(1,2),设运动时间为t (t >0)秒.问:是否存在这样的t ,使S △ODP =S △ODQ ?若存在,请求出t 的值;若不存在,请说明理由;(3)点F 是线段AC 上一点,满足∠FOC=∠FCO ,∠OEC=∠CAO+∠ACE ,点G 是第二象限中一点,连OG ,使得∠AOG=∠AOF .点E 是线段OA 上一动点,连CE 交OF 于点H ,当点E 在线段OA 上运动的过程中,OECACEOHC ∠∠+∠的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.解:(1)∵(a-2b )2+|b-2|=0,∴a-2b=0,b-2=0,解得a=4,b=2,∴A(0,4),C(2,0);故答案为(2,0),(0,4).(2)如图1中,由条件可知:P点从C点运动到O点时间为2秒,Q点从O点运动到A点时间为2秒,∴0<t≤2时,点Q在线段AO上,即 CP=t,OP=2-t,OQ=2t,AQ=4-2t,∴S△DOP=21OP•yD=21(2-t)×2=2-t,S△DOQ=21OQ•xD=21×2t×1=t,∵S△ODP=S△ODQ,∴2-t=t,∴t=1;(3)OECACEOHC∠∠+∠的值不变,其值为2.理由如下:如图2中,∵∠2+∠3=90°,又∵∠1=∠2,∠3=∠FCO,∴∠GOC+∠ACO=180°,∴OG∥AC,∴∠1=∠CAO,∴∠OEC=∠CAO+∠4=∠1+∠4,如图,过H点作AC的平行线,交x轴于P,则∠4=∠PHC,PH∥OG,∴∠PHO=∠GOF=∠1+∠2,∴∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,∴OECACEOHC∠∠+∠=241)41(2414421=∠+∠∠+∠=∠+∠∠+∠+∠+∠.7.在平面直角坐标系中,△ABC 的三个顶点坐标为A (4,-1),B (1,4),C (1,-1). (1)请画出△ABC ,并画出△ABC 向左平移6个单位长度后得到的图形△A 1B 1C 1; (2)点P 是线段AB 上的一动点,连接A 1P ,B 1P ,求证:∠BB 1P +∠AA 1P =∠A 1PB 1; (3)在坐标轴上是否存在一点D ,使得△BCD 的面积是△ACD 面积的2倍?若存在,求出点D 的坐标;若不存在,请说明理由.解:(1)△ABC ,△A 1B 1C 1如图所示:(2)如图,过点P 作PQ ∥AA 1交A 1B 1于点Q ,连接BB 1,AA 1,∴PQ ∥AA 1,PQ ∥BB 1,∴∠BB 1P =∠B 1PQ ,∠AA 1P =∠A 1PQ , ∴∠BB 1P +∠AA 1P =∠A 1PB 1; (3)假设存在,分情况讨论:①当点D 在y 上时,设点D (0,m ),则15=51=22BCD S ⨯⨯△,1=312ACD S m ⨯⨯+△,∴5=2=312BCD ACD S S m +=△△, 解得:116m =-,2116m =-,此时点D 的坐标为(0,16-)或(0,116-);②当点D 在x 轴上时,设点D (m ,0),则1=512BCD S m ⨯⨯-△,13=31=22ACD S ⨯⨯△,∴5=2=132BCD ACD S S m -=△△,解得:1115m =,215m =-, 此时点D 的坐标为(115,0)或(15-,0); 综上所述,存在点D 的坐标为(0,16-)或(0,116-)(115,0)或(15-,0)。
七年级数学下册期末代几综合复习题(压轴题)
TP.若∠ABO=n°,请探究∠APT 与∠PTE 之间的数量关系?(注:可用含 n 的式子表
达并说明理由)
(3)若 S△BOD≥S△AOD,求出 m 的取值范围.
10.在平面直角坐标系中,A(6,a),B(b,0),M(0,c),P 点为 y 轴上一动点,
且(b﹣2)2+|a﹣6|+
=0.(1)求点 B、M 的坐标;
6
13.在平面直角坐标系中,已知点 A(a,0),B(0,b).
(1)若|a+b+1|+
=0,已知点 C(m,﹣m).
①AC∥y 轴,求 m 的值;
②若△ABC 的面积不超过 8,求 m 的取值范围;
(2)若∠ABO=60°,射线 BA 以每秒 9°的速度绕点 B 顺时针方向旋转至射线 BA1,M
8. 在 直 角 坐 标 系 中 , 已 知 点 A(a , 0) , B ( b , c ), C ( d , 0 ) 且 a 是 -8 的 立 方 根 ; 方 程
是关于 x,y 的二元一次方程,d 为不等式组
的最大整数解。
(1)求 A、B、C 的坐标; (2)如图 1,若 D 为 y 轴负半轴上的一个动点,连 BD 交 x 轴于点 E,问是否存在点 D,
且 a 6 | b 4 | 0
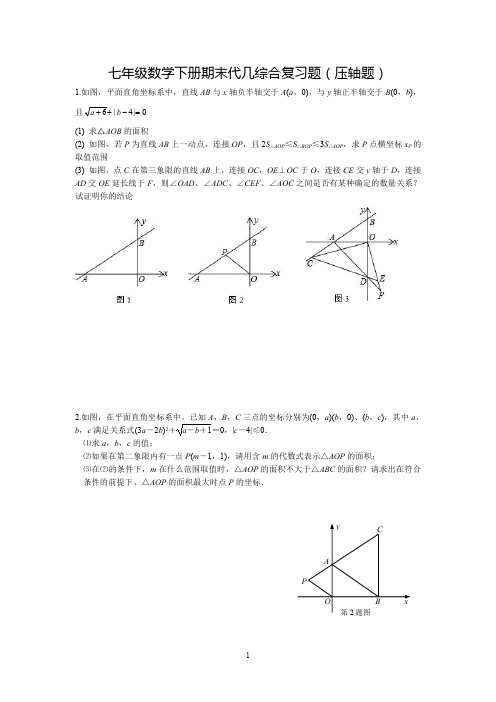
(1) 求△AOB 的面积 (2) 如图,若 P 为直线 AB 上一动点,连接 OP,且 2S△AOP≤S△BOP≤3S△AOP,求 P 点横坐标 xP 的 取值范围 (3) 如图,点 C 在第三象限的直线 AB 上,连接 OC,OE⊥OC 于 O,连接 CE 交 y 轴于 D,连接 AD 交 OE 延长线于 F,则∠OAD、∠ADC、∠CEF、∠AOC 之间是否有某种确定的数量关系? 试证明你的结论
平面直角坐标系必刷常考题七年级数学下学期期中期末满分必刷常考压轴题人教版

专题03 平面直角坐标系必刷常考题选择题必练1.在平面直角坐标系中,点M(﹣2,3)在()A.第一象限B.第二象限C.第三象限D.第四象限2.在平面直角坐标系中,点(﹣1,m2+1)一定在()A.第一象限B.第二象限C.第三象限D.第四象限3.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为()A.2B.3C.4D.54.课间操时,小华、小军、小刚的位置如图1,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成()A.(5,4)B.(4,5)C.(3,4)D.(4,3)5.如图为小杰使用手机内的通讯软件跟小智对话的纪录.根据图中两人的对话纪录,若下列有一种走法能从邮局出发走到小杰家,则此走法为何?()A.向北直走700公尺,再向西直走100公尺B.向北直走100公尺,再向东直走700公尺C.向北直走300公尺,再向西直走400公尺D.向北直走400公尺,再向东直走300公尺6.点P(﹣2,﹣3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为()A.(﹣3,0)B.(﹣1,6)C.(﹣3,﹣6)D.(﹣1,0)7.若点P是第二象限内的点,且点P到x轴的距离是4,到y轴的距离是3,则点P的坐标是()A.(﹣4,3)B.(4,﹣)C.(﹣3,4)D.(3,﹣4)8.如果P(m+3,2m+4)在y轴上,那么点P的坐标是()A.(﹣2,0)B.(0,﹣2)C.(1,0)D.(0,1)9.如图,小手盖住的点的坐标可能为()A.(5,2)B.(﹣6,3)C.(﹣4,﹣6)D.(3,﹣4)10.在平面直角坐标系中,点P(﹣2,x2+1)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限11.如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A′的坐标是()A.(6,1)B.(0,1)C.(0,﹣3)D.(6,﹣3)12.点P的坐标为(2﹣a,3a+6),且到两坐标轴的距离相等,则点P的坐标为()A.(3,3)B.(3,﹣3)C.(6,﹣6)D.(3,3)或(6,﹣6)13.根据下列表述,能确定位置的是()A.红星电影院2排B.北京市四环路C.北偏东30°D.东经118°,北纬40°14.如图,点A(﹣2,1)到y轴的距离为()A.﹣2B.1C.2D.15.已知点A(1,0),B(0,2),点P在x轴上,且△P AB的面积为5,则点P的坐标为()A.(﹣4,0)B.(6,0)C.(﹣4,0)或(6,0)D.无法确定填空题必练16.剧院里5排2号可以用(5,2)表示,则7排4号用表示.17.如果点P(a,2)在第二象限,那么点Q(﹣3,a)在.18.线段CD是由线段AB平移得到的,点A(﹣1,4)的对应点为C(4,7),则点B(﹣4,﹣1)的对应点D的坐标是.19.已知点M(3,﹣2),将它先向左平移4个单位,再向上平移3个单位后得到点N,则点N的坐标是.20.若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是.21.如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(﹣4,2)、(﹣2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是.22.已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为.23.如图,△A′B′C′是△ABC经过某种变换后得到的图形,如果△ABC中有一点P的坐标为(a,2),那么变换后它的对应点Q的坐标为.24.点P(m+3,m+1)在直角坐标系的x轴上,则P点坐标为.25.在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:(1)f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);(2)g(m,n)=(﹣m,﹣n),如g(2,1)=(﹣2,﹣1)按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣3,2)]=.26.将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9,则表示实数17的有序实数对是.27.如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2013的直角顶点的坐标为.解答题必练28.如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).(1)写出点A、B的坐标:A(,)、B(,)(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).(3)△ABC的面积为.29.在平面直角坐标系中,已知点M(m,2m+3).(1)若点M在x轴上,求m的值;(2)若点M在第二象限内,求m的取值范围;(3)若点M在第一、三象限的角平分线上,求m的值.30.如图,平面直角坐标系中,四边形ABCD的顶点坐标分别为A(1,0),B(5,0),C(3,3),D(2,4),求四边形ABCD的面积.31.如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3.(1)求点B的坐标;(2)求△ABC的面积;(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.专题03 平面直角坐标系必刷常考题选择题必练1.在平面直角坐标系中,点M(﹣2,3)在()A.第一象限B.第二象限C.第三象限D.第四象限【答案】B【解答】解:∵﹣2<0,3>0,∴(﹣2,3)在第二象限,故选:B.2.在平面直角坐标系中,点(﹣1,m2+1)一定在()A.第一象限B.第二象限C.第三象限D.第四象限【答案】B【解答】解:因为点(﹣1,m2+1),横坐标﹣1<0,纵坐标m2+1一定大于0,所以满足点在第二象限的条件.故选:B.3.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为()A.2B.3C.4D.5【答案】A【解答】解:由B点平移前后的纵坐标分别为1、2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2、3,可得A点向右平移了1个单位,由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,所以点A、B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2.故选:A.4.课间操时,小华、小军、小刚的位置如图1,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成()A.(5,4)B.(4,5)C.(3,4)D.(4,3)【答案】D【解答】解:如果小华的位置用(0,0)表示,小军的位置用(2,1)表示,如图所示就是以小华为原点的平面直角坐标系的第一象限,所以小刚的位置为(4,3).故选:D.5.如图为小杰使用手机内的通讯软件跟小智对话的纪录.根据图中两人的对话纪录,若下列有一种走法能从邮局出发走到小杰家,则此走法为何?()A.向北直走700公尺,再向西直走100公尺B.向北直走100公尺,再向东直走700公尺C.向北直走300公尺,再向西直走400公尺D.向北直走400公尺,再向东直走300公尺【答案】A【解答】解:依题意,OA=OC=400=AE,AB=CD=300,DE=400﹣300=100,所以邮局出发走到小杰家的路径为,向北直走AB+AE=700,再向西直走DE=100公尺.故选:A.6.点P(﹣2,﹣3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为()A.(﹣3,0)B.(﹣1,6)C.(﹣3,﹣6)D.(﹣1,0)【答案】A【解答】解:根据题意,得点P(﹣2,﹣3)向左平移1个单位,再向上平移3个单位,所得点的横坐标是﹣2﹣1=﹣3,纵坐标是﹣3+3=0,即新点的坐标为(﹣3,0).7.若点P是第二象限内的点,且点P到x轴的距离是4,到y轴的距离是3,则点P的坐标是()A.(﹣4,3)B.(4,﹣3)C.(﹣3,4)D.(3,﹣4)【答案】C【解答】解:∵点P在第二象限,∴P点的横坐标为负,纵坐标为正,∵到x轴的距离是4,∴纵坐标为:4,∵到y轴的距离是3,∴横坐标为:﹣3,∴P(﹣3,4),故选:C.8.如果P(m+3,2m+4)在y轴上,那么点P的坐标是()A.(﹣2,0)B.(0,﹣2)C.(1,0)D.(0,1)【答案】B【解答】解:∵P(m+3,2m+4)在y轴上,∴m+3=0,解得m=﹣3,2m+4=﹣2,∴点P的坐标是(0,﹣2).故选:B.9.如图,小手盖住的点的坐标可能为()A.(5,2)B.(﹣6,3)C.(﹣4,﹣6)D.(3,﹣4)【答案】D【解答】解:根据图示,小手盖住的点在第四象限,第四象限的点坐标特点是:横正纵负;分析选项可得只有D符合.故选:D.10.在平面直角坐标系中,点P(﹣2,x2+1)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:∵x2≥0,∴x2+1≥1,∴点P(﹣2,x2+1)在第二象限.故选:B.11.如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A′的坐标是()A.(6,1)B.(0,1)C.(0,﹣3)D.(6,﹣3)【答案】B【解答】解:四边形ABCD先向左平移3个单位,再向上平移2个单位,因此点A也先向左平移3个单位,再向上平移2个单位,由图可知,A′坐标为(0,1).故选:B.12.点P的坐标为(2﹣a,3a+6P的坐标为()A.(3,3)B.(3,﹣3)C.(6,﹣6)D.(3,3)或(6,﹣6)【答案】D【解答】解:∵点P的坐标为(2﹣a,3a+6),且到两坐标轴的距离相等,∴|2﹣a|=|3a+6|,∴2﹣a=±(3a+6)解得a=﹣1或a=﹣4,即点P的坐标为(3,3)或(6,﹣6).故选:D.13.根据下列表述,能确定位置的是()A.红星电影院2排B.北京市四环路C.北偏东30°D.东经118°,北纬40°【答案】D【解答】解:在平面内,点的位置是由一对有序实数确定的,只有D能确定一个位置,故选:D.14.如图,点A(﹣2,1)到y轴的距离为()A.﹣2B.1C.2D.【答案】C【解答】解:点A的坐标为(﹣2,1),则点A到y轴的距离为2.故选:C.15.已知点A(1,0),B(0,2),点P在x轴上,且△P AB的面积为5,则点P的坐标为()A.(﹣4,0)B.(6,0)C.(﹣4,0)或(6,0)D.无法确定【答案】C【解答】解:∵A(1,0),B(0,2),点P在x轴上,∴AP边上的高为2,又△P AB的面积为5,∴AP=5,而点P可能在点A(1,0)的左边或者右边,∴P(﹣4,0)或(6,0).故选:C.填空题必练16.剧院里5排2号可以用(5,2)表示,则7排4号用表示.【答案】(7,4)【解答】解:∵5排2号可以表示为(5,2),∴7排4号可以表示为(7,4).故答案填:(7,4).17.如果点P(a,2)在第二象限,那么点Q(﹣3,a)在.【答案】第三象限【解答】解:∵点P(a,2)在第二象限,∴a<0,∴点Q的横、纵坐标都为负数,∴点Q在第三象限.故答案为第三象限18.线段CD是由线段AB平移得到的,点A(﹣1,4)的对应点为C(4,7),则点B(﹣4,﹣1)的对应点D的坐标是.【答案】(1,2)【解答】解:∵线段CD是由线段AB平移得到的,而点A(﹣1,4)的对应点为C(4,7),∴由A平移到C点的横坐标增加5,纵坐标增加3,则点B(﹣4,﹣1)的对应点D的坐标为(1,2).故答案为:(1,2).19.已知点M(3,﹣2),将它先向左平移4个单位,再向上平移3个单位后得到点N,则点N的坐标是.【答案】(﹣1,1)【解答】解:原来点的横坐标是3,纵坐标是﹣2,向左平移4个单位,再向上平移3个单位得到新点的横坐标是3﹣4=﹣1,纵坐标为﹣2+3=1.则点N的坐标是(﹣1,1).故答案填:(﹣1,1).20.若第二象限内的点P(x,y)满足|x|=3,y2=25,则点P的坐标是.【答案】(﹣3,5)【解答】解:∵|x|=3,y2=25,∴x=±3,y=±5,∵第二象限内的点P(x,y),∴x<0,y>0,∴x=﹣3,y=5,∴点P的坐标为(﹣3,5),故答案为:(﹣3,5).21.如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(﹣4,2)、(﹣2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是.【答案】(5,4)【解答】解:∵两眼间的距离为2,且平行于x轴,∴右图案中右眼的横坐标为(3+2).则右图案中右眼的坐标是(5,4).故答案为:(5,4).22.已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为.【答案】(﹣2,2)或(8,2)【解答】解:已知AB∥x轴,点B的纵坐标与点A的纵坐标相同,都是2;在直线AB上,过点A向左5单位得(﹣2,2),过点A向右5单位得(8,2).∴满足条件的点有两个:(﹣2,2),(8,2).故答案填:(﹣2,2)或(8,2).23.如图,△A′B′C′是△ABC经过某种变换后得到的图形,如果△ABC中有一点P的坐标为(a,2),那么变换后它的对应点Q的坐标为.【答案】(a+5,﹣2)【解答】解:由图可知,A(﹣4,3),A′(1,﹣1),所以,平移规律为向右5个单位,向下4个单位,∵P(a,2),∴对应点Q的坐标为(a+5,﹣2).故答案为:(a+5,﹣2).24.点P(m+3,m+1)在直角坐标系的x轴上,则P点坐标为.【答案】(2,0)【解答】解:∵点P(m+3,m+1)在直角坐标系的x轴上,∴这点的纵坐标是0,∴m+1=0,解得,m=﹣1,∴横坐标m+3=2,则点P的坐标是(2,0)25.在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:(1)f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);(2)g(m,n)=(﹣m,﹣n),如g(2,1)=(﹣2,﹣1)按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣3,2)]=.【答案】(3,2)【解答】解:∵f(﹣3,2)=(﹣3,﹣2),∴g[f(﹣3,2)]=g(﹣3,﹣2)=(3,2),故答案为:(3,2).26.将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9,则表示实数17的有序实数对是.【答案】(6,5)【解答】解:观察图表可知:每排的数字个数就是排数;且奇数排从左到右,从小到大,而偶数排从左到右,从大到小.实数15=1+2+3+4+5,则17在第6排,第5个位置,即其坐标为(6,5).故答案为:(6,5).27.如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2013的直角顶点的坐标为.【答案】(8052,0)【解答】解:∵点A(﹣3,0)、B(0,4),∴AB==5,由图可知,每三个三角形为一个循环组依次循环,一个循环组前进的长度为:4+5+3=12,∵2013÷3=671,∴△2013的直角顶点是第671个循环组的最后一个三角形的直角顶点,∵671×12=8052,∴△2013的直角顶点的坐标为(8052,0).故答案为:(8052,0).解答题必练28.如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).(1)写出点A、B的坐标:A(,)、B(,)(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(,)、B′(,)、C′(,).(3)△ABC的面积为.【答案】(1)A(2,﹣1)、B(4,3)(2)A′(0,0)、B′(2,4)、C′(﹣1,3).(3)5【解答】解:(1)写出点A、B的坐标:A(2,﹣1)、B(4,3)(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,则A′B′C′的三个顶点坐标分别是A′(0,0)、B′(2,4)、C′(﹣1,3).(3)△ABC的面积=3×4﹣2××1×3﹣×2×4=5.29.在平面直角坐标系中,已知点M(m,2m+3).(1)若点M在x轴上,求m的值;(2)若点M在第二象限内,求m的取值范围;(3)若点M在第一、三象限的角平分线上,求m的值.【答案】(1)m=﹣1.5;(2)﹣1.5<m<0;(3)m=﹣3.【解答】解:(1)∵点M在x轴上,∴2m+3=0解得:m=﹣1.5;(2)∵点M在第二象限内,∴,解得:﹣1.5<m<0;(3)∵点M在第一、三象限的角平分线上,∴m=2m+3,解得:m=﹣3.30.如图,平面直角坐标系中,四边形ABCD的顶点坐标分别为A(1,0),B(5,0),C (3,3),D(2,4),求四边形ABCD的面积.【答案】8.5【解答】解:如图,作CE⊥x轴于点E,DF⊥x轴于点F.则S△ADF=×(2﹣1)×4=2,S梯形DCEF=×(3+4)×(3﹣2)=3.5,S△BCE=×(5﹣3)×3=3,∴S四边形ABCD=2+3.5+3=8.5,答:四边形ABCD的面积是8.5.31.如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=3.(1)求点B的坐标;(2)求△ABC的面积;(3)在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.【答案】(1)(2,0)或(﹣4,0);(2)5 (3)(0,)或(0,﹣).【解答】解:(1)点B在点A的右边时,﹣1+3=2,点B在点A的左边时,﹣1﹣3=﹣4,所以,B的坐标为(2,0)或(﹣4,0);(2)△ABC的面积=×3×4=6;(3)设点P到x轴的距离为h,则×3h=10,解得h=,点P在y轴正半轴时,P(0,),点P在y轴负半轴时,P(0,﹣),综上所述,点P的坐标为(0,)或(0,﹣).。
七年级下学期压轴题(平面直角坐标系的综合题)含答案

七年级下学期压轴题(平面直角坐标系的综合题)含答案七年级下学期压轴题(平面直角坐标系的综合题)1、如图,在长方形ABCD中,边AB=8,BC=4,以点O为原点,OA,OC所在的直线为y轴和x轴,建立直角坐标系.1) 点A的坐标为(2,4),则B点坐标为(10,4),C点坐标为(10,0);2) 当点P从C出发,以2单位/秒速度向CO方向移动(不过O点),Q从原点O出发以1单位/秒速度向OA方向移动(不过A点),P,Q同时出发,在移动过程中,四边形OPBQ的面积是否变化?若不变,求其值;若变化,求其变化范围.解:(1) a-2=0,a=2;b-3=0,b=3;c-4=0,c=4;故答案为:A(2,4),B(10,4),C(10,0);2) 设运动时间为t,则CP=2t,AQ=4-t。
S四边形OPBQ=S矩形ABCD-S△ABQ-S△BPC。
4×8-1/2×8(4-t)-1/2×4t。
32-16+4t-4t。
16。
所以,四边形OPBQ的面积不变,为16.2、如图,在平面直角坐标系中,已知A(2,a)、B(b,0)、C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)^2+c-4=0。
1) 满足条件的解为a=2,b=3,c=4;2) 四边形ABOP的面积为:S△ABC-1/2×(b-2)×|a-2|;3) 当m=0时,S△ACP=2S△ABC,此时P的坐标为(2,0);4) 当x=b/2时,S△BCQ=2S△ABC。
3、如图,△ABC的三个顶点位置分别是A(1,0),B(-2,3),C(-3,0).1) △ABC的面积为5;2) 三角形ACP的面积为:1/2×(a-1)×|m|;3) 当m=10时,S△ACP=2S△ABC,此时点P的坐标为(1,10);4) 当x=-3时,S△BCQ=2S△ABC。
4、如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)^2+b-2=4,过C作CB⊥x轴于B.解:由(a+2)^2+b-2=4得b=6-2a-a^2.因为BC⊥x轴,所以CB的斜率为0,即CB的方程为y=2.代入b=6-2a-a^2得a^2+2a-2=0,解得a=-1±√3.所以A的坐标为(-1+√3,0)或(-1-√3,0),C的坐标为(1-√3,2)或(1+√3,2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级下册数学直角坐标系压轴题
1.在平面直角坐标系中,O为坐标原点,点A的坐标为(a,3),点B的坐标为(b,6)。
如果AB与坐标轴平行,求AB的长度。
解析:由于AB与坐标轴平行,可以得到AB的长度为|6-3|=3.
如果a、b、c满足AC⊥x轴,垂足为C,BD⊥x轴,垂足为D,则需要求四边形ACDB的面积和△OAB的面积。
解析:首先可以得到点C的坐标为(a,0),点D的坐标为(b,0)。
因此,四边形ACDB的面积为|a-b|*3/2.连接OA和OB,可以得到△OAB的面积为1/2*3*|a-b|。
由于
6<2*△OAB<10,可以得到2<|a-b|<20/3,即a-b的取值范围为(2,20/3)。
2.在平面直角坐标系中,O为坐标原点,点A的坐标为(a,-a),点B的坐标为(b,c)。
如果a没有平方根,则
需要判断点A在第几象限,并说明理由。
解析:如果a没有平方根,则a不等于0.因此,可以得到
点A在第三象限,因为a为正,而y坐标为负。
如果点A到x轴的距离是点B到x轴距离的3倍,则需
要求点B的坐标。
解析:可以得到点A到x轴的距离为|a|,点B到x轴距
离为|c|。
由于|a|=3|c|,可以得到c=-a/3.因此,点B的坐标为(b,-a/3)。
如果△OAB的面积是△DAB面积的2倍,且点D的坐标
为(4,-2),则需要求点B的坐标。
解析:可以得到△OAB的面积为1/2*|a-b|^2,△DAB的
面积为1/2*|a-b|*6.因此,可以得到|a-b|=4.由于a-b不能等于0,可以得到a-b的取值为4或-4.如果a-b=4,则可以得到点B的
坐标为(a-4,-a+4)。
如果a-b=-4,则可以得到点B的坐标
为(a+4,-a-4)。
3.如图,在平面直角坐标系中,A(a,y1),D(6,4),将线段AD平移到BC,使B(x2,b),且a,b满足|2-a|=0.
解析:由于|2-a|=0,可以得到a=2.因此,点A的坐标为(2,y1)。
将线段AD平移到BC,可以得到点B的坐标为
(x2,y1+2)。
如果设点M(-3,n),且△ABM的面积为16,则需要
求n的值。
解析:可以得到△ABM的面积为1/2*|a-x2|*|y1+2-n|=16.
由于|2-a|=0,可以得到a=2.因此,可以得到|y1+2-n|=8/|x2-2|。
由于点A在第三象限,可以得到y1<0.因此,可以得到
n=y1+2-8/(x2-2)。
如果∠DAO=150°,设点P是x轴上的一动点(不与点A 重合),需要问∠APC与∠PCB存在什么具体的数量关系,并写出证明结论并证明。
解析:由于∠DAO=150°,可以得到点A在第三象限。
因此,点P在x轴的左侧。
设点P的坐标为(p,0),则可以得到点C的坐标为(a,0)。
由于AB平行于CD,可以得到
∠APC=∠PCB。
