matlab课后习题及答案详解(修改版)
matlab课后习题及答案详解

第1章 MATLAB概论1.1与其他计算机语言相比较,MATLAB语言突出的特点是什么?MATLAB具有功能强大、使用方便、输入简捷、库函数丰富、开放性强等特点。
1.2 MATLAB系统由那些部分组成?MATLAB系统主要由开发环境、MATLAB数学函数库、MATLAB语言、图形功能和应用程序接口五个部分组成。
1.3 安装MATLAB时,在选择组件窗口中哪些部分必须勾选,没有勾选的部分以后如何补安装?在安装MATLAB时,安装内容由选择组件窗口中个复选框是否被勾选来决定,可以根据自己的需要选择安装内容,但基本平台(即MATLAB选项)必须安装。
第一次安装没有选择的内容在补安装时只需按照安装的过程进行,只是在选择组件时只勾选要补装的组件或工具箱即可。
1.4 MATLAB操作桌面有几个窗口?如何使某个窗口脱离桌面成为独立窗口?又如何将脱离出去的窗口重新放置到桌面上?在MATLAB操作桌面上有五个窗口,在每个窗口的右上角有两个小按钮,一个是关闭窗口的Close按钮,一个是可以使窗口成为独立窗口的Undock按钮,点击Undock按钮就可以使该窗口脱离桌面成为独立窗口,在独立窗口的view菜单中选择Dock ……菜单项就可以将独立的窗口重新防止的桌面上。
1.5 如何启动M文件编辑/调试器?在操作桌面上选择“建立新文件”或“打开文件”操作时,M文件编辑/调试器将被启动。
在命令窗口中键入edit命令时也可以启动M文件编辑/调试器。
1.6 存储在工作空间中的数组能编辑吗?如何操作?存储在工作空间的数组可以通过数组编辑器进行编辑:在工作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输入修改内容即可。
1.7 命令历史窗口除了可以观察前面键入的命令外,还有什么用途?命令历史窗口除了用于查询以前键入的命令外,还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中。
MATLAB习题与答案详解
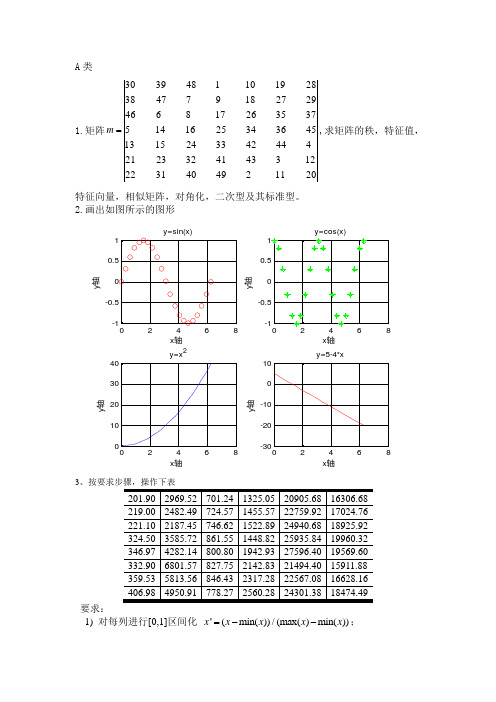
A 类1.矩阵20112494031221234341322321444423324151345363425161453735261786462927189747382819101483930=m ,求矩阵的秩,特征值,特征向量,相似矩阵,对角化,二次型及其标准型。
2.画出如图所示的图形y=sin(x)x 轴y 轴y=cos(x)x 轴y轴2468010203040y=x 2x 轴y 轴2468-30-20-10010y=5-4*xx 轴y轴3要求:1) 对每列进行[0,1]区间化 '(min())/(max()min())x x x x x =--;2) 把区间化后的表的右边3列,连接在左边3列下边,构成16行3列的表;3) 把16行3列进行转置,得到3行16列的表。
然后对列进行操作,把3行16列的表变成一列,后转置成一行,得到最终的结果。
4、下表为81)2) 把任意两点距离的表中,自己到自己的距离,转变成无穷大5.附件1给出了100个学生的学号和五门课程成绩。
1)求五门课总分最高分和最低分及相应学生的学号。
2)设计一个成绩查询系统,要求输入某学生的学号能够返回该学生各科成绩,总分以及在100个人中的名次。
B类(三选二)6.假设排列着100个乒乓球,由两个人轮流拿球装入口袋,能拿到第100个乒乓球的人为胜利者。
条件是:每次拿球者至少要拿1个,但最多不能超过5个,问:如果你是最先拿球的人,你该拿几个?以后怎么拿就能保证你能得到第100个乒乓球?7、模拟猫跑一条轨迹,轨迹为倒“8”字,轨迹如下:(条件自行拟定)8.当一个球从h米自由下落后,被地面弹起h1,再一次下落,直至平衡,如图所示,请模拟这个过程。
1 2 3 4 5 6 7 8x 4.22 7.92 6.56 8.49 6.79 7.43 6.55 7.06y 9.16 9.59 0.36 9.34 7.58 3.92 1.71 0.32。
matlab课后习题答案

习题二1.如何理解“矩阵就是MATLAB最基本得数据对象”?答:因为向量可以瞧成就是仅有一行或一列得矩阵,单个数据(标量)可以瞧成就是仅含一个元素得矩阵,故向量与单个数据都可以作为矩阵得特例来处理。
ﻩ因此,矩阵就是MATLAB最基本、最重要得数据对象。
2.设A与B就是两个同维同大小得矩阵,问:(1)A*B与A。
*B得值就是否相等?答:不相等。
(2)A。
/B与B。
\A得值就是否相等?答:相等。
(3)A/B与B\A得值就是否相等?答:不相等、(4)A/B与B\A所代表得数学含义就是什么?答:A/B等效于B得逆右乘A矩阵,即A*inv(B),而B\A等效于B矩阵得逆左乘A矩阵,即inv(B)*A。
3.写出完成下列操作得命令。
(1)将矩阵A第2~5行中第1,3, 5列元素赋给矩阵B。
答:B=A(2:5,1:2:5); 或B=A(2:5,[1 3 5])(2)删除矩阵A得第7号元素、答:A(7)=[](3)将矩阵A得每个元素值加30、答:A=A+30;(4)求矩阵A得大小与维数、答:size(A);ndims(A);(5)将向量t得0元素用机器零来代替。
答:t(find(t==0))=eps;(6)将含有12个元素得向量x转换成矩阵、答:reshape(x,3,4);(7)求一个字符串得ASCII码。
答:abs(‘123’); 或double(‘123');(8)求一个ASCII码所对应得字符、答:char(49);4.下列命令执行后,L1、L2、L3、L4得值分别就是多少?A=1:9;B=10-A;。
.、L1=A==B;L2=A<=5;L3=A〉3&A〈7;L4=find(A>3&A<7);答:L1得值为[0, 0, 0, 0, 1, 0, 0,0, 0]L2得值为[1, 1, 1, 1, 1,0, 0, 0, 0]L3得值为[0, 0, 0, 1,1, 1, 0, 0, 0]L4得值为[4,5, 6]5.已知完成下列操作:(1)取出A得前3行构成矩阵B,前两列构成矩阵C,右下角子矩阵构成矩阵D,B与C得乘积构成矩阵E。
matlab课后习题答案

习题二1.如何理解“矩阵是MATLAB 最基本的数据对象”?答:因为向量可以看成是仅有一行或一列的矩阵,单个数据(标量)可以看成是仅含一个元素的矩阵,故向量和单个数据都可以作为矩阵的特例来处理。
因此,矩阵是MATLAB 最基本、最重要的数据对象。
2.设A 和B 是两个同维同大小的矩阵,问:(1)A*B 和A.*B 的值是否相等?答:不相等。
(2) A./B 和B.\A 的值是否相等?答:相等。
(3)A/B 和B\A 的值是否相等?答:不相等。
(4)A/B 和B\A所代表的数学含义是什么?答:A/B等效于B的逆右乘A矩阵,即A*inv(B),而B\A等效于B 矩阵的逆左乘 A 矩阵,即inv(B)*A。
3.写出完成下列操作的命令。
(1)将矩阵A第2~5行中第1, 3, 5列元素赋给矩阵B。
答:B=A(2:5,1:2:5); 或B=A(2:5,[1 3 5])(2)删除矩阵A的第7号元素。
答:A(7)=[](3)将矩阵A的每个元素值加30。
答:A=A+30;(4)求矩阵A的大小和维数。
答:size(A);ndims(A);(5)将向量t的0 元素用机器零来代替。
答:t(find(t==0))=eps;(6)将含有12 个元素的向量x转换成34矩阵。
答:reshape(x,3,4);(7)求一个字符串的ASCII 码。
答:abs(‘123'); 或double(‘123');(8)求一个ASCII 码所对应的字符。
答:char(49);4.下列命令执行后,L1、L2、L3、L4的值分别是多少?A=1:9;B=10-A;...L1=A==B;L2=A<=5;L3=A>3&A<7;L4=find(A>3&A<7);答:L1的值为[0, 0, 0, 0, 1, 0, 0, 0, 0]L2的值为[1, 1, 1, 1, 1, 0, 0, 0, 0]L3的值为[0, 0, 0, 1, 1, 1, 0, 0, 0]L4的值为[4, 5, 6]5.已知23 10 -0.778 041 -45 65 5A=32 5 0 326 -9.54 54 3.14完成下列操作:(1)取出A 的前3 行构成矩阵B,前两列构成矩阵C,右下角32子矩阵构成矩阵D,B 与C的乘积构成矩阵E。
matlab课后习题答案(附图)

matlab课后习题答案(附图)习题2.1画出下列常见曲线的图形y (1)⽴⽅抛物线3x命令:syms x y;ezplot('x.^(1/3)')(2)⾼斯曲线y=e^(-X^2);命令:clearsyms x y;ezplot('exp(-x*x)')(3)笛卡尔曲线命令:>> clear>> syms x y;>> a=1;>> ezplot(x^3+y^3-3*a*x*y)(4)蔓叶线命令:>> clear>> syms x y;>> a=1ezplot(y^2-(x^3)/(a-x))(5)摆线:()()tsin-=,=-by1命令:>> clear>> t=0:0.1:2*pi;>> x=t-sin(t);>>y=2*(1-cos(t)); >> plot(x,y)7螺旋线命令:>> clear >> t=0:0.1:2*pi; >> x=cos(t); >> y=sin(t); >> z=t;>>plot3(x,y,z)(8)阿基⽶德螺线命令:clear>> theta=0:0.1:2*pi;>> rho1=(theta);>> subplot(1,2,1),polar(theta,rho1)(9) 对数螺线命令:cleartheta=0:0.1:2*pi;rho1=exp(theta);subplot(1,2,1),polar(theta,rho1)(12)⼼形线命令:>> clear >> theta=0:0.1:2*pi; >> rho1=1+cos(theta); >> subplot(1,2,1),polar(theta,rho1)练习2.21. 求出下列极限值(1)nnn n3→命令:>>syms n>>limit((n^3+3^n)^(1/n)) ans = 3(2))121(lim n n n n ++-+∞→命令:>>syms n>>limit((n+2)^(1/2)-2*(n+1)^(1/2)+n^(1/2),n,inf) ans = 0(3)x x x 2cot lim 0→命令:syms x ;>> limit(x*cot(2*x),x,0) ans = 1/2 (4))(coslimcm xx ∞→命令:syms x m ; limit((cos(m/x))^x,x,inf) ans = 1(5))111(lim 1--→exx x命令:syms x>> limit(1/x-1/(exp(x)-1),x,1) ans =(exp(1)-2)/(exp(1)-1) (6))(2lim x x xx -+∞>> limit((x^2+x)^(1/2)-x,x,inf)ans = 1/2练习2.41. 求下列不定积分,并⽤diff 验证:(1)+x dxcos 1>>Clear >> syms x y >> y=1/(1+cos(x)); >> f=int(y,x) f =tan(1/2*x) >> y=tan(1/2*x); >> yx=diff(y ,x); >> y1=simple(yx) y1 =1/2+1/2*tan(1/2*x)^2 (2)+exdx1clear syms x yy=1/(1+exp(x));f=int(y,x) f =-log(1+exp(x))+log(exp(x)) syms x yy=-log(1+exp(x))+log(exp(x)); yx=diff(y,x); y1=simple(yx) y1 = 1/(1+exp(x)) (3)dx x x ?sin 2syms x yy=x*sin(x)^2; >> f=int(y,x) f =x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2 clearsyms x y y=x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2; yx=diff(y,x); >> y1=simple(yx) y1 = x*sin(x)^2 (4)xdx ?sec3syms x y y=sec(x)^3;f=int(y,x) f =1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x)) clear syms x yy=1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x)); yx=diff(y,x); y1=simple(yx) y1 =1/cos(x)^32. 求下列积分的数值解 1)dx x-10clearsyms xy=int(x^(-x),x,0,1) y =int(x^(-x),x = 0 .. 1) vpa(y,10) ans =1.291285997 2)xdx e x cos3202?πclearsyms xy=int(exp(2*x)*cos(x)^3,x, clear syms xy=int((1/(2*pi)^(1/2))*exp(-x^2/2),x,0,1) y =7186705221432913/36028797018963968*erf(1/2*2^(1/2))*2^(1/2)*pi^(1/0,2*pi) y =22/65*exp(pi)^4-22/65vpa(ans,10)(3)dx xe21221-π>> clear >> syms x>> y=int(1/(2*pi)^(1/2)*exp(-x^2/2),0,1); >> vpa(y,14) ans =.341344746068552(4)>> clear >> syms x>> y=int(x*log(x^4)*asin(1/x^2),1,3); Warning: Explicit integral could not be found. > In sym.int at 58 >> vpa(y,14) ans = 2.45977212823752(5) >> clear >> syms x1判断下列级数的收敛性,若收敛,求出其收敛值。
matlab课后习题答案(1-9章)

1 数字1.5e2,1.5e3 中的哪个与1500相同吗?1.5e32 请指出如下5个变量名中,哪些是合法的?abcd-2xyz_33chan a 变量ABCDefgh 2、5是合法的。
3 在MATLAB 环境中,比1大的最小数是多少? 1+eps4 设 a = -8 , 运行以下三条指令,问运行结果相同吗?为什么?w1=a^(2/3) w2=(a^2)^(1/3) w3=(a^(1/3))^2w1 = -2.0000 + 3.4641i ;w2 = 4.0000 ;w3 =-2.0000 + 3.4641i 5 指令clear, clf, clc 各有什么用处?clear 清除工作空间中所有的变量。
clf 清除当前图形。
clc 清除命令窗口中所有显示。
第二章1 说出以下四条指令产生的结果各属于哪种数据类型,是“双精度”对象,还是“符号”符号对象?3/7+0.1双; sym(3/7+0.1)符; sym('3/7+0.1') 符;; vpa(sym(3/7+0.1)) 符;2 在不加专门指定的情况下,以下符号表达式中的哪一个变量被认为是自由符号变量. sym('sin(w*t)'),sym('a*exp(-X)'),sym('z*exp(j*th)') symvar(sym('sin(w*t)'),1) w a z3 (1)试写出求三阶方程05.443=-x 正实根的程序。
注意:只要正实根,不要出现其他根。
(2)试求二阶方程022=+-a ax x 在0>a 时的根。
(1)reset(symengine)syms x positive solve(x^3-44.5) ans =(2^(2/3)*89^(1/3))/2(2)求五阶方程022=+-a ax x 的实根 syms a positive %注意:关于x 的假设没有去除 solve(x^2-a*x+a^2)Warning: Explicit solution could not be found. > In solve at 83 ans =[ empty sym ]syms x clear syms a positivesolve(x^2-a*x+a^2) ans =a/2 + (3^(1/2)*a*i)/2 a/2 - (3^(1/2)*a*i)/24 观察一个数(在此用@记述)在以下四条不同指令作用下的异同。
matlab课后习题与答案

习题二1.如何理解“矩阵是MATLAB最基本的数据对象”?答:因为向量可以看成是仅有一行或一列的矩阵,单个数据(标量)可以看成是仅含一个元素的矩阵,故向量和单个数据都可以作为矩阵的特例来处理。
因此,矩阵是MATLAB最基本、最重要的数据对象。
2.设A和B是两个同维同大小的矩阵,问:(1)A*B和A.*B的值是否相等?答:不相等。
(2)A./B和B.\A的值是否相等?答:相等。
(3)A/B和B\A的值是否相等?答:不相等。
(4)A/B和B\A所代表的数学含义是什么?答:A/B等效于B的逆右乘A矩阵,即A*inv(B),而B\A等效于B矩阵的逆左乘A矩阵,即inv(B)*A。
3.写出完成下列操作的命令。
(1)将矩阵A第2~5行中第1, 3, 5列元素赋给矩阵B。
答:B=A(2:5,1:2:5); 或B=A(2:5,[1 3 5])(2)删除矩阵A的第7号元素。
答:A(7)=[](3)将矩阵A的每个元素值加30。
答:A=A+30;(4)求矩阵A的大小和维数。
答:size(A);ndims(A);(5)将向量t的0元素用机器零来代替。
答:t(find(t==0))=eps;(6)将含有12个元素的向量x转换成34矩阵。
答:reshape(x,3,4);(7)求一个字符串的ASCII码。
答:abs(‘123’); 或double(‘123’);(8) 求一个ASCII 码所对应的字符。
答:char(49);4. 下列命令执行后,L1、L2、L3、L4的值分别是多少?A=1:9;B=10-A;...L1=A==B;L2=A<=5;L3=A>3&A<7;L4=find(A>3&A<7);答:L1的值为[0, 0, 0, 0, 1, 0, 0, 0, 0]L2的值为[1, 1, 1, 1, 1, 0, 0, 0, 0]L3的值为[0, 0, 0, 1, 1, 1, 0, 0, 0]L4的值为[4, 5, 6]5. 已知23100.7780414565532503269.5454 3.14A -⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥-⎣⎦完成下列操作:(1) 取出A 的前3行构成矩阵B ,前两列构成矩阵C ,右下角32⨯子矩阵构成矩阵D ,B 与C 的乘积构成矩阵E 。
(完整版)MATLAB)课后实验答案[1]
![(完整版)MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/306ff29b690203d8ce2f0066f5335a8102d266cb.png)
(完整版)MATLAB)课后实验答案[1]实验⼀ MATLAB 运算基础1. 先求下列表达式的值,然后显⽰MATLAB ⼯作空间的使⽤情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =,其中2120.455i x +??=?- (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--L (4) 2242011122123t t z t t t t t ?≤=-≤,其中t =0:0.5:2.5 解:4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建⽴⼀个字符串向量,删除其中的⼤写字母。
解:(1) 结果:(2). 建⽴⼀个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:实验⼆ MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S=?,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对⾓阵,试通过数值计算验证2 2E R RS A O S +??=。
解: M ⽂件如下;5. 下⾯是⼀个线性⽅程组:1231112340.951110.673450.52111456x x x ??=???(1) 求⽅程的解。
(2) 将⽅程右边向量元素b 3改为0.53再求解,并⽐较b 3的变化和解的相对变化。
(3) 计算系数矩阵A 的条件数并分析结论。
解: M ⽂件如下:123d4e56g9实验三选择结构程序设计1. 求分段函数的值。
2226035605231x x x x y x x x x x x x ?+-<≠-?=-+≤<≠≠??--?且且及其他⽤if 语句实现,分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。
解:M ⽂件如下:2. 输⼊⼀个百分制成绩,要求输出成绩等级A、B、C、D、E。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1章MATLAB概论1.1与其他计算机语言相比较,MA TLAB语言突出的特点是什么?MATLAB具有功能强大、使用方便、输入简捷、库函数丰富、开放性强等特点。
1.2 MA TLAB系统由那些部分组成?MATLAB系统主要由开发环境、MA TLAB数学函数库、MATLAB语言、图形功能和应用程序接口五个部分组成。
1.3 安装MATLAB时,在选择组件窗口中哪些部分必须勾选,没有勾选的部分以后如何补安装?在安装MA TLAB时,安装内容由选择组件窗口中个复选框是否被勾选来决定,可以根据自己的需要选择安装内容,但基本平台(即MATLAB选项)必须安装。
第一次安装没有选择的内容在补安装时只需按照安装的过程进行,只是在选择组件时只勾选要补装的组件或工具箱即可。
1.4 MA TLAB操作桌面有几个窗口?如何使某个窗口脱离桌面成为独立窗口?又如何将脱离出去的窗口重新放置到桌面上?在MA TLAB操作桌面上有五个窗口,在每个窗口的右上角有两个小按钮,一个是关闭窗口的Close按钮,一个是可以使窗口成为独立窗口的Undock按钮,点击Undock按钮就可以使该窗口脱离桌面成为独立窗口,在独立窗口的view菜单中选择Dock ……菜单项就可以将独立的窗口重新防止的桌面上。
1.5 如何启动M文件编辑/调试器?在操作桌面上选择“建立新文件”或“打开文件”操作时,M文件编辑/调试器将被启动。
在命令窗口中键入edit命令时也可以启动M文件编辑/调试器。
1.6 存储在工作空间中的数组能编辑吗?如何操作?存储在工作空间的数组可以通过数组编辑器进行编辑:在工作空间浏览器中双击要编辑的数组名打开数组编辑器,再选中要修改的数据单元,输入修改内容即可。
1.7 命令历史窗口除了可以观察前面键入的命令外,还有什么用途?命令历史窗口除了用于查询以前键入的命令外,还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中。
1.8 如何设置当前目录和搜索路径,在当前目录上的文件和在搜索路径上的文件有什么区别?当前目录可以在当前目录浏览器窗口左上方的输入栏中设置,搜索路径可以通过选择操作桌面的file菜单中的Set Path菜单项来完成。
在没有特别说明的情况下,只有当前目录和搜索路径上的函数和文件能够被MATLAB运行和调用,如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件,如果没有特别说明,数据文件将存储在当前目录上。
1.9 在MA TLAB中有几种获得帮助的途径?在MATLAB 中有多种获得帮助的途径:(1)帮助浏览器:选择view 菜单中的Help 菜单项或选择Help 菜单中的MATLAB Help 菜单项可以打开帮助浏览器;(2)help 命令:在命令窗口键入“help ” 命令可以列出帮助主题,键入“help 函数名”可以得到指定函数的在线帮助信息;(3)lookfor 命令:在命令窗口键入“lookfor 关键词”可以搜索出一系列与给定关键词相关的命令和函数(4)模糊查询:输入命令的前几个字母,然后按Tab 键,就可以列出所有以这几个字母开始的命令和函数。
注意:lookfor 和模糊查询查到的不是详细信息,通常还需要在确定了具体函数名称后用help 命令显示详细信息。
第2章 MATLAB 矩阵运算基础2.1 在MA TLAB 中如何建立矩阵⎥⎦⎤⎢⎣⎡194375,并将其赋予变量a ?>> a=[5 7 3;4 9 1]2.2 有几种建立矩阵的方法?各有什么优点?可以用四种方法建立矩阵:①直接输入法,如a=[2 5 7 3],优点是输入方法方便简捷;②通过M 文件建立矩阵,该方法适用于建立尺寸较大的矩阵,并且易于修改;③由函数建立,如y=sin(x),可以由MA TLAB 的内部函数建立一些特殊矩阵;④通过数据文件建立,该方法可以调用由其他软件产生数据。
2.3 在进行算术运算时,数组运算和矩阵运算各有什么要求?进行数组运算的两个数组必须有相同的尺寸。
进行矩阵运算的两个矩阵必须满足矩阵运算规则,如矩阵a 与b 相乘(a*b )时必须满足a 的列数等于b 的行数。
2.4 数组运算和矩阵运算的运算符有什么区别?在加、减运算时数组运算与矩阵运算的运算符相同,乘、除和乘方运算时,在矩阵运算的运算符前加一个点即为数组运算,如a*b 为矩阵乘,a.*b 为数组乘。
2.5 计算矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡897473535与⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡638976242之和。
>> a=[5 3 5;3 7 4;7 9 8]; >> b=[2 4 2;6 7 9;8 3 6]; >> a+b ans = 2.6 求⎥⎦⎤⎢⎣⎡+-+-+-+-++=i 44i 93i 49i 67i 23i 57i 41i 72i 53i 84x 的共轭转置。
>> x=[4+8i 3+5i 2-7i 1+4i 7-5i;3+2i 7-6i 9+4i 3-9i 4+4i]; >> x ’ ans = 2.7 计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。
>> a=[6 9 3;2 7 5];>> b=[2 4 1;4 6 8]; >> a.*b ans =2.8 “左除”与“右除”有什么区别?在通常情况下,左除x=a\b 是a*x=b 的解,右除x=b/a 是x*a=b 的解,一般情况下,a\b ≠b/a 。
2.9 对于B AX =,如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ,求解X 。
>> A=[4 9 2;7 6 4;3 5 7]; >> B=[37 26 28]’; >> X=A\B X =2.10 已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ,分别计算a 的数组平方和矩阵平方,并观察其结果。
>> a=[1 2 3;4 5 6;7 8 9]; >> a.^2 ans = >> a^2 ans = 2.11 ⎥⎦⎤⎢⎣⎡-=463521a ,⎥⎦⎤⎢⎣⎡-=263478b ,观察a 与b 之间的六种关系运算的结果。
>> a=[1 2 3;4 5 6]; >> b=[8 –7 4;3 6 2]; >> a>b ans = >> a>=b ans = >> a<b ans = >> a<=b ans =>> a==b ans = >> a~=b ans =2.12 []7.0802.05--=a ,在进行逻辑运算时,a 相当于什么样的逻辑量。
相当于a=[1 1 0 1 1]。
2.13 在sin(x )运算中,x 是角度还是弧度?在sin(x)运算中,x 是弧度,MA TLAB 规定所有的三角函数运算都是按弧度进行运算。
2.14 角度[]604530=x ,求x 的正弦、余弦、正切和余切。
>> x=[30 45 60]; >> x1=x/180*pi; >> sin(x1) ans = >> cos(x1) ans = >> tan(x1) ans = >> cot(x1) ans =2.15 用四舍五入的方法将数组[2.4568 6.39823.9375 8.5042]取整。
>> b=[2.4568 6.3982 3.9375 8.5042]; >> round(b) ans =2.16 矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=728365219a ,分别对a 进行特征值分解、奇异值分解、LU 分解、QR 分解及Chollesky 分解。
>> [v,d]=eig(a,b) v = d =>> a=[9 1 2;5 6 3;8 2 7]; >> [u,s,v]=svd(a)u = s = v =>> [l,u]=lu(a) l = u =>> [q,r]=qr(a) q = r =>> c=chol(a) c = 2.17 将矩阵⎥⎦⎤⎢⎣⎡=5724a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵:(1)组合成一个4⨯3的矩阵,第一列为按列顺序排列的a 矩阵元素,第二列为按列顺序排列的b 矩阵元素,第三列为按列顺序排列的c 矩阵元素,即⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574(2)按照a 、b 、c 的列顺序组合成一个行矢量,即 []296531877254>> a=[4 2;5 7]; >> b=[7 1;8 3]; >> c=[5 9;6 2]; % (1)>> d=[a(:) b(:) c(:)] d = % (2)>> e=[a(:);b(:);c(:)]' e =或利用(1)中产生的d >> e=reshape(d,1,12)ans = 第3章 数值计算基础3.1 将(x -6)(x -3)(x -8)展开为系数多项式的形式。
>> a=[6 3 8]; >> pa=poly(a); >> ppa=poly2sym(pa) ppa =x^3-17*x^2+90*x-144 3.2 求解多项式x 3-7x 2+2x +40的根。
>> r=[1 -7 2 40]; >> p=roots(r);3.3 求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。
>> p=poly([1 2 3 4]); >> polyvalm(p,8) ans =3.4 计算多项式乘法(x 2+2x +2)(x 2+5x +4)。
>> c=conv([1 2 2],[1 5 4]) c =3.5 计算多项式除法(3x 3+13x 2+6x +8)/(x +4)。
>> d=deconv([3 13 6 8],[1 4]) d =3.6 对下式进行部分分式展开:27243645232345234+++++++++x x x x x x x x x>> a=[1 3 4 2 7 2]; >> b=[3 2 5 4 6]; >> [r,s,k]=residue(b,a) r = s = k =3.7 计算多项式9514124234++--x x x x 的微分和积分。
