MATlab课后习题答案周开利
MATLAB基础及其应用教程-周开利-邓春晖课后答案,第三章
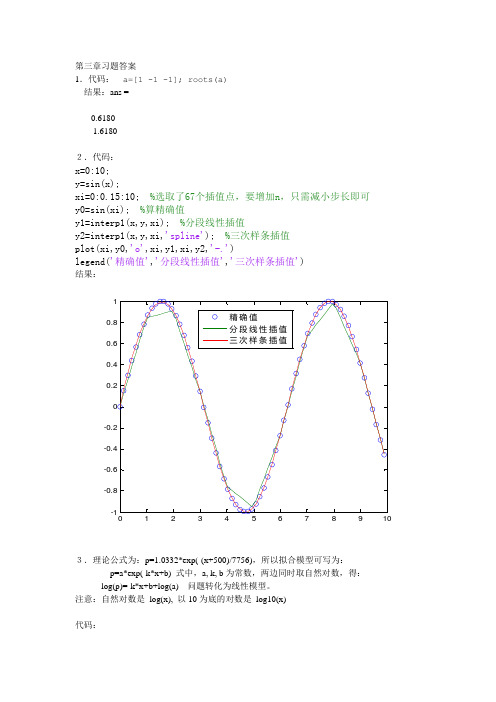
第三章习题答案1．代码：a=[1 -1 -1]; roots(a)结果：ans =-0.61801.6180２．代码：x=0:10;y=sin(x);xi=0:0.15:10; %选取了67个插值点，要增加n，只需减小步长即可y0=sin(xi); %算精确值y1=interp1(x,y,xi); %分段线性插值y2=interp1(x,y,xi,'spline'); %三次样条插值plot(xi,y0,'o',xi,y1,xi,y2,'-.')legend('精确值','分段线性插值','三次样条插值')结果：３．理论公式为：p=1.0332*exp(-(x+500)/7756)，所以拟合模型可写为：p=a*exp(-k*x+b) 式中，a, k, b为常数，两边同时取自然对数，得：log(p)=-k*x+b+log(a)问题转化为线性模型。
注意：自然对数是log(x), 以10为底的对数是log10(x)代码：clear;x=[0 300 600 1000 1500 2000];p=[0.9689 0.9322 0.8969 0.8519 0.7989 0.7491];lnp=log(p); %转化为 p 的自然对数值,模型转化为线性模型pk=polyfit(x,lnp,1); % 线性拟合,得到模型的斜率pk(1)和常数pk(2) 模型为: p=exp(pk(1)*x)*exp(pk(2))xi=0:50:2000;p0=1.0332*exp(-(xi+500)/7756); %理论值p1=exp(pk(1)*xi+pk(2)); %拟合模型值p2=interp1(x,p,xi,'spline'); %三次样条插值plot(x,p,'p',xi,p0,xi,p1,'--',xi,p2,'-.');legend('测量值','理论值','拟合值','三次样条值');format long % 数据显示格式为15位有效数字x2=0:200:2000 % 取10个点，比较差异pp1=1.0332*exp(-(x2+500)/7756) %理论值pp2=exp(pk(1)*x2+pk(2)) % 拟合值pp3=interp1(x,p,x2,'spline') % 样条插值err1=sum(abs(pp2-pp1).^2) % 拟合值的误差绝对值总和err2=sum(abs(pp3-pp1).^2) % 样条值的误差绝对值总和结果：0200400600800100012001400160018002000从图像上，都符合得很好，但很难看出差异。
matlab课后习题答案 (附图)
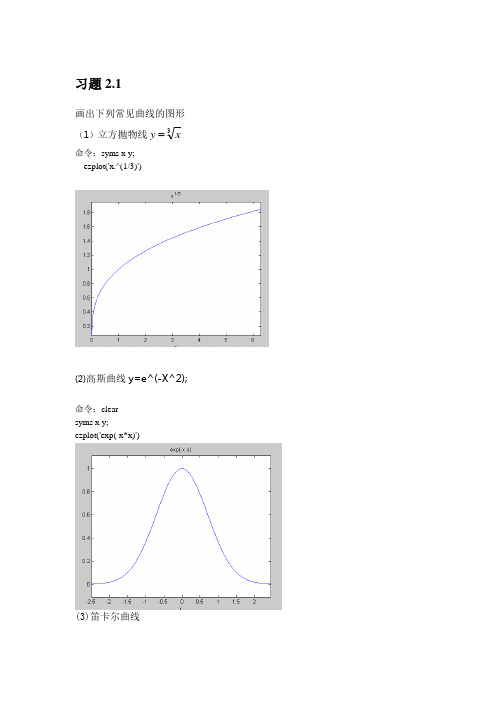
习题2.1画出下列常见曲线的图形y （1）立方抛物线3x 命令：syms x y;ezplot('x.^(1/3)')(2)高斯曲线y=e^(-X^2);命令：clearsyms x y;ezplot('exp(-x*x)')(3)笛卡尔曲线命令：>> clear>> syms x y;>> a=1;>> ezplot(x^3+y^3-3*a*x*y)(4)蔓叶线命令：>> clear>> syms x y;>> a=1 ezplot(y^2-(x^3)/(a-x))(5)摆线:()()t b y t t a x cos 1,sin -=-=命令：>> clear>> t=0:0.1:2*pi;>> x=t-sin(t);>>y=2*(1-cos(t)); >> plot(x,y)7螺旋线命令：>> clear >> t=0:0.1:2*pi; >> x=cos(t); >> y=sin(t);>> z=t;>>plot3(x,y,z) (8)阿基米德螺线>> theta=0:0.1:2*pi;>> rho1=(theta);>> subplot(1,2,1),polar(theta,rho1)(9) 对数螺线命令：cleartheta=0:0.1:2*pi;rho1=exp(theta);subplot(1,2,1),polar(theta,rho1) (12)心形线>> theta=0:0.1:2*pi;>> rho1=1+cos(theta);>> subplot(1,2,1),polar(theta,rho1)练习2.21. 求出下列极限值（1）nn n n 3lim 3+∞→命令：>>syms n>>limit((n^3+3^n)^(1/n))ans =3（2）)121(lim n n n n ++-+∞→命令：>>syms n>>limit((n+2)^(1/2)-2*(n+1)^(1/2)+n^(1/2),n,inf)ans =（3）x x x 2cot lim 0→命令：syms x ；>> limit(x*cot(2*x),x,0)ans =1/2（4）)(cos lim c m xx ∞→ 命令：syms x m ；limit((cos(m/x))^x,x,inf)ans =1（5）)111(lim 1--→e x x x 命令：syms x>> limit(1/x-1/(exp(x)-1),x,1)ans =(exp(1)-2)/(exp(1)-1)（6）)(2lim x x x x -+∞→命令：syms x>> limit((x^2+x)^(1/2)-x,x,inf)ans =1/2练习2.41. 求下列不定积分，并用diff 验证：（1）⎰+xdx cos 1 >>Clear>> syms x y>> y=1/(1+cos(x));>> f=int(y,x)f =tan(1/2*x)>> y=tan(1/2*x);>> yx=diff(y,x);>> y1=simple(yx)y1 =1/2+1/2*tan(1/2*x)^2 (2)⎰+e x dx 1clearsyms x yy=1/(1+exp(x));f=int(y,x)f =-log(1+exp(x))+log(exp(x))syms x yy=-log(1+exp(x))+log(exp(x));yx=diff(y,x);y1=simple(yx)y1 =1/(1+exp(x))(3)dx x x ⎰sin 2syms x yy=x*sin(x)^2;>> f=int(y,x)f =x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2clearsyms x y y=x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2;yx=diff(y,x);>> y1=simple(yx)y1 =x*sin(x)^2(4) xdx ⎰sec 3syms x yy=sec(x)^3;f=int(y,x)f =1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x))clearsyms x yy=1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x));yx=diff(y,x);y1=simple(yx)y1 =1/cos(x)^32. 求下列积分的数值解1）dx x x ⎰-10clearsyms xy=int(x^(-x),x,0,1)y =int(x^(-x),x = 0 .. 1)vpa(y,10)ans =1.2912859972）xdx e x cos 3202⎰πclearsyms xy=int(exp(2*x)*cos(x)^3,x, clearsyms xy=int((1/(2*pi)^(1/2))*exp(-x^2/2),x,0,1)y =7186705221432913/36028797018963968*erf(1/2*2^(1/2))*2^(1/2)*pi^(1/0,2*pi) y =22/65*exp(pi)^4-22/65vpa(ans,10)(3) dx x e 210221-⎰π>> clear>> syms x>> y=int(1/(2*pi)^(1/2)*exp(-x^2/2),0,1);>> vpa(y,14)ans =.341344746068552（4）>> clear>> syms x>> y=int(x*log(x^4)*asin(1/x^2),1,3);Warning: Explicit integral could not be found.> In sym.int at 58>> vpa(y,14)ans =2.45977212823752（5）>> clear>> syms x>> y=int(1/(2*pi)^(1/2)*exp(-x^2/2),-inf,inf);>> vpa(y,14)ans =.99999999999999练习2.51判断下列级数的收敛性，若收敛，求出其收敛值。
matlab课后习题解答第二章
matlab课后习题解答第⼆章第2章符号运算习题2及解答1 说出以下四条指令产⽣的结果各属于哪种数据类型，是“双精度”对象，还是“符号”符号对象3/7+; sym(3/7+; sym('3/7+'); vpa(sym(3/7+)〖⽬的〗不能从显⽰形式判断数据类型，⽽必须依靠class指令。
〖解答〗c1=3/7+c2=sym(3/7+c3=sym('3/7+')c4=vpa(sym(3/7+)Cs1=class(c1)Cs2=class(c2)Cs3=class(c3)Cs4=class(c4)c1 =c2 =37/70c3 =c4 =Cs1 =doubleCs2 =symCs3 =symCs4 =sym2 在不加专门指定的情况下，以下符号表达式中的哪⼀个变量被认为是⾃由符号变量.sym('sin(w*t)'),sym('a*exp(-X)'),sym('z*exp(j*th)')〖⽬的〗理解⾃由符号变量的确认规则。
〖解答〗symvar(sym('sin(w*t)'),1)ans =wsymvar(sym('a*exp(-X)'),1)ans = asymvar(sym('z*exp(j*th)'),1) ans = z5求符号矩阵=333231232221131211a a a a a a a a a A 的⾏列式值和逆，所得结果应采⽤“⼦表达式置换”简洁化。
〖⽬的〗理解subexpr 指令。
〖解答〗A=sym('[a11 a12 a13;a21 a22 a23;a31 a32 a33]')DA=det(A) IA=inv(A);[IAs,d]=subexpr(IA,d) A =[ a11, a12, a13] [ a21, a22, a23] [ a31, a32, a33] DA =a11*a22*a33 - a11*a23*a32 - a12*a21*a33 + a12*a23*a31 + a13*a21*a32 - a13*a22*a31 IAs =[ d*(a22*a33 - a23*a32), -d*(a12*a33 - a13*a32), d*(a12*a23 - a13*a22)] [ -d*(a21*a33 - a23*a31), d*(a11*a33 - a13*a31), -d* (a11*a23 - a13*a21)] [ d*(a21*a32 - a22*a31), -d*(a11*a32 - a12*a31), d*(a11*a22 - a12*a21)] d =1/(a11*a22*a33 - a11*a23*a32 - a12*a21*a33 + a12*a23*a31 + a13*a21*a32 - a13*a22*a31)8（1）通过符号计算求t t y sin )(=的导数dtdy。
（完整版）MATLAB）课后实验答案[1]
![（完整版）MATLAB）课后实验答案[1]](https://img.taocdn.com/s3/m/306ff29b690203d8ce2f0066f5335a8102d266cb.png)
（完整版）MATLAB）课后实验答案[1]实验⼀ MATLAB 运算基础1. 先求下列表达式的值，然后显⽰MATLAB ⼯作空间的使⽤情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =，其中2120.455i x +??=?- (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--L (4) 2242011122123t t z t t t t t ?≤=-≤，其中t =0:0.5:2.5 解：4. 完成下列操作：(1) 求[100,999]之间能被21整除的数的个数。
(2) 建⽴⼀个字符串向量，删除其中的⼤写字母。
解：(1) 结果：(2). 建⽴⼀个字符串向量例如：ch='ABC123d4e56Fg9';则要求结果是：实验⼆ MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S=?，其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对⾓阵，试通过数值计算验证2 2E R RS A O S +??=。
解: M ⽂件如下；5. 下⾯是⼀个线性⽅程组：1231112340.951110.673450.52111456x x x ??=???(1) 求⽅程的解。
(2) 将⽅程右边向量元素b 3改为0.53再求解，并⽐较b 3的变化和解的相对变化。
(3) 计算系数矩阵A 的条件数并分析结论。
解： M ⽂件如下：123d4e56g9实验三选择结构程序设计1. 求分段函数的值。
2226035605231x x x x y x x x x x x x ?+-<≠-?=-+≤<≠≠??--?且且及其他⽤if 语句实现，分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。
解：M ⽂件如下：2. 输⼊⼀个百分制成绩，要求输出成绩等级A、B、C、D、E。
MATLAB基础及其应用教程周开利邓春晖课后答案
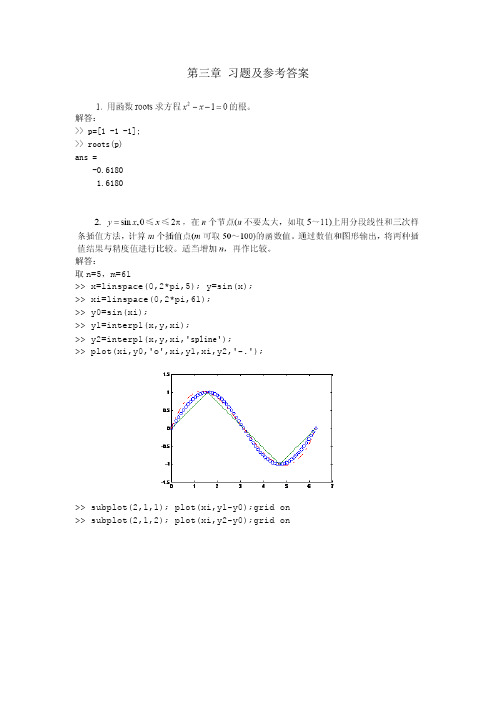
第三章习题及参考答案解答：>> p=[1 -1 -1];>> roots(p)ans =-0.61801.6180解答：取n=5，m=61>> x=linspace(0,2*pi,5); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on >> subplot(2,1,2); plot(xi,y2-y0);grid on分段线性和三次样条插值方法与精确值之差取n=11，m=61>> x=linspace(0,2*pi,11); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on>> subplot(2,1,2); plot(xi,y2-y0);grid on分段线性和三次样条插值方法与精确值之差解答：>> x=[0,300,600,1000,1500,2000];>> y=[0.9689,0.9322,0.8969,0.8519,0.7989,0.7491]; >> xi=0:100:2000;>> y0=1.0332*exp(-(xi+500)/7756);>> y1=interp1(x,y,xi,'spline');>> p3=polyfit(x,y,3);>> y3=polyval(p3,xi);>> subplot(2,1,1);plot(xi,y0,'o',xi,y1,xi,y3,'-.'); >> subplot(2,1,2);plot(xi,y1-y0,xi,y3-y0);grid on插值和拟合方法相比较，都合理，误差也相近。
MATLAB基础及其应用教程周开利邓春晖课后答案
第三章习题及参考答案解答：>> p=[1 -1 -1];>> roots(p)ans =-0.61801.6180解答：取n=5，m=61>> x=linspace(0,2*pi,5); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on>> subplot(2,1,2); plot(xi,y2-y0);grid on分段线性和三次样条插值方法与精确值之差取n=11，m=61>> x=linspace(0,2*pi,11); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on>> subplot(2,1,2); plot(xi,y2-y0);grid on分段线性和三次样条插值方法与精确值之差解答：>> x=[0,300,600,1000,1500,2000];>> y=[0.9689,0.9322,0.8969,0.8519,0.7989,0.7491]; >> xi=0:100:2000;>> y0=1.0332*exp(-(xi+500)/7756);>> y1=interp1(x,y,xi,'spline');>> p3=polyfit(x,y,3);>> y3=polyval(p3,xi);>> subplot(2,1,1);plot(xi,y0,'o',xi,y1,xi,y3,'-.');>> subplot(2,1,2);plot(xi,y1-y0,xi,y3-y0);grid on插值和拟合方法相比较，都合理，误差也相近。
matlab课后习题答案
第2章 MATLAB 矩阵运算基础2.1 在MA TLAB 中如何建立矩阵⎥⎦⎤⎢⎣⎡194375，并将其赋予变量a ？ >> a=[5 7 3;4 9 1]2.5 计算矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡897473535与⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡638976242之和。
>> a=[5 3 5;3 7 4;7 9 8]; >> b=[2 4 2;6 7 9;8 3 6];>> a+bans =7 7 7 9 14 13 15 12 142.6 求⎥⎦⎤⎢⎣⎡+-+-+-+-++=i 44i 93i 49i 67i 23i 57i 41i 72i 53i 84x 的共轭转置。
>> x=[4+8i 3+5i 2-7i 1+4i 7-5i;3+2i 7-6i 9+4i 3-9i 4+4i]; >> x’ans =4.0000 - 8.0000i 3.0000 - 2.0000i 3.0000 -5.0000i 7.0000 +6.0000i 2.0000 +7.0000i 9.0000 - 4.0000i 1.0000 - 4.0000i 3.0000 + 9.0000i 7.0000 + 5.0000i 4.0000 - 4.0000i2.7 计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。
>> a=[6 9 3;2 7 5];>> b=[2 4 1;4 6 8]; >> a.*b ans =12 36 3 8 42 402.9 对于B AX =，如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ，求解X 。
>> A=[4 9 2;7 6 4;3 5 7];>> B=[37 26 28]’;-0.5118 4.0427 1.33182.10 已知：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ，分别计算a 的数组平方和矩阵平方，并观察其结果。
matlab课后习题答案
习题二之阳早格格创做1.怎么样明白“矩阵是MATLAB最基础的数据对于象”？问：果为背量不妨瞅成是仅有一止或者一列的矩阵，单个数据（标量）不妨瞅成是仅含一个元素的矩阵，故背量战单个数据皆不妨动做矩阵的惯例去处理.果此，矩阵是MATLAB最基础、最要害的数据对于象.2.设A战B是二个共维共大小的矩阵，问：(1)A*B战A.*B的值是可相等？问：没有相等.(2)A./B战B.\A的值是可相等？问：相等.(3)A/B战B\A的值是可相等？问：没有相等.(4)A/B战B\A所代表的数教含意是什么？问：A/B等效于B的顺左乘A矩阵，即A*inv(B)，而B\A等效于B矩阵的顺左乘A矩阵，即inv(B)*A.3.写出完毕下列支配的下令.(1)将矩阵A第2~5止中第1, 3, 5列元素赋给矩阵B.问：B=A(2:5,1:2:5); 或者B=A(2:5,[1 3 5])(2)简略矩阵A的第7号元素.问：A(7)=[](3)将矩阵A的每个元素值加30.问：A=A+30;(4)供矩阵A的大小战维数.问：size(A);ndims(A);(5)将背量t的0元素用呆板整去代替.问：t(find(t==0))=eps;(6)将含有12个元素的背量x变换成34 矩阵.问：reshape(x,3,4);(7)供一个字符串的ASCII码.问：abs(‘123’); 或者double(‘123’);(8)供一个ASCII码所对于应的字符.问：char(49);4.下列下令真止后，L1、L2、L3、L4的值分别是几？A=1:9;B=10-A;...L1=A==B;L2=A<=5;L3=A>3&A<7;L4=find(A>3&A<7);问：L1的值为[0, 0, 0, 0, 1, 0, 0, 0, 0]L2的值为[1, 1, 1, 1, 1, 0, 0, 0, 0]L3的值为[0, 0, 0, 1, 1, 1, 0, 0, 0]L4的值为[4, 5, 6]5.已知完毕下列支配：(1)与出A的前3止形成矩阵B，前二列形成矩阵C，左下角32⨯子矩阵形成矩阵D，B与C的乘积形成矩阵E.问：B=A(1:3,:);C=A(:,1:2);D=A(2:4,3:4);E=B*C;(2)分别供E<D、E&D、E|D、~E|~D战find(A>=10&A<25).问：E<D=010001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，E&D=110111⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，E|D=111111⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，~E|~D=001000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦find(A>=10&A<25)=[1; 5].6.当A=[34, NaN, Inf, -Inf, -pi, eps, 0]时，分解下列函数的真止截止：all(A)，any(A)，isnan(A)，isinf(A)，isfinite(A).问：all(A)的值为0any(A)的值为1isnan(A)的值为[0, 1, 0, 0, 0, 0, 0]isinf(A)的值为[0, 0, 1, 1, 0, 0, 0]isfinite(A)的值为[1, 0, 0,0, 1, 1, 1]7.用结构体矩阵去保存5名教死的基础情况数据，每名教死的数据包罗教号、姓名、博业战6门课程的结果.问：student(1).id='0001';student(1).name='Tom';student(1).major='computer';student(1).grade=[89,78,67,90,86,85];8.修坐单元矩阵B并回问有闭问题.B{1,1}=1;B{1,2}='Brenden';B{2,1}=reshape(1:9,3,3);B{2,2}={12,34,2;54,21,3;4,23,67};(1)size(B)战ndims(B)的值分别是几？问：size(B)的值为2,2.ndims(B)的值为2.(2)B(2)战B(4)的值分别是几？问：B(2)=147258369⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦，B(4)=[12][34][2][54][21][3][4][23][67]⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦(3)B(3)=[]战B{3}=[]真止后，B的值分别是几？问：当真止B(3)=[]后，B={1, [1, 4, 7; 2, 5, 8; 3, 6, 9], {12, 34, 2; 54, 21, 3; 4, 23, 67}}当真止B{3}=[]后，B={1,[]; [1, 4, 7; 2, 5, 8; 3, 6, 9],{12, 34, 2; 54, 21, 3; 4, 23, 67}}习题三1.写出完毕下列支配的下令.(1)修坐3阶单位矩阵A.问：A=eye(3);(2)修坐5×6随机矩阵A，其元素为[100,200]范畴内的随机整数.问：round(100+(200-100)*rand(5,6));(3)爆收均值为1，圆好为0.2的500个正态分散的随机数.问：1+sqrt(0.2)*randn(5,100);(4)爆收战A共样大小的幺矩阵.问：ones(size(A));(5)将矩阵A对于角线的元素加30.问：A+eye(size(A))*30;(6)从矩阵A提与主对于角线元素，并以那些元素形成对于角阵B.问：B=diag(diag(A));2.使用函数，真止圆阵左旋90o或者左旋90o的功能.比圆，本矩阵为A，A左旋后得到B，左旋后得到C.问：B=rot90(A);C=rot90(A,-1);3.修坐一个圆阵A，供A的顺矩阵战A的止列式的值，并考证A与A-1是互顺的.问：A=rand(3)*10;B=inv(A);C=det(A);先估计B*A，再估计A*B，由估计可知B*A=A*B，即A·A-1=A-1·A是互顺.4.供底下线性圆程组的解.问：A=[4,2,-1;3,-1,2;12,3,0];b=[2;10;8];x=inv(A)*b圆程组的解为x=6.000026.666727.3333 -⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦5.供下列矩阵的主对于角线元素、上三角阵、下三角阵、秩、范数、条件数战迹.(1)112351423052111509A-⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦(2)0.434328.9421B⎡⎤=⎢⎥-⎣⎦问：(1)与主对于角线元素：diag(A);上三角阵：triu(A)；下三角阵：tril(A);秩：rank(A);范数：norm(A,1); 或者 norm(A);或者 norm(A,inf);条件数：cond(A,1); 或者 cond(A,2); 或者 cond(A,inf)迹：trace(A);(2)【请参照(1)】.6.供矩阵A的特性值战相映的特性背量.问：[V,D]=eig(A);习题四1.从键盘输进一个4位整数，按如下准则加稀后输出.加稀准则：每位数字皆加上7，而后用战除以10的余数与代该数字；再把第一位与第三位接换，第二位与第四位接换.问：a=input('请输进4位整数：');A=[a/1000,a/100,a/10,a];A=fix(rem(A,10));A=rem(A+7,10);b=A(3)*1000+A(4)*100+A(1)*10+A(2);disp(['加稀后的值为：',num2str(b)]);2.分别用if语句战switch语句真止以下估计，其中a、b、c 的值从键盘输进.问：(1) 用if语句真止估计：a=input('请输进a的值：');b=input('请输进b的值：');c=input('请输进c的值：');x=input('请输进x的值：');y=a*x^2+b*x+c;endy=a*((sin(b))^c)+x;endy=log(abs(b+c/x));enddisp(['y=',num2str(y)]);(2) 用switch语句真止估计：a=input('请输进a的值：');b=input('请输进b的值：');c=input('请输进c的值：');x=input('请输进x的值：');switch fix(x/0.5)case {1,2}y=a*x^2+b*x+c;case num2cell(3:6)y=a*((sin(b))^c)+x;case num2cell(7:10)y=log(abs(b+c/x));enddisp(['y=',num2str(y)]);3.爆收20个二位随机整数，输出其中小于仄衡值的奇数.问：A=fix(10+89*rand(1,20));sum=0;for i=1:20sum=sum+A(i);endB=A(find(A<(sum/20)));C=B(find(rem(B,2)==0));disp(C);4. 输进20个数，供其中最大数战最小数.央供分别用循环结媾战调用MATLAB 的max 函数、min 函数去真止. 问：(1) 用循环结构真止：v_max=0;v_min=0;for i=1:20x=input(['请输进第', num2str(i), '数：']);if x>v_maxv_max=x;end;if x<v_minv_min=x;end;enddisp(['最大数为：', num2str(v_max)]);disp(['最小数为：', num2str(v_min)]);(2) 用max 函数、min 函数真止：for i=1:5A(i)=input(['请输进第', num2str(i), '数：']);enddisp(['最大数为：', num2str(max(A))]);disp(['最小数为：', num2str(min(A))]);5. 已知：236312222s =+++++，分别用循环结媾战调用MATLAB 的sum 函数供s 的值.问：(1) 用循环结构真止：s=0;for i=0:63s=s+2^i;ends(2) 调用sum函数真止：s=0:63;s=2.^s;sum(s)6.当n分别与100、1000、10000时，供下列各式的值.(1)111111(1)(ln2) 234nn+-+-++-+=(2)1111() 3574π-+-+=(3) 11111() 4166443n+++++=(4)224466(2)(2)133557(21)(21)2n nn nπ⎛⎫⨯⨯⨯⨯⎛⎫⎛⎫⎛⎫⎛⎫=⎪⎪⎪⎪ ⎪⨯⨯⨯-⨯+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭央供分别用循环结媾战背量运算（使用sum或者prod函数）去真止.问：(1) 用循环结构真止：sum=0;for k=1:100sum=sum+(-1)^(k+1)/k;endsum使用sum函数：x=[];for k=1:10000x=[x, (-1)^(k+1)/k];endsum(x)(2)用循环结构真止：sum=0;for k=1:100sum=sum+(-1)^(k+1)/(2*k-1);endsum使用sum函数：x=[];for k=1:100x=[x, (-1)^(k+1)/(2*k-1)];endsum(x)(3)用循环结构真止：sum=0;for k=1:100sum=sum+1/(4^k);endsum使用sum函数真止：x=[];for k=1:100x=[x, 1/(4^k)];endsum(x)(4)用循环结构真止：t=1;for k=1:100t=t*(((2*k)*(2*k))/((2*k-1)*(2*k+1)));endt使用prod函数真止：x=[];for k=1:100x=[x, ((2*k)*(2*k))/((2*k-1)*(2*k+1))];endprod(x)7. 编写一个函数文献，供小于任性自然数n的斐波那契（Fibnacci）数列各项.斐波那契数列定义如下：问：function x=fibnacci(n)for i=1:nif i<=2x(i)=1;elsex(i)=x(i-1)+x(i-2);endend8.编写一个函数文献，用于供二个矩阵的乘积战面乘，而后正在下令文献中调用该函数.问：函数文献myfnc.m：function [x, y]=myfnc(A, B)tryx=A*B;catchx=[];endy=A.*B;下令文献myexe.m：A=input('请输进矩阵A：');B=input('请输进矩阵B：');[x, y]=myfnc(A, B);if length(x)==0display('二矩阵的维数没有匹配，无法举止乘积运算！');disp('矩阵A 战矩阵B 的乘积为：'); xenddisp('矩阵A 战矩阵B 的面乘为：'); y9. 先用函数的递归调用定义一个函数文献供1n m i i =∑，而后调用该函数文献供100501021111k k k k k k ===++∑∑∑. 问：函数文献myfnc.m ：function sum=myfnc(n, m)if n<=1sum=1;elsesum= myfnc (n-1, m)+n^m;end正在下令窗心中调用myfnc.m 文献，估计100501021111k k k k k k ===++∑∑∑： sum=myfnc(100, 1)+myfnc(50, 2)+myfnc(10,-1) 10.写出下列步调的输出截止.① s=0;a=[12,13,14;15,16,17;18,19,20;21,22,23]; for k=afor j=1:4if rem(k(j),2)~=0s=s+k(j);endendends问：真止截止为②下令文献exe.m真止后的截止为：x =41220y=2 4 6。
matlab课后答案完整版
matlab课后答案完整版ones表⽰1矩阵zeros表⽰0矩阵ones(4)表⽰4x4的1矩阵zeros(4)表⽰4x4的0矩阵zeros(4,5)表⽰4x5的矩阵eye(10,10)表⽰10x10的单位矩阵rand(4,5)表⽰4x5的伴随矩阵det(a)表⽰计算a的⾏列式inv(a)表⽰计算a的逆矩阵Jordan(a)表⽰求a矩阵的约当标准块rank(a)表⽰求矩阵a的秩[v,d]=eig(a)对⾓矩阵b=a’表⽰求a矩阵的转置矩阵sqrt表⽰求平⽅根exp表⽰⾃然指数函数log⾃然对数函数abs绝对值第⼀章⼀、5（1）b=[97 67 34 10;-78 75 65 5;32 5 -23 -59]; >> c=[97 67;-78 75;32 5;0 -12]; >> d=[65 5;-23 -59;54 7];>> e=b*ce =5271 11574-11336 6641978 3112（2）a=50:1:100⼆、1 、x=-74;y=-27;z=(sin(x.^2+y.^2))/(sqrt(tan(abs(x+y)))+pi) z =-0.09012、a=-3.0:0.1:3.0;>> b=exp(-0.3*a).*sin(a+0.3)y =0.7218 1.0474-0.2180 1.15624、a*b表⽰a矩阵和b矩阵相乘a.*b表⽰a矩阵和b矩阵单个元素相乘A(m,n)表⽰取a矩阵第m⾏，第n列A(m,:)表⽰取a矩阵第m⾏的全部元素A(:,n)表⽰取a矩阵的第n列全部元素A./B表⽰a矩阵除以b矩阵的对应元素，B.\A等价于A./BA.^B表⽰两个矩阵对应元素进⾏乘⽅运算A.^2表⽰a中的每个元素的平⽅A^2表⽰A*A例：x=[1,2,3];y=[4,5,6];z=x.^yz=1 32 729指数可以是标量（如y=2）.底数也可以是标量（如x=2）5、a=1+2i;>> b=3+4i;>> c=exp((pi*i)/6)c =0.8660 + 0.5000id=c+a*b/(a+b)d =1.6353 + 1.8462i第⼆章⼆、4、（1）y=0;k=0;>> while y<3k=k+1;>> display([k-1,y-1/(2*k-1)])ans =56.0000 2.9944第三章⼆1（1） x=0:pi/10:2*pi; >> y=x-x.^3/6; >> plot(x,y)1234567-40-35-30-25-20-15-10-505（2）x=0:pi/10:2*pi; y=(exp(-x.^2/2))/2*pi;plot(x,y)012345670.20.40.60.811.21.41.6（3）x=-8:0.01:8; y=sqrt((64-x.^2)/2);plot(x,y)-8-6-4-2024680123456（4）t=0:0.1:8*pi; >> x=t.*sin(t); >> y=t.*cos(t);-25-20-15-10-50510152025-30-20-10102030例3.4x=0:pi/100:2*pi; y1=exp(-0.5*x);y2=exp(-0.5*x).*sin(2*x); plot(x,y1,x,y2)>> title('x from 0 to 2{\pi} '); >> xlabel('variable x'); >> ylabel('variable y'); >> text(1.5,0.5,'曲线y1=e^(-0.5x)'); >> text(3,0.1,'曲线y2=cos(4{\pi}x)e^{-0.5x}'); >> legend('y1','y2')1234567-0.4-0.20.20.40.60.81x from 0 to 2πvariable xv a r i a b l e y曲线y1=e (-0.5x)曲线y2=cos(4πx)e -0.5xy1y22、(1)y1=2*x-0.5;t=linspace(0,pi,100); x=sin(3*t).*cos(t); y=sin(3*t).*sin(t);>> k=find(abs(y-x)<1e-2); >> t1=t(k) t1 =0 0.7933 1.04722.0944>> z=sin(3.*(t1)).*cos(t1) z =0 0.4841 0.0000 0.0000 -0.0000>> plot(t,x,t,y,'k:',t1,z,'bp');0.511.522.533.5-1-0.8-0.6-0.4-0.200.20.40.60.81（2）subplot(1,2,1); >> scatter(x1,y1,10)； >> title('y=2x-0.5')； >> subplot(1,2,2); >> scatter(x,y,10)-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.63、subplot(1,2,1); x=0:0.01:pi; y=sin(1./x); plot(x,y)subplot(1,2,2);fplot('sin(1./x)',[1,100])1234-1-0.8-0.6-0.4-0.200.20.40.60.81204060801000.10.20.30.44、t=0:pi:2*pi; y=1./(1+exp(-t));subplot(2,2,1);%图形窗⼝的分割bar(t,'group'); %绘制柱形图（分组） subplot(2,2,2);barh(t,'stack');%绘制柱形图（堆积） subplot(2,2,3);loglog(t,y); %函数使⽤全对数坐标，x,y 均采⽤常⽤对数刻度 subplot(2,2,4); semilogy(t,y); %函数使⽤半对数坐标，y 轴为常⽤对数刻度，x 轴仍为线性刻度1230246802468123100.5100.710-0.01810-0.0010246810-0.310-0.210-0.15、（1）theta=linspace(-pi,pi,100); ro=5.*cos(theta)+4; polar(theta,ro); （2）x=linspace(0,2*pi,100);a=1>> r=a.*(1+cos(x)); polar(x,r);3021060240902701203001503301806、（1）t=0:pi/10:2*pi;>> x=exp((-t)/20).*cos(t); >> y=exp((-t)/20).*sin(t); >> z=t; >> plot3(x,y,z);-1-0.50.51-1-0.50.5102468（2）t=0:0.01:1; x=t;>> y=t.^2; >> z=t.^3;>> plot3(x,y,z);0.20.40.60.800.20.40.60.817、x=-30:0.1:0; >> y=0:0.1:30;>> [x,y]=meshgrid(x,y); >>z=10.*sin(sqrt(x.^2+y.^2))./sqrt(1+x.^2+y.^2);>> meshc(x,y,z);绘制曲⾯图和等⾼线-30-20-10102030-4-202468、x=linspace(-3,3,100); >> y=linspace(-3,3,100); >> [x y]=meshgrid(x,y); %可以将向量转化为矩阵 >> fxy=-5./(1+x.^2+y.^2); >> i=find(abs(x)<=0.8 & abs(y)<=0.5); >> fxy(i)=NaN; >>surf(x,y,fxy) %绘制三维曲⾯图-4-224-4-224-4-3-2-19、u=linspace(1,10,100); v=linspace(-pi,pi,100);[u v]=meshgrid(u,v); x=3.*u.*sin(v); y=2.*u.*cos(v); z=4*u.^2; surf(x,y,z); shading interp;-40-20-1010200100200300400第五章⼆1、a=rand(1,30000);mean(a) %求平均数 ans =0.5010 >>b=std(a) %求标准差 b =0.2882 >> c=max(a) c =0.9999 >> d=min(a) d =3.5706e-005size(find(a>0.5))/size(a) %求⼤于0.5的随机数个数占总数的百分⽐ans =0.50322、h=[466,715,950,1422,1635]; >> w=[7.04,4.28,3.40,2.52,2.13]; >> hh=[500,900,1500]; >> ww=interp1(h,w,hh,'spline')ww =6.4903 3.5226 2.3845 3、x=linspace(1,10,50); y=log(x);f=polyfit(x,y,5); %求曲线的拟合 >> yy=polyval(f,x); >> plot(x,y,'r-',x,yy,'g.') 123456789100.511.522.55、（1）、（2） p1=[1,2,0,7]; p2=[1,-2]; p3=[1,0,5,1]; p12=conv(p1,p2); >>p=p12+[zeros(1,size(p12,2)-size(p3,2)),p3]; >> roots(p) ans =-3.4656 0.6128 + 1.6278i 0.6128 - 1.6278i 1.2400-29 291 95 19 -3 697 -13 697 1427 >>y2=polyvalm(p,a)%以矩阵a 为⾃变量 y2 =391 2084 3273 502 2693 4207 720 3775 5892 6、（1）z=fzero('3*x-sin(x)+1',0) %求x=0时附近的根 z =-0.4903 第⼋章⼆、2t=0:pi/20:2*pi; x=sin(t); y=cos(t); x1=sin(7*t); y1=cos(7*t);h=plot(x,y,x1,y1);set(h,'marker','x','linewidth',2); set(gca,'xtick',-1:0.1:1); title('篮筐')-1-0.9-0.8-0.7-0.6-0.5-0.4-0.3-0.2-0.100.10.20.30.40.50.60.70.80.91 -1-0.8-0.6-0.4-0.200.20.40.60.81篮筐3、x=0:pi/10:5*pi;y=exp(-0.2*x).*cos(x)+2; h=plot(x,y);set(gca,'color','red','linestyle','-','linewidth',3);text(5,2.4,'y=exp(-0.2*x).*cos(x)+2');02468101214161.41.61.822.22.42.62.83y=exp(-0.2*x).*cos(x)+24、t=-pi:pi/100:pi; x=cos(t); y=sin(t); z=t;h=plot(t,x,t,y,t,z);set(h,'linestyle','-','linewidth',3);-4-3-2-101234-4-3-2-101234字符串例ch='Welcome to Beijing';subch=ch(12:18) 选12~18个字符串（空格也算）ans =WELCOME TO BEIJING >> length(k)统计⼩写字母的个数ans = 14 例：已知y=1-1/2+1/3-1/4.........-1/100求y 的值y=0; >> n=100; >> for i=1:100; y=y+(-1)^(i-1)/i; end>> disp(y)0.6882绘制⼆维曲线图x=0:pi/100:2*pi; >> y1=0.2*exp(-0.5*x).*cos(4*pi*x); >> y2=1.5*exp(-0.5*x).*cos(pi*x); >> plotyy(x,y1,x,y2); 7-0.20.20123456-202绘制三维图像例：x=sint+tcost y=cost-tsint z=tt=0:pi/10:10*pi; x=sin(t)+t.*cos(t); y=cos(t)-t.*sin(t); z=t; plot3(x,y,z); axis([-30 30 -30 30 0 35]); 坐标轴的最⼤值与最⼩值title('line in 3-D space'); 图形的题⽬ >> xlabel('x');ylabel('y');zlabel('z'); 标注坐标>> grid on; 加⽹格线 -30-20-10102030-20205101520253035xline in 3-D spaceyz三维例]2/,0[],,0[,cos sin 22ππ∈∈+=y x y x z [x,y]=meshgrid(0:pi/100:pi,0:pi/100:pi/2);>> z=sin(x.^2)+cos(y.^2);>> mesh(x,y,z);>> axis([0 4 0 1.8 -1.5 1.5]); 012340.511.5-1.5-1-0.500.511.5例3.16t=0:pi/20:2*pi; subplot(1,2,1);[x,y,z]=cylinder(sin(t),30);surf(x,y,z); 绘制三维曲⾯图subplot(1,2,2);>> [x,y,z]=peaks(100);>> mesh(x,y,z); 绘制三维⽹格图-11-10100.20.40.60.81-55-505-10-5510多项式求导例：f(x)=1/x^2+5 p=[1];>> q=[1,0,5];>> [p,q]=polyder(p,q)注：c=conv(a,b) 表⽰a 多项式与b 多项式乘积[p,r]=deconv(a,b) 表⽰a 多项式与b 多项式相除其中p 为商向量 r 为余数向量p=polyder(p) 表⽰求p 的导数 p=poleder(p,q) 表⽰求p 乘以q 的导数[p,q]=poleder(p,q) 表⽰p 除以q 的导数多项式求根例：f(x)=2x^4-12x^3+3x^2+5 p=[2,-12,3,0,5]; >> x=roots(p); >> p=[2,-12,3,0,5]; x=roots(p) 求⽅程f(x)=0的根 x =5.7246 0.8997 -0.3122 + 0.6229i -0.3122 - 0.6229i>> g=poly(x) 已知多项式的根求多项式 g =1.0000 -6.0000 1.5000 -0.00002.5000符号求导例7.3x=a(t-tsint)y=b(1-cost) 求y 对x 的⼀阶导数 syms x y a b t;>> f21=a*(t-sin(t)); >> f22=b*(1-cos(t));>> diff(f22)/diff(f21) 求y 对x 的⼀阶导数ans =b*sin(t)/a/(1-cos(t))注：diff(f1,x,2) 表⽰f1对x 的⼆阶导数diff （f3,x ）表⽰z 对x 的偏导 diff （f3,y ）表⽰z 对y 的偏导求不定积分int(f) 求f 的不定积分 f1=int(f,a,b) 求f 在a ，b 之间的定积分eval （f1）计算积分值符号求极限例7.2 syms x h>> f=(sin(x+h)-sin(x))/h;>> limit(f,h,0) h 趋向于0ans =cos(x)例2f=sym('(1+t/x)^x');limit(f,inf) f趋向于⽆穷ans =exp(t)例3f=sym('x*(sqrt(x^2+1)-x)');limit(f,sym('x'),inf,'left') x 趋向于正⽆穷ans =1/2⼤⼩写ch='Welcome to Beijing';subch=ch(12:18)subch =Beijing>> k=find(ch>='A'&ch<='Z'); ch(k)=ch(k)-('A'-'a');>> char(ch)ans =welcome to beijing>> length(k)ans =2。
MATLAB 课后部分答案
P77 第2章1、>> x=2;>> y=power(x,3)+(x-0.98).^2./(x+1.35).^3-5*(x+1./x)>> x=4;>> y=power(x,3)+(x-0.98).^2./(x+1.35).^3-5*(x+1./x)7、>> mat=rand(4,5);>> m=1;>> for i=1:2for j=1:5if mat(i,j)>0.3b(m)=mat(i,j);m=m+1;endendend>> b8、>> V=inv(A)>> A=rand(5,5);10、>> A=[1 4 8 13;-3 6 -5 -9;2 -7 -12 -8];B=[5 4 3 -2;6 -2 3 -8;-1 3 -9 7]; >> C=A*B??? Error using ==> mtimesInner matrix dimensions must agree.>> C=A.*BC =5 16 24 -26-18 -12 -15 72-2 -21 108 -5611、>> x=linspace(0,2*pi,125);>> y=cos((x).*(0.5+3*sin(x)./(1+x.^2)));>> plot(x,y)13、>> x=-2:0.1:2;y=-2:0.1:2;>> [X,Y]=meshgrid(x,y);>> Z=X.^2.*exp(-X.^2-Y.^2);>> mesh(Z)建立一个M函数文件mycos.m，程序如下：function y=mycos(x)clear allx=input('请输入x的值')y=1./((x-2).^2+0.1)+1./((x-3).^3+0.01)在命令窗口输入：mycosP123 第3章1、>> x=[446 714 950 1422 1634];y=[7.04 4.28 3.40 2.54 2.13];>> xi=500:500:1500;>> yi=interp1(x,y,xi,'linear')4、>> p=[3 4 7 2 9 12];>> roots(p)8、>> a=[2 4 9;4 2 4;9 4 18];>> [V,D]=eig(a) %V的列向量是相应的特征向量,对角阵D的对角元素为a的特征值10、>> p1=[-1 4 0];p2=[-1 -4 0];>> A=polyder(p1);B=polyder(p2);>> A1=roots(A);B1=roots(B);>> y=4*A1-4*B1-A1.^2-B1.^213、>> syms x y>> Ex=int(int(x.*12.*y.^2,y,0,x),x,0,1)>> Ey=int(int(y.*12.*y.^2,x,y,1),y,0,1)>> Exy=Ex.*Ey14、>> A=rand(4,4);>> [L,U]=lu(A)>> [Q,R]=qr(A)P183 第4章1、>> n=-2*pi:0.01:2*pi;>> N=12;x=cos(n*pi./6);>> X=fft(x,N)>> nx=((n>=0)&(n<=11)); hx=((n>=0)&(n<=5)); >> xn=0.8*nx;hn=hx;>> y=conv(xn,hn)4、>> n=0:11;h=0:5;>> nx=((n>=0)&(n<=11)); hx=((n>=0)&(n<=5)); >> xn=0.8*nx;hn=hx;>> M=length(xn);N=length(hn);>> L=pow2(nextpow2(M+N-1));>> Xk=fft(xn,L);Hk=fft(hn,L);>> Yk=Xk.*Hk;>> yn=ifft(Yk,L)5、>> num=[2 3 0];den=[1 0.4 1];>> [z,p,k]=tf2zp(num,den)6、>> num=[4 15.6 6 2.4 -6.4];den=[3 2.4 6.3 -11.4 6]; >> [z,p,k]=tf2zp(num,den)>> zplane(z,p)7、>> num=[18 0 0 0];den=[18 3 -4 -1];>> [r,p,k]=residuez(num,den)9、建立一个M函数文件，程序如下：clear allN=10;[z,p,k]=buttap(N);[A,B,C,D]=zp2ss(z,p,k);wc1=100;wc2=200;[At,Bt,Ct,Dt]=lp2bp(A,B,C,D,wc1,wc2);[num1,den1]=ss2tf(At,Bt,Ct,Dt);[num2,den2]=impinvar(num1,den1);dimpulse(num2,den2)10、建立一个M函数文件，程序如下：clear allwp=100*2*pi;ws=200*2*pi;Rp=2;Rs=15;Fs=500;[N,Wc]=buttord(wp,ws,Rp,Rs,'s'); %选择滤波器的最小阶数[z,p,k]=buttap(N);[B,A]=zp2tf(z,p,k);[num,den]=bilinear(B,A,Fs); %模拟滤波器的传递函数转换为数字滤波器的传递函数freqz(num,den)11、建立一个M函数文件，程序如下：clear allN=48;w=[0.35,0.65];B=fir1(N,w,'bandpass'); %返回一个N阶的带通滤波器freqz(B) %绘制滤波器的频率响应曲线12、建立一个M函数文件，程序如下：clear allN=37;wc=0.3*pi;B=fir1(N,wc);freqz(B) %绘制滤波器的频率响应曲线13、建立一个M函数文件，程序如下：clear allN=55;F=[0:1/55:1];A=[ones(1,28),zeros(1,N-27)];B=fir2(N,F,A);freqz(B) %绘制滤波器的频率响应曲线15、建立一个M函数文件，程序如下：clear allwc=0.4*pi/(2*pi);N=12;[B,A]=butter(N,wc);%设计N阶截止频率为wc的Butterworth低通数字滤波器的传递函数模型m=dimpulse(B,A,101);stem(m,'.')P277 第6章2、建立一个M函数文件，程序如下：function [h,l]=huffmancode(P)if length(find(P<0))~=0,error('Not a prod.vector')endif abs(sum(P)-1)>10e-10error('Not a prod.vector')endn=length(P);for i=1:n-1for j=i:nif P(i)<=P(j)p=P(i);P(i)=P(j);P(j)=p;endendenddisp('概率分布'),PQ=P;m=zeros(n-1,n);for i=1:n-1[Q,l]=sort(Q);m(i,:)=[l(1:n-i+1),zeros(1,i-1)];Q=[Q(1)+Q(2),Q(3:n),1];endfor i=1:nc(i,:)=blanks(n*n);endc(n-1,n)='0';c(n-1,2*n)='1';for i=2:n-1c(n-i,1:n-1)=c(n-i+1,n*(find(m(n-i+1,:)==1))-(n-2):n*(find(m(n-i+1,:)==1)));c(n-1,n)='0';c(n-i,n+1:2*n-1)=c(n-i,1:n-1);c(n-i,2*n)='1';for j=1:i-1c(n-i,(j+1)*n+1:(j+2)*n)=c(n-i+1,n*(find(m(n-i+1,:)==j+1)-1)+1:n*find(m(n-i+1,:)==j+1));endendfor i=1:nh(i,1:n)=c(1,n*(find(m(1,:)==i)-1)+1:find(m(1,:)==i)*n);ll(i)=length(find(abs(h(i,:))~=32));endl=sum(P.*ll); %计算平均码长在命令窗口中输入：>> P=[0.20 0.15 0.13 0.12 0.1 0.09 0.08 0.07 0.06];>> [h,l]=huffmancode(P)3、建立一个M函数文件，程序如下：function[sqnr,a_quan,code]=u_pcm(a,n)% U_PCM 一个序列均匀的PCM编码.% n=量化级数的数目（偶数）.% sqnr=输入信号量化噪声比（偶数）。
MATLAB-课后实验答案
实验一 MATLAB 运算基础1. 先求下列表达式的值，然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin851z e =+(2) 21ln(2z x =，其中2120.455i x +⎡⎤=⎢⎥-⎣⎦(3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=--(4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩，其中t =0:: 解：2. 已知：1234413134787,2033657327A B --⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦求下列表达式的值：`(1) A+6*B 和A-B+I （其中I 为单位矩阵）(2) A*B 和A.*B(3) A^3和A.^3(4) A/B 及B\A(5) [A,B]和[A([1,3],:);B^2] 解：运算结果：3. 设有矩阵A 和B123453166789101769,111213141502341617181920970212223242541311A B ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(1) 求它们的乘积C 。
(2) 将矩阵C 的右下角3×2子矩阵赋给D 。
(3) 查看MATLAB 工作空间的使用情况。
解：. 运算结果：4. 完成下列操作：）(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量，删除其中的大写字母。
解：(1) 结果：(2). 建立一个字符串向量例如：ch='ABC123d4e56Fg9';则要求结果是：实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦，其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵，试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。
(完整版)MATLAB)课后实验答案[1]
![(完整版)MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/d27ebaa958fb770bf78a55b8.png)
实验一 MATLAB 运算基础1. 先求下列表达式的值，然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =，其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=--L (4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩，其中t =0:0.5:2.5 解：4. 完成下列操作：(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量，删除其中的大写字母。
解：(1) 结果：(2). 建立一个字符串向量例如：ch='ABC123d4e56Fg9';则要求结果是：实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦，其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵，试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。
解: M 文件如下；5. 下面是一个线性方程组：1231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦(1) 求方程的解。
(2) 将方程右边向量元素b 3改为0.53再求解，并比较b 3的变化和解的相对变化。
(3) 计算系数矩阵A 的条件数并分析结论。
解： M 文件如下： 123d4e56g9实验三 选择结构程序设计1. 求分段函数的值。
2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现，分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。
matlab课后习题答案(1-9章)要点
1 数字1.5e2，1.5e3 中的哪个与1500相同吗？1.5e32 请指出如下5个变量名中，哪些是合法的？abcd-2xyz_3 3chan a 变量ABCDefgh 2、5是合法的。
3 在MATLAB 环境中，比1大的最小数是多少？ 1+eps4 设 a = -8 , 运行以下三条指令，问运行结果相同吗？为什么？w1=a^(2/3) w2=(a^2)^(1/3) w3=(a^(1/3))^2w1 = -2.0000 + 3.4641i ;w2 = 4.0000 ;w3 =-2.0000 + 3.4641i 5 指令clear, clf, clc 各有什么用处？clear 清除工作空间中所有的变量。
clf 清除当前图形。
clc 清除命令窗口中所有显示。
第二章1 说出以下四条指令产生的结果各属于哪种数据类型，是“双精度”对象，还是“符号”符号对象？3/7+0.1双; sym(3/7+0.1)符; sym('3/7+0.1') 符;; vpa(sym(3/7+0.1)) 符;2 在不加专门指定的情况下，以下符号表达式中的哪一个变量被认为是自由符号变量. sym('sin(w*t)'),sym('a*exp(-X)'),sym('z*exp(j*th)') symvar(sym('sin(w*t)'),1) w a z3 （1）试写出求三阶方程05.443=-x 正实根的程序。
注意：只要正实根，不要出现其他根。
（2）试求二阶方程022=+-a ax x 在0>a 时的根。
（1）reset(symengine)syms x positive solve(x^3-44.5) ans =(2^(2/3)*89^(1/3))/2（2）求五阶方程022=+-a ax x 的实根 syms a positive %注意：关于x 的假设没有去除 solve(x^2-a*x+a^2)Warning: Explicit solution could not be found. > In solve at 83 ans =[ empty sym ]syms x clear syms a positivesolve(x^2-a*x+a^2) ans =a/2 + (3^(1/2)*a*i)/2 a/2 - (3^(1/2)*a*i)/24 观察一个数（在此用@记述）在以下四条不同指令作用下的异同。
matlab课后练习习题及答案详解
matlab课后习题及答案详解第1章MATLAB概论与其余计算机语言对比较，MATLAB语言突出的特色是什么？MATLAB拥有功能强盛、使用方便、输入简捷、库函数丰富、开放性强等特色。
MATLAB系统由那些部分构成？MATLAB系统主要由开发环境、MATLAB数学函数库、MATLAB语言、图形功能和应用程序接口五个部分组成。
安装MATLAB时，在选择组件窗口中哪些部分一定勾选，没有勾选的部分此后怎样补安装？在安装MATLAB时，安装内容由选择组件窗口中个复选框能否被勾选来决定，能够依据自己的需要选择安装内容，但基本平台（即MATLAB选项）一定安装。
第一次安装没有选择的内容在补安装时只要依据安装的过程进行，不过在选择组件时只勾选要补装的组件或工具箱即可。
MATLAB操作桌面有几个窗口？怎样使某个窗口离开桌面成为独立窗口？又怎样将离开出去的窗口从头搁置到桌面上？在MATLAB操作桌面上有五个窗口，在每个窗口的右上角有两个小按钮，一个是封闭窗口的Close按钮，一个是能够使窗口成为独立窗口的Undock 按钮，点击Undock按钮就能够使该窗口离开桌面成为独立窗口，在独立窗口的view菜单中选择Dock,,菜单项就能够将独立的窗口从头防备的桌面上。
怎样启动M文件编写/调试器？在操作桌面上选择“成立新文件”或“翻开文件”操作时，M文件编写/调试器将被启动。
在命令窗口中键入edit命令时也能够启动M文件编写/调试器。
储存在工作空间中的数组能编写吗？怎样操作？储存在工作空间的数组能够经过数组编写器进行编写：在工作空间阅读器中双击要编写的数组名翻开数组编写器，再选中要改正的数据单元，输入改正内容即可。
命令历史窗口除了能够察看前方键入的命令外，还有什么用途？命令历史窗口除了用于查问从前键入的命令外，还能够直接履行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中。
怎样设置目前目录和搜寻路径，在目前目录上的文件和在搜寻路径上的文件有什么差别？目前目录能够在目前目录阅读器窗口左上方的输入栏中设置，搜寻路径能够经过选择操作桌面的file菜单中的SetPath菜单项来达成。
matlab课后习题答案
习题二之南宫帮珍创作2.如何理解“矩阵是MATLAB最基本的数据对象”？答：因为向量可以看成是仅有一行或一列的矩阵, 单个数据（标量）可以看成是仅含一个元素的矩阵, 故向量和单个数据都可以作为矩阵的特例来处置.因此, 矩阵是MATLAB最基本、最重要的数据对象.3.设A和B是两个同维同年夜小的矩阵, 问：(1)A*B和A.*B的值是否相等？答：不相等.(2)A./B和B.\A的值是否相等？答：相等.(3)A/B和B\A的值是否相等？答：不相等.(4)A/B和B\A所代表的数学含义是什么？答：A/B等效于B的逆右乘A矩阵, 即A*inv(B), 而B\A等效于B矩阵的逆左乘A矩阵, 即inv(B)*A.4.写出完成下列把持的命令.(1)将矩阵A第2~5行中第1, 3, 5列元素赋给矩阵B.答：B=A(2:5,1:2:5); 或B=A(2:5,[1 3 5])(2)删除矩阵A的第7号元素.答：A(7)=[](3)将矩阵A的每个元素值加30.答：A=A+30;(4)求矩阵A的年夜小和维数.答：size(A);ndims(A);(5)将向量t的0元素用机器零来取代.答：t(find(t==0))=eps;(6)将含有12个元素的向量x转换成34 矩阵.答：reshape(x,3,4);(7)求一个字符串的ASCII码.答：abs(‘123’); 或double(‘123’);(8)求一个ASCII码所对应的字符.答：char(49);5.下列命令执行后, L1、L2、L3、L4的值分别是几多？A=1:9;B=10-A;...L1=A==B;L2=A<=5;L3=A>3&A<7;L4=find(A>3&A<7);答：L1的值为[0, 0, 0, 0, 1, 0, 0, 0, 0]L2的值为[1, 1, 1, 1, 1, 0, 0, 0, 0]L3的值为[0, 0, 0, 1, 1, 1, 0, 0, 0]L4的值为[4, 5, 6]6.已知完成下列把持：(1)取出A的前3行构成矩阵B, 前两列构成矩阵C, 右下角32⨯子矩阵构成矩阵D, B与C的乘积构成矩阵E.答：B=A(1:3,:);C=A(:,1:2);D=A(2:4,3:4);E=B*C;(2)分别求E<D、E&D、E|D、~E|~D和find(A>=10&A<25).答：E<D=010001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦, E&D=110111⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦, E|D=111111⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦, ~E|~D=001000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦find(A>=10&A<25)=[1; 5].7.当A=[34, NaN, Inf, -Inf, -pi, eps, 0]时, 分析下列函数的执行结果：all(A), any(A), isnan(A), isinf(A), isfinite(A).答：all(A)的值为0any(A)的值为1isnan(A)的值为[0, 1, 0, 0, 0, 0, 0]isinf(A)的值为[0, 0, 1, 1, 0, 0, 0]isfinite(A)的值为[1, 0, 0,0, 1, 1, 1]8.用结构体矩阵来存储5名学生的基本情况数据, 每名学生的数据包括学号、姓名、专业和6门课程的成果.答：student(1).id='0001';student(1).name='Tom';student(1).major='computer';student(1).grade=[89,78,67,90,86,85];9.建立单位矩阵B并回答有关问题.B{1,1}=1;B{1,2}='Brenden';B{2,1}=reshape(1:9,3,3);B{2,2}={12,34,2;54,21,3;4,23,67};(1)size(B)和ndims(B)的值分别是几多？答：size(B)的值为2,2.ndims(B)的值为2.(2)B(2)和B(4)的值分别是几多？答：B(2)=147258369⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦, B(4)=[12][34][2][54][21][3][4][23][67]⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦(3)B(3)=[]和B{3}=[]执行后, B的值分别是几多？答：当执行B(3)=[]后,B={1, [1, 4, 7; 2, 5, 8; 3, 6, 9], {12, 34, 2; 54, 21, 3; 4, 23, 67}}当执行B{3}=[]后,B={1,[]; [1, 4, 7; 2, 5, 8; 3, 6, 9],{12, 34, 2; 54, 21, 3; 4, 23, 67}}习题三1.写出完成下列把持的命令.(1)建立3阶单位矩阵A.答：A=eye(3);(2)建立5×6随机矩阵A, 其元素为[100,200]范围内的随机整数.答：round(100+(200-100)*rand(5,6));(3)发生均值为1, 方差为0.2的500个正态分布的随机数.答：1+sqrt(0.2)*randn(5,100);(4)发生和A同样年夜小的幺矩阵.答：ones(size(A));(5)将矩阵A对角线的元素加30.答：A+eye(size(A))*30;(6)从矩阵A提取主对角线元素, 并以这些元素构成对角阵B.答：B=diag(diag(A));2.使用函数, 实现方阵左旋90o或右旋90o的功能.例如, 原矩阵为A, A左旋后获得B, 右旋后获得C.答：B=rot90(A);C=rot90(A,-1);3.建立一个方阵A, 求A的逆矩阵和A的行列式的值, 并验证A与A-1是互逆的.答：A=rand(3)*10;B=inv(A);C=det(A);先计算B*A, 再计算A*B, 由计算可知B*A=A*B, 即A·A-1=A-1·A是互逆.4.求下面线性方程组的解.答：A=[4,2,-1;3,-1,2;12,3,0];b=[2;10;8];x=inv(A)*b方程组的解为x=6.000026.666727.3333 -⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦5.求下列矩阵的主对角线元素、上三角阵、下三角阵、秩、范数、条件数和迹.(1)112351423052111509A-⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦(2)0.434328.9421B⎡⎤=⎢⎥-⎣⎦答：(1)取主对角线元素：diag(A);上三角阵：triu(A)；下三角阵：tril(A);秩：rank(A);范数：norm(A,1); 或 norm(A);或 norm(A,inf);条件数：cond(A,1); 或 cond(A,2); 或 cond(A,inf)迹：trace(A);(2)【请参考(1)】.6.求矩阵A的特征值和相应的特征向量.答：[V,D]=eig(A);习题四1.从键盘输入一个4位整数, 按如下规则加密后输出.加密规则：每位数字都加上7, 然后用和除以10的余数取代该数字；再把第一位与第三位交换, 第二位与第四位交换.答：a=input('请输入4位整数：');A=[a/1000,a/100,a/10,a];A=fix(rem(A,10));A=rem(A+7,10);b=A(3)*1000+A(4)*100+A(1)*10+A(2);disp(['加密后的值为：',num2str(b)]);2.分别用if语句和switch语句实现以下计算, 其中a、b、c的值从键盘输入.答：(1) 用if语句实现计算：a=input('请输入a的值：');b=input('请输入b的值：');c=input('请输入c的值：');x=input('请输入x的值：');y=a*x^2+b*x+c;endy=a*((sin(b))^c)+x;endy=log(abs(b+c/x));enddisp(['y=',num2str(y)]);(2) 用switch语句实现计算：a=input('请输入a的值：');b=input('请输入b的值：');c=input('请输入c的值：');x=input('请输入x的值：');switch fix(x/0.5)case {1,2}y=a*x^2+b*x+c;case num2cell(3:6)y=a*((sin(b))^c)+x;case num2cell(7:10)y=log(abs(b+c/x));enddisp(['y=',num2str(y)]);3.发生20个两位随机整数, 输出其中小于平均值的偶数.答：A=fix(10+89*rand(1,20));sum=0;for i=1:20sum=sum+A(i);endB=A(find(A<(sum/20)));C=B(find(rem(B,2)==0));disp(C);4. 输入20个数, 求其中最年夜数和最小数.要求分别用循环结构和调用MATLAB 的max 函数、min 函数来实现.答：(1) 用循环结构实现：v_max=0;v_min=0;for i=1:20x=input(['请输入第', num2str(i), '数：']);if x>v_maxv_max=x;end;if x<v_minv_min=x;end;enddisp(['最年夜数为：', num2str(v_max)]);disp(['最小数为：', num2str(v_min)]);(2) 用max 函数、min 函数实现：for i=1:5A(i)=input(['请输入第', num2str(i), '数：']);enddisp(['最年夜数为：', num2str(max(A))]);disp(['最小数为：', num2str(min(A))]);5. 已知：236312222s =+++++, 分别用循环结构和调用MATLAB 的sum 函数求s 的值.答：s=0;for i=0:63s=s+2^i;ends(2) 调用sum函数实现：s=0:63;s=2.^s;sum(s)6.当n分别取100、1000、10000时, 求下列各式的值.(1)111111(1)(ln2) 234nn+-+-++-+=(2)1111() 3574π-+-+=(3) 11111() 4166443n+++++=(4)224466(2)(2)133557(21)(21)2n nn nπ⎛⎫⨯⨯⨯⨯⎛⎫⎛⎫⎛⎫⎛⎫=⎪⎪⎪⎪ ⎪⨯⨯⨯-⨯+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭要求分别用循环结构和向量运算（使用sum或prod函数）来实现.答：(1) 用循环结构实现：sum=0;for k=1:100sum=sum+(-1)^(k+1)/k;endsum使用sum函数：x=[];for k=1:10000x=[x, (-1)^(k+1)/k];endsum(x)sum=0;for k=1:100sum=sum+(-1)^(k+1)/(2*k-1);endsum使用sum函数：x=[];for k=1:100x=[x, (-1)^(k+1)/(2*k-1)];endsum(x)(3)用循环结构实现：sum=0;for k=1:100sum=sum+1/(4^k);endsum使用sum函数实现：x=[];for k=1:100x=[x, 1/(4^k)];endsum(x)(4)用循环结构实现：t=1;for k=1:100t=t*(((2*k)*(2*k))/((2*k-1)*(2*k+1)));endt使用prod函数实现：x=[];for k=1:100x=[x, ((2*k)*(2*k))/((2*k-1)*(2*k+1))];endprod(x)7. 编写一个函数文件, 求小于任意自然数n的斐波那契（Fibnacci）数列各项.斐波那契数列界说如下：答：function x=fibnacci(n)for i=1:nif i<=2x(i)=1;elsex(i)=x(i-1)+x(i-2);endend8.编写一个函数文件, 用于求两个矩阵的乘积和点乘, 然后在命令文件中调用该函数.答：函数文件myfnc.m：function [x, y]=myfnc(A, B)tryx=A*B;catchx=[];endy=A.*B;命令文件myexe.m：A=input('请输入矩阵A：');B=input('请输入矩阵B：');[x, y]=myfnc(A, B);if length(x)==0display('两矩阵的维数不匹配, 无法进行乘积运算！');elsedisp('矩阵A 和矩阵B 的乘积为：');xenddisp('矩阵A 和矩阵B 的点乘为：');y9. 先用函数的递归调用界说一个函数文件求1n m i i =∑, 然后调用该函数文件求100501021111k k k k k k ===++∑∑∑. 答：函数文件myfnc.m ：function sum=myfnc(n, m)if n<=1sum=1;elsesum= myfnc (n-1, m)+n^m;end在命令窗口中调用myfnc.m 文件, 计算100501021111k k k k k k ===++∑∑∑： sum=myfnc(100, 1)+myfnc(50, 2)+myfnc(10,-1) 10.写出下列法式的输出结果.① s=0;a=[12,13,14;15,16,17;18,19,20;21,22,23];for k=afor j=1:4if rem(k(j),2)~=0s=s+k(j);endendends答：执行结果为s=108②命令文件exe.m执行后的结果为：x =41220y=。
精讲多练MATLAB课后习题答案
第 1 章练习题答案1-2.A= ;B= ;C= ;D= ;E=;T=atan((2*pi*A+E/(2*pi*B*C))/D)1-3clearx=45;(sin(x*pi/180)+sqrt(35))/(72^(1/5))1-4cleara=;b=;exp(a+b)/log10(a+b)1-5clearx=3;y=sqrt(x)-6*(x+1/x)+^2/(x+^31-6clearr=15;d=2*rc=2*pi*rs=pi*r*r1-7cleara=;b=;c=;s=(a+b+c)/2;area=sqrt(s*(s-a)*(s-b)*(s-c))第 2 章练习题答案2-1 c learA=[ 3 1 1;2 1 2;1 2 3]; B=[1 1 -1;2 -1 0;1 -1 1]; 2*A+B,4*(A^2)-3*(B^2),A*B,B*A,A*B-B*A 2-2 clearA=[1/3 0 0;0 1/4 0;0 0 1/7];B=inv(inv(A)-eye(3))*62-3clearB=[1 2 -3 -2;0 1 2 -3;0 0 1 2;0 0 0 1];C=[1201;0120;0012;0001];A=(inv(2*eye(4)-inv(C)*B)*inv(C))'2-4clearA=[2 -1;-1 2];B=[0 -2;-2 0];X=(1/2)*(B+2*A)2-5clearA=[2 -3 0 2;1 5 2 1;3 -1 1 -1;4 1 2 2];B=[8;2;7;12];X=A\B2-6A=[3 12 4 7 0 8 1];p=poly2str(A,'x')x=roots(A)2-7A=[3 12 4 7 0 8 1];B=[1 -3 5 -15 0];[div,rest]=deconv(A,B)第三章=sym('x');limit((cos(sqrt(x)))^(pi/x),x,0,'right')ans =exp(-1/2*pi)=sym('x');f=sym('(3*sin(x)+x^2*cos(1/x))/((1+cos(x))*log(1+x))');limit(f,x,0)ans =3/2=sym('x');f=sym('(sqrt(4*x^2+x-1)+x+1)/sqrt(x^2+sin(x))');limit(f,x,-inf)ans =1x y;f=sym('(x^2+y^2)^(x^2*y^2)');limit(limit(f,x,0),y,0) ans =1 =sym('x');y=sym('(tan(sqrt(x+sqrt(x+sqrt(2*x)))))^2');diff(y,x)ans=tan((x+(x+2^(1/2)*x^(1/2))^(1/2))^(1/2))*(1+tan((x+(x+2^(1/2)*x^(1/2 ))^(1/2))^(1/2))^2)/(x+(x+2^(1/2)*x^(1/2))^(1/2))^(1/2)*(1+1/2/(x+2^(1/2)*x^(1/2))^(1/2)*(1+1/2*2^(1/2)/x^(1/2)))3-6.x=sym('x');y=sym('cos(x^2)*sin(1/x)^2');diff(y,x)ans =-2*sin(x^2)*x*sin(1/x)^2-2*cos(x^2)*sin(1/x)*cos(1/x)/x^23-7 .x=sym('x');y=sym('sqrt(sin(x)-sin(x)^3)');int(y,x,0,pi)ans =4/3=sym('x');y=sym('sqrt((x+1)/(x-1))/x');int(y,x)ans=-((1+x)/(x-1))^(1/2)*(x-1)*(atan(1/(-1+x^2)^(1/2))-log(x+(-1+x^2)^(1 /2)))/((1+x)*(x-1))^(1/2)('D2y+4*Dy+4*y=exp(-2*x)','x')ans =1/2*exp(-2*x)*(2*C2+2*x*C1+x^2)3-10.dsolve('x^2*Dy+x*y=y^2','y(1)=1')ans =x*exp(1/x)/(exp(1/x)+exp(1/x*t)*x-exp(1/x*t))第四章4-1.plot([1 2 4 0 5 10 11 21 3 1])4-2.t=0:pi/100:2*pi;x=cos(t);y=sin(t);plot(x,y);axis('square');4-3.R=[1 5 10 20];I=0::10;U=I'*R;plot(I,U);4-4.mon=1:12;temp=[];rainf=[];plot(mon,temp,'r-p',mon,rainf,'b:s');xlabel('month');ylabel('temperature and rainfall');%title('Temperature and Rainfall Curve');%text(3,1,'rainfall');%text(9,,'temperature');flag=12;while(flag)text(mon(flag),temp(flag),[num2str(mon(flag)),num2str(temp(flag))]); text(mon(flag),rainf(flag),[num2str(mon(flag)),num2str(rainf(flag))]);flag=flag-1;end4-5.A=[1111111;1222221;1223221;1222221;111111 1]; plot(A);4-6.x=-10::10;y=x;[X,Y]=meshgrid(x,y);Z=X.^2+Y.^2;surf(X,Y,Z);4-7.clccleartheta=(0::2)*pi;phi=(0::2)*pi;x=zeros(length(theta),length(phi));y=x;z=x;for i=1:length(theta)for j=1:length(phi)x(i,j)=2*sin(theta(i))*cos(phi(j));y(i,j)=3*sin(theta(i))*sin(phi(j));endz(i,:)=4*cos(theta(i));endaxis squaresubplot(2,2,1);mesh(x,y,z)title('三维 ')subplot(2,2,2);mesh(x,y,z)view(90,0)title('X轴视图 ')subplot(2,2,3);mesh(x,y,z)view(0,0)title('Y轴视图 ')subplot(2,2,4);mesh(x,y,z)view(0,90)title('Z轴视图 ')第五章5-1 ：clear;x=-2::2;for ii=1:401if(x(ii)<0)y(ii)=x(ii)+1;elseif (x(ii)<1)&(x(ii)>=0)y(ii)=1;elseif(x(ii)>=1)y(ii)=x(ii)^3;endendplot(x,y);5-2 ：function y=fenduan(x)if(x<0)y=x+1;elseif (x<1)&(x>=0)y=1;elseif(x>=1)y=x^3;end5-3 ：成立文件以下：function y=arcsin(x)if abs(x)>1disp('输入参数的绝对值一定小于1');return;endn=0;y=0;u=x;while u>epsu=(jiecheng(2*n)*x^(2*n+1))/(2^(2*n)*(jiecheng(n)^2*(2*n+1)));y=y+u;n=n+1;end成立文件以下：function y=jiecheng(n)if(n<0)disp('输入参数一定为大于或等于0 的整数 ');return;endif n==0 | n==1y=1;elsey=n*jiecheng(n-1);end5-4 ：成立文件以下：function [tu,ji]=shuliang(tou,jiao)tu=jiao/2-tou;ji=2*tou-jiao/2;在命令窗口中履行： >>[a,b]=shuliang(36,100)5-5 ：for i=2:999ge=rem(i,10);shi=rem(fix(i/10),10);bai=fix(i/100);if rem((ge+shi+bai),2) & isprime(i)disp(i);endend5-6 ：function y=issushu(n)y=1;for ii=2:fix(n/2)if(rem(n,ii)==0)y=0;endend习题 1（程序段后边的是其运转的结果）例题function lt12a=1+2*i;b=3-4*i;disp(['a+b=',num2str(a+b)])disp(['a-b=',num2str(a-b)])disp(['a*b=',num2str(a*b)])disp(['a/b=',num2str(a/b)])>> lt12a+b=4-2i a-b=-2+6i a*b=11+2ia/b=+ >>例题function z=lt13x=*pi/180;y=*pi/180;z=sin(abs(x)+abs(y))/sqrt(cos(abs(x+y))); >> lt13 ans =>>例题function p1=lt14r=;n=2015-2000;p0=;p1=p0*+r)^n;>>lt14ans =+009>>例题function lt15a=1;b=2;c=3;d=sqrt(b^2-4*a*c);x1=(-b+d)/2*a;x2=(-b-d)/2*a;disp('原方程的根是：')disp(['x1=',num2str(x1)])disp(['x2=',num2str(x2)])>>lt15原方程的根是：x1=-1+ x2=>>。