5.1振幅调制的基本原理
振幅调制

振幅调制(AM及DSB)摘要:信号调制可以将信号的频谱搬移到任意位置,从而有利于信号的传送,并且使频谱资源得到充分利用。
调制作用的实质就是使相同频率范围的信号分别依托于不同频率的载波上,接收机就可以分离出所需的频率信号,不致互相干扰。
这也是在同一信道中实现多路复用的基础。
而要还原出被调制的信号就需要解调电路。
所以现在调制与解调在高频通信领域有着更为广泛的应用。
关键词:振幅调制,单频信号引言:调制的作用是把消息置入消息载体,便于传输或处理。
在通信系统中为了适应不同的信道情况(如数字信道或模拟信道、单路信道或多路信道等),常常要在发信端对原始信号进行调制,得到便于信道传输的信号,调制是各种通信系统的重要基础,也广泛用于广播、电视、雷达、测量仪等电子设备。
一.振幅调制的原理振幅调制常用于长波,中波,短波和超短无线电广播,通信,电视,雷达等系统。
这种调制方式是用传递的低频信号去控制作为传送媒体的高频震荡波的幅度,使已调波的幅度随调制信号的大小线性变化,而保持载波的角频率不变。
标准调幅(AM)就是其中一种。
标准振幅调制是一种相对便宜的质量不高的调制形式。
主要用于声频和视频的商业广播。
AM调制器是非线性设备,有2个输入端口和1个输出端口,一端输入振幅为常数的单频载波信号,另一端输入低频载波信息信号。
在调制器中,信息作用在载波上,就产生了振幅随调制信号瞬时值而变化的已调波。
通常已调波是能有效地通过天线发射,并在自由空间中传播的射频波。
二单频信号调制1.AM调幅波的数学表达式如果设单频调制信号为uI =UImcosΩt,设载波为u c=U cm cosωCt,那么调幅信号(已调波)就可以表示为:uAM =UAM(t) cosωCt, (1)在该式子中UAM(t)称为已调波的瞬时幅值(也称为调幅波的包络函数)。
由于调幅信号的瞬时振幅与调制信号成线性关系,则有:UAM (t)= U cm+kaUImcosΩt= U cm(1+ ka UImcosΩt/ U cm)= U cm(1+macosΩt) (2)式中ka 为比例常数,一般由调制电路的参数决定;ma= kaUIm/ U cm,为调制系数(或称调制深度)ma反映了调幅波振幅的改变量,常用百分比表示,将(2)式代入(1)式可得到单频信号调幅波的表达式如下:uAM = U cm(1+macosΩt) cosωCt基于以上原理,我们做的是单二极管开关状态调幅电路,图2.1单二极管调幅电路设负载Z L 为LC 选频回路,分析可知回路谐振时Z L =R L ,且流过负载回路的电流为:i d =Ld R r +1S(t)u d 式中u d = u I (t)+ u c (t); S(t)为开关函数,且有:S(t)=1,u c >0; S(t)=0, u c <0; S(t)为周期函数,其傅里叶级数为: S(t)=∙∙∙+-+t t c c ωπωπ3cos 32cos 221i d =L d R r +1⎥⎦⎤⎢⎣⎡∙∙∙+-+t t c c ωπωπ3cos 32cos 221 (U Im cos Ωt+ U cm cos ωC t) 如果LC 回路谐振在频率ωC 处,由谐振时负载阻抗Z L =R L ,则可得出回路的输出电压为:u L (t)=()()[]t t R U g t R U g c c L In d c L cm d Ω-+Ω++ωωπωcos cos 1cos 21 =t t U U R U g c cm InL cm d ωπcos cos 4121⎪⎪⎭⎫ ⎝⎛Ω+=()t t m U c Lm ωcos cos 1Ω+ 式中d g =Ld R r +1,m=cm In U U π4,Lm U =L cm d R U g 21;如果我们给定元件的参数,固定载波的振幅U cm 与频率ωC 不变,只改变调制信号的振幅U Im ,R L =900Ω,r d =100Ω, L=100H,C=0.01 μF;可知谐振频率为:LCc 1=ω=1000 rad/s ,载波信号给定为u c =6cos (200πt)当u I =43πcos(20πt )时, m=0.5. 在matlab 中编写代码实现AM 波的调幅,代码如下: 1)调制信号的程序代码: fs=1000;%设定采样频率 N=1024;%设定数据长度 i=0:N-1; t=i/fs;f=10;%设定信号频率 %生成正弦信号 x=(3*pi/4)*cos(2*pi*f*t); subplot(231);plot(t,x);%信号的时域波形 axis([0,0.3,-4,4]); xlabel('t'); ylabel('y');title('信号时域波形');grid;%进行FFT变换并做频谱图y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:N-1)*fs/N;%横坐标频率的表达式为f=(0:M-1)*Fs/M; subplot(232);plot(f,mag);%做频谱图axis([0,200,0,2000]);xlabel('频率(Hz)');ylabel('幅值');title('信号幅频谱图')下面是调制信号的时域波形图与频谱图的截图:图2.22)载波信号的程序代码:fs=1000;%设定采样频率N=1024;%设定数据长度i=0:N-1;t=i/fs;f=100;%设定信号频率x=6*cos(2*pi*f*t); %生成余弦信号subplot(231);plot(t,x);%作信号的时域波形axis([0,0.05,-8,8]);xlabel('t');ylabel('y');title('载波信号时域波形');grid;%进行FFT变换并做频谱图y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:N-1)*fs/N;%横坐标频率的表达式为f=(0:M-1)*Fs/M; subplot(232);plot(f,mag);%做频谱图axis([0,200,0,300]);xlabel('频率(Hz)');ylabel('幅值');title('信号幅频谱图')下面是载波信号的时域波形图与频谱图的截图:图2.33)两个信号叠加以后即为已调波,已调波代码如下fm=10; %调制信号频率fc=100; %载波信号频率t=0:0.000001:0.5;x=0:0.000001:2;m1=0.5;s_am1=6*(1+m1.*cos(2*pi*fm*t)).*cos(2*pi*fc*t); figure(2) %图2为ma=0.5时的已调波plot(t,s_am2); grid on;title('m=0.5时AM调制信号');xlabel('t'); ylabel('v');运行后其调幅波波形如下:图2.44)现在再来看m=0.5时已调波的频谱图,其代码如下:t=i/fs;fm=10; %调制信号频率Hzfc=100; %载波信号频率Hzma1=0.5;x=6*(1+ma1.*cos(2*pi*fm*t)).*cos(2*pi*fc*t);y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:N-1)*fs/N;%横坐标频率的表达式为f=(0:M-1)*Fs/M; subplot(232);plot(f,mag);%做频谱图axis([0,200,0,1500]);xlabel('频率(Hz)');ylabel('幅值');title('已调波信号频谱图(m=0.5时)')下图是已调波的频谱图:图2.5由以上各图可知m=0.5时可以保证已调波的包络真实地反映出调制信号的变化规律当uI =23 cos(20πt)时, m=1.调制信号程序代码如下:fs=1000;%设定采样频率N=1024;%设定数据长度i=0:N-1;t=i/fs;f=10;%设定信号频率x=(3*pi/2)*cos(2*pi*f*t); %生成余弦信号subplot(231);plot(t,x);%信号的时域波形axis([0,0.3,-6,6]);xlabel('t');ylabel('y');title('调制信号时域波形');grid;%进行FFT变换并做频谱图y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:N-1)*fs/N;%横坐标频率的表达式为f=(0:M-1)*Fs/M; subplot(232);plot(f,mag);%做频谱图axis([0,200,0,2000]);xlabel('频率(Hz)');ylabel('幅值');title('信号幅频谱图')下面是调制信号的时域波形图与频谱图:图2.6再来看已调波的波形图,程序的代码如下:fm=10; %调制信号频率fc=100; %载波信号频率t=0:0.000001:0.5;x=0:0.000001:2;m2=1;s_am2=6*(1+m2.*cos(2*pi*fm*t)).*cos(2*pi*fc*t); figure(2) %为m1=1时的已调波plot(t,s_am2); grid on;title('m=1时AM调制信号');xlabel('t'); ylabel('v');程序运行的结果如下:图2.7再来看m=1时已调波的频谱图,其代码如下:fs=1000;%设定采样频率N=1024;%设定数据长度i=0:N-1;t=i/fs;fm=10; %调制信号频率Hzfc=100; %载波信号频率Hzma2=1;x=6*(1+ma2.*cos(2*pi*fm*t)).*cos(2*pi*fc*t);y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:N-1)*fs/N;%横坐标频率的表达式为f=(0:M-1)*Fs/M; subplot(232);plot(f,mag);%做频谱图axis([0,200,0,2500]);xlabel('频率(Hz)');ylabel('幅值');title('已调波信号频谱图(m=1时)')下图为程序运行后的结果图:图2.8由上图知m=1时,调制系数的百分比达到100%,此时包络振幅的最小值为0当uI =49 cos(20πt)时, m=1.5. 调制信号程序代码如下:fs=1000;%设定采样频率N=1024;%设定数据长度i=0:N-1;t=i/fs;f=10;%设定信号频率x=(9*pi/4)*cos(2*pi*f*t); %生成余弦信号subplot(231);plot(t,x);%作信号的时域波形axis([0,0.3,-8,8]);xlabel('t');ylabel('y');title('调制信号时域波形');grid;%进行FFT变换并做频谱图y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:N-1)*fs/N;%横坐标频率的表达式为f=(0:M-1)*Fs/M; subplot(232);plot(f,mag);%做频谱图axis([0,200,0,2000]);xlabel('频率(Hz)');ylabel('幅值');title('信号幅频谱图')图2.9下面再来看已调波的波形图,程序的代码如下:fm=10; %调制信号频率fc=100; %载波信号频率t=0:0.000001:0.5;x=0:0.000001:2;m3=1.5;s_am2=6*(1+m3.*cos(2*pi*fm*t)).*cos(2*pi*fc*t); figure(2) %图2为ma=0.5时的已调波plot(t,s_am2); grid on;title('m=1.5时AM调制信号');xlabel('t'); ylabel('v');程序运行的结果如下:图2.10再来看m=1.5时已调波的频谱图,其代码如下:fs=1000;%设定采样频率N=1024;%设定数据长度i=0:N-1;t=i/fs;fm=10; %调制信号频率Hzfc=100; %载波信号频率Hzma3=1;x=6*(1+ma3.*cos(2*pi*fm*t)).*cos(2*pi*fc*t);y=fft(x,N);%进行fft变换mag=abs(y);%求幅值f=(0:N-1)*fs/N;%横坐标频率的表达式为f=(0:M-1)*Fs/M; subplot(232);plot(f,mag);%做频谱图axis([0,200,0,2500]);xlabel('频率(Hz)');ylabel('幅值');title('已调波信号频谱图(m=1.5时)')下图为程序运行后的结果图:图2.11由图知此时已调波的包络形状与调制信号不一样,产生了严重的包络失真,这种情况称为过量调幅,实际应用时应尽量避免。
第五章 振幅调制、解调及混频讲解
(5)相位调制:调制信号控制载波相位,使已调波的相位随调 制信号线变化。
( 6)解调方式:
振幅检波 振幅调制的逆过程 鉴频 调频的逆过程 鉴相 调相的逆过程 (7)振幅调制分三种方式:
普通调幅( AM ) 抑制载波的双边带调幅(DSB ) 单过带调制(SSB )
密码
信号 载波信号:(等幅)高频振荡信号
正弦波 方波 三角波 uc Uc cos(ct )
锯齿波
已调信号(已调波):经过调制后的高频信号(射频信号)
(1) 调制:用调制信号去控制载波信号的某一个参量的过程。 (2)解调:调制的逆过程,即从已调波中恢复原调制信号的过程。
休息1 休息2
(3)振幅调制:由调制信号去控制载波振幅,使已调信号的振 幅 随调制信号线性变化。
)t
可见,调幅波并不是一个简单的正弦波,包含有三个频率分量:
载波分量(c ) : 不含传输信息
上边频分量c : 含传输信息 下边频分量c : 含传输信息
调制信号
Ω
载波
调幅波
U
ωc
c
下边频
1 2 maUc
1 2
maU
c
上边频
ωc - Ω ωc +Ω
(2) 限带信号的调幅波
第5章 振幅调制、解调及混频
5.1 概述 5.2 振幅调制原理及特性 5.3 振幅调制电路 5.4 调幅信号的解调 5.5 混频器原理及电路
返回 休息1 休息2
5.1概述
振幅调制
解调(检波)
属于 频谱线性搬移电路
混频(变频)
语言
定义: 调制信号:需要传输的信号(原始信号)
幅度调制的原理

5.1 幅度调制〔线性调制〕的原理
调幅定义:载波的振幅随调制信号的变化而变化
m(t)
s(t) H() sm(t)
适中选择带通滤波器
Acos(ct 0)
的特性,便可以得到 各种幅度调制信号。
正弦型载波为 c(t)Acosct0
式中, A — 载波幅度;
c — 载波角频率;
0 — 载波初始相位〔以后假定 0 = 0〕。
s (t) f1 (t)c o sc t f2 (t)s inc t
消息信号
f1(t)
乘积调 制器
复合信号 s(t)
乘积调 制器
1
低通滤 2 f 1 ( t ) 波器
cos( ct)
cos( c t )
-90o移相器
sin(ct)
消息信号 乘积调
f2(t)
制器
复合信号 s(t)
-90o移相器
sin(ct )
18
5.1.1 AM信号:普通调幅波
5 频谱:假设m(t)为确知信号,那么AM信号的频谱
为
因为
m(t)M()
cosct (c)(c)
A0 2A0()
且
S m ( t) S A M ( t) A 0 m ( t) c o sc t
S A M () F ( A 0 c o s c t F m ( t ) c o s c t
幅度调制的原理
5.0 根本概念
根本概念
调制信号-指来自信源的基带信号〔低频〕 载波-未受调制的周期性振荡信号,它可以是正弦波,也可 以是非正弦波〔高频〕 调制-用调制信号去控制载波信号的某个参数,使参数随调 制信号的变化而变化,把信号转换成适合在信道中传输的形式的一 种过程。 已调信号-载波受调制后称为已调信号,调制信号和载波的合 成信号(高频〕 解调〔检波〕-调制的逆过程,其作用是将已调信号中的调 制信号恢复出来。
振幅调制和解调电路

02
振幅调制原理
振幅调制定义
01
振幅调制是指将低频信号调制到 高频载波上,改变载波的幅度大 小的过程。
02
振幅调制是一种线性调制方式, 其原理是将输入信号的幅度变化 ,通过改变高频载波的幅度来实 现信号的传输。
01
03
同时,随着物联网、云计算、大数据等新兴技术的发 展,振幅调制和解调电路的应用领域也将不断拓展,
为人们的生活和工作带来更多的便利和价值。
04
未来发展方向包括采用新型的调制方式、提高调制效 率、降低解调误差率、增强抗干扰能力等。
THANKS
感谢观看
振幅调制优点与缺点
振幅调制的优点包括实现简单、抗干扰能力强、信道利用率 高等。
振幅调制的缺点包括对非线性失真敏感、对信道特性变化敏 感等。
03
振幅调制电路
模拟振幅调制电路
01
模拟振幅调制电路主要 由调制信号、载波信号 和调制器组成。
02
03
04
调制信号通常是音频信 号或低频信号,载波信 号是高频信号。
移动通信
在移动通信系统中,振幅调制用于传 输语音和数据信号。解调电路在接收 端将调制的信号还原为原始信号,以 便用户接收。
有线通信系统中的应用
有线电视
在有线电视系统中,振幅调制用于传 输多路电视信号。解调电路用于将各 个电视频道还原为原始信号,以便用 户选择观看。
DSL宽带接入
在DSL宽带接入中,振幅调制用于传 输高速数据信号。解调电路在接收端 将调制信号还原为原始数据信号,提 供互联网接入服务。
振幅调制原理

振幅调制原理
振幅调制(Amplitude Modulation,简称AM)是一种调制技术,它通过改变载波的振幅,来传输要调制的信号。
具体而言,振幅调制是将调制信号的幅度(即振幅)与高频载波信号相乘,得到一个新的带有调制信号特征的调制信号。
在振幅调制中,调制信号通常是音频信号,比如人声或者音乐。
而载波信号是具有固定频率和振幅的高频信号。
调制信号和载波信号相乘的结果,就是振幅调制信号。
振幅调制过程中,调制指数(也称调制深度)是一个关键参数。
调制指数是调制信号的幅度变化与载波幅度的比值。
调制指数的大小会影响到调制信号的功率和频谱分布。
振幅调制的原理可以用以下几个步骤来解释:
1. 调制信号:将要传输的音频信号作为调制信号。
2. 载波信号:选择一个高频信号作为载波信号。
3. 调制过程:将调制信号的幅度与载波信号相乘,得到一个新的调制信号。
4. 调制指数:调节调制指数,控制调制信号的幅度变化。
5. 传输信号:将调制后的信号传输到接收端。
在接收端,需要进行解调过程,将调制信号还原为原始的调制信号。
解调过程是振幅调制的逆过程,在解调过程中,通过将收到的调制信号与一个参考信号(通常是与发送端相同的载波信号)相乘,就可以获得原始的调制信号。
振幅调制在广播和电视等领域中得到了广泛应用。
它可以实现信号的远距离传输,同时具有一定的抗干扰能力。
然而,振幅调制也存在一些问题,比如在传输过程中容易受到噪声和干扰的影响,以及只能传输一个信号的限制。
因此,在一些特定的应用场景中,人们也使用其他调制技术,比如频率调制(FM)和相位调制(PM)。
第5章 振幅调制与解调

振幅调制与解调
本节的主要内容包括:
5.1.1 标准调幅信号的特点 5.1.2 抑制载波的双边带与单边带调幅信号
振幅调制与解调
5.1.1 标准调幅信号的特点
定义:振幅调制就是用低频调制信号去控制高频载波信号的 振幅,使载波的振幅随调制信号成正比的变化;经过振幅调 制的高频载波称为振幅调制波,简称调幅波(AM)。 一、普通调幅波的表达式 设载波uc(t)的表达式和调制信号uΩ(t)的表达式分别为:
例如,语音信号的频率范围为300~3400Hz,则语音信号 的调幅波带宽为2×3400=6800Hz。 小结: 调幅波调制过程为频谱的线性搬移过程,即将调制信号的 频谱不失真地搬移到载频的两旁。因此,调幅称为线性调制。 调幅电路则属于频谱的线性搬移电路。
振幅调制与解调
三、普通调幅波的功率关系
若调制信号为单频余弦信号,负载电阻为RL,
其中:
பைடு நூலகம்
U cm (1 ma cos t ) cos c t
(式5.1)
K为比例系数,是由调制电路决定的比例常数;
m a为调幅系数或调幅度,它表示了载波振幅受调制信号控制的程 度。
振幅调制与解调
ma
U cm KU m U cm U cm
U max U min U cm U min 2U cm Ucm
1 maU cm 2
c-
2(
1 maU cm 2
c- c+
c+
) 2
信号 带宽
2(
2
振幅调制与解调
例1:已知信号电压的频谱如下图示,试写出该信号电压的数 学表达式,并指出已调波性质,并计算在单位电阻上消耗的 边带功率和总功率以及已调波的频带宽度。
振幅调制电路

uo(t)= Amuc(t)uΩ(t)
=AmUΩm cosΩt Ucmcosωct
(5―10)
由上式可得双边带调幅信号的波形,如图5.9(a)所示。
根据(5―10)式可得双边带调幅信号的频谱表达式为
uo
(t)
1 2
AmUmUcm[cos(c
)t
cos(c
)t]
(5―11)
u(t)
Am uo(t)=Amu(t)uc(t)
(5―2)
4) 普通调幅信号的频谱结构和频谱宽度
将式(5―1)用三角函数展开:
Uo (t) Uomct mUom cos t cosct
Uom
cosct
1 2
maUom
cos(c
)t
1 2
maUom
cos(c
)t
(5―3)
u(t)
t uc(t)
t
uo(t)
Uo mmax
Uo mmin
t
Uo m(1+macos t)
(5―5)
可以看到,uo(t)的频谱结构中,除载波分量外, 还有由相乘器产生的上、下边频分量,其角频率为
(ωc±Ω)、(ωc+2Ω)…(ωc±nmaxΩ)。这些上、下 边频分量是将调制信号频谱不失真地搬移到ωc两边, 如图5.7所示。不难看出,调幅信号的频谱宽度为调制 信号频谱宽度的两倍,即
振幅调制和解调的原理及MATLAB编程实现
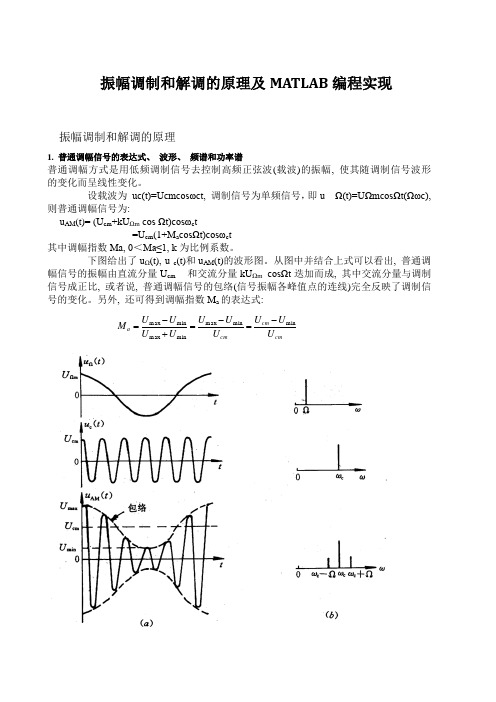
振幅调制和解调的原理及MATLAB 编程实现振幅调制和解调的原理1. 普通调幅信号的表达式、 波形、 频谱和功率谱普通调幅方式是用低频调制信号去控制高频正弦波(载波)的振幅, 使其随调制信号波形的变化而呈线性变化。
设载波为 uc(t)=Ucmcosωct, 调制信号为单频信号,即u Ω(t)=UΩmcosΩt(Ωωc), 则普通调幅信号为:u AM (t)= (U cm +kU Ωm cos Ωt)cosωc t=U cm (1+M a cosΩt)cosωc t 其中调幅指数Ma, 0<Ma≤1, k 为比例系数。
下图给出了u Ω(t), u c (t)和u AM (t)的波形图。
从图中并结合上式可以看出, 普通调幅信号的振幅由直流分量U cm 和交流分量kU Ωm cosΩt 迭加而成, 其中交流分量与调制信号成正比, 或者说, 普通调幅信号的包络(信号振幅各峰值点的连线)完全反映了调制信号的变化。
另外, 还可得到调幅指数M a 的表达式:cmcm cm a U U U U U U U U U U M minmin max min max min max -=-=+-=调幅的波形与频谱显然, 当Ma >1时, 普通调幅波的包络变化与调制信号不再相同, 产生了失真, 称为过调制。
所以, 普通调幅要求Ma 必须不大于1。
上式又可以写成u AM (t)=U cm cosωc t+ ·[cos (ωc +Ω)t+cos (ωc -Ω)t ]可见, uAM(t)的频谱包括了三个频率分量:ωc (载波)、 ωc +Ω(上边频)和ωc -Ω(下边频)。
原调制信号的频带宽度是 Ω或(F= ) , 而普通调幅信号的频带宽度是2Ω(或2F), 是原调制信号的两倍。
普通调幅将调制信号频谱搬移到了载频的左右两旁,如下图所示还可以看到, 若此单频调幅信号加在负载R 上, 则载频分量产生的平均功率为:P c =两个边频分量产生的平均功率相同, 均为:PSB=调幅信号总平均功率为: P av =P c +2P SB =根据信号分析理论, 一般非周期调制信号u Ω(t)的频谱是一连续频谱, 假设其频率范围是Ωmin ~Ωmax , 如载频仍是ωc , 则这时的普通调幅信号可看成是调制信号中所有π2Ωca cm a p M U M R 2241)2(21=R U cm 221c n p M )211(2+2MaUcm频率分量分别与载频调制后的迭加, 各对上、下边频的迭加组成了上、 下边带。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m 2a Po (1 ) 2
当 ma = 1时,边频功率最大,但仅为PAV / 3 实际使用中, ma在0.1~1之间,平均值为0.3。可见普通 调幅波中边频分量所占的功率非常小,而载波占绝大多数。 信息含于边频分量中,载波不含有用信息,但载波占 有很大能量。不经济。要抑制载波。
高频电子线路
5.1 振幅调制的基本原理
5.1.2 抑制载波的双边带和单边带调幅波
一、双边带调幅波 1. 表达式
DSB波:抑制载波分量 只含上、下边带分量
uDSB (t ) ka u (t ) cos(c t )
通过相乘实现!
kaU m cos(t ) cos(ct )
1 1 kaU m cos[( c )t ] kaU m cos[( c )t ] 2 2
载波分量功率
1 U cm Po 2 RL
边频分量功率:
PSB1 PSB2
1 ( maU cm ) 2 RL
1 2
2
1 m 2 aU 2 cm 1 2 m a Po 4 8 RL
高频电子线路
5.1 振幅调制的基本原理
调幅波在调制信号一个周期内的平均功率:
PAV Po PSB1 PSB2
高频电子线路
5.1 振幅调制的基本原理
5.1.3 调幅电路的组成模型
一、相乘器
ux
uy
X AMXY Y
uo
AM —增益系数或乘积系数,1/V
理想相乘器符号
理 1. 实现相乘,而对输入电压波形、幅度、极性、频率 无要求。 想 相 2. u 、u 中有一个为恒值时,相乘器相当于线性放大器。 x y 乘 uO = AM UxmUymcosxt cosyt 器 3. 产生新的频率分量 1 功 AMU xmU ym[cos( x y ) cos( x y )] 2 能
无载频分量!
高频电子线路
5.1 振幅调制的基本原理
2. 双边带调幅波波形
高频电子线路
5.1 振幅调制的基本原理
3. 双边带调幅波频谱
BW = 2F
高频电子线路
5.1 振幅调制的基本原理
二、单边带调幅波 表达式
SSB波:只含一个边带分量
或
1 uSSB ( t ) kaU m cos( c )t 2 1 uSSB ( t ) kaU m cos( c )t 2
5.1 振幅调制的基本原理
4. 单频调制时AM调幅波的功率 由于
uAM (t ) U cm ( 1 macost〕 cos(c t )
2
1 Ucm cos(ωc t ) 1 m U [cos( ω Ω ) t ] m U cos[(ωc Ω)t ] c 2 a cm 2 a cm
单频调制的AM波 的频带宽度:
BW = 2F
c 、c、c
高频电子线路
5.1 振幅调制的基本原理
多音频调制的普通调幅波的频谱
多频调制的AM波 的频带宽度:
B 2Fmax
结论
调幅过程是一种线性频谱搬移过程。调制信号的频谱由 低频被搬移到载频附近,成为上、下边频带。
高频电子线路
高频电子线路
5.1 振幅调制的基本原理
5.1.1 普通调幅波
一、普通调幅表达式 载波信号
AM调幅波
uc (t ) Ucm cosc t Ucm cos2 fc t
调制信号
uΩ ( t )
ka由调制电路决定
普通调幅波信号
uAM (t ) [U cm ka u (t )] cos(ct ) U m (t ) cos(ct )
高频电子线路
5.1 振幅调制的基本原理
DSB信号频谱含有上边带和下边带,没有载频分量, 其表达式为 uDSB (t ) ka u (t ) cos(ct ) ,其振幅在零值上 下按调制信号的规律变化,当 u (t ) 自正值或负值通 o 过零值变化时,调幅信号波形将发生180 的相位突变, 其包络不再反映调制信号的形状。 SSB信号频谱含有上边带或下边带分量,已调波波形 的包络也不直接反映调制信号的变化规律。单边带信 号一般是由双边带信号经除去一个边带而获得。 幅度调制就是频谱线性搬移。 频谱线性搬移只有采用相乘器才能实现。
四、SSB调幅电路组成模型
思路
DSB 除去一个边带 SSB
滤波
高频电子线路
5.1 振幅调制的基本原理
滤波法 uc(t) u(t) X AMXY uDSB(t) Y uSSB(t)
BPF
fc–Fmax
fc
Fc+ Fmax
f
fc–Fmin Fc+ Fmin
滤波法的关键是高频带 通滤波器。要能有效滤 除不要的边带,而不失 真地通过需要的边带。
高频电子线路
5.1 振幅调制的基本原理
第 5 章 振幅调制、解调与混频电路
振幅调制:用待传输的低频信号去控制高频载波信号的幅值 解调:从高频已调信号中还原出原调制信号 混频:将已调信号的载波载频变成另一个载频 振幅调制、解调和混频电路都是频谱线性搬移电路
地位 通信系统的基本电路
高频电子线路
5.1 振幅调制的基本原理
kaU m ma U cm
通常 F<<fc
调幅系数或调幅度 表示载波振幅受调幅波的包络。
高频电子线路
5.1 振幅调制的基本原理
2. 单频调制时AM调幅波波形
最大振幅
U cm (1 ma )
最小振幅
Ucm (1 ma )
ma>1时 过调幅失真
高频电子线路
5.1 振幅调制的基本原理
当ma≤1时,已调波振幅的包络形状与调制信号一样 不失真调幅 当ma>1时,将产生过量调制如下图所示。 包络形状会产生严重失真,必须尽力避免 。
包络 失真
高频电子线路
5.1 振幅调制的基本原理
3. 单频调制时AM调幅波频谱
uAM (t ) U cm ( 1 macost〕 cos(c t ) 1 Ucm cos(ωc t ) 1 m U [cos( ω Ω ) t ] m U cos[(ωc Ω)t ] c 2 a cm 2 a cm
当滤波器边带相对距离 f / fc小时,直接滤波很困难。
高频电子线路
例
5.1 振幅调制的基本原理
求带宽
(设ωc为Ω的整数倍)
解: 普通调幅信号, ma 1
BW = 2F
高频电子线路
例
5.1 振幅调制的基本原理
求带宽
(设ωc为Ω的整数倍)
解:
抑制载频双边带调辐信号
BW = 2F
高频电子线路
高频电子线路
5.1 振幅调制的基本原理
二、AM调幅电路组成模型 uc(t) u(t) + UQ uc(t) X AMXY Y uAM(t)
或
u(t)
+ + – – UQ
X AMXY Y
uAM(t)
uAM (t ) AM[UQ u (t )]Ucm cosc t [ AMUQUcm AMUcmu (t )]cosc t
普通调幅波幅值
Um (t ) Ucm ka u (t )
高频电子线路
5.1 振幅调制的基本原理
二、单频调制 1. 表达式
uΩ (t ) U Ωm cos Ωt U Ωm cos 2Ft
uAM (t ) 〔U cm ka u (t ) 〕 cos(c t ) 〔U cm kaU mcost〕 cos(c t ) U cm ( 1 macost〕 cos( c t )
高频电子线路
5.1 振幅调制的基本原理
高频电子线路
5.1 振幅调制的基本原理
第 5 章 振幅调制、解调与混频电路
振幅调制的基本原理
相乘器电路
振幅调制电路
振幅检波电路 混频电路 本章小结
高频电子线路
5.1 振幅调制的基本原理
5.1 振幅调制的基本原理
主要要求:
掌握普通调幅波、双边带调幅波和单边带调幅波 的表达式、波形特点、频谱图和频带宽度的计算 掌握线性频谱搬移电路的构成要素和频谱特点 掌握调幅电路的组成模型 理解调幅度的概念与应用
[Um ka u (t )]cosc t
Um AMUQUcm
ka AMUcm
高频电子线路
5.1 振幅调制的基本原理
三、DSB调幅电路组成模型 uc(t) u(t) X AMXY Y
uDSB(t)
uDSB (t ) AM u (t )uc (t )
uDSB (t ) AMUcmUm cos(t ) cos( c t ) Um cos(t ) cos( c t )
5.1 振幅调制的基本原理
求带宽
例
(设ωc为Ω的整数倍)
解:
单边带调幅信号
BW = F
高频电子线路
5.1 振幅调制的基本原理
求带宽
例
(设ωc为Ω的整数倍)
解:
低频信号与高频信号相叠加
高频电子线路
5.1 振幅调制的基本原理
小结
振幅调制有普通调幅信号(AM)、双边带(DSB) 和单边带(SSB)调制信号。 AM信号频谱含有载频、上边带和下边带,其中,上 下边带频谱结构反映调制信号频谱结构(下边带频谱 与调制信号频谱成倒置关系),其表达式 为 uAM (t ) 〔U cm ka u (t ) 〕 cos(c t ),其振幅在载波振幅 上下按调制信号的规律变化,即已调波的包络直接反 映调制信号的变化规律。
