第二章理论力学作业
理论力学(周衍柏 第二版)第2章习题解答

把⑥代入⑦得,
R1 = m1m2 cosθ g ⑧ m2 + m1 sin 2 θ
水平面对劈的反作用力 R2 。仍用隔离法。因为劈在垂直水皮方向上无加速度, 所以
R2 − m2 g − R1 cosθ = 0 ⑨
于是
R2 = m2 ( m1 + m2 ) g ⑩ m2 + m1 sin 2 θ
6
2.5解 因为质点组队某一固定点的动量矩 J = ∑ ri × mi v i
m 相对于地固连的坐标系 Oxy 的绝对速度
V绝对 = V相 + V牵
V相 为 m 相对 M 的运动速度
② u = aθ
故水平方向 vx = u cosθ − V ③ 竖直方向
v y = usiaθ ④
在 m 下滑过程中,只有保守力(重力)做功,系统机械能守恒: (以地面为重力零势能面)
8
mga cos α = mga cos θ +
(M + M ′) − M 2 μg M′ u− 2mM M
2
2.16 雨滴落下时,其质量的增加率与雨滴的表面积成正比例,求雨滴速度与时间的关系。 2.17 设用某种液体燃料发动的火箭, 喷气速度为 2074 米/秒, 单位时间内所消耗的燃料为 原始火箭总质量的 1 。如重力加速度 g 的值可以认为是常数,则利用此种火箭发射人造太
i =1 n
所以对于连续物体对某一定点或定轴,我们就应该把上式中的取和变为积分。如 图 2.5.1 图所示薄圆盘,任取一微质量元,
O
dθ
dr
dm = ρ ⋅ rdθdr
ρ=
所以圆盘绕此轴的动量矩 J
J =
M πa 2
∫∫ r × ( dm v ) = ∫∫ r ⋅ ρ rdrd
理论力学第2章答案

2 平面力系(3)一、是非题1、 平面力系的主矢量是力系的合力。
(×)2、 平面力系的力多边形不封闭,则该力系对任意一点的主矩都不可能为零。
(×)3、 当平面一般力系向某点简化为力偶时,如果向另一点简化其结果相同。
(√)4、 首尾相接构成一封闭力多边形的平面力系是平衡力系。
(×)5、 若一平面力系对某点主矩为零,且主矢亦为零,则该力系为一平衡力系。
(√)6、 作用在刚体上的一个力,可以从原来的作用位置平行移动到该刚体内任意指定点,但必须附加一个力偶,附加力偶的矩等于原力对指定点的矩。
(√)7、平面力系向某点简化之主矢为零,主矩不为零。
则此力系可合成为一个合力偶,且此力系向任一点简化之主矩与简化中心的位置无关。
(√)8、若平面力系对一点的主矩为零,则此力系不可能合成为一个合力。
(×)二、填空题1、0,902、10kN , →3、10kN ,←4、题目误,应在C 加支座。
5、2P ,↑6、R=10kN ,方向与AB 平行,d=2m三、A 点是固定端约束,有约束反力偶(设为逆时针方向)。
解:1) 选AB 研究,画受力图。
分布载荷的大小 q m *4/2,作用点距A 点4/3处。
2) 建坐标系,列解平衡方程优先用对A 点的力矩平衡方程,F 对A 点的力矩用合力矩定理。
kNm12 M 03)45sin -(F 4)45cos (F -M M 34)2q 4(0)F (ΣM A A m i A ==︒︒++⋅-= 066F 0)2126(3F 0F Ax Ax xi ===⋅+=--)24(∑ kN 6F 02126F 0F Ay Ay yi ==-= )( ∑ Ax F Ay F A M。
理论力学第二章习题答案

理论力学第二章习题答案理论力学是物理学中研究物体运动规律和相互作用的分支学科,它以牛顿运动定律为基础,通过数学方法来描述物体的运动和力的作用。
本章习题答案将帮助学生更好地理解和掌握理论力学的基本概念和计算方法。
习题1:考虑一个质量为m的物体在重力作用下自由下落。
忽略空气阻力,求物体下落过程中的速度和位移。
答案:物体自由下落时,受到的力只有重力,大小为mg,方向向下。
根据牛顿第二定律,F=ma,可以得到加速度a=g。
物体的速度v随时间t变化,可以使用公式v=gt计算。
物体的位移s随时间变化,可以使用公式s=1/2gt^2计算。
习题2:一个质量为m的物体在水平面上以初速度v0开始运动,受到一个大小为k的恒定摩擦力作用。
求物体停止前所经过的距离。
答案:物体在水平面上运动时,受到的摩擦力与物体的位移成正比,即F=-kx。
根据牛顿第二定律,F=ma,可以得到加速度a=-k/m。
物体的位移x随时间t变化,可以使用公式x=v0t - 1/2(k/m)t^2计算。
当物体速度减至0时,物体停止,此时t=2v0/k,代入公式得到x=2v0^2/k。
习题3:一个质量为m的物体在斜面上,斜面与水平面的夹角为θ。
物体受到一个向上的拉力F,使得物体沿斜面匀速上升。
求拉力F的大小。
答案:物体沿斜面匀速上升时,拉力F与重力分量mgsinθ和摩擦力μmgcosθ平衡。
根据平衡条件,F=mgsinθ + μmgcosθ。
如果摩擦系数为μ,可以进一步简化为F=mg(sinθ + μcosθ)。
习题4:考虑一个质量为m的物体在竖直平面内做圆周运动,圆心位于物体的正下方。
物体的运动由一个弹簧连接到圆心,弹簧的劲度系数为k。
求物体在圆周运动中的角速度。
答案:物体在圆周运动中,受到弹簧力和重力的作用。
根据牛顿第二定律,向心力Fc=mv^2/r=ma,其中r为圆的半径。
由于物体做圆周运动,向心力由弹簧力和重力的垂直分量提供。
因此,Fc=kx - mgcosθ,其中x为弹簧的伸长量,θ为物体与竖直方向的夹角。
理论力学第二次作业

本次作业是本门课程本学期的第2次作业,注释如下:一、单项选择题(只有一个选项正确,共15道小题)1. 平面任意力系有个独立的平衡方程。
(A)1(B) 2(C) 3(D) 4正确答案:C解答参考:2. 平面平行力系有个独立的平衡方程。
(A) 1(B) 2(C) 3(D) 4正确答案:B解答参考:3.图示结构是()。
(A) 静定(B) 一次超静定(C) 二次超静定(D)三次超静定正确答案:B解答参考:4.图示为两个相互啮合的齿轮。
作用在齿轮A上的切向力平移到齿轮B的中心。
(A) 不可以(B) 可以(C) 不能确定正确答案:A解答参考:5.图示桁架中杆件内力等于零,即所谓“零杆”为。
(A) BC, AC(B) BC, AC, AD(C) BC(D) AC[前面作业中已经做正确] [正确]正确答案:A解答参考:6.沿正立方体的前侧面作用一力,则该力。
(A) 对轴x、y、z之矩均相等(B) 对轴x、y、z之矩均不相等(C) 对轴x、y、之矩相等(D) 对轴y、z之矩相等你选择的答案: [前面作业中已经做正确] [正确]正确答案:D解答参考:7.空间力对点之矩是。
(A) 代数量(B) 滑动矢量(C) 定位矢量(D)自由矢量正确答案:C解答参考:8. 力对轴之矩是。
(A) 代数量(B) 滑动矢量(C) 定位矢量(D) 自由矢量你选择的答案: [前面作业中已经做正确] [正确]正确答案:A解答参考:9.空间力偶矩矢是。
(A) 代数量(B) 滑动矢量(C) 定位矢量(D) 自由矢量正确答案:D解答参考:10. 空间任意力系有个独立的平衡方程。
(A) 3(B) 4(C) 5(D)6你选择的答案: [前面作业中已经做正确] [正确]正确答案:D解答参考:11. 空间汇交力系有个独立的平衡方程。
(A) 3(B) 4(C) 5(D) 6正确答案:A解答参考:12. 空间力偶系有个独立的平衡方程。
(A) 3(B) 4(C) 5(D) 6正确答案:A解答参考:13. 空间平行力系有个独立的平衡方程。
理论力学作业答案

解:力系对O点的主矩在轴上的投影为
M Ox M x F F2 cos a .100 F3 sin .300 51.8 N .m M Oy M y F F1 .200 F2 sin a .100 36.64 N .m M Oz M z F F2 cos a .200 F3 cos .300 103.6 N .m
FCy
P1
FDx
解得: FCy 4550 N
P
3、研究杆ABC
FCy
C
M F F
y
C
0
M A 6FAx 3FBx 0 0
B
FCx
FBy
FAy FBy FCy P3 0
x
0
FBx
FAx FBx FCx 0
MA P3 FAy
A
解得: FBx 22800, FBy 17850
M M FAx tan , FAy , M A M a a
3-9(b)
已知:q, M, a,. 不计梁自重,求支座A、B、C约束反力。 FNC FBy FBx
解:BC段梁受力分析如图,平面任意力系平衡方程为
F F
解得:
FNC
x y
0 FBx FNC sin 0 0 FBy qa FNC cos 0
解得: FAx 0, FAy 1 F M , FNB 1 3F M 2 a 2 a
3-5(b)
已知:F, M, q, a, 求支座A、B约束反力。
q
M
解:梁受力分析如 图,平面任意力系 平衡方程为
FAx
理论力学习题及解答1
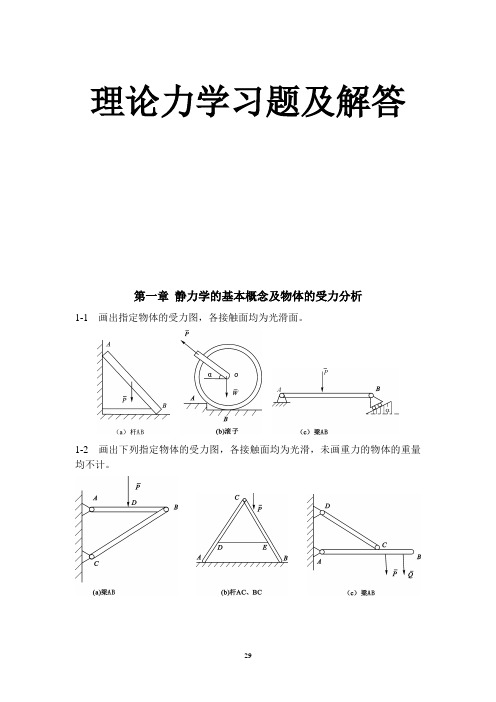
理论力学习题及解答第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图,各接触面均为光滑面。
1-2 画出下列指定物体的受力图,各接触面均为光滑,未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图,除注明者外,各物体自重不计,所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起,设滑轮的大小及滑轮转轴处的摩擦忽略不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体,求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN,P2=800kN及制动力T=193kN,桥墩自重W=5280kN,风力Q=140kN。
各力作用线位置如图所示,求将这些力向基底截面中心O简化的结果,如能简化为一合力,试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示,试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中,已知q=15kN/m,求A、B、C处的约束力。
2-6 图示平面结构,自重不计,由AB、BD、DFE三杆铰接组成,已知:P=50kN,M=40kN·m,q=20kN/m,L=2m,试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计,D、E处为铰链,B、C为链杆约束,A为固定端,已知:q G=1kN/m,q=1kN/m,M=2kN·m,L1=3m,L2=2m,试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成,O、B处为铰链,A、E是固定铰支座,尺寸如图,已知:r=20cm,在滑轮上吊有重Q=1000N的物体,杆及轮重均不计,试求支座A和E以及AO杆上的O处约束反力。
理论力学习题

第一章 质点运动学填空1. 在平面极坐标系中,单位向量的微分为: , ,速度的两个分量为 , ,加速度的两个分量为 。
2. 在自然坐标系下,单位向量的微分为: , 速度表示为: ,切向加速度为: ,法向加速度为: 。
3. 点M 沿螺旋线自外向内运动,如图所示。
它走过的弧长与时间的一次方成正比,则点的加速度越来越 (填:大、小、不变),点M 越跑越 (填:快、慢、不变)。
选择题1. 在直角坐标系下,某质点速度随时间的变化为:2234 (m/s)t i t j - ,则在1s 时,质点轨迹的曲率半径ρ= ( ) A. 0 m B. m ∞ C. 1 m D. 5 m计算和证明题:1. 有一作平面曲线运动的质点,其速度在y 轴上的投影于任何时刻均为常数c .试证:任何情况下,加速度的值可用下式表示3v a c ρ= ,其中v 为速率,ρ为轨道曲率半径.M·3. 质点作平面运动,其速率保持为常数.试证此质点速度矢量与加速度矢量相互垂直。
4. 一质点沿抛物线22y px =运动. 其切向加速度的量值为法向加速度量值的2k -倍.如此质点从弦的一端(,)2pp 以速率u 出发,试求其达到正焦弦另一端时的速率.)p )p5,质点沿着半径为r 的圆周运动,其加速度矢量与速度矢量间的夹角α保持不变。
求:(1),质点的速率随时间而变化的规律,(2),质点速率关于速度与x 之间夹角θ之间的函数关系。
已知初始时,速率为0v ,速度与x 轴夹角为0θ。
6,如图所示,细长杆A 端沿半径为R 的半圆槽底滑动,杆紧靠槽边以角速度ω倒下。
求:当杆与x 轴的夹角为ϕ时,杆的端点A 和杆上与槽边的接触点C 的速度。
开始时A 点在半圆槽底端A 0处。
x第二章 质点动力学填空题1.如果运动质点所受的力的作用线始终通过某一定点,我们称此力为有心力,而这个定点叫 。
2. 在直角坐标系下,某质点的动量为:32cos te i t j -- ,则作用在质点上的力F= 。
理论力学作业参考答案

平面任意力系(一)一、填空题1、平面任意力系的主矢RF '与简化中心的位置 无 关,主矩o M 一般与简化中心的位置 有 关,而在__主矢为零___的特殊情况下,主矩与简化中心的位置 无 __ 关.2、当平面力系的主矢等于零,主矩不等于零时,此力系合成为_一个合力偶.3、如右图所示平面任意力系中,F F F F 1234===,此力系向A 点简化的结果是 0R F '≠,0A M ≠ ,此力系向B 点简化的结果是0RF '≠,0A M = . 4、如图所示x 轴与y 轴夹角为α,设一力系在oxy 平面内对y 轴和x轴上的A ,B 点有∑A m 0)(=F ,∑B m 0)(=F ,且∑=0y F ,但∑≠0x F ,l OA =,则B 点在x 轴上的位置OB =___/cos l θ ____.(题4图) (题5图)5、折杆ABC 与CD 直杆在C 处铰接,CD 杆上受一力偶m N 2⋅=M 作用,m 1=l ,不计各杆自重,则A 处的约束反力为___2N___. 二、判断题(√ ) 1.若一平面力系对某点之主矩为零,且主矢亦为零,则该力系为一平衡力系.(√ ) 2.在平面力系中,合力一定等于主矢.(× ) 3.在平面力系中,只要主矩不为零,力系一定能够进一步简化.1F 2F 3F 4F AB(√ ) 4.当平面任意力系向某点简化结果为力偶时,如果再向另一点简化,则其结果是一样的.(×) 5.平面任意力系的平衡方程形式,除一矩式,二矩式,三矩式外,还可用三个投影式表示.(× ) 6.平面任意力系平衡的充要条件为力系的合力等于零.(× ) 7.设一平面任意力系向某一点简化得一合力,如另选适当的点为简化中心,则力系可简化为一力偶.(√ ) 8.作用于刚体的平面任意力系主矢是个自由矢量,而该力系的合力(若有合力)是滑动矢量,但这两个矢量等值,同向.( × ) 9.图示二结构受力等效.三、选择题1、关于平面力系与其平衡方程式,下列的表述正确的是_____D_ ___A.任何平面任意力系都具有三个独立的平衡方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章作业
1.求图示机构的A、B支座反力。
(提示:整体分析受平面汇交力系作用)
2.两球A和B分别重P和Q,用长为2l的杆连接,然后放在有光滑内表面的球形穴中,此球形穴的半径为R。
如不计杆重,求物系平衡时,在接触点A和B处的约束反力以及杆的内力。
3.系统如图,AB杆上作用矩为M的力偶,设AC=2R,R为轮C的半径,各物体的重量及摩擦不计。
求AC段绳子的拉力和铰A对AB杆的约束反力及地面对轮C的反力。
4.求图示静定梁的支座A、B、D约束反力。
4.结构的荷载和尺寸如图,CE=ED,试求固定端A和铰支座B的约束反力。
(提示:先局部分析)。
