圆盘剪分条剪切力计算方法
剪切力的计算方法

第3章剪切和挤压的实用计算3.1剪切的概念在工程实际中,经常遇到剪切问题。
剪切变形的主要受力特点是构件受到与其轴线相垂直的大小相等、方向相反、作用线相距很近的一对外力的作用(图3-1a),构件的变形主要表现为沿着与外力作用线平行的剪切面(m - n面)发生相对错动(图3-1b)。
图3-1工程中的一些联接件,如键、销钉、螺栓及铆钉等,都是主要承受剪切作用的构件。
构件剪切面上的内力可用截面法求得。
将构件沿剪切面m-n假想地截开,保留一部分考虑其平衡。
例如,由左部分的平衡,可知剪切面上必有与外力平行且与横截面相切的内力F Q (图3-1C)的作用。
F Q称为剪力,根据平衡方程',=0,可求得F Q二F。
剪切破坏时,构件将沿剪切面(如图3-la所示的m-n面)被剪断。
只有一个剪切面的情况,称为单剪切。
图3-1a所示情况即为单剪切。
受剪构件除了承受剪切外,往往同时伴随着挤压、弯曲和拉伸等作用。
在图3-1中没有完全给出构件所受的外力和剪切面上的全部内力,而只是给出了主要的受力和内力。
实际受力和变形比较复杂,因而对这类构件的工作应力进行理论上的精确分析是困难的。
工程中对这类构件的强度计算,一般采用在试验和经验基础上建立起来的比较简便的计算方法,称为剪切的实用计算或工程计算。
3.2剪切和挤压的强度计算3.2.1剪切强度计算剪切试验试件的受力情况应模拟零件的实际工作情况进行。
图试验装置的简图,试件的受力情况如图 3-2b 所示,这是模拟某种销钉联接的工作情形。
当载荷F 增大至破坏载荷 F b 时,试件在剪切面 m - m 及n - n 处被剪断。
这种具有两个剪切面的情况,称为双剪切。
由图 3-2c 可求得剪切面上的剪力为F Q图3-2由于受剪构件的变形及受力比较复杂,剪切面上的应力分布规律很难用理论方法确定,因而工程上一般采用实用计算方法来计算受剪构件的应力。
在这种计算方法中,假设应力在剪切面内是均匀分布的。
剪切力计算公式角度怎么算

剪切力计算公式角度怎么算剪切力是指在材料受到剪切力作用时所产生的内部应力。
在工程中,剪切力是一个非常重要的参数,它可以影响材料的强度和耐久性。
因此,了解如何计算剪切力是非常重要的。
本文将从角度的角度出发,介绍如何计算剪切力的公式和方法。
首先,让我们来了解一下什么是剪切力。
当一个物体受到外部力的作用时,如果这个力是沿着物体的表面平行方向作用的,那么这个力就是剪切力。
在材料力学中,剪切力是一种产生剪切应力的力,它可以导致材料的形变和破坏。
剪切力的计算公式可以通过角度来进行推导。
假设有一个物体受到一个剪切力F的作用,这个力是沿着物体的表面平行方向作用的。
如果我们知道这个力的大小和作用的角度,那么我们就可以通过角度来计算剪切力。
设物体受到的剪切力F的大小为F,作用的角度为θ。
那么根据三角函数的定义,我们可以得到剪切力的计算公式:F = F sin(θ)。
其中,F是剪切力的大小,θ是剪切力的作用角度。
这个公式告诉我们,剪切力的大小与作用角度的正弦值成正比。
也就是说,当剪切力的作用角度增大时,剪切力的大小也会增大。
通过这个公式,我们可以很容易地计算剪切力的大小。
只需要知道剪切力的大小和作用的角度,就可以通过这个公式来进行计算。
这对于工程实践中的设计和分析工作非常有帮助。
除了剪切力的大小,还有一个重要的参数是剪切应力。
剪切应力是指在材料受到剪切力作用时所产生的内部应力。
剪切应力与剪切力之间的关系可以通过角度来进行推导。
设物体受到的剪切力F的大小为F,作用的角度为θ。
根据材料力学的知识,我们知道剪切应力τ与剪切力F之间的关系可以通过下面的公式来表示:τ = F / A。
其中,τ是剪切应力,F是剪切力的大小,A是物体受力的截面积。
根据三角函数的定义,我们可以得到剪切应力与剪切力之间的关系:τ = F / A = F sin(θ) / A。
从这个公式可以看出,剪切应力与剪切力的大小和作用的角度都有关系。
当剪切力的大小和作用角度增大时,剪切应力也会增大。
剪切力的计算方法精编版

剪切力的计算方法精编版首先,我们先来了解一下剪切力的概念和背景知识。
剪切力是指物体在受到垂直于其截面的剪切应力时,所受到的力的大小。
剪切应力是指物体内部由于受到力的作用而产生的应力,其沿截面施加的作用力垂直于截面。
1.应力-应变关系法应力-应变关系法是计算剪切力最常用的方法之一、根据钢材等材料的线性弹性特性,剪切应力和应变之间存在线性关系,可以通过杨氏模量来计算剪切力。
公式如下所示:剪切力=剪切应力×截面积其中,剪切应力可以通过应力-应变关系得出,应变根据物体的受力情况和形状可以进行计算。
2.扭矩法扭矩法是一种通过扭转杆件来计算剪切力的方法。
当杆件受到扭矩作用时,杆件会在截面上产生剪切应力,从而产生剪切力。
根据弹性力学理论,扭矩和剪切力之间存在线性关系,公式如下所示:剪切力=扭矩×距离/截面极性矩其中,截面极性矩可以通过截面形状进行计算。
3.力矩法力矩法是一种通过受力物体的力矩平衡条件来计算剪切力的方法。
根据力矩平衡定律,物体受到的剪切力和力矩之间存在平衡关系,公式如下所示:剪切力=ΣM/距离其中,ΣM表示所有受力物体的力矩的代数和,距离表示力矩的作用距离。
4.梁的转角法梁的转角法是一种通过梁的转角来计算剪切力的方法。
当梁受到外力作用时,会产生转角,根据梁的弹性力学公式可以计算出剪切力。
公式如下所示:剪切力=F×L/θ其中,F表示梁所受外力的大小,L表示梁的长度,θ表示梁的转角。
这些方法可以根据具体情况和需求来选择使用。
在进行剪切力的计算时,需要明确剪切应力、截面积、扭矩、距离、力矩和转角等参数的具体值,并进行合理的单位换算以确保计算结果的准确性。
需要注意的是,剪切力的计算方法可能会受到材料的非线性特性、几何形状的复杂性等多种因素的影响,因此在实际应用中需要进行合理的简化和适当的修正。
综上所述,剪切力的计算方法包括应力-应变关系法、扭矩法、力矩法和梁的转角法等。
选择适当的计算方法需要根据具体情况和实际需求来决定,同时需要注意考虑材料的特性以及几何形状的复杂性等因素。
剪切力的计算方法剪力强度公式

第3章剪切与挤压的实用计算3、1剪切的概念在工程实际中,经常遇到剪切问题。
剪切变形的主要受力特点就是构件受到与其轴线相垂直的大小相等、方向相反、作用线相距很近的一对外力的作用(图3-la),构件的变形主要表现为沿着与外力作用线平行的剪切而(加-"面)发生相对错动(图3-lb)o图3-1工程中的一些联接件,如键、销钉、螺栓及钏钉等,都就是主要承受剪切作用的构件。
构件剪切而上的内力可用截而法求得。
将构件沿剪切而〃L”假想地截开,保留一部分考虑其平衡。
例如,由左部分的平衡,可知剪切而上必有与外力平行且与横截而相切的内力匚(图3-lc)的作用° F Q称为剪力,根据平衡方程工丫= 0,可求得F Q=F°剪切破坏时,构件将沿剪切而(如图3-la所示的川-舁而)被剪断。
只有一个剪切而的情况,称为单剪切。
图3-"所示情况即为单剪切。
受剪构件除了承受剪切外,往往同时伴随着挤压、弯曲与拉伸等作用。
在图3-1 中没有完全给出构件所受的外力与剪切而上的全部内力•而只就是给出了主要的受力与内力。
实际受力与变形比较复杂,因而对这类构件的工作应力进行理论上的精确分析就是困难的。
工程中对这类构件的强度计算,一般采用在试验与经验基础上建立起来的比较简便的计算方法,称为剪切的实用讣算或工程计算。
3、2剪切与挤压的强度计算3、2、1剪切强度计算剪切试验试件的受力情况应模拟零件的实际工作情况进行。
图3-2a为一种剪切试验装巻的简图,试件的受力情况如图3-2b所示,这就是模拟某种销钉联接的工作情形。
当载荷F增大至破坏载荷几时,试件在剪切面加-加及处被剪断。
这种具有两个剪切面的情况,称为双剪切匚由图3-2c可求得剪切而上的剪力为图3-2由于受剪构件的变形及受力比较复杂,剪切而上的应力分布规律很难用理论方法确泄,因而工程上一般采用实用il•算方法来计算受剪构件的应力。
在这种计算方法中, 假设应力在剪切而内就是均匀分布的。
中板圆盘剪剪切跑偏分析及改进实践

中板圆盘剪剪切跑偏分析及改进实践摘要:本文结合现场生产实际,通过对圆盘剪剪切原理及剪切过程进行分析,总结圆盘剪剪切过程中发生的钢板跑偏设备故障产生的原因,提出了有效技术措施。
关键词:圆盘剪跑偏剪切重叠量调整1前言福建三钢集团有限公司中厚板轧钢厂于2007年2月全线建成投产,是福建省第一条的中厚板生产线,二期工程改造完成后产能达到120万吨/年,圆盘式双边剪是中厚板生产线精整区主要设备之一,用于对轧制钢板进行边部纵切,将钢板剪切至要求的成品宽度。
在实际生产过程中,由圆盘剪剪刃间隙调整、剪刃直径,钢板对中精度,轧制板型、碎边剪及设备安装制造精度等原因引起钢板剪切时产生跑偏,造成剪切不及时,严重影响了剪切效率及产品质量,本文结合现场生产实际对圆盘剪剪切过程中发生的钢板跑偏的原因进行总结,并提出有效的改进措施。
2圆盘剪设备技术参数3 圆盘剪剪切跑偏原因分析及改进措施经过几年的生产实践过程观察总结,造成圆盘剪剪切跑偏的主要原因有剪刃间隙调整、刀盘直径,钢板对中精度,刀口钝化、碎边剪及设备安装制造精度等。
具体原因分析及改进措施如下:3.1 两侧剪刃垂直间隙和水平间隙调整的影响圆盘剪剪切钢板过程中理论两侧刀盘垂直间隙和水平间隙是完全一致的,实际上剪刃间隙是影响跑偏和剪切质量最重要的因素,生产过程中,由于存在刀轴窜动,剪刃间隙调整机构传动动精度,刀口直径磨损及钝化差异,操作人员需要根据剪切实际现象进行剪刃间隙补偿性调整,而非理论上严格的将两侧间隙调整一致。
首先我们通过圆盘剪剪切过程中的剪切力分析来找出剪刃垂直间隙即重叠量大小剪切力之间的关系,进而找出剪刃垂直间隙和水平间隙影响跑偏的解决办法。
圆盘剪剪切力公式为:Z1 被剪掉的板边宽度与板厚的比值d/h,影响因素系数由式3-1可以看出,当剪切钢板材质、板型一定时,剪切力大小主要与剪切时剪刃的咬入角a以及受d/h影响的系数Z1有关。
式中ε0 为钢板断裂时的相对切入深度,s为剪刃垂直间隙,D为剪刃直径。
剪切力的计算方法

第3章 剪切和挤压的实用计算3.1 剪切的概念在工程实际中,经常遇到剪切问题。
剪切变形的主要受力特点是构件受到与其轴线相垂直的大小相等、方向相反、作用线相距很近的一对外力的作用(图3-1a),构件的变形主要表现为沿着与外力作用线平行的剪切面(n m -面)发生相对错动(图3-1b)。
图3-1工程中的一些联接件,如键、销钉、螺栓及铆钉等,都是主要承受剪切作用的构件。
构件剪切面上的内力可用截面法求得。
将构件沿剪切面n m -假想地截开,保留一部分考虑其平衡。
例如,由左部分的平衡,可知剪切面上必有与外力平行且与横截面相切的内力Q F (图3-1c)的作用。
Q F 称为剪力,根据平衡方程∑=0Y ,可求得F F Q =。
剪切破坏时,构件将沿剪切面(如图3-la 所示的n m -面)被剪断。
只有一个剪切面的情况,称为单剪切。
图3-1a 所示情况即为单剪切。
受剪构件除了承受剪切外,往往同时伴随着挤压、弯曲和拉伸等作用。
在图3-1中没有完全给出构件所受的外力和剪切面上的全部内力,而只是给出了主要的受力和内力。
实际受力和变形比较复杂,因而对这类构件的工作应力进行理论上的精确分析是困难的。
工程中对这类构件的强度计算,一般采用在试验和经验基础上建立起来的比较简便的计算方法,称为剪切的实用计算或工程计算。
3.2 剪切和挤压的强度计算3.2.1 剪切强度计算剪切试验试件的受力情况应模拟零件的实际工作情况进行。
图3-2a 为一种剪切试验装置的简图,试件的受力情况如图3-2b 所示,这是模拟某种销钉联接的工作情形。
当载荷F 增大至破坏载荷b F 时,试件在剪切面m m -及n n -处被剪断。
这种具有两个剪切面的情况,称为双剪切。
由图3-2c 可求得剪切面上的剪力为2F F Q =图3-2由于受剪构件的变形及受力比较复杂,剪切面上的应力分布规律很难用理论方法确定,因而工程上一般采用实用计算方法来计算受剪构件的应力。
在这种计算方法中,假设应力在剪切面内是均匀分布的。
剪切力的计算公式

剪切力的计算公式
剪切力是在固体力学中使用的一个重要概念,它是指单位面积上
作用的垂直于面的力与该面所承受的剪切应力的比值。
在实际应用中,剪切力的计算需要了解剪切应力和力学模型的基础知识。
剪切力的计算公式是F=τA,其中,F表示剪切力,τ表示剪切应力,A表示所承受剪切应力的面积。
该公式的实际应用中,需要考虑多种因素的影响,如剪切应力的方向、大小、面积的大小和形状等。
对于一个物体而言,当剪切应力作用于其表面时,会产生相应的
剪切力,从而导致物体在其表面产生形变。
剪切力的大小和方向取决
于剪切应力的大小和方向,以及作用面积的大小和形状。
在力学分析中,通常采用二维模型进行计算,以简化计算过程。
要计算剪切力的值,需要首先确定剪切应力的大小和方向。
然后
根据作用面积的大小和形状,确定所承受剪切应力的面积。
最后,根
据剪切力公式计算得到剪切力的值。
在工程中,剪切力的计算常常与材料的剪切强度有关。
一般来说,当剪切力超过材料的剪切强度时,材料就会发生破坏。
因此,在实际
应用中,需要根据材料的性质和使用环境的特点,合理地计算剪切力,以确保材料的安全运行。
总之,剪切力的计算对于实际工程应用具有重要意义,需要以理论和实践相结合的方式进行研究和应用。
在进行计算时,需要考虑多种因素的影响,以确保计算结果的准确性和可靠性。
圆盘剪分条剪切力计算方法
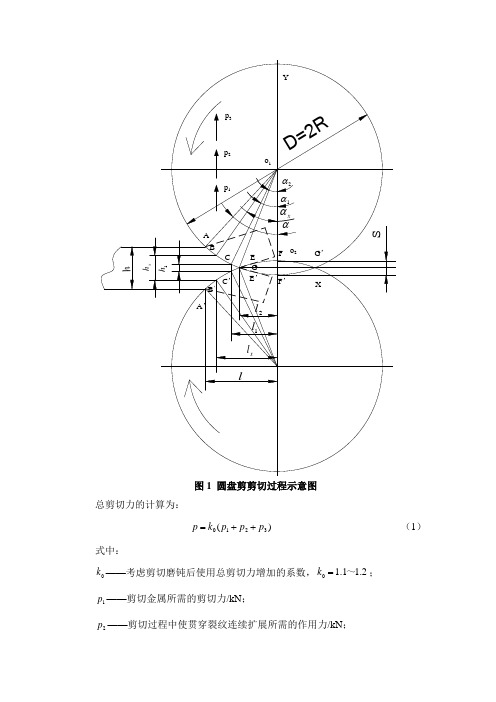
sD =2R xh 1h h2l 1l xl lα1αx α2αA ’BB ’CE F G A C ’G ’E ’F ’XYp 1p 2p 3o 1o 2 图1 圆盘剪剪切过程示意图总剪切力的计算为: )(3210p p p k p ++= (1)式中:0k ——考虑剪切磨钝后使用总剪切力增加的系数,.211.10~=k ;1p ——剪切金属所需的剪切力/kN ; 2p ——剪切过程中使贯穿裂纹连续扩展所需的作用力/kN ;3p ——弯曲切边所需的作用力/kN 。
1、1p 计算当D 、h 、S 一定后,咬入角0a 为 )1(c o s 10DS h a +-=- (2)式中:h——被切板厚/mm ;S ——剪刃重叠量/mm ; D ——圆盘剪直径/mm 。
与咬入角0a 相应的x坐标为l24422Sh hSRh RS l ---+= (3)在剪切区内,与任一坐标x所对应的瞬时被剪件高度为x h2222)(22x R lR h h x ---+= (4)式中:R ——圆盘剪半径/mm 。
设金属开始断裂时的相对切入深度为1ε,剪切薄板时取5125.1σε≈,5σ为被剪板的延伸率。
开始断裂时被剪件瞬时高度为1h )1(11ε-=h h (5)与1h 所对应的x坐标为1l由式(4)21222122l R lR h h ---+=得:21221212214⎥⎦⎤⎢⎣⎡---=l R h h l l εε (6)稳定的剪切面积0F180)sin(sin)2()()(11122122212201πR l Rl R l R lR h l l R h l x d h F ll x -------+--+==⎰(7)从而可得10m a x 1F k F p b στ== (8)式中:1k ——应力换算系数,5.707.0max 1~==bk στb σ——被切板抗拉强度极限/Mpa;2、2p 计算cG l p 32= (9)式中:c G ——裂纹扩展单位面积所需的能量sc h G σβεμμ1)21)(1(-+≈ (10)μ——被剪金属波桑系数,钢板3.0≈μ;β——断裂力学中的COD 降低系数,高强钢取1.0,中等钢取1.5,低强钢取2.0~2.6;3l ——裂纹长度/mm ;sσ——被切板屈服强度极限/Mpa看图1所示,当0221>=-s o o R 时,213l l l -= (11)2l ——上、下剪刃空间相交点G 的x坐标长/mm 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
s
D =
2R x
h 1
h h
2l 1
l x
l l
α
1
αx α2
αA ’
B
B ’C
E F G A C ’
G ’
E ’
F ’
X
Y
p 1
p 2
p 3
o 1
o 2 图1 圆盘剪剪切过程示意图
总剪切力的计算为: )
(3210p p p k p ++= (1)
式中:
0k ——考虑剪切磨钝后使用总剪切力增加的系数,.2
11.10~=k ;
1p ——剪切金属所需的剪切力/kN ; 2
p ——剪切过程中使贯穿裂纹连续扩展所需的作用力/kN ;
3
p ——弯曲切边所需的作用力/kN 。
1、1p 计算
当D 、h 、S 一定后,咬入角0a 为 )
1(c o s 1
0D
S h a +-
=- (2)
式中:
h
——被切板厚/mm ;
S ——剪刃重叠量/mm ; D ——圆盘剪直径/mm 。
与咬入角0a 相应的x
坐标为l
2
4
4
2
2
Sh h
S
Rh RS l -
-
-
+= (3)
在剪切区内,与任一坐标x
所对应的瞬时被剪件高度为x h
2
22
2
)
(22
x R l
R h h x ---+= (4)
式中:
R ——圆盘剪半径/mm 。
设金属开始断裂时的相对切入深度为1ε,剪切薄板时取5
1
25.1σε≈,5σ为被
剪板的延伸率。
开始断裂时被剪件瞬时高度为1h )
1(11ε-=h h (5)
与1h 所对应的x
坐标为1l
由式(4)
2
1
22
212
2
l R l
R h h ---+=
得:
2
1
2
2
1
2
1
2214⎥
⎦
⎤⎢⎣
⎡---=l R h h l l εε (6)
稳定的剪切面积0F
180
)
sin
(sin
)2
()()(1
1
1
22122
212
201
π
R l R
l R l R l
R h l l R h l x d h F l
l x ------
-+--+==
⎰
(7)
从而可得
10m a x 1F k F p b στ== (8)
式中:
1k ——应力换算系数,5
.707.0max 1~==
b
k στ
b σ——被切板抗拉强度极限/Mpa;
2、2p 计算
c
G l p 32= (9)
式中:
c G ——裂纹扩展单位面积所需的能量
s
c h G σ
βεμμ1)21)(1(-+≈ (10)
μ——被剪金属波桑系数,钢板3.0≈μ
;
β——断裂力学中的COD 降低系数,高强钢取1.0,中等钢取1.5,低强钢取2.0~2.6;
3l ——裂纹长度/mm ;
s
σ
——被切板屈服强度极限/Mpa
看图1所示,当0
221>=-s o o R 时,
213l l l -= (11)
2
l ——上、下剪刃空间相交点G 的x
坐标长/mm 。
当
2l x <后,切边和母体金属将完全费力并以不同方向运动。
当0
221==-s o o R
时,2l =0,则3l =1l ;
当0
221<=-s o o R
时,上下剪刃没有空间相交点,所以不存在2l ,即2l =0,
3l =1l 。
3、3p 计算
产生贯穿裂纹后,剪刃作用在切边上的压力,是切边被弯曲并改变运动方向的主要原因。
设在1l 范围内剪刃作用在切边上的压力合力3p 作用在2
l 的作用线上,在力的
作用下,切边在咬入处产生塑性弯曲,则
)
2
(4)
21(412
12
3l l bh l bh p s
s
-
=
-
=
σσ
(12)
式中:
b
——切边宽度
因3p 与1p 、2p 不在同一作用线上,根据等效力矩原则,将其换算到1p 、2
p 作用线上。
对剪刃中心取力矩,换算到1p 、2p 的3p 为
)
2
)((4112
13l l l l bh l p s
-
+=
σ
(13)
由式(1)知:总的剪切力为:P?
考虑到刀刃磨钝的影响,增大15%~20%,这里取20%,
%)
201(+=p P
圆盘剪上的剪切力可根据作用在刀片的力矩来计算,在上下刀片直径、速度都相等而且都驱动时,则与简单轧制情况相似,合力p 垂直作用在刀片上,这时转动刀盘所需的力矩为:
α
sin 1PD M =
驱动圆盘剪的总力矩为:
)
(21M M n M +=
式中,n ——刀片对数
2
M
——一对刀片轴上的摩擦力矩,μ
Pd M =2
,其中d 为刀片轴轴颈的直径
这里取d=170mm ,μ为刀片轴承处的摩擦系数,查手册取0.004,
所以,总力矩为:
)
(21M M n M +=
查文献圆盘剪电动机功率可按下式确定
η
μD Mv N 100021
=
式中:
1μ——考虑刀片与钢板间摩擦系数,1μ=1.1~1.2;
v
——钢板运动速度,m/s η
——传动系统效率,95
.093.0~=η
(因未给出材料的屈服强度、抗拉强度、分条宽度、材料的延伸率,剪切力无法计算)。
