三角函数基础知识点(整理)
高中数学三角函数知识点整理
高中数学三角函数知识点整理在高中数学课程中，三角函数是一个非常重要且基础的概念。
三角函数包括正弦函数、余弦函数、正切函数等，它们在数学中有着广泛的应用。
一、正弦函数正弦函数是三角函数中的一种，通常用sin表示。
正弦函数的定义域为实数集，值域为[-1, 1]。
正弦函数的图像是一条周期性振荡的曲线，其周期为2π。
在直角三角形中，正弦函数可以表示为对边与斜边的比值，即sinθ=对边/斜边。
二、余弦函数余弦函数是三角函数中的另一种常见函数，通常用cos表示。
余弦函数的定义域为实数集，值域为[-1, 1]。
余弦函数的图像也是一条周期性的曲线，其周期也为2π。
在直角三角形中，余弦函数可以表示为邻边与斜边的比值，即cosθ=邻边/斜边。
三、正切函数正切函数是三角函数中的另一重要函数，通常用tan表示。
正切函数的定义域不包括所有使余弦函数值为零的实数，其值域为所有实数。
正切函数的图像是一条振荡的曲线，不存在周期。
在直角三角形中，正切函数可以表示为对边与邻边的比值，即tanθ=对边/邻边。
四、三角函数的基本性质三角函数具有一些基本性质，如周期性、奇偶性和对称性等。
正弦函数和余弦函数都是偶函数，而正切函数是奇函数。
正弦函数和余弦函数都是周期函数，其周期为2π。
而正切函数是无周期性的。
五、三角函数的图像和性质正弦函数的图像为一条周期性振荡的曲线，对称于y轴。
余弦函数的图像也是一条周期性振荡的曲线，对称于x轴。
而正切函数的图像则是在一些点上有无穷大的奇点。
综上所述，三角函数是数学中非常重要的一部分，学习三角函数知识有助于理解数学中的许多问题和现象，特别是在几何和物理等领域有着广泛的应用。
希望通过本文的整理，能够帮助读者更好地理解和掌握高中数学中的三角函数知识点。
九年级三角函数知识点整理
九年级三角函数知识点整理三角函数是数学中一个重要的概念，特别是在处理角度、弧度、三角形和圆等方面。
以下是九年级三角函数知识点整理：1. 锐角三角函数的定义：锐角角A的正弦（sin），余弦（cos）和正切（tan），余切（cot）以及正割（sec），余割（csc）都叫做角A的锐角三角函数。
正弦（sin）：等于对边比斜边，即sinA=a/c。
余弦（cos）：等于邻边比斜边，即cosA=b/c。
正切（tan）：等于对边比邻边，即tanA=a/b。
余切（cot）：等于邻边比对边，即cotA=b/a。
正割（sec）：等于斜边比邻边，即secA=c/b。
余割（csc）：等于斜边比对边，即cscA=c/a。
2. 特殊角的三角函数值：对于一些特定的角度，三角函数有特定的值。
例如，当角度为30°、45°和60°时，正弦、余弦和正切的值分别是1/2、√2/2、√3/3等。
3. 互余角的关系：sin(π-α)=cosα，cos(π-α)=sinα，tan(π-α)=cotα，cot(π-α)=tanα。
4. 平方关系：sin^2(α)+cos^2(α)=1，tan^2(α)+1=sec^2(α)，cot^2(α)+1=csc^2(α)。
5. 积的关系：sinα=tanα·cosα，cosα=cotα·sinα。
6. 诱导公式：对于角度的和差、倍角等运算，可以通过诱导公式简化计算。
例如，sin(A+B)和cos(A+B)可以通过诱导公式转化为sinAcosB+cosAsinB 和cosAcosB-sinAsinB。
7. 图像与性质：正弦、余弦和正切的图像是周期函数，具有对称性。
例如，正弦函数在y轴两侧对称，余弦函数在x轴上对称。
此外，三角函数的最大值和最小值以及对应的x值也是重要的知识点。
8. 应用：三角函数在日常生活和科学研究中有着广泛的应用。
例如，在测量、航海、工程、物理和数学等领域中，经常需要用到三角函数的知识。
三角函数整理
一、三角函数公式1、两角和公式sin(A＋B) = sinAcosB＋cosAsinB cos(A＋B) = cosAcosB－sinAsinB sin(A－B) = sinAcosB－cosAsinB cos(A－B) = cosAcosB＋sinAsinB tan(A＋B) = (tanA＋tanB)/(1－tanAtanB)tan(A－B) = (tanA－tanB)/(1＋tanAtanB)cot(A＋B) = (cotAcotB－1)/(cotB＋cotA)cot(A－B) = (cotAcotB＋1)/(cotB－cotA)2、倍角公式sin2A=2sinA•cosA cos2A = cos2 A－sin2 A=2cos2 A－1 tan2A = 2tanA/(1－tan2 A) =1－2sin2 A 3、三倍角公式sin3A = 3sinA－4sin3A cos3A = 4cos3A－3cosAtan3A = tanA • tan(π/3＋A)• tan(π/3－A)4、半角公式sin(A/2) = √{(1－cosA)/2} tan(A/2)=sin(A/2)/cos(A/2)cos(A/2) = √{(1 ＋cosA)/2} =[2sin(A/2)cos(A/2)]/[2cos2(A/2)] tan(A/2) = √{(1－cosA)/(1＋cosA)} =sinA/(1＋cosA)cot(A/2) = √{(1＋cosA)/(1－cosA)} = (1－cosA)/sinA5、和差化积sinA＋sinB = 2sin[(A＋B)/2]cos[(A－B)/2]sinA－sinB = 2cos[(A＋B)/2]sin[(A－B)/2]cosA－cosB = －2sin[(A＋B)/2]sin[(A－B)/2]tanA＋tanB = sin(A＋B)/cosAcosB6、积化和差sinAsinB =－1/2•[cos(A＋B)－cos(A－B)]cosAcosB = 1/2•[cos(A＋B)＋cos(A－B)]sinAcosB = 1/2•[sin(A＋B)＋sin(a－b)]cosAsinB = 1/2•[sin(A＋B)-－sin(A－B)]7、诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）= sinαtan（2kπ＋α）= tanαcos（2kπ＋α）= cosαcot（2kπ＋α）= cotα(以上k∈Z)公式二：设α为任意角，π＋α的三角函数值与α的三角函数值之间的关系：sin（π＋α）= －sinαtan（π＋α）= tanαcos（π＋α）=－cosαcot（π＋α）= cotα公式三：任意角α与－α的三角函数值之间的关系：sin（－α）=－sinαtan（－α）=－tanαcos（－α）= cosαcot（－α）=－cotα公式四：利用公式二和公式三可以得到π－α与α的三角函数值之间的关系：sin（π－α）= sinαtan（π－α）=－tanαcos（π－α）=－cosαcot（π－α）=－cotα公式五：利用公式一和公式三可以得到2π－α与α的三角函数值之间的关系：sin（2π－α）=－sinαtan（2π－α）= －tanαcos（2π－α）= cosαcot（2π－α）=－cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin（π/2＋α）= cosαtan（π/2＋α）= －cotαcos（π/2＋α）= －sinαcot（π/2＋α）= －tanαsin（π/2－α）= cosαtan（π/2－α）= cotαcos（π/2－α）= sinαcot（π/2－α）= tanαsin（3π/2＋α）=－cosαtan（3π/2＋α）=－cotαcos（3π/2＋α）= sinαcot（3π/2＋α）=－tanαsin（3π/2－α）=－cosαtan（3π/2－α）= cotαcos（3π/2－α）=－sinαcot（3π/2－α）= tanα8、万能公式sinA= 2tan(A/2) / {1+[tan(A/2)]2}cosA= {1－[tan(A/2)]2} / {1＋[tan(A/2)]2}tanA= [2tan(A/2)]/{1－[tan(A/2)]2}9、其他公式a•sinA＋b•cosA = [√(a2＋b2) ]•sin[A+arctan (b/a) ]a•sinA＋b•cosA = [√(a2＋b2) ]•cos[A－arctan (a/b) ]1＋sinA = [ sin(A/2)＋cos(A/2) ]21－sinA = [ sin(A/2)－cos(A/2) ]210、其他非重点三角函数cscA = 1/sinAsecA = 1/cosA二、双曲函数sh= (e x－e－x)/2ch = (e x＋e－x)/2th = sh/ch =(e x－e－x)/(e x＋e－x)cth = ch /sh =(e x＋e－x)/(e x－e－x)sech(x) = 1 / ch = 2 / (e x＋e－x)csch(x) = 1 / sh = 2 / (e x－e－x）三、特殊公式A•sin(ωt＋θ)＋B•sin(ωt＋φ)=√{(A2＋B2＋2ABcos(θ－φ)}• sin{ ωt＋arcsin (A•sinθ＋B•sinφ) / √{A2＋B2＋2ABcos(θ－φ)} }√表示根号,包括{……}中的内容。
高中三角函数知识点整理
高中三角函数知识点整理三角函数是数学中重要的概念，存在于高中数学课程中，是几何、代数、微积分等领域的基础知识。
下面整理了高中三角函数的重要知识点，希望对学生们的学习有帮助。
一、三角函数的基本概念1.弧度制：角的度量单位，一个角所对应的弧长等于半径的长度时，这个角的大小为1弧度。
2.角的三要素：顶点，始边，终边，顶点为角的端点，始边为角的起始边，终边为角的结束边。
3.弧度与角度的转换：角度数×π/180=弧度。
4.等角：具有相同角度的两个角是等角。
5. 正弦：给定一个锐角∠A，对于 A 的任何弧 B，就有 sin A = sin B。
二、正弦、余弦和正切函数1. 正弦函数：在数轴上，根据半径 r 的终端点 (x, y)，它的正弦函数值定义为 y / r，可以表示为sinθ。
2. 余弦函数：在数轴上，根据半径 r 的终端点 (x, y)，它的余弦函数值定义为 x / r，可以表示为cosθ。
3. 正切函数：在数轴上，根据半径 r 的终端点 (x, y)，它的正切函数值定义为 y / x，可以表示为tanθ。
4.三角函数的性质：正弦和余弦函数的值在-1到1之间，正切函数的值没有限制。
三、三角函数的基本性质1.三角函数的周期性：正弦和余弦函数周期为2π，正切函数周期为π。
2.函数图像：正弦函数和余弦函数的图像为曲线，正切函数的图像为直线。
3.函数值的变化：正弦函数和余弦函数的值在一个周期内从-1到1变化，正切函数在不同区间内的值无限制变化。
4. 正弦函数和余弦函数的图像对称：sin(-θ) = -sinθ，cos(-θ) = cosθ。
5. 周期性的性质：sin(θ + 2πn) = sinθ，cos(θ + 2πn) =cosθ，n为整数。
6. 三角函数的诱导公式：sin(α + β) = sinαcosβ +cosαsinβ，cos(α + β) = cosαcosβ - sinαsinβ。
三角函数的基本概念与公式整理
三角函数的基本概念与公式整理三角函数是数学中重要的概念，它们在几何学、物理学、工程学等领域中有广泛的应用。
本文将对三角函数的基本概念及其相关的公式进行整理和归纳。
一、正弦函数（Sine Function）正弦函数是最基本的三角函数之一，以sin表示，其定义域是所有实数集合，值域为[-1, 1]。
正弦函数的图像是一条连续的正弦曲线。
正弦函数的主要公式如下：1. 正弦函数的周期性：sin(x) = sin(x + 2πn)，其中n为整数。
2. 正弦函数的奇偶性：sin(-x) = -sin(x)。
3. 正弦函数的和差角公式：- sin(x ± y) = sin(x)cos(y) ± cos(x)sin(y)- sin(x ± π/2) = ±cos(x)4. 正弦函数的倍角公式：- sin(2x) = 2sin(x)cos(x)- sin(3x) = 3sin(x) - 4sin^3(x)- sin(4x) = 8sin^4(x) - 8sin^2(x) +1二、余弦函数（Cosine Function）余弦函数也是三角函数中常见的一种，以cos表示，其定义域是所有实数集合，值域为[-1, 1]。
余弦函数的图像是一条连续的余弦曲线。
余弦函数的主要公式如下：1. 余弦函数的周期性：cos(x) = cos(x + 2πn)，其中n为整数。
2. 余弦函数的奇偶性：cos(-x) = cos(x)。
3. 余弦函数的和差角公式：- cos(x ± y) = cos(x)cos(y) ∓ sin(x)sin(y)- cos(x ± π/2) = ∓sin(x)4. 余弦函数的倍角公式：- cos(2x) = cos^2(x) - sin^2(x)- cos(3x) = 4cos^3(x) - 3cos(x)- cos(4x) = 8cos^4(x) - 8cos^2(x) + 1三、正切函数（Tangent Function）正切函数是另一种常见的三角函数，以tan表示，其定义域为所有实数，但在某些角度上没有定义，值域为整个实数集合。
三角函数基础知识点(整理)
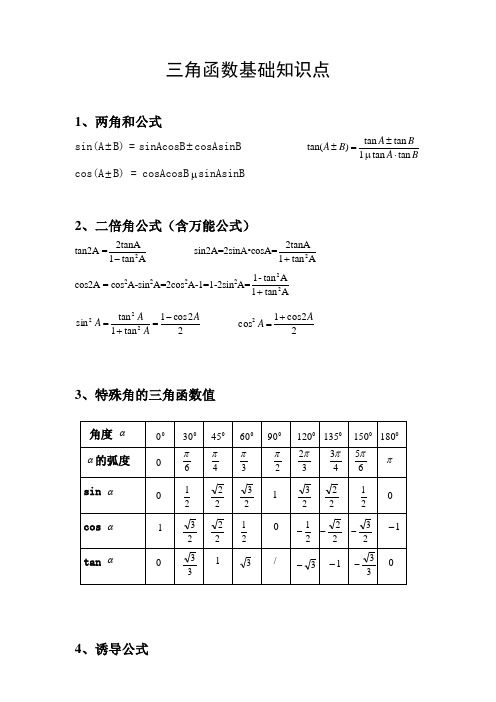
三角函数基础知识点1、两角和公式sin(A ±B) = sinAcosB ±cosAsinB BA BA B A tan tan 1tan tan )tan(⋅±=±μcos(A ±B) = cosAcosB μsinAsinB2、二倍角公式（含万能公式）tan2A =A tan 12tanA 2- sin2A=2s inA•cosA=Atan 12tanA2+ cos2A = cos 2A-sin 2A=2cos 2A-1=1-2sin 2A=A tan 1Atan -122+ 22cos 1tan 1tan sin 222A A A A -=+= 22cos 1cos 2A A +=3、特殊角的三角函数值4、诱导公式公式一： απαsin )2sin(=+k ；απαcos )2cos(=+k ；απαtan )2tan(=+k ．（其中Z ∈k ）．公式二： ααπ-sin sin(=+）；ααπ-cos cos(=+）；ααπtan tan(=+）． 公式三： sin()-sin αα-=；cos()cos αα-= ；tan()tan αα-=-． 公式四： ααπsin sin(=-）；ααπ-cos cos(=-）；ααπtan tan(-=-） 公式五： sin(2sin παα-=-）；cos(2cos παα-=）；tan(2tan παα-=-）公式六： sin(2π) = cos ； cos(2π) = sin ． 公式七： sin(2π+) = cos ；cos(2π+) = sin ．公式八： sin(32π)=- cos ； cos(32π) = -sin ．公式九： sin(32π+) = -cos ；cos(32π+) = sin ．以上九组公式可以推广归结为：要求角2k πα⋅±的三角函数值，只需要直接求角α的三角函数值的问题．这个转化的过程及结果就是十字口诀“奇变偶不变，符号看象限”。
初三数学三角函数知识点整理
初三数学三角函数知识点整理
三角函数知识：
（一）基本概念：
1. 三角函数：三角函数是一类变化比较复杂的可以描述出来的函数，它们可以用来描述各种具有特殊的几何关系的函数关系。
2. 周期性特征：三角函数都具有周期性的特征，正弦函数的周期长度为2π，余弦、正切函数的周期有π。
3. 区间形态特征：三角函数的话，一个比较方便的办法是先分析函数图像的区间变化形态，分析一下函数的一般变化规律，进而猜测出变化规律。
（二）三角函数求值
1. 小角度求值法：小角度求值法是把角极限值和角转换为弧度来进行求解，这种方法的优点是可以把角的大小任意进行变量，从而实现任意角度的三角函数求值。
2. 单位圆三角等价：单位圆三角等价是把圆上的位置用三角函数来表示，其中圆心为(0,0)，半径为1。
3. 唯一方程法：唯一方程法就是把三角函数问题变成一般代数方程来求解，这样就可以利用代数方法解决三角函数问题了。
（三）三角函数运算
1. 三角函数对数：三角函数对数可以得到两个三角函数的乘积，除法
或求幂的值。
2. 三角形关系：三角形关系是指把一个等腰三角形的一条边的长度按照给定的一定比例缩放得到另外两边的长度。
3. 余弦定理：余弦定理是指任意一个三角形的两边的长度乘积等于它的最短的三条边的三次方再乘以一个特别的常数。
初中数学三角函数知识点整理
初中数学三角函数知识点整理【初中数学】三角函数知识点整理一、概念介绍三角函数是研究三角形各边与角度之间关系的数学函数，包括正弦函数（sin）、余弦函数（cos）、正切函数（tan）等。
它们在数学、物理、工程等领域中有非常广泛的应用，对于初中学生来说，掌握三角函数的基本概念和性质是重要的数学基础。
二、正弦函数（sin）1. 定义：在平面直角坐标系中，以原点为顶点，与x轴正半轴的夹角（弧度或角度）对应的纵坐标值。
2. 特点：a. 值域：[-1, 1]，即正弦函数的取值范围在-1到1之间。
b. 周期性：sin(x) = sin(x + 2πk)，其中k为整数，即正弦函数的图象在每个周期内重复。
c. 对称性：sin(-x) = -sin(x)，即正弦函数关于原点对称。
三、余弦函数（cos）1. 定义：在平面直角坐标系中，以原点为顶点，与x轴正半轴的夹角（弧度或角度）对应的横坐标值。
2. 特点：a. 值域：[-1, 1]，即余弦函数的取值范围在-1到1之间。
b. 周期性：cos(x) = cos(x + 2πk)，其中k为整数，即余弦函数的图象在每个周期内重复。
c. 对称性：cos(-x) = cos(x)，即余弦函数关于y轴对称。
四、正切函数（tan）1. 定义：在平面直角坐标系中，以原点为顶点，与x轴正半轴的夹角（弧度或角度）对应的纵坐标除以横坐标的比值。
2. 特点：a. 值域：(-∞, +∞)，即正切函数的取值范围为所有实数。
b. 周期性：tan(x) = tan(x + πk)，其中k为整数，即正切函数的图象在每个周期内重复。
五、三角函数的相关性质1. 三角函数的正负关系：在0到π/2之间，sin函数为正，cos函数为正；在π/2到π之间，sin函数为正，cos函数为负；在π到3π/2之间，sin函数为负，cos函数为负；在3π/2到2π之间，sin函数为负，cos函数为正。
2. 三角函数的互相关系数：tan(x) = sin(x) / cos(x)，cot(x) = cos(x) / sin(x)，sec(x) = 1 / cos(x)，csc(x) = 1 / sin(x)。
(完整版)高中数学三角函数复习专题
高中数学三角函数复习专题一、知识点整理 :1、角的看法的推行：正负，范围，象限角，坐标轴上的角；2、角的会集的表示：①终边为一射线的角的会集：x x2k, k Z=|k 360o, k Z②终边为向来线的角的会集：x x k, k Z；③两射线介定的地域上的角的会集：x 2k x2k, k Z④两直线介定的地域上的角的会集：x k x k, k Z；3、任意角的三角函数：（1）弧长公式： l a R R 为圆弧的半径，a为圆心角弧度数， l 为弧长。
（2）扇形的面积公式：S 1lR R 为圆弧的半径， l 为弧长。
2（3）三角函数定义：角中边上任意一点 P 为 ( x, y) ，设 | OP |r 则：sin y, cos x ,tan y r= a 2b2 r r x反过来，角的终边上到原点的距离为r 的点P的坐标可写为：P r cos, r sin 比如：公式 cos()cos cossin sin的证明（4）特别角的三角函数值α032 64322sin α012310-10222cosα13210-101222tan α0313不存不存0 3在在（5）三角函数符号规律：第一象限全正，二正三切四余弦。
（6）三角函数线：（判断正负、比较大小，解方程或不等式等）y T 如图，角的终边与单位圆交于点P，过点 P 作 x 轴的垂线，P 垂足为 M ，则Ao 过点 A(1,0)作 x 轴的切线，交角终边OP 于点 T，则M x。
（7）同角三角函数关系式：①倒数关系： tana cot a 1sin a ②商数关系： tan acosa③平方关系： sin 2 a cos2 a1（ 8)引诱公试sin cos tan三角函数值等于的同名三角函数值，前方-- sin+ cos- tan加上一个把看作锐角时，原三角函数值的- tan-+ sin- cos符号；即：函数名不变，符号看象限+- sin- cos+ tan2-- sin+ cos- tan2k++ sin+ cos+ tansin con tan2+ cos+ sin+ cot三角函数值等于的异名三角函数值，前方2+ cos- sin- cot加上一个把看作锐角时，原三角函数值的3- cos- sin+ cot2符号 ;3- cos+ sin- cot2即：函数名改变，符号看象限 : sin x cos x cos x比方444cos x sin x444.两角和与差的三角函数：（1）两角和与差公式：cos() cos a cos sin a sin sin( a) sin a coscosa sintan a(atan a tan注：公式的逆用也许变形)1 tan a tan．．．．．．．．．（2）二倍角公式：sin 2a 2sin acosa cos 2a cos2 a sin 2 a12 sin2 a 2 cos2 a 12 tan atan 2a1 tan2 a(3)几个派生公式：①辅助角公式：a sinx bcosx a2b2 sin(x)a22 cos()b x比方： sinα± cosα＝ 2 sin4＝ 2 cos4．sinα±3 cosα＝ 2sin3＝2cos3等．②降次公式： (sin cos) 21sin 2cos21cos2,sin 21cos222③ tan tan tan()(1 tan tan)5、三角函数的图像和性质：（此中 k z ）三角函数y sin x定义域（- ∞， +∞）值域[-1,1]最小正周期T2奇偶性奇[ 2k,2k]22单调性单调递加[ 2k,2k3 ]22单调递减x k对称性2(k ,0)零值点x ky cosx（- ∞， +∞）[-1,1]T 2偶[( 2k 1) ,2k ]单调递加[( 2k , (2k 1) ]单调递减x k(k,0)2x k2y tan xx k2（-∞，+∞）T奇(k,k)22单调递加k(,0)x kx k2x 2 k，最值点y max1ymax 1；无x k2x(2k 1) ，y min1y min1 6、 .函数y Asin( x) 的图像与性质：（本节知识观察一般能化成形如y Asin( x) 图像及性质）（ 1）函数 y Asin( x) 和 y Acos( x2 ) 的周期都是T（ 2）函数y A tan( x) 和 y Acot( x) 的周期都是T（ 3）五点法作y Asin( x) 的简图，设t x，取0、、、3、2来求相应x22的值以及对应的y 值再描点作图。
九年级数学三角函数全章知识点整理
一、角度与弧度制1.角度的定义：角度是从一个弧中截取的一部分，一个完整圆共有360度。
一个度可以被继续等分为60分，每一分可以被继续等分为60秒。
2.弧度的定义：弧度是弧与半径相对应的圆心角所对的弧长的比值。
一个圆的周长为2πr，一个圆的弧长等于其半径乘以所对的圆心角的弧度数。
一个圆的周长为2π弧度。
3.角度与弧度的互相转化：360度=2π弧度；1度=π/180弧度；1弧度=180/π度。
二、单位圆与三角比1.单位圆的定义：单位圆是一个半径为1的圆，在坐标系中，圆心坐标为(0,0)。
2. 正弦、余弦、正切的定义：对于单位圆上任意一点P(x,y)，假设与x轴正方向的夹角为θ，则点P的坐标(x,y)可以表示为(x,y)=(cosθ,sinθ)。
3. 正弦、余弦、正切与角度的关系：sinθ = y，cosθ = x，tanθ = y/x。
4. 余弦、正弦、正切与弧度的关系：sinθ = y，cosθ = x，tanθ = y/x。
5.三角函数的周期性：三角函数的周期是2π。
三、基本三角函数恒等式1. 余弦与正弦的关系：cos²θ + sin²θ = 12. 正切与余切的关系：tanθ = 1/cotθ。
3. 正弦与余切的关系：sinθ = 1/cscθ。
4. 余弦与正切的关系：cosθ = 1/secθ。
5. 正弦与正切的关系：sinθ = tanθ/cosθ。
四、三角函数的图像与性质1. 正弦函数的图像与性质：y = sinθ，函数图像为典型的正弦曲线，周期为2π，在(0,0)处取得最小值0，最大值1，满足奇函数性质。
2. 余弦函数的图像与性质：y = cosθ，函数图像为典型的余弦曲线，周期为2π，在(0,0)处取得最大值1，最小值-1，满足偶函数性质。
3. 正切函数的图像与性质：y = tanθ，函数图像为典型的正切曲线，周期为π，无定义点为θ = (2n+1)π/2，其中n为整数。
高一数学三角函数知识整理
⾼⼀数学三⾓函数知识整理⾼⼀数学三⾓函数知识整理⼀、正弦函数图像函数y=sin x 的定义域，值域，奇偶性，单调性，周期性 1、函数y=sin x 的定义域是R ，值域为[-1，1] 2、当x ∈{x| x=22 k ππ+,k ∈Z}时，y 有最⼤值为1，当x ∈{x|x=322k ππ+,k ∈Z}时，y 有最⼩值为-13、函数y=sin x 的图像关于原点对称是奇函数，可以根据sin(-x)=-sinx 证明。
对称中⼼为（k π，0）对称轴为x=k π+2π(k ∈Z)。
4、在[22k ππ-，22k ππ+]k ∈Z 上单调递增，在[22k ππ+，322k ππ+]k∈Z 上单调递减。
5、函数y=sin x 的周期为2k π（k ∈Z 且k ≠0），最⼩正周期为2π注意有界性：sin 1x ≤ ⼆、余弦函数图像函数y=cosx 的定义域，值域，奇偶性，单调性，周期性 1、函数y=cos x 的定义域是实数集R ，值域是[-1，1]2、当x ∈{x | x=2k π，k ∈Z}时y 有最⼤值为1，当x ∈{x | x=2k π+π,k∈Z}时，y 有最⼩值为-1。
3、函数y=cosx 关于y 轴对称是偶函数，可以通过诱导公式cos(-x)=cosx 证明。
对称中⼼[2k ππ+，0]，对称轴为x= k π4、在[2k ππ-，2k π]上单调递增，在[2k π，2k ππ+]上单调递减。
5、函数y=cosx 的周期为2k π（k ∈Z 且k ≠0）最⼩正周期为2π。
注意有界性：cos 1x ≤ 三、正切函数图像函数y=tanx 定义域，值域，奇偶性，单调性，周期性1、 y=tan x 的定义域是{x| x ∈R 且x ≠2k ππ+,k ∈Z}。
因为定义域不连贯，所以当有题⽬说该函数在定义域上怎么怎么样是错误的（同样⽤于其它所有函数）。
值域是⼀切实数R2、 y=tan x 的定义域关于原点对称是奇函数，根据诱导公式且tan(-x)=-tan x 可以证明。
三角函数所有公式及基本性质[整理]
![三角函数所有公式及基本性质[整理]](https://img.taocdn.com/s3/m/967dc291daef5ef7ba0d3c95.png)
一、任意角的三角比（一）诱导公式ααπsin )2sin(=+k ααπcos )2cos(=+k ααπtg k tg =+)2( ααπctg k ctg =+)2( ααsin )sin(-=- ααcos )cos(=- ααtg tg -=-)( ααctg ctg -=-)( ααπsin )sin(-=+ααπcos )cos(-=+ααπtg tg =+)(ααπctg ctg =+)(ααπsin )sin(=- ααπcos )cos(-=- ααπtg tg -=-)( ααπctg ctg -=-)( ααπsin )2sin(-=- ααπcos )2cos(=- ααπtg tg -=-)2( ααπctg ctg -=-)2( ααπcos )2sin(=- ααπsin )2cos(=-ααπctg tg =-)2(ααπtg ctg =-)2(ααπcos )2sin(=+ααπsin )2cos(-=+ ααπctg tg -=+)2(ααπtg ctg -=+)2(ααπcos )23sin(-=- ααπsin )23cos(-=- ααπctg tg =-)23( ααπtg ctg =-)23(ααπcos )23sin(-=+ ααπsin )23cos(=+ ααπctg tg -=+)23( ααπtg ctg -=+)23(（二）关系结构图（三）三角比符号αsin αsec αtg αctg αcos αcsc 1++ __ cos α&sec αsin α&csc α+ + __++ _ _tg α&ctg α1.同角三角比的关系 倒数关系 1csc sin =αα 1sec cos =αα1=ααctg tg商数关系 αααcos sin =tg αααsin cos =ctg平方关系 1cos sin 22=+αα αα22sec 1=+tg αα22csc 1=+ctg2.两角和与差的三角比两角差的余弦公式 βαβαβαsin sin cos cos )cos(+=- 两角和的余弦公式 βαβαβαsin sin cos cos )cos(-=+ 两角差的正弦公式 βαβαβαsin cos cos sin )sin(-=- 两角和的正弦公式 βαβαβαsin cos cos sin )sin(+=+ 两角差的正切公式 βαβαβαtg tg tg tg tg +-=-1)(两角和的正切公式 βαβαβαtg tg tg tg tg -+=+1)(形式)sin(ϕα+Aπϕϕϕϕααα20,sin ,cos )sin(cos sin 222222<≤+=+=++=+ba b ba ab a b a3.二倍角的三角比ααααααααααα22222122sin 211cos 2sin cos 2cos cos sin 22sin tg tg tg -=-=-=-==4.半角的三角比αααααααααααsin cos 1cos 1sin cos 1cos 122cos 12cos 2cos 12sin -=+=+-±=+±=-±=tg5.万能置换公式21222121cos 2122sin 2222αααααααααtg tgtg tg tg tg tg-=+-=+=_1. 三角形的面积C ab B ca A bc S sin 21sin 21sin 21===∆ 2. 正弦定理)2(sin sin sin R Cc B b A a === 3. 余弦定理abc b a C ca b a c B bc a c b A C ab b a c B ca c a b A bc c b a 2cos 2cos 2cos cos 2cos 2cos 2222222222222222222-+=⇔-+=⇔-+=-+=⇔-+=⇔-+=或三角比补充概念或公式一、 有关sin α与cos α，tg α与tg α，|sin α|与|cos α|，|tg α|与|ctg α|大小比较1.sin α与cos α（下左图）当α的终边在第一、第三象限的角平分线上时，sin α=cos α 当α的终边在此角平分线的上方，即图中区域①时，sin α>cos α 当α的终边在此角平分线的下方，即图中区域②时，sin α<cosα2.tg α与ctg α（上右图）当α的终边在第一、第三象限，或第二、第四象限的角平分线上时，tg α=ctg α 当α的终边在图中区域①、或③、或⑤、或⑦时（不包括坐标轴），tg α>ctg α 当α的终边在图中区域②、或④、或⑥、或⑧时（不包括坐标轴），tg α<ctg α3. |sin α|与|cos α|（下左图）当α的终边在第一、第三象限，或第二、第四象限的角平分线上时，|sin α|=|cos α| 当α的终边在图中区域①或③时，|sin α|>|cos α| 当α的终边在图中区域②或④时，|sin α|<|cosα|4. |tg α|与|ctg α|（上右图）当α的终边在第一、第三象限，或第二、第四象限的角平分线上时，|tg α|=|ctg α| 当α的终边在图中区域①或③时（不包括坐标轴），|tg α|>|ctg α| 当α的终边在图中区域②或④时（不包括坐标轴），|tg α|<|ctg α| 二、三角中常用的手法（sin α+sin β）与（cos α+cos β）分别平方后相加，可以产生cos(α-β) （sin α+sin β）与（cos α+cos β）分别平方后相加，可以产生sin(α+β) 三、1.在非直角ΔABC 中，有tgAtgBtgC tgC tgB tgA =++2.在tgA ，tgB ，tgC 存在的前提下，A+B+C=k π（k 属于整数）是tgAtgBtgC tgC tgB tgA =++的充要条件。
三角函数知识点整理
1.角的有关概念(1)角的概念：角可以看成是由一条射线绕着它的端点旋转而成的始时的射线叫做角的始边；旋转终止时的射线叫做角的终边。
(2)正角、负角和零角按逆时针方向旋转而成的角叫做正角；按顺时针方向旋转而成的角叫做负角；当一条射线没有作任何旋转时而成的角叫做零角⑶象限角在平面直角坐标系下,使角的顶点与坐标原点重合的始边与x轴的正半轴重合，角的终边落在第几象限，就把这个角称做第几象限角，若角的终边落在坐标轴上,称为轴线角,这个角不属于任何象限.(4)各个象限的半角范围可以用下图记忆，图中的I、H、m、IV分别指第一、二、三、四象限角的半角范围；(5)终边相同的角与a角终边相同的角所组成的集合：S={P|P =a +2k n,k w z}2.角度制与弧度制设扇形的弧长为l圆心角为a (rad),半径为R,面积为S角a的弧度数公式 2 兀 X a /360 )角度与弧度的换算①360° =2 兀 rad②1° =兀/180rad③ 1rad= 180° 15718' =57.3°弧长公式l =a|R扇形的面积公式 1S ='lR23. 任意角的三角函数三角函数(6个)表示：a为任意角，角a的终边上任意点P的坐标为(x, y),它与原点的距离为r=V x2+y2A0(r>0,当点P在单位圆上时，r=1 )那么角a的正弦、余弦、正切、余切、正割、余割分别是:y x y xr rsina=—, cosa =—，tan a = — , cot a = — , seca=—，csca =—.r r x yx y4.同角三角函数关系式射线的端点叫做角的顶点；旋转开, cosa cot a=sin a③ 倒数关系：tanacota=1 ②商数关系：tana=sn-acosa ③平方关系：sin2 a cos2 a = 15.6.l 特殊锐角(0° , 30° , 45° , 60° , 90° )的三角比的值三角函数角度正弦余弦正切余切 0° 0 1 0不存在30° 1 ~Z W 2叵 3展45口72 ~z21 1 60°2 _L 2V3V3 3 90°P 1不存在7.诱导公式：(奇变偶不变，符号看象限)k •冗/2+a 所谓奇偶指的是整数 k 的奇偶性公式三角函数sin acosatana诱导公式一 sin( a + k 0) = sin acos( a + k 2冗)=cos a tan( 口 + k ，2兀)=tan a诱导公式二sin(冗十 a ) = -sin acos( n + a ) = - cos 。
三角函数知识点整理
，已知其中一个式子的值，其余二式均可求出，且必要时可以换元。
6．函数的最值（几种常见的函数及其最值的求法）：
① （或 型：利用三角函数的值域，须注意对字母的讨论
② 型:引进辅助角化成 再利用有界性
③ 型：配方后求二次函数的最值,应注意 的约束
④ 型：反解出 ，化归为 解决
⑥ 型:常用到换元法： ,但须注意 的取值范围: 。
（3)三角形中常用的关系：
, , ,
,
三角函数值域总结：
注意：定义域的取值
1、应用提斜公式，形如 可直接用公式。
形如 ，逆用倍角公 式化成提斜的形式。
形如 或 的的函数（式中也可以是同名函数），先 、
用和差化积公式展开,化归为例1、例２的形式求最值．
单调性
单调递增
单调递减
单调递增
单调递减
单调递增
对称性
(对称轴）
(对称中心）
（对称轴）
(对称中心)
（对称中心)
零值点
最值点
,
,
， ;
，
无
１0．函数 的图像与性质:
(本节知识考察一般能化成形如 图像及性质）
（1）函数 和 的周期都是
（2）函数 和 的周期都是
（3）五点法作 的简图,设 ，取0、 、 、 、 来求相应 的值以及对应的y值再描点作图。
（6）结构变化：在三角变换中常常对条件、结论的结构进行调整，或重新分组,或移项，或变乘为除，或求差等等。在形式上有时需要和差与积的互化、分解因式、配方等。
（7）消元法:如果所要证明的式子中不含已知条件中的某些变量,可用此法
（8）思路变换:如果一种思路无法再走下去，试着改变自己的思路，通过分析比较去选择更合适、简捷的方法去解题目。
三角函数知识点整理
三角函数知识点整理三角函数是数学中研究角度和角度关系的重要内容。
它在几何、代数、物理等领域都有广泛的应用。
本文将对常见的三角函数及其性质进行整理，以便帮助读者更好地理解和掌握相关知识。
一、三角函数的定义与关系在平面直角坐标系中，假设有一个单位圆，以原点为圆心，半径为1，任意选取一个角θ ，则角θ 的终边与单位圆交于一点 P(x, y)，其中x 和 y 分别表示点 P 的横坐标和纵坐标。
根据这个定义，我们可以定义以下三角函数：1. 正弦函数sin θ = y2. 余弦函数cos θ = x3. 正切函数tan θ = y / x其中，θ 表示角度，y / x 是 y 除以 x 的商。
注意，在数学中，角度是用弧度制来表示的。
根据三角函数的定义，我们可以得到以下重要的关系：1. sin²θ + cos²θ = 1：这是三角恒等式中的重要等式，也是勾股定理在三角函数中的应用。
2. tanθ = sinθ / cosθ：这是正切函数与正弦函数以及余弦函数的关系。
二、三角函数的性质了解三角函数的性质对于解题和理解相关概念非常重要。
下面是一些常见的性质：1. 周期性：正弦函数、余弦函数、正切函数都是周期函数，周期为2π或π。
即在一个周期内，函数的值会重复出现。
2. 奇偶性：正弦函数是奇函数，即 sin(-θ) = -sinθ；余弦函数是偶函数，即 cos(-θ) = cosθ；正切函数是奇函数，即 tan(-θ) = -tanθ。
3. 定义域和值域：正弦函数和余弦函数的定义域是全体实数，值域是[-1, 1]；正切函数的定义域是全体实数除去使得x = π/2 + kπ (k为整数) 的点，值域是全体实数。
4. 单调性：在定义域内，正弦函数的单调性是：[-π/2 + kπ, π/2+ kπ] 单调递增，[π/2 + kπ, 3π/2 + kπ] 单调递减；余弦函数的单调性是：[kπ,π + kπ] 单调递减, [π + kπ, 2π + kπ] 单调递增；正切函数的单调性是：(kπ - π/2, kπ + π/2) 单调递增。
九年级数学三角函数全章知识点整理
一、角度与弧度制度量1.角度的定义与表示方法：度、分、秒2.角度的换算：度与弧度的换算3.弧度制度量的定义与表示方法4.弧度与角度之间的换算二、三角函数的定义与基本性质1.正弦函数：定义、图像、性质（周期性、奇偶性、单调性）2.余弦函数：定义、图像、性质（周期性、奇偶性、单调性）3.正切函数：定义、图像、性质（周期性、奇偶性、单调性）4.函数值的范围与周期性5.三角函数的基本关系式和恒等式6.正弦、余弦的诱导公式和和差公式7.三角函数的同角关系式三、常用角的三角函数值1.0度、30度、45度、60度和90度的三角函数值2.零点的三角函数值3.常用角的三角函数值的对称性四、图像与性质1.角度对应的弧度的图像与性质2.角度对应的三角函数图像与性质3.三角函数的周期性、奇偶性和对称性4.幅度与峰值五、三角函数的性质与变换1. 函数y=A*sin(Bx+C)+D和y=A*cos(Bx+C)+D的基本性质和变换2.三角函数的峰值、最小值和最大值3.三角函数图像的平移、伸缩、翻转等变换4.三角函数的同位角恒等式与诱导公式的应用5.反三角函数的性质与定义六、三角函数的应用1.正弦定理与余弦定理：直角三角形、任意三角形的应用2.解三角形的基本步骤和技巧3.短边与短边之间的关系（余弦定理）4.弧度与扇形面积、扇形弧长的关系5.三角函数在测量、工程设计等方面的应用七、用三角函数解直角三角形1.斜边和斜边所对应的角的关系2.已知两边求角度3.已知两边求第三边4.解一般直角三角形问题的基本步骤八、平面向量与复数1.平面向量的定义、表示方法和性质2.平面向量的共线与平行3.向量在平面内的平移九、极坐标与复数1.平面极坐标系的定义与性质2.复数的定义与基本性质3.复数运算：加法、减法、乘法、除法4.复数的共轭、模和辐角5.复数的指数形式与三角形式以上为九年级数学三角函数全章的知识点整理，其中包括角度与弧度制度量、三角函数的定义与基本性质、常用角的三角函数值、图像与性质、三角函数的性质与变换、三角函数的应用、用三角函数解直角三角形、平面向量与复数、极坐标与复数等内容，共计1200字以上。
三角函数知识点整理复习
三角函数知识点整理复习三角函数是初等数学的重要分支，是描述直角三角形中各个角的函数关系。
在几何、力学、电磁学等学科中都有广泛的应用。
下面是对三角函数常识的整理和复习。
1. 正弦函数（sin）：正弦函数是一个周期性的函数，其定义域为所有实数，值域为[-1,1]。
根据单位圆的定义，正弦函数可以表示为一些角的斜边长度与半径长度之比。
在单位圆上，角度为θ时，正弦函数的值等于斜边长度（垂直边）与半径长度之比。
2. 余弦函数（cos）：余弦函数也是一个周期性函数，其定义域为所有实数，值域也是[-1,1]。
余弦函数可以表示为一些角的直角边长度与半径长度之比。
在单位圆上，角度为θ时，余弦函数的值等于直角边长度（底边）与半径长度之比。
3. 正切函数（tan）：正切函数也是一个周期性函数，其定义域为所有实数，值域为整个实数集。
正切函数可以表示为一些角的直角边长度的比值。
在单位圆上，角度为θ时，正切函数的值等于直角边长度（垂直边）与直角边长度（底边）之比。
4. 余切函数（cot）：余切函数也是一个周期性函数，其定义域为所有实数，值域为整个实数集。
余切函数可以表示为一些角的直角边长度的比值。
在单位圆上，角度为θ时，余切函数的值等于直角边长度（底边）与直角边长度（垂直边）之比。
5.正弦函数和余弦函数的关系：正弦函数和余弦函数是互为余弦的关系，即sin(θ) = cos(π/2 - θ) 和cos(θ) = sin(π/2 - θ)。
这意味着两个角的正弦值相等，当且仅当这两个角互为余弦。
6.正切函数和余切函数的关系：正切函数和余切函数是互为余切的关系，即tan(θ) = cot(π/2 - θ) 和cot(θ) = tan(π/2 - θ)。
这意味着两个角的正切值相等，当且仅当这两个角互为余切。
7.正弦函数和余切函数的关系：正弦函数和余切函数是互为正弦的关系，即sin(θ) = 1/csc(θ) 和csc(θ) = 1/sin(θ)。
三角函数基础知识点
三角函数基础知识点三角函数是数学中的重要概念，是研究三角形及其相关性质的有力工具。
下面将整理三角函数的基础知识点。
一、三角函数的定义1. 正弦函数：定义为对于任意实数x，都有sin(x) = y，其中y为以x为角度的单位圆上的点的纵坐标。
2. 余弦函数：定义为对于任意实数x，都有cos(x) = y，其中y为以x为角度的单位圆上的点的横坐标。
3. 正切函数：定义为tan(x) = sin(x) / cos(x)。
4. 余切函数：定义为cot(x) = 1 / tan(x) = cos(x) / sin(x)。
5.值域：正弦函数和余弦函数的值域为[-1,1]；正切函数和余切函数的值域为整个实数集。
二、三角函数的性质1.周期性：正弦函数和余弦函数的周期都是2π；正切函数和余切函数的周期都是π。
2. 对称性：正弦函数是奇函数，即sin(-x) = -sin(x)；余弦函数是偶函数，即cos(-x) = cos(x)；正切函数是奇函数，即tan(-x) = -tan(x)；余切函数是奇函数，即cot(-x) = -cot(x)。
3.正交性：正弦函数和余弦函数在同一角度的情况下，它们的积分等于0。
4.互补性：正弦函数和余弦函数在同一角度的情况下，它们的平方和等于15.三角恒等式：(1) 正弦函数和余弦函数的平方和等于1，即sin^2(x) + cos^2(x)= 1(2) 正切函数和余切函数的平方差等于1，即tan^2(x) - cot^2(x)= 1(3) 正切函数可以用正弦函数和余弦函数表示，即tan(x) = sin(x) / cos(x)。
(4) 余切函数可以用正弦函数和余弦函数表示，即cot(x) = cos(x) / sin(x)。
6.三角函数的图像性质：正弦函数和余弦函数的图像是连续的周期函数；正切函数和余切函数的图像有无数个奇点。
三、三角函数的应用1.几何应用：三角函数可以用于求解三角形的各种性质，例如计算边长、角度、面积等。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三角函数基础知识点
1、两角和公式
sin(A ±B) = sinAcosB ±cosAsinB B
A B
A B A tan tan 1tan tan )tan(⋅±=±
cos(A ±B) = cosAcosB sinAsinB
2、二倍角公式（含万能公式）
tan2A =
A tan 12tanA 2- sin2A=2sinA •cosA=A
tan 12tanA
2
+ cos2A = cos 2
A-sin 2
A=2cos 2
A-1=1-2sin 2
A=A tan 1A
tan -12
2+ 22cos 1tan 1tan sin 222
A A A A -=+= 2
2cos 1cos 2
A A +=
3、特殊角的三角函数值
4、诱导公式
公式一： απαsin )2sin(=+k ；απαcos )2cos(=+k ；απαtan )2tan(=+k ．（其中Z ∈k ）．
公式二： ααπ-sin sin(=+）；ααπ-cos cos(=+）；ααπtan tan(=+）． 公式三： sin()-sin αα-=；cos()cos αα-= ；tan()tan αα-=-． 公式四： ααπsin sin(=-）；ααπ-cos cos(=-）；ααπtan tan(-=-） 公式五： sin(2sin παα-=-）；cos(2cos παα-=）；tan(2tan παα-=-）
公式六： sin(2π-α) = cos α； cos(2π
-α) = sin α．
公式七： sin(2π+α) = cos α；cos(2π
+α) =- sin α．
公式八： sin(32π-α)=- cos α； cos(32π
-α) = -sin α．
公式九： sin(32π+α) = -cos α；cos(32
π
+α) = sin α．
以上九组公式可以推广归结为：要求角2
k π
α⋅±的三角函数值，
只需要直接求角α的三角函数值的问题．这个转化的过程及结果就是十字口诀“奇变偶不变，符号看象限”。
即诱导公式的左边为k ·900＋α（k ∈Z ）的正弦（切）或余弦（切）函数，当k 为奇数时，右边的函数名称正余互变；当k 为偶数时，右边的函数名称不改变，这就是“奇变偶不变”的含义，再就是将α“看成”锐角（可能并不是锐角，也可能是大于锐角也可能小于锐角还有可能是任意角），然后分析k ·900＋α（k ∈Z ）为第几象限角，再判断公式左边这个三角函数在此象限是正还是负，也就是公式右边的符号。
5、正弦定理和余弦定理
正弦定理
1、正弦定理：在△ABC 中，
R C
c
B b A a 2sin sin sin ===（R 为△AB
C 外接圆半径）。
2、变形公式：（1）化边为角：2sin ,2sin ,2sin ;a R A b R B c R C === （2）化角为边：sin ,sin ,sin ;222a b c
A B C R R R
=
== （3）::sin :sin :sin a b c A B C = （4）
2sin sin sin sin sin sin a b c a b c R A B C A B C
++====++.
3、三角形面积公式：
21111sin sin sin 2sin sin sin 22224ABC abc S ah ab C ac B bc A R A B C R
∆======
余弦定理
A bc c b a cos 22
2
2
-+=⇔bc
a c
b A 2cos 2
2
2
-+=
B ac a c b cos 22
2
2
-+=⇔ca
b a
c B 2cos 2
22-+=
C ab b a c cos 22
2
2
-+=⇔ab
c b a C 2cos 2
22-+=
1、（山东卷）要得到函数y=sin （4x-3
π
）的图像，只需要将函数y=sin4x 的图像（B ） （A ）向左平移
12
π
个单位 （B ）向右平移
12
π
个单位
（C ）向左平移3π个单位 （D ）向右平移3
π个单位 2、（新课标1卷）sin20°cos10°-cos160°sin10°=（D ）
（A ）（B （C ）12- （D ）1
2
3、已知),2
(ππα∈,5
5
sin =
α.
(1)求)4
sin(απ+的值；
(2)求)26
5cos(απ-的值.
4、已知函数()2
cos sin 3f x x x x π⎛⎫=⋅+-+ ⎪
⎝
⎭
x R ∈. （Ⅰ）求()f x 的最小正周期；
（Ⅱ）求()f x 在闭区间,44ππ
⎡⎤
-⎢⎥⎣⎦
上的最大值和最小值.
5、已知函数1()cos (sin cos )2
f x x x x =+-.
（1）若02
π
α<<
，且sin 2
α=
，求()f α的值； （2）求函数()f x 的最小正周期及单调递增区间.
6、已知函数
2()cos 222
x x x
f x =
．
(Ⅰ) 求()f x 的最小正周期；
(Ⅱ) 求()f x 在区间[π0]-，上的最小值．
7、（重庆卷）（本小题满分13分，（I ）小问7分，（II ）小问6分）
已知函数()2
sin sin 2
f x x x x π
⎛⎫=- ⎪⎝
⎭
（I ）求()f x 的最小正周期和最大值； （II ）讨论()f x 在2,
6
3ππ⎡⎤
⎢⎥⎣⎦
上的单调性.
1.（2013·北京高考文科·Ｔ5）在△ABC 中，a=3,b=5,sinA=13
,则sinB=( )
A.15
B.59
C.
5
3
D.1 2.（2013·新课标全国Ⅱ高考文科·Ｔ4）ABC ∆的内角,,A B C 的对边分别为,,a b c ，已知2b =，6
B π=，4
C π
=
，则ABC ∆的面积为（ ）
A.232+
B.31+
C.232-
D.31-
3.设△ABC 的内角A , B , C 所对的边分别为a, b, c , 若
cos cos sin b C c B a A +=, 则△ABC
的形状为 ( )
A. 直角三角形
B. 锐角三角形
C. 钝角三角形
D. 不确定
4．(2013·天津卷)在△ABC 中，∠ABC ＝π
4，AB ＝2，BC ＝3，则sin
∠BAC ＝( )
A.1010
B.105
C.31010
D.55
5．已知A ，B 两地的距离为10 km ，B ，C 两地的距离为20 km ，现测得∠ABC ＝120°，则A 、C 两地的距离为________km.
6.（2013·上海高考文科·T5）已知∆ABC 的内角A 、B 、C 所对的边
分别是a、b、c.若a2+ab+b2-c2=0，则角C的大小是 .
7．在ABC
∆中，角,,
A B C的对边分别为,,
a b c且cos3
cos
C a c
B b
-
=.
(1)求sin B;
(2)若
b a c
==，求ABC
∆的面积.
8．在△ABC中，角A，B，C的对边分别为a，b，c，已知cos cos cos cos
a C
b C
c B c A
-=-，且C＝120°．
（1）求角A；（2）若a＝2，求c．
9．在△ABC，已知.
sin
sin
3
)
sin
sin
)(sin
sin
sin
(sin C
B
A
C
B
C
B
A=
-
+
+
+
(1)求角A值；
(2)求C
B cos
sin
3-的最大值.。